Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 6 Electromagnetic Induction Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Physics Chapter 6 Electromagnetic Induction
PSEB 12th Class Physics Guide Electromagnetic Induction Textbook Questions and Answers
Question 1.
Predict the direction of induced current in the situations described by the following Figs. 6.18 (a) to (f).
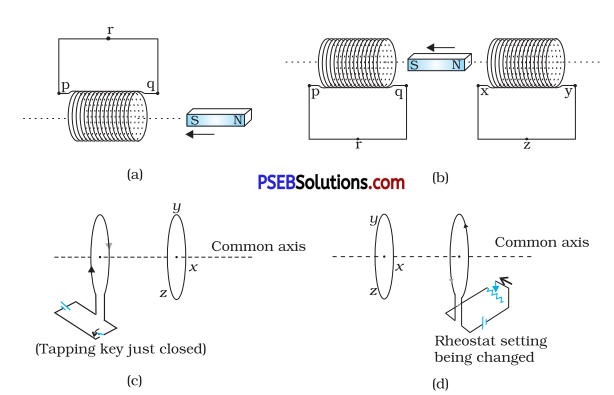
Answer:
(a) As the magnet moves towards the solenoid, the magnetic flux linked with the solenoid increases. According to Lenz’s law, the induced e.m.f. produced in the solenoid in such that it opposes the very cause producing it i. e., it opposes the motion of the magnet. Hence the face q of it becomes the south pole and p becomes north pole. Therefore, the current will flow along pqin the coili. e., along qrpqin this figurei. e., clockwise when seen from the side of the magnet according to clock rule.
(b) As the north pole moves away from xy coil, so the magnetic flux linked with this coil decreases. Thus according to Lenz’s law, the induced e.m.f. produced in the coil will oppose the motion of the magnet. Hence the face, X becomes S-pole, so the current will flow in the clockwise direction i.e., along yzx in the cone.
For coil pq, the south pole of the magnet moves towards end q and thus this end will acquire south polarity so as to oppose the motion of the magnet, hence the current will flow along prq in the coil.
(c) The induced current will be in the anticlockwise direction i.e., along yzx.
(d) The induced current will be in the clockwise direction i.e., along zyx.
(e) The battery current in the left coil will be from right to left, so by mutual induction, the induced current in the right coil will be in the opposite direction i.e., from left to right or along xry.
(f) In this case, there is no change in magnetic flux linked with the wire, so no current will flow through the wire since there is no induced current as the field lines lie in the plane of the loop.
![]()
Question 2.
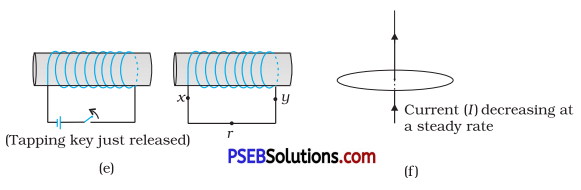
Use Lenz’s law to determine the direction of induced current in the situations described by Fig. 6.19.
(a) A wire of irregular shape turning into a circular shape;
(b) A circular loop being deformed into a narrow straight wire.
(a) When a wire of irregular shape turns into a circular loop, the magnetic flux linked with the loop increases due to increase in area. The circular loop has greater area than the loop of irregular shape. The induced e.m.f. will cause current to flow in such a direction so that the wire forming the loop is pulled inward from all sides i.e., current must flow in the direction adcba as shown in Fig. (a) i.e., in anticlock-wise direction so that the magnetic field produced by the current ((directed out of the paper) opposes the applied field.
In Fig. (b), a circular loop deforms into a narrow straight wire i.e., upper side of loop should move downwards and lower end should move upwards to oppose the motion of the circular loop, thus its area decreases as a result of which the magnetic flux linked with it decreases. To oppose the decrease in magnetic flux, the induced current should flow anti clockwise in the loop i. e., along a’d’ d b’ a’. Due to the flow of anti-clockwise current, the magnetic field produced will be out of the page and hence the applied field is supplemented.
Question 3.
A long solenoid with 15 turns per cm has a small loop of area 2.0 cm2 placed inside the solenoid normal to its axis. If the current carried hy the solenoid changes steadily from 2.0 A to
4.0 A in 0.1 s, what is the induced emf in the loop while the current is changing?
Answer:
Number of turns per unit length of the solenoid, n = 15 turns/cm = 1500 turns/m
The solenoid has a small loop of area, A = 2.0 cm2 = 2 × 10-4 m2
Current carried by the solenoid changes from 2 A to 4 A.
.-. Change in current in the solenoid, dI = 4 – 2 = 2A
Change in time, dt = 0.1 s
We know that the magnetic field produced inside the solenoid is given by
B = μ0nI
If Φ be the magnetic flux linked with the loop, then
Φ = BA = μ0nI A
Induced emf in the solenoid is given by Faraday’s law as
e = –\(\frac{d \phi}{d t}\)
e = – \(\frac{d}{d t}\) (Φ) = –\(\frac{d}{d t}\) μ0nI A
μ0n A \(\frac{d I}{d t}\)
∴ Magnitude of e is given by
= A μ0n × (\(\frac{d I}{d t}\))
= 2 × 10-4 × 4π × 10-7 × 500 × \(\frac{2}{0.1}\)
7.54 × 10 -6 V
Hence, the induced voltage in the loop is = 7.54 × 10 -6 V
![]()
Question 4.
A rectangular wire loop of sides 8 cm and 2 cm with a small cut is moving out of a region of uniform magnetic field of magnitude 0.3 T directed normal to the loop. What is the emf developed across the cut if the velocity of the loop is 1 cm s-1 in a direction normal to the (a) longer side, (b) shorter side of the loop? For how long does the induced voltage last in each case?
Answer:
Length of the rectangular wire, l = 8 cm = 0.08 m
Width of the rectangular wire, b = 2 cm = 0.02 m
Hence, area of the rectangular loop A = lb
= 0.08 × 0.02
= 16 × 10-4 m2
Magnetic field strength, B = 0.3 T
Velocity of the loop, v = 1 cm/s = 0.01 m / s
(a) Emf developed in the loop is given as
e = Blv
= 0.3 × 0.08 × 0.01 = 2.4 × 10-4 V

= \(\frac{b}{v}\) = \(\frac{0.02}{0.01}\) = 2 s
Hence, the induced voltage is 2.4 × 10-4 V which lasts for 2s.
(b) Emf developed,
e = Bbv = 0.3 × 0.02 × 0.01 = 0.6 × 10-4 V

\(\frac{l}{v}\) = \(\frac{0.08}{0.01}\) 8s
Hence, the induced voltage is 0.6 × 10-4 V which lasts for 8 s.
Question 5.
A 1.0 m long metallic rod is rotated with an angular frequency of 400 rad s-1 about an axis normal to the rod passing through its one end. The other end of the rod is in contact with a circular metallic ring. A constant and uniform magnetic field of 0.5 T parallel to the axis exists everywhere. Calculate the emf developed between the centre and the ring.
Answer:
Length of the rod, l = 1m
Angular frequency, ω = 400 rad/s
Magnetic field strength, B = 0.5 T
One end of the rod has zero linear velocity, while the other end has a linear velocity of l ω.
Average linear velocity of the rod, v = \(\frac{l \omega+0}{2}=\frac{l \omega}{2}\)
Emf developed between the centre and the ring,
e = Blv = Bl(\(\frac{l \omega}{2}\)) = \(\frac{B l^{2} \omega}{2}\)
= \(\frac{0.5 \times(1)^{2} \times 400}{2}\) = 100V
Hence, the emf developed between the centre and the ring is 100 V.
![]()
Question 6.
A circular coil of radius 8.0 cm and 20 turns is rotated about its vertical diameter with an angular speed of 50 rad s-1 in a uniform horizontal magnetic field of magnitude 3.0 × 10-2 T. Obtain the maximum and average emf induced in the coil. If the coil forms a closed loop of resistance 10 Ω, calculate the maximum value of current in the coil. Calculate the average power loss due to Joule heating. Where does this power come from?
Answer:
Here, n = number of turns in the coil = 20
r = radius ofcoil = 8.0 cm = 8 × 10-2 m
ω = angular speed of the coil = 50 rad s-1.
B = magnetic field = 3.0 × 10-2 T
Let e0 be the maximum e.m.f. in the coil = ?
and eav be the average e.m.f. in the coil = ?
We know that the instantaneous e.m.f. produced in a coil is given by
e = BA ω sinωt.
for e to be maximum emax, sin ωt = 1.
∴ emax = B A n ω = B.πr2 nω
where A = πr2 is the area of the coil

i.e., eav is zero as the average value of sincot for one complete cycle is always zero.
Now R = resistance of the closed loop formed by the coil = 10 Ω
Let Imax = maximum current in the coil = ?
∴ Using the relation,
Imax = \(\frac{e_{\max }}{R}\), we get
Imax = \(\frac{0.603}{10}\) = 0.0603 A
Let Pav be the average power loss due to Joule heating = ?
∴ Pav = \(\frac{e_{\max } \cdot I_{\max }}{2}\) = \(\frac{0.603 \times 0.0603}{2}\)
= 0.018 Watt
The induced current causes a torque opposing the rotation of the coil. An external agent must supply torque and do work to counter this torque in order to keep the coil rotating uniformly. Thus the source of the power dissipated as heat in the coil is the external agent i. e., rotor.
Question 7.
A horizontal straight wire 10 m long extending from east to west is falling with a speed of 5.0 m s-1, at right angles to the horizontal component of the earth’s magnetic field, 0.30 × 10-4 Wb m-2.
(a) What is the instantaneous value of the emf induced in the wire?
(b) What is the direction of the emf?
(c) Which end of the wire is at the higher electrical potential?
Answer:
Length of the wire, l = 10 m
Falling speed of the wire, v = 5.0 m/s
Magnetic field strength, B = 0.3 × 10-4 Wb m-2
(a) emf induced in the wire,
e = Blv = 0.3 × 10-4 × 5 × 10
= 1.5 × 10-3 V
(b) Using Fleming’s right hand rule, it can be inferred that the direction of the induced emf is from west to east.
(c) The eastern end of the wire is at a higher electrical potential.
![]()
Question 8.
Current in a circuit falls from 5.0 A to 0.0 A in 0.1 s. If an average emf of 200 V induced, give an estimate of the self-inductance of the circuit.
Initial current, I1 = 5.0 A
Final current, I2 = 0.0 A
Change in current, dl = I1 – I2 = 5 – 0 = 5 A
Time taken for the change, dt = 0.1 s
Average emf, e = 200 V
For self-inductance (I) of the circuit, we have the relation for average emf as
e = L\(\frac{d I}{d t}\)
L = \(\frac{e}{\left(\frac{d I}{d t}\right)}\)
= \(\frac{200}{\frac{5}{0.1}}=\frac{200 \times 0.1}{5}\) 4H
Hence, the self induction of the circuit is 4 H.
Question 9.
A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from 0 to 20 A in 0.5 s, what is the change of flux linkage with the other coil?
Answer:
Mutual inductance of the pair of coils, μ = 1.5 H
Initial current, I1 = 0 A
Final current, I2 – 20 A
Change in current, dI = I2 – I1 = 20 – 0 = 20 A
Time taken for the change, dt = 0.5 s
Induced emf, e = \(\frac{d \phi}{d t}\) ………… (1)
Where d Φ is the change in the flux linkage with the coil.
Emf is related with mutual inductance as
e = μ\(\frac{d I}{d t}\) ……………. (2)
Equating equations (1) and (2), we get
\(\frac{d \phi}{d t}\) = μ\(\frac{d I}{d t}\)
or dΦ = μdI
∴ dΦ = 1.5 × (20) = 30 Wb
Hence, the change in the flux linkage is 30 Wb.
![]()
Question 10.
A jet plane is travelling towards west at a speed of 1800 km/h. What is the voltage difference developed between the ends of the wings having a span of 25 m, if the Earth’s magnetic field at the location has a magnitude of 5 × 10-4 T and the dip angle is 30°.
Answer:
Speed of the jet plane, v = 1800 km/h = 1800 × \(\frac{5}{18}\) = 500 m/s
Wing span of the jet plane, l = 25 m
Earth’s magnetic field strength, B = 5.0 × 10-4 T
Angle of dip, δ = 30°
Vertical component of Earth’s magnetic field,
BV = B sinδ
= 5 × 10-4 × sin30°
= 5 × 10-4 × \(\frac{1}{2}\) = 2.5 × 10-4 T
Voltage difference between the ends of the wing can be calculated as
e = (BV) × l × v
= 2.5 × 10-4 × 25 × 500 = 3.125 V
Hence, the voltage difference developed between the ends of the wings is 3.125 V.
Question 11.
Suppose the loop in Exercise 6.4 is stationary but the current feeding the electromagnet that produces the magnetic field is gradually reduced so that.the field decreases from its initial value of 0.3 T at the rate of 0.02 Ts-1. If the cut is joined and the loop has a resistance of 1.6 Ω, how much power is dissipated by the loop as heat? What is the source of this power?
Answer:
Sides of the rectangular wire loop are 8 cm and 2 cm.
Hence, area of the rectangular wire loop,
A = length × width = 8 × 2 = 16 cm
= 16 × 10-4 m2
Initial value of the magnetic field, B = 0.3 T
Rate of decrease of the magnetic field, \(\frac{d B}{d t}\) = 0.02 T/s
emf developed in the loop is given as
e = \(\frac{d \phi}{d t}\)
where, Φ = Change in flux through the loop area
= AB
∴ e = \(\frac{d(A B)}{d t}=\frac{A d B}{d t}\)
= 16 × 10-4 × 0.02 =0.32 × 10-4 V
= 3.2 × 10-5 V
Resistance of the loop, R = 1.6 Ω
The current induced in the loop is given as
i = \(\frac{e}{R}\)
= \(\frac{0.32 \times 10^{-4}}{1.6}\) = 2 × 10-5A
Power dissipated in the loop in the form of heat is given as
P = i2R
= (2 × 10-5)2 × 1.6
= 6.4 × 10-10 W
The source of this heat loss is an external agent, which is responsible for changing the magnetic field with time.
![]()
Question 12.
A square loop of side 12 cm with its sides parallel to X and F axes is moved with a velocity of 8 cm s-1 in the positive x-direction in an environment containing a magnetic field in the positive 2-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10-3 T cm-1 along the negative jtr-direction (that is it increases by 10-3 T cm-1 as one moves in the negative x-direction), and it is decreasing in time at the rate of 10-3 T s1. Determine the direction and magnitude of the induced current in the loop if its resistance is 4.50 mΩ.
Answer:
Here, a = side of the square loop = 12 cm = 12 × 10-2 m
\(\vec{v}\) = velocity of loop parallel to x-axis = 8 cms-1
= 8 × 10-2 ms-1.
Let B = variable magnetic field acting away from us ⊥ ar to the XY plane along z axis i. e., plane of paper represented by x.
\(\) = 10-3 Tcm-1
= 10-3 × 102 Tm-1
= 0.1 Tm-1
= field gradient along – ve x direction.

\(\frac{d B}{d t}\) = rate of variation with me
= 10-3 Ts-1
R = resistance of the loop = 4.5 mΩ = 4.5 × 10-3 Ω
Let I = induced current = ? and its direction = ?
∴ A = area of loop = a2 = (12 × 10-2)2 m2 = 144 × 10-4 m2.
The magnetic flux changes (i) due, to the variation of B with time and
(ii) due to motion of the loop in non-uniform \(\vec{B}\).
Thus if Φ be the total magnetic flux of the loop, then Φ is calculated as Area of shaded part = adx
Let dΦ = magnetic flux linked with shaded part = B(x,t)adx

∴ From (3), \(\) = 144 × 10-7 + 1152 × 10-7
= 1296 × 10-7 Wbs-1
Clearly the two effect add up as these cause a decrease in flux along the + z direction.
∴ If e be the induced e.m.f. produced, then
e = –\(\frac{d \phi}{d t}\) = -1296 × 10-7 V
= -12.96 × 10-5 V
∴ e = 12.96 × 10-5 V
∴ I = \(\frac{e}{R}\) = \(\frac{12.96 \times 10^{-5}}{4.5 \times 10^{-3}}\) 2.88 × 10-2 A.
The direction of induced current is such as to increase the flux through the loop along +z-direction. Thus if for the observer, the loop moves to the right, the current will be seen to be anti-clockwise.
![]()
Question 13.
It is desired to measure the magnitude of field between the poles of a powerful loud speaker magnet. A small fiat search coil of area 2 cm2 with 25 closely wound turns, is positioned normal to the field direction, and then quickly snatched out of the field region. Equivalently, one can give it a quick 90° turn to bring its plane parallel to the field direction. The total charge flown in the coil (measured by a ballistic galvanometer connected to coil) is 7.5 mC. The combined resistance of the coil and the galvanometer is 0.50 Q. Estimate the field strength of magnet.
Answer:
Area of the small flat search coil, A = 2cm2 = 2 × 10-4m2
Number of turns on the coil, N = 25
Total charge flown in the coil, Q = 7.5 mC = 7.5 × 10 -3 C
Total resistance of the coil and galvanometer, R = 0.50 Ω
Induced current in the coil,
I = \(\frac{\text { Induced emf }(e)}{R}\) ………….. (1)
Induced emf is given us
e = -N\(\frac{d \phi}{d t}\) ……………… (2)
Combining equations (1) and (2), we get


Hence, the field strength of the magnet is 0.75 T.
![]()
Question 14.
Figure 6.20 shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod, and the magnetic Held are in three mutual perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod = 15 cm, B = 0.50 T, resistance of the closed loop containing the rod = 9.0 mfl. Assume the field to be uniform.
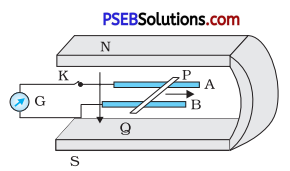
(a) Suppose K is open and the rod is moved with a speed of 12 cm s-1 in me airection snown. dive me polarity ana magnitude of the induced emf.
(b) Is there an excess charge built up at the ends of the rods when K is open? What if K is closed?
(c) With K open and the rod moving uniformly, there is no net force on the electrons in the rod PQ even though they do experience magnetic force due to the motion of the rod. Explain.
(d) What is the retarding force on the rod when K is closed?
(e) How much power is required (by an external agent) to keep the rod moving at the same speed (= 12 cm s-1) when K is closed? How much power is required when K is open?
(f) How much power is dissipated as heat in the closed circuit? What is the source of this power?
(g) What is the induced emf in the moving rod if the magnetic field is parallel to the rails instead of being perpendicular?
Answer:
Here, B = 0.50 T
l = length of the rod = 15 cm = 15 × 10-2 m
R = resistance of the closed loop containing the rod = 9.0 mΩ
= 9 × 10-3 Ω.
(a) v = speed of the rod = 12 cms-1 = 12 × 10-2 ms-1.
The magnitude of the induced e.m.f. is
E = Blv = 0.50 × 15 × 10-2 × 12 × 10-12 = 9 × 10-3 V
According to Fleming’s left hand rule, the direction of Lorentz force —^ ^ ^
\(\vec{F}\) = -e(\(\vec{V} \times \vec{B}\)) on electrons in PQ is from P to Q. So the end P of the rod will acquire positive charge and Q will acquire negative charge,
(b) Yes. When the switch K is open, the electrons collect at the end Q, so excess charge is built up at the end Q. But when the switch K is closed, the accumulated charge at the end Q is maintained by the continuous flow of current.
(c) This is because the presence of excess charge at the ends P and Q of the rod sets up an electric field \(\vec{E}\). The force due to the electric field (q\(\vec{E}\)) balances the Lorentz magnetic force q(\(\vec{V} \times \vec{B}\)). Hence the net force on the electrons is zero.
(d) When the key K is closed, current flows through the rod. The retarding force experienced by the rod is
F = BIl = B(\(\frac{E}{R}\)) l
where, I = \(\) is the induced current. R
F = \(\frac{0.50 \times 9 \times 10^{-3} \times 15 \times 10^{-2}}{9 \times 10^{-3}}\)
= 7.5 × 10-2 N.
(e) The power required by the external agent against the above retarding force to keep the rod moving uniformly at speed 12 cms-1 (= 12 × 10-2 m/s) when K is closed is given by
p = FV = 7. 5 × 10-2 × 12 × 10-2
= 90 × 10-4 W
= 9 × 10-3 W
(f) Power dissipated as heat is given by
P = I2R = (\(\frac{E}{R}\))2 R = \(\frac{E^{2}}{R}\)
= \(\frac{\left(9 \times 10^{-3}\right)^{2}}{9 \times 10^{-3}}\)
= 9 × 10-3 W.
The source of this power is the power provided by the external agent calculated in (e).
Zero. This is because when the magnetic field is parallel to the rails, θ = 0°, so induced e.m.f. E = Blv sinθ = Blv sin 0 = 0. In this situation, the moving rod does not cut the field lines, so there is no change in the magnetic flux, hence E = 0.
![]()
Question 15.
An air-cored solenoid with length 30 cm, area of cross-section 25 cm2 and number of turns 500, carries a current of 2.5 A. The current is suddenly switched off in a brief time of 10-3 s. How much is the average back emf induced across the ends of the open switch in the circuit? Ignore the variation in magnetic Held near the ends of the solenoid.
Answer:
Length of the solenoid, l = 30 cm = 0.3 m
Area of cross-section, A = 25 cm2 = 25 x 10-4 m2
Number of turns on the solenoid, N = 500
Current in the solenoid, I = 2.5 A
Current flows for time, t = 10-3 s
Average back emf, e = \(\frac{d \phi}{d t}\) ……………. (1)
where,
dΦ = NAB ………….. (2)
and B = μ0 \(\frac{N I}{l}\) …………. (3)
Using equations (2) and (3) in equation (1), we get
e = \(\frac{\mu_{0} N^{2} I A}{l t}\)
\(=\frac{4 \pi \times 10^{-7} \times(500)^{2} \times 2.5 \times 25 \times 10^{-4}}{0.3 \times 10^{-3}}\)
= 6.5 V
Hence, the average back emf induced in the solenoid is 6.5 V.
Question 16.
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in Figure 6.21.
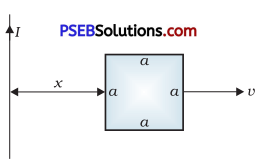
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.
Answer:
(a) Take a small element dy in the loop at a distance y from the long straight wire (as shown in the given figure).
Magnetic flux associated with element dy, dΦ = BdA
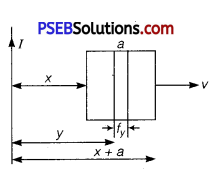
= where,
dA = Area of element dy = a dy
B = Magnetic field at distance y = \(\frac{\mu_{0} I}{2 \pi y}\)
I = Current in the wire

![]()
Question 17.
A line charge λ per unit length is lodged uniformly onto the rim of a wheel of mass M and radius R. The wheel has light non-conducting spokes and is free to rotate without friction about its axis as shown in Fig. 6.22. A uniform magnetic field extends over a circular region within the rim. It is given by,
B = -Bk (r ≤ a; a < R)
= 0 (otherwise)
What is the angular velocity of the wheel after the field is suddenly switched off?
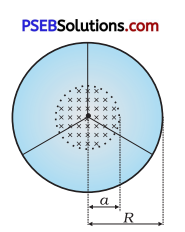
Answer:
Let ω be the angular velocity of the wheel of mass M and radius R.
Let e = Induced e.m.f. produced.
The rotational K.E. of the rotating wheel = \(\frac{1}{2}\) Iω2 ………… (1)
where, I = Moment of inertia of wheel
= \(\frac{1}{2}\) MR2 …………… (2)
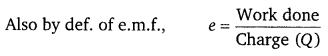
or Work done = eQ
Applying the work energy theorem, we get
Rotational K.E. = Work done
or RotationalK.E. = Q × e …………… (3)
We know that the e.m.f. of a rod rotating in a uniform magnetic field is
given by \(\frac{1}{2}\) Bωa2 , since here the magnetic field is changing, we assume the average over the time span and thus average value of e.m.f. is given by
