Punjab State Board PSEB 12th Class Physics Important Questions Chapter 6 Electromagnetic Induction Important Questions and Answers.
PSEB 12th Class Physics Important Questions Chapter 6 Electromagnetic Induction
Very short answer type questions
Question 1.
The motion of copper plate is damped when it is allowed to oscillate between the two poles of a magnet. What is the cause of this damping?
Answer:
As the plate oscillate, the changing magnetic flux through the plate produces a strong eddy current in the direction, which opposes the cause. Also, copper being substance, it gets magnetised in the opposite direction, so the plate motion gets damped.
Question 2.
On what factors does the magnitude of the emf induced in the circuit due to magnetic flux depend ?
Answer:
Depends on the time rate of change in magnetic flux (or simply change in Magnetic flux)
\(|\varepsilon|=\frac{\Delta \phi}{\Delta t}\)
![]()
Question 3.
A light metal disc on the top of an electromagnet is thrown up as the current is switched on. Why? Give reason.
Answer:
When the current begins to grow through the electromagnet, the magnetic flux through the disc begins to increase. This sets up eddy current in the disc in the same direction as that of the electromagnetic current.
Thus, if the upper surface of electromagnetic acquires AT-polarity, the lower surface of the disc also acquires N-polarity. As, same magnetic poles repel each other, the light metallic disc is thrown up.
Question 4.
State the Faraday’s law’ of electromagnetic induction.
Answer:
On the basis of his experiment, Faraday gave the following two laws:
First Law: Whenever magnetic flux linked with a circuit changes, an emf is induced in it which lasts, so long as change in flux continuous.
Second Law: The emf induced in loop or closed circuit is directly proportional to the rate of change of magnetic flux linked with the loop
i.e., ε ∝ \(\frac{(-) d \phi}{d t}\) or ε = -N \(\frac{d \phi}{d t}\)
where, N= number of turns in the coil. Negative sign indicates the Lenz’s law.
Question 5.
State Lenz’s law. A metallic rod held horizontally along East-West direction, is allowed to fall under gravity. Will there be an emf induced at its ends? Justify your answer.
Answer:
Lenz’s Law: The direction of the induced emf, or the current, in any circuit is such as to oppose the cause that produces it.
Yes, emf will be induced in the rod as there is change in magnetic flux. When a metallic rod held horizontally along East-West direction, is allowed to fall freely under gravity i.e., fall from North to South, the intensity of magnetic lines of the earth’s magnetic field changes through it, i.e., the magnetic flux changes and hence emf induced in it.
Question 6.
How does the mutual inductance of a pair of coils change, when
(i) distance between the coils is increased and
(ii) number of turns in the coils is increased?
Answer:
(i) AΦ = MI, with the increase in the distance between the coils the magnetic flux linked with the secondary coil decreases and hence, the mutual inductance of the two coils will decreases with the increase of separation between them.
(ii) Mutual inductance of two coils can be found out by
M = μ0N1N2 Al i.e.,
M ∝ N1N2, SO, with the increase in number of turns mutual inductance increases.
![]()
Question 7.
Why is the core of a transformer laminated?
Answer:
The core of a transformer is laminated because of preventing eddy current being produced in the core.
Question 8.
How can the self-inductance of a given coil having N number of turns, area of cross-section A and lengths l be increased?
Answer:
The self-inductance can be increased by the help of electric fields. It does not depend on the current through circuit but depends upon the permeability of material from which the core is made up off.
Question 9.
Consider a magnet surrounded by a wire with an on/off switch S (as shown in figure). If the switch is thrown from the off position (open circuit) to the on position (closed circuit), will a current ?Explain (NCERT Exemplar)

Answer:
No part of the wire is moving and so motional e.m.f. is zero. The magnet is stationary and hence the magnetic field does not change with time. This means no electromotive force is produced and hence no current will flow in the circuit.
Question 10.
A wire in the form of a tightly wound solenoid is connected to a DC source, and carries a current. If the coil is stretched so that there are gaps between successive elements of the spiral coil, will the current increase or decrease? Explain. (NCERT Exemplar)
Answer:
The current will increase. As the wires are pulled apart the flux will leak through the gaps. Lenz’s law demands that induced emf resist this decrease, which can be done by an increase in current.
![]()
Question 11.
A solenoid is connected to a battery so that a steady current flows through it. If an iron core is inserted into the solenoid, will the current increase or decrease? Explain. (NCERT Exemplar)
Answer:
The current will decrease. As the iron core is inserted in the solenoid, the magnetic field increases and the flux increases. Lenz’s law implies that induced emf should resist this increase, which can be achieved by a decrease in current. However, this change will be momentarily.
Question 12.
Consider a metal ring kept (supported by a cardboard) on top of a fixed solenoid carrying a current /. The centre of the ring coincides with the axis of the solenoid. If the current in the solenoid is switched off, what will happen to the ring? (NCERT Exemplar)
Answer:
When the current in the solenoid decreases a current flows in the same direction in the metal ring as in the solenoid. Thus there will be a downward force. This means the ring will remain on the cardboard. The upward reaction of the cardboard on the ring will increase.
Short answer type questions
Question 1.
Consider a closed loop C in a magnetic field (figure). The flux passing through the loop is defined by choosing a surface whose edge coincides with the loop and using the formula Φ = B1 dA1, B2 dA2…. Now, if we choose two different surfaces S1 and S2 having C as their edge, would we get the same answer for flux. Justify your answer. (NCERTExemplar)

The magnetic flux linked with the surface can considered as the number of magnetic field lines passing through the surface. So, let dΦ = BdA represents magnetic lines in an area A to B.
By the concept of continuity of lines B cannot end or start in space, therefore the number of lines passing through surface S1 must be the same as the number of lines passing through the surface S2. Therefore, in both the cases we gets the same answer for flux.
![]()
Question 2.
What are eddy currents? Write their two applications.
Answer:
Eddy Current: Eddy currents are the currents induced in the bulk pieces of conductors when the amount of magnetic flux linked with the conductor changes.
Eddy currents can be minimised by taking laminated core, consists of thin metallic sheet insulated from each other by varnish instead of a single solid mass. The plane of the sheets should be kept perpendicular to the direction of the currents. The insulation provides high resistance hence, eddy current gets minimised.
Applications
(i) Electromagnetic damping
(ii) Induction furnace.
Question 3.
(i) A rod of length l is moved horizontally with a uniform – velocity v in a direction perpendicular to its length through a region in which a uniform magnetic field is acting vertically downward. Derive the expression for the emf induced across the ends of the rod.
(ii) How does one understand this motional emf by invoking the Lorentz force acting on the free charge carriers of the conductor? Explain.
Answer:
(i) Consider a straight conductor moving with velocity v and U shaped conductor placed in perpendicular magnetic field as shown in the figure.
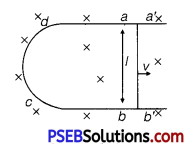
Let conductor shifts from ab to a’ b’ in time dt, then change in magnetic flux
dΦ = B × change in area
= B × (areaa’b’ab)
= B × (l × vdt)
∴ \(\frac{d \phi}{d t}\) Bvl
∴ Induced emf lei \(|\varepsilon|=\frac{d \phi}{d t}\) = Bvl
(ii) During motion, free e– are shifted at one end due to magnetic force so due to polarisation of rod electric field is produced which applies electric force on free e– on opposite direction.
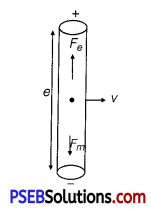
At equilibrium of Lorentz force,
Fe + Fm = 0
qE + q(v × B) = 0
E = -v × B = B × v
\(|E|=|B v \sin 90|\)
\(\frac{d v}{d r}\) = Bv
PD = Bvl
![]()
Question 4.
(a) How does the mutual inductance of a pair of coils change when
(i) distance between the coils is increased and
(ii) number of turns in the coils is increased?
(b) A plot of magnetic flux (Φ) versus current (I), is shown in the figure for two inductors A and B. Which of the two has large value of self-inductance?
(c) How is the mutual inductance of a pair of coils affected when
(i) separation between the coils is increased?
(ii) the number of turns in each coil is increased?
(iii) a thin iron sheet is placed between the two coils, other factors remaining the same?
Justify your answer in each case.

Answer:
(a)
(i) Mutual inductance decreases.
(ii) Mutual inductance increases.
Concept
(i) If distance between two coils is increased as shown in figure.
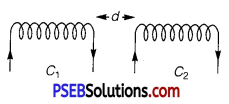
It causes decrease in magnetic flux linked with the coil C2. Hence induced emf in coil C2 decreases by relation ε2 = \(\frac{-d \phi_{2}}{d t}\). Hence mutual inductance decreases.
(ii) From relation M21 = μ0N1N2 Al, if number of turns in one of the coils or both increases, means mutual inductance will increase.
(b) Φ = LI ⇒ \(\frac{\phi}{I}\) = L
The slope of \(\frac{\phi}{I}\) of straight line is equal to self-inductance L. It is larger for inductor A; therefore inductor A has larger value of self inductanc ‘ L’.
(c)
(i) When the relative distance between the coil is increased, the leakage
of flux increases which reduces the magnetic coupling of the coils. So magnetic flux linked with all the turns decreases. Therefore, mutual inductance will be decreased.
(ii) Mutual inductance for a pair of coil is given by
M = K\(\sqrt{L_{1} L_{2}}\)
where, L = \(\frac{\mu N^{2} A}{l}\) and L is called self inductance. Therefore, when the number of turns in each coil increases, the mutual inductance also increases.
(iii) When a thin iron sheet is placed between the two coils, the mutual inductance increases because M ∝ permeability. The permeability of the medium between coils increases.
Question 5.
Consider a metallic pipe with an inner radius of 1 cm. If a cylindrical bar magnet of radius 0.8 cm is dropped through the pipe, It takes more time to come down than It takes for a similar
unmagnetised cylindrical iron bar dropped through the metallic pipe. Explain. (NCERT Exemplar)
Answer:
For the magnet, eddy currents are produced in the metallic pipe. These currents will oppose the motion of the magnet. Therefore magnet’s downward acceleration will be less than the acceleration due to gravity g. On the other hand, an unmagnetised iron bar will not produce eddy
currents and will fall an acceleration g. Thus the magnet will take more time.
![]()
Question 6.
A magnetic field B = B0 sin(ωt) k̂ covers a large region where a wire AB slides smoothly over two parallel conductors separated by a distance d (figure). The wires are in the x-y plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity y, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity? (NCERT Exemplar)
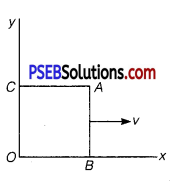
Answer:
Let us assume that the parallel wires are at y = 0 i. e., along x-axis and y = d. At t = 0, AB has x = 0, i. e., along y-axis and moves with a velocity v. Let at time t, wire is at x (t) = vt.
Now, the motional emf across AB is
= (B0sinωt) vd(-ĵ)
emf due to change in field (along OBAC)
= -B0ωcosωt (t)d
Total emf in the circuit = emf due to change in field (along OBAC) + the motional emf across AB = -B0d[ωxcos(ωt) + vsin (ωt)]
Electric current in clockwise direction is given by,
= \(\frac{B_{0} d}{R}\) = (ωxcosωt + vsinωt)
The force acting on the conductor is given by F = ilB sin 90° = ilB
Substituting the values, we have
Force needed along i = \(\frac{B_{0} d}{R}\) (ωx cos ωt + vsinωt) × d × B sinωt
= \(\frac{B_{0}^{2} d^{2}}{R}\)(ωx cos ωt + vsinωt) sinωt
This is the required expression for force.
Long answer type questions
Question 1.
(i) How is magnetic flux linked with the armature coil changed in a generator ?
(ii) Derive the expression for maximum value of the induced emf and state the rule that gives the direction of the induced emf.
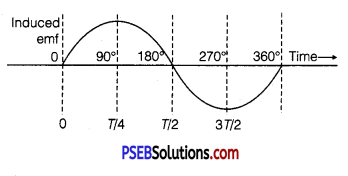
(iii) Show the variation of the emf generated versus time as the armature is rotated with respect to the direction of the magnetic fields.
Answer:
(i) The direction of flow of current in resistance R get changed alternatively after every half cycle.
Thus, AC is produced in coil.
(ii) Let at any instant total magnetic flux linked with the armature coil is G. and θ = ωt is the angle made by area vector of coil with magnetic field.
Φ = NBA cosθ = NBA cosωt
\(\frac{d \phi}{d t}\) = -NBAω sin ωt
– \(\frac{d \phi}{d t}\) = NBAω sin ωt
By Faraday’s law of emf, e = \(\frac{-d \phi}{d t}\)
Induced emf in coil is given by,
e = NBAω sinωt
e = e0 sinωt
where, e0 = NBAω = peak value of induced emf
(iii) The mechanical energy spent in rotating the coil in magnetic field appears in the form of electrical energy.
![]()
Question 2.
State the working of AC generator with the help of a labelled diagram.
The coil of an AC generator having N turns, each of area A, is rotated with a constant angular velocity to. Deduce the expression for the alternating emf generated in the coil.
What is the source of energy generation in this device?
Answer:
AC Generator: A dynamo or generator is a device which converts mechanical energy into electrical energy.
Principle: It works on the principle of electromagnetic induction. When a coil rotates continuously in a magnetic field, the effective area of the coil linked normally with the magnetic field lines, changes continuously with time. This variation of magnetic flux with time results in the production of an alternating emf in the coil.
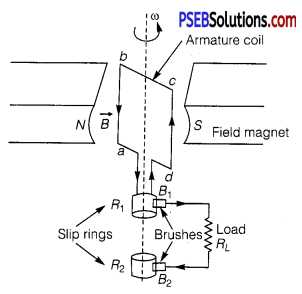
Construction: It consists of the four main parts
(i) Field magnet: It produces the magnetic field. In the case of a low power dynamo, the magnetic field is generated by a permanent magnet, while in the case of large power dynamo, the magnetic field is produced by an electromagnet.
(ii) Armature: It consists of a large number of turns of insulated wire in the soft iron drum or ring. It can revolve an axle between the two poles of the field magnet. The drum or ring serves the two purposes: (a) It serves as a support to coils and (b) It increases the magnetic field due to air core being replaced by an iron core.
(iii) Slip rings: The slip rings R1 and R2 are the two metal rings to which the ends of armature coil are connected. These rings are fixed to the shaft which rotates the armature coil so that the rings also rotate along with the armature.
(iv) Brushes: There are two flexible metal plates or carbon rods (B1 and B2) which are fixed and constantly touch the revolving rings. The output current in external load RL is taken through these brushes.
Working: When the armature coil is rotated in the strong magnetic field, the magnetic flux linked with the coil changes and the current is induced in the coil, its direction being given by Fleming’s right hand rule. Considering the armature to be in vertical position and as it rotates in anticlockwise direction, the wire ab moves upward and cd downward, so that the direction of induced current is shown in fig. In the external circuit, the current flows along B1RlB2. The direction of current remains unchanged during the first half turn of armature. During the second half revolution, the wire ab moves downward and cd upward, so the direction of current is reversed and in external circuit it flows along B2RLB1 Thus the direction of induced emf and current changes in the external circuit after each half revolution.
Expression for Induced emf: If N is number of turns in coil, f the frequency of rotation, A area of coil and B the magnetic induction, then induced emf
e = – \(\frac{d \phi}{d t}\) = –\(\frac{d}{d t}\) {NBA (cos 2π ft)} dt dt
= 2π NBA f sin 2π ft
Obviously, the emf produced is alternating and hence the current is also alternating.
Current produced by an AC generator cannot be measured by moving coil ammeter; because the average value of AC over full cycle is zero.
The source of energy generation is the mechanical energy of rotation of armature coil.