Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 15 Communication Systems Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Physics Chapter 15 Communication Systems
PSEB 12th Class Physics Guide Communication Textbook Questions and Answers
Question 1.
Which of the frequencies will be suitable for beyond-the-horizon communication using sky waves?
(a) 10 kHz
(b) 10 MHz
(C) 1 GHz
(d) 1000 GHz
Answer:
(b) 10 MHz.
For beyond-the-horizon communication, it is necessary for the signal waves to travel a large distance. 10 kHz signals cannot be radiated efficiently because of the antenna size. The high-energy signal waves (1 GHz – 1000 GHz) penetrate the ionosphere. 10 MHz frequencies get reflected easily from the ionosphere. Hence, signal waves of such frequencies are suitable for beyond-the-horizon communication.
Question 2.
Frequencies in the UHF range normally propagate by means of:
(a) Ground waves
(b) Sky waves
(c) Surface waves
(d) Space waves
Answer:
(d) Space waves
Owing to its high frequency, an ultra-high frequency (UHF) wave can neither travel along the trajectory of the ground nor can it get reflected by the ionosphere. The signals having UHF are propagated through line-of-sight communication, which is nothing but space wave propagation.
Question 3.
Digital signals
(i) do not provide a continuous set of values,
(ii) represent values as discrete steps,
(iii) can utilize binary system, and
(iv) can utilize decimal as well as binary systems.
Which of the above statements are true?
(a) (i) and (ii) only
(b) (ii) and (iii) only
(c) (i), (ii) and (iii) but not (iv)
(d) All of (i), (ii), (iii) and (iv)
Answer:
(c) A digital signal uses the binary (0 and 1) system for transferring message signals. Such a system cannot utilize the decimal system (which corresponds to analogue signals). Digital signals represent discontinuous values.
![]()
Question 4.
Is it necessary for a transmitting antenna to be at the same height as that of the receiving antenna for line-of-sight communication? A TV transmitting antenna is 81 m tall. How much service area can it cover if the receiving antenna is at the ground level?
Answer:
Line-of-sight communication means that there is no physical obstruction between the transmitter and the receiver.
In such communications, it is not necessary for the transmitting and receiving antennas to be at the same height.
Height of the given antenna, h = 81 m
Radius of earth, R = 6.4 x 106 m
For range, d = 2Rh, the service area of the antenna is given by the relation
A = πd2 = π(2Rh)
= 3.14 x 2 x 6.4 x 106 x 81
= 3255.55 x 106 m2
= 3255.55 ~ 3256 km2.
Question 5.
A carrier wave of peak voltage 12 V is used to transmit a message signal.
What should be the peak voltage of the modulating signal in order to have a modulation index of 75%?
Answer:
Amplitude of the carrier wave, Ac =12,
Modulation index, m = 75% = 0.75
Amplitude of the modulating wave = Am
Using the relation for modulation index,
m = \(\frac{A_{m}}{A_{c}}\)
∴ Am =mAc
= 0.75 x 12 = 9 V
Hence, amplitude of the modulating wave is 9 V.
Question 6.
A modulating signal is a square wave, as shown in Fig. 15.14.
The carrier wave is given by c(t) = 2 sin (8πt) volts.
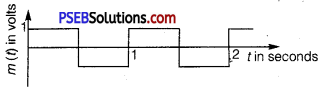
(i) Sketch the amplitude modulated waveform.
(ii) What is the modulation index?
Answer:
Given, the equation of carrier wave
c(t) = 2sin(8πt) ……………………………… (i)
(i) According to the diagram.
Amplitude of modulating signal, Am = 1V
Amplitude of carrier wave,
Ac = 2V [By eq.(1)]
Tm = 1s (From diagram)
From eq.(1) ωm = \(\frac{2 \pi}{T_{m}}=\frac{2 \pi}{1}\) = 2π rad/s ………………. (2)
c(t) = 2sin8πt = Ac sinωc t
ωc =8π
So,
From Eq.(2)
So, ωc = 4ωm
Amplitude of modulated wave
A = Am +Ac =2+1 =3V
The sketch of the amplitude modulated waveform is shown below :
For carrier signal, ω = 8π,T = \(\frac{2 \pi}{\omega}=\frac{2}{8}=\frac{1}{4}\) = 0.25s
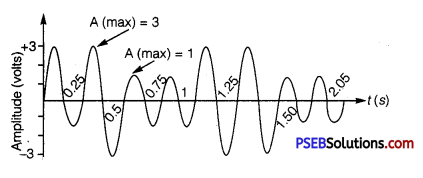
(ii) Modulation index, µ = \(\frac{A_{m}}{A_{c}}=\frac{1}{2}\) = 0.5
Question 7.
For an amplitude modulated wave, the maximum amplitude is found to be 10 V while the minimum amplitude is found to be 2 V. Determine the modulation index, p.
What would be the value of p if the minimum amplitude is zero volts?
Answer:
Maximum amplitude, Amax = 10 V
Minimum amplitude, Amin = 2 V
Modulation index µ, is given by the relation
µ = \(\frac{A_{\max }-A_{\min }}{A_{\max }+A_{\min }}\)
= \(\frac{10-2}{10+2}=\frac{8}{12} \) = 0.67
If Amin=0,
Then µ = \(\frac{A_{\max }}{A_{\max }}=\frac{10}{10}\) = 1
Hence, µ = 1, if the minimum amplitude is zero volts.
![]()
Question 8.
Due to economic reasons, only the upper sideband of an AM wave is transmitted, but at the receiving station, there is a facility for generating the carrier. Show that if a device is available which can multiply two signals, then it is possible to recover the modulating signal at the receiver station.
Answer:
Let ωc be the angular frequency of carrier waves and com by the angular frequency of signal waves.
Let the signal received at the receiving station be
e = E1 cos(ωc +ωm )t
Let the instantaneous voltage of carrier wave
ec = Ec cosωc t
is available at receiving station.
Multiplying these two signals, we get
e x ec = E1Ec coscωc t cos(ωc+ωm)t

Now, at the receiving end as the signal passes through filter, it will pass the high frequency (2ωc + ωm) but obstruct the frequency ωm. So, we can \(\frac{E_{1} E_{c}}{2} \cos \omega_{m_{s}} t\) record the modulating signal frequency ωm.