Punjab State Board PSEB 12th Class Physics Important Questions Chapter 11 Dual Nature of Radiation and Matter Important Questions and Answers.
PSEB 12th Class Physics Important Questions Chapter 11 Dual Nature of Radiation and Matter
Very short answer type questions
Question 1.
In the photoelectric effect, why should the photoelectric current increase as the intensity of monochromatic radiation incident on a photosensitive surface is increased? Explain.
Answer:
The photoelectric current increases proportionally with the increase in intensity of incident radiation. Larger the intensity of incident radiation, larger is the number of incident photons and hence larger is the number of electrons ejected from the photosensitive surface.
Question 2.
Define the term ‘threshold frequency’ in relation to photoelectric effect.
Answer:
Threshold frequency is defined as the minimum frequency of incident radiation which can cause photoelectric emission. It is different for different metal.
![]()
Question 3.
WrIte the basic features of photon picture of electromagnetic radiation on which Einstein’s photoelectric equation is based.
Answer:
Features of the photons are as:
- Photons are particles of light having energy E = hv and momentum p = \(\frac{h}{\lambda}\), where h is Planck’s constant.
- Photons travel with the speed of light in vacuum, independent of the frame of reference.
- Intensity of light depends on the number of photons crossing unit area in a unit time.
Question 4.
Define Intensity of radiation on the basis of photon picture of light. Write its SI unit.
Answer:
The amount of light energy or photon energy incident per meter square per second is called intensity of radiation1 Its SI unit is \(\frac{\mathrm{W}}{\mathrm{m}^{2}}\) or J/s m
Question 5.
State de Broglie hypothesis.
Answer:
According to the hypothesis of de Brogue “The atomic particles of matter moving with a given velocity, can display the wave-like properties.” i.e., λ = \(\frac{h}{m v}\) (mathematically)
Question 6.
Write the relationship of de Brogue wavelength λ associated with a particle of mass m terms of its kinetic energy E.
Answer:
Kinetic energy EK = \(\frac{p^{2}}{2 m}\)
where, p = momentum
m = mass and EK = kinetic energy
⇒ p = \(\sqrt{2 m E_{K}} \)
de Brogue wavelength,
λ = \(\frac{h}{p}\)
Where, p = \(\sqrt{2 m E_{K}} \)
⇒ λ = \(\frac{h}{\sqrt{2 m E_{K}}}\)
Question 7.
Name the phenomenon which shows the quantum nature of electromagnetic radiation.
Answer:
Photoelectric effect.
Question 8.
Do all the electrons that absorb a photon comes out as photoelectrons? (NCERT Exemplar)
Answer:
No, most electrons get scattered into the metal. Only a few come out of the surface of the metal.
![]()
Question 9.
There are materials which absorb photons of shorter wavelength and emit photons of longer wavelength. Can there be stable substances which absorb photons of larger wavelengths and emit light of shorter wavelengths? (NCERT Exemplar)
Answer:
In the first case, energy given out is less than the energy supplied. In the second case, the material has to supply the energy as the emitted photon has more energy. This cannot happen for stable substances.
Question 10.
There are two sources of light, each emitting with a power 100W.
One emits X-rays of wavelength 1 nm and the other visible light at 500 nm.
Find the ratio of number of photons of X-rays the photons of visible light of the given wavelength. (NCERT Exemplar) Ans. Total E is constant.
Let n1 and n2 be the number of photons of X-rays and visible region.
n1E2 = n2E2

Short answer type questions
Question 1.
What is meant by work function of a metal? How does the value of work function influence the kinetic energy of electrons liberated during photoelectron emission?
Answer:
Work Function: The minimum energy required to free an electron from metallic surface is called the work function.
Smaller the work function, larger the kinetic energy of emitted electron.
Question 2.
Show mathematically how Bohr’s postulate of quantization of orbital angular momentum in hydrogen atom is explained by de Broglie’s hypothesis.
Answer:
According to de Broglie’s hypothesis,
λ = \(\frac{h}{m v}\) …………………………… (1)
According to de Broglie’s condition of stationary orbits, the stationary orbits are those which contain complete de Broglie wavelength.
2πr = nλ …………………………………… (2)
Substituting value of λ from (1) in (2), we get
2πr = n\(\frac{h}{m v}\)
⇒ mvr = n\(\frac{h}{2 \pi}\) ……………………………………… (3)
This is Bohr’s postulate of quantization of energy levels.
![]()
Question 3.
Write briefly the underlying principle used in the Davison-Germer experiment to verify wave nature of electrons experimentally. What is the de Broglie wavelength of an electron with kinetic energy (EK) 120 eV?
Answer:
Principle: Diffraction effects are observed for beams of electrons scattered by the crystals.
λ = \(\frac{h}{p}=\frac{h}{\sqrt{2 m E_{K}}}=\frac{h}{\sqrt{2 m e V}}\)
= \(\frac{6.63 \times 10^{-34}}{\sqrt{2 \times 9.1 \times 10^{-31} \times 1.6 \times 10^{-19} \times 120}}\)
λ = 0.112 nm.
Question 4.
(i) Describe briefly three experimentally observed features in the phenomenon of photoelectric effect.
(ii) Discuss briefly how wave theory of light cannot explain these features.
Answer:
(i) Three experimentally observed features in the phenomenon of photoelectric effect are as follows :
- Intensity: When intensity of incident light increases as one photon ejects one electron, the increase in intensity will increase the number of ejected electrons. Frequency has no effect on photoelectron.
- Frequency: When the frequency of incident photon increases, the kinetic energy of the emitted electrons increases. Intensity has no effect on kinetic energy of photoelectrons.
- No Time Lag: When energy incident photon is greater than the work function, the photoelectron is immediately ejected. Thus, there is no time lag between the incidence of light and emission of photoelectrons.
(ii) These features cannot be explained in the wave theory of light because wave nature of radiation cannot explain the following :
- The instantaneous ejection of the photoelectrons.
- The existence of threshold frequency for a metal surface.
- The fact that kinetic energy of the emitted electrons is independent of the intensity of light and depends upon its frequency.
Question 5.
A beam of monochromatic radiation is incident on a photosensitive surface. Answer the following questions :
(i) Do the emitted photoelectrons have the same kinetic energy?
(ii) Does the kinetic energy of the emitted electrons depend on the intensity of incident radiation?
(iii) On what factors does the number of emitted photoelectrons depend?
Answer:
In photoelectric effect, an electron absorbs a quantum of energy hv of radiation, which exceeds the work function, an electron is emitted with maximum kinetic energy.
EK max = hv – W
(i) No, all electrons are bound with different forces in different layers of the metal. So, more tightly bound electron will emerge with less kinetic energy. Hence, all electrons do not have same kinetic energy.
(ii) No, because an electron cannot emit out if quantum energy hv is less than the work function of the metal. The KE depends on the energy of each photon.
(iii) Number of emitted photoelectrons depends on the intensity of the radiations provided the quantum energy hv is greater than the work function of the metal.
Question 6.
Define the term “cut-off frequency” in photoelectric emission. The threshold frequency of a metal is f. When the light of frequency 2f is incident on the metal plate, the maximum velocity of photoelectrons is v1. When the frequency of the incident radiation is increased to 5f, the maximum velocity of photoelectrons is v2. Find the ratio v1: v2.
Answer:
Cut-off Frequency: It is that maximum frequency of incident radiation below which no photoemission takes place from a photoelectric material. According to Einstein’s photoelectric equation
EK max = \(\frac{h c}{\lambda}-\phi \) = \(h v-\phi\)
Given that threshold frequency of the metal is f. If light of frequency, 2f is incident on metal plate, maximum velocity of photoelectron is v1 then,
\(\frac{1}{2} m v_{1}^{2}\) = h (2f-f)
⇒ \(\frac{1}{2} m v_{1}^{2}\) = hf …………………….. (1)
If light of frequency, 5f is incident and maximum velocity of photoelectron is v2.
\(\frac{1}{2} m v_{1}^{2}\) = h(5f-f)
⇒ \(\frac{1}{2} m v_{1}^{2}\) = 4hf ………………………………… (2)
Dividing (1) by (2), we get
\(\left(\frac{v_{1}}{v_{2}}\right)^{2}=\frac{1}{4}\)
⇒ \(\frac{v_{1}}{v_{2}}=\frac{1}{2}\)
∴ v1 = v2 = 1:2
![]()
Question 7.
Two monochromatic beams A and B of equal intensity I hit a screen. The number of photons hitting the screen by beam A is twice that by beam B. Then what inference can you make about their frequencies? (NCERTExemplarl
Answer:
Let no. of photons falling per second of beam A = nA
No. of photons falling per second of beam B = nB
Energy of beam A = hvA
Energy of beam B = h vB
According to question, I = nAvA = nBvB
\(\frac{n_{A}}{n_{B}}=\frac{v_{B}}{v_{A}}\) or \(\frac{2 n_{B}}{n_{B}}=\frac{v_{B}}{v_{A}}\)
⇒ vB = 2 vA
The frequency of beam B is twice that of A.
Question 8.
Consider Fig. for photoemission.
How would you reconcile with momentum- conservation? No light (Photons) have momentum in a different direction than the emitted electrons. (NCERT Exemplar)
Answer:
The momentum is transferred to the metal. At the microscopic level, atoms absorb the photon and its momentum is transferred mainly to the nucleus and electrons. The excited electron is emitted. Conservation of momentum needs to be accounted for the momentum transferred to the nucleus and electrons.
Long answer type questions
Question 1.
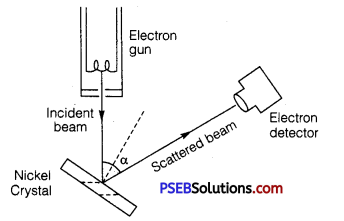
Describe Davisson and Germer’s experiment to demonstrate the wave nature of electrons. Draw a labeled diagram of apparatus used.
Answer:
Davisson and Germer Experiment: In 1927 Davisson and Germer performed a diffraction experiment with electron beam in analogy with X-ray diffraction to observe the wave nature of matter.
Apparatus: It consists of three parts
(i) Electron gun : It gives a fine beam of electrons, de Brogue used electron beam of energy 54 eV. de Brogue wavelength associated with this beam
λ = \(\frac{h}{\sqrt{2 m E_{k}}}\)
Here, m = mass of electron = 9.1 x 10-31 kg
EK = Kinetic energy of electron = 54eV
= 54 x 1.6 x 10-19 J = 86.4 x 10-19 J
∴ λ = \(\frac{6.63 \times 10^{-34}}{\sqrt{2 \times 9.1 \times 10^{-31} \times 86.4 \times 10^{-19}}}\)
= 1.66 x 10-10 = 1.66 Å
(ii) Nickel crystal: The electron beam was directed on nickel crystal against the electron detector. The smallest separation between nickel atoms is O.914Å. Nickel crystal behaves as diffraction grating.
(iii) Electron detector: It measures the intensity of electron beam diffracted from nickel crystal. It may be an ionization chamber fitted with a sensitive galvanometer. The energy of electron beam, the angle of incidence of beam on nickel crystal and the position of detector can all be varied.
Method: The crystal is rotated in small steps to change the angle (α say) between incidence and scattered directions and the corresponding intensity (I) of scattered beam is measured. The variation of the intensity (I) of the scattered electrons with the angle of scattering a is obtained for different accelerating voltages.
The experiment was performed by varying the accelerating voltage from 44 V to 68 V. k was noticed that a strong peak appeared in the intensity (I) of the scattered electron for an accelerating voltage of 54 V at a scattering angle α = 50°.
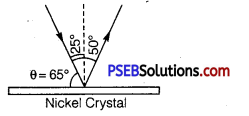
From Bragg’s law, 2d sinθ = nλ
Here, n =1,d =0.914 Å,θ =65°
∴ λ = \(\frac{2 d \sin \theta}{n}=\frac{2 \times(0.914 \AA) \sin 65^{\circ}}{1}\)
=2 x 0.914 x 0.9063Å =1.65Å
The measured wavelength is in close agreement with the estimated de Broglie wavelength. Thus the wave nature of electrons is verified. Later on G.P. Thomson demonstrated the wave nature of fast electrons. Due to their work Davisson and G.P. Thomson were awarded Nobel Prize in 1937.