Punjab State Board PSEB 12th Class Chemistry Book Solutions Chapter 3 Electrochemistry Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Chemistry Chapter 3 Electrochemistry
PSEB 12th Class Chemistry Guide Electrochemistry InText Questions and Answers
Question 1.
Arrange the following metals in the order in which they displace each other from the solution of their salts.
Al, Cu, Fe, Mg and Zn
Answer:
The following is the order in which the given metals displace each other from the solution of their salts.
Mg > Al > Zn > Fe > Cu
Question 2.
Given the standard electrode potentials,
K+/K = – 2.93 V, Ag+/Ag = 0.80V, Hg2+/Hg = 0.79V
Mg2+/Mg = -2.37 V,Cr3+/Cr = -0.74V
Arrange these metals in their increasing order of reducing power. .
Answer:
The lower the reduction potential, the higher is the reducing power. The given standard electrode potentials increase in the order of K+/K < Mg2+/Mg < Cr3+/Cr < Hg2+/Hg < Ag+/Ag.
Hence, the reducing power of the given metals increases in the ‘ following order:
Ag < Hg < Cr < Mg < K
![]()
Question 3.
Depict the galvanic cell in which the reaction
Zn(s) + 2Ag+ (aq) → Zn2+ (aq) + 2Ag(s) takes place. Further show:
(i) Which of the electrode is negatively charged?
(ii) The carriers of the current in the cell.
(iii) Individual reaction at each electrode.
Answer:
The galvanic cell in which the given reaction takes place is depicted as:
Zn(s) | Zn2+ (aq) || Ag+(aq) | Ag(s)
(i) Zn electrode (anode) is negatively charged.
(ii) Ions are carriers in the cell and in the external circuit, current will flow from silver to zinc.
(iii) The reaction taking place at the anode is given by,
Zn (s) → Zn2+ (aq) + 2e–
The reaction taking place at the cathode is given by,
Ag+ (aq) + e– → Ag(s)
Question 4.
Calculate the standard cell potentials of galvanic cell in which the following reactions take place:
(i) 2Cr(s) + 3Cd2+(aqr) → 2Cr3+(aq) + 3Cd(s)
(ii) Fe2+(aq) + Ag+(aq) → Fe3+(aq) + Ag(s)
Calculate the ΔrGΘ and equilibrium constant of the reactions.
Solution:
(i) EΘCr3+/Cr = -0.74 V
EΘCd2+/Cd = – 0.40 V
Now, the standard cell potential is
\(E_{\text {cell }}^{\ominus}\) = \(E_{\text {cathode }}^{\ominus}\) – \(E_{\text {anode }}^{\ominus}\)
= -0.40 – (-0.74)
= + 0.34 V
ΔrGΘ = -nF\(E_{\text {cell }}^{\ominus}\)
ΔrGΘ = – 6 mol × 96500 C mol-1 × 0.34 V
= -196860 CV
= -196.86 kJ
Again,
ΔrGΘ = -2.303 RT InKC
=> log KC = – \(\frac{\Delta_{r} G}{2.303 R T}\)
= \(\frac{(-196860 \mathrm{~J})}{2.303 \times\left(8.314 \mathrm{JK}^{-1}\right) \times(298 \mathrm{~K})}\)
= 34.501
∴ KC = antilog (34.501)
= 3.192 × 1034
(ii) EΘ Fe3+/Fe2+ = 0.77 V
EΘ Ag+/Ag = 0.80 V
Now, the standard cell potential is
\(E_{\text {cell }}^{\ominus}\) = \(E_{\text {cathode }}^{\ominus}\) – \(E_{\text {anode }}^{\ominus}\)
= 0.80 -0.77 = 0.03 V A
ΔrGΘ = – nF\(E_{\text {cell }}^{\ominus}\)
= -1 mol × 96500 C mol-1 × 0.03 V
= – 2895 CV
= – 2895 J
ΔrGΘ = – 2.895 kJ
Again, ΔrGΘ = – 2.303 RT In KC
=> log KC = – \(\frac{\Delta_{r} G}{2.303 R T}\)
= \(\frac{-2895 \mathrm{~J}}{2.303 \times\left(8.314 \mathrm{JK}^{-1}\right) \times(298 \mathrm{~K})}\)
= 0.5074
∴ KC = antilog (0.5074)
= 3.22
![]()
Question 5.
Write the Nernst equation and emf of the following cells at 298 K:
(i) Mg(s) | Mg2+ (0.001M) || CU2+(0.0001M) | Cu(s)
(ii) Fe(s) | Fe2+ (0.001M) ||H+(1M)|H2(g)(lbar) | Pt(s)
(iii) Sn(s) | Sn2+ (0.050 M) ||H+(0.020 M) | H2(g) (1 bar) | Pt(s)
(iv) Pt(s) | Br2(l) | Br– (0.010M)||H+(0.030M) | H2(g) (lbar) | Pt(s).
Solution:
(i) Cell reaction : Mg(s) + Cu2+ (aq) → Mg2+ (aq) + Cu(s) (n = 2)
For the reaction, the Nernst equation can be given as:

(iii) Cell reaction : Sn(s) + 2H+ (aq) → Sn2+ (aq) + H2 (g) (n = 2)
For the reaction, the Nernst equation can be given as
Ecell = \(E_{\text {cell }}^{\ominus}\) – \(\frac{0.0591}{n}\) log \(\frac{\left[\mathrm{Sn}^{2+}\right]}{\left[\mathrm{H}^{+}\right]^{2}}\)
EMF of cell Ecell = [ 0 – (-0.14)} – \(\frac{0.0591}{2}\) log \(\frac{0.050}{(0.020)^{2}}\)
= 0.14 – 0.0295 × log 125
= 0.14 -0.062
= 0.078 V
= 0.08 V
(iv) Cell reaction : 2Br–(l) + 2H+ (aq) → Br2(l) + H2(g) (n = 2)
For the reaction, the Nernst equation can be given as
Ecell = \(E_{\text {cell }}^{\ominus}\) – \(\frac{0.0591}{n}\) log \(\frac{1}{\left[\mathrm{Br}^{-}\right]^{2}\left[\mathrm{H}^{+}\right]^{2}}\)
EMF of cell Ecell = (0 – 1.09) – \(\frac{0.0591}{2}\) log \(\frac{1}{(0.010)^{2}(0.030)^{2}}\)
= -1.09 – 0.02955 × log \(\frac{1}{0.00000009}\)
= -1.09 – 0.02955 × log \(\frac{1}{9 \times 10^{-8}}\)
= -1.09 – 0.02955 × log (1.11 × 107 )
= -1.09 – 0.02955 (0.0453 + 7)
= -1.09 – 0.208
= -1.298 V
Question 6.
In the button cells widely used in watches and other devices the following reaction takes place:
Zn(s)+ Ag20(s) + H20(Z) → Zn2+ (aq) + 2Ag(s)+ 20H– (aq)
Determine ΔrGΘ and EΘ for the reaction.
Solution:
Zn(s) → Zn2+ (aq) + 2e–; EΘ = – 0.76 V

∴ EΘ = 1.11 V
Weknow that
ΔrGΘ = -nFEΘ
= -2 × 96500 × 1.11
= -214230 CV or .2.1423 × 105J
![]()
Question 7.
Define conductivity and molar conductivity for the solution of an electrolyte. Discuss their variation with concentration.
Answer:
Conductivity: The conductivity of a solution is defined as the conductance of a solution of 1 cm in length and area of cross-section 1 sq. cm. The inverse of resistivity is called conductivity or specific conductance. It is represented by the symbol K. If p is resistivity, then
we can write:
K = \(\frac{1}{\rho}\)
The conductivity of a solution at any given concentration is the conductance (G) of one unit volume of solution kept between two platinum electrodes with the unit area of cross-section and at a distance of unit length.
G = K\(\frac{a}{l}\) = K.1 = K
i. e.,
(Since a = 1,1 = 1)
Conductivity always decreases with a decrease in concentration, both for weak and strong electrolytes. This is because the number of ions per unit volume that carry the current in a solution decreases with a decrease in concentration.
Molar conductivity: The molar conductivity of a solution at a given concentration is the conductance of volume V of a solution containing 1 mole of the electrolyte kept between two electrodes with the area of cross-section A and distance of unit length.
∧m = K\(\frac{A}{l}\)
Now, l = 1 and A = V (volume containing a mole of the electrolyte).
∧m = KV
Its unit is ohm-1 cm2 or Scm2 mol-1
Molar conductivity increases with a decrease in concentration. This is because the total volume V of the solution containing one mole of the electrolyte increases on dilution.
The variation of ∧m with √e for strong and weak electrolytes is shown in the following plot:
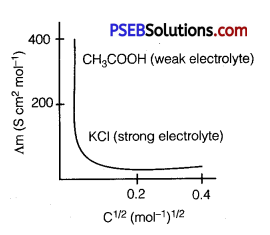
Question 8.
The conductivity of 0.20 M solution of KCI at 298 K is 0.0248 Scm-1. Calculate its molar conductivity.
Solution:
Given,
Conductivity (K) = 0.0248 Scm-1
Molar concentration (C) = 0.20 M
∴ Molar conductivity, ∧m = \(\frac{\kappa \times 1000}{C}\)
= \(\frac{0.0248 \times 1000}{0.2}\)
= 124 Scm2 mol-1
![]()
Question 9.
The resistance of a conductivity cell containing 0.001 M KCI solution at 298 K is 1500 Ω. What is the cell constant if conductivity of 0.001M KCI solution at 298 K is 0.146 × 10-3 S cm-1.
Solution:
Given,
Conductivity, (K) = 0.146 × 10-3 Scm-1
Resistance, R = 1500Ω
Cell constant = K × R
= 0.146 × 10-3 × 1500 ’
= 0.219 cm-1
Question 10.
The conductivity of sodium chloride at 298 K has been determined at different concentrations and the results are given below:

Calculate ∧m for all concentrations and draw a plot between ∧m
and \(\mathbf{C}^{\frac{1}{2}}\). Find the value of \(\Lambda_{m}^{0}\).
Solution:
\(\frac{1 \mathrm{~S} \mathrm{~cm}^{-1}}{100 \mathrm{Sm}^{-1}}\) = 1 (Unit conversion factor)
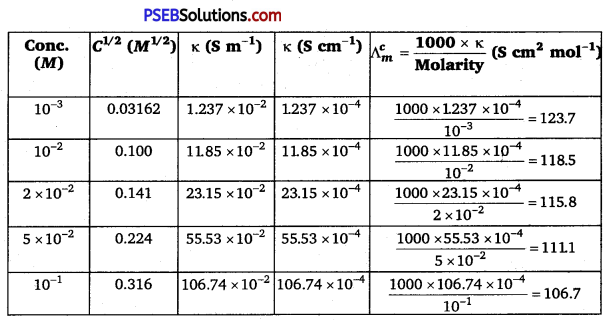
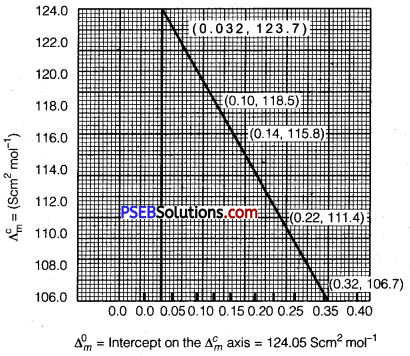
Question 11.
Conductivity of 0.00241 M acetic acid is 7.896 × 10-5 S cm-1. Calculate its molar conductivity. If \(\Lambda_{m}^{0}\) for acetic acid is 390.5 S cm2 mol-1, what is its dissociation constant?
Solution:
Given, K = 7.896 × 10-5 S cm-1
C = 0.00241 mol L -1
Then, molar conductivity, \(\Lambda_{m}^{c}\) = \(\frac{\kappa}{C}\) × 1000
= \(\frac{7.896 \times 10^{-5} \mathrm{~S} \mathrm{~cm}^{-1} \times 1000 \mathrm{~cm}^{3} \mathrm{~L}^{-1}}{0.00241 \mathrm{~mol} \mathrm{~L}^{-1}}\)
= 32.76S cm2 mol-1
Again, \(\Lambda_{m}^{0}\) = 390.5 S cm2 mol-1
Now, α = \(\frac{\Lambda_{m}^{c}}{\Lambda_{m}^{0}}\) = \(\frac{32.76 \mathrm{~S} \mathrm{~cm}^{2} \mathrm{~mol}^{-1}}{390.5 \mathrm{~S} \mathrm{~cm}^{2} \mathrm{~mol}^{-1}}\)
= 0.084
∴ Dissociation constant, Ka = \(\frac{C \alpha^{2}}{(1-\alpha)}\)
= \(\frac{\left(0.00241 \mathrm{~mol} \mathrm{~L}^{-1}\right)(0.084)^{2}}{(1-0.084)}\)
= 1.86 × 10-5 mol L-1
![]()
Question 12.
How much charge is required for the following reductions:
(i) 1 mol of Al3+ to Al.
(ii) 1 mol of Cu2+ to Cu.
(iii) 1 mol of \(\mathrm{MnO}_{4}^{-}\) to Mn2+.
Solution:
(i) Al3+ + 3e– → Al
Quantity of charge required for reducing 1 mol of Al3+ to Al
= 3 Faraday = 3 × 96500 C
= 289500 C
(ii) Cu2+ + 2e– → Cu
Quantity of charge required for reducing 1 mol of Cu2+ to Cu
= 2F = 2 × 96500 C = 193000 C
(iii) \(\mathrm{MnO}_{4}^{-}\) + 5e– → Mn2+
Quantity of charge required for reducing 1 mol
of \(\mathrm{MnO}_{4}^{-}\) to Mn2+ = 5F = 5 × 96500 C = 482500 C
Question 13.
How much electricity in terms of Faraday is required to produce
(i) 20.0 g of Ca from molten CaCl2.
(ii) 40.0 g of Al from molten Al2O3.
Solution:
(i) According to the question,
![]()
Electricity required to produce 40g of calcium = 2F
Therefore, electricity required to produce 20 g of calcium = \(\frac{2 \times 20}{40}\) F
= IF
(ii) According to the question,
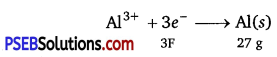
Electricity required to produce 27 g of Al = 3F
Therefore, electricity required to produce 40 g of Al = \(\frac{3 \times 40}{27}\) F
= 4.44 F
Question 14.
How much electricity is required in coulomb for the oxidation of
(i) 1 mol of H2O to O2
(ii) 1 mol of FeO to Fe2O3
Solution:
(i) According to the question,
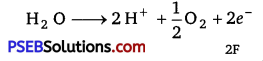
Electricity required for the oxidation of 1 mol of H2O to O2 = 2 F
= 2 × 96500 C = 19300 C
(ii) According to the question,

Electricity required for the oxidation of 1 mol of FeO to Fe203 = 1F
= 1 × 96500 C = 96500 C
![]()
Question 15.
A solution of Ni(NO3)2 is electrolysed between platinum
electrodes using a current of 5 amperes for 20 minutes. What mass of Ni is deposited at the cathode?
Solution:
Given, Current = 5A, Time = 20 × 60 = 1200 s
∴ Charge = current × time
= 5 × 1200 = 6000 C
According to the reaction,
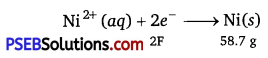
Nickel deposited by 2 × 96500 C = 58.7 g
Therefore, nickel deposited by 6000 C = \(\frac{58.7 \times 6000}{2 \times 96500}\)g
= 1.825 g
Hence, 1.825 g of nickel will be deposited at the cathode.
Question 16.
Three electrolytic cells A,B,C containing solutions of ZnS04, AgNO3 and CuS04, respectively are connected in series. A steady current of 1.5 amperes was passed through them until 1.45 g of silver deposited at the cathode of cell B. How long did the current flow? What mass of copper and zinc were deposited?
Solution:
(a)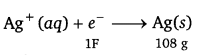
i.e., 108 g of Ag is deposited by electricity = 96500 C.
Therefore, 1.45 g of Ag is deposited by electricity = \(\frac{96500 \times 1.45}{108}\)C
= 1295.6 C
Current (I) = 1.5A
∴ Time (t) = \(\frac{Q}{I}\) = \(\frac{1295.6}{1.5}\)s
= 863.6 s = 864 s
(b) 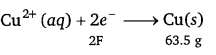
i.e., 2 × 96500 C of charge deposit = 63.5 g of Cu
Therefore, 1295.6 C of charge will deposit = \(\frac{63.5 \times 1295.6}{2 \times 96500}\)g
= 0.426 g of Cu

i.e., 2 × 96500 Cof charge deposit = 65.4 g of Zn
Therefore, 1295.6 C of charge will deposit = \(\frac{65.4 \times 1295.6}{2 \times 96500}\)g
= 0.439 g of Zn
![]()
Question 17.
Using the standard electrode potentials given in Table 3.1, predict if the reaction between the following is feasible:
(i) Fe3+(aq) and I– (aq)
(ii) Ag+ (aq) and Cu(s)
(iii) Fe3+(aq) and Br– (aq)
(iv) Ag(s) and Fe3+ (aq)
(v) Br2(aq) and Fe2+ (aq).
Answer:

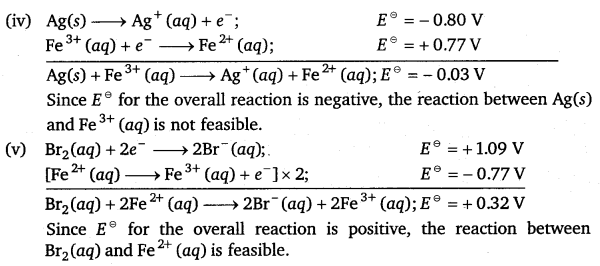
![]()
Question 18.
Predict the products of electrolysis in each of the following:
(i) An aqueous solution of AgNO3 with silver electrodes.
(ii) An aqueous solution of AgNO3 with platinum electrodes.
(iii) A dilute solution of H2SO4 with platinum electrodes.
(iv) An aqueous solution of CuCl2 with platinum electrodes.
Answer:
(i) An aqueous solution of AgNO3 with silver electrodes.
In aqueous solution, ionisation of AgNO3 and H2O takes place.

At cathode: Ag+ ions have less discharge potential than H+ ions so silver will be deposited at cathode.
Ag+ (aq) + e– → Ag(s)
At anode: An equivalent amount of silver will be oxidised to Ag+ ions by releasing electrons.
Ag(s) → Ag+ (aq) + e–
Ag anode is attacked by \(\mathrm{NO}_{3}^{-}\) ions, so it will also produce Ag+ in the solution.
(ii) An aqueous solution of AgNO3 with platinum electrodes.
In aqueous solution ionisation of AgNO3 and H2O occurs
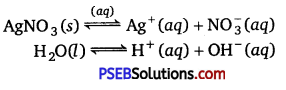
As platinum electrodes are non-attackable electrodes, they will not be reacted upon by\(\mathrm{NO}_{3}^{-}\) ions.
At cathode: Ag will be deposited at cathode.
Ag+(aq) + e– → Ag(s)
At anode: Out of \(\mathrm{NO}_{3}^{-}\) and OH– ions, only OH– ions will be oxidised (due to less discharge potential) preferentially and \(\mathrm{NO}_{3}^{-}\) ions will remain in the solution.
OH–(aq) → OH + e–
40H → 2H2O(l) + O2(g)
So, oxygen gas is produced at anode. The solution remains acidic due to the presence of HNO3.
![]()
(iii) A dilute solution of H2SO4 with platinum electrodes.
Both H2S04 and water ionise in the solution.

At cathode: H+ ions will be reduced and hydrogen gas is produced at cathode.
H+ (aq) + e– → H(g)
H(g) + H(g) → H2(g)
At anode: OH– ions will be released preferentially and not \(\) ions due to less discharge potential.
OH–(aq) → OH + e–
4 OH → 2H2oa) + 02(g)
Oxygen gas is produced at anode.
Solution will be acidic and will contain H2S04.
(iv) An aqueous solution of CuCl2 with platinum electrodes.
Both CuCl2, and water ionise as usual.

At cathode : Cu2+ ions will be reduced preferentially due to less discharge potential than H+ ions.
Cu2+ (aq) + 2e– > Cu(s)
Copper metal is deposited at cathode.
At anode: Cl– ions will be discharged in preference to OH– ions and chlorine gas is produced at anode.
Cl– (aq) → Cl(g) + e–
Cl(g) + Cl(g) → Cl2(g)
![]()
Chemistry Guide for Class 12 PSEB Electrochemistry Textbook Questions and Answers
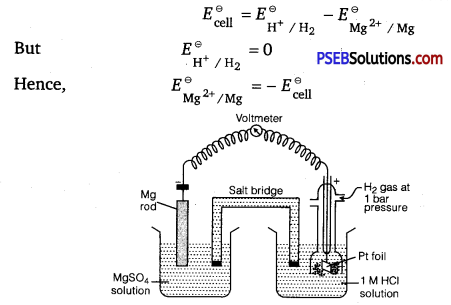
Question 1.
How would you determine the standard electrode potential of the system Mg2+| Mg?
Answer:
The standard electrode potential of the system Mg2+|Mg can be determined with respect to the standard hydrogen electrode, represented by
Pt(s), H2(g) (1 atm) |H+(aq)(lM).
A cell, consisting of Mg|MgS04(aq1 M) as the anode and the standard hydrogen electrode as the cathode, is set up.
Mg|Mg2+ || H+ (aq, 1M) H2 (g, 1 bar), Pt(s)
Then, the emf of the cell is measured and this measured emf is the
standard electrode potential of the magnesium electrode.
Question 2.
Can you store copper sulphate solutions in a zinc pot?
Ans. No, zinc pot cannot store copper sulphate solutions because the standard electrode potential (EΘ) value of zinc is less than that of copper. So, zinc is stronger reducing agent than copper.
Zn2+ (aq) + 2e– → Zn(s); EΘ = – 0.76 V
Cu2+ (aq) + 2e– → Cu(s); EΘ = – 0.34 V
So, zinc will loss electrons to Cu2+ ions and redox reaction will occur as follows:
Zn(s) + Cu2+ (aq) → Zn2+ (aq) + Cu(s)
Question 3.
Consult the table of standard electrode potentials and suggest three substances that can oxidise ferrous ions under suitable conditions.
Answer:
Substances that are stronger oxidising agents than ferrous (Fe2+ ) ions
can oxidise ferric (Fe3+) ions.
Fe2+ → Fe3+ + e–;EΘ = – 0.77 V
This implies that the substances having higher reduction potentials than + 0.77 V can oxidise ferrous ions to ferric ions. Three substances that can do so are F2, Cl2, and 02.
![]()
Question 4.
Calculate the potential of hydrogen electrode in contact with a solution whose pH is 10.
Solution:

= – 0.0591 log 1010
= – 0.0591 × 10 log 10
= -0.591V [∵ log 10=1]
Question 5.
Calculate the emf of the cell in which the following reaction takes place:
Ni(s) + 2Ag+ (0.002 M) → Ni2+ (0.160 M) + 2Ag(s)
Given that \(\boldsymbol{E}_{\text {(cell) }}^{\ominus}\) = 1.05 V
Solution:
Applying Nemst.equation, we have
E(cell) = \(\boldsymbol{E}_{\text {(cell) }}^{\ominus}\) – \(\frac{0.0591}{n}\) log \(\frac{\left[\mathrm{Ni}^{2+}\right]}{\left[\mathrm{Ag}^{+}\right]^{2}}\)
= 1.05 – \(\frac{0.0591}{2}\) log \(\frac{(0.160)}{(0.002)^{2}}\)
= 1.05 – 0.02955 log \(\frac{0.16}{0.000004}\)
= 1.05-0.02955 log 4 × 104
= 1.05 – 0.02955 (log 10000 + log 4)
= 1.05 – 0.02955 (4 + 0.6021)
= 0.914 V
Question 6.
The cell in which the following reaction occurs:
2Fe3+ (aq) + 2I– (aq) → 2Fe2+ (aq) + I2(s)
has EΘcell = 0.236 V at 298 K.
Calculate the standard Gibbs energy and the equilibrium constant of the cell reaction.
Solution:
Here, n = 2, \(\boldsymbol{E}_{\text {(cell) }}^{\ominus}\) = 0.236 V, T = 298 K
We know that,
ΔrGΘ = – nFEΘcell
= – 2 x 96500 x 0.236
= – 45548 CV
= – 45548 J
ΔrGΘ = -45.55 kJ
Again, ΔrGΘ = – 2.303RT log Kc
=> log Kc = – \(\frac{\Delta_{r} G^{\ominus}}{2.303 R T}\)
= – \(\frac{-45.55 \mathrm{~kJ}}{2.303 \times 8.314 \times 10^{-3} \times 298}\)
= 7.983
> Kc = Antilog (7.983)
= 9.616 × 107
![]()
Question 7.
Why does the conductivity of a solution decrease with dilution?
Answer:
The conductivity of a solution is the conductance of ions present in a unit volume of the solution. The number of ions (responsible for carrying current) decreases when the solution is diluted. As a result, the conductivity of a solution decreases with dilution.
Question 8.
Suggest a way to determine the \(\Lambda_{\boldsymbol{m}}^{\mathrm{o}}\) value of water.
Answer:
Applying Kohlrausch’s law of independent migration of ions, the \(\Lambda_{\boldsymbol{m}}^{\mathrm{o}}\) value of water can be determined as fallows:
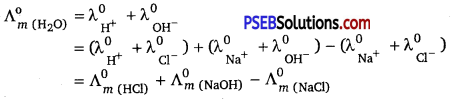
Hence, by knowing the \(\Lambda_{\boldsymbol{m}}^{\mathrm{o}}\) values of HCl, NaOH, and NaCl, the \(\Lambda_{\boldsymbol{m}}^{\mathrm{o}}\) value of water can be determined.
Question 9.
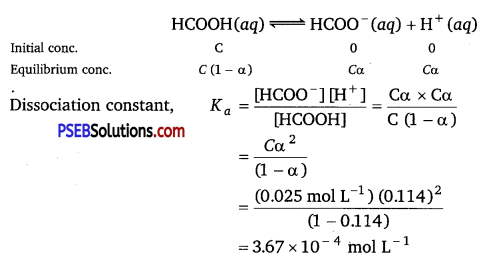
The molar conductivity of 0.025 mol L-1 methanoic acid is 46.1 S cm2 mol-1.
Calculate its degree of dissociation and dissociation constant.
Given \(\lambda_{\mathbf{H}^{+}}^{\mathbf{0}}\) = 349.6 S cm2 mol-1 and \(\lambda_{\text {HCOо }^{-}}^{\text {0 }}\) = 54.6 cm2 mol-1.
Solution:
Calculation of degree of dissociation (a) of HCOOH Given,
C = 0.025 mol L-1
∧m = 46.1 S cm2 mol-1
\(\lambda^{0}{ }_{\left(\mathrm{H}^{+}\right)}\) – = 349.6 S cm2 mol-1
\(\lambda^{0}{ }_{\left(\mathrm{HCOO}^{-}\right)}\) = 54.6 S cm2 mol-1
\(\Lambda_{m}^{\circ}(\mathrm{HCOOH})\) = λ0(H+) + λ0(HCOO–)
= 349.6 + 54.6
= 404.2 S cm2 mol-1
Now, degree of dissociation,
α = \(\frac{\Lambda_{m(\mathrm{HCOOH})}}{\Lambda_{m(\mathrm{HCOOH})}^{o}}\)
= \(\frac{46.1}{404.2}\) = 0.114
Calculation of dissociation constant
![]()
Question 10.
If a current of 0.5 ampere flows through a metallic wire for 2 hours, then how many electrons would flow through the wire?
Solution:
Given, I = 0.5 A, t = 2 hours = 2 × 60 × 60 s = 7200 s
Thus, Q = It = 0.5A × 7200 s = 3600 C
We know that 96487C = 6.023 × 1023 number of electrons.
Then,
3600C = \(\frac{6.023 \times 10^{23} \times 3600}{96487}\) number of electrons
= 2.25 × 1022 number of electrons
Hence, 2.25 × 1022 number of electrons will flow through the wire.
Question 11.
Suggest a list of metals that are extracted electrolytically.
Answer:
Metals that are on the top of the reactivity series such as sodium, potassium, calcium, lithium, magnesium, aluminium are extracted electrolytically.
Question 12.
Consider the reaction : \(\mathrm{Cr}_{2} \mathrm{O}_{7}^{2-}\) + 14H+ + 6e– → 2Cr3+ + 7H2O What is the quantity of electricity in coulombs needed to reduce 1 mol of \(\mathrm{Cr}_{2} \mathrm{O}_{7}^{2-}\)?
Solution:
The given reaction is
\(\mathrm{Cr}_{2} \mathrm{O}_{7}^{2-}\) + 14H+ + 6e– → 2Cr3+ + 7H2O
Therefore, to reduce 1 mol of \(\mathrm{Cr}_{2} \mathrm{O}_{7}^{2-}\), the required quantity of electricity will be:
= 6 F = 6 × 96487 C = 578922 C
Question 13.
Write the chemistry of recharging the lead storage battery, highlighting all the materials that are involved during recharging.
Answer:
During recharging, electrical energy is supplied to the cell from an external source. The reactions are reverse of those that takes place during discharge.
At anode: PbSO4(s) + 2e– → Pb(s) + \(\mathrm{SO}_{4}^{2-}\) (aq)
At cathode: PbSO4(s) + 2H2O(l) → Pb02(s) + \(\mathrm{SO}_{4}^{2-}\) (aq) + 2e–
The overall cell reaction is given by,
2PbSO4(s) + 2H2O(l) → Pb(s) + PbO2(s) + 2H2SO4(aq)
Question 14.
Suggest two materials other than hydrogen that can be used as fuels in fuel cells.
Answer:
Methane (CH4) and methanol (CH3OH) can be used as fuels in fuel cells.
![]()
Question 15.
Explain how rusting of iron is envisaged as setting up of an electrochemical cell.
Answer:
In corrosion, a metal is oxidised by loss of electrons to oxygen with the formation of oxides. So, an electrochemical cell is set up. e.g., Rusting of iron involves following terms:
The water layer present on the surface of iron dissolves acidic oxides of air like CO2 to form acids which dissociate to give H+ ions.
![]()
In the presence of H+ ions, iron starts losing electrons at some spot to form ferrous ions. Hence, this spot acts as the anode:
Fe(s) → Fe2+ (aq) + 2e–;[\(E_{\left(\mathrm{Fe}^{2+} / \mathrm{Fe}\right)}^{\ominus}\) =-0.44V]
The electrons thus released move through the metal to reach another
spot where H+ ions and the dissolved oxygen gain these electrons and
reduction reaction takes place. Hence, this spot acts as the cathode:
O2(g) + 4H+ (aq) + 4e– > 2H2O(l; [\(E^{\ominus}{\left(\mathrm{H}^{+} / \mathrm{O}_{2} / \mathrm{H}_{2} \mathrm{O}\right)}\) = 1.23V]
The overall reaction is given as:
2Fe(s) + O2(g) + 4H+ (aq) > 2Fe2+ (aq) + 2H2O(Z) ; [\(E_{\text {cell }}^{\ominus}\) = 1.67V]
Therefore, an electrochemical cell is set up on the surface.
Ferrous ions are further oxidised by the atmospheric oxygen to ferric ions which combine with water molecules to form hydrated ferric oxide, Fe2O3.xH0, which is rust.
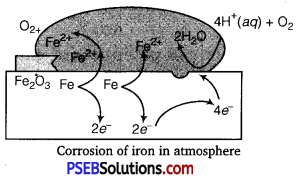
Oxidation: Fe(s) → Fe2+ (aq) + 2e–
Reduction: O2(g) + 4H+ (aq) + 4e– → 2H2O(l)
Atmospheric
Oxidation: 2Fe2+ (aq) + 2H2O(l) + \(\frac{1}{2}\)O2(g) → Fe2O3(s) + 4H– (aq)