Punjab State Board PSEB 12th Class Chemistry Important Questions Chapter 1 The Solid State Important Questions and Answers.
PSEB 12th Class Chemistry Important Questions Chapter 1 The Solid State
Very short answer type questions
Question 1.
Give an example each of a molecular solid and an ionic solid.
Answer:
Molecular solids: CO2, I2, HCl
Ionic solids: NaCl, ZnS, CaF2
Question 2.
Why does the window glass of the old buildings look milky?
Answer:
It is due to heating during the day and cooling at night, i.e., due to annealing over a number of years, glass acquires crystalline character.
Question 3.
What would be the nature of solid if there is no energy gap between valence band and conduction band?
Answer:
Conductor.
![]()
Question 4.
Express the relationship between atomic radius (r) and the edge length (a) in the bcc unit cell,
Answer:
Atomic radius (r) = \(\frac{\sqrt{3}}{4}\) a (edge length of unit cell).
Question 5.
Which point defect in its crystal units increases the density of a solid?
Answer:
Interstitial defect.
Question 6.
What is meant by the term ‘forbidden zone’ in reference to band theory of solids?
Answer:
The energy gap between valence band and conduction band is known as forbidden zone.
Question 7.
‘Crystalline solids are anisotropic in nature.’ What does this statement mean?
Answer:
It means that some of their physical properties like electrical conductivity, refractive index, etc., are diferent in different directions.
Question 8.
Why does the electrical conductivity of semiconductors increase with rise in temperature? [NCERT Exemplar)
Answer:
The gap between conduction band and valence band is small in semiconductors. Therefore, electrons from the valence band can jump to the conduction band on increasing temperature. Thus, they become more conducting as the temperature increases.
Question 9.
Why does table salt NaCl sometimes appear yellow in colour?
(NCERT Exemplar)
Answer:
Yellow colour in NaCl is due to metal excess defect due to which unpaired electrons occupy anionic sites, known as F-centres. These electrons absorb energy from the visible region for the excitation which makes crystal appear yellow.
![]()
Question 10.
Why are liquids and gases categorised as fluids? (NCERT Exemplar)
Answer:
Liquids and gases have the tendency to flow, i.e., their molecules can move freely from one place to another. Therefore, they are known as fluids.
Short answer type questions
Question 1.
(i) What type of stoichiometric defect is shown by KC1 and why?
(ii) What type of semiconductor is formed when silicon is doped with As?
(iii) Which one of the following is an example of molecular solid : CO2 or SiO2?
Answer:
(i) KCl shows Schottky defect as the cation, K+ and anion, Cl– are of almost similar sizes.
(ii) n-type semiconductor.
(iii) CO2
Question 2.
Iron has a body centred cubic unit cell with a cell dimension of 286.65 pm. The density of iron is 7.874 g cm-3. Use this information to calculate Avogadro’s number. (At. mass of Fe = 55.845 u)
Solution:
Given, a =286.65 pm = 286.65 × 10-10 cm; M = 55.845 g mol-1;
d = 7.874 g cm-3
For bee unit cell, z = 2
Substituting the values in the expression, NA = \(\frac{z \times M}{a^{3} \times d}\), we get
NA = \(\frac{2 \times 55.845 \mathrm{~g} \mathrm{~mol}^{-1}}{\left(286.65 \times 10^{-10} \mathrm{~cm}\right)^{3} \times 7.874 \mathrm{~g} \mathrm{~cm}^{-3}}\)
NA = 6.022 × 1023 mol-1
Question 3.
An element crystallises in a fee lattice with cell edge of 400 pm. The density of the element is 7 g cm-3. How many atoms are present in 280 g of the element?
Solution:
Given, a = 400 pm = 400 × 10-10 cm = 4 x× 10-8 cm
Volume of the unit cell = a3
= (4 × 10-8 cm)3 = 6.4 × 10-23cm3

Since each fee unit cell contains 4 atoms, therefore, the total number of atoms in 280 g = 4 × 6.25 × 1023 = 2.5 × 1024 atoms
![]()
Question 4.
An element crystallises in a fee lattice with cell edge of 400 pm. Calculate the density if 200 g of this element contain 2.5 × 1024 atoms.

Molar mass M = 48.18 g mol-1
Here, z = 4, M = 48.18 g mol-1, NA = 6.022 × 1023 mol-1
a = 400 pm = 400 × 10-10 cm = 4 × 10-8 cm
Substituting these values in the expression,
d = \(\frac{z \times M}{a^{3} \times N_{A}}\) , we get
d = \(\frac{4 \times 48.18 \mathrm{~g} \mathrm{~mol}^{-1}}{\left(4 \times 10^{-8} \mathrm{~cm}\right)^{3} \times\left(6.022 \times 10^{23} \mathrm{~mol}^{-1}\right)}\) = 5 g cm-3
Question 5.
Explain why does conductivity of germanium crystals increase on doping with galium?
Answer:
On doping germanium with galium some of the positions of lattice of germanium are occupied be galium. Galium atom has only three valence electrons. Therefore, fourth valency of nearly germanium atom is not satisfied. The place remains vacant. This place is deficient of electrons and is therefore called electron hole or electron vacancy. Electron from neighbouring atom comes and fills the hole, thereby creating a hole in its original position. Under the influence of electric field electrons move towards positively charged plates through these and conduct electricity. The holes appear to move towards negatively charged plates.
Long answer type questions
Question 1.
A sample of ferrous oxide has actual formula Fe0.93O1.00In this
sample what fraction of metal ions are Fe2+ ions? What type of non-stoichiometric defect is present in this sample? (NCERT Exemplar)
Solution:
Let the formula of the sample be (Fe2+ )x (Fe3+ )y O
On looking at the given formula of the compound
x + y = 0.93 ………….. (i)
Total positive charge on ferrous and ferric ions should balance the two units of negative charge on oxygen.
Therefore, 2x + 3y = 2 ……….. (ii)
x + \(\frac{3}{2}\)y = 1 ……………..(iii)
On subtracting equation (i) from equation (iii) we have
\(\frac{3}{2}\) y – y = 1 – 0.93 ⇒ \(\frac{1}{2}\)y = 0.07 ⇒ y = 0.14
On putting the value of y in equation (i), we get
x + 0.14 = 0.93
⇒ x = 0.93 – 0.14 ⇒ x = 0.79
Fraction of Fe2+ ions present in the sample = \(\frac{0.79}{0.93}\) = 0.849
Metal deficiency defect is present in the sample because iron is less in amount than that required for stoichiometric composition.
![]()
Question 2.
(i) Following is the schematic alignment of magnetic moments:

Identify the type of magnetism. What happens when these substances are heated?
(ii) If the radius of the octahedral void is ‘r’ and radius of the atoms in close packing is ‘R’ What is the relation between ‘r’ and ‘R’?
(iii) Tungsten crystallises in body centred cubic unit cell. If the edge of the unit cell is 316.5 pm. What is the radius of tungsten atom?
Answer:
(i) The given schematic alignment of magnetic moments shows ferrimagnetism. When these substances are heated they lose ferrimagnetism and become paramagnetic.
(ii) The radius of the octahedral void = r
The radius of the atoms in close packing = R
Relation between r and R is given as :
r = 0.414 R
(iii) Given, a = 316.5 pm
Vs
We know that for body centred cubic unit cell r = \(\frac{\sqrt{3}}{4}\) a
∴ r = \(\frac{\sqrt{3}}{4}\) × 316.5 pm = 136.88 pm
![]()
Question 3.
(i) Identify the type of defect shown in the following figure:

What type of substances show this defect?
(ii) A metal crystallises in a body centred cubic structure. If ‘a’ is the edge length of its unit cell, ‘r’ is the radius of the sphere. What is the relationship between ‘r’ and ‘a’?
(iii) An element with molar mass 63 g/ mol forms a cubic unit cell with edge length of 360.8 pm. If its density is 8.92 g/cm 3. What is the nature of the cubic unit cell?
Answer:
(i) The given figure shows Schottky defect. This defect arises when equal number of cations and anions are missing from the lattice. It is a common defect in ionic compounds of high coordination number.
Where born cations and anion are of the same size, e.g., KCl, NaCl, KBr etc.
(ii) Edge length of the unit cell = a
Radius of the sphere = r
For body centred cubic structure ,
r = \(\frac{\sqrt{3}}{4}\)
(iii) We know that,
Density d = \(\frac{z \times M}{a^{3} \times N_{A}}\) or z = \(\frac{d \times a^{3} \times N_{A}}{M}\)
Given,
M = 63 g-mol-1 6.3 × 10-2 kg mol-1
a = 360.8 pm = 360.8 × 10-12 m = 3.608 × 10-10m
d = 8.92 g/cm2 = 0.892 kgm-3
NA = 6.022 × 1023 mol-1
On putting the given values in formula,
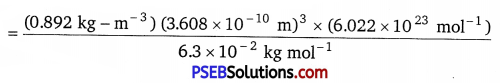
= 3.97 ≅ 4.
Since, 4 atoms of the element present per unit cell. Hence, the cubic unit cell must be face-centered.