Punjab State Board PSEB 11th Class Physics Important Questions Chapter 12 Thermodynamics Important Questions and Answers.
PSEB 11th Class Physics Important Questions Chapter 12 Thermodynamics
Very Short Answer Type Questions
Question 1.
Can a system be heated and its temperature remain constant? (NCERT Exemplar)
Answer:
If the system does work against the surroundings so that it compensates for the heat supplied, the temperature can remain constant.
Question 2.
Air pressure in a car tyre increases during driving. Explain. (NCERT Exemplar)
Answer:
- During driving, temperature of the gas increases while its volume remains constant.
- So, according to Charles’ law, at constant V, p ∝ T.
- Therefore, pressure of gas increases.
Question 3.
Write conditions for an isothermal process.
Answer:
The conditions for an isothermal process are :
- The walls should be diathermic.
- The process should be quasi-static.
Question 4.
Why air quickly leaking out of a balloon becomes cooler?
Answer:
Leaking of air is adiabatic expansion and adiabatic expansion produces cooling.
![]()
Question 5.
If a refrigerator’s door is kept open, will the room become cool or hot? Explain.
Answer:
Here, heat removed is less than the heat supplied and hence the room become hotter.
Question 6.
Is reversible process is possible in nature?
Answer:
A reversible process is never possible in nature because of dissipative forces and condition for a quasi-static process is not practically possible.
Question 7.
On what factors, the efficiency of a Carnot engine depends?
Answer:
On the temperature of source of heat and the sink.
Question 8.
Which thermodynamic law put restrictions on the complete conversion of heat into work?
Answer:
According to second law of thermodynamics, heat energy cannot converted into work completely.
Short Answer Type Questions
Question 1.
What are the limitations of the first law of thermodynamics?
Answer:
Following are the limitations of the first law of thermodynamics :
- It does not tell us about the direction of flow of heat.
- It fails to explain why heat cannot be spontaneously converted into work.
Question 2.
Two bodies at different temperatures T1 and T2 are brought in contact.
Under what condition, they settle to mean temperature? (after they attain equilibrium)
Answer:
Let m1 and m2 are masses of bodies with specific heats s1 and s2, then if their temperature after they are in thermal equilibrium is T.
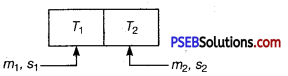
Then, if > T1> T2 and assuming no heat loss.
Heat lost by hot body = heat gained by cold body
m1s1(T1-T)=m2s2(T-T2)
⇒ \(\frac{m_{1} s_{1} T_{1}+m_{2} s_{2} T_{2}}{m_{1} s_{1}+m_{2} s_{2}}\) = T[equilibrium temperature]
So for, bodies to settle down to mean temperature,
m1 = m2 and s1 = s2
means bodies have same specific heat and have equal masses.
Then, T = \(\frac{T_{1}+T_{2}}{2}\) [mean temperature]
![]()
Question 3.
When ice melts, then change in internal energy, is greater than the heat supplied, why?
Solution:
When ice melts, volume of water formed is less than that of ice. So, surroundings (environment) does work on the system (ice). And by first law,
ΔQ = ΔW+ΔU
⇒ ΔU = ΔQ-ΔW
(ΔW = negative as work is done on the system)
⇒ ΔU>ΔQ
Question 4.
Calculate the work done for adiabatic expansion of a gas.
Solution:
Consider (say µ mole) an ideal gas, which is undergoing an adiabatic expansion.
Let the gas expands by an infinitesimally small volume dV, at pressure p, then the infinitesimally small work done given by
dW = pdV
The net work done from an initial volume V1 to final volume V2 is given by
W= ∫v1v2 pdV
For an adiabatic process, pVγ = constant = K

For an adiabatic process, K = p1Vγ = p2Vγ
For an ideal gas, p1V1 = μRT1 and p2V2 = μRT2.
So, we have
W = \(\frac{1}{(1-\gamma)}\left[\mu R T_{2}-\mu R T_{1}\right]=\frac{\mu R}{(\gamma-1)}\left[T_{1}-T_{2}\right]\)
Question 5.
What is a heat engine? What is the best way to increase efficiency of a heat engine? Is it possible to design a thermal engine that has 100% efficiency?
Solution:
A heat engine is a device (or a combination) which converts heat into work.
Its efficiency, η = \(\frac{\text { Work output }}{\text { Heat input }}=1-\frac{T_{2}}{T_{1}}\)
where, T2 = temperature of sink
T1 = temperature of source.
From above expression, we can see that for 100% efficiency, T2 =0
It is impossible to design a thermal engine that has 100% efficiency because it is not possible to have a sink with kelvin temperature.
![]()
Question 6.
An ideal engine works between temperatures T1 and T2. It derives an ideal refrigerator that works between temperatures T3 and T4. Find the ratio Q3/Q1 in terms of T1, T2, T3, and T4.
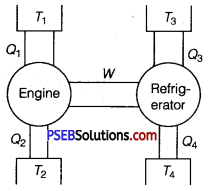
Solution:
W = work done by engine = Q1 – Q2
and W = work done supplied to refrigerator = Q3 -Q4
Q1 – Q2 =Q3 – Q4
Dividing by Q1, on both sides of the above equation, we get

Question 7.
Under what condition, an ideal Carnot engine has 100% efficiency?
Solution:
Efficiency of a Carnot engine is given by η = \(\left(1-\frac{T_{2}}{T_{1}}\right)\)
where, T2 = temperature of sink
and T1 = temperature of sink source
So for η = 1 or 100%, T2 = 0 K or heat is rejected into a sink at 0 K temperature.
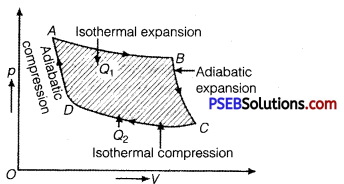
Question 8.
Draw p-V diagram of a Carnot cycle.
Solution:
p-V diagram for Carnot cycle
Long Answer Type Questions
Question 1.
A cycle followed by a machine (made of one mole of a perfect gas in a cylinder with a piston) is shown in figure
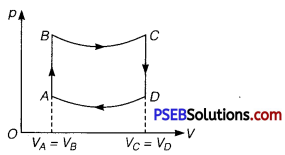
A to B: volume constant B to C: adiabatic
C to D: volume constant D to A : adiabatic
VC = VD = 2 VA = 2 VB
(i) In which part of the cycle, heat is supplied to the machine from outside?
(ii) In which part of the cycle, heat is being given to the surrounding by the machine?
(iii) What is the work done by the machine in one cycle? Write your answer in terms of PA’ PB’ VA.
(iv) What is the efficiency of the machine?
Take γ = \(\frac{5}{3}\) for the gas and CV =R for one mole.
Solution:
(i) A to B because TB > TA, as p ∝ T [ ∴ V = constant]
(ii) C to D because TC>TD, as P ∝ T [∴ V=constant]
(iii) WAB = \(\int_{B}^{C} \) pdV=O and WCD =0 [∴ V= constant]
Similarly,
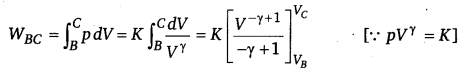
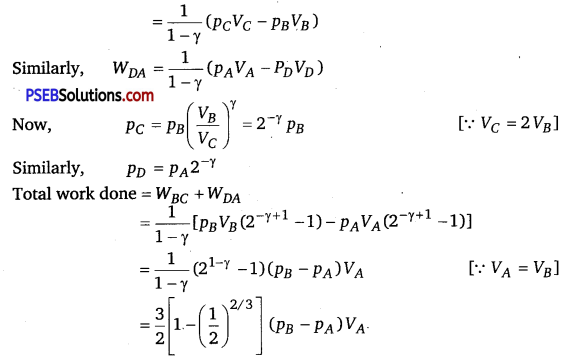
(iv) Heat supplied during process A to B
dQAB = dUAB
QAB = \(\frac{3}{2} n R\left(T_{B}-T_{A}\right)=\frac{3}{2}\left(p_{B}-p_{A}\right) V_{A}\)
∴ Efficiency = \(=\frac{\text { Net work done }}{\text { Heat supplied }}=\left[1-\left(\frac{1}{2}\right)^{2 / 3}\right]\)
![]()
Question 2.
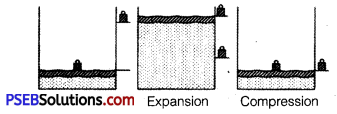
Explain with the suitable example that a reversible process must be carried slowly and a fast process is necessarily irreversible.
Answer:
A reversible process must pass through equilibrium states which are very close to each other so that when process is reversed, it passes back through these equilibrium states. Then, it is again decompressed or it passes through same equilibrium states, system can be restored to its initial state without any change in surroundings. e.g., If a gas is compressed as shown But a reversible process can proceed without reaching equilibrium in intermediate states.