PSEB 11th Class Economics Solutions Chapter 20 रेखाचित्रों द्वारा प्रस्तुतीकरण

Punjab State Board PSEB 11th Class Economics Book Solutions Chapter 20 रेखाचित्रों द्वारा प्रस्तुतीकरण Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 11 Economics Chapter 20 रेखाचित्रों द्वारा प्रस्तुतीकरण

PSEB 11th Class Economics रेखाचित्रों द्वारा प्रस्तुतीकरण Textbook Questions and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
रेखाचित्रीय प्रदर्शन के लाभ लिखें।
उत्तर-
रेखाचित्रीय प्रदर्शन आंकड़ों को प्रस्तुत करने का आकर्षक, सरल व प्रभावशाली साधन है।

प्रश्न 2.
आवृत्ति आयत चित्र किसे कहते हैं ?
उत्तर-
आवृत्ति आयत चित्र वह रेखाचित्र है जिसमें अखण्डित श्रृंखला से सम्बन्धित मदों तथा उनकी आवृत्तियों को आयतों के रूप में ग्राफ पेपर पर प्रदर्शित किया जाता है।

प्रश्न 3.
संचयी आवृत्ति वक्र अथवा ओजाइव किसे कहते हैं ?
उत्तर-
संचयी आवृत्ति वक्र संचयी आवृत्ति वितरण को ग्राफ के रूप में प्रस्तुत करने वाला वक्र है। संचयी वक्र को ओजाइव (Ogive) भी कहते हैं।

प्रश्न 4.
आवृत्ति बहुभुज किसे कहते हैं ?
उत्तर-
आवृत्ति बहुभुज वह रेखाचित्र है जो आवृत्ति आयत चित्र (Histogram) के प्रत्येक आयत के शीर्ष के मध्य बिन्दुओं को सरल रेखाओं द्वारा मिलाकर बनाया जाता है।

प्रश्न 5.
कृत्रिम आधार रेखा किसे कहते हैं?
उत्तर-
शून्य रेखा अथवा मूल बिन्दु से कुछ ऊपर बनाई जाने वाली टेढ़ी-मेढ़ी रेखा जिस से धनात्मक प्रमाप आरम्भ की जाती है।

प्रश्न 6.
संचयी आवृत्ति वक्र को ओजाइव भी कहा जाता है।
उत्तर-
सही।

प्रश्न 7.
जब अखण्डित श्रृंखला को उनकी मदों के अनुसार आवृत्ति का प्रगटावा एक ग्राफ पेपर पर किया जाता है तो इसको …………………. कहते हैं।
(a) आवृत्ति वितरण
(b) आवृत्ति वक्र
(c) आवृत्ति आयत
(d) आवृत्ति बहुभुज।
उत्तर-
(c) आवृत्ति आयत।

प्रश्न 8.
आवृत्ति आयत (Histogram) की सभी आयतों के मध्य बिन्दुओं को सरल रेखा द्वारा मिला दिया जाता है तो इसको ……………….. कहते हैं।
उत्तर-
आवृत्ति बहुभुज (Polygon)।

प्रश्न 9.
आवृत्ति आयत का क्षेत्रफल = ……………………….. का क्षेत्रफल
उत्तर-
आवृत्ति वक्र।

प्रश्न 10.
संचयी आवृत्ति वक्र अथवा ओजाइव दो प्रकार की होती है
(i) ऊपरी सीमा से कम
(ii) ……….
उत्तर-
निचली सीमा से अधिक।

प्रश्न 11.
चित्रमयी और बिन्दु रेखीय प्रस्तुतीकरण में कोई एक अन्तर बताएँ।
उत्तर-
बिन्दु रेखीय चित्र को ग्राफ पर बनाते हैं और चित्रमयी को साधारण कागज़ पर बनाते हैं।

प्रश्न 12.
समय श्रेणी चित्र ………. के आधार पर बनाए जाते हैं।
उत्तर-
समय।

प्रश्न 13.
आवृत्ति आयत का क्षेत्रफल = …………….. का क्षेत्रफल।
उत्तर-
आवृत्ति वक्र।

प्रश्न 14.
संचयी आवृत्ति वक्र अथवा ओजाइव दो प्रकार की होती हैं।
(i) ऊपरी सीमा से कम
(ii) …………….
उत्तर-
निचली सीमा से अधिक।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
ग्राफ द्वारा प्रदर्शन का क्या अर्थ है ?
उत्तर-
आंकड़ों को प्रस्तुत करने की एक महत्त्वपूर्ण विधि ग्राफ विधि अथवा बिन्दु रेखीय विधि होती है। इस विधि में आंकड़ों को ग्राफ पेपर (Graph Paper) पर प्रस्तुत किया जाता है। जब हम ग्राफ पेपर आंकड़ों को स्पष्ट करते हैं तो कम समय या कम परिश्रम से एक मनुष्य आंकड़ों को समझने योग्य हो जाता है। इसलिए क्राक्सटन तथा काउडन ने ठीक कहा है, “ग्राफ विधियां सीमित सूचना को जल्दी तथा प्रभावशाली ढंग से प्रस्तुत करने की लाभदायक विधियां हैं।”

प्रश्न 2.
ग्राफ द्वारा प्रदर्शन के कोई दो गुण बताएं।
उत्तर-

1. आंकड़ों को सरल बनाना (To make data simple) आंकड़े मूल रूप में जटिल होते हैं, जिनको स्पष्ट करना तथा समझना कठिन होता है। इसलिए ग्राफ द्वारा आंकड़ों को आसानी से समझा जा सकता है।
2. तुलना के लिए आसान (To make easy comparison)-जब आंकड़ों को ग्राफ की विधि द्वारा दिखाया जाता है तो इनमें तुलना करनी बहुत आसान हो जाती है जैसे कि पंजाब स्कूल शिक्षा बोर्ड के 10 + 2 कक्षा के विद्यार्थियों द्वारा प्राप्त किए प्रतिशत अंकों की तुलना पिछले वर्ष के प्रतिशत अंकों से करते समय ग्राफ विधि लाभदायक होती है। इसी तरह एक मरीज़ के बुखार की स्थिति का अनुमान ग्राफ को देखकर डॉक्टर आसानी से लगा लेता है।

प्रश्न 3.
ग्राफ द्वारा प्रदर्शन की कोई दो सीमाएं बताएं।
उत्तर-

1. निश्चितता की कमी (Lack of Accuracy)-ग्राफ विधि द्वारा आंकड़ों की प्रवृत्ति का पता चलता है। परन्तु इन आंकड़ों में निश्चितता की कमी होती है। ग्राफ द्वारा प्रदान की गई सूची युद्ध परिणाम प्रदान नहीं करती।
2. गलत परिणाम (Wrong Results) -ग्राफ विधि द्वारा कई बार गलत परिणाम भी निकाले जा सकते हैं। क्योंकि रेखाचित्र द्वारा रेखाओं के उतार-चढ़ाव को देखकर 100% शुद्ध परिणाम प्राप्त नहीं किए जा सकते।

प्रश्न 4.
आवृत्ति आयत से क्या अभिप्राय है ?
उत्तर-
आवृत्ति आयत (Histogram)-आवृत्ति आयत चित्र वह चित्र है, जिनमें अखण्डित आवृत्ति वितरण (Continuous Frequency Distribution) को उनकी मदों के अनुसार आवृत्तियों का प्रकटावा एक ग्राफ पेपर पर किया जाता है। इस चित्र में OX पर मदों के वर्गांतर (Class Intervals) तथा OX पर वर्गांतर की आवृत्ति (Frequency) को प्रकट करते हैं। इस प्रकार आयतों के रूप में जो चित्र बन जाता है, उसको आयत आवृत्ति (Histogram) चित्र कहा जाता है।

प्रश्न 5.
आवृत्ति बहुभुज का अर्थ बताएं।
उत्तर-
आवृत्ति बहुभुज (Frequency Polygon) आवृत्ति बहुभज वह चित्र होता है जोकि आवृत्ति आयत (Histrogram) की सभी आयतों के ऊपरी भागों के मध्य बिन्दुओं को सीधी रेखा द्वारा मिलाकर बनाया जाता है। इसमें आवृत्ति बहुभुज के दोनों किनारों को आधार रेखाओं तक दोनों ओर बढ़ा दिया जाता है। इससे आवृत्ति बहुभुज का निर्माण हो जाता है। आवृत्ति बहुभुज तथा आवृत्ति आयतों का क्षेत्रफल एक-दूसरे के समान होता है।

III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 1.
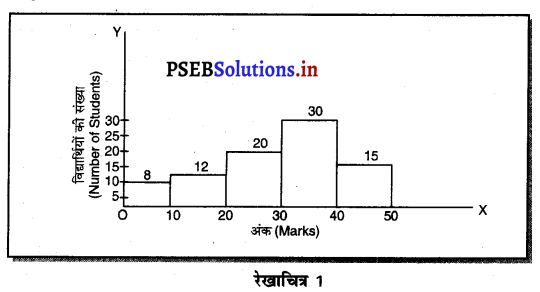
निम्नलिखित तालिका में विद्यार्थियों द्वारा प्राप्त किए अंकों का विवरण दिया गया है। आवृत्ति आयत चित्र द्वारा प्रदर्शित करो।

अंक :	0-10	10-20	20-30	30-40	40-50
विद्यार्थियों की संख्या :	8	12	20	30	15

उत्तर-
आवृत्ति आयत (Histogram)

प्रश्न 2.
आवृत्ति बहुभुज से क्या अभिप्राय है ? निम्नलिखित आंकड़ों की सहायता से आवृत्ति बहुभुज का निर्माण करो।

अंक :	0-5	5-10	10-15	15-20	20-25	25-30
विद्यार्थी :	10	18	30	50	40	20

उत्तर-
आवृत्ति बहुभुज का अर्थ (Meaning of Frequency Polygon)-आवृत्ति बहुभुज का निर्माण करने से पहले हम आवृत्ति आयत (Histogram) का निर्माण करते हैं। आवृत्ति आयत के ऊपर के किनारों के मध्य बिन्दु को लेकर उनको आपस में मिला दिया जाए तो आधार रेखा तक बढ़ा दिया जाए तो इस प्रकार हमारे पास आवृत्ति बहुभुज का निर्माण हो जाता है।
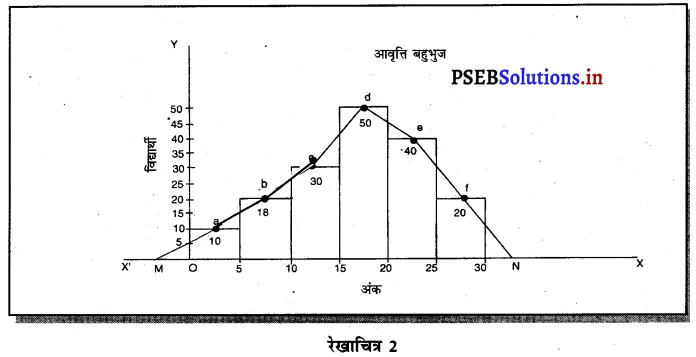नोट-प्रश्न अनुसार दिए आंकड़ों की सहायता से आवृत्ति आयत का निर्माण करने के पश्चात् आवृत्ति आयतों के ऊपर के भागों का मध्य a, b, c, d, e, f किया जाता है। इनको आपस में मिलाकर आधार रेखा तक बढ़ाने से बिन्दु M, N प्राप्त हो जाते हैं। इस प्रकार M & N को आवृत्ति बहुभुज कहा जाता है। इसमें आवृत्ति आयतों का क्षेत्रफल आवृत्ति बहुभुज के क्षेत्रफल के समान होता है।

प्रश्न 3.
संचयी आवृत्ति वक्र से क्या अभिप्राय है ? संचयी आवृत्ति वक्र का निर्माण ऊँची सीमा पर कम विधि (Less than method) द्वारा स्पष्ट कीजिए।

अंक :	0-10	10-20	20-30	30-40	40-50
विद्यार्थी :	5	10	12	15	8

उत्तर-
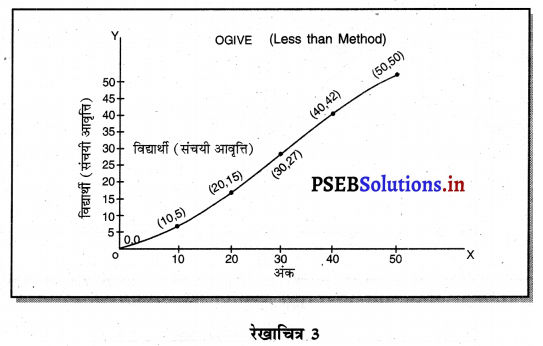
संचयी आवृत्ति वक्र अथवा ओजाइव का अर्थ ऐसे वक्र से होता है, जिसमें आवृत्ति का जोड़ करके ग्राफ पेपर पर दिखाने से जो वक्र बन जाता है, उसको ओजाइव कहते हैं। इसको संचयी आवृत्ति वक्र भी कहा जाता है। इसका. निर्माण दो तरह से किया जाता है। वर्ग अन्तर की ऊँची सीमा तथा कम विधि (Less than method) तथा वर्ग अन्तर की नीचे वाली सीमा से अधिक विधि (More than method) से ओजाइव बनाई जाती है।

ओजाइव वक्र ऊँची सीमा से कम विधि की ओर (Ogive with less than method)-जब हम ऊँची सीमा से कम विधि की आवृत्ति के जोड़ को प्रकट करते हैं तो इससे संचयी आवृत्ति का निर्माण किया जाता है।

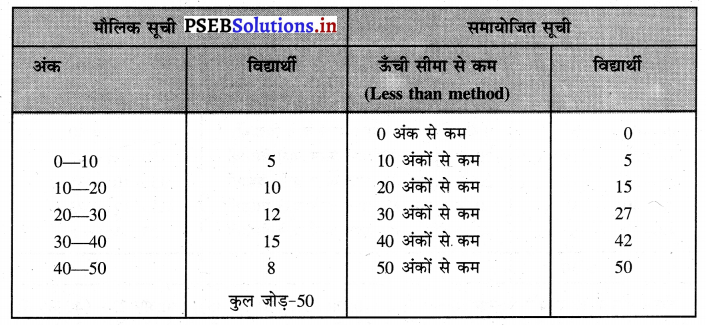
नोट-समायोजित सूची अनुसार (0 तथा 0), (10 तथा 5) (20 तथा 15), (30 तथा 27) (40 तथा 42), (50 तथा 50) को आपस में मिलाने से जो बिन्दु प्राप्त होते हैं, उनको जिस रेखा द्वारा दिखाया जाता है, उस रेखा को ओजाइव कहते हैं।

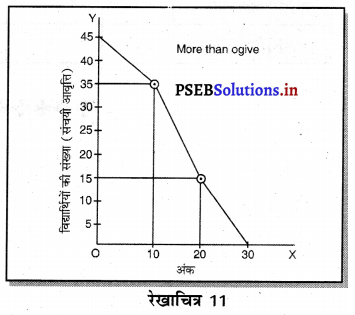
प्रश्न 4.
निम्नलिखित आंकड़ों द्वारा निम्न सीमा से अधिक विधि (More than Method) द्वारा संचित आवृत्ति वक्र का निर्माण करें।

अंक :	0-10	10-20	20-30	30-40	40-50
विद्यार्थियों की संख्या:	5	10	12	15	8

हल (Solution)-संचय आवृत्ति वक्र निम्न सीमा से अधिक विधि द्वारा (Ogive with More than Method)
इस विधि द्वारा समायोजित सूची का निर्माण अग्रलिखित अनुसार किया जाता है-

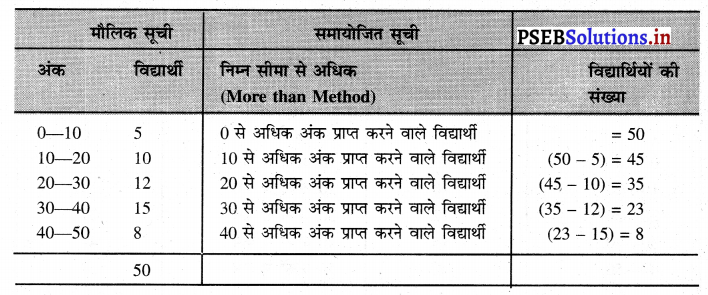
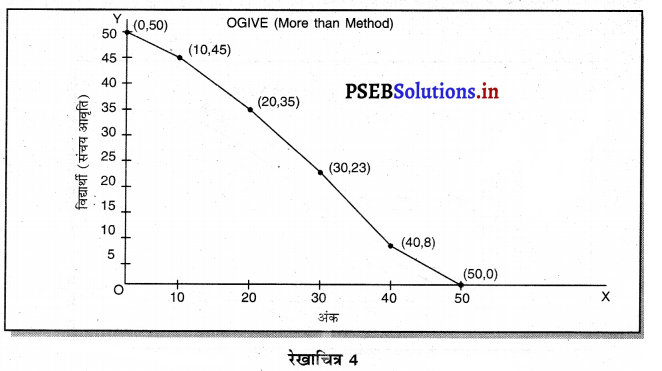
नोट-समायोजित सूची के अनुसार (0 और 50), (10 और 45), (20 और 35), (30 और 23), (40 और 8) अथवा 50 से अधिक अंक प्राप्त करने वाला कोई विद्यार्थी नहीं है, इसलिए (50 और 0) के मिलाने से जो बिंदु प्राप्त होते हैं। उनको मिला दिया जाए तो उस रेखा को निम्न सीमा से अधिक विधि द्वारा ओजाइव कहा जाता है।

IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
ग्राफ द्वारा प्रदर्शन के अर्थ बताओ। ग्राफ की रचना सम्बन्धी साधारण नियमों की व्याख्या करें।
(Explain the meaning of Graphic Presentation of Data. Explain the general rules for the construction of a Graph.)
उत्तर-
आंकड़ों को प्रस्तुत करने की एक महत्त्वपूर्ण विधि ग्राफ विधि अथवा बिन्दु रेखीय विधि होती है। इस विधि में आंकड़ों को ग्राफ पेपर (Graph Paper) पर प्रस्तुत किया जाता है। जब हम ग्राफ पेपर पर आंकड़ों को स्पष्ट करते हैं तो कम समय तथा कम परिश्रम से एक मनुष्य आंकड़ों को समझने योग्य हो जाता है। इसलिए क्राक्सटन तथा काउडन ने ठीक कहा है, “ग्राफ विधियां सीमित सूचना को जल्दी तथा प्रभावशाली ढंग से प्रस्तुत करने की लाभदायक विधियां हैं।” (“Graphic devices are extremely useful and effective for quickly presenting a limited amount of information.” —Croxton and Cowden)

ग्राफ प्रदर्शन के अर्थ (Meaning of Graphic Presentation)-ग्राफ प्रदर्शन आंकड़ों को प्रस्तुत करने की वह विधि होती है, जिसमें एक ग्राफ पेपर पर इनको रेखाओं तथा चित्रों के रूप में दिखाया जाता है। इस प्रकार आंकड़ों को ग्राफ पेपर पर प्रदर्शन करने के ढंग को आंकड़ों का ग्राफ द्वारा प्रदर्शन कहा जाता है।

ग्राफ निर्माण के नियम (Rules for constructing a Graph)-ग्राफ का निर्माण करते समय निम्नलिखित नियमों को ध्यान में रखना चाहिए –

1. शीर्षक (Title)-प्रत्येक ग्राफ का शीर्षक स्पष्ट होना चाहिए। शीर्षक को पढ़ने से ही इस बात का पता लगना अनिवार्य होता है कि ग्राफ किस सूचना की जानकारी देता है।
2. पैमाना (Scale)- चित्र बनाने से पहले पैमाने का चयन कर लेना चाहिए। पैमाने का चयन एकत्रित किए आंकड़ों पर निर्भर करता है। पैमाना इतना लेना चाहिए जो सभी आंकड़े सरलता से ग्राफ पर प्रस्तुत किए जा सकें।
3. बिन्दुओं का मिलान (Plotting the Points)- ग्राफ पेपर पर OX अक्ष तथा OY अक्ष पर लिए गए तत्त्वों के सम्बन्ध को स्पष्ट किया जाता है। साधारण तौर पर अर्थशास्त्रियों के आंकड़े धनात्मक होते हैं। इसलिए OX अक्ष को बाएं से दाएं हाथ की ओर तथा OY अक्ष के नीचे से ऊपर की ओर दिखाया जाता है। यदि हम तथ्यों के सम्बन्ध को OX तथा OY रेखाओं पर लम्ब खींचकर स्पष्ट करते हैं तो हमारे पास बिन्दु प्राप्त हो जाते हैं।
4. रेखाओं का प्रयोग (Use of lines) – ग्राफ में जब अधिक रेखाओं को प्रस्तुत किया जाता है तो इस स्थिति में सीधी रेखाएँ (straight lines), टूटी रेखाएँ (Dotted lines) अथवा बिन्दु रेखाएँ (Point Lines) का प्रयोग किया जाता है।
5. बनावटी आधार रेखा (False Base Line)-हम जानते हैं कि OX तथा OY रेखाओं का आरम्भ 0 अथवा

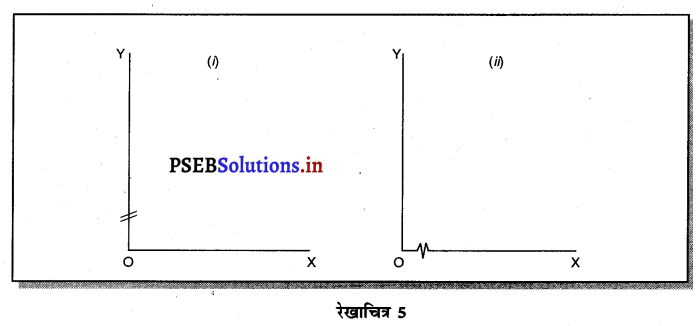
शून्य से होता है अर्थात् जहाँ OX तथा OY पर मदों की संख्या को दिखाने की आवश्यकता पड़ती है। ऐसी स्थिति में बनावटी आधार रेखा का निर्माण किया जाता है। इस उद्देश्य के लिए हम जिस ओर बनावटी आधार को दिखाना चाहते हैं, उस ओर रेखा पर कटाव पैदा कर देते हैं, क्योंकि वह सभी आंकड़े Ox अथवा OY पर दिखाने से रेखाचित्र का आकार बहुत विशाल हो जाता है, जिसको रेखा चित्र में स्पष्ट करना कठिन होता है। रेखाचित्र 5 (i), (ii) में OY रेखा पर बनावटी आधार रेखा लेने के अलग-अलग ढंग बताए गए हैं। भाग-1 अनुसार दो तिरछी रेखाएं (I/) बनाई जा सकती हैं। भाग-2 अनुसार बनावटी रेखाएं लहरों की तरह बढ़ती घटती हो सकती हैं।

प्रश्न 2.
ग्राफ अथवा रेखाचित्र द्वारा प्रदर्शन के लाभ बताओ। ग्राफ प्रदर्शन की सीमाएँ भी लिखो । (Explain the advantages of Graphic Presentation. Discuss its limitations.)
उत्तर-
ग्राफ द्वारा आंकड़ों को प्रदर्शन करने के बहुत लाभ होते हैं। जैसे कि प्रो० वैसेलो ने ठीक कहा है, “आंकड़ों को समझने का सबसे सरल ढंग उन बिन्दु रेखाओं द्वारा अध्ययन करना होता है।” (“The simplest and commonest aid to the numerical reading is the graph.’ – Vesselo)

ग्राफ विधि द्वारा आंकड़ों को प्रदर्शन करने के मुख्य उद्देश्य तथा लाभ इस प्रकार हैं-
1. आंकड़ों को सरल बनाना (To make data simple)-आंकड़े मूल रूप में जटिल होते हैं, जिनको स्पष्ट करना तथा समझना कठिन होता है। इसलिए ग्राफ द्वारा आंकड़ों को आसानी से समझा जा सकता है।

2. तुलना के लिए आसान (To Make easy comparison)-जब आंकड़ों को ग्राफ की विधि द्वारा दिखाया जाता है तो इनमें तुलना करनी बहुत आसान हो जाती है जैसे कि पंजाब स्कूल शिक्षा बोर्ड के 10 + 2 कक्षा के विद्यार्थियों द्वारा प्राप्त किए प्रतिशत अंकों की तुलना पिछले वर्ष के प्रतिशत अंकों से करते समय ग्राफ विधि लाभदायक होती है। इसी तरह एक मरीज़ के बुखार की स्थिति का अनुमान ग्राफ को देखकर डॉक्टर आसानी से लगा लेता है।

3. आंकड़ों को रोचक बनाना (To make data interesting) आंकड़ों को आकर्षक बनाने के लिए ग्राफ अथवा रेखाचित्र द्वारा प्रदर्शन लाभदायक होता है। कीमत स्तर में परिवर्तनों को देखने के लिए ग्राफ विधि बहुत लाभदायक परिणाम प्रदान करती है।

4. समय श्रेणियों का प्रदर्शन (Presentation of time series)-ग्राफ समय श्रेणियों को प्रदर्शन करने के लिए अच्छी विधि मानी जाती है। इस द्वारा रेखा चित्रों द्वारा आंकड़ों को लाभदायक तथा प्रभावशाली ढंग द्वारा प्रदर्शन किया जा सकता है, जिससे लाभदायक परिणाम प्राप्त किए जाते हैं।

5. सांख्यिकी विधियों का अध्ययन (Study of Statistical methods)-आंकड़ा शास्त्र की बहुत-सी विधियों की व्याख्या ग्राफ विधि द्वारा की जा सकती है, जैसे कि मध्यका, बहुलक, सह-सम्बन्ध इत्यादि को रेखा चित्रों द्वारा प्रस्तुत किया जा सकता है।

ग्राफ विधियों की सीमाएं (Limitations of Graphic method)—ग्राफ द्वारा आंकड़ों का प्रदर्शन करने की मुख्य सीमाएं इस प्रकार हैं –

1. निश्चितता की कमी (Lack of Accuracy)-ग्राफ विधि द्वारा आंकड़ों की प्रवृत्ति का पता चलता है। परन्तु इन आंकड़ों में निश्चितता की कमी होती है। ग्राफ द्वारा प्रदान की सूची युद्ध परिणाम प्रदान नहीं करती।
2. गलत परिणाम (Wrong Results)-ग्राफ विधि द्वारा कई बार गलत परिणाम भी निकाले जा सकते हैं। क्योंकि रेखाचित्र द्वारा रेखाओं के उतार-चढ़ाव को देखकर 100% शुद्ध परिणाम प्राप्त नहीं किए जा सकते।
3. केवल तुलनात्मक अध्ययन (Only Comparative Study)-ग्राफ विधि द्वारा केवल तुलनात्मक अध्ययन करना ही सम्भव होता है। जब हम आंकड़ों द्वारा मनोवैज्ञानिक अथवा सामाजिक परिणाम प्राप्त करना चाहते हैं तो ऐसा करना सम्भव नहीं होता।।
4. बहमुखी सूचना का मुश्किल प्रदर्शन (Difficult Presentation of Multiple Information)-ग्राफ की विधि द्वारा जब किसी तत्त्व की बहुमुखी विशेषताओं को दिखाना हो तो ऐसा करना भी मुश्किल होता है। सारणीकरण की सहायता से हम कई प्रकार की सूचनाएँ एकत्रित तौर पर प्रदर्शित कर सकते हैं।

प्रश्न 3.
आवृत्ति वितरण ग्राफ से क्या अभिप्राय है ? आवृत्ति वितरण ग्राफ की प्रदर्शन विधियां बताएँ।
(What is Frequency Distribution Graph? Explain the methods of presentation of Frequency Distribution Graphs.)
उत्तर-
ग्राफ मुख्य तौर पर दो प्रकार के होते हैंसमय श्रेणी ग्राफ (Time Series Graphs) तथा आवृत्ति वितरण ग्राफ (Frequency Distribution Graphs) आवृत्ति वितरण ग्राफ का अर्थ (Meaning of Frequency Distribution Graph) आवृत्ति विवरण ग्राफ वह चित्र होते हैं, जिनमें चरों की आवृत्ति वितरण अनुसार उनको प्रस्तुत किया जाता है। इसमें आंकड़ों का प्रदर्शन समय अनुसार नहीं किया जाता, बल्कि मदों के मूल्यों की आवृत्ति के अनुसार ग्राफ बनाने की विधि को आवृत्ति वितरण ग्राफ कहा जाता है।

आवृत्ति वितरण प्रदर्शन की विधियां-आवृत्ति वितरण प्रदर्शन की मुख्य विधियां निम्नलिखित अनुसार हैं –

1. रेखा आवृत्ति चित्र (Line Frequency Diagram)
2. आवृत्ति आयत (Frequency Histogram)
3. आवृत्ति बहुभुज (Frequency Polygon)
4. आवृत्ति वक्र (Frequency Curve)
5. संचयी आवृत्ति वक्र अथवा

ओजाइव (Cumulative Frequency curve or ogive)-
1. रेखा आवृत्ति चित्र (Line Frequency Diagram) रेखा आवृत्ति चित्र खण्डित आवृत्ति वितरण (Discrete Frequency Distribution) को प्रकट करने के लिए प्रयोग किया जाता है। इस चित्र में OX वक्र पर मदों (Items) तथा OY वक्र पर आवृत्ति (Frequency) को अंकित किया जाता है। उदाहरण-एक फैक्टरी में पैनों का उत्पादन किया जाता है। मई में तीन लाख, जून में 5 लाख, जुलाई में 4 लाख पैनों का उत्पादन किया गया। इसको रेखा आवृत्ति रेखा आवृत्ति चित्र चित्र कहा जाता है।

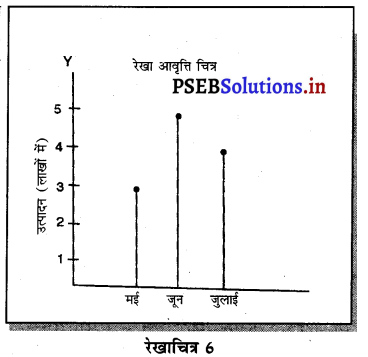
2. आवृत्ति आयत (Histogram)-आवृत्ति आयत चित्र वह चित्र है, जिनमें अखण्डित आवृत्ति वितरण (Continuous Frequency Distribution) को उनकी मदों के अनुसार आवृत्तियों का प्रकटावा एक ग्राफ पेपर पर किया जाता है। इस चित्र में OX पर मदों के वर्गांतर (Class Intervals) तथा OX पर वर्गांतर की आवृत्ति (Frequency) को प्रकट करते हैं। इस प्रकार आयतों के रूप में जो चित्र बन जाता है, उसको आयत आवृत्ति (Histogram) चित्र कहा जाता है।
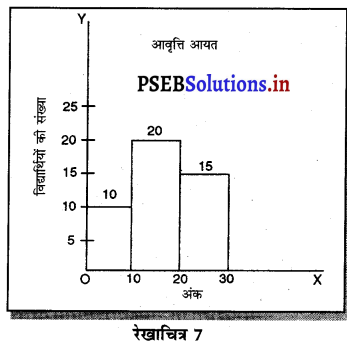अंक 0-10 10-20 20-30 . 30-40 विद्यार्थी 10 20
15
उदाहरण-एक कक्षा में 0-10 अंक प्राप्त करने वाले विद्यार्थियों की संख्या 10 है। 10-20 अंक प्राप्त करने वाले आवृत्ति बहुभुज 20 विद्यार्थी हैं तथा 20-30 तक अंक प्राप्त करने वाले 15 20B विद्यार्थी हैं, 30-40 तक अंक प्राप्त करने वाले 8 विद्यार्थी हैं। इस प्रकार के ग्राफ को आवृत्ति आयत (Histogram) कहा जाता है।

3. आवृत्ति बहुभुज (Frequency Polygron)-आवृत्ति बहुभुज वह चित्र होता है जोकि आवृत्ति आयत (Histogram) की सभी आयतों के ऊपरी भागों के मध्य बिन्दुओं को सीधी रेखा द्वारा मिलाकर बनाया जाता है। इसमें आवृत्ति बहुभुज के दोनों किनारों को आधार रेखाओं तक दोनों ओर बढ़ा दिया जाता है। इससे आवृत्ति बहुभुज का निर्माण हो जाता है। आवृत्ति रेखाचित्र 8 बहुभुज तथा आवृत्ति आयतों का क्षेत्रफल एक-दूसरे के समान होता है।

उदाहरण-ऊपर दी गई विधि अनुसार पहले आवृत्ति आयत बनाई जाती है। ऊपरी किनारों के मध्यों को आपस में मिलाकर ABC चित्र का निर्माण होता है, जिसको आवृत्ति बहुभुज कहा जाता है। इसमें धनात्मक किनारों (++) का क्षेत्र जोड़ा जाता है तथा ऋणात्मक किनारा (–) का क्षेत्र कम किया जाता है। इस प्रकार आवृत्ति आयत तथा आवृत्ति बहुभुज का क्षेत्रफल एक-दूसरे के समान हो जाता है।

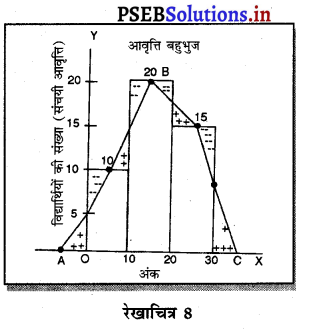
4. आवृत्ति वक्र (Frequency Curve)-आवृत्ति वक्र वह चित्र है जो कि आवृत्ति बहुभुज की तरह सीधी रेखाएं नहीं, बल्कि स्वतन्त्र हाथ से वक्र बनाने की विधि होती है। आवृत्ति वक्र अर्थात् आवृत्ति आयत का निर्माण करने के पश्चात् ऊपर के किनारों के मध्यों को स्वतन्त्र हाथ मिलाकर आधार रेखा से मिला दिया जाए तो आवृत्ति वक्र का निर्माण हो जाता है। उदाहरण-रेखाचित्र में ABC आवृत्ति बहुभुज है, जिसको डॉटड रेखा में दिखाया है। यदि स्वतन्त्र हाथ से एक रेखा DBE खींच देते हैं तो इस रेखा को आवृत्ति वक्र कहते है।

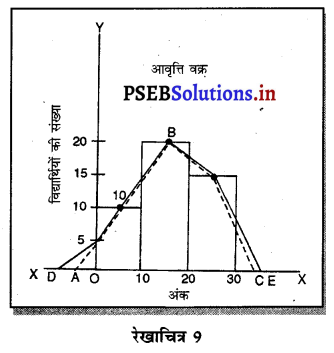
5. संचयी आवृत्ति वक्र अथवा ओजाइव (Cummulative Frequency curve or ogive)—जब आवृत्ति को संचयी अथवा जोड़ कर लिया जाए तो उस जोड़ की हुई आवृत्ति का चित्र बनाया जाए तो इसको संचयी आवृत्ति वक्र अथवा ओजाइव (Ogive) कहा जाता है।
(i) उदाहरण-ऊँची सीमा से कम (Less than Method)

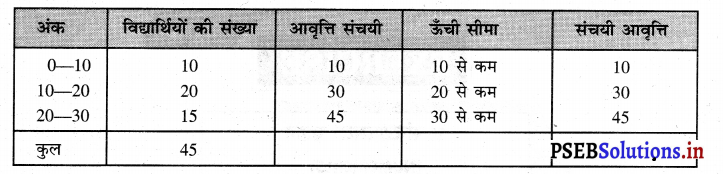
रेखाचित्र में सूची पत्र अनुसार 10 अंक से कम अंक प्राप्त करने वाले विद्यार्थी 10 हैं। 20 अंक से कम अंक प्राप्त करने वाले 10 + 20 = 30 विद्यार्थी हैं। 30 अंक से कम अंक प्राप्त करने वाले 10 + 20 + 15 = 45 विद्यार्थी हैं। इसलिए (10 तथा 10), (20 तथा 30), (30 तथा 45) को मिलाकर हमारे पास ऊँची सीमा से कम ओजाइव (Ogive) वक्र बन जाती है।

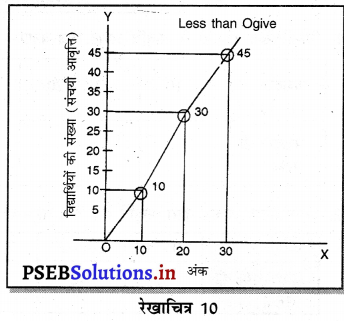
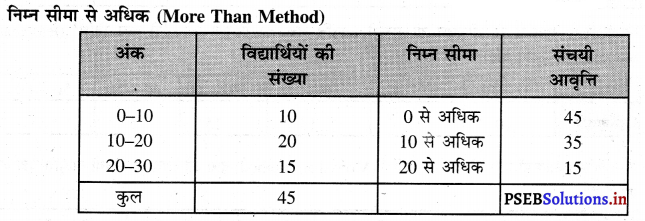
सूची पत्र तथा रेखाचित्र अनुसार 0 से अधिक अंक प्राप्त करने वाले विद्यार्थियों की संख्या 45 है। 10 से अधिक अंक प्राप्त करने वाले विद्यार्थियों की संख्या 35 तथा 20 से अधिक अंक प्राप्त करने वाले विद्यार्थियों की संख्या 15 है। 30 से अधिक अंक प्राप्त वाला कोई विद्यार्थी नहीं है। यदि हम (0, 45), (10, 35), (20, 15) को आपस में मिला दें तो हमारे पास जो रेखा प्राप्त होती है उसको आगे रेखा से अधिक का ओजाइव कहा जाता है।