Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
Question 1.
Which of the following pairs of linear equations has unique solution, no solution, or infinitély many solutions. In case there is a unique solution, find it by using cross multiplication method.
(i) x – 3y – 3 = 0
3x – 9y – 2 = 0
(ii) 2x + y = 5
3x + 2y = 8
(iii) 3x – 5y = 20
6x – 10y = 40
(iv) x – 3y – 7 = 0
3x – 3y – 15 = 0
Solution:
(i) Given pair of linear equation is:
x – 3y – 3 = 0
and 3x – 9y – 2 = 0
Here a1 = 1, b1 = -3, c1 = -3
a2 = 3, b2 = -9, c2 = -2
Now, \(\frac{a_{1}}{a_{2}}=\frac{1}{3}\);
\(\frac{b_{1}}{b_{2}}=\frac{-3}{-9}=\frac{1}{3}\);
\(\frac{c_{1}}{c_{2}}=\frac{-3}{-2}=\frac{3}{2}\)
∵ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Hence, given system of equations has no solution.
![]()
(ii) Given pair of linear equations
2x + y = 5
and 3x + 2y = 8
or 2x + y – 5 = 0
and 3x + 2y – 8=0
Here a1 = 2, b1 = 1, c1 = -5
a2 = 3,b2 = 2, c2 = 8
Now,
\(\frac{a_{1}}{a_{2}}=\frac{2}{3}\);
\(\frac{b_{1}}{b_{2}}=\frac{1}{2}\);
\(\frac{c_{1}}{c_{2}}=\frac{-5}{-8}=\frac{5}{8}\)
∵ \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
∴ given system of equation have unique solution.
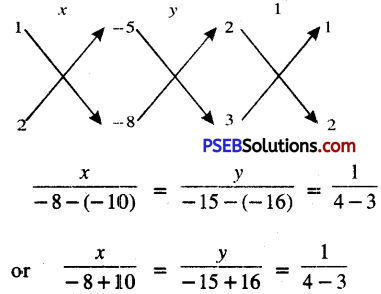
or \(\frac{x}{2}=\frac{y}{1}=\frac{1}{1}\)
I II III
From I and III, we get:
\(\frac{x}{2}=\frac{1}{1}\)
⇒ x = 2
From I and III, we get:
\(\frac{y}{1}=\frac{1}{1}\)
⇒ y = 1
Hence, x = 2 and y = 1.
![]()
(iii) Given pair of linear equations is :
3x – 5y = 20
and 6x – 10y = 40
or 3x – 5y – 20 = 0
and 6x – 10y – 40 =0
Here a1 = 3, b1 = -5, c1 = -20
a2 = 6, b2 = -10, c2 = -40
Now,
\(\frac{a_{1}}{a_{2}}=\frac{3}{6}=\frac{1}{2}\);
\(\frac{b_{1}}{b_{2}}=\frac{-5}{-10}=\frac{1}{2}\);
\(\frac{c_{1}}{c_{2}}=\frac{-20}{-40}=\frac{1}{2}\)
∵ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
Hence, given system have infinite solution.
(iv) Given pair of linear equation is:
x – 3y – 7 = 0
and 3x – 3y – 15 = 0
Here a1 = 1, b1 = -3, c1 = -7
a2 = 3, b2 = -3, c2 = -15
Now,
\(\frac{a_{1}}{a_{2}}=\frac{1}{3}\);
\(\frac{b_{1}}{b_{2}}=\frac{-3}{-3}=1\);
\(\frac{c_{1}}{c_{2}}=\frac{-7}{-15}=\frac{7}{15}\)
∵ \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
∴ given system have unique solution.
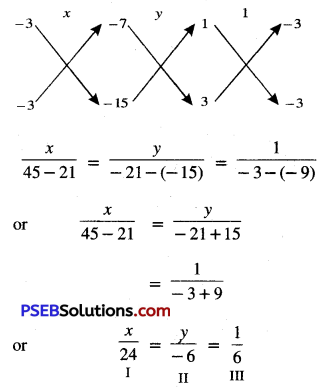
From I and III, we get:
\(\frac{x}{24}=\frac{1}{6}\)
⇒ x = 4
From I and III, we get:
\(\frac{y}{-6}=\frac{1}{6}\)
⇒ y = -1
Hence, x = 4, y = -1.
![]()
Question 2.
(i) For which values of a and b does the following pair of linear eqU1tions have an infinite number of solutions?
2x + 3y = 7
(a – b)x ÷ (a + b)y = 3a + b – 2
(ii) For which value of k wifi the following pair of linear equations have no solution?
3x + y = 1
(2k – 1) x + (k – 1) y = 2k + 1
Solution:
(i) Given pair of linear equation are
2x + 3y = 7
and (a – b)x + (a + b)y = 3a + b – 2
or 2x + 3y – 7 = 0
and (a – b)x + (a + b)y – (3a + b – 2) = 0
Here a1 = 2, b1 = 3, c1 = -7
a2 = a – b, b2 = a + b, c2 = -(3a + b – 2)
∵ System of equation have an infinite number of solutions.
∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
\(\frac{2}{a-b}=\frac{3}{a+b}=\frac{-7}{-(3 a+b-2)}\)
Fron I and III, we get:
\(\frac{2}{a-b}=\frac{7}{3 a+b-2}\)
or 6a + 2b – 4 = 7a – 7b
or -a + 9b – 4 = 0
or a = 9b – 4 …………..(1)
From II and III. we get:
\(\frac{3}{a+b}=\frac{7}{3 a+b-2}\)
or 9a + 3b – 6 = 7a + 7b
or 2a – 4b – 6 = 0
or a – 2b – 3 = 0
Substitute the value of a from (1) in above, we get:
9b – 4 – 2b – 3 = 0
or 7b – 7 = 0
or 7b = 7
b = 1
Substitute this value of b in (1), we get
a = 9 × 1 – 4 = 9 – 4
a = 5
Hence a = 5 and b = 1
(ii) Given pair of linear equation are
3x + y = 1
and (2k – 1)x + (k – 1)y = 2k + 1
or 3x + y – 1 = 0
and(2k – 1)x + (k – 1)y – (2k + 1) = 0
Here a1 = 3, b1 = -1, c1 = -1
a2 = (2k – 1), b2 = k – 1, c2 = -(2k + 1)
∵ system of equations have no solution.
∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
\(\frac{3}{2 k-1}=\frac{1}{k-1} \neq \frac{-1}{-(2 k+1)}\)
I II III
From I and III, we get:
\(\frac{3}{2 k-1} \neq \frac{1}{(2 k+1)}\)
⇒ 6k + 3 ≠ 2k – 1
⇒ 4k ≠ -4
⇒ k ≠ –\(\frac{4}{4}\)
⇒ k ≠ -1
From II and III, we get:
\(\frac{3}{2 k-1}=\frac{1}{k-1}\)
⇒ 3k – 3 = 2k – 1
⇒ k = 2
Hence k = 2 and k ≠ -1.
![]()
Question 3.
Solve the following pair of linear equations by the substitution and cross- multiplication methods:
8x + 5y = 9
3x + 2y = 4
Solution:
Given pair of linear equation is:
8x + 5y = 9 ………….(1)
3x + 2y = 4 …………..(2)
Substitution Method:
From (2), 2y = 4 – 3x
y = \(\frac{4-3 x}{2}\) …………….(3)
Substitute this value of y in (1), we get:
8x + 5\(\frac{4-3 x}{2}\) = 9
or \(\frac{16 x+20-15 x}{2}\) = 9
or x + 20 = 18
or x = 18 – 20 = -2
Substitute this value of x in (3), we get:
y = \(\frac{4-3(-2)}{2}=\frac{4+6}{2}\)
= \(\frac{10}{2}\) = 5
Hence, x = -2 and y = 5.
Cross-multiplication Method:
Given pair of linear equation is:
8x + 5y – 9 = o
and 3x + 2y – 4= 0
Here a1 = 8, b1 = 5, c1 = -9
a2 = 3, b2 = 2, c2 = -4
Now,
\(\frac{a_{1}}{a_{2}}=\frac{8}{3}\);
\(\frac{b_{1}}{b_{2}}=\frac{5}{2}\);
\(\frac{c_{1}}{c_{2}}=\frac{-9}{-4}=\frac{9}{4}\)
∵ \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
∴ system have unique solution.
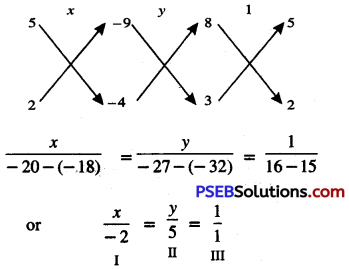
From I and III, we get:
\(\frac{x}{-2}=\frac{1}{1}\)
⇒ x = -2
From II and III, we get:
\(\frac{y}{5}=\frac{1}{1}\)
⇒ y = 5
Hence, x = -2 and y = 5.
![]()
Question 4.
Form the pair of linear equations in the following problems and find their solutions (If they exist) by any algebraic method.
(i) A part of monthly hostel charges Is fixed and the remaining depends on the number of days one has taken food
in the mess. When a student A takes food for 20 days she has to pay 1000 as hostel charges whereas a student B, who takes food for 26 days, pays 1180 as hostel charges. Find the fixed charges and the cost of food per day.
(ii) A fraction becomes when 1 is subtracted from the numerator and it becomes when 8 is added to its denominator. Find the fraction.
(iii) Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash ‘would have scored 50 marks. How many questions were there in the test?
(iv) Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time, If the cars travel in the same direction at differ it speeds they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
(v) The area of a rectangle gets reduced by 9 square units if Its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 units. Find the dimensions of the rectangle.
![]()
Solution:
(i) Let monthly fixed hostel charges = ₹ x
and cost of food per day = ₹ y
According to 1st condition
x + 20y = 1000 ………….(1)
According to 2nd condition
x + 26y = 1180 …………..(2)
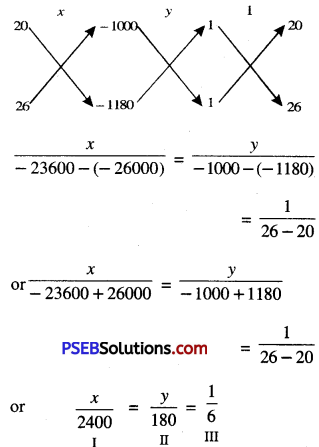
From I and III, we get:
\(\frac{x}{2400}=\frac{1}{6}\)
⇒ x = \(\frac{2400}{6}\) = 400
From II and III, we get:
\(\frac{y}{180}=\frac{1}{6}\)
⇒ y = \(\frac{180}{6}\) = 30
Hence, monthly fixed hostel charges and cost of food per day are 400 and 30 respectively.
![]()
(ii) Let numerator of fraction = x
Denominator of fraction = y
∴ required fraction = \(\frac{x}{y}\)
According to 1st condition,
\(\frac{x-1}{y}=\frac{1}{3}\)
or 3x – 3 = y
or 3x – y – 3 = 0 …………..(1)
According to 2nd condition,
\(\frac{x}{y+8}=\frac{1}{4}\)
or 4x = y + 8
or 4x – y – 8 = 0 …………….(2)
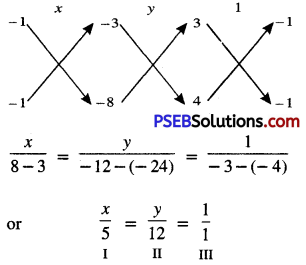
From I and III, we get:
\(\frac{x}{5}=\frac{1}{1}\)
⇒ x = 5
From II and III, we get:
\(\frac{y}{12}=\frac{1}{1}\)
⇒ y = 12
Hence, required fraction is \(\frac{5}{12}\).
![]()
(iii) Let, number of right questions attempted by Yash = x
and Number of wrong questions attempted by Yash = y
According to 1st condition,
3x – y = 40
or 3x – y – 40 = 0 …………….(1)
According to 2nd condition,
4x – 2y = 50
or 4x – 2y – 50 = 0 ……………(2)
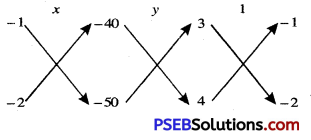
\(\frac{x}{50-80}=\frac{y}{-160-(-150)}=\frac{1}{-6-(-4)}\)
or \(\frac{x}{-30}=\frac{y}{-10}=\frac{1}{-2}\)
From I and III, we get:
\(\frac{x}{-30}=\frac{1}{-2}\)
x = \(\frac{-30}{-2}\)
⇒ x = 15
From II and III, we get:
\(\frac{y}{-10}=\frac{1}{-2}\)
y = \(\frac{-10}{-2}\)
⇒ y = 5
∴ Number of right questions = 15
Number of wrong questions = 5
Hence, total number of questions = [No. of right questions] + [No. of wrong questions]
=15 + 5 = 20.
![]()
(iv) Let speed of car at place A = x km/hour
and speed of car at place B = y km/hour
Distance between places A and B = 100 km
In case of 5 hours
Distance covered by car A = 5x km
[∵ Distance = Speed × Time]
Distance covered by car B = 5y km
According to I st condition,
5x – 5y = 100
or x – y = 20
or x – y – 20 = 0
In case of one hour
Distance covered by car A = x km
[∵ Distance = Speed × Time]
Distance covered by car B = y km
According to 2nd condition,
x + y = 100
or x + y – 100 = 00 ……………….(2)
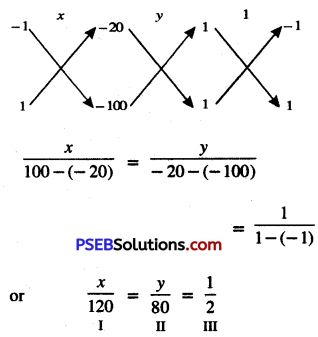
From I and III, we get:
\(\frac{x}{120}=\frac{1}{2}\)
x = \(\frac{1}{2}\) × 120
⇒ x = 60
From II and III, we get:
\(\frac{y}{171}=\frac{1}{19}\)
y = \(\frac{171}{19}\)
⇒ y = 9
Hence, length and breadth of rectangle are 17 units and 9 units respectively.