Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
Question 1.
Solve the following pair of equations by the elimination method and the substitution method.
(i) x + y = 5 and 2x – 3y = 4
(ii) 3x + 4y = 10 and 2x – 2y = 2
(iii) 3x – 5y – 4= 0 and 9x = 2y + 7
(iv) \(\frac{x}{2}+\frac{2 y}{3}\) and x – \(\frac{y}{3}\) = 3
Solution:
(i) Given pair of linear equations
x + y = 5 …………..(1)
and 2x – 3y = 4 ………….(2)
Elimination Method
Multiplying (1) by 2, we get:
2x + 2y = 10 …………..(3)
Now, (3) – (2) gives
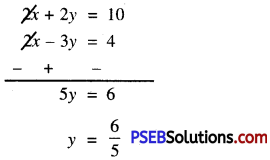
Substitute this value of y in (1), we get:
x + \(\frac{6}{5}\) = 5
or x = 5 – \(\frac{6}{5}\)
= \(\frac{25-6}{5}\) = \(\frac{19}{5}\)
Hence, x = \(\frac{19}{5}\) and \(\frac{6}{5}\)
![]()
Substitution Method:
From(2), 2x =4 + 3y
or x = \(\frac{4+3 y}{2}\) ……………..(4)
Substitute this value of x in (I), we get :
\(\frac{4+3 y}{2}\) + y = 5
Or \(\frac{4+3 y+2 y}{2}\)
Or 4 + 5y = 10
Or 5y = 10 – 4 = 6
Or y = \(\frac{6}{5}\)
Substitute this value of y in (4). we get:
x = \(\frac{4+\left(3 \times \frac{6}{5}\right)}{2}=\frac{4+\frac{18}{5}}{2}\)
= \(\frac{20+18}{5 \times 2}=\frac{38}{5 \times 2}\) = \(\frac{19}{5}\)
Hence x = \(\frac{19}{5}\) and y = \(\frac{6}{5}\)
(ii) Given pair of linear equation is :
3x + 4y = 10 …………….(1)
and 2x – 2y = 2 …………………(2)
Elimination Method
Multiplying equation (2) by 2, we get:
4x – 4y = 4 ……………(3)
Now, (3) + (1) gives
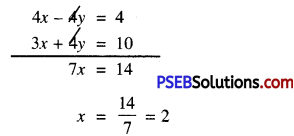
Substitute this value of x in (1), we get:
3(2) + 4y = 10
or 6 + 4y = 10
or 4y = 10 – 6
or 4y = 4
or y = \(\frac{4}{4}\) = 1
Hence x = 2 and y = 1.
![]()
Substitution method:
From (2),
2x = 2 + 2y
or x = y + 1 ………..(3)
Substitute this value of x in (1), we get :
3(y + 1) +4y = 10
or 3y + 3 + 4y = 10
or 7y = 10 – 3
or 7y = 7
or y = 1
Substitute this value of y in (3), we get :
x = 1 + 1 = 2
Hence, x = 2 and y = 1.
(iii) Given pair of linear equation is :
3x – 5y – 4 = 0 ……..(1)
and 9x = 2y + 7
or 9x – 2y – 7 = 0
Elimination Method:
Multiplying (1) by 3, we get:
9x – 15y – 12 = 0 ……………(3)
Now, (3) – (2) gives
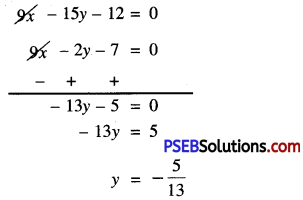
Substitute this value of y in (1), we get:
3x – 5(-\(\frac{5}{13}\)) – 4 = 0
or 3x + \(\frac{25}{13}\) – 4 = 0
or 3x = 4 – \(\frac{25}{13}\)
or 3x = \(\frac{52-25}{13}\) = \(\frac{27}{13}\)
or x = \(\frac{27}{13} \times \frac{1}{3}\)
= \(\frac{9}{13}\)
Hence, x = \(\frac{9}{13}\) and y = – \(\frac{5}{13}\).
![]()
Substitution Method:
From(2), x = \(\frac{2 y+7}{9}\) …………..(4)
Substitute this value of x in (1), we get:
3\(\frac{2 y+7}{9}\) – 5y – 4 = 0
or \(\frac{2 y+7-15 y-12}{3}\) = 0
or – 13y – 5 = 0
or -13y = 5
or y = \(-\frac{5}{13}\)
Substitute this value of y in (4), we get:
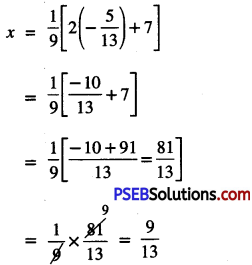
Hence x = \(\frac{9}{13}\) and y = –\(\frac{5}{13}\)
(iv) Given pair of linear equation is:
\(\frac{x}{2}+\frac{2 y}{3}\) = -1
or \(\frac{3 x+4 y}{6}\) = -1
or 3x + 4y = -6 ……………(1)
x – \(\frac{y}{3}\) = 3
or \(\frac{3 x- y}{3}\) = 3
or 3x – y = 9 ……………(2)
Elimination Method:
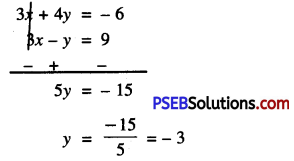
Substitute this value of y in (1), we get :
3x + 4(-3) = -6
or 3x – 12 = -6
or 3x = -6 + 12
or 3x = 6
x = \(\frac{6}{3}\) = 2
Hence x = 2, y = – 3.
![]()
Substitution Method:
From (2), y = 3x – 9 …………..(4)
Substitute this value of y in (1), we get :
3x + 4(3x – 9) = -6
or 3x + 12x – 36 = -6
or 15x = -6 + 36
or 15x = 30
or x = \(\frac{30}{15}\) = 2
Substitute this value of x in (4), we get :
y = 3 (2) – 9
= 6 – 9 = -3
Hence x = 2, y = -3.
Question 2.
Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method:
(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes if
we only add 1 to the denominator. What ¡s the fraction?
(ii) Five years ago, Nun was thrice as old as Sonu. Ten years later, Nun will be twice as old as Sonu. How old are Nun
and Sonti?
(iii) The sum of the digits of a two-digit nunaber ¡s 9. Also, nine times this number is twice the number obtained by reversing the order of the number. Find the number.
(iv) Meena went to a bank to withdraw ₹ 2000. She asked the cashier to give her ₹ 50 and ₹ 100 notes only. Meena got ₹ 25 notes in all. Find how many notes of ₹ 50 and ₹ 100 she received.
(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹ 27 for a book kept for seven days, while Susy paid ₹ 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day.
![]()
Solution:
(i) Let numerator of fraction = x
Denominator of fraction = y
Required fraction = \(\frac{x}{y}\)
According to 1st condition,
\(\frac{x+1}{y-1}\) = 1
or x + 1 = y – 1
or x – y + 2 = 0 …………….(1)
According to 2nd condition,
\(\frac{x}{y+1}=\frac{1}{2}\)
or 2x = y + 1
or 2x – y – 1 = 0 ……………..(2)
Now, (2) – (1) gives
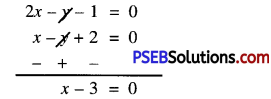
or x = 3
Substitute this value of x in (2), we get :
2 × 3 – y – 1 = 0
or 6 – y – 1 = 0
or 5 – y = 0
or y = 5
Hence, required fraction is \(\frac{3}{5}\).
(ii) Let Nun’s present age = x years
Sonus present age = y years
Five years ago
Nun’s age = (x – 5) years
Sonus age = (y – 5) years
According to 1st condition,
x – 5 = 3(y – 5)
or x – 5 = 3y – 15
or x – 3y + 10 = 0 …………….(1)
Ten years later
Nun’s age = (x + 10) years
Sonu’s age = (y + 10) years
According to 2nd condition,
x + 10 = 2 (y + 10)
or x + 10 = 2y + 20
or x – 2y – 10 = 0
Now, (1) – (2) gives
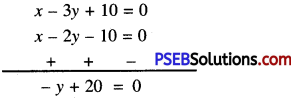
or -y = -20
or y = 20
Substitute this value of y in (2), we get:
x – 2(20) – 10 = 0
or x – 40 – 10 = 0
or x = 50
Hence, Nun’s present age = 50 years
Sonu’s present age = 20 years.
![]()
(iii) Let unit’s digit = x
Ten’s digit = y
∴ Required Number = 10y + x
According to 1st condition,
x + y = 9 …………..(1)
On reversing
Unit’s digit = y
Ten’s digit = x
∴ Number = 10x + y
According to 2nd condition,
9[10y + x] = 2[10x + y]
or 90y + 9x = 20x + 2y
or 90y + 9x – 20x – 2y = 0
or -11x + 88y = 0
or x – 8y = 0 ………………(2)
Now, (2) – (1) gives
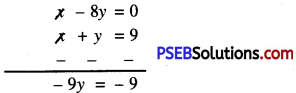
y = 1
Substitute this value of y in (2), we get :
x – 8 × 1 = 0
or x = 8
Hence, required number = 10y + x
= 10 × 1 + 8 = 18.
(iv) Let, Meena received number of Rs. 50 notes = x
also, Meena received number of Rs. 100 notes = y
According to 1st condition,
x + y = 25 ……………(1)
According to 2nd condition,
50x + 100y = 2000
or x + 2y = 40 ………………(2)
Now, (2) – (1) gives
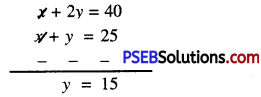
Substitute this value of y in (1), we get:
x + 15 = 25
or x = 25 – 15 = 10
Hence, Meena received number of notes of
Rs. 50 and Rs. 100 are 10 and 15 respectively.
![]()
(v) Let fixed charges for first three days = ₹ x
An additional charge for each day thereafter = ₹ y
In case of Saritha,
x + 4y = 27 …………..(1)
In case of Susy,
x + 2y = 21
Now, (1) – (2) gives

or y = \(\frac{6}{2}\) = 3
Substitute this value of y in (2), we get:
x + 2(3) = 21
or x + 6 = 21
or x = 21 – 6 = 15
Hence, fixed charges for first three days and an additional charge for each day thereafter ₹ 15 and ₹ 3.