Class 7

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 4 Simple Equations Ex 4.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.4

Question 1.
If 7 is added to five times a number, the result is 57. Find the number.
Solution:
Let the required number = x
Five times the number = 5x
7 added to five times the number = 5x + 7
According to the problem
5x + 7 = 57
5x = 57 – 7
5x = 50
x = \(\frac {50}{5}\)
So, x = 10
Hence the required number is 10.

Question 2.
9 decreased from four times a number yields 43. Find the number.
Solution:
Let the required number = x
Four times the number = 4x
9 decreased from four times the number = 4x – 9
According to the problem
4x – 9 = 43
4x = 43 + 9
4x = 52
x = \(\frac {52}{4}\)
x = 13
Hence, the required number is 13.

Question 3.
If one-fifth of a number minus 4 gives 3, find the number.
Solution:
Let the required number = x
One fifth of the number = \(\frac {1}{5}\)x
One fifth of the number minus 4 = \(\frac {1}{5}\)x – 4
According to problem
\(\frac {1}{5}\)x – 4 = 3
\(\frac {1}{5}\)x = 3 + 4
\(\frac {1}{5}\)x = 7
x = 35
Hence the required number is 35.

Question 4.
In a class of 35 students, the number of girls is two-fifth the number of boys. Find the number of girls in the class.
Solution:
Let the number of boys = x
∴ number of girls = \(\frac {2}{5}\)x
Total number of students = 35
x + \(\frac {2}{5}\)x =35
\(\frac{5 x+2 x}{5}\) = 35
7x = 5 × 35
x = \(\frac{5 \times 35}{7}\)
x = 25
Therefore number of boys = 25
Number of girls = 35 – 25 = 10.

Question 5.
Sham’s father’s age is 5 years more than three times Sham’s age. Find Sham’s age, if his father is 44 years old.
Solution:
Let Sham’s age = x years
Then Sham’s father age = 3x + 5
But Sham’s fathers age = 44
According to question
3x + 5 = 44
3x = 44 – 5
3x = 39
Dividing both sides by 3
\(\frac{3 x}{3}=\frac{39}{3}\)
or x = 13
Hence Sham’s age is 13 years.

Question 6.
In an isosceles triangle the base angles are equal, the vertex angle is 40°. What are the base angles of the triangle ? (Remember, the sum of three angles of a triangle is 180°)
Solution:
Let each base angle of an isosceles triangle = x (in degrees)
Vertex angle = 40°
The sum of angles of a triangle = 180°
∴ x + x + 40° = 180°
2x = 180° – 40°
2x = 140°
Divide both sides by 2
\(\frac{2 x}{2}-\frac{140^{\circ}}{2}\)
Or x = 70°
Each equal angle is of 70°

Question 7.
Irfan says that he has 7 marbles more than five times the marbles Pannit has. Irfan has 37 marbles. How many marbles does Pannit have ?
Solution:
Let marbles Parmit has = x
Marbles Irfan has = 5x + 7
But Marbles Irfan has = 37
∴ 5x + 7 = 37
5x = 37 – 7
5x = 30
x = \(\frac {30}{5}\) = 6
Therefore Parmit has 6 marbles.

Question 8.
The length of a rectangle is 3 units more than its breadth and the perimeter is 22 units. Find the breadth and length of a rectangle.
Solution:
Let breadth of rectangle (l)
= x units
∵ length of rectangle (b) = (x + 3) units
∴ Perimeter of rectangle = 2(l + b)
= 2 (x + x + 3) units
= 2(2x + 3) units
According to the question
Perimeter = 22 units
2 (2x + 3) =22
\(\frac{2(2 x+3)}{2}=\frac{22}{2}\)
2x + 3 = 11
2x = 11 – 3
or 2x = 8
Dividing both sides by 2 we get
\(\frac{2 x}{2}=\frac{8}{2}\)
x = 4
∴ breadth = 4 units
Length = (4 + 3) units
= 7 units

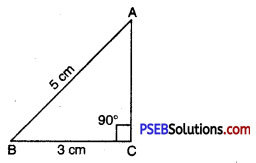
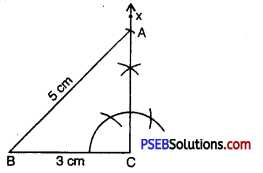
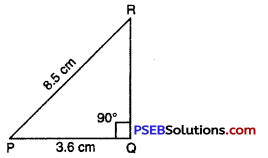
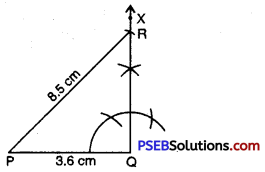
Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 4 Simple Equations Ex 4.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.3

1. Solve each of the following equation.

Question (i).
6x + 10 = – 2
Answer:
Given equation is 6x + 10 = – 2
Transposing + 10 from L.H.S to R.H.S
we get
6x = -2 – 10
or 6x = -12
Dividing both sides by 6, we get
\(\frac{6 x}{6}=\frac{-12}{6}\)
or x = – 2, which is the required solution.

To check Put x = – 2 in the LHS of the equation 6x + 10 = – 2
L.H.S. = 6x + 10
= 6 × -2 + 10
= -12 + 10
= – 2 = R.H.S.
∴ L.H.S. = R.H.S.

Question (ii).
2y – 3 = 2
Answer:
Given equation is 2y – 3 = 2
Transposing – 3 from L.H.S. to R.H.S,
we get
2y = 2 + 3
or 2y = 5
Dividing both sides by 2, we get:
\(\frac{2 y}{2}=\frac{5}{2}\)
or y = \(\frac {5}{2}\), which is the required solution

To check. Put y = \(\frac {5}{2}\) in the L.H.S of the equation 2y – 3 = 2
L.H.S = 2y – 3 = 2 × \(\frac {5}{2}\) – 3
= 5 – 3 = 2 = R.H.S.
∴ L.H.S. = R.H.S.

Question (iii).
\(\frac{a}{5}\) + 3 = 2
Answer:
Given equation is \(\frac{a}{5}\) + 3 = 2
Transposing + 3 from L.H.S to R.H.S., we get
\(\frac{a}{5}\) = 2 – 3
or \(\frac{a}{5}\) = -1
Multiplying both sides, by 5, we get
5 × \(\frac{a}{5}\) = 5 × – 1
or a = – 5, which is the required solution.

To Check: Put a = – 5 in the L.H.S of the equation
\(\frac{a}{5}\) + 3 = 2,
L.H.S. = \(\frac{a}{5}\) + 3
= \(\frac {-5}{5}\) + 3
= – 1 + 3
= 2 = R.H.S.
∴ L.H.S. = R.H.S.

Question (iv).
\(\frac{3 x}{2}=\frac{2}{3}\)
Answer:
Given equation is \(\frac{3 x}{2}=\frac{2}{3}\)
Multiplying both sides by 2, we get
2 × \(\frac{3 x}{2}\) = 2 × \(\frac {2}{3}\)
or 3x = \(\frac {4}{3}\)
Dividing both sides by 3 we get
\(\frac{3 x}{3}=\frac{4}{3} \times \frac{1}{3}\)
or x = \(\frac {4}{9}\), which is the required solution.

To Check. Put x = \(\frac {4}{9}\) in the L.H.S. of equation \(\frac{3 x}{2}=\frac{2}{3}\)
L.H.S. = \(\frac{3 x}{2}=\frac{3}{2} \times \frac{4}{9}\) = \(\frac {2}{3}\) = R.H.S.
∴L.H.S. = R.H.S.

Question (v).
\(\frac {5}{2}\)x = -5
Answer:
Given equation is \(\frac {5}{2}\) x = – 5
Multiplying both sides by 2, we get
2 × \(\frac {5}{2}\) x = 2 × – 5
or 5x = – 10
Dividing both sides by 5, we get
\(\frac{5 x}{5}=\frac{-10}{5}\)
or x = – 2, which is the required solution.

To Check. Put x = – 2 in L.H.S. of the equation \(\frac {5}{2}\)x = – 5
L.H.S. = \(\frac {5}{2}\)x = \(\frac {5}{2}\) × -2
= – 5 = R.H.S.
∴ L.H.S. = R.H.S.

Question (vi).
2x + \(\frac {5}{2}\) = \(\frac {37}{2}\)
Answer:
Given equation is 2x + \(\frac {5}{2}\) = \(\frac {37}{2}\)
Subtract \(\frac {5}{2}\) from both sides, we get
2x + \(\frac {5}{2}\) – \(\frac {5}{2}\)
= \(\frac {37}{2}\) – \(\frac {5}{2}\)
or 2x = \(\frac{37-5}{2}\)
or 2x = \(\frac {32}{2}\)
or 2x = 16
Dividing both sides by 2, we get
\(\frac{2 x}{2}=\frac{16}{2}\)
or x = 8, which is the required solution.

To Check. Put x = 8 in the L.H.S. of the equation 2x + \(\frac {5}{2}\) = \(\frac {37}{2}\)
L.H.S. = 2x + \(\frac {5}{2}\)
= 2 × 8 + \(\frac {5}{2}\)
= 16 + \(\frac {5}{2}\)
= \(\frac{32+5}{2}\)
= \(\frac {37}{2}\) = R.H.S.
∴ L.H.S. = R.H.S.

2. Solve the following equation

Question (i).
5 (x + 1) = 25
Answer:
Given equation is 5 (x + 1) = 25
Dividing both sides by 5 we get
\(\frac{5(x+1)}{5}=\frac{25}{5}\)
or x + 1 = 5
Transposing 1 from L.H.S. to R.H.S. we get
x = 5 – 1
or x = 4, which is the required solution.

To Check. Put x = 4 in the L.H.S. of the equation 5 (x + 1) = 25
L.H.S. = 5 (x + 1)
= 5 (4 + 1)
= 5 (5)
= 25 = R.H.S.
∴ L.H.S. = R.H.S.

Question (ii).
2 (3x – 1) = 10
Answer:
Given equation is 2 (3x – 1) = 10
Dividing both sides by 2, we get
\(\frac{2(3 x-1)}{2}=\frac{10}{2}\)
or 3x – 1 = 5
Transposing – 1 from L.H.S. to R.H.S we get
3x = 5 + 1
3x = 6
Dividing both sides by 3, we get \(\frac{3 x}{3}=\frac{6}{3}\)
or x = 2, which is the required solution.

To Check. Put x = 2, in the L.H.S. of the equation 2 (3x – 1) = 10
L.H.S. = 2 (3x – 1) = 10
L.H.S = 2 (3x – 1) = 2 (3 × 2 – 1)
= 2 (6 – 1)
= 2 × 5
= 10 = R.H.S.
∴L.H.S. = R.H.S.

Question (iii).
4 (2 – x) = 8
Answer:
Given equation is 4 (2 – x) = 8
Dividing both sides by 4, we get
\(\frac{4(2-x)}{4}=\frac{8}{4}\)
or 2 – x= 2
Transposing 2 from L.H.S. to R.H.S. we get
-x = 2 – 2
or – x = 0
Multiplying both sides by – 1, we get
-x × – 1 = x – 1
or x = 0, which is the required solution.

To Check. Put x = 0 in the L.H.S. of the equation 4 (2 – x) = 8
L.H.S. = 4 (2 – x) = 4 (2 – 0)
= 4 × 2
= 8 = R.H.S.
∴ L.H.S. = R.H.S.

Question (iv).
– 4 (2 + x) = 8.
Answer:
Given equation is – 4 (2 + x) = 8
Dividing both sides by – 4, we get
\(\frac{-4(2+x)}{-4}=\frac{8}{-4}\)
Transposing 2 from L.H.S. to R.H.S. we get :
x = – 2 – 2
or x = – 4, which is the required solution

To Check. Put x = – 4 in the L.H.S. of equation – 4 (2 + x) = 8
L.H.S. = – 4 (2 + x) = – 4 [2 + (- 4)]
= – 4 (2 – 4)
= – 4 (- 2)
= 8 = R.H.S.
∴ L.H.S. = R.H.S.

3. Solve the following equations :

Question (i).
4 = 5 (x – 2)
Answer:
Given equation is 4 = 5 (x – 2)
or 4 = 5x – 10
Transposing 5x to L.H.S. and 4 to R.H.S.,
we get
– 5x = – 4 – 10
or – 5x = – 14
Dividing both sides by – 5, we get
\(\frac{-5 x}{-5}=\frac{-14}{-5}\)
or, x = \(\frac {14}{5}\), which is the required solution.

To Check. Put x = \(\frac {14}{5}\) in the R.H.S. of the equation 4 = 5 (x – 2)
R.H.S. = 5 (x – 2) = 5\(\left(\frac{14}{5}-2\right)\)
= 5\(\left(\frac{14-10}{5}\right)\)
= 5 \(\left(\frac{4}{5}\right)\)
= 4 = L.H.S.
∴ L.H.S. = R.H.S.

Question (ii).
– 4 = 5 (x – 2)
Answer:
Given equation is – 4 = 5 (x – 2)
or – 4 = 5x – 10
Transposing -4 to R.H.S and 5x to L.H.S
we get
-5x = 4 – 10 or -5x = -6
Dividing both sides by – 5 we get
\(\frac{-5 x}{-5}=\frac{-6}{-5}\)
or x = \(\frac {6}{5}\), which is the required solution.

To Check. Put x = \(\frac {6}{5}\) in the R.H.S. of the equation – 4 = 5 (x – 2)
L.H.S. = 5 (x – 2)
= 5\(\left(\frac{6}{5}-2\right)\)
= 5\(\left(\frac{6-10}{5}\right)\)
= 5\(\left(\frac{-4}{5}\right)\)
= -4 = L.H.S.
L.H.S. = R.H.S.

Question (iii).
4 + 5 (p – 1) = 34
Answer:
Given equation is 4 + 5(p – 1) = 34
Transposing 4 to R.H.S. we get
5(p – 1) = 34 – 4
5(p – 1) = 30
Dividing both sides, by 5, we get
\(\frac{5(p-1)}{5}=\frac{30}{5}\)
p – 1=6
Transposing -1 to R.H.S. we get
p = 6 + 1
p = 7 which is the required solution.

To Check : Put p = 7 in L.H.S. of the equation 4 + 5 (p – 1) = 34
L.H.S. = 4 + 5 (p – 1)
= 4 + 5 (7 – 1)
= 4 + 5 (6)
= 4 + 30
= 34 = R.H.S.
∴ L.H.S. = R.H.S.

Question (iv).
6y – 1 = 2y + 1.
Answer:
Given equation is 6y – 1 = 2y + 1
Transposing – 1 to R.H.S. and 2y to L.H.S,
we get
6y – 2y = 1 + 1
or 4y = 2 or y = \(\frac {2}{4}\)
or y = \(\frac {1}{2}\), which is the required solution.

To Check Put y = \(\frac {1}{2}\) in both L.H.S. and R.H.S. of the equation
6y – 1 = 2y + 1
L.H.S. = 6y – 1 = 6 × \(\frac {1}{2}\) – 1 = 3 – 1 = 2
R.H.S. = 2y + 1 = 2 × \(\frac {1}{2}\) + 1 = 1 + 1 = 2.
∴ L.H.S. = R.H.S.

4.

Question (i).
Construct 3 equations starting with x = 2
Answer:
First Equation.
(i) Start with x = 2
Multiplying both sides by 10
10x = 20
Adding 2 to both sides
10x + 2 = 20 + 2
or 10x + 2 = 22
This has resulted in an equation.

Second Equation. Start with x = 2
Divide both sides by 5
∴ \(\frac{x}{5}=\frac{2}{5}\)
This has resulted in an equation.

Third Equation. Start with x = 2
Multiply both sides by 5, we get
5x = 5 × 2
or 5x = 10
Subtracting 3 from both sides, we get
5x – 4 = 10 – 3
or 5x – 3 = 7
This has resulted in an equation.

Question (ii).
Construct 3 equation starting with x = – 2
Answer:
First Equation. Start with x = – 2
Multiplying both sides with 3, we get
3x = – 6
This has resulted in an equation

Second Equation. Start with x = – 2
Multiplying both sides with 3, we get 3x = -6
Adding 7 to both sides, we get 3x + 7
= -6 + 7 or 3x + 7 = 1
This has resulted in an equation.

Third Equation. Start with x = – 2
Multiplying both side with 2 we get 3x = – 6
Adding 10 to both sides we get
3x+ 10 = -6 + 10
or 3x + 10 = 4
This has resulted in an equation.

Multiple Choice Questions :

5. If 7x + 4 = 39, then x is equal to :
(a) 6
(b) -4
(c) 5
(d) 8
Answer:
(c) 5

6. If 8m – 8 = 56 then m is equal to :
(a) -4
(b) -2
(c) -14
(d) 8
Answer:
(d) 8

7. Which of the following number satisfies the equation – 6 + x = -18 ?
(a) 10
(b) – 13
(c) – 12
(d) – 16.
Answer:
(a) 10

8. If \(\frac{x}{2}\) = 14, then the value of 2x + 6 is equal to :
(a) 62
(b) -64
(c) 16
(d) -62.
Answer:
(a) 62

9. If 3 subtracted from twice a number is 5, then the number is :
(a) -4
(b) -2
(c) 2
(d) 4
Answer:
(d) 4

10. If 5 added to thrice an integer is – 7, then the integer is :
(a) – 6
(b) – 5
(c) -4
(d) 4
Answer:
(c) -4

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 4 Simple Equations Ex 4.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 4 Simple Equations Ex 4.2

1. Write the first step that you will use to separate the variable and then solve the equation.

Question (i).
x + 1 = 0
Answer:
Given equation x + 1 = 0
Subtracting 1 from both sides, we get
x + 1 – 1 = -1
or x = – 1

Question (ii).
x – 1 = 5
Answer:
Given equation is x – 1 = 5
Adding 1 to both sides we get
x – 1 + 1 = 5 + 1
or x = 6
Thus x = 6 is the solution of the given equation

Question (iii).
x + 6 = 2
Answer:
Given equation is x + 6 = 2
Subtracting 6 from both sides, we get:
x + 6 – 6 = 2 – 6
or x = – 4
Thus, x = – 4 is the solution of the given equation.

Question (iv).
y + 4 = 4
Answer:
Given equation is y + 4 = 4
Subtracting 4 from both sides we get
y + 4 – 4 = 4 – 4
or y = 0
Thus, y = 0 is the solution of the given equation.

Question (v).
y – 3 = 3
Answer:
Given equation is y – 3 = 3
Adding 3 to both sides we get
y – 3 + 3 = 3 + 3
or y = 6
Thus, y = 6 is the solution of the given equation.

2. Write the first step that you will use to separate the variable and then sotye the equation :

Question (i).
3x = 15
Answer:
Given equation is 3x = 15
Dividing both sides by 3 we get
\(\frac{3 x}{3}=\frac{15}{3}\)
or x = 5

Question (ii).
\(\frac{P}{7}\) = 4
Answer:
Given equation is \(\frac{P}{7}\) = 4
Multiplying both sides by 7, we get
7 × \(\frac{P}{7}\) = 7 × 4
or p = 28
Thus, p = 28 is the solution of the given equation.

Question (iii).
8y = 36
Answer:
Given equation is 8y = 36
Dividing both sides by 8, we get
\(\frac{8 y}{8}=\frac{36}{8}\)
or y = \(\frac {9}{2}\)

Question (iv).
20x = – 10
Answer:
Given equation is
20x = – 10
Dividing both sides by 20
\(\frac{20 x}{20}=\frac{-10}{20}\)
or x = \(\frac {-1}{2}\)

3. Give the steps you will use to separate the variable and then solve the equation.

Question (i).
5x + 7 = 17
Answer:
Given equation is 5x + 7 = 17
Subtracting 7 from both sides, we get
5x + 7 – 7 = 17 – 7
or 5x = 10
Dividing both sides by 5, we get
\(\frac{5 x}{5}=\frac{10}{5}\)
or x = 2

Question (ii).
\(\frac{20 x}{3}\) = 40
Answer:
Given equation is \(\frac{20 x}{3}\) = 40
Multiplying both sides by 3, we get
3 × \(\frac{20 x}{3}\) = 3 × 40
or 20x = 3 × 40
Dividing both sides by 20, we get
\(\frac{20 x}{20}\) = \(\frac{3 \times 40}{20}\)
or x = 6

Question (iii).
3p – 2 = 46
Answer:
Given equation is 3p – 2 = 46
Adding 2 to both sides, we get
3p – 2 + 2 = 46 + 2
or 3 p = 48
Dividing both sides by 3, we get:
\(\frac{3 p}{3}=\frac{48}{3}\)
or p = 16

4. Solve the following equations :

Question (i).
10x + 10 = 100
Answer:
Given equation is 10x + 10 = 100
Subtracting 10 from both sides, we get
10x + 10 – 10 = 100 – 10
or 10x = 90
Dividing both sides by 10, we get
\(\frac{10 x}{10}=\frac{90}{10}\)
or x = 9
Thus x = 9 is the solution of the given equation.

Question (ii).
\(\frac{-p}{3}\) = 5
Answer:
Given equation is \(\frac{-p}{3}\) = 5
Multiplying both sides by – 3, we get
– 3 × \(\frac{-p}{3}\) = -3 × 5
or p = -15
Thus p = – 15 is the solution of the given equation.

Question (iii).
3x + 12 = 0
Answer:
Given equation is 3x + 12 = 0
Subtracting 12 from both sides, we get
3x + 12 – 12 = – 12
or 3x = – 12
Dividing both sides by 3, we get
\(\frac{3 x}{3}=\frac{-12}{3}\)
or x = -4
Thus x = – 4 is the solution of the given equation.

Question (iv).
2q – 6 = 0
Answer:
The given equation is 2q – 6 = 0
Adding 6 to both sides, we get
2q – 6 + 6 = 0 + 6
or 2q = 6
Dividing both sides by 2, we get
\(\frac{2 q}{2}=\frac{6}{2}\)
or q = 3
Thus, q = 3 is the solution of the given equation.

Question (v).
3p = 0
Answer:
The given equation is 3p = 0
Dividing both sides by 3, we get
\(\frac{3 p}{3}=\frac{0}{3}\)
or p = 0
Thus, p = 0 is the solution of the given equation.

Question (vi).
3s = -9
Answer:
The given equation is
3s = -9
Dividing both sides by 3, we get
\(\frac{3 s}{3}=-\frac{9}{3}\)
or s = – 3
Thus, s = – 3 is the solution of the given equation.

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry MCQ Questions with Answers.

PSEB 7th Class Maths Chapter 10 Practical Geometry MCQ Questions

Multiple Choice Questions :

Question 1.
Number of parallel lines that can be drawn passing through a point not lying on the given line is :
(a) 0
(b) 1
(c) 2
(d) 3.
Answer:
(b) 1

Question 2.
The sum of three angles of a Δ is :
(a) 90°
(b) 180°
(c) 360°
(d) None
Answer:
(b) 180°

Question 3.
A triangle can be constructed by taking its sides of these :
(a) 3 cm, 5 cm, 7 cm
(b) 4 cm, 5 cm, 9 cm
(c) 4 cm, 3 cm, 8 cm
(d) 3 cm, 2 cm, 5 cm.
Answer:
(a) 3 cm, 5 cm, 7 cm

Question 4.
Two angles of a triangle are 40° and 50°. Third angle is :
(a) 40°
(b) 50°
(c) 90°
(d) 60°
Answer:
(c) 90°

Question 5.
The angles of a triangle are 30° and 50°, third angle is :
(a) 100°
(b) 60°
(c) 80°
(d) 50°.
Answer:
(a) 100°

Fill in the blanks :

Question 1.
Sum of lengths of any two sides of a triangle is …………….
Answer:
greater than third side

Question 2.
In right angled triangle.
(Hypotenuse)² = (…………….)² + (…………….)²
Answer:
Base, Perpendicular

Question 3.
SAS stands for …………….
Answer:
Side, angle, Side

Question 4.
RHS stands for …………….
Answer:
Right angle hypotenuse side

Question 5.
ASA stands for …………….
Answer:
Angle, side, angle.

Write True or False

Question 1.
Exterior angle of a triangle is equal to the sum of opposite interior angles. (True/False)
Answer:
True

Question 2.
The lengths of three sides can be used to construct a triangle. (True/False)
Answer:
True

Question 3.
The sum of the three angles of a triangle is 160°. (True/False)
Answer:
False

Question 4.
Construction of a triangle is possible when some of too angle is 180°. (True/False)
Answer:
True

Question 5.
Each angle of equilateral triangle is 60°. (True/False)
Answer:
True

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.5

1. Construct a right angled triangle ABC with ∠C = 90°, AB = 5 cm and BC = 3 cm.
Solution:
Given : Two sides of ΔABC as
AB = 5 cm,
BC = 3 cm
and ∠C = 90°.
To construct : A triangle with these two sides and one right angle.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle ABC and indicate the measure of these two sides and mark the right angle.

Step 2. Draw BC of length 3 cm.

Step 3. At C, draw CX ⊥ BC. (A should be somewhere on this perpendicular).

Step 4. With B as centre, draw an arc of radius 5 cm. (A must be on this arc since it is at a distance of 5 cm from B).

Step 5. A has to be on the perpendicular line CX as well as on the arc drawn with centre C.
∴ A is the meeting point of these two.
ΔABC is now obtained.

2. Construct an isosceles right angled triangle DEF where ∠E = 90° and EF = 6 cm.
Solution:
Given : An isoscele right angled ΔDEF where ∠E = 90° and EF = 6 cm.
To Construct: A right angled triangle with one side.
Steps of Construction:
Steps 1. Draw a rough sketch of given measures.

Step 2. Draw a line segment EF = 6 cm.

Step 3. With the help of compass taking E as centre, draw a ray EX making an angle of 90° with EF.

Step 4. With E as centre and radius 6 cm (= DE) draw an arc intersecting EX at D.

Step 5. Join D and F. Therefore ΔDEF is required isosceles right triangle.

3. Construct a right-angled triangle PQR in which :
∠Q= 90°, PQ = 3.6 cm and PR = 8.5 cm
Solution:
Given : Right triangle be PQR; right-angled at Q
i. e. ∠Q = 90°
and PQ = 3.6 cm,
PR = 8.5 cm
To construct : A triangle with these two sides and one right angle.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle PQR and indicate the measure of these two sides and mark the right angle.

Step 2. Draw PQ of length 3.6 cm.

Step 3. At Q, draw QX ⊥ PQ.
(R should be somewhere on this perpendicular).

Step 4. With P as centre, draw arc of radius
(R must be on this arc, since it is at a distance of 8.5 cm from P).

Step 5. R has to be on the perpendicular line QX as well as on the arc drawn with centre P.
∴ R is the meeting point of these two.
ΔPQR is now obtained.

4. Question (i).
Which of the following is a pythagorian triplet ?
(a) 1, 2, 3
(b) 2, 3, 4
(c) 4, 5, 6
(d) 12, 13, 5
Answer:
(d) 12, 13, 5

Question (ii).
Construction of unique triangle is not possible when :
(a) Three sides are given.
(b) Two sides and an included angle are given.
(c) Three angles are given.
(d) Two angles & included side are given.
Answer:
(c) Three angles are given.

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 11 Perimeter and Area Ex 11.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.2

1. Estimate the area of the following figures by counting unit squares.

Question (i).

Solution:
In the given figure, number of squares covered completely = 135
Area of a square = 1 sq. unit
Area of (135 square) figure = 135 sq. units, (approx.)

Question (ii).

Solution:
In the given figure number of square covered completely = 114
Area of one square = 1 unit
∴ Area of 114 squares = 114 sq units approx
Thus area of given figure = 114 sq units approx.

2. In the following figures find the area of 

Question (i).
ΔABC

Solution:
Given length of rectangle = 15 cm
Breadth of rectangle = 8 cm
The diagonal AC divides the rectangle into two triangles ΔABC and ΔADC
So, area of ΔABC = \(\frac {1}{2}\) × Area of rectangle ABCD
= \(\frac {1}{2}\) × length × breadth
= \(\frac {1}{2}\) × 15 × 8
= 60 cm²

Question (ii).
ΔCOD

Solution:
Given side of square = 6 cm
The diagonals AC and BD divides the square into four equal posses (triangles)
So, area of ΔCOD = \(\frac {1}{4}\) × Area of square
= \(\frac {1}{4}\) × 6 × 6
= 9 cm²

3. Find the area of following parallelograms.

Question (i).

Solution:
Given base of parallelogram = 9 cm
Height of parallelogram = 6 cm
Area of parallelogram = Base × height
= 9 × 6
= 54 cm²

Question (ii).

Solution:
Given base of parallelogram = 6.5 cm
Height of parallelogram= 8.4 cm
Area of parallelogram = Base × height
= 6.5 × 8.4
= 54.6 cm²

4. Find the value of x in the following parallelograms.

Question (i).

Solution:
Given base (AD) of parallelogram = 5.6 cm
Corresponding height of parallelogram = 9 cm
Area of parallelogram = 5.6 × 9 cm² ….(1)
Also in the paralleogram, base (AB) = x
Corresponding height of parallelogram = 7 cm
Area of parallelogram will be = x × 7 ….(2)
From (1) and (2), we get
x × 7 = 5.6 × 9
x = \(\frac{5.6 \times 9}{7}\)
= 7.2

Question (ii).

Solution:
Given base (AB) of parallelogram = 15 cm
Corresponding height = 6 cm
Area of parallelogram =15 × 6 cm² ….(1)
Also Base (AD || BC) of parallelogram = 9 cm
Corresponding height = x
So area of parallelogram = 9 × x ….(2)
From (1) and (2)
9 × x = 15 × 6
x = \(\frac{15 \times 6}{9}\)
= 10 cm.

5. The adjacent sides of a parallelogram are 28 cm and 45 cm and the altitude on longer side is 18 cm. Find the area of parallelogram.
Solution:
Given base of the parallelogram = 45 cm
Corresponding height = 18 cm
Area of parallelogram = Base × Height
= 45 × 18
= 810 cm2

6. ABCD is a parallelogram given in figure. DN and DM are the altitudes on side AB and CB respectively. If area of the parallelogram is 1225 cm², AB = 35 cm and CB = 25 cm, find DN and DM.

Solution:
In the given parallelogram ABCD
Base (AB) = 35 cm
Let height (DN) = x cm
So area of parallelogram = 35 × x cm²
But given area of parallelogram (ABCD) = 1225 cm²
Therefore 35x = 1225
x = \(\frac {1225}{35}\)
= 35 cm
Similarly, for base (BC) and height (DM)
1225 = BC × DM
\(\frac{1225}{\mathrm{BC}}\) = DM
or DM = \(\frac {1225}{25}\)
= 49 cm.

7. Find the area of the following triangles.

Question (i).

Solution:
Given base of triangle = 7 cm
Height of triangle = 4.8 cm
Area of triangle = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × 7 × 4.8
= 16.8 cm².

Question (ii).

Solution:
Given base of triangle =6 cm
Height of triangle = 9 cm
Area of triangle = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × 6 × 9
= 27 cm²

8. Find the value of x in the following triangles.

Question (i).

Solution:
In ΔABC, BC = 8 cm, AC = 15 cm
Area of triangle ABC = \(\frac {1}{2}\) × Base × height
= \(\frac {1}{2}\) × BC × AC
= \(\frac {1}{2}\) × 8 × 15
= 60 cm² …(1)
Also, in ΔABC, AB = 20 cm
height = x
Area of triangle ABC = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × 20 × x ….(2)
From (1) and (2)
\(\frac {1}{2}\) × 20 × x = 60
x = \(\frac{60 \times 2}{20}\)
x = 6 cm.

Question (ii).

Solution:
In ΔABC, base (AC) = 25 cm
height = 14 cm
Area of triangle ABC = \(\frac {1}{2}\) × Base × height
\(\frac {1}{2}\) × 14 × 25 ….(1)
Also, in ΔABC, base AB = x cm
height = 20 cm
So, area of ΔABC = \(\frac {1}{2}\) × Base × Height
= \(\frac {1}{2}\) × x × 20 ….(2)
From (1) and (2) we get
\(\frac {1}{2}\) × x × 20 = \(\frac {1}{2}\) × 14 × 25
x = 17.5 cm

9. ABCD is a square, M is a point on AB such that AM = 9 cm and area of ΔDAM is 171 cm². What is the area of the square ?

Solution:
Given area of ΔDAM = 171 cm²
Base of triangle = 9 cm
As, area of triangle ΔDAM = \(\frac {1}{2}\) × base × height
171 = \(\frac {1}{2}\) × 9 × (DA)
Hence height (DA) = \(\frac{171 \times 2}{9}\)
= 18 cm
Hence side of square (DA) = 18 cm
Therefore area of square = (side)²
= (18)²
= 324 cm²

10. ΔABC is right angled at A as shown in figure. AD is perpendicular to BC, if AB = 9 cm, BC = 15 cm and AC = 12 cm. Find the area of ΔABC, also find file length of AD.

Solution:
Given AB = 9 cm
BC = 15 cm
AC = 12 cm
Let AD = x cm
Area of triangle = \(\frac {1}{2}\) × Base × height
= \(\frac {1}{2}\) × 12 × 9 cm².
= 54 cm² ….(1)
Since, AD is perpendicular to BC
So, area of triangle = \(\frac {1}{2}\) × BC × AD
= \(\frac {1}{2}\) × 15 × AD ….(2)
From (1) and (2) we get
\(\frac {1}{2}\) × 15 × AD = 54
AD = \(\frac{54 \times 2}{15}\)
AD = 7.2 cm

11. ΔABC is isosceles with AB = AC = 9 cm, BC = 12 cm and the height AD from A to BC is 4.5 cm. Find the area of ΔABC. What will be the height from B to AC i.e. BN ?

Solution:
In triangle ABC, Base (BC) = 12 cm
AD = 4.5 cm
AD is perpendicular to BC
So, Area of ΔABC = \(\frac {1}{2}\) × base × height
= \(\frac {1}{2}\) × 12 × 4.5 cm
= 27 cm ….(1)
Also, in ΔABC, Base (AC) = 9 cm
Let corresponding height (BN) = x
So area of ΔABC = \(\frac {1}{2}\) × base × height
= \(\frac {1}{2}\) × 9 × BN ….(2)
From (1) and (2)
\(\frac {1}{2}\) × 9 × BN = 27
BN = \(\frac{27 \times 2}{9}\)
= 6 cm.

12. Multiple choice questions :

Question (i).
Find the height of a parallelogram whose area is 246 cm² and base is 20 cm.
(a) 1.23 cm²
(b) 13.2 cm²
(c) 12.3 cm²
(d) 1.32 cm²
Answer:
(c) 12.3 cm²

Question (ii).
One of the side and the corresponding height of a parallelogram are 7 cm and 3.5 cm respectively. Find the area of the parallelogram.
(a) 21 cm²
(b) 24.5 cm²
(c) 21.5 cm²
(d) 24 cm²
Answer:
(b) 24.5 cm²

Question (iii).
The height of a triangle whose base is 13 cm and area is 65 cm² is :
(a) 12 cm
(b) 15 cm
(c) 10 cm
(d) 20 cm
Answer:
(c) 10 cm

Question (iv).
Find the area of an isosceles right angled triangle, whose equal sides are of length 40 cm each.
(a) 400 cm²
(b) 200 cm²
(c) 600 cm²
(d) 800 cm²
Answer:
(d) 800 cm²

Question (v).
If the sides of a parallelogram are increased to twice of its original length, how much will be the perimeter of the new parallelogram ?
(a) 1.5 times
(b) 2 times
(c) 3 times
(d) 4 times
Answer:
(b) 2 times

Question (vi).
In a right angled triangle one leg is double the other and area is 64 cm² find the smaller leg.
(a) 8 cm
(b) 16 cm
(c) 24 cm
(d) 32 cm.
Answer:
(a) 8 cm

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 11 Perimeter and Area Ex 11.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.1

1. Find the perimeter and the area of a rectangle having :
(i) Length = 28 cm, Breadth = 15 cm
(ii) Length = 9.4 cm Breadth = 2.5 cm
Solution:
(i) Given length of rectangle = 28 cm
Breadth of rectangle = 15 cm
Perimeter of rectangle = 2 [length + Breadth]
= 2 [28 + 15]
= 2 × 43
= 86 cm

Area of rectangle = length × Breadth
= 28 × 15
= 420 cm²

(ii) Perimeter of rectangle = 2 [9.4 + 2.5]
= 2 × 11.9
= 23.8 cm
Area of rectangle = 9.4 × 2.5
= 23.5 cm²

2. Find the perimeter and the area of a square whose side measures
(i) 29 cm
(ii) 8.3 cm
Solution:
(i) Given side of square = 29 cm
Perimeter of square = 4 × side
= 4 × 29
= 116 cm
Area of square = (side)²
= (29)²
= 841 cm²

(ii) Perimeter of square = 4 × 8.3
= 33.2 cm
Area of square = 8.3 × 8.3
= 68.89 cm²

3. The perimeter of a square park is 148 m. Find its area.
Solution:
Given the perimeter of square park = 148 m
Side of the square park = \(\frac{perimeter}{4}\)
= \(\frac {148}{4}\)
Area of the square park = (side)²
= (37)²
= 1369 m²

4. The area of a rectangle is 580 cm². Its length is 29 cm. Find its breadth and also, the perimeter.
Solution:
Given area of rectangle = 580 cm²
Length of the rectangle = 29 cm
Let breadth of the rectangle = b cm
Area of the rectangle = length × breadth
580 = 29 × b
\(\frac {580}{29}\) = b
b = 20 cm
Perimeter of rectangle = 2 [length + breadth]
= 2 [29 + 20]
= 2 × 49
= 98 cm

5. A wire is in the shape of a rectangle. Its length is 48 cm and breadth is 32 cm. If the same wire is rebent into the shape of a square, what will be the measure of each side. Also, find which shape encloses more area and by how much ?
Solution:
Given length of the rectangle = 48 cm
Breadth of the rectangle = 32 cm
Perimeter of the rectangle = 2 [length + breadth]
= 2 [48 + 32]
= 2 × 80
= 160 cm
Let side of square = a cm
Perimeter of the square = 4 × a
Since wire is rebent into the shape of a square
Perimeter of square = Perimeter of rectangle
4 a = 160
Therefore, a = \(\frac {160}{4}\)
= 40 cm
Area of square = (side)²
= 40 × 40
= 1600 cm²
Area of rectangle = length × breadth
= 48 × 32
= 1536 cm²
∴ Square encloses more area by 64 cm²

6. The area of a square park is the same as that of a rectangular park. If the side of the square park is 75 m and the length of the rectangular park is 125 m, find the breadth of the rectangular park. Also, find the perimeter of rectangular park.
Solution:
Given side of square park = 75 m
Area of square park = (75)²
= 75 × 75
= 5625 m²
Length of rectangular park = 125 m
Let breadth of rectangular park = b m
Area of rectangular park = length × breadth
= 125 × b m²
Given that
Area of rectangular park = Area of square park
125 × b = 5625
= 45 m
Perimeter of rectangular park = 2 [length + breadth]
= 2 [125 + 45]
= 2 × 170
= 340 m

7. A door of length 2.5 m and breadth 1.5 m is fitted in a wall. The length of wall, is 9 m and breadth is 6 m. Find the cost of painting the wall, if the rate of painting the wall is ₹ 30 per m².

Solution:
Length of door = 2.5 m
Breadth of door = 1.5 m
Area of door = length × breadth
= 2.5 × 1.5
= 3.75 m²
Area of wall = 9 × 6
= 54 m²
Area of wall painting = Area of wall including door – Area of door
= 54 – 3.75
= 50.25 m²
Cost of painting 1 m² of wall = ₹ 30
Cost of painting 50.25 m² of wall = ₹ 50.25 × 30
= ₹ 1507.50

8. A door of dimensions 3 m × 2 m and a window of dimensions 2.5 m × 1.5 m is fitted in a wall. The length of the wall is 7.8 m and breadth is 3.9 m. Find the cost of painting the wall, if the rate of painting the wall is ₹ 25 per m².
Solution:
Area of door = 3 × 2 = 6 m²
Area of window = 2.5 m × 1.5 m
= 3.75 m²
Area of wall = 7.8 m × 3.9 m
= 30.42 m²
Area of painting the wall = Area of wall – Area of door – Area of window
= 30.42 – 6 – 3.75
= 20.67 m²
Cost of painting the wall = ₹ 25 × 20.67
= ₹ 516.75

9. Find the area and the perimeter of the following figures.

Solution:
(i) Perimeter of the given figure
= AB + BC + CD + DE + EF + FG + GH + HA
= 2 + 3.5 + 3 + 2 + 5 + 3.5 + 10 + 9
= 38 cm²
Area of the figure = Area of rectangle ABCJ + Area of rectangle JDEI + Area of rectangle IFGH
= 2 × 3.5 + 5 × 2 + 10 × 3.5
= 7 + 10 + 35
= 52 cm²

(ii) Perimeter of the given figure
= 8cm + 5 cm + 1.5 cm + 2.5 cm + 2.5 cm + 1.5 cm + 1.5 cm + 1.5 cm + 2.5 cm + 1.5 cm
= 29 cm
Area of the given figure = Area of rectangle I + Area of rectangle II + Area of rectangle III
= 8 cm × 1.5 cm + 3.5 cm × 1.5 cm + 1.5 cm × 1.5 cm
= 12 cm² + 5.25 cm² + 2.25 cm
= 19.5 cm²

10. Multiple Choice Questions :

Question (i).
What is the area of a rectangle of dimensions 12 cm × 10 cm ?
(a) 44 cm²
(b) 120 cm²
(c) 1200 cm²
(d) 1440 cm²
Answer:
(b) 120 cm²

Question (ii).
Find the breadth of a rectangle whose length is 12 cm and perimeter is 36 cm.
(a) 6 cm
(b) 3 cm
(c) 9 cm
(d) 12 cm
Answer:
(a) 6 cm

Question (iii).
If each side of a square is 1 m then its area is ?
(a) 10 cm²
(b) 100 cm²
(c) 1000 cm²
(d) 10000 cm²
Answer:
(d) 10000 cm²

Question (iv).
Find the area of a square whose perimeter is 96 cm.
(a) 576 cm²
(b) 626 cm²
(c) 726 cm²
(d) 748 cm².
Answer:
(a) 576 cm²

Question (v).
The area of a rectangular sheet is 500 cm². If the length of the sheet is 25 cm, what is its breadth ?
(a) 30 cm
(b) 40 cm
(c) 20 cm
(d) 25 cm.
Answer:
(c) 20 cm

Question (vi).
What happens to the area of a square, if its side is doubled ?
(a) The area becomes 4 times, the area of original square.
(b) The area becomes \(\frac {1}{4}\) times, the area of original square.
(c) The area becomes 16 times, the area of original square.
(d) The area becomes \(\frac {1}{6}\) times, 6 the area of original square.
Answer:
(a) The area becomes 4 times, the area of original square.

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.4

1. Construct ΔABC, given AB = 6 cm, ∠A = 30° and ∠B = 75°.
Solution:
Given. One side of ΔABC as AB = 6 cm, m∠A = 30° and m∠B = 75°.
To construct: A triangle with one side and these two angles.
Steps of Construction :
Step 1. We first draw a rough sketch of ΔABC and indicate the measures of side and two angles.

Step 2. Draw a ray AB of length 6 cm.

Step 3. At A; draw a ray AX making an angle 30° with AB.

Step 4. With the help of compass. At B; draw a ray BY making an angle of 75° with AB.

Step 5. Both rays AX and BY intersect, at a point. So the point of intersection of the two rays is C Then. ΔABC is now obtained.

2. Construct an isosceles ΔABC such that AB = 5.3 cm and each base angle = 45°.
Solution:
Given : Isosceles ΔABC with AB = 5.3 cm each base angle = 45°.
To Construct: A triangle with one side and two base angles.
Steps of construction :
Step 1. Draw a rough sketch of ΔABC with given measures

Step 2. Draw a line segment AB = 5.3 cm.

Step 3. Taking A as centre with the help of compass. Draw a ray AX making an angle 45° with AB.

Step 4. With the help of compass and taking B as a centre. Draw a ray BY making an angle 45° with the line segment AB.

Step 5. Rays AX and BY intersect, at a point say C, then ABC is the required triangle.

3. Construct ΔXYZ if XY = 4 cm, ∠X = 45° and ∠Z = 60°.
[Hint : ∠Y = 180° – 45° – 60° = 75°]
Solution:
One side of ΔXYZ as
XY = 4 cm,
∠X = 45°
and ∠Z = 60°.
As we know that by angle-sum property of a triangle; sum of all three angles of a triangle is equal to 180°.
∴ ∠X + ∠Y + ∠Z = 180°
⇒ 45° + ∠Y + 60° = 180°
⇒ 105° + ∠Y = 180°
⇒ ∠Y = 75°.
Now it will be easy to construct triangle with side
XY = 4 cm,
∠X = 45°
and ∠Y = 75°.
Steps of Construction :
Step 1. We first draw a rough sketch of ΔXYZ and indicate the measure of side and two angles.

Step 2. Draw a ray XY of length 4 cm.

Step 3. At X draw a ray XA making an angle of 45° with XY.

Step 4. At Y; draw a ray YB making an angle of 75° with XY.

Step 5. Z has to lie on both rays XA and YB. So, the point of intersection of two rays is Z.
ΔXYZ is now obtained.

4. Examine whether you can construct ΔPQR such that ∠P = 100°, ∠Q = 90° and PQ = 4.3 cm If not possible given reason.
Solution:
No, we cannot construct given ΔPQR.
Reason :
As we know that by angle sum property of a triangle; sum of all three angles a triangle is equal to 180°. But in given question sum of two angles;
m∠P + m∠Q
= 100° + 90°
= 190°
The sum of these two angles should be less than 180°. So triangle with given measures cannot be constructed as it violates the angle sum property of a triangle.

5. Question (i).
In which of the following cases a unique triangle can be drawn ?
(a) BC = 5 cm, ∠B = 90° and ∠C = 100°
(b) AB = 4 cm, BC = 7 cm and CA = 2 cm
(c) XY = 5 cm, ∠X = 45°, ∠Y = 60°
(d) An isosceles triangle with length of each equal side equal to 5 cm.
Answer:
(c) XY = 5 cm, ∠X = 45°, ∠Y = 60°

Question (ii).
A triangle can be constructed by taking two of its angles as.
(a) 110°, 40°
(b) 70°, 115°
(c) 135°, 45°
(d) 90°, 90°
Answer:
(a) 110°, 40°

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.3

1. Construct ΔABC such that AB = 4 cm, ∠B = 30°, BC = 4 cm. Also name the type of triangle on the basis of sides.
Solution:
Given : Two sides of ΔABC as AB = 4 cm, BC = 4 cm and ∠B = 30°.
To construct: A triangle with these two sides and included angle.
Step of Construction :
Step 1. We first draw a rough sketch of the ΔABC and indicate the measure of these two sides and included angle.

Step 2. Draw a line segment BC of length 4 cm.

Step 3. At B draw BX making an angle of 30° with BC (The point A must be somewhere on this ray of the angle).

Step 4. (To fix A, the distance AB has been given) With B as centre, draw an arc of radius 3 cm. It cuts BX at the point A.

Step 5. Join AC.
ΔDEF is now obtained.

Since two sides of triangle are equal.
Therefore ΔABC is an isosceles triangle.

2. Construct ΔABC with AB = 7.5 cm, BC = 5 cm and ∠B = 30°.
Solution:
Given. Two sides of ΔABC as AB = 7.5 cm,
BC = 5 cm
and ∠B = 30°
To construct A triangle with these two sides and included angle.
Steps of Construction.
Step 1. We first draw a rough sketch of the ΔABC and indicate the measures of these two sides and included angle.

Step 2. Draw a line segment BC of length 5 cm.

Step 3. At B draw BX making an angle of 30° with BC. (The point A must be somewhere on this ray of the angle)

Step 4. (To fix A; the distance BC has been given) With B as centre draw an arc of radius 7.5 cm. It cuts CX at the point A.

Step 5 : Join AC.
ΔABC is now obtained.

3. Construct a triangle XYZ, such that XY = 6 cm, YZ = 6 cm and ∠Y = 60°. Also name the type of this triangle.
Solution:
Step 1. Draw a rough sketch of XYZ with given measures.

Step 2. Draw a line segment XY of length 6 cm.

Step 3. With the help of compass, at Y, draw a ray YA making an angle 60°

Step 4. With Y as centre and radius 6 cm. draw an arc intersecting the ray YX at point Z.

Step 5. Join XZ.ΔXYZ is required triangle, Measure the third side. We see that ZX = 6 cm
∴ In Δ XYZ
XY = YZ = ZX = 6 cm
Therefore XYZ is an equilateral triangle.

4. Which of the following triangle can be constructed using SAS criterion.
(a) AB = 5 cm, BC = 5 cm, CA = 6 cm
(b) AB = 5 cm, BC = -5 cm, ∠B = 40°
(c) ∠A = 60°, ∠B = 60°, ∠C = 60°
(d) BC = 5 cm, ∠B = ∠C = 45°
Answer:
(b) AB = 5 cm, BC = -5 cm, ∠B = 40°

Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.2

1. Construct ΔABC in which AB = 3.5 cm, BC = 5 cm and CA = 7 cm.
Solution:
Given : Three sides of a triangle as AB = 3.5 cm, BC = 5 cm and CA = 7 cm.
To construct : A triangle with these three sides.
Step 1. We first draw a rough sketch of the triangle ABC and indicate the lengths of the three sides.

Step 2. Draw a line segment BC = 5 cm.

Step 3 : From B; point A is at a distance 3.5 cm. So, with B as centre, draw an arc of radius
3.5 cm (Now point A will be some where on this arc. Our job is to find where exactly A is.)

Step 4. From C, point A is at a distance of 7 cm. So, with C as centre; draw an arc of radius 7 cm. (A will be some where on this arc. We have to fix it).

Step 5. A has to be on both the arcs drawn. So it is the point of intersection of arcs.
Mark the point of intersection of arcs as A. Join AB and AC.
Thus we obtain ΔABC.

2. Construct a triangle ABC in which AB = BC = 6.5 cm and CA = 4 cm. Also name the kind of triangle drawn.
Solution:
Given : Three sides of triangle as AB = BC = 6.5 cm. and CA = 4 cm.
To construct : A triangle with these three sides.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle ABC and indicate the lengths of the three sides.

Step 2. Draw a line segment AC = 4 cm.

Step 3. From A; point B is at a distance of 6.5 cm. So, with A as centre, draw an arc of radius 6.5 cm. (Now point B will be somewhere on this arc. Our job is to find where exactly A is.)

Step 4. From C; point B is at a distance of 6.5 cm. So; with C as centre; draw an arc of radius 6.5 cm. (B will be some where on this arc. We have to fix it.)

Step 5. B has to be on both the arcs drawn. So it is the point of intersection of arcs. Mark the point of intersection of arcs as B. Join AB and BC.

We observe that AB = BC = 6.5 cm.
Since two sides are of equal length. Thus we obtain an isosceles ΔABC.

3. Construct a triangle XYZ such that length of each side is 5 cm. Also name the kind of triangle drawn.
Solution:
Given : A triangle XYZ in which XY = YZ = ZX = 5 cm..
To Construct. A triangle XYZ with each side 5 cm.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle XYZ and indicate the lengths of the three sides.

Step 2. Draw a line segment YZ = 5 cm.

Step 3. From Y; point X is at a distance of 5 cm. So, with Y as centre, draw an arc of radius 5 cm. (Now point X will be somewhere on this arc. Our job is to find where exactly X is.)

Step 4. From Z, point X is at a distance of 5 cm. So, with Z as centre, draw an arc of radius 5 cm. (X will be somewhere oh this arc. We have to fix it.)

Step 5. Point X has to be on both the arcs drawn. So, it is the point of intersection of arcs.
Mark the point of intersection of arcs as X. Join XY and XZ.

Thus we obtain an equilateral ΔXYZ each of whose side is 5 cm.

4. Construct a triangle PQR such that PQ = 2.5 cm, QR = 6 cm and RP = 6.5 cm. Measure ∠PQR and also name the kind of triangle drawn.
Solution:
Given. Three sides of triangle as PQ = 2.5 cm, QR = 6 cm and RP = 6.5 cm.
To construct. A triangle with these three sides.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle PQR and indicate the lengths of the three sides.

Step 2. Draw a line segment QR of length 6 cm.

Step 3. From Q; point P is at a distance of 2.5 cm. So, with Q as centre, draw an arc of radius 2.5 cm. (Now point P will be some where on this arc. Our job is to find where exactly P is.)

Step 4. From R; point P is at a distance of 6.5 cm. So; with R as centre; draw an arc of radius 6.5 cm. (P will be somewhere on this arc. We have to fix it.)

Step 5. Point P has to be on both the arcs drawn. So, it is the point of intersection of arcs. Mark a point of intersection of arcs as P. Join PQ and PR.

Thus we obtain ΔPQR; on measuring ∠PQR, we observe that ∠PQR = 90° so it is a right angled triangle.

5. Construct a triangle ABC, in which AB = 6 cm, BC = 2 cm, CA = 3 cm. (If possible). If not possible give the reason.
Solution:
Since AB = 6 cm, BC = 2 cm, CA = 3 cm
Here BC + CA = 2 cm + 3 cm
= 5 cm < 6 cm < AB
Which is not possible because the sum of two sides of a triangle is always greater than third side of the triangle.

6. Question (i).
Which of the following can be used to construct a triangle ?
(a) The lengths of the three sides
(b) The perimeter of the triangle
(c) The measures of three angles
(d) The name of three vertices
Answer:
(a) The lengths of the three sides

Question (ii).
A triangle can be constructed by taking its sides as :
(a) 1.8 cm, 2.6 cm, 4.4 cm
(b) 3 cm, 4 cm, 8 cm
(c) 4 cm, 7 cm, 2 cm
(d) 5 cm, 4 cm, 4 cm.
Answer:
(d) 5 cm, 4 cm, 4 cm.