Punjab State Board PSEB 7th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 7 Maths Chapter 10 Practical Geometry Ex 10.2
1. Construct ΔABC in which AB = 3.5 cm, BC = 5 cm and CA = 7 cm.
Solution:
Given : Three sides of a triangle as AB = 3.5 cm, BC = 5 cm and CA = 7 cm.
To construct : A triangle with these three sides.
Step 1. We first draw a rough sketch of the triangle ABC and indicate the lengths of the three sides.
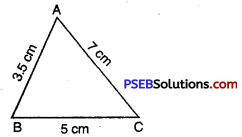
Step 2. Draw a line segment BC = 5 cm.
![]()
Step 3 : From B; point A is at a distance 3.5 cm. So, with B as centre, draw an arc of radius
3.5 cm (Now point A will be some where on this arc. Our job is to find where exactly A is.)
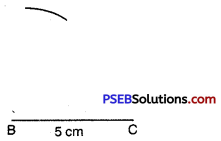
Step 4. From C, point A is at a distance of 7 cm. So, with C as centre; draw an arc of radius 7 cm. (A will be some where on this arc. We have to fix it).
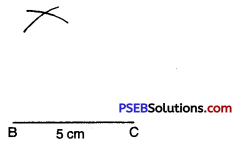
Step 5. A has to be on both the arcs drawn. So it is the point of intersection of arcs.
Mark the point of intersection of arcs as A. Join AB and AC.
Thus we obtain ΔABC.
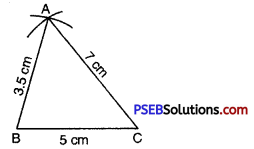
![]()
2. Construct a triangle ABC in which AB = BC = 6.5 cm and CA = 4 cm. Also name the kind of triangle drawn.
Solution:
Given : Three sides of triangle as AB = BC = 6.5 cm. and CA = 4 cm.
To construct : A triangle with these three sides.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle ABC and indicate the lengths of the three sides.
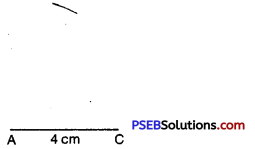
Step 2. Draw a line segment AC = 4 cm.
![]()
Step 3. From A; point B is at a distance of 6.5 cm. So, with A as centre, draw an arc of radius 6.5 cm. (Now point B will be somewhere on this arc. Our job is to find where exactly A is.)
Step 4. From C; point B is at a distance of 6.5 cm. So; with C as centre; draw an arc of radius 6.5 cm. (B will be some where on this arc. We have to fix it.)
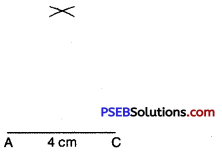
Step 5. B has to be on both the arcs drawn. So it is the point of intersection of arcs. Mark the point of intersection of arcs as B. Join AB and BC.
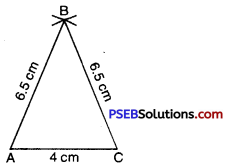
We observe that AB = BC = 6.5 cm.
Since two sides are of equal length. Thus we obtain an isosceles ΔABC.
![]()
3. Construct a triangle XYZ such that length of each side is 5 cm. Also name the kind of triangle drawn.
Solution:
Given : A triangle XYZ in which XY = YZ = ZX = 5 cm..
To Construct. A triangle XYZ with each side 5 cm.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle XYZ and indicate the lengths of the three sides.
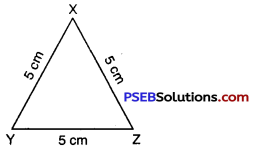
Step 2. Draw a line segment YZ = 5 cm.
![]()
Step 3. From Y; point X is at a distance of 5 cm. So, with Y as centre, draw an arc of radius 5 cm. (Now point X will be somewhere on this arc. Our job is to find where exactly X is.)
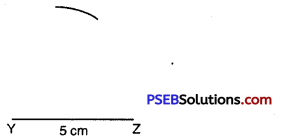
Step 4. From Z, point X is at a distance of 5 cm. So, with Z as centre, draw an arc of radius 5 cm. (X will be somewhere oh this arc. We have to fix it.)
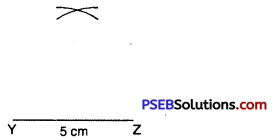
Step 5. Point X has to be on both the arcs drawn. So, it is the point of intersection of arcs.
Mark the point of intersection of arcs as X. Join XY and XZ.
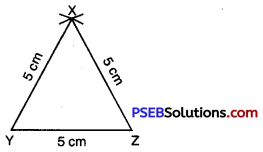
Thus we obtain an equilateral ΔXYZ each of whose side is 5 cm.
![]()
4. Construct a triangle PQR such that PQ = 2.5 cm, QR = 6 cm and RP = 6.5 cm. Measure ∠PQR and also name the kind of triangle drawn.
Solution:
Given. Three sides of triangle as PQ = 2.5 cm, QR = 6 cm and RP = 6.5 cm.
To construct. A triangle with these three sides.
Steps of Construction :
Step 1. We first draw a rough sketch of the triangle PQR and indicate the lengths of the three sides.
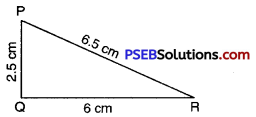
Step 2. Draw a line segment QR of length 6 cm.
![]()
Step 3. From Q; point P is at a distance of 2.5 cm. So, with Q as centre, draw an arc of radius 2.5 cm. (Now point P will be some where on this arc. Our job is to find where exactly P is.)

Step 4. From R; point P is at a distance of 6.5 cm. So; with R as centre; draw an arc of radius 6.5 cm. (P will be somewhere on this arc. We have to fix it.)
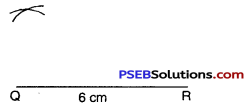
Step 5. Point P has to be on both the arcs drawn. So, it is the point of intersection of arcs. Mark a point of intersection of arcs as P. Join PQ and PR.
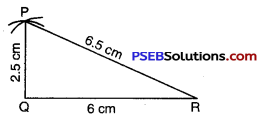
Thus we obtain ΔPQR; on measuring ∠PQR, we observe that ∠PQR = 90° so it is a right angled triangle.
![]()
5. Construct a triangle ABC, in which AB = 6 cm, BC = 2 cm, CA = 3 cm. (If possible). If not possible give the reason.
Solution:
Since AB = 6 cm, BC = 2 cm, CA = 3 cm
Here BC + CA = 2 cm + 3 cm
= 5 cm < 6 cm < AB
Which is not possible because the sum of two sides of a triangle is always greater than third side of the triangle.
6. Question (i).
Which of the following can be used to construct a triangle ?
(a) The lengths of the three sides
(b) The perimeter of the triangle
(c) The measures of three angles
(d) The name of three vertices
Answer:
(a) The lengths of the three sides
Question (ii).
A triangle can be constructed by taking its sides as :
(a) 1.8 cm, 2.6 cm, 4.4 cm
(b) 3 cm, 4 cm, 8 cm
(c) 4 cm, 7 cm, 2 cm
(d) 5 cm, 4 cm, 4 cm.
Answer:
(d) 5 cm, 4 cm, 4 cm.