Class 12

Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 29 धारणीय आर्थिक विकास, आर्थिक विकास का वातावरण पर प्रभाव तथा ग्लोबल वार्मिंग Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 12 Economics Chapter 29 धारणीय आर्थिक विकास, आर्थिक विकास का वातावरण पर प्रभाव तथा ग्लोबल वार्मिंग

PSEB 12th Class Economics धारणीय आर्थिक विकास, आर्थिक विकास का वातावरण पर प्रभाव तथा ग्लोबल वार्मिंग Textbook Questions, and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
चिरकालीन विकास की परिभाषा दीजिए।
उत्तर-
चिरकालीन विकास वह क्रिया है, जिसमें आर्थिक विकास द्वारा न केवल वर्तमान पीढ़ी बल्कि भविष्य की पीढ़ी की लम्बे समय तक की आवश्यकताओं की अधिकतम पूर्ति की जाती है।

प्रश्न 2.
हरित शुद्ध राष्ट्रीय आय की धारणा को स्पष्ट करो।
उत्तर-
हरित शुद्ध राष्ट्रीय आय = शुद्ध राष्ट्रीय आय – राष्ट्रीय पूंजी की घिसावट।

• शुद्ध राष्ट्रीय आय-एक देश में निवासियों द्वारा उत्पादित अंतिम वस्तुओं, सेवाओं के बाजार मूल्य को शुद्ध राष्ट्रीय आय कहा जाता है।
• राष्ट्रीय पूंजी की घिसावट-प्राकृतिक साधनों में कमी + वातावरण की अधोगति।

प्रश्न 3.
साधनों की सीमित उपलब्धता से क्या अभिप्राय है ?
उत्तर-
साधनों की सीमित उपलब्धता से अभिप्राय है, प्राकृतिक साधनों भूमि, जल, खनिज, जंगल इत्य, की मात्रा का आवश्यकता से कम पाया जाना। आर्थिक विकास के लिए सीमित साधनों के उचित प्रयोग के लिए चयन की समस्या उत्पन्न होती है।

प्रश्न 4.
भारत में वनों की स्थिति का वर्णन कीजिए।
उत्तर-
सन् 2011 के आंकड़ों के अनुसार, भारत में 67.6 मिलियन हेक्टेयर भूमि पर वन पाए जाते थे जोकि कुल क्षेत्रफल का 20% हिस्सा है। एक देश के वातावरण को संतुलित रखने के लिए देश में 33 प्रतिशत क्षेत्रफल पर वन होने चाहिए।

प्रश्न 5.
वातावरण की अधोगति से क्या अभिप्राय है ?
उत्तर-
वातावरण की अधोगति से अभिप्राय है जल, भूमि, खनिज तथा जलवायु का दुरुपयोग होना जिससे देश की धरती बंजर हो जाती है, जिससे कृषि तथा औद्योगिक विकास रुक जाता है।

प्रश्न 6.
औद्योगिक प्रदूषण से क्या अभिप्राय है ?
उत्तर-
औद्योगिक विकास के परिणामस्वरूप जल, वायु, शोर, भूमि तथा मौसम की अधोगति को औद्योगिक प्रदूषण कहा जाता है।

प्रश्न 7.
एक अर्थव्यवस्था की वास्तविक आय में इस प्रकार वृद्धि होना जिससे पर्यावरण संरक्षण तथा जीवन की गुणवत्ता बनी रहे, जिससे न केवल वर्तमान पीढ़ी बल्कि भावी पीढ़ी को अधिकतम लाभ प्राप्त हो सके को चिरकालीन विकास कहते हैं।
उत्तर-
सही।

प्रश्न 8.
धारणीय विकास का अर्थ है ……….
(a) प्राकृतिक साधनों का कुशल प्रयोग
(b) भावी पीढ़ी के जीवन की गुणवत्ता बनी रहे।
(c) प्रदूषण में वृद्धि न हो
(d) उपरोक्त सभी।
उत्तर-
(d) उपरोक्त सभी।

प्रश्न 9.
हरित शुद्ध राष्ट्रीय आय = शुद्ध राष्ट्रीय आय (-) ………….
उत्तर-
पूंजी की घिसावट।

प्रश्न 10.
विशुद्ध बचतें (Genuine Savings) = बचत की दर (-) मनुष्य निर्मित पूंजी की घिसावट (-)
उत्तर-
प्राकृतिक पूंजी की घिसावट।

प्रश्न 11.
भूमि की अधोगति से क्या अभिप्राय है ?
उत्तर-
मिट्टी के कटाव तथा पानी के जमाव के कारण भूमि के उपजाऊपन की क्षति को भूमि की अधोगति कहते हैं।

प्रश्न 29.
आर्थिक वृद्धि (Economic Growth) से क्या अभिप्राय है?
उत्तर-
आर्थिक वृद्धि से अभिप्राय है दीर्घकाल में प्रति व्यक्ति वास्तविक आय में वृद्धि होना।

प्रश्न 13.
आर्थिक विकास (Economic Development) से क्या अभिप्राय है ?
उत्तर-
आर्थिक विकास से अभिप्राय है प्रति व्यक्ति वास्तविक आय और आर्थिक कल्याण में दीर्घकाल में वृद्धि होना।

प्रश्न 14.
चिरकालीन विकास (Sustainable Development) से क्या अभिप्राय है ?
उत्तर-
चिरकालीन विकास का अर्थ है प्रति व्यक्ति आय, आर्थिक कल्याण में वृद्धि के साथ-साथ भविष्य की पीढ़ी के आर्थिक कल्याण को बनाए रखना।

प्रश्न 15.
जीवन की गुणवत्ता का अर्थ लोगों के स्वास्थ्य तथा शिक्षा जीवन से होता है।
उत्तर-
सही।

प्रश्न 16.
वायु प्रदूषण का अर्थ है वायु में जीवन के लिए ज़रूरी तत्त्वों में प्रदूषण।
उत्तर-
सही।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
चिरकालीन विकास से क्या अभिप्राय है ?
उत्तर-
धारणीय आर्थिक विकास का अर्थ-धारणीय आर्थिक विकास (Sustainable Economic Development) की धारणा बरंट्रडलैंड रिपोर्ट (Brendtland Report) में पहली बार 1987 में प्रयोग की गई। इस सम्बन्ध में विकास तथा पर्यावरण के लिए विश्व कमीशन (World Commission on environment and development) की स्थापना की गई थी। इस कमीशन के अनुसार विकास की प्रक्रिया का सम्बन्ध वर्तमान की कम समय की आवश्यकताओं से नहीं है, बल्कि इसका सम्बन्ध लम्बे समय के आर्थिक विकास से होता है। रॉबर्ट रिपीटो के शब्दों में, “धारणीय विकास एक ऐसी विकास नीति है जोकि प्राकृतिक तथा मानवीय साधनों, वित्तीय तथा भौतिक भण्डारों का प्रबन्धीकरण इस प्रकार करती है जिससे दीर्घकाल में धन तथा भलाई में वृद्धि हो।”

प्रश्न 2.
पर्यावरण की अधोगति (Environment Degradation) से क्या अभिप्राय है ?
उत्तर–
स्वतन्त्रता के पश्चात् भारत में आर्थिक विकास की वृद्धि के लिए कृषि उत्पादन तथा उद्योगों का विकास किया गया ताकि बढ़ रही जनसंख्या की आवश्यकताओं को पूरा किया जा सके। परन्तु मशीनीकरण पर अधिक ज़ोर तथा खनिज पदार्थों के बिना सोचे-समझे अधिक प्रयोग से पर्यावरण की अधोगति में वृद्धि हुई है। पर्यावरण की अधोगति से अभिप्राय जल, भूमि, खनिज तथा जलवायु का दुरुपयोग होना जिससे एक देश की धरती बंजर हो जाती है।

प्रश्न 3.
वायु प्रदूषण से क्या अभिप्राय है ?
उत्तर-
वायु प्रदूषण-वायु में मुख्य तौर पर 21% ऑक्सीजन, 1% कार्बन डाइऑक्साइड तथा 78.09% नाइट्रोजन की मात्रा पाई जाती हैं। उद्योगों के विकास से वायु में सल्फर डाइऑक्साइड, कार्बन डाइऑक्साइड तथा कार्बन मोनोऑक्साइड गैसें शामिल हो जाती हैं। इन गैसों के शामिल होने से टी०बी०, दमा, खांसी इत्यादि बीमारियां फैल जाती हैं। इसको वायु प्रदूषण कहा जाता है।

प्रश्न 4.
जल प्रदूषण से क्या अभिप्राय है ?
उत्तर-
जल प्रदूषण-उद्योगों के विकास से जो रासायनिक कूड़ा-कर्कट तथा गन्दा जल निकलता है, इसको नदियों, झीलों तथा नहरों में छोड़ दिया जाता है। इससे जहरीले पदार्थ तथा हानिकारक धातुओं के कण पानी में शामिल हो जाते हैं यह पानी पीने के लिए प्रयोग किया जाता है, जिस कारण बीमारियां फैलती हैं। इसको जल प्रदूषण कहा जाता

प्रश्न 5.
ध्वनि प्रदूषण से क्या अभिप्राय है ?
उत्तर-
ध्वनि प्रदूषण-उद्योगों में मशीनों के चलने के कारण शोर उत्पन्न होता है। इससे मज़दूरों की सुनने की शक्ति पर बुरा प्रभाव पड़ता है। मशीनों में से निकलने वाला धुआं तथा कण बहुत-सी बीमारियों को जन्म देते हैं। इससे टी०बी०, दमा, ब्लड प्रैशर तथा दिमागी तनाव इत्यादि बीमारियां उत्पन्न होती हैं।

III. लघु उत्तरीय प्रश्न | (Short Answer Type Questions)

प्रश्न 1.
धारणीय विकास के मुख्य लक्षण बताओ।
उत्तर-
धारणीय विकास एक ऐसी प्रक्रिया है, जिसमें वर्तमान पीढ़ी की आवश्यकताओं की पूर्ति इस ढंग से की जाती है, ताकि भविष्य की पीढ़ी अपनी आवश्यकताओं की पूर्ति आसानी से कर सके। धारणीय आर्थिक विकास के मुख्य लक्षण निम्नलिखित हैं-

1. लम्बे समय तक प्रति व्यक्ति आय तथा आर्थिक भलाई में वृद्धि हो।
2. प्राकृतिक साधनों का प्रयोग वर्तमान में आवश्यकता से अधिक न किया जाए।
3. भविष्य की पीढ़ी अपनी आवश्यकताओं को आसानी से पूरा कर सके।
4. बिना प्रदूषण के अच्छा जीवन स्तर व्यतीत किया जा सके।

प्रश्न 2.
धारणीय आर्थिक विकास का माप कैसे किया जाता है ?
उत्तर-
धारणीय आर्थिक विकास का माप दो धारणाओं से किया जाता है-

1. हरित शुद्ध राष्ट्रीय आय (Green Net National Income)-हरित शुद्ध राष्ट्रीय आय = शुद्ध राष्ट्रीय आय (-) प्राकृतिक साधनों का प्रयोग (-) पर्यावरण अधोगति।
2. वास्तविक बचत (Genuine Savings)-वास्तविक बचत = बचत की दर (-) मनुष्य द्वारा उत्पादित पूंजी की घिसावट (-) प्राकृतिक साधनों का प्रयोग (-) पर्यावरण अधोगति।

प्रश्न 3.
भारत में साधनों की प्राप्ति का वर्णन करो।
उत्तर-
भारत सम्बन्धी कहा जाता है कि यह एक अमीर देश है परन्तु इसमें रहने वाले लोग ग़रीब हैं। भारत में साधन अधिक मात्रा में पाए जाते हैं। लोहा तथा कोयला अधिक मात्रा में हैं परन्तु खनिज, पेट्रोल तथा तेल की कमी पाई जाती है। भारत में जल साधनों की कोई कमी नहीं। भारत का क्षेत्रफल भी विशाल है। मानवीय साधन बहुत अधिक हैं, परन्तु इन साधनों का प्रयोग उचित ढंग से नहीं किया गया। वन साधनों की कमी पाई जाती है। प्रत्येक देश क्षेत्रफल का 33% भाग वनों के अधीन होना चाहिए, परन्तु भारत में केवल 20% हिस्से पर वन हैं। 54% भूमि पर कृषि नहीं की जाती। भू-क्षरण, सेम, बाढ़ इत्यादि समस्याएं हैं। उद्योगों का विकास किया गया है जिससे औद्योगिक प्रदूषण की समस्या उत्पन्न हो गई है। इसलिए साधनों की प्राप्ति तो काफ़ी है परन्तु इसका उचित तरह से प्रयोग नहीं किया गया।

प्रश्न 4.
भारत में प्राकृतिक साधनों पर नोट लिखो।
उत्तर-
भारत में प्राकृतिक साधन निम्नलिखित हैं-

1. भूमि साधन-भारत का भौगोलिक क्षेत्र 329 मिलियन हेक्टेयर है। इस क्षेत्र में से 46 प्रतिशत भाग कृषि उत्पादन अधीन है।
2. जल साधन-भारत में जल साधन काफ़ी मात्रा में हैं। पूरे वर्ष बहने वाली नदियां हैं, परन्तु जल साधनों के 38 प्रतिशत भाग का प्रयोग किया जाता है।
3. वन-भारत में कुल क्षेत्र का 20 प्रतिशत भाग वनों के अधीन है।
4. खनिज-भारत में लोहा तथा कोयला काफ़ी मात्रा में है, परन्तु तांबा, जिंक, निकल, सल्फर तथा पेट्रोल इत्यादि कम मात्रा में प्राप्त होते हैं।

प्रश्न 5.
पर्यावरण की अधोगति से क्या अभिप्राय है ?
उत्तर-
पर्यावरण की अधोगति से अभिप्राय यह है कि स्वतन्त्रता के पश्चात् कृषि उत्पादन तथा उद्योगों का विकास इतनी तीव्रता से किया गया, जिससे भूमि बंजर हो गई, खनिज पदार्थों का दुरुपयोग किया गया, वायु तथा जल प्रदूषित हो गए, कृषि उत्पादन के कारण क्षार तथा सेम की समस्याएं उत्पन्न हो गई हैं। इसको पर्यावरण की अधोगति कहा जाता है।

प्रश्न 6.
कृषि उत्पादन द्वारा भूमि की अधोगति कैसे हुई है ?
उत्तर-
भारत में स्वतन्त्रता के पश्चात् बढ़ती हुई जनसंख्या की आवश्यकता को पूरा करने के लिए कृषि उत्पादन में वृद्धि की गई। वनों की कटाई करके कृषि की गई। इससे भूमि की अधोगति हुई है। जैसे कि भारत का कुल क्षेत्रफल 329 मिलियन हेक्टेयर है। इस क्षेत्रफल में से 144 मिलियन हेक्येटर भूमि, भूमि कटाव की शिकार हो गई है। 30 मिलियन हेक्टेयर भूमि, काला शोरा, सेम तथा भूमि कटाव के कारण खराब हो गई है। इस प्रकार 54% हिस्से की अधोगति हो चुकी है जिसमें सुधार करने की आवश्यकता है।

प्रश्न 7.
प्रदूषण की किस्में बताएं।
उत्तर-

1. वायु प्रदूषण-वायु में मुख्य तौर पर 21% ऑक्सीजन, 1% कार्बन डाइऑक्साइड तथा 87% नाइट्रोजन की मात्रा पाई जाती है। उद्योगों के विकास से वायु में सल्फर डाइऑक्साइड, कार्बन डाइऑक्साइड तथा कार्बन मोनोऑक्साइड गैसें शामिल हो जाती हैं। इन गैसों के शामिल होने से टी० बी०, दमा, खांसी इत्यादि बीमारियां फैल जाती हैं। इसको वायु प्रदूषण कहा जाता है।
2. जल प्रदूषण-उद्योगों के विकास से जो रासायनिक कूड़ा-कर्कट तथा गन्दा जल निकलता है, इसको नदियों, झीलों तथा नहरों में छोड़ दिया जाता है। इससे जहरीले पदार्थ तथा हानिकारक धातुओं के कण पानी में शामिल हो जाते हैं यह पानी पीने के लिए प्रयोग किया जाता है, जिस कारण बीमारियां फैलती हैं। इसको जल प्रदूषण कहा जाता है।
3. ध्वनि प्रदूषण-उद्योगों में मशीनों के चलने के कारण शोर उत्पन्न होता है। इससे मजदूरों की सुनने की शक्ति पर बुरा प्रभाव पड़ता है। मशीनों में से निकलने वाला धुआं तथा कण बहुत-सी बीमारियों को जन्म देते हैं। इससे टी० बी०, दमा, ब्लड प्रैशर तथा दिमागी तनाव इत्यादि बीमारियां उत्पन्न होती हैं।

IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
धारणीय आर्थिक विकास से क्या अभिप्राय है ? इसकी मुख्य विशेषताएं बताओ। इसका माप कैसे किया जाता है ?
(What is sustainable Economic Growth? Explain the main features of sustainable Economic Growth. How is it measured ?)
उत्तर-
धारणीय आर्थिक विकास का अर्थ-धारणीय आर्थिक विकास (Sustainable Economic Development) की धारणा बरंट्रडलैंड रिपोर्ट (Brendtland Report) में पहली बार 1987 में प्रयोग की गई। इस सम्बन्ध में विकास तथा पर्यावरण के लिए विश्व कमीशन (World Commission on environment and development) की स्थापना की गई थी। इस कमिशन के अनुसार विकास की प्रक्रिया का सम्बन्ध वर्तमान की कम समय की आवश्यकताओं से नहीं है, बल्कि इसका सम्बन्ध लम्बे समय के आर्थिक विकास से होता है। वर्तमान काल के लोगों की आवश्यकताओं की पूर्ति के लिए भूमि, जल, खनिज पदार्थों तथा वनों इत्यादि का प्रयोग लापरवाही से न किया जाए ताकि भविष्यकाल के लोगों की आवश्यकताओं की अवहेलना की जाए तथा पर्यावरण का दुरुपयोग किया जाए।

पर्यावरण में भूमि तथा मौसम को ही शामिल नहीं किया जाता बल्कि इसमें जानवर, पशु, पक्षी, पौधे, जंगल, इत्यादि भी शामिल होते हैं। इस प्रकार धारणीय विकास का अर्थ आर्थिक विकास के परिणामस्वरूप वर्तमान तथा भविष्य की नस्लें अधिकतम लाभ प्राप्त कर सकें। रोबर्ट रिपीटो के शब्दों में, “धारणीय विकास एक ऐसी विकास नीति है जोकि प्राकृतिक तथा मानवीय साधनों, वित्तीय तथा भौतिक भण्डारों का प्रबन्धीकरण इस प्रकार करती है, जिससे दीर्घकाल में धन तथा भलाई में वृद्धि हो।” धारणीय आर्थिक विकास की विशेषताएं-धारणीय विकास की मुख्य विशेषताएं निम्नलिखित हैं-

1. प्रति व्यक्ति आय तथा आर्थिक भलाई में धारणीय वृद्धि।
2. प्राकृतिक साधनों का आवश्यकता से अधिक प्रयोग न किया जाए।
3. वर्तमान पीढ़ी, प्राकृतिक साधनों का प्रयोग इस प्रकार करें कि भविष्य की पीढ़ी के लिए आवश्यकताएं पूरी करने के लिए साधनों की कमी न हो।
4. प्राकृतिक साधनों का प्रयोग इस प्रकार किया जाए, जिससे जल प्रदूषण, वायु प्रदूषण तथा ध्वनि प्रदूषण में वृद्धि न हो। आर्थिक विकास से प्रदूषण की समस्या उत्पन्न हो सकती है। जिससे वर्तमान तथा भविष्य की नस्लों की जीवन गुणवत्ता (Quality of life) पर बुरा प्रभाव पड़ सकता है।
5. इसमें वातावरण सुरक्षा की ओर अधिक जोर दिया गया है।
6. इसमें संरचनात्मक, तकनीकी तथा संस्थागत परिवर्तन पर अधिक ज़ोर नहीं दिया गया।
7. धारणीय विकास का अर्थ जीवन गुणवत्ता का विकास है। अच्छी जीवन गुणवत्ता से अभिप्राय अच्छा स्वास्थ्य, अच्छी शिक्षा, शुद्ध वातावरण, शुद्ध जल, वायु तथा अच्छी सामाजिक सुरक्षा से होता है।

धारणीय विकास के सूचक तथा शर्ते-

• प्रति व्यक्ति आय तथा जीवन गुणवत्ता का विकास।
• प्राकृतिक साधनों पर वातावरण का सद् उपयोग।
• ग्रामीण जीवन का सर्वपक्षीय विकास तथा आधुनिक सुविधाएं, पानी, बिजली, टी० वी०, टेलीफोन इत्यादि सुविधाओं में वृद्धि।
• कृषि उत्पादन में कीटनाशक तथा रासायनिक खादों का कम प्रयोग।
• उद्योगों द्वारा जल, वायु, तथा ध्वनि प्रदूषण में कमी।

धारणीय आर्थिक विकास की माप विधिधारणीय विकास का माप दो समष्टि धारणाओं द्वारा किया जा सकता है –
1. हरित शुद्ध राष्ट्रीय आय (Green Net National Income) हरित शुद्ध राष्ट्रीय आय का माप निम्नलिखित सूत्र द्वारा किया जाता है हरित शुद्ध राष्ट्रीय आय = शुद्ध राष्ट्रीय आय ( – ) प्राकृतिक पूंजी की घिसावट |

• शुद्ध राष्ट्रीय आय-देश में अंतिम वस्तुओं तथा सेवाओं के एक वर्ष के उत्पादन को शुद्ध राष्ट्रीय आय कहा जाता है।
• प्राकृतिक पूंजी की घिसावट-प्राकृतिक पूंजी का अर्थ है प्राकृतिक साधन तथा वातावरण का योग।

प्राकृतिक साधनों तथा वातावरण की घिसावट का अर्थ है, इन साधनों के प्रयोग द्वारा मूल्य में कमी। वास्तविक बचत (Genuine Savings)-वास्तविक बचत द्वारा भी चिरकालीन विकास का माप किया जाता है। इस उद्देश्य के लिए निम्नलिखित सूत्र का प्रयोग होता है| वास्तविक बचत = बचत की दर (-) मनुष्य द्वारा बनाई पूंजी की घिसावट – प्राकृतिक पूंजी की घिसावट |

वास्तविक बचत अधिक होने का अर्थ है अधिक चिरकालीन विकास की दर।

1. बचत की दर-आय में से उपभोग खर्च घटाकर जो राशि शेष बच जाती है।
2. मनुष्य द्वारा बनाई पूंजी की घिसावट-मनुष्य द्वारा बनाई मशीनों तथा औज़ारों की घिसावट।
3. प्राकृतिक पूंजी की घिसावट-प्राकृतिक पूंजी की घिसावट में प्राकृतिक साधनों तथा वातावरण के निरन्तर प्रयोग द्वारा मूल्य में हुए नुकसान को शामिल किया जाता है।

प्रश्न 2.
साधनों की सीमित उपलब्धता से क्या अभिप्राय है ? भारत में साधनों की प्राप्ति का वर्णन कीजिए।
(What do you mean by Limited Availability of Resources? Explain the availability of Resources in India.)
उत्तर-
प्रो० लईस के अनुसार, “किसी देश में साधनों की मात्रा, उस देश के आर्थिक विकास की मात्रा तथा सीमा का निर्धारण करती है।” अल्पविकसित देशों का विकास उस देश में प्राप्त साधनों पर निर्भर करता है। प्राकृतिक साधनों में भूमि, जल साधन, खनिज पदार्थ, वन, मौसम इत्यादि को शामिल किया जाता है। मनुष्यों को देश के कुछ साधनों का ज्ञान होता है, परन्तु कुछ साधन प्रकृति की गोद में छिपे होते हैं, जिनको ढूंढ़ने की आवश्यकता होती है। इस तरह कुछ साधन जैसे कि भूमि, जल, मछलियां, वन इत्यादि का पुनर्निर्माण होता रहता है परन्तु कुछ साधन जैसे कि खनिज, पेट्रोल इत्यादि समाप्त होने वाले होते हैं। इस प्रकार प्रत्येक देश में साधनों की सीमित उपलब्धता पाई जाती है।

आर्थिक विकास के लिए इन साधनों के उचित प्रयोग की आवश्यकता होती है। साधन विकास के निर्देशक सिद्धान्त-

1. साधनों का प्रयोग इस प्रकार किया जाए ताकि साधनों का दुरुपयोग कम-से-कम हो।
2. पूर्ण निर्मित साधनों तथा नष्ट योग्य साधनों का प्रयोग अच्छे ढंग से किया जाए।
3. साधनों द्वारा बहुपक्षीय उद्देश्यों की पूर्ति की जाए, जैसे कि डैमों द्वारा बिजली, सिंचाई, बाढ़ नियंत्रण इत्यादि उद्देश्यों की पूर्ति होती है।
4. उद्योगों की स्थापना साधनों की प्राप्ति के स्थानों पर करके उत्पादन लागत में कमी की जाए।
5. शक्ति की पूर्ति में वृद्धि करके दूसरे साधनों का उत्तम प्रयोग किया जाए।

भारत में प्राकृतिक साधन-
1. भूमि साधन-भारत का भौगोलिक क्षेत्रफल 329 मिलियन हेक्टेयर है। इसमें से 306 मिलियन हेक्टेयर सम्बन्धी आंकड़े उपलब्ध हैं। यदि हम बंजर, भूमि, वन अधीन क्षेत्र, चरागाहें तथा बेकार भूमि को छोड़ देते हैं तो कृषि योग्य 141 मिलियन हेक्टेयर भूमि रह जाती है, जोकि कुल भूमि का 46% हिस्सा है। सरकार को 54% भूमि जिस पर कृषि नहीं होती इसलिए उचित नीति बनाने की आवश्यकता है।

2. वन साधन-ग्याहरवीं पंचवर्षीय योजना अनुसार भारत में सन् 2017 में 69 मिलियन हेक्टेयर क्षेत्र पर वन पाए जाते थे, जोकि कुल क्षेत्रफल का लगभग 20 प्रतिशत हिस्सा है, भूमि के 33 प्रतिशत क्षेत्र पर वन होने चाहिए। परन्तु वन साधन बढ़ने की जगह पर कम होते जा रहे हैं। प्रत्येक वर्ष 1.3 से 1.5 मिलियन हेक्टेयर भूमि पर वन काटे जाते हैं, जिससे प्राप्त लकड़ी टीक, बोर्ड, प्लाई इत्यादि के उद्योगों में प्रयोग होती है। सरकार ने 2015 में वनों सम्बन्धी नीति का निर्माण किया है। 33% क्षेत्र पर वन बढ़ाने का लक्ष्य रखा गया है।

3. जल साधन-भारत में जल साधन काफ़ी मात्रा में पाए जाते हैं। प्रो० बी० एस० नाग तथा जी० एन० कठपालिया ने अनुमान लगाया कि 1974 से 2005 तक 4000 कुइबक किलोमीटर वर्षा हुई। इसको तीन भागों में विभाजित कर सकते हैं। 2150 कुइबक किलोमीटर जल नदियों में चला जाता है तथा 700 कुइब्रक किलोमीटर जल वायुमडल में भाप बनकर उड़ जाता है। 1974 में 380 कुइबक किलोमीटर मीट्रिक जल का प्रयोग किया जाता था जोकि 2017 में बढ़कर 250 कुइबक किलोमीटर होने का अनुमान है। भारत में पूरे वर्ष बहने वाली नदियाँ हैं, जिन पर डैम बनाएं गए हैं। नहरों, टैंकों तथा ट्यूबवैलों द्वारा सिंचाई की जाती है। नदियों की सफाई की ओर और अधिक ध्यान दिया जा रहा है।

4. मछली पालन-भारत, विश्व में मछली पालने के क्षेत्र में तीसरा स्थान रखता है। समुद्र के किनारे पर रहने वाले एक मिलियन मछुआरे, मछलियों द्वारा जीवन पोषण करते हैं। 1951 में 0.7 मिलियन टन मछलियों का उत्पादन किया गया जोकि 2017-18 में बढ़कर 9.9% मिलियन टन हो गया। परन्तु भारत द्वारा एशिया में 9 प्रतिशत मछलियों का उत्पादन किया जाता है जबकि जापान द्वारा 43 प्रतिशत उत्पादन किया जाता है।

5. खनिज साधन-भारत में कोयला तथा लोहा काफ़ी मात्रा में पाए जाते हैं परन्तु कॉपर, जिंक, निकल, सल्फर, पेट्रोल इत्यादि खनिज पदार्थों की कमी पाई जाती है। परन्तु भारत में कोयले की खानें बहुत नीचे पाई जाती हैं, जिनमें से कोयला निकालने की लागत बहुत अधिक आती है। 1994 में सरकार ने नई खनिज नीति की घोषणा की है। जिस द्वारा खनिज पदार्थों को निजी क्षेत्र तथा विदेशी निवेशकों को सौंपने की योजना है। दसवीं योजना में खनिज साधनों को निजी क्षेत्र में विकसित करने का प्रोग्राम है।
भारत में साधनों को देखकर यह कह सकते हैं कि साधन सीमित मात्रा में हैं। इनका प्रयोग करने के लिए उचित नीति की आवश्यकता है।

प्रश्न 3.
पर्यावरण की अधोगति (Environmental Degradation) से क्या अभिप्राय है ? भारत में साधनों की अधोगति पर प्रकाश डालें।
(What is meant by Environment Degradation? Discuss its effects on degradation of Resources in India.)
उत्तर-
स्वतन्त्रता के पश्चात् भारत में आर्थिक विकास की वृद्धि के लिए कृषि उत्पादन तथा उद्योगों का विकास किया गया ताकि बढ़ रही जनसंख्या की आवश्यकताओं को पूरा किया जा सके। परन्तु मशीनीकरण पर अधिक ज़ोर तथा खनिज पदार्थों के बिना सोचे-समझे अधिक प्रयोग से पर्यावरण की अधोगति में वृद्धि हुई है। पर्यावरण की अधोगति से अभिप्राय जल, भूमि, खनिज तथा जलवायु का दुरुपयोग होना, जिससे एक देश की धरती बंजर हो जाती है।

भारत में साधनों की अधोगति अग्रलिखित अनुसार हुई है –
1. कृषि तथा भूमि अधोगति (Agriculture and Land Degradation)-भारत के कृषि उत्पादन मंत्रालय अनुसार भारत में भूमि अधोगति तथा भू-क्षरण (Soil Erosion) की समस्या गंभीर रूप धारण कर चुकी है। बाढ़ों तथा आंधियां इत्यादि ऋतु उपद्रवों के कारण भूमि की ऊपरी परत के हट जाने को भू-क्षरण कहा जाता है। भारत में कुल भौगोलिक क्षेत्र 329 मिलियन हेक्टेयर में से 144 मिलियन हेक्टेयर भूमि, भू-अपरदन का शिकार हो चुकी है। 30 मिलियन हेक्टेयर भूमि भूमि कटाव, काला शोरा तथा सेम के कारण खराब हो गई है। इस प्रकार कुल भूमि के 534 प्रतिशत भाग की अधोगति हो चुकी हैं। इसके अतिरिक्त सरकार ने चरागाहों की देखरेख की ओर कोई ध्यान नहीं दिया। इस प्रकार 11 मिलियन हेक्टेयर चरागाह का क्षेत्र बंजर भूमि बन गया है।

2. वनों की कटाई तथा भूमि अधोगति-भारत में भूमि अधोगति के अन्य कारणों में वनों की कटाई सबसे महत्त्वपूर्ण कारण है। भारत में 1951 से 1972 तक वनों अधीन 34 लाख हेक्टेयर भूमि पर कटाई की गई। इस क्षेत्र में से 72 प्रतिशत क्षेत्र पर कृषि तथा 17 प्रतिशत क्षेत्र पर उद्योग, सड़कें, यातायात, संचार, डैम इत्यादि बनाए गए। इसकी ज़िम्मेदारी राज्य सरकारों तथा वन विभाग की है, जिन्होंने वनों की देख-रेख की ओर कोई ध्यान नहीं दिया।

3. जल संसाधन अधोगति-भारत को विश्व का जल साधन भरपूर देश कहा जाता है। वनों की बेरहमी से कटाई के कारण, वर्षा के पानी का अधिक भाग समुद्र में चला जाता है। भारत में लगभग 250 मिलियन लोग बाढ़ वाले क्षेत्र पर निवास करते हैं। विश्व के 70 प्रतिशत लोग जो बाढ़ का शिकार होते हैं, भारत तथा बंगलादेश में रहते हैं। भारत के आर्थिक नियोजन की बड़ी गलती जल संसाधनों का उचित प्रयोग नहीं करना है। बाढ़ों के कारण वार्षिक 12000 करोड़ से 18000 करोड़ रु० की हानि होती है। पंजाब तथा हरियाणा में सेम की समस्या के कारण हज़ारों एकड़ भूमि बेकार हो गई है। शोरे की समस्या का भी सामना करना पड़ता है। सरकार ने जल संसाधनों के प्रयोग की ओर उचित नीति का निर्माण नहीं किया।

4. खनन तथा पर्यावरण समस्याएं-भारत ने खानों में से खनिज पदार्थों का अधिक प्रयोग किया, परन्तु सरकार ने पर्यावरण की ओर कोई ध्यान नहीं दिया। इससे भूमि, जल, वन तथा वायु, अधोगति में वृद्धि हुई है, जोकि इस प्रकार स्पष्ट किया जा सकता है –

• खानों के मालिकों ने कृषि भूमि पर सड़कें, रेलों, नहरों तथा नगरों का निर्माण किया
• खनिजों की धूल (Dust) द्वारा वायु प्रदूषण की समस्या के साथ कृषि उत्पादकता के कम होने की समस्या उत्पन्न हुई है।
• कोयले की खानों में आग लगने से जान, माल के नुकसान के अतिरिक्त लाखों हेक्टेयर भूमि बेकार हो गई है।
• वर्षा का पानी खानों में से निकलकर नदियों, टैंकों में प्रदूषण पैदा करता है।
• इस कारण जंगलों की कटाई होती है तथा भूमि कटाव की समस्या उत्पन्न हो जाती है।
• जो लोग खानों में काम करते हैं, उनको दमा तथा अन्य बीमारियां लग जाती हैं। इसलिए भारत को अमेरिका की तरह खानों सम्बन्धी कानून बनाकर उचित नीति द्वारा खानों का सद्उपयोग करना चाहिए।

प्रश्न 4.
भारत में पर्यावरण अधोगति के कारण बताओ। वातावरण को कैसे बचाया जा सकता है ? (What are the causes of degradation of Environment in India ? How can Environment he saved ?)
उत्तर-
भारत में वातावरण अधोगति के मुख्य कारण निम्नलिखित हैं-

1. जनसंख्या की वृद्धि– भारत में 1951 में जनसंख्या 36 करोड़ थी। 2011 में जनसंख्या 121 करोड़ हो गई है। जनसंख्या की आवश्यकताओं को पूरा करने के लिए उद्योगों तथा कृषि के विकास के कारण साधनों की अधोगति हुई है।
2. औद्योगीकरण में वृद्धि-उद्योगों के विकास के कारण देश में जल, वायु तथा ध्वनि प्रदूषण में वृद्धि हुई है। इससे बीमारियां बढ़ गई हैं।
3. शहरीकरण की ओर झुकाव-गांवों के लोग शहरों में रहने के लिए आ गए हैं। उनको सुविधाएं प्रदान करना एक समस्या बन गई है। इस कारण साधनों की अधोगति में वृद्धि हुई है।
4. कृषि उत्पादन में वृद्धि-लोगों की आवश्यकताओं को पूरा करने के लिए कृषि उत्पादकता में वृद्धि की गई। नई कृषि नीति अनुसार रासायनिक खाद, कीटनाशक दवाइयों का अधिक प्रयोग किया गया, इससे प्रदूषण में वृद्धि हुई
5. निर्धनता–भारत के लोगों में निर्धनता के कारण जलाने के लिए लकड़ी तथा गोबर के उपलों का प्रयोग किया जाता है। इससे प्राकृतिक पूंजी की अधोगति हुई है।
6. यातायात के साधनों का कम विकास-देश में सड़कों का विस्तार उतनी तीव्रता से न हुआ, जितनी तीव्रता से वाहनों (स्कूटर, कारों) की संख्या में वृद्धि हुई है।

पर्यावरण के बचाव के लिए उपाय-

1. जनसंख्या पर नियंत्रण-भारत में तीव्रता से बढ़ रही जनसंख्या पर नियंत्रण करने की आवश्यकता है। इससे पर्यावरण की अधोगति को रोका जा सकता है।
2. सामाजिक चेतना-लोगों में हवा, पानी, खनिज तथा प्रदूषण सम्बन्धी चेतना उत्पन्न करने की आवश्यकता है। प्रत्येक व्यक्ति पर्यावरण में शुद्धता लाने के लिए योगदान डाल सकता है।
3. वन लगाना-पर्यावरण को शुद्ध करने के लिए वनों का विस्तार करना चाहिए।
4. कृषि प्रदूषण-कृषि उत्पादन क्षेत्र में प्रदूषण रोकने के लिए रासायनिक खादों का कम प्रयोग किया जाए। वृक्ष लगाकर भू-अपरदन की समस्याओं को घटाना चाहिए।
5. औद्योगिक प्रदूषण-उद्योगों द्वारा जल, वायु तथा ध्वनि प्रदूषण फैलता है। भारत सरकार ने 17 उद्योगों की सूची तैयार की है जोकि अधिक प्रदूषण फैलाते हैं। नए उद्योगों को स्थापित करते समय प्रदूषण मापदंड स्थापित करने चाहिए।
6. जल प्रबन्ध-भारत में लोगों को शुद्ध जल पीने के लिए प्रदान करने के लिए जल प्रदूषण को रोकने की आवश्यकता है। इससे सभी लोगों के स्वास्थ्य पर अच्छा प्रभाव पड़ सकता है। इस प्रकार लोगों के रहन-सहन सम्बन्धी सुधार करके पर्यावरण की अधोगति पर रोक लगाई जा सकती है। विश्व बैंक के अनुसार भारत में पर्यावरण की अधोगति को ठीक करने के लिए सकल घरेलू उत्पाद (GDP) 5.7% भाग व्यय करना पड़ रहा है।

प्रश्न 5.
ग्लोबल वार्मिंग से क्या अभिप्राय है? ग्लोबल वार्मिंग के कारण तथा प्रभाव स्पष्ट करो। (What is Global Warming ? Discuss its causes and effects ?)
उत्तर-
ग्लोबल वार्मिंग का अर्थ (Meaning of Global Warming) ग्लोबल वार्मिंग अथवा वैश्विक तापन का अर्थ विश्व भर में वातावरण में बढ़ रही गर्मी से है। विश्व में जब से औद्योगिक क्रान्ति पैदा हुई है तब से लेकर आज तक विश्व के तापमान में वृद्धि हो रही है। 20वीं शताब्दी के मध्य से लेकर आज तक तापमान में जो वृद्धि हुई है वह पिछले 150 वर्ष में इतनी वृद्धि तापमान में नहीं देखी गई। अमरीका के वैज्ञानिकों का यह विचार है कि विश्व के तापमान में 10 Degree तक वृद्धि हो सकती है। वैश्विक तापन का मुख्य कारण मानवीय गतिविधियों के कारण वातावरण में ग्रीन हाउस गैसों की मात्रा में वृद्धि होना है। ग्रीन आऊस गैसों में मुख्य रूप से कार्बनडाईआक्साईड (CO₂), मीथेन (CH₄), नाइट्रस आक्साइइ (N₂O), ओजोन (O₃), क्लोरोफ्लोरो कार्बन (CFCs) आदि गैसें शामिल हैं। ग्लोबल वार्मिंग विश्व की कितनी बड़ी समस्या है यह साधारण आदमी समझ नहीं पाता। आम लोग समझते हैं कि ग्लोबल वार्मिंग से फिलहाल संसार को कोई खतरा नहीं है। परन्तु यह धारणा ठीक नहीं है।

बढ़ते हुए तापमान को न रोका गया तो इसके घातक परिणाम हो सकते हैं। ग्लोबल वार्मिंग के कारण (Causes of Global warming)-
1. जंगलों की कटाई (Deforestation)ग्लोबल वार्मिंग का सबसे बड़ा कारण जंगलों की कटाई है। आधुनिकीकरण के कारण पेड़ों की कटाई गांवों को शहरीकरण में बदलाव, हर खाली जगह पर बिल्डिंग, कारखाना या अन्य कोई कमाई के लिए स्रोत खोले जा रहे हैं। लकड़ी का प्रयोग इमारतो के निर्माण, खाना बनाने आदि के लिए बड़े स्तर पर होने के कारण अमरीका तथा आस्ट्रेलिया जैसे देशों में जहां जंगल अधिक मात्रा में हैं वहां जंगलों को अपने आप आग लग जाती है जिसको बुझाने के लिए सरकार को बहुत मेहनत करनी पड़ती है।

2. उद्योगों का विकास (Growth of Industries) ग्लोबल वार्मिंग का एक कारण विश्व में औद्योगिकरण को भी माना जाता है। फ्रांस में औद्योगिक क्रान्ति के पश्चात विश्व में बड़े पैमाने पर उद्योगों का विकास हुआ है। इस से प्रदूषण में वृद्धि हुई है। ग्रीन हाउस गैसों कार्बन डाईआक्साइड, मीथेन, ओजोन आदि की वृद्धि के कारण विश्व के तापमान में वृद्धि तेजी से हो रही है।

3. मोटर वाहनों का विकास (Growth of Automobiles)-जैसे-जैसे विश्व ने आर्थिक विकास किया है उसके साथ लोगों की आय में तेजी से वृद्धि हुई है। इससे लोगों ने मोटर वाहनों का अधिक प्रयोग करना शुरू कर दिया है। मोटर वाहनों के अधिक प्रयोग के कारण विश्व में कार्बन डाईआक्साइड की मात्रा में वृद्धि हुई है। इस कारण तापमान में वृद्धि हुई है।

4. वातावरण में गैसों का विकास (Growth of Gases in Atmosphere)-कुछ वैज्ञानिकों का विचार है कि ज्वालापुखी विस्फोट के कारण भी विश्व में गैसों की वृद्धि हुई है। इस कारण भी ग्लोबल वार्मिंग हुई है। जब ज्वालामुखी में विस्फोट होता है तो अन्त कार्बन डाईआक्साईड का प्रवाह होता है। इस कारण भी ग्लोबल वार्मिंग में वृद्धि होती है।

5. मानव क्रियाओं का विकास (Growth of Human Activities) मानव क्रियाएं भी ग्लोबल वार्मिंग का कारण बन गई है। हम घरों में एयरकंडीशनर, फ्रिज, कोल्ड स्टोर आदि अधिक मात्रा में प्रयोग करने लगे हैं। इससे भी ग्रीन हाउस प्रभाव पैदा हैता है अर्थात् जहरीली गैसें निकलती हैं जिस कारण तापमान में वृद्धि होती है जनसंख्या में वृद्धि प्रदूषण के कारण अधिक अनाज़ पैदा करने के लिए आधुनिक खादों का प्रयोग तथा कीट नाशकों के प्रयोग कारण भी प्रदूषण में वृद्धि होती है। वातावरण में प्रदूषण के फैलने से भी ग्लोबल वार्मिंग हो रही है।

ग्लोबल वार्मिंग के प्रभाव (Effects of Global Warming) – ग्लोबल वार्मिंग तेजी से बढ़ रही है इस के दुष्प्रभाव इस प्रकार हो सकते हैं –
1. ग्लेशियरों का पिघलना (Melting of Glaciers)-ताप बढ़ने से ग्लेशियर पिघलने लगते हैं और उनका आकार कम होने लगता है। भारत में उत्तराखण्ड में 8 फरवरी 2021 को ग्लेशियर के पिघले से बाढ़ की स्थिति उत्पन्न हो गई जिससे बहुत से लोगों की मृत्यु हुई है और बहुत से लोग लापता हैं। इस प्रकार ग्लेशियर लगातार कम हो रहे हैं जिसका कारण ग्लोबल वार्मिंग है।

2. बढ़ता समुद्री जलस्तर (Rising Sea Level)-ग्लेशियरों के पिघलने से प्राप्त जल सागरों में मिलता हो तो समुद्री जल स्तर में वृद्धि हो जाती है। समुद्री जलस्तर बढ़ने से समुद्री तटों पर जो शहर बसे हुए हैं उन में बाढ़ का खतरा बन जाता है।

3. नदियों में बाढ़ (Floods in Rivers) ग्लेशियरों से कई बार हमारी नदियां निकलती है। इन नदियों में जल का प्रवाह बढ़ने से बाढ़ की स्थिति उत्पन्न हो जाती है जिस कारण बहुत से शहरों तथा गांवों में बाढ़ के कारण बहुत हानि सहन करनी पढ़ती है।

4. कृषि पर प्रभाव (Effect on Agriculture)-ग्लोबल वार्मिंग के कारण कभी गर्म तेज़ हवाएं चलती हैं और कभी अधिक वर्षा होती है। इस कारण कृषि में उत्पादन पर बुरा प्रभाव पड़ता है। मछली उद्योग को भी ग्लोबल वार्मिंग से नुकसान होता है।

5. मानव तथा जानवरों पर बुरा प्रभाव (Bad Effect on Living Beings) ग्लोबल वार्मिंग के कारण मनुष्यों को बहुत सी बीमारियों का सामना करना पड़ता है। पशुओं तथा पक्षियों की बहुत सी प्रजातियां लुप्त हो रही हैं। इसलिए ग्लोबल वार्मिंग की तरफ़ ध्यान देने की ज़रूरत है।

Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 28 बुनियादी ढांचा और ऊर्जा Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 12 Economics Chapter 28 बुनियादी ढांचा और ऊर्जा

PSEB 12th Class Economics बुनियादी ढांचा और ऊर्जा Textbook Questions, and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
बुनियादी ढांचा शब्द किस भाषा से लिया गया है?
(a) लैटिन
(b) ग्रीक
(c) फ्रैंच
(d) संस्कृत।
उत्तर-
(c) फ्रैंच।

प्रश्न 2.
बुनियादी ढांचे से क्या अभिप्राय है?
उत्तर-
किसी देश में आर्थिक तथा सामाजिक सेवाएं प्रदान करना बुनियादी ढांचा कहलाता है।

प्रश्न 3.
Infra शब्द का अर्थ नीचे का और Structure का अर्थ ढांचा होता है।
उत्तर-
सही।

प्रश्न 4.
देश में शिक्षा संस्थान, अस्पताल, पार्क आदि के विकास को ……. बुनियादी ढांचा कहा जाता
उत्तर-
सामाजिक अथवा नरम बुनियादी ढांचा (Soft-Infrastructure)।

प्रश्न 5.
देश में सड़कें, रेलें, पुल, बिजली, पानी सहूलतों को ……. बुनियादी ढांचा कहा जाता है।
उत्तर-
सख्त (सथूल) बुनियादी ढांचा (Hard Infrastructure)।

प्रश्न 6.
सामाजिक बुनियादी ढांचे का विकास देश में आर्थिक उत्पादन की वृद्धि के लिए सहायक होता है। (सही/गलत)
उत्तर-
सही।

प्रश्न 7.
आर्थिक और सामाजिक बुनियादी ढांचा एक दूसरे पर निर्भर करते हैं।
उत्तर-
सही।

प्रश्न 8.
बुनियादी ढांचे के विकास का आर्थिक-विकास पर प्रभाव नहीं पड़ता।
उत्तर-
गलत।

प्रश्न 9.
मानव पूँजी का विकास …………… बुनियादी ढांचे का भाग है।
उत्तर-
सामाजिक।

प्रश्न 10.
आर्थिक बुनियादी ढांचे और सामाजिक बुनियादी ढांचे में कोई अन्तर नहीं है।
उत्तर-
गलत।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
बुनियादी ढांचे से क्या अभिप्राय है?
उत्तर-
बुनियादी ढांचे का अर्थ उन आधारभूत सहूलतों से हैं जिन द्वारा देशवासियों को यातायात तथा जीवन स्तर के लिए सहूलते प्रदान की जा सकें। इनका उद्देश्य देश में कृषि, उद्योग, यातायात, संचार का विकास करके चिरकालीन आर्थिक विकास करना होता है। बुनियादी ढांचे में रेलों, सड़कों, सिंचाई, बिजली, पानी, सेहत, ऊर्जा आदि सुविधा प्रदान की जाती है।

प्रश्न 2.
आर्थिक बुनियादी ढांचे से क्या अभिप्राय है?
उत्तर-
आर्थिक बुनियादी ढांचा (Economic Infrastructure) देश के आर्थिक विकास में महत्त्वपूर्ण योगदान डालता है। इसमें यातायात, संचार, सड़कों, रेलों, बिजली पानी कौशल, तकनीक के विकास द्वारा कृषि और उद्योगों के उत्पादन में वृद्धि की जाती है। इस द्वारा देश में चिरकालीन विकास होता है।

प्रश्न 3.
सामाजिक बुनियादी ढांचे से क्या अभिप्राय है?
उत्तर–
सामाजिक बुनियादी ढांचे (Social Infrastructure) से अभिप्राय उन सहूलतों से है जो लोगों के जीवन स्तर को ऊंचा उठाने के लिए सहयोगी होती हैं। इन सहूलतों में शिक्षा, सेहत, घर निर्माण, पार्क, अस्पताल, सभ्याचारक केन्द्र सथापित करना होता है।

प्रश्न 4.
ऊर्जा के मुख्य स्त्रोत बताओ?
उत्तर-
ऊर्जा के मुख्य स्त्रोत इस प्रकार हैं-

प्रश्न 5.
परंपरागत ऊर्जा के किसी एक स्त्रोत का वर्णन करें।
उत्तर-
कोयला (Coal) कोयला ऊर्जा का महत्त्वपूर्ण परंपरागत स्रोत है। भारत में कोयले के 326 बिलियन भंडार हैं। इस का वार्षिक उत्पादन 396 मिलियन टन किया जाता है। इसके भंडार, बिहार, उड़ीसा, मध्य प्रदेश और बंगाल में पाए जाते हैं।

प्रश्न 6.
किसी एक गैर पारम्परिक ऊर्जा के स्रोत का वर्णन करें।
उत्तर-
सूर्य ऊर्जा (Solar Energy)-यह ऊर्जा सूर्य की रोशनी द्वारा उत्पन्न होती है। फोटोवोल्टैनिक सैल, सूर्य की किरणों की ओर लगाए जाते हैं। इस द्वारा जो बिजली उत्पन्न होती है उस का प्रयोग घरेलू कामों के लिए किया जाता है। जैसे कि खाना बनाने, रोशनी और जल साफ़ करने आदि कामों के लिए किया जाता है।

III. लघु उत्तरीय प्रश्न | (Short Answer Type Questions)

प्रश्न 1.
बुनियादी ढाचे का अर्थ बताएं, बुनियादी ढांचे का वर्गीकरण स्पष्ट करें।
उत्तर-
बुनियादी ढांचे का अर्थ (Meaning of Infrastructure)-बुनियादी ढांचे का अर्थ उन आधारभूत सहूलतों से है जिन के द्वारा अर्थव्यवस्थता के संचालन को चिरकालीन विकास के लिए प्रयोग किया जा सकता है। इसमें उन आधारभूत सहूलतों को शामिल किया जाता है जो आर्थिक विकास का आधार बनती हैं। बुनियादी ढांचे में सड़कों, रेलों, पुल, जल आपूर्ति, बिजली संचार, इंटरनैट आदि को शामिल किया जाता है।

बुनियादी ढांचे का वर्गीकरण (Classification of Infrastructure) बुनियादी ढांचे के वर्गीकरण को दो भागों में बांटा जा सकता है।

1. स्थूल बुनियादी ढांचा (Hard Infrastructure)-इसको आर्थिक बुनियादी ढांचा भी कहा जाता है। इसमें भौतिक वस्तुओं को शामिल किया जाता है जैसे कि सड़कें, रेलवे, फ्लाईओवर, बिजली आदि का विकास शामिल किया जाता है।
2. नरम बुनियादी ढांचा (Soft Infrastructure)-नरम बुनियादी ढांचे को सामाजिक ढांचा भी कहा जाता है। इसमें अस्पताल, शिक्षा संस्थान, पार्क, मनोरंजन सहूलतों को शामिल किया जाता है।

प्रश्न 2.
आर्थिक बुनियादी ढांचे और सामाजिक बुनियादी ढांचे से क्या अभिप्राय है? ।
उत्तर-

• आर्थिक बुनियादी ढांचा (Economic Infrastructure)-इस बुनियादी ढांचे में स्थूल वस्तुओं को शामिल किया जाता है जिसमें सड़कें, रेलवे, बिजली, कृषि विकास औद्योगिक सुविधाएं, ऊर्जा आदि शामिल होते हैं। इससे उत्पादन क्रियाओं में गति पैदा होती है और देश का आर्थिक विकास तेज़ हो जाता है। लोगों की आय और रोजगार में वृद्धि होती है।
• सामाजिक बुनियादी ढांचा (Social Infrastructure)-सामाजिक बुनियादी ढांचे को नरम बुनियादी ढांचा भी कहा जाता है। इसमें सामाजिक सेवाएं शामिल होती हैं। जिनकी सहायता से उत्पादन शक्ति में वृद्धि होती है। सरकार द्वारा लोगों को शिक्षा, सेहत, तकनीकी शिक्षा, खेल के मैदान, पार्क आदि सहूलतें प्रदान की जाती हैं। इन सहूलतों के कारण लोगों की उत्पादन शक्ति में वृद्धि होती है और आर्थिक विकास पर अच्छा प्रभाव पड़ता है।

प्रश्न 3.
बुनियादी ढांचे के महत्त्व को स्पष्ट करें।
उत्तर-
बुनियादी ढांचे का महत्त्व (Importance of Infrastructure) –

1. आर्थिक विकास में वृद्धि-बुनियादी ढांचे द्वारा देश में आर्थिक विकास की गति तेज़ हो जाती है। आर्थिक विकास ही प्रत्येक देश का मुख्य उद्देश्य होता है इसके लिए बुनियादी ढांचा अति आवश्यक है।
2. रोज़गार में वृद्धि-जब देश में आर्थिक ढांचे का निर्माण होता है जिस द्वारा सड़कें, नहरें, पुल आदि बनते हैं तो इसके निर्माण के समय रोज़गार में वृद्धि होती है और बनने के पश्चात् और बहुत से उद्योग स्थापित हो जाते हैं। इसलिए रोजगार में वृद्धि होने लगती है।
3. उत्पाद शक्ति में वृद्धि-आधारभूत ढांचे के विकास से लोगों की उत्पादन शक्ति में वृद्धि होती है। उत्पादन शक्ति बढ़ने से न केवल देश के लोगों की आवश्यकताएं पूरी होती हैं बल्कि विदेशों में वस्तुओं का निर्यात बढ़ने से विदेशी मुद्रा के रूप में आय प्राप्त होती है।
4. जीवन स्तर के लिए सहायक–देश में साफ सुथरा वातावरण, सेहत सहूलतों के बढ़ने से लोगों के काम करने की समर्था में वृद्धि होती है। उन की आय बढ़ जाती है और इस से राष्ट्रीय आय में वृद्धि होती है।

प्रश्न 4.
ऊर्जा के परम्परागत तथा गैर परम्परागत स्रोतों का वर्णन करें।
उत्तर-

1. परम्परागत स्रोत (Conventional Sources)-इनको गैर-नवीनीकरण (Non-Renewable Source) भी कहा जाता है अर्थात इनका प्रयोग एक बार ही किया जा सकता है जितनी देर तक देश में इन स्रोतों के भंडार होते हैं तब तक ही यह प्रयोग में आ सकते हैं जैसे कि कोयला (Coal), पैट्रोल तथा गैस (Patrol and Gas) और बिजली (Electricity) आदि।
2. गैर परम्परागत स्रोत (Non-Conventional Sources)-इनको नवीनीकरण स्रोत (Renewable Sources) कहा जाता है। यह प्रकृति की मुफ्त देन होती है जिसका प्रयोग हम बार बार कर सकते हैं। इन स्रोतों द्वारा ऊर्जा पैदा करना आसान होता है। जैसे कि सूर्य ऊर्जा (Solar Energy), वायु ऊर्जा (Wind Energy), बायो गैस ऊर्जा (BioGas Energy) आदि इसके महत्त्वपूर्ण रूप हैं। ये स्रोत प्रकृति द्वारा दिये जाते हैं और इनका अन्त नहीं होता। इन स्रोतों को विकसित करने की आवश्यकता है जिससे दीर्घकाल तक विकास किया जा सकता है।

IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
बुनियादी ढांचे से क्या अभिप्राय है? बुनियादी ढांचे की किस्में बताएं। (What is meant by Infrastructure ? Explain the types of Infrastructure.)
उत्तर-
बुनियादी ढांचे का अर्थ (Meaning of Intrastructure)-बुनियादी ढांचे शब्द का प्रयोग सबसे पहले फ्रांस में 1880 में किया गया। यह फ्रेन्च भाषा के दो शब्दों को मिलाकर बनाया गया। Infra जिसका अर्थ है नीचे का (Below) और Structure का अर्थ है ढांचा (Building) बुनियादी ढांचा आधार होता है जिसके ऊपर अर्थव्यवस्था का ढांचा तैयार किया जाता है। 1987 में अमरीका की राष्ट्रीय खोज कौंसिल (National Reserach Council) ने सार्वजनिक ढांचे के रूप में इसका प्रयोग किया जिससे हाईवेज़, हवाई अड्डे, टैलीकमिनीकेशन और जल आपूर्ति के लिए इसका प्रयोग किया गया।

बुनियादी ढांचे से अभिप्राय उन सहूलतों से है जिन के द्वारा अर्थव्यवस्था का संचालन किया जाता है जिससे चिरकालीन विकास हो सके। बुनियादी ढांचे में सार्वजनिक अथवा निजी ढांचे को शामिल किया जाता है। इसमें सड़कें (Roads), रेलवे (Railways), पुल (Bridges) जल आपूर्ति (Water Supply), सीवरेज़ (Sewage), बिजली (Electricity), संचार (Telecommunication) और इन्टरनेट (Internet) आदि को शामिल किया जाता है। इसको परिभाषा देते हुए जैफ़री फलमर (Joffery Fulmer) ने कहा है, “बुनियादी ढांचा अन्तर सम्बन्धत प्रणाली को कहा जाता है जिस द्वारा वस्तुओं तथा सेवाओं की सुविधा प्रदान करके चिरकालीन विकास अथवा सामाजिक जीवन स्थितियाँ पैदा करके वातावरण को ठीक रखा जाता है।” (“Infrastructure is the physical components of inter-related system providing commodities and services essential to enable sustain or enhance social living conditions to maintain the surrounding or environment.” Jaffery Fulmer).

बुनियादी ढांचे का वर्गीकरण (Classification of Infrastructure) बुनियादी ढांचे को दो भागों में बांटा जा सकता है-

1. सख्त और स्थूल बुनियादी ढांचा (Hard Infrastructure)-सख्त बुनियादी ढांचे में भौतिक काम (Physical Network) होते हैं। जिस के द्वारा उद्योगों (Industries) का संचालन किया जाता है। इनमें सड़कें, पुल, फ्लाईओवर, रेलें आदि का विकास शामिल होता है। इस को आर्थिक बुनियादी ढांचा (Economic Infrastructure) भी कहा जाता है।
2. नरम बुनियादी ढांचा (Soft Infrastructure)-नरम बुनियादी ढांचे में वे संस्थाएं शामिल होती हैं जिन के द्वारा आर्थिक, सेहत, सामाजिक वातावरण और अस्पताल, पार्क, मनोरंजन सहूलतें, कानून व्यवस्था आदि सेवाओं को शामिल किया जाता है। इस को सामाजिक बुनियादी ढांचा भी कहा जाता है।

बुनियादी ढांचे की किस्में (Types of Infrastructure)-बुनियादी ढांचे की मुख्य किस्में इस प्रकार हैं-
1. आर्थिक बुनियादी ढांचा (Economic Infrastructure)-आर्थिक बुनियादी ढांचे में सड़कें, यातायात के साधन, जलापूर्ति, सीवरेज, कृषि का विकास, औद्योगिक विकास ऊर्जा आदि के विकास को शामिल किया जाता है। जिस से उत्पादन में वृद्धि होती है।

2. सामाजिक बुनियादी ढांचा (Social Infrastructure)-इसमें समाजिक सुविधाओं को शामिल किया जाता है जिनमें शिक्षा संस्थान, अस्पताल, पार्क आदि के विकास पर बल दिया जाता है। इसकी व्याख्या 1965 में प्रो. हैलसेन ने की थी।

3. निजी बुनियादी ढांचा (Personal Infrastructure)-निजी बुनियादी ढांचे में मानव पूँजी (Human Capital) को शामिल किया जाता है। जब लोग शिक्षा प्राप्त करके अपने कौशल का विकास करते हैं और उनकी सेहत अच्छी होती है तो उत्पादन शक्ति में वृद्धि होती है। इसको निजी बुनियादी ढांचा कहा जाता है।

4. भौतिक बुनियादी ढांचा (Material Infrastructure)-भौतिक बुनियादी ढांचे में अचल पूँजी (Immoveable Capital) को शामिल किया जाता है। इस में उद्योगों का विकास, कृषि की उत्पादन शक्ति में वृद्धि करके लोगों की आवश्यकता को पूरा किया जाता है।

5. ज़रूरी बुनियादी ढांचा (Core Infrastructure)-कुछ अर्थशास्त्रियों ने बुनियादी ढांचे क्षेत्रों में जरूरी बुनियादी ढांचे को शामिल किया है इसमें निवेश द्वारा आय में वृद्धि, मुद्रा स्फीति को काबू में रखना, उद्योगों का विकास, सड़कें, नहरें, बिजली आदि को शामिल किया जाता है।

6. आधारभूत बुनियादी ढांचा (Basic Infrastructure)-इसमें सड़कें, नहरें, रेलें, बंदरगाहों का विकास, भूमि की उपज में वृद्धि आदि को शामिल किया जाता है। यदि हम देखें तो बुनियादी ढांचे को दो किस्मों आर्थिक बुनियादी ढांचा और सामाजिक बुनियादी ढांचे को अलगअलग नाम दिये गए हैं।

प्रश्न 2.
बुनियादी ढांचे से क्या अभिप्राय है? इसके महत्त्व को स्पष्ट करें। (What is meant by Infrastructure ? Discuss the importantce of Infrastructure)
उत्तर-
बुनियादी ढांचे का अर्थ (Meaning of Infrastructure)-बुनियादी ढांचे से अभिप्राय उन आधारभूत सुविधाओं से है जिन के द्वारा देश का आर्थिक विकास तेजी से किया जा सकता है। इन में कृषि पैदावार, औद्योगिक विकास, सड़कें, यातायात के साधन, रेलवे, बिजली, जलापूर्ति आदि सुविधाओं को शामिल किया जाता है।

बुनियादी ढांचे का महत्त्व (Importance of Infrastructure)-

1. आर्थिक विकास में वृद्धि (Increase in Economic Development)-प्रत्येक देश का मुख्य उद्देश्य आर्थिक विकास प्राप्त करना होता है। इस के लिए बुनियादी ढांचे का महत्त्वपूर्ण योगदान होता है। देश में उत्पादन में वृद्धि होती है। मानव पूँजी का विकास होता है तो आर्थिक विकास तेजी से होता है।
2. रोज़गार में वृद्धि (Increase in Employment)-बुनियादी ढांचे के विकास से देश में रोज़गार के नए अवसर पैदा होते हैं। जब देश में सड़कें, पुल, डैम आदि का निर्माण होता है तो रोज़गार में वृद्धि होती है। यह काम पूरा होते ही उद्योग स्थापित होते हैं, कृषि पैदावार बढ़ जाती है, होटल, बैंक, सुविधाएं अधिक हो जाती हैं तो रोज़गार में और वृद्धि होती है।
3. उत्पादन शक्ति में वृद्धि (Increase in Productivity)-उत्पादन शक्ति में वृद्धि बुनियादी ढांचे पर निर्भर करती है। जब देश में आर्थिक तथा सामाजिक बुनियादी ढांचे का विकास होता है तो लोगों की उत्पादन शक्ति बढ़ जाती है जिस द्वारा न केवल देश के लोगों की आवश्यकताएं पूरी होती हैं बल्कि विदेशों की ज़रूरतों को पूरा किया जाता है।
4. अर्थव्यवस्था के संचालन में सहायक (Helpful in Functioning of the Economy)-किसी देश के प्राकृतिक तथा मानव संसाधनों के उचित उपयोग के लिए भी बुनियादी ढांचा महत्त्वपूर्ण होता है। यातायात, संचार, बिजली, पानी, बैंकिंग आदि सहूलतें आर्थिक विकास के लिए अति आवश्यक होती हैं। इस से देश के साधनों का पूर्ण उपयोग संभव होता है।
5. विदेशी काम के लिए सहायक (Helpful in Outsourcing)-जब विदेशी कंपनियां आपना काम दूसरे देशों में प्रारंभ करती हैं तो वहाँ के लोगों से सहयोग लिया जाता है। यदि लोगों को काम करने का ज्ञान है और वे आधुनिक, कम्पूयटर आदि को संचालन कर सकते हैं तो काल सैंटर (Call Center) खोल कर आय प्राप्त कर सकते हैं।
6. जीवन स्तर के लिए सहायक (Helpful in Standard of Living)-जिस देश में बुनियादी ढांचा विकसित हो जाता है उस देश के लोगों को रोजगार प्राप्त होता है। उनकी आय बढ़ जाती है।

इससे रहन-सहन पर अच्छा प्रभाव पढ़ता है। लोग अपने बच्चों को शिक्षा और उच्च शिक्षा दिलवाने के काबिल हो जाते हैं। इससे लोगों की काम करने की शक्ति पर अच्छा प्रभाव पड़ता है। प्रति व्यक्ति आय में वृद्धि होती है और आर्थिक विकास होता है।

प्रश्न 3.
भारत में ऊर्जा के स्रोतों को वर्णन करो। Explain the sources of Energy in India.
उत्तर-
ऊर्जा आर्थिक विकास के लिए महत्त्वपूर्ण स्रोत है। इसको दो भागों में बांट कर स्पष्ट किया जा सकता है|

(A) परम्परागत स्रोत (Conventional Source)-परम्परागत स्रोत को गैर नवीनीकरण स्रोत भी कहा जाता है। जैसे जैसे हम परम्परागत स्रोतों का प्रयोग करते हैं तो धीरे-धीरे इन के भंडार समाप्त हो जाते हैं। इस कारण इन को गैर नवीनीकरण स्रोत कहा जाता है।

परम्परागत स्रोत दो प्रकार के होते हैं।

• व्यापारिक स्रोत (Conventional Source)
• गैर-व्यापारिक स्त्रोत (Non-conventional Source) ।

व्यापारिक स्त्रोंतो में मुख्य स्रोत

1. कोयला
2. पैट्रोल और प्राकृतिक गैस
3. बिजली होते है और गैर

व्यापारिक स्रोत

• लकड़ी
• कृषि कूड़ा करकट
• सूखा गोबर (उपले)।

इस अध्याय में हम व्यापारिक परम्परागत स्रोतों का अध्ययन करेंगे-
1. कोयला (Coal)-भारत में व्यापारिक परम्परागत स्रोत कुल स्रोतों का 74% हैं जिनमे कोयले का भाग 44% हैं। 2020-21 में अनुमान लगाया गया है कि कोयले के भंडार 100 साल के पश्चात समाप्त हो जाएंगे। कोयला उत्पादन में भारत का विश्व में चौथा स्थान है। भारत में कोयला थर्मल प्लांटों, फैक्ट्रियों, रेलों आदि में प्रयोग किया जाता है। कोयले के भंडार उड़ीसा, बिहार, बंगाल तथा मध्य प्रदेश में पाए जाते हैं। भारत में भूरे कोयले (Liginite) के भंडार भी हैं जो कि नवेली (Neyveli) में पाए जाते हैं। इस कोयले का भंडार लगभग 3300 मिलियन टन है।

2. पैट्रोल तथा प्राकृतिक गैस (Petrol & Natural Gas)-पैट्रोल भी ऊर्जा का महत्त्वपूर्ण स्रोत है। इसका प्रयोग विश्व भर में किया जाता है। पैट्रोल का प्रयोग वाहनों (Automobiles) रेल गाड़ियों (Railway), हवाई जहाजों (Aeroplans) और समुद्री जहाजों (Ships) आदि के लिए किया जाता है। भारत में पैट्रोल आसाम, बाम्बे हाई और गुजरात में मिलता है। 2000-01 में अनुमान लगाया गया था कि भारत में 32 मिलियन टन पैट्रोल के भण्डार हैं यह देश की 25% आवश्यकताओं को पूरा करता है।

बाकी पैट्रोल खाड़ी देशों से आयात किया जाता है। भारत में तेल साफ करने की पहली रिफाइनरी आसाम में लगाई गई थी। इस के पश्चात भारत में 13 और रिफाइनरियाँ स्थापत की गई हैं जिन की तेल शोधक क्षमता 604 लाख टन है। यदि इस रफ्तार से पैट्रोल का प्रयोग भारत के पैट्रोल भण्डारों से किया गया तो 20-25 वर्ष में यह भंडार समाप्त हो जाएंगे। प्राकृतिक गैस भी ऊर्जा का स्रोत है। यह रासायनिक खाद और कैमीकल के उद्योगों में प्रयोग होती है। इस को खाना बनाने में भी प्रयोग किया जाता है।

3. बिजली (Electricity)-बिजली सब से अधिक प्रयोग किया जाने वाला और सब से अधिक प्रचलित ऊर्जा स्रोत है। इस का प्रयोग व्यापारिक कार्यों तथा घरेलू उद्देश्यों के लिए किया जाता है। इस का प्रयोग खाना बनाने, पंखे, ऐ०सी० फ्रिज, कपड़ा धोने की मशीनों आदि के लिए किया जाता है। इस को कृषि उपकरणों को चलाने, उद्योगों के संचालन, व्यापारिक संस्थानों तथा घरेलू उपयोग के लिए किया जाता है।

भारत में कुल बिजली का 25% भाग कृषि के लिए, 36% भाग उद्योगों के लिए 24% भाग घरेलू कामों के लिए तथा अन्य 15% भाग और कामों के लिए प्रयोग किया जाता है। भारत में बिजली पैदा करने के तीन स्रोत हैं।

• थर्मल शक्ति (Thermal Power)
• हाईड्रो इलैक्ट्रिक शक्ति (Hydro Electric Power)
• अणु शक्ति (Neuclear Power)।

31 मार्च 2020 तक भारत में बिजली पैदा करने की क्षमता 356100 MW है। जिसमें 68% थर्मल प्लांटों द्वारा प्राप्त की जाती है जिसका हिस्सा अब कम हो रहा है।

गैर-परम्परागत स्रोत (Non-Conventional Source)-गैर-परम्परागत स्रोतों को नवीनीकरण स्रोत (Renewable Source) भी कहा जाता है। गैर-परम्परागत स्रोत निम्नलिखित अनुसार हैं-
1. सौर ऊर्जा (Solar Energy)-सौर ऊर्जा एक महत्त्वपूर्ण और ऊर्जा का मुफ्त स्रोत है। विश्व में जितनी कुल ऊर्जा की ज़रूरत है उससे 15000 गुणा अधिक सौर ऊर्जा प्राप्त की जा सकती है। एक वर्ग km में 20 MW प्लांट की स्थापना की जा सकती है। सौर ऊर्जा को तीन भागों में बांटा जा सकता है। कम तापमान वाले यंत्र (100°C), मध्य ताप यत्र (100°C से 300°C) और उच्च ताप यंत्र 300°C से अधिक ऊर्जा पैदा करने के लिए यंत्र। इन का प्रयोग होटलों में, डेयरी फार्मों में, कपड़ा उद्योगों में तथा घर के कामों के लिए किया जा सकता है।

2. वायु ऊर्जा (Wind Energy) वायु द्वारा भी ऊर्जा पैदा की जा सकती है। भू-मध्य रेखा पर अधिक गर्म जलवायु होती है। जैसे हम उत्तरी पोल तथा दक्षणी पोल की तरफ जाते हैं। गर्मी कम होती जाती है। जहां पर वायु 15 km/h (15 km प्रति घंटा) की रफ्तार से चलती है वहां पर वायु ऊर्जा यन्त्र लगाए जा सकते हैं। यदि वायु 25 km/ h से 30 km/h की रफ्तार से चलती है वहाँ पर ज्यादा ऊर्जा पैदा की जा सकती है। भारत में अनुमान है कि 20,000 MW ऊर्जा वायु ऊर्जा द्वारा पैदा की जा सकती है।

3. बायो-ऊर्जा (Bio-Energy)-बायो ऊर्जा भी ऊर्जा का एक महत्त्वपूर्ण स्रोत माना जाता है। यह लकड़ी उद्योग, कृषि तथा घरों से निकलने वाले कचरे के प्रयोग से ऊर्जा के निर्माण में सहायक होता है। पशुओं के गोबर से भी गैस प्राप्त की जा सकती है जिस का प्रयोग घर में खाना बनाने के लिये किया जा सकता है। कचरे द्वारा जो ऊर्जा पैदा की जाती है इस का दोहरा लाभ होता है। एक तो कचरे से पैदा होने वाला प्रदूषण समापत हो जाता है तथा इस के प्रयोग द्वारा जो बिजली उत्पन्न होती है उस का प्रयोग भी होता है। विकसित देशों में बायो ऊर्जा द्वारा भी ऊर्जा प्राप्त की जा रही है। आधुनिक युग में अनु ऊर्जा (Atomic Energy) के प्लांट भी स्थापित किये जा रहे हैं जिस द्वारा ऊर्जा पैदा करके देश की आवश्यकताओं को पूरा करने के यत्न किये जा रहे हैं।

प्रश्न 4.
बुनियादी ढांचे से क्या अभिप्राय है? आर्थिक बुनियादी ढांचे के अंश बताएं।
(What do you mean by Infrastructure? Give brief account of components of economic Infrastructure?)
उत्तर-
बुनियादी ढांचे से अभिप्राय वह सुविधायें, काम अथवा सेवाएं हैं जो कि अर्थव्यवस्था के भिन्न-भिन्न क्षेत्रों का विकास करने के लिए योगदान डालते हैं। देश का पूँजी भण्डार जो अर्थव्यवस्था के विकास के लिए आवश्यक सेवाएं प्रदान करता है उस को बुनियादी ढांचा कहा जाता है। (“Infrastructure means the services and facilities which are helpful in development of Primary secondary & teritary sectors of the economy.”)
आर्थिक बुनियादी ढांचे के अंश- (Components of Economic Infrastructure) आर्थिक बुनियादी ढांचे के तीन अंश होते हैं –
1. ऊर्जा (Energy)
2. यातायात (Transportation)
3. संचार (Communication)
1. ऊर्जा (Energy)-ऊर्जा के बगैर औद्योगिक विकास संभव नहीं होता। ऊर्जा दो प्रकार की होती है। व्यावहारिक ऊर्जा (Commercial Energy) जिसमें कोयला (Coal), पैट्रोल (Petrol) प्राकृतिक गैस (Natural Gas) और बिजली (Electricity) को शामिल किया जाता है। गैर परंपरागत ऊर्जा में लकड़ी, पशुओं तथा कृषि का कचरा शामिल किया जाता है।

व्यावहारिक ऊर्जा के स्रोत इस प्रकार हैं-

• कोयला (Coal)-कोयला ऊर्जा का पुरातन तथा महत्त्वपूर्ण स्रोत है। भारत में कोयला काफी मात्रा में पाया जाता है। इस के भण्डार 100 वर्ष तक चलने की संभावना है।
• पैट्रोल (Petrol)-पैट्रोल भी ऊर्जा का महत्त्वपूर्ण स्रोत है। भारत में यह आसाम, बांबे हाई और गुजरात में पाया जाता है। इस के भण्डार देश की 25% आवश्यकताओं को पूरा करते हैं।
• प्राकृतिक गैस (Natural Gas)-प्राकृतिक गैस भी बुनियादी ढांचे का अंश है। इस का प्रयोग घरों में खाना बनाने तथा खाद बनाने के लिए किया जाता हैं।
• बिजली (Electricity)-बिजली भारत में थर्मल प्लांटों हाईड्रो इलैक्ट्रिक पावर और अणु शक्ति से प्राप्त की जाती है।

(A) गैर परंपरागत स्रोत (Non Conventional Sources)-

• सूर्य ऊर्जा (Solar Energy)-भारत में यह महत्त्वपूर्ण स्रोत हो सकता है क्योंकि वर्ष के 365 दिनों में से 325 से 335 दिन तक सूर्य ऊर्जा उत्पादन की जा सकती है।
• वायु ऊर्जा (Wind Energy)-भारत के पठारी इलाके में वायु ऊर्जा उत्पादन की जा सकती है।
• बायो ऊर्जा (Bio-Energy)-यह पशुओं तथा कृषि के कचरे से पैदा की जा सकती है।

(B) यातायात (Transportation) यातायात भी बुनियादी ढांचे का महत्त्वपूर्ण अंश है। यातायात में रेलवे, सड़कें, जल यातायात, हवाई यातायात को शामिल किया जाता है।

• रेल यातायात (Rail Transportation)-भारत में रेल यातायात सब से महत्त्वपूर्ण यातायात का स्रोत है। इस समय रेलों का जाल देश भर में फैला हुआ है। भारत में रेलवे ट्रैक 1,15,000 km है। यह एशिया में सब से अधिक और विश्व में दूसरे स्थान पर है। यह ट्रैक 67368 km क्षेत्र में फैला हुआ है।
• सड़क यातायात (Road Transportation)-भारत में मार्च 2019 तक 1,32,500 km राष्ट्रीय सड़क मार्ग तथा 1,76,166 km राज्य सड़क मार्ग से सड़कों द्वारा मुसाफिरों तथा माल का आवागमन होता है।
• जल यातायात (Water Transportation)-जल यातायात भी बुनियादी ढांचे का महत्त्वपूर्ण साधन है। यह भारत में 14,500 km क्षेत्र में फैला हुआ है जिसमें से 5,685 km व्यापारिक वाहनों के लिये प्रयोग किया जाता है।
• हवाई यातायात (Air Transportation)-हवाई यातायात से लोग एक स्थान से दूसरे स्थानों तक सफर करते हैं तथा माल भी दूसरे स्थानों पर भेजा जाता है। भारत में दो हवाई कंपनियां हैं। पहली Air India जिस द्वारा 28 अन्तर्राष्ट्रीय तथा 13 घरेलू उड़ानें भरी जाती हैं। दूसरी Indian Airlines जो देश में 58 स्थानों को आपस में जोड़ती है।

(C) संचार (Communication)-संचार में डाक सेवाएं (Postal Services), टैलीफोन सेवाएं (Telephone Services) तथा टैलीग्राम सेवाएं (Telegraphic Services) को शामिल किया जाता है।

1. डाक सेवाएं (Postal Services) भारत में डाक विभाग बहुत पुरातन संचार का साधन है। भारत में इस समय लगभग 1,56,000 डाकखाने हैं। जिन में से 1,39,000 डाकखाने गाँव में स्थित है। प्रत्येक डाकखाने को पिन कोड दिया गया है। यह डाकखाने E Post, Speed Post, Express Post, Satellite Post आदि सेवाएं प्रदान करते हैं।
2. टैलीफोन सेवाएं (Telephone Services)-भारत में टैलीफोन भी संचार का साधन है। टैलीफोन सेवाओं में भारत एशिया भर में पहले स्थान पर है। STD की सुविधा 23000 से अधिक स्थान पर दी जाती है।
3. टैलीग्राफ सेवाएं (Telegraph Services)-भारत में लगभग 45,000 टैलीग्राफ दफ्तर हैं। इनके द्वारा देश में लिखती संदेश भेजे जाते हैं। इन आर्थिक सेवाओं द्वारा देश के आर्थिक विकास में वृद्धि होती है। प्रत्येक बजट में आर्थिक बुनियादी ढांचे का निर्माण करने के लिए यत्न किये जा रहे हैं। इस द्वारा देश के आर्थिक विकास में तेजी से वृद्धि होने की संभावना है|

Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 27 भारत में शिक्षा, स्वास्थ्य तथा बेरोजगारी Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 12 Economics Chapter 27 भारत में शिक्षा, स्वास्थ्य तथा बेरोजगारी

PSEB 12th Class Economics भारत में शिक्षा, स्वास्थ्य तथा बेरोजगारी Textbook Questions, and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
भारत में साक्षरता की क्या स्थिति है ?
उत्तर-
भारत में 1951 में साक्षरता दर 18.3% थी। 2019 में साक्षरता दर बढ़कर 75% प्रतिशत हो गई है।

प्रश्न 2.
भारत में शिक्षा संस्थाओं की संख्या पर प्रकाश डालें।
उत्तर-
भारत में 2019-20 में 828 यूनिवर्सिटियां, 25938 प्रोफैशनल कॉलेज, 40,000 कॉलेज, 92275 सैकेण्डरी स्कूल, 139539 हाई स्कूल, 2 लाख 74 हज़ार से अधिक मिडिल स्कूल तथा 7 लाख 48 हज़ार से अधिक प्राइमरी स्कूल थे।

प्रश्न 3.
शिक्षा के व्यवसायीकरण से क्या अभिप्राय है ?
उत्तर-
शिक्षा के व्यवसायीकरण से अभिप्राय है शिक्षा के साथ किसी व्यवसाय की शिक्षा देना।

प्रश्न 4.
1986 की नई शिक्षा नीति के उद्देश्य बताओ।
उत्तर-
शत-प्रतिशत प्राइमरी शिक्षा प्रदान करना। ग्रामीण क्षेत्र में शिक्षा का प्रसार करना।

प्रश्न 5.
भारत में स्वतन्त्रता के पश्चात् जन्म दर तथा मृत्यु दर में क्या परिवर्तन हुआ है ?
उत्तर-
भारत में स्वतन्त्रता के पश्चात् जन्म दर तथा मृत्यु दर में बहुत कमी हुई है। 1951 में मृत्यु दर 18 प्रति हज़ार थी जोकि कम होकर 7.3 प्रति हज़ार रह गई है।

प्रश्न 6.
भारत में जीवन प्रत्याशा को स्पष्ट करो।
उत्तर-
भारत में स्वतन्त्रता के पश्चात् जीवन प्रत्याशा में काफ़ी वृद्धि हुई है। 1951 में भारत में लोगों की औसत आयु 41 वर्ष थी। 2019 में लोगों की औसत आयु बढ़कर 70.4 वर्ष हो गई है।

प्रश्न 7.
रोज़गार से क्या अभिप्राय है?
उत्तर-
वे सभी व्यक्ति (पुरुष तथा स्त्रियां) जो पारिश्रमिक के लिए किसी प्रकार की नौकरी अथवा अपना कार्य करते हैं, उनको रोज़गार पर लगे गिना जाता है।

प्रश्न 8.
श्रम शक्ति (Labour Force) से क्या अभिप्राय है ?
उत्तर-
जो व्यक्ति असल में काम करते हैं अथवा काम करने के इच्छुक हैं, उनको श्रम शक्ति कहा जाता है। श्रम शक्ति में 15 वर्ष से अधिक तथा 60 वर्ष से कम आयु के व्यक्तियों को गिना जाता है।

प्रश्न 9.
सामाजिक संरचना के तीन महत्त्वपूर्ण घटक बताएं।
उत्तर-

1. शिक्षा
2. स्वास्थ्य
3. आवास।

प्रश्न 10.
लोगों के पढ़ने-लिखने तथा समझने की योग्यता को शिक्षा कहते हैं।
उत्तर-
सही।

प्रश्न 11.
भारत में शिक्षित बेरोज़गारी का मुख्य कारण शिक्षा को व्यवसाय से नहीं जोड़ा जाना है।
उत्तर-
सही।

प्रश्न 12.
2011 की जनगणना के अनुसार भारत में साक्षरता दर ………… प्रतिशत हो गई है।
(a) 64%
(b) 74.04%
(c) 84%
(d) इनमें से कोई नहीं।
उत्तर-
(b) 74.04%.

प्रश्न 13.
भारत में औसत जीवन अवधि …………….. वर्ष है।
(a) 53.5 वर्ष
(b) 63.5 वर्ष
(c) 73.5 वर्ष
(d) इनमें से कोई नहीं।
उत्तर-
(b) 63.5 वर्ष।

प्रश्न 14.
सम्भोग द्वारा जो बीमारियां एक व्यक्ति से दूसरे व्यक्ति में फैल जाती हैं उनको कहा जाता है।
उत्तर-
रजित रोग (Sexually Transmitted Diseases)

प्रश्न 15.
HIV से क्या अभिप्राय है ?
उत्तर-
ह्यूमन इमयुनो डैफीशेन्सी वायरस (HIV) का अर्थ शरीर में सफेद सैलज की कमी हो जाना जिनसे बीमारियों की रोकथाम होती है।

प्रश्न 16.
भारत में प्रारंभिक शिक्षा का कुल दाखिलों के अनुपात का अनुमान कैसे लगाया जाता है ?
उत्तर-
प्रारंभिक शिक्षा का कुल शिक्षा अनुपात-

प्रश्न 17.
सैकेण्डरी शिक्षा में शिक्षा के व्यवसायीकरण के लिए विशेष सफलता प्राप्त नहीं हुई है ?
उत्तर-
सही।

प्रश्न 18.
भारत में उच्च शिक्षा पर नियंत्रण तथा मार्गदर्शन कौन करता है ?
(a) केंद्र सरकार
(b) राज्य सरकार
(c) विश्वविद्यालय अनुदान आयोग
(d) उपरोक्त सभी।
उत्तर-
(c) विश्वविद्यालय अनुदान आयोग।

प्रश्न 19.
भारत में बेरोज़गारी का एक कारण शिक्षा का व्यवसायीकरण न होना है।
उत्तर-
सही।

प्रश्न 20.
भारत में शिक्षा पर सरकार द्वारा किया जाने वाला व्यय संतोषजनक है।
उत्तर-
ग़लत।

प्रश्न 21.
भारत में शिक्षा पर अधिक व्यय कौन करता है ?
(a) केंद्र सरकार
(b) राज्य सरकार
(c) निजी संस्था
(d) माता-पिता।
उत्तर-
(b) राज्य सरकार।

प्रश्न 22.
एड्ज़ (AIDS) से क्या अभिप्राय है ?
उत्तर-
एड्ज़ से अभिप्राय (एकुआयर्ड इमीनियो डैफीसेन्सी सिंड्रोम) रोगों से लड़ने की शक्ति की घाट।

प्रश्न 23.
औद्योगीकरण सेहत के लिए कैसे हानिकारक होता है ?
उत्तर-
औद्योगीकरण द्वारा वायु प्रदूषण, जल प्रदूषण और ध्वनि प्रदूषण फैलता है जो कि सेहत के लिए हानिकारक होता है।

प्रश्न 24.
भारत में बेरोज़गारी कितनी है ?
उत्तर-
भारत में 6.1% बेरोज़गार हैं।

प्रश्न 25.
भारत में शिक्षत बेरोज़गार कितने है ?
उत्तर-
भारत में 11.4% शिक्षत बेरोज़गार हैं।

II. अति लयु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
भारत में शिक्षा की स्थिति पर संक्षेप नोट लिखो।
उत्तर-
इस समय भारत में 74.04 प्रतिशत लोग साक्षर हैं। स्वतन्त्रता के पश्चात् शिक्षा के प्रसार की ओर अधिक ध्यान दिया गया है।

1. साधारण शिक्षा का प्रसार-शिक्षित लोगों की संख्या में वृद्धि हुई है। भारत में 82.14% पुरुष तथा 65.46% स्त्रियां साक्षर हैं।
2. शिक्षा संस्थाएं-भारत में स्कूल, कॉलेज तथा यूनिवर्सिटियों की संख्या में बहुत वृद्धि हुई है।

प्रश्न 2.
श्रम शक्ति तथा मानवीय शक्ति में अन्तर बताओ।
उत्तर-

• श्रम शक्ति उन व्यक्तियों की संख्या होती है जो वास्तव में काम पर लगे होते हैं अथवा काम करने के लिए तैयार होते हैं। कार्य शक्ति उन व्यक्तियों की संख्या होती है, जोकि वास्तव में कार्य पर लगे हुए होते हैं। उनमें उन व्यक्तियों को शामिल नहीं किया जाता, जो कार्य करने के लिए तैयार होते हैं।
• श्रम शक्ति में उन व्यक्तियों को शामिल करते हैं, जो देश में कार्य करने के लिए उपलब्ध होते हैं। कार्य शक्ति में उन व्यक्तियों को शामिल किया जाता है, जो वास्तव में काम पर लगे होते हैं।

प्रश्न 3.
रोज़गार से क्या अभिप्राय है ?
उत्तर-
रोज़गार का अर्थ है आर्थिक क्रिया में लगे होना। वह सभी व्यक्ति (पुरुष तथा स्त्रियां) जो किसी प्रकार के पारिश्रमिक के लिए किसी प्रकार की नौकरी अथवा अपना कार्य करते हैं को रोज़गार पर लगे हुए गिना जाता है। जब हम रोज़गार पर लगे व्यक्तियों की बात करते हैं तो उन व्यक्तियों को शामिल किया जाता है जो 15-60 वर्ष की आयु के हैं। 15 वर्ष से कम तथा 60 वर्ष से ऊपर की आयु के लोगों को कार्य शक्ति (Work Force) में शामिल नहीं किया जाता।

प्रश्न 4.
शहरी बेरोज़गारी पर टिप्पणी लिखें।
उत्तर-
शहरी बेरोज़गारी-भारत में 2017-18 में 991 लाख रजिस्टर्ड बेरोज़गार थे। इनमें औद्योगिक क्षेत्र के बेरोज़गार, शिक्षित बेरोज़गार जिनमें लड़के तथा लड़कियां शामिल हैं, उनमें बेरोज़गारी पाई जाती है। ग्रामीण तथा शहरी क्षेत्र में निम्नलिखित किस्म की बेरोज़गारी पाई जाती है –

1. खुली बेरोज़गारी-जब काम करने योग्य श्रम शक्ति काम करना चाहती है परन्तु उनको काम नहीं मिलता तो उसको खुली बेरोज़गारी कहा जाता है।
2. अल्प बेरोज़गारी-नैशनल सैम्पल सर्वे अनुसार यदि किसी व्यक्ति को साप्ताहिक 28 घण्टे काम प्राप्त होता है तो उसको अति अल्प बेरोजगार कहा जाता है। 29 से 42 घण्टे साप्ताहिक काम करने वाले श्रमिक को सीमित अल्प बेरोज़गार कहते हैं। जब कोई व्यक्ति किसी अन्य कार्य में अधिक उत्पादन कर सकता है तो वह वर्तमान कार्य में अल्प बेरोज़गार है।
3. संरचनात्मक बेरोज़गारी-किसी देश में संरचनात्मक ढांचे में परिवर्तन हो जाए अर्थात् तकनीक तथा मांग में परिवर्तन के कारण बेरोज़गारी उत्पन्न हो जाए तो इसको संरचनात्मक बेरोज़गारी कहते हैं।

प्रश्न 5.
बेरोज़गारी के आर्थिक प्रभाव बताएँ।
उत्तर-
बेरोज़गारी के आर्थिक प्रभाव-

• जब बेरोज़गारी होती है तो मानवीय शक्ति का पूर्ण प्रयोग नहीं होता।
• देश में उत्पादन कम हो जाता है।
• देश में प्रति व्यक्ति पैदावार कम हो जाती है।
• पूंजी निर्माण के कम होने से निवेश पर बुरा प्रभाव पड़ता है।

III. लघु उत्तरीय प्रश्न (Short Answer Type Question)

प्रश्न 1.
भारत में शिक्षा की स्थिति पर संक्षेप नोट लिखो।
उत्तर-
सन् 2011 में भारत में 74.04 प्रतिशत लोग साक्षर थे। स्वतन्त्रता के पश्चात शिक्षा प्रणा की ओर अधिक ध्यान दिया गया है।

1. साधारण शिक्षा का प्रसार-शिक्षित लोगों की संख्या 74.04% हो गई है। भारत में 82.14%, पुरुष तथा 65.46% स्त्रियां साक्षर हैं।
2. शिक्षा संस्थाएं-भारत में स्कूल, कॉलेज तथा यूनिवर्सिटियों की संख्या में बहुत वृद्धि हुई है।
3. विद्यार्थियों की संख्या-विद्यार्थियों की संख्या 2011 में बढ़कर 2 करोड़ हो गई है।
4. शिक्षा का व्यवसायीकरण-शिक्षा को व्यवसाय आधारित बनाया जा रहा है।

प्रश्न 2.
भारत में स्वास्थ्य स्थिति का संक्षेप वर्णन करो।
उत्तर-
भारत की स्वास्थ्य स्थिति के सूचक इस प्रकार हैं –

• जन्म दर-भारत में 1951 में जन्म दर 40 प्रति हज़ार से घट कर 2019-20 में 17 प्रति हज़ार रह गई है।
• मृत्यु दर-मृत्यु दर 1951 में 18 प्रति हज़ार थी जोकि 2019-20 में घटकर 7.3 प्रति हज़ार रह गई है।
• जीवन स्तर-भारत में औसत आयु 1951 में 41 वर्ष प्रति हज़ार थी जोकि 2019-20 में 70.4 वर्ष हो गई है।
• अस्पताल तथा डॉक्टरों की संख्या-भारत में 70000 अस्पताल हैं, जिनमें कुल 8 लाख 890130 डॉक्टर तथा 19 लाख 4 हज़ार नर्से हैं।

प्रश्न 3.
श्रम पूर्ति तथा श्रम शक्ति में अन्तर बताओ।
उत्तर-

1. श्रम पूर्ति का अर्थ मज़दूरी की दर के विभिन्न स्तर पर काम करने के लिए तैयार होते हैं। श्रम शक्ति का अर्थ वह मजदूरों की संख्या है जोकि काम कर रही है अथवा काम करने को तैयार है, परन्तु श्रम शक्ति का सम्बन्ध मज़दूरी की दर से नहीं होता।
2. श्रम पूर्ति अधिक अथवा कम हो सकती है, जब मज़दूरी में परिवर्तन होता है, इसका माप मानवीय दिन (8 घण्टे) के अनुसार किया जाता है। श्रम शक्ति का अर्थ मज़दूरों की संख्या से होता है। इसको मानवीय दिन (8 घण्टे) द्वारा मापा नहीं जाता।

IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
स्वतन्त्रता के पश्चात् भारत में शिक्षा के विकास की व्याख्या करो। (Explain the status of Education in India after Independence.)
अथवा
भारत में वर्तमान शिक्षा स्थिति का वर्णन करो। शिक्षा सम्बन्धी सरकार की नीति को स्पष्ट करो।
(Explain the present education condition of India. Discuss the Policy of the Government regarding Educations.)
उत्तर-
स्वतन्त्रता के पश्चात् भारत में शिक्षा के विकास को बहुत महत्त्व दिया गया है। 1950-51 में शिक्षा पर 114 करोड़ रुपए व्यय किए गए थे। 2019-20 में शिक्षा के क्षेत्र के लिए 1.78 लाख करोड़ रुपए व्यय करने का लक्ष्य है। भारत में शिक्षा प्रणाली की वर्तमान स्थिति अग्रलिखित अनुसार है –

1. साधारण शिक्षा का प्रसार-भारत में 1951 में कुल जनसंख्या का 16% भाग शिक्षित था। 2019-20 में शिक्षित लोगों की संख्या बढ़कर 74.4% हो गई है। इस प्रकार शिक्षा का प्रसार अधिक हुआ है। पुरुषों में शिक्षित लोग 82.14% तथा स्त्रियों में 65.46% प्रतिशत हैं।
2. शिक्षा संस्थाएं तथा विश्वविद्यालय-भारत में इस समय (2019-20) 900 विश्वविद्यालय (Universities) तथा अनुसन्धान केन्द्र हैं। 25938 प्रोफेशनल शिक्षा संस्थाएं तथा 40000 कॉलेज हैं। सीनियर सैकेण्डरी स्कूलों की संख्या 233517, मिडिल स्कूल 18 लाख 10 हज़ार तथा प्राइमरी स्कूलों की संख्या 18 लाख 12 हज़ार से अधिक है। भारत में प्राइमरी शिक्षा निःशुल्क तथा अनिवार्य है।
3. विद्यार्थियों की संख्या-1951 में 6 वर्ष से 11 वर्ष की आयु के 42 प्रतिशत विद्यार्थी स्कूल जाते थे। अब 80 प्रतिशत से अधिक विद्यार्थी स्कूल जाते हैं। विश्वविद्यालय में पढ़ने वाले विद्याथिर्यों की संख्या 1951 में 3.5 लाख थी जोकि 2019 में बढ़कर 2.9 करोड़ हो गई है।
4. शिक्षा का व्यवसायीकरण-भारत में केन्द्र सरकार ने 1986 की नई शिक्षा नीति अनुसार सैकेण्डरी स्तर पर शिक्षा के व्यवसायीकरण की योजना आरम्भ की है। व्यावसायिक शिक्षा प्राप्त विद्यार्थियों के लिए निजी क्षेत्र, सार्वजनिक क्षेत्र तथा उनके स्व-रोज़गार के लिए योजनाबद्ध नीतियां बनाई गई हैं।
5. प्रौढ़ तथा स्त्रियों की शिक्षा-भारत में बड़ी आयु के अनपढ़ पुरुषों तथा स्त्रियों के लिए शिक्षा को प्रौढ़ शिक्षा कहा जाता है। भारत में 15 वर्ष से 35 वर्ष के 11 करोड़ अनपढ़ हैं। सन् 2019-20 में 5.2 लाख लोगों के लिए शिक्षा का प्रबन्ध किया है। भारत में स्त्रियों की संख्या की ओर विशेष ध्यान दिया गया है।
6. स्कूलों में विज्ञान का विषय-1988 के पश्चात् स्कूलों में विज्ञान की शिक्षा आरम्भ की गई है। इसका उद्देश्य शिक्षा के स्तर का सुधार करना तथा वैज्ञानिक दृष्टिकोण उत्पन्न करना है।

सरकार की शिक्षा नीति-भारत में नई शिक्षा नीति की घोषणा 1986 में की गई। इस नीति अनुसार केन्द्र तथा राज्य सरकारें शिक्षा पर व्यय सकल घरेलू उत्पाद का 6 प्रतिशत करेंगी। दसवीं योजना में शिक्षा पर 24908 करोड़ रु० व्यय किए गए। 2020-21 में शिक्षा पर 360000 करोड़ रु० व्यय होने का अनुमान है। नई नीति में निम्नलिखित बातों पर जोर दिया गया है-

1. देश में सभी लोगों के लिए प्राथमिक शिक्षा प्रदान करना। इस उद्देश्य के लिए सर्वशिक्षा अभियान नवम्बर 2000 में आरम्भ किया गया। इस उद्देश्य के लिए 2020 में GDP का 3.9% भाग व्यय किया गया।
2. जुलाई 2019 में लड़कियों की शिक्षा के लिए सर्व शिक्षा अभियान के स्थान पर “प्राथमिक स्तर पर लड़कियों की शिक्षा के लिए राष्ट्रीय प्रोग्राम” की घोषणा की है । इस योजना के अधीन पिछड़े क्षेत्रों में जहां स्त्री संख्या कम है, उन क्षेत्रों में स्त्री शिक्षा का विस्तार किया जाएगा।
3. पिछड़ी जातियों तथा जनजाति की लड़कियों को प्राथमिक शिक्षा प्रदान करने के लिए ग्रामीण क्षेत्रों में रिहायशी स्कूल स्थापित करने का निर्णय लिया गया है। इस उद्देश्य के लिए 2014-15 में कस्तूरबा गांधी बालिका विद्यालय स्थापित करने के लिए बाहरवीं के वर्ष 2019-20 में 27 हज़ार करोड़ रु० व्यय करने का लक्ष्य है जिससे 750 रिहायशी स्कूल स्थापित किए जाएंगे।
4. सरकार ने प्रत्यक्ष तथा अप्रत्यक्ष करों पर 3 प्रतिशत अतिरिक्त कर (Cess) लगाया है, जिसको प्राथमिक शिक्षा कोष का नाम दिया गया है। इस कर द्वारा 2019-20 में 2500 करोड़ रु० व्यय किए गए।
5. तकनीकी शिक्षा के प्रसार पर भी जोर दिया गया है। बारहवीं योजना (2012-17) में स्कूल शिक्षा पर 360000 करोड़ अथवा उच्च शिक्षा पर 99300 लाख करोड़ रु० व्यय किये गए।

प्रश्न 2.
भारत में वर्तमान स्वास्थ्य स्थिति का वर्णन करो। इस सम्बन्धी सरकार की नीति स्पष्ट करो।
(Explain the present status of Health in India. Explain the Policy of Government in this regard.)
उत्तर-
किसी देश के साधनों में मानवीय साधनों को सबसे महत्त्वपूर्ण माना जाता है। किसी देश का आर्थिक विकास इस बात पर निर्भर करता है कि उस देश के मानवीय साधनों का शिक्षा, स्वास्थ्य, जीवन स्तर इत्यादि के रूप में कितना विकास हुआ है। प्रो० ड्रकर के अनुसार, “मनुष्यों के बिना पूंजी व्यर्थ होती है। पूंजी के बिना भी लोग पहाड़ों को हिलाने की शक्ति रखते हैं।” स्वतन्त्रता के पश्चात् भारत में मानवीय स्वास्थ्य पर बहुत बल दिया गया है। इसका अनुमान निम्नलिखित सूची पत्र द्वारा लगाया जा सकता है

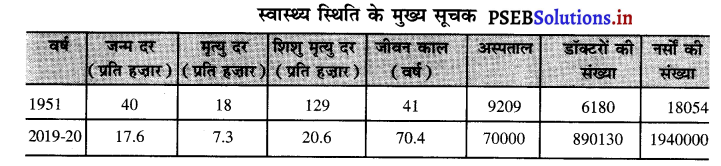
भारत में स्वास्थ्य स्थिति का अनुमान ऊपर दी सूची से लगाया जा सकता है।

1. जन्म दर-भारत में 1951 में जन्म दर 40 प्रति हज़ार थी जोकि 2019-20 में घटकर 17.6 प्रति हज़ार रह गई है। जन्म दर में कमी आई है जोकि जनसंख्या की वृद्धि पर रोक लगाने के लिए अच्छी है।
2. मृत्यु दर-भारत में मृत्यु दर भी काफ़ी घट गई है। 1951 में मृत्यु दर 18 प्रति हज़ार थी। यह घटकर 2019-20 में 7.3 प्रति हज़ार रह गई है। इसका कारण स्वास्थ्य सुविधाओं का विकास है।
3. शिशु मृत्यु दर-भारत में बच्चों के जन्म समय शिशुओं की मृत्यु हो जाती थी। 1951 में शिशु मृत्यु दर 129 प्रति हजार से घटकर 2019-20 में 26.6 प्रति हज़ार रह गई है। यह भी स्वास्थ्य सुविधाओं में वृद्धि का प्रतीक है।
4. जीवन प्रत्याशा-भारत में औसत जीवन प्रत्याशा में वृद्धि हुई है। 1951 में औसत जीवन प्रत्याशा 41 वर्ष थी। 2019-20 में औसत जीवन प्रत्याशा 70.4 वर्ष हो गई है। पुरुषों की जीवन प्रत्याशा 67 वर्ष तथा स्त्रियों की जीवन प्रत्याशा 74.4 वर्ष है।
5. अस्पतालों की संख्या-भारत में 1951 में अस्पतालों की संख्या 70000 थी। यह संख्या 2019-20 में बढ़कर 593320 हो गई है। इससे लोगों को विभिन्न बीमारियों का इलाज करवाना आसान हो गया है।
6. डॉक्टरों तथा नौं की संख्या- भारत में डॉक्टरों की संख्या में भी निरन्तर वृद्धि हुई है। 1951 में 61810 डॉक्टर थे। 2019-20 में डॉक्टरों की संख्या बढ़कर 890130 हो गई है। देश के प्रत्येक प्रान्त में मेडिकल कलेज स्थापित हो गए हैं। मरीजों की देखभाल तथा इलाज में नौं का योगदान भी महत्त्वपूर्ण होता है। 1951 में भारत में नों की संख्या 18054 थी जोकि बढ़कर 2019-20 में 1940000 हो गई।

स्वास्थ्य सम्बन्धी समस्याएं- भारत में स्वास्थ्य सम्बन्धी सुविधाओं की कुछ समस्याएं है जैसे कि –

• गांवों तथा शहरों में स्वास्थ्य सुविधाएं एक समान नहीं है। गांवों में स्वास्थ्य सुविधाओं की कमी है।
• एड्ज, शूगर, ब्ल्ड प्रैशर बीमारियों में वृद्धि हो रही है।
• निजीकरण के कारण स्वास्थ्य सम्भाल की लागत बढ़ रही है।
• साफ-सुथरे वातावरण तथा स्वास्थ्य सुविधाओं की कमी पाई जाती है।

स्वास्थ्य सम्बन्धी नीति-दसवीं पंचवर्षीय योजना में स्वास्थ्य सुविधाओं पर सकल घरेलू उत्पाद का 2-3 प्रतिशत हिस्सा व्यय करने की सिफ़ारिश की गई है। इस नीति के मुख्य उद्देश्य निम्नलिखित हैं

1. 2019-20 में एड्ज़ पर नियन्त्रण करने के लिए 2100 करोड़ रुपए व्यय किए गए।
2. प्राइमरी स्वास्थ्य केन्द्र गांवों में स्थापित किए गए हैं, जिनकी संख्या 2019-20 में 192166 हो गई है।
3. 2019-20 के बजट में स्वास्थ्य सुविधाओं पर 2998 करोड़ रु० व्यय किए गए।
4. देश के 19 राज्यों में कुष्ठ की बीमारी को समाप्त किया गया है। बारहवीं योजना के अन्त तक इस बीमारी को समाप्त कर दिया जाएगा।
5. देश में 2019-20 में 14 से 16 मिलियन पुरुष, स्त्रियां तथा बच्चे एड्ज़/एच० आई० वी० के शिकार हो चुके थे। यह देश में स्वास्थ्य सुविधाओं की कमी का सूचक है।
6. भारत में आयुर्वेद, योगा, यूनानी तथा होमियोपैथी को विकसित किया जा रहा है। इन इलाजों के विकास के लिए बारहवीं योजना में 13999 करोड़ रु० व्यय किए जाएंगे।
7. बारहवीं योजना में स्वास्थ्य पर 842481 करोड़ रु० व्यय किये जाएंगे।

प्रश्न 3.
भारत में बेरोज़गारी की किस्में बताओ। बेरोज़गारी के आर्थिक तथा सामाजिक प्रभाव बताओ।
(Explain the types of unemployment in India. Discuss the Economic and Social Effects and Education.)
उत्तर-
भारत में बेरोजगारी दिन-प्रतिदिन बढ़ रही है। जब एक मनुष्य काम पर नहीं होता परन्तु वह मनुष्य वर्तमान मज़दूरी की दर पर काम करना चाहता है तो उनको बेरोज़गार कहा जाता है। भारत में 2000 में 26.6 मिलियन, 2004 में 34.3 मिलियन तथा 2009 में 28 मिलियन तथा 2019-20 में 20.9 मिलियन श्रम शक्ति बेरोज़गार थी। भारत में बेरोज़गारी का वर्गीकरण निम्नलिखित अनुसार किया जा सकता है –
1. ग्रामीण बेरोज़गारी-गांवों में दो-तिहाई श्रम शक्ति स्व:रोज़गार पर कृषि उत्पादन में लगी हुई है। भारत में 2016 में 8.52% लोग बेरोज़गार थे। परन्तु गांवों में छिपी बेरोज़गारी भी पाई जाती है। छिपी बेरोज़गारी का अर्थ है कि कृषि उत्पादन में एक खेत पर पांच व्यक्तियों की आवश्यकता है परन्तु आठ व्यक्ति काम पर लगे हुए हैं, यदि 3 व्यक्तियों को अन्य काम पर लगाया जाए परन्तु कृषि के उत्पादन में कोई कमी न आए तो तीन श्रमिकों को छिपे बेरोज़गार कहा जाता है। इसी तरह गांवों में कृषि उत्पादन मौसमी कार्य है। इस कारण मौसमी बेरोज़गारी भी पाई जाती है।

2. शहरी बेरोज़गारी- भारत में 2019-20 में 11.4% बेरोज़गार थे। इनमें औद्योगिक क्षेत्र के बेरोज़गार, शिक्षित बेरोज़गार जिनमें लड़के तथा लड़कियां शामिल हैं, उनमें बेरोज़गारी पाई जाती है। ग्रामीण तथा शहरी क्षेत्र में निम्नलिखित किस्म की बेरोज़गारी पाई जाती है –

• खुली बेरोज़गारी-जब काम करने योग्य श्रम शक्ति काम करना चाहती है परन्तु उनको काम नहीं मिलता तो उसको खुली बेरोज़गारी कहा जाता है।
• अल्प बेरोज़गारी-नैशनल सैम्पल सर्वे अनुसार यदि किसी व्यक्ति को साप्ताहिक 28 घण्टे काम प्राप्त होता है तो उसको आत अल्प बेरोज़गार कहा जाता है। 29 से 42 घण्टे साप्ताहिक काम करने वाले श्रमिक को सीमित अल्प गेज़गार कहते हैं। जब कोई व्यक्ति किसी अन्य कार्य में अधिक उत्पादन कर सकता है तो वह नमान कार्य में अल्प बेरोज़गार है।
• संरचनात्मक बेरोज़गारी-किसी देश में संरचनात्मक ढांचे में परिवर्तन हो जाए अर्थात् तकनीक तथा मांग में परिवर्तन के कारण बेरोज़गारी उत्पन्न हो जाए तो इसको संरचनात्मक बेरोज़गारी कहते हैं।
• अस्थिर बेरोज़गारी-अस्थिर बेरोज़गारी देश में श्रम की गतिहीनता तथा श्रम बाज़ार की अपूर्णता के कारण उत्पन्न होती है, जब मजदूरों को बाज़ार का ज्ञान नहीं होता तो इस प्रकार की बेरोज़गारी उत्पन्न हो जाती है।
• चक्रीय बेरोज़गारी-किसी देश में मन्दीकाल के कारण उत्पन्न हुई बेरोज़गारी को चक्रीय बेरोज़गारी कहा जाता है।
• मौसमी बेरोज़गारी-मौसम में परिवर्तन होने से कुछ उद्योग बन्द हो जाते हैं तो इस प्रकार की बेरोज़गारी को मौसमी बेरोज़गारी कहा जाता है।

बेरोजगारी के आर्थिक प्रभाव-

1. जब बेरोज़गारी होती है तो मानवीय शक्ति का पूर्ण प्रयोग नहीं होता।
2. देश में उत्पादन कम हो जाता है।
3. देश में प्रति व्यक्ति पैदावार कम हो जाती है।
4. पूंजी निर्माण के कम होने से निवेश पर बुरा प्रभाव पड़ता है।

बेरोज़गारी पर सामाजिक प्रभाव-

• जीवन की गुणवत्ता कम हो जाती है।
• समाज में अमीर तथा गरीब वर्ग उत्पन्न हो जाते हैं।
• आर्थिक तथा सामाजिक असमानता में वृद्धि होती है।
• सामाजिक अशान्ति फैल जाती है जैसे कि नक्सलवादी तथा आतंकवादी समाज में अशान्ति उत्पन्न करते हैं।

प्रश्न 4.
भारत में शहरी तथा ग्रामीण रोजगार के लिए सरकार द्वारा कौन-सी योजनाएं बनाई गई हैं ? इनका उल्लेख करें।
(Explain the programs of the Government of India regarding rural and urban employment.)
उत्तर-
भारत में रोजगार की वृद्धि के लिए सरकार द्वारा निम्नलिखित पग उठाए गए हैंशहरी रोज़गार में वृद्धि के लिए उठाए गए पग-

1. संगठित क्षेत्रों का विकास-भारत में निजी क्षेत्र तथा सार्वजनिक क्षेत्र में अर्थात् उद्योग, खनिज, यातायात निर्माण इत्यादि में बहुत-से लोगों को रोजगार प्रदान करवाया जा रहा है।
2. रोज़गार के दफ़्तर-सरकार ने रोज़गार की सुविधाएं बढ़ाने के लिए 915 रोज़गार दफ़्तर स्थापित किए हैं। सरकार बेरोज़गारी भत्ता देने के बारे भी विचार कर रही है।
3. शिक्षित लोगों को स्व:रोज़गार-भारत में शिक्षित लोगों को स्व:रोज़गार दिलवाने के लिए सरकार बहुत-सी योजनाएं लागू कर रही है। शिक्षित लोगों को ऋण की सुविधाएं प्रदान की जा रही हैं।
4. रोज़गार गारण्टी योजना-कुछ राज्यों जैसे कि महाराष्ट्र, पश्चिमी बंगाल, केरल तथा राजस्थान इत्यादि में रोज़गार गारण्टी योजना आरम्भ की है। महाराष्ट्र में 2019 में 326 करोड़ रु० व्यय किए गए।

ग्रामीण रोज़गार में वृद्धि के लिए उठाए गए पग-
1. रोजगार के लिए धमाकेदार प्रोग्राम-1971 में बेरोज़गारी तथा अल्प बेरोज़गारी को दूर करने के लिए प्रत्येक जिले में श्रम सघन योजना आरम्भ की गई। इससे प्रत्येक परिवार के कम-से-कम एक व्यक्ति को रोज़गार प्रदान किया जाता है। इस योजना पर प्रत्येक वर्ष 100 करोड़ रु० व्यय किए गए हैं।

2. राष्ट्रीय ग्रामीण रोजगार प्रोग्राम-1980-81 में पहले काम के बदले अनाज योजना बनाई गई थी जिसका नाम बदलकर राष्ट्रीय ग्रामीण रोजगार प्रोग्राम रखा गया। इस योजना के तीन उद्देश्य थे

• गांवों में अधिक रोज़गार के अवसर पैदा करना।
• ग्रामीण लोगों का जीवन स्तर ऊँचा उठाना
• लोगों की आय में वृद्धि करना।

3. स्व:रोज़गार के लिए प्रशिक्षण-ग्रामीण स्वरोजगार प्रशिक्षण योजना (TRYSEM) 1979 में आरम्भ की गई। इस योजना के अन्तर्गत 12 लाख युवकों को प्रशिक्षण दिया गया। प्रत्येक युवक को 3000 अथवा 5000 रु० तक की आर्थिक सहायता भी दी गई ताकि वह अपना कार्य आरम्भ कर सकें।

4. जवाहर रोज़गार योजना-28 अप्रैल, 1989 में स्वर्गीय प्रधानमन्त्री श्री राजीव गांधी ने जवाहर रोज़गार योजना (JRY) आरम्भ की। इस योजना अधीन प्रत्येक गरीब ग्रामीण परिवार के एक सदस्य को 50 से 100 दिनों तक का रोज़गार देना है। इस योजना में स्त्रियों के लिए 30 प्रतिशत हिस्सा सुरिक्षत किया गया। इस योजना पर 2019-20 में 7200 करोड़ रु० व्यय किए गए।

5. जवाहर ग्राम समृद्धि योजना-यह योजना अप्रैल 1999 में आरम्भ की गई। इसमें केन्द्र तथा राज्य सरकारों का योगदान 75:25 की अनुपात में रखा गया। इस योजना का उद्देश्य गांवों में पक्की नालियां, गलियां, धर्मशालाएं इत्यादि चिरकालीन चलने वाले भण्डारों का विकास करना है। 2018-19 में केन्द्र सरकार ने 61500 करोड़ की राशि का योगदान इस योजना में पाया।

6. स्वर्ण जयन्ती ग्राम स्व:रोज़गार-यह योजना एकीकृत ग्रामीण विकास प्रोग्राम तथा स्वरोजगार के लिए प्रशिक्षण योजना को शामिल करके तैयार की गई। इसमें पहले चलाई जा रही योजनाओं को चालू रखना इसका उद्देश्य रखा गया।

7. सम्पूर्ण ग्रामीण रोजगार योजना-यह योजना 1 सितम्बर, 2001 में आरम्भ की गई। जवाहर ग्राम समृद्धि योजना तथा रोज़गार आश्वासन योजना को मिला दिया गया। इस योजना का उद्देश्य मज़दूरों को रोजगार के अधिक अवसर प्रदान करना, क्षेत्रीय आर्थिक तथा सामाजिक दशाओं का विकास करना है। इस योजना अधीन 2018-19 में 82 लाख टन चावल तथा 44 लाख टन गेहूं का वितरण किया गया।

8. प्रधानमन्त्री रोज़गार योजना-यह योजना शिक्षित बेरोजगार युवकों के लिए बनाई गई है। 2017-18 में इस योजना द्वारा 88 लाख युवकों को रोजगार दिया जा चुका है।

9. रोज़गार गारण्टी एक्ट 2005-यह योजना सितम्बर 2004 में लागू की गई है। इस योजना अनुसार प्रत्येक ग्रामीण, शहरी तथा निर्धन परिवार में से एक सदस्य को 100 दिनों का काम प्रदान किया जाएगा। 2018-19 में इस योजना पर व्यय करने के लिए 30 हज़ार करोड़ रुपये रखे गए हैं जोकि सकल घरेलू उत्पाद का 1.3% हिस्सा है।

10. प्रधानमन्त्री कौशल विकास योजना-NDA सरकार ने 2015 में कौशल विकास योजना का निर्माण किया। इसमे बेरोजगार युवकों को कौशल प्रदान करके रोजगार दिया जाएगा। इसमें अब तक 4.30 लाख बेरोजगारों को शिक्षा प्रदान की जा चुकी है।

11. दीन दयाल उपाध्याय ग्राम कौशल योजना-यह योजना 2019-20 में आरम्भ की गई इस योजना द्वारा 2.78 लाख ग्रामीण बेरोजगार युवकों को सिखलाई दी गई है।

12. बारहवीं योजना और रोज़गार-भारत की बारहवीं योजना (2012-17) के अन्त तक श्रम शक्ति में वृद्धि 65 करोड़ होगी तथा 42 करोड़ श्रम शक्ति के लिये रोज़गार प्रदान किया जाएगा। योजना के अन्त तक 5% बेरोज़गारी रह जाने की सम्भावना है। इस योजना में बेरोजगारों को शिल्प (Skill) सिखलाई देकर देश का विकास किया जाएगा।

13. बजट 2020-21-बजट 2020-21 में वित्त मंत्री निर्मला सीतारमण ने ग्रामीण क्षेत्र में रोजगार की वृद्धि के लिए 69000 करोड़ की राशि व्यय करने का लक्ष्य रखा है।

Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 26 आर्थिक विकास में मानव पूँजी का योगदान Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 12 Economics Chapter 26 आर्थिक विकास में मानव पूँजी का योगदान

PSEB 12th Class Economics आर्थिक विकास में मानव पूँजी का योगदान Textbook Questions, and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
मानव पूंजी से क्या अभिप्राय है ?
उत्तर-
मनुष्यों की कार्य कुशलता, ज्ञान और कौशल में वृद्धि को मानव पूँजी कहा जाता है।

प्रश्न 2.
मशीन, औज़ार और फैक्ट्रियां ही पूँजी निर्माण होते हैं ?
उत्तर-
गलत।

प्रश्न 3.
मनुष्य भी पूँजी निर्माण का महत्त्वपूर्ण स्रोत है ?
उत्तर-
सही।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
क्या जनसंख्या पूँजी निर्माण का स्रोत हो सकती है ?
उत्तर-
जनसंख्या का अधिक होना भी पूँजी निर्माण का स्रोत हो सकती है। इस बारे में प्रो० लुईस ने एक सिद्धान्त पेश किया है जिसमें वह कहते है कि बढ़ती जनसंख्या भी पूंजी निर्माण का साधन होती है ? चीन ने यह सिद्ध किया है कि अधिक जनसंख्या का अच्छी तरह प्रयोग करके उत्पादन में वृद्धि की जा सकती है। आज चीन दुनिया की एक महत्त्वपूर्ण शक्ति बन चुका है। इसलिए जनसंख्या पूँजी निर्माण का स्रोत बन सकती है।

प्रश्न 2.
मानव पूँजी द्वारा आर्थिक विकास के दो स्रोत बताएं।
उत्तर-

1. आर्थिक विकास के लिए मानव पूँजी योगदान पा सकती है। मानव पूँजी द्वारा उच्च शिक्षा, अच्छी सेहत और विज्ञान के प्रयोग से उत्पादन में वृद्धि करके आर्थिक विकास संभव हो सकता है।
2. मानव पूँजी आर्थिक विकास के औज़ार के रूप में भी प्रयोग की जा सकती है। मानव पूँजी उत्पादन के नए ढंगों का प्रयोग करके आर्थिक विकास में तेजी ला सकती है।

III. लघु उत्तरीय प्रश्न (Short Answer Type Question)

प्रश्न-
मानव पूँजी द्वारा आर्थिक विकास के औज़ार के रूप में कोई चार बिन्दु स्पष्ट करें।
उत्तर-
मानव पूँजी का अर्थ उच्च शिक्षा, अच्छी सेहत और खोज के नए ढंगों का प्रयोग करना होता है। इसलिए मानव पूँजी द्वारा आर्थिक विकास तेज़ी से किया जा सकता है –

1. उत्पादन में वृद्धि-यदि अधिक जनसंख्या होती है तो ऋण की लागत कम होती है। विकसित देश उस देश में पूँजी निवेश करके ऋण का प्रयोग करते है तो उत्पादन में तेज़ी से वृद्धि होती है।
2. उत्पादन शक्ति में वृद्धि-मानव पूँजी से न केवल उत्पादन में वृद्धि होती है और इसके साथ ही प्रति व्यक्ति उत्पादन बढ़ जाता है। इस प्रकार वस्तु की उत्पादन लागत कम हो जाती है और वस्तु कम कीमत पर आसानी से बेची जा सकती है। जिससे आर्थिक विकास में वृद्धि होती है।
3. प्रति व्यक्ति आय में वृद्धि-मानव पूँजी द्वारा प्रति व्यक्ति आय में वृद्धि होती है जो कि आर्थिक विकास का महत्त्वपूर्ण माप कहा जाता है। लोग अपने जीवन स्तर को ऊँचा करने का प्रत्यन करते हैं और बच्चे कम लिए जाते हैं।
4. उच्च शिक्षा का प्रसार-लोग आपने बच्चों को अच्छी उच्च शिक्षा प्रदान करते हैं जिससे उनको जीवन में कभी भी मुश्किल का सामना न करना पड़े। इस प्रकार बच्चों की उत्पादन शक्ति बढ़ जाती है और आर्थिक विकास में वृद्धि होती है।

IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
मानव पूँजी का आर्थिक विकास में योगदान स्पष्ट करें। (Explain the Role of Human Capital in Economic Development.)
उत्तर–
पुरातन समय में पूंजी का अर्थ केवल, मशीन, औज़ार, फैक्ट्रियाँ आदि भौतिक रूप में लिया जाता था। परन्तु रैंगवर वर्कस ने कहा कि भौतिक पूँजी के बिना मानव पूँजी भी आर्थिक विकास में महत्त्वपूर्ण योगदान पा सकती है। जब मानव उच्च शिक्षा, अच्छी सेहत, ज्ञान में वृद्धि करके अपने कौशल का विकास करते हैं तो इसको मानव पूंजी कहा जाता है। प्रो० एफ० एच० हारबीसन के अनुसार, “मानव पूँजी निर्माण का अर्थ उस प्रक्रिया से है जिसमें उन मनुष्यों की संख्या में वृद्धि की जाती है जो अधिक शिक्षित, कुशलता और तजुर्बे वाले होते हैं और देश के विकास प्रति आर्थिक तथा राजनीतिक विकास को आलोचनात्मक दृष्टि से देखते हैं। मानव पूँजी का सम्बन्ध मनुष्य के निवेश बढ़ाने से है जिससे वह उत्पादन में नए ढंगों का निर्माण कर सकें।” (“The term Human Capital Formation refers to the process of acquiring and increasing the number of persons who have the skill, education and experience which are critical for economic and political development of the country.” F.H. Harbison) प्रो० शुल्ज़ (Schultz) ने मानव पूंजी विकास के पाँच माप दण्ड बताए हैं जिनके द्वारा मानव पूँजी का विकास किया जा सकता है –

• सेहत सहूलतों में वृद्धि जिससे जीवन काल में वृद्धि हो। लोगों की काम करने की क्षमता बढ़ जाए और लोग हृष्ट-पुष्ट हों।
• काम करने की ट्रेनिंग जो कि फैक्ट्रियों द्वारा दी जाती है।
• शिक्षा प्रदान करना जो स्कूलों कालेजों और विश्वविद्यालयों में दी जाती है उसमें वृद्धि है।
• कृषि के क्षेत्र में लोगों को आधुनिक ढंगों का ज्ञान प्रदान करना।
• लोगों में गतिशीलता पैदा करना जिससे नए काम की खोज आसानी से की जा सके। इसमें विदेशी पूँजी और तकनीक को भी शामिल किया जा सकता है।

अधिक जनसंख्या होती है यह देश जनसंख्या को संसाधन का स्रोत बना सकते हैं जैसे कि चीन और भारत में विश्व की जनसंख्या का बहुत अधिक भाग है। चीन ने अपनी मानव शक्ति की सहायता से इतनी उन्नति की है कि अब विश्व की एक शक्ति बन गया है। अधिक जनसंख्या के कारण यूरोप और अमेरिका जैसे देशों ने पूंजी लगाकर सस्ते श्रम का लाभ उठाने का यत्न किया। फलस्वरूप जनसंख्या चीन के लिए पूंजी निर्माण का स्रोत बन गया। भारत भी अपनी जनसंख्या को पूंजी निर्माण का स्रोत बना सकता है।

इससे पता चता है कि कम विकसित देश इस कारण पिछड़े हुए नहीं हैं कि उनके पास साधनों की कमी है। बल्कि इस कारण पिछड़े हुए हैं कि उन देशों ने अपने साधनों का उचित प्रयोग नहीं किया। भारत के सम्बन्ध में ठीक कहा जाता है कि “भारत एक अमीर देश है इसमें रहने वाले लोग गरीब हैं।” “India is a rich country in habited by poor people.” भारत में प्राकृतिक साधन कोयला, लोहा, अच्छी उपजाऊ भूमि, दरिया आदि बहुत मात्रा में पाए जाते हैं। परन्तु इनका ठीक उपयोग न होने के कारण भारत पिछड़ा देश रह गया है। प्राकृतिक स्रोतों का उपयोग लोगों की कुशलता से बढ़ाया जा सकता है इसलिए मानव संसाधनों का अधिक योगदान हो सकता है।

मानव शक्ति के विकास के लिए तत्त्व (Factors to Improve quality of Human Power) – मानव शक्ति के विकास के लिए निम्नलिखित तत्त्व महत्त्वपूर्ण होते हैं-
1. शिक्षा (Education)-कम विकसित देशों के पिछड़ेपन का एक कारण वहां के लोगों का अशिक्षित होना है। शिक्षा से लोगों की विचारधारा विशाल होती है। वह उत्पादन के नए-नए स्रोत ढूंढ़ने लगते हैं। इस द्वारा राष्ट्रीय भावना उत्पन्न होती है। लोगों में मेहनत करने की भावना उत्पन्न होती है। देश का उत्पादन बढ़ जाता है। इस प्रकार लोगों की आय में भी वृद्धि होती है। देश के तीनों क्षेत्र प्राथमिक, गौण तथा टरशरी, सभी में विकास होना प्रारंभ हो जाता है। इस प्रकार शिक्षा द्वारा देश में आर्थिक विकास होने लगता है।

2. सेहत (Health)-ठीक कहा जाता है सेहतमंद शरीर में सेहतमंद दिमाग होता है। (A healthy body keeps a healthy mind) यदि देश के लोग स्वस्थ हैं तो उनमें काम करने की भावना उत्पन्न होती है। वर्ष 2021 का बजट पेश करते हुए वित्त मंत्री निर्मला सीतारमण ने सबसे अधिक राशि स्वास्थ्य के लिए व्यय करने का प्रस्ताव रखा है। जब लोग सेहतमंद होते हैं तो काम करने की इच्छा अधिक होती है। इससे उनकी आय में वृद्धि होती है और जीवन स्तर उच्चा हो जाता है। अच्छा खाना पीना सेहत के लिए अच्छा होता है इससे उनकी आय में वृद्धि होती है। प्रति व्यक्ति आय बढ़ने से राष्ट्रीय आय में वृद्धि होती है।

3. कौशल विकास (Skill Development) भगवान प्रत्येक मनुष्य को कोई ना कोई कौशल देकर भेजता है। यदि लोगों के कौशल को विकसित किया जाए तो उनकी उत्पादन शक्ति में वृद्धि होती है। कौशल विकास से नई-नई वस्तुएं बनाने की रुचि उत्पन्न होती है। इस प्रकार लोगों को अलग-अलग प्रकार के कौशल की शिक्षा देकर उनकी उत्पादन शक्ति में वृद्धि की जा सकती है। स्कूलों में पढ़ाई के साथ-साथ काम धन्धे के कौशल की सिखलाई दी जाए तो पढ़ाई समाप्त होते ही लोग नौकरी की तलाश की बजाय अपने काम चालू कर सकते हैं। इस प्रकार के लोग संसाधन का स्रोत बन सकते हैं।

4. तकनीक (Technology)-तकनीक का ज्ञान भी लोगों को संसाधन का स्रोत बना देता है। प्रकृति ने भूमि के नीचे लोहा, कोयला, हीरे, मोती, पैट्रोल आदि खनिज पदार्थ दिए हैं। तकनीक का ज्ञान न हो तो उनकी खोज नहीं की जा सकती। इसलिए लोगों को संसाधन का स्रोत बनाने के लिए तकनीक का विकास भी आवश्यक है। तकनीक के विकास के कारण यूरोप के लोग अधिक विकसित हो सके हैं। इस प्रकार नई-नई तकनीकों का आविष्कार करके आर्थिक विकास किया जा सकता है। इस प्रकार शिक्षा, सेहत, कौशल और तकनीक के विकास से लोगों को संसाधन का स्रोत बनाया जा सकता है।

Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 25 सहकारिता, कृषि में विभिन्नता और जैविक खेती Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 12 Economics Chapter 25 सहकारिता, कृषि में विभिन्नता और जैविक खेती

PSEB 12th Class Economics सहकारिता, कृषि में विभिन्नता और जैविक खेती Textbook Questions, and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
सहकारी समितियों का कृषि में क्या महत्त्व है ?
उत्तर-
सहकारी समितियों द्वारा ग्रामीण विकास संभव है।

प्रश्न 2.
सरकारी समितियाँ ………….. में सहायक होती है।
उत्तर-
ग्रामीण विकास।

प्रश्न 3.
कृषि में विभिन्नता से क्या अभिप्राय है ?
उत्तर-
एक प्रकार की उपज के स्थान पर विभिन्न फसलों की बिजाई को कृषि में विभिन्नता कहते हैं।

प्रश्न 4.
सहज कृषि से क्या अभिप्राय है ?
उत्तर-
सहज कृषि (Organic Agriculture) का अर्थ है पुरातन ढंगों से कृषि करके उत्पादन करना।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
सहकारी समितियों का कृषि में महत्त्व स्पष्ट करें।
उत्तर-
सहकारी समितियाँ बहुत छोटे तथा मध्यम वर्ग के किसानों के लिए लाभदायक सिद्ध हो सकती हैं। यदि छोटे किसान अपने छोटे-छोटे कृषि के टुकड़ों को सहकारिता की सहायता से इकट्ठा करते तो उन पर आधुनिक मशीनों का प्रयोग किया जा सकता है। इस प्रकार उनकी आय में बहुत वृद्धि की जा सकती है। प्रम: कृषि में विभिन्नता के दो लाभ बताएं।
उत्तर-
कृषि में विभिन्नता के बहुत से लाभ हैं। दो मुख्य लाभ इस प्रकार हैं

• द्वारा छोटे और मध्यम वर्ग के किसानों की आय में बहुत वृद्धि की जा सकती है।
• निषि आधुनिक रासायनिक खाद के स्थान पर पुरातन गोबर खाद डालकर जैविक कृषि को अपनाया जा सकता है।

आज कल बहुत से लोग रासायनिक खाद के कारण बीमारी का शिकार हो रहे हैं इसलिए लोग लेविक अनाज, फल और सब्जियां खरीदना पसंद करते हैं जिससे जीवन स्तर में वृद्धि होगी।

प्रश्न 3.
सहज कृषि के लाभ बताएं।
उत्तर-
आधुनिक खादों के कारण ब्लड प्रैशर, मधुमेह और कई तरह की बीमारियां नज़र आ रही हैं। इसलिए लोगों का रुझान सहज कृषि (Organic Agriculture) की तरफ बढ़ रहा है। इसमें गोबर द्वारा पुरातन ढंग से कृषि की जाती है। जिससे न केवल मनुष्य के जीवन में सुधार होता है और इसके साथ-साथ धरती की उपजाऊ शक्ति में भी परिवर्तन होता है। इसलिए सहज कृषि आजकल प्रचलित हो रही है।

III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न-
भारत में कृषि में विभिन्नता की आवश्यकता क्यों है ?
उत्तर-
भारत में अनाज की आवश्यकता को ध्यान में रखते हुए 1966 में हरित क्रांति द्वारा अनाज वृद्धि पर जोर दिया गया। इससे रासायनिक खादों का अति अधिक प्रयोग किया गया। उत्पादन तो बढ़ गया परन्तु इससे न केवल भूमि की उपरी सतह पर बुरा प्रभाव पड़ा बल्कि भूमि के नीचे जल भी प्रदूषित हो गया। अधिक उद्योग स्थापित होने के कारण नदियों का जल प्रदूषित हो गया और अधिक रासायनिक खाद के कारण धरती के नीचे का जल भी प्रदूषित हो गया है। इस प्रकार पीने के पीने का संकट उत्पन्न हो गया है। इसलिए न केवल भारत में बल्कि विश्व भर में कृषि में विभिन्नता की ओर ध्यान दिया जा रहा है।

कृषि में विभिन्नता का अर्थ है कि एक प्रकार की फसल लगातार बीजने के स्थान पर दूसरी प्रकार की फसलों की बिजाई करना। जैसे कि गेहूँ और चावल की कृषि के स्थान पर दालों, फल, सब्जियों आदि को सहज ढंग से बीज कर जैविक अनाज पैदा करना। जैविक अनाज की कीमत भी अधिक मिलती है और यह मनुष्य के स्वास्थ्य को भी ठीक रखते हैं। इसलिए आजकल लोग सहज कृषि की तरफ अधिक ध्यान दे रहे हैं।

IV. दीर्य उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
सहकारी समितियों का ग्रामीण विकास में महत्त्व स्पष्ट करें। (Explain the Role of Co-operatives in Rural development.)
उत्तर-
ग्रामीण विकास में सहकारी समितियों का योगदान महत्त्वपूर्ण स्थान प्राप्त कर गया है। भारत में किसान के पास ज़मीन कम हो रही है, छोटे-छोटे टुकड़े हो गए हैं जिन पर कृषि करना लाभदायक नहीं रहा है। इसलिए किसान का गुजारा इन छोटे आकार के खेतों पर कृषि करके निर्वाह मुश्किल से हो रहा है। किसान को कृषि करने के लिए कर्ज लेना पड़ता है और उस उधार की वापसी बहुत कठिन हो रही है। इसलिए सहकारी समितियों की सहायता से ही छोटे किसान अपनी आय बढ़ा सकते हैं और इससे कृषि करने के ढंग में सुधार हो सकता है।
सहकारी समितियों का कृषि में योगदान इस प्रकार से स्पष्ट किया जा सकता है-

1. यदि किसान अपने छोटे-छोटे जमीन के टुकड़ों पर कृषि के स्थान पर सहकारी खेती करना शुरू कर दे तो इससे बड़े पैमाने पर आधुनिक मशीनों का प्रयोग करके ऊपज में वृद्धि की जा सकती है।
2. कृषि में जो उपज पैदा होती है उस को बाज़ार में बेचने के स्थान पर तैयार सामान बनाकर बेचा जा सकता है-जैसे कि गेहूँ के स्थान पर आटा बेचा जा सकता है। फल बेचने के स्थान पर जूस बना कर बेच सकते हैं। सरसों के स्थान पर सरसों का तेल बना कर बेचा जा सकता है। इससे किसान की आय में वृद्धि हो जाएगी।
3. कृषि में उपज के मण्डीकरण में भी सुधार हो सकता है। छोटे किसान अपनी उपज बाजार में तुरन्त बेच के लिए मजबूर होते हैं। सहकारी समितियों द्वारा अनाज का भण्डार किया जा सकता है। जब कीमत में वृद्धि हो तब उसको बेच कर अधिक दाम प्राप्त किया जा सकता है। इसके लिए भारत में NAFED राष्ट्रीय कृषि बिक्री फैडरेशन बनाई गई है।
4. कृषि के लिए आधुनिक औजारों का प्रयोग करके ऑर्गेनिक फसलें तैयार की जा सकती हैं। आजकल ऑर्गेनिक उपज की मांग बढ़ रही है जिसके द्वारा किसानों की आय में बहुत वृद्धि की संभावना है जो कि सहकारिता द्वारा ही संभव है।
5. छोटे किसानों को उधार प्राप्त करने में तकलीफ का सामना करना पड़ता है। सहकारी समितियां बैंकों से आसानी से उधार लेकर कृषि कार्य पूर्ण कर सकती हैं। इससे सहकारी समिति के प्रत्येक सदस्य को लाभ प्राप्त हो सकता है।

इस क्षेत्र में NABARD का योगदान बहुत ही अच्छा है। कृषि में सहकारी समितियां बनाने के लिए लोगों को उत्साहित किया जा रहा है इसके फलस्वरूप भारत में KRIBCO और KD Milk Producers Co-operative समितियों की स्थापना हुई है। इस तरफ किसानों को और ध्यान देने की जरूरत है।

सहकारी समितियों का ग्रामीण विकास में योगदान (Role of Co-operatives in Rural Development) – भारत में कृषि ग्रामीण जीवन की आय और रोजगार का मुख्य स्रोत है। ग्रामीण जीवन के सुधार के लिए सहकारी समितियां महत्त्वपूर्ण योगदान डालती हैं। इस का वर्णन निम्नलिखित अनुसार किया जा सकता है –

1. रोज़गार का स्रोत (Source of Employment)-गांवों में 65% जनसंख्या कृषि पर निर्भर है। गांवों के लोग कृषि, मछलीपालन, जंगलात और पशुधन द्वारा अपनी जीविका का प्रबन्ध करते हैं। सीमान्त किसान के लिए सहकारी समितियाँ रोजगार का स्रोत बन जाती हैं।
2. आधुनिक कृषि तकनीक का प्रयोग (Use of Modern Cultivation Techniques) कृषि में अच्छी खाद, अच्छे बीज, औजार, भंडारण, यातायात आदि सहूलतों में सहकारी समितियों द्वारा वृद्धि की जाती है। इससे आय में वृद्धि होती है।
3. धारणीय अर्थव्यवस्था (Sustainable Economy)-कृषि में हर काम में सहकारी समितियाँ सहायता करती हैं। जिससे उत्पादन में वृद्धि होती है और इससे धारणीय विकास किया जा सकता है।
4. वस्तुओं की पूर्ति में वृद्धि (Increase in Supply of Goods)-सहकारी समितियाँ ग्रामीण क्षेत्र में बहुत सी सेवाएं प्रदान करती हैं। गाँव में लोगों के पास वित्तीय साधन कम होते हैं इसलिए यह समितियां लोगों को शिक्षा, ऋण, नई तकनीकों की जानकारी देकर उनकी आय में वृद्धि करती है क्योंकि वह वस्तुओं की पूर्ति में वृद्धि करते हैं।
5. ऋण की सुविधा (Credit Facilities)-ग्रामीण जीवन में लोगों को हर काम के लिए ऋण की जरूरत पड़ती है। फसल बीजने से लेकर कटाई तक पैसे की आवश्यकता होती है। वह सहकारी समितियों के सहयोग से प्राप्त किया जा सकता है।

सहकारी समितियों के प्रकार (Types of Co-operative Societies) सहकारी समितियों के विभिन्न प्रकार इस प्रकार हैं –

• उपभोक्ता सहकारी समितियाँ (Consumer Co-operative Societies) सहकारी समितियाँ गांवों में लोगों को प्रत्यक्ष रूप से आवश्यक वस्तुएँ, बीज, खादें, उपभोगी वस्तुएं, उत्पादकों से प्रत्यक्ष तौर पर खरीदकर प्रदान करती हैं। इससे मध्यस्थों का लाभ समाप्त हो जाता है और कम कीमत पर उपभोक्ता वस्तुएं मिल जाती
• उत्पादक सहकारी समितियाँ (Producer Co-operative Societies)-सीमान्त तथा लघु किसानों के लिए सहकारी समितियाँ लाभदायक सिद्ध होती है, उत्पादन के लिए औज़ार, मशीनें, कच्चा माल आदि इन समितियों द्वारा प्रदान किया जाता है।
• मंडीकरण सहकारी समितियाँ (Marketing Co-operative Societies)-सीमान्त तथा लघु किसानों की उपज की बिक्री के लिए सहकारी समितियाँ लाभदायक होती हैं। किसानों को उपज की बिक्री में बहुत सी मुश्किलें सहन करनी पड़ती हैं जिनके लिए यह समितियाँ सहायता करती हैं।
• सहकारी ऋण समितियाँ (Co-operative Credit Societies)-किसानों को ऋण की सहूलत प्रदान करने में भी सहकारी समितियाँ सहयोग करती हैं। यह समितियाँ अपने सदस्यों से उनकी बचत को इकट्ठा करती हैं और दूसरे सदस्यों को उधार देती हैं।

ग्रामीण क्षेत्रों में सहकारी समितियों की समस्याएं (Problems faced by Co-operative Societies in Rural Areas) सहकारी समितियों की मुख्य समस्याएं इस प्रकार हैं –

1. असन्तोषजनक फंड (Insufficient Funds)-सहकारी समितियों के पास जो फंड होते हैं वह संतोषजनक नहीं होते हैं। जब इन समितियों के पास फंड की कमी होती है तो वे अपने सदस्यों को उधार नहीं दे पातीं। इस कारण बहुत सी समितियां असफल हो जाती हैं।
2. केवल कृषि ऋण (Agricultural Loans Only)ये समितियाँ किसानों की हर प्रकार की वित्तीय जरूरतें पूरी नहीं करती। यह केवल कृषि ऋण ही प्रदान करती हैं। इसलिए किसान इन समितियों से पूरा लाभ प्राप्त नहीं कर पाते।
3. राजनीतिक दखल (Political Intrusion)-सहकारी समितियाँ किसी न किसी राजनीतिक दल द्वारा प्रभावित होती हैं। राजनीतिक नेता अपने पक्ष के लोगों की आवश्यकताओं को पूरा करते हैं और दूसरे पक्ष के लोगों को ऋण देते समय बहुत सी शर्ते लगा देते हैं। इस कारण सभी लोग इन समितियों से पूरा लाभ नहीं उठा पाते।
4. निजी हित (Personal Interests)-बहुत से सहकारी समितियों के सदस्य निजी हित को ध्यान में रखते हैं। वे सभी सदस्यों के हितों का ध्यान नहीं रखते। इससे गरीब सदस्यों को ऋण लेने में तकलीफ होती है और ये समितियाँ असफल हो जाती हैं।

प्रश्न 2.
कृषि में विविधीकरण के महत्व को स्पष्ट करें। (Explain the role of Diversification in Agriculture.)
उत्तर-
विविधीकरण का अर्थ (Meaning of Diverssification)-विविधीकरण का अर्थ है कि कृषि में कम मूल्य की फसलों के स्थान पर अधिक मूल्य वाली फसलों को उगाना अथवा अधिक आय देने वाले काम को शुरू करना। इससे डेयरी (Dairy), पोल्ट्री (Poultary), बागवानी (Horticulture) और मछली पालन (Pisciculture) क्षेत्र में पुरानी फसलों के स्थान पर इन क्षेत्रों को अपनाने को विविधीकरण कहा जाता है। एक फसल (गेहूँ अथवा चावल) के स्थान पर विभिन्न प्रकार की अलग-अलग फसलों की बीजाई करके आय में वृद्धि करना कृषि में विविधीकरण कहलाता है।

भारत में विविधीकरण का अर्थ स्पष्ट करते हुए अराधना सिंह ने कहा, “विविधीकरण का अर्थ एक फसल के स्थान पर अधिक फसलों का उत्पादन करना है जिससे आय में वृद्धि हो।” (Diversification means shift from the regional dominance of one crop to regional production of a number of crops for enhancing the income of the farmers.” Aradhna Singh)
विविधीकरण की आवश्यकता (Need for Diversification)-विविधीकरण करने की आवश्यकता क्यों है इसके मुख्य कारण इस प्रकार हैं –

1. उपभोक्ता माँग में परिवर्तन (Changing Consumer Demand)-विकासशील देशों में लोगों की माँग में अधिक परिवर्तन हो रहा है। पहले लोग एक ही अनाज को आहार में प्रयोग करते थे। परन्तु अब आहार में मीट, अण्डे, और दूध, मक्खन, पनीर आदि वस्तुओं ने स्थान ले लिया है। इसलिए उपभोक्ता माँग में परिवर्तन आने से विविधीकरण की आवश्यकता है।
2. जनसंख्या में वृद्धि (Increase in Population) विश्व की जनसंख्या बहुत तेजी से बढ़ रही है। अब विश्व की जनसंख्या 7 मिलियन है और 2050 तक 9.5 बिलियन होने का अनुमान है। भारत में भी आज़ादी के समय जनसंख्या 36 करोड़ थी जो 2020-21 में 136 करोड़ के लगभग हो गई है। इस प्रकार तेजी से बढ़ रही जनसंख्या के लिए अनाज पैदा करना एक चुनौती है। इस कारण भी कृषि में विविधीकरण की आवश्यकता
3. निर्यात बाज़ार की मांग में वृद्धि (Increase in Export Market Demand) विकासशील देशों में किसान विश्व बाजार में बढ़ रही माँग को देखते हुए, निर्यात करने के लिए विविधीकरण को अपना रहे हैं। आजकल निर्यात करके अधिक आय प्राप्त की जा सकती है, इसलिए भी विविधीकरण की जरूरत है।
4. सपर बाजार में बिक्री में वृद्धि (Increases in sale in Super-Market)-आजकल विश्व में बड़े बड़े सुपर स्टोर खुल रहे हैं। यहाँ पर इतनी किस्म की वस्तुएं खरीदी जा सकती हैं कि ग्राहक प्रचून विक्रेता के पास जाने के स्थान पर सुपर बाज़ार में जाकर खरीदारी करनी पसंद करने लगा है। इसलिए विविधीकरण द्वारा सुपर बाज़ार में बिक्री के लिए वस्तुएं पैदा करना अधिक लाभकारी हो गया है।
5. सरकार की नीतियों में परिवर्तन (Change in Government Policies)-बाज़ार की संभावना अब बढ़ गई हैं क्योंकि सरकार भी किसानों को वह अनाज अधिक मात्रा में पैदा करने को उत्साहिक करती है जिस की बिक्री बदलते बाज़ार के अनुकूल हो। अब किसान अपनी वस्तु मध्यस्थों के द्वारा बिक्री के स्थान पर सीधे खरीददारों को बेच सकता है इससे भी विविधीकरण को उत्साह प्राप्त हुआ है।
6. पौष्टिक आहार (Nutrient Food)-पुरानी एक अनाज के प्रयोग के आहार में अब परिवर्तन हुआ है और इसके स्थान पर पौष्टिक आहार के विविधीकरण की ओर रुझान बढ़ रहा है।
7. जोखिम (Risk)-एक ही अनाज को उगाने में अब किसान को अधिक जोखिम उठाना पड़ता है क्योंकि कृषि प्रकृति पर निर्भर है। इसलिए विविधीकरण द्वारा इस जोखिम को कम किया जा सकता है।
8. शहरीकरण (Urbanization)-शहरीकरण में वृद्धि होने से किसान अब उन वस्तुओं की खेती करना अधिक लाभदायक समझता है जिससे उसकी आय में वृद्धि हो। शहरों में अधिक फल, सब्जियों की माँग होती है इसलिए विविधीकरण की आवश्यकता है।
9. मौसम में परिवर्तन (Climate Change)-ग्लोबल वार्मिंग के कारण मौसम में परिवर्तन हो रहा है। . बेमौसमी वर्षा के कारण फसलें नष्ट हो जाती हैं। इसलिए बहुत से देशों, जैसे कि कैनेडा, कीनिया, भारत, श्रीलंका आदि में विविधीकरण पर बल दिया जा रहा है।
10. घरेलू नीति (Domestic Policy)-कृषि में बहुत प्रकार की सहायता दी जाती है। यदि कृषि में सबसिडी (Subsidy) न दी जाए तो किसान अपनी लागत पूरी नहीं कर सकता। इसलिए सरकार अब इस सहायता में परिवर्तन करके विविधीकरण के लिए सहायता दे रही है जिससे किसान आत्मनिर्भर हो सके।

विविधीकरण के प्रकार
(Types of Diversification) विविधीकरण दो प्रकार से किया जाता है –

• फसल उत्पादन में विविधीकरण (Diversification of Crop Pattern)-जब एक फसल गेहूँ और चावल के स्थान पर बहुत सी फसलें पैदा की जाती हैं तो इसको फसल उत्पादन में विविधीकरण कहा जाता है।
• उत्पादन क्रिया में विविधीकरण (Diversification of Productive Activities)-इसका अर्थ है कि जब श्रम शक्ति को कृषि के स्थान पर अन्य सम्बन्धित कार्यों और गैर-कृषि कार्यों में लगाया जाता है इसको उत्पादन क्रिया में विविधीकरण कहा जाता है। जैसा कि पशुपालन द्वारा मीट, अण्डे, पशम आदि की पैदावार, दूध तथा दूध उत्पादों में वृद्धि, मछली पालन और बागवानी में श्रम शक्ति का प्रयोग करके किसान की आय में वृद्धि करना।

विविधीकरण के लाभ (Benefits of Diversification) विविधीकरण के मुख्य लाभ इस प्रकार हैं –
1. आय में वृद्धि (Increase in Income)-विविधीकरण द्वारा किसान एक ही फसल पर निर्भर होने के स्थान पर बहुत सी फसलों को बीजता है तो उसका जोखिम कम हो जाता है और आय में वृद्धि होती है।

2. अनाज सुरक्षा (Food Security)-जब किसान एक फसल की बिजाई करता है और मौसम खराब होने से अनाज नष्ट हो जाता है तो इससे अनाज की कमी हो जाती है। विविधीकरण द्वारा अलग-अलग वस्तुओं के उत्पादन से अनाज सुरक्षा बनी रहती है।

3. रोज़गार में वृद्धि (Increase in Employment)-जब एक फसल के स्थान पर विभिन्न प्रकार की वस्तुओं की पैदावार की जाती है, तो इससे रोज़गार में वृद्धि होती है। फल सब्जियां, और प्रोसैस्ड फूड में अधिक लोगों को काम मिलता है। इस प्रकार दूध, मुर्गी पालन, मछली पालन आदि काम करने से भी रोजगार में वृद्धि होती है।

4. गरीबी को कम करना (Reducing Poverty)-विकासशील देशों में गरीबी की समस्या भी जटिल समस्या है। विविधीकरण द्वारा गरीबी को कम किया जा सकता है। जब विविधीकरण किया जाता है तो गरीब लोगों को काम प्राप्त होता है जिससे उनकी आय में वृद्धि होती है। आय बढ़ने से गरीबों के जीवन स्तर में सुधार होता है। दूसरे जब विविधीकरण किया जाता है तो निर्यात में वृद्धि होती है इससे भी लोगों की आय में वृद्धि होती है।

5. सीमित साधनों की अधिक उत्पादकता (More Productivity of Scarce Resources)-प्रकृति ने जो साधन दिये हैं वे सीमित मात्रा में हैं जैसे जल, कोयला आदि। इनका उत्तम प्रयोग करने के लिए भी विविधीकरण की जरूरत है। कम जल का प्रयोग करके हम पोल्ट्री फार्म, पशु पालन करके आय अधिक प्राप्त कर सकते हैं।

6. निर्यात में वृद्धि (Increase in Exports) विविधीकरण द्वारा विदेशी उपभोक्ताओं की माँग के अनुसार उत्पादन करके निर्यात में वृद्धि की जा सकती है इससे आय में और वृद्धि होती है।

7. मूल्य में वृद्धि (Adding Value)-यूरोप, अमेरिका आदि देशों में लोगों को तैयार आहार चाहिए जैसे कटा हुआ सलाद, बर्गर, पीज़ा आदि। यदि विविधीकरण द्वारा इन वस्तुओं का उत्पादन बढ़ाया जाता है तो अनाज के मूल्य में वृद्धि की जा सकती है।

8. सरकार की नीति (Government Policies)-सरकार भी किसानों को विविधीकरण के लिए प्रेरित करती है जिससे किसानों की आय में वृद्धि हो। बहुत सी सहायता देकर नए किस्म की वस्तुओं को प्रोत्साहित किया जाता है।

9. शहरीकरण (Urbanization)–लोग ज्यादा शहरों में रहना पसंद करते हैं। इससे लोगों के आहार में परिवर्तन हो रहा है जिसको लोगों की माँग के अनुसार बदल कर लाभ प्राप्त किया जा सकता है।

10. वातावरण (Environment)-विविधीकरण द्वारा हम भूमि, जल प्रदूषण पर नियन्त्रण कर सकते हैं। इससे धारणीय विकास (Sustainable Development) हो सकता है। इस प्रकार विविधीकरण द्वारा देश में आर्थिक विकास की गति को तेज़ किया जा सकता है। यह न केवल किसानों के हित में है इससे देश का विकास भी तीव्र गति से होगा।

प्रश्न 3.
जैविक खेती से क्या अभिप्राय है ? जैविक खेती के सिद्धान्त बताएं। इसके लाभ तथा त्रुटियाँ बताएँ।
(What is Organic Farming? Explain the principles of organic farming. Explain its merits & limitations.)
उत्तर-
जैविक खेती कृषि की वह विधि है जो संश्लेषित उर्वरकों एवं संश्लेषित कीटनाशकों के अप्रयोग या न्यूनतम प्रयोग पर आधारित है तथा जो भूमि की उर्वरक शक्ति को बनाए रखने के लिए आवश्यक तथा लाभकारी होता है। विश्व में जनसंख्या की वृद्धि के कारण हरित क्रान्ति ने जन्म लिया। इससे विश्व में रासायनिक खादों का प्रयोग करके अधिक अनाज पैदा करने के लिए यत्न किये गए। इस द्वारा अनाज के उत्पादन में बहुत वृद्धि हुई है परन्तु खाद तथा कीटनाशकों के अधिक प्रयोग के कारण उत्पादन में जहरीला असर बढ़ गया। लोगों को कैंसर, ब्लड प्रेशर, शूगर आदि बीमारियों का शिकार होना पड़ा। इसलिए विश्व भर में जैविक खेती की तरफ रुझान बढ़ रहा है। इसमें पुरातन ढंग से खेती करने का रुझान बढ़ गया है। इसमें पशुओं का गोबर और कूड़ा-कर्कट का प्रयोग करके अनाज की पैदावार की जाती है। इसको जैविक खेती (Organic Farming) कहा जाता है।

जैविक खेती के मुख्य सिद्धान्त (Main principles of Organic Farming)-UNO के विशेषज्ञों के अनुसार, “जैविक खेती प्राकृतिक तथा धारणीय प्रबन्धक विधि के विशेष मूल्यों पर आधारित है।” (Organic Farming is based on unique values of natural & sustainable farm management practices.” U.N.O. Experts. यह विधि निम्नलिखित सिद्धान्तों पर आधारित है –
1. सेहत का सिद्धान्त (Principle of Health)-जैविक खेती सेहत के सिद्धान्त को ध्यान में रख कर अपनाई जाती है। इससे भूमि, जल, वायु आदि को प्रदूषित होने से रोका जाता। यह विधि मनुष्य, पशुओं तथा पक्षियों के लिए भी लाभदायक है।

2. वातावरण का सिद्धान्त (Principle of Ecology)-जैविक खेती वातावरण को ठीक रखने के उद्देश्य से अपनाई जाती है। इसके द्वारा न केवल भूमि, जल, वायु और सूर्य की ऊर्जा को ठीक रखा जाता है। बल्कि इस विधि द्वारा मनुष्यों, जानवरों, पशु-पक्षियों को भी प्रदूषण से बचाया जाता है। इसलिए यह विधि वातावरण को शुद्ध रखने के लिए भी उचित मानी जाती है।

3. उचित्ता का सिद्धान्त (Principle of Fairness)-जैविक खेती में लोगों के आहार सम्बन्धी आवश्यकताओं की पूर्ति के लिए पैदावार करते समय यह ध्यान रखा जाता है कि इसका देश पर आर्थिक, सामाजिक तथा मनोविज्ञानिक बुरा प्रभाव न पड़े।

4. पूर्ण ध्यान रखने का सिद्धान्त (Principle of Care)-इस विधि द्वारा यह ध्यान रखा जाता है कि जो लोग अलग-अलग किस्म के काम करते हैं उन का सेहत तथा लागत में अधिक प्रभाव न पड़े। इस से लोगों की भलाई को भी ध्यान में रखा जाता है।

जैविक खेती में फसलों के बदलाव (Crop Rotation), देशी खाद, अच्छे शुद्ध बीज, पौधों में उचित दूरी पर पैदावार की जाए, जिससे प्राप्त अनाज की गुणवत्ता कायम रहे। भारत में जैविक खेती को सबसे पहले मध्य प्रदेश में चालू किया गया। पहले प्रत्येक जिले में एक गाँव का चुनाव किया। जिसमें जैविक खेती शुरू की गई। बाद में 2 गाँवों और फिर 5 गाँवों में जैविक खेती चाल की गई। इन गाँवों को जैविक गाँवों का नाम दिया गया। इस समय करीब 4000 गाँवों में जैविक खेती की जा रही है। जैविक खेती से उपजाई गई फसल का रेट काफी अधिक होता है। गेहूँ जोकि जैविक खेती से बनाया जाता है उसका आटा लगभग ₹ 60 प्रति किलो निर्धारित किया जाता है। इस प्रकार जैविक खेती से अधिक आय भी होती है।

जैविक खेती के लाभ (Merits of Organic Farming) –

1. इस द्वारा सेहत के लिए शुद्ध वातावरण प्राप्त होता है।
2. इस द्वारा भूमि, जल, वायु आदि को प्रदूषण से हानि नहीं होती।
3. इस द्वारा भूमि की चिरकालीन उपजाऊ शक्ति बनी रहती है।
4. प्राकृतिक साधनों का उचित प्रयोग होता है और इससे भविष्य में आने वाली नस्लों को भी अच्छा वातावरण मिलता है।
5. जैविक खेती से इंधन की लागत कम हो जाती है। इससे प्रत्येक को अच्छा अनाज उचित कीमतों पर प्राप्त होता है।

जैविक खेती में कम ऊर्जा का प्रयोग होता है और फसलों के खराब होने की सम्भावना घट जाती है। इससे कैमीकल क्रियाओं से होने वाला खतरा कम हो जाता है।

जैविक खेती की सीमाएं (Limitations of Organic Farming) –

• जैविक खाद की सीमित मात्रा होने के कारण सभी लोगों को खाद प्राप्त करने में कठिनाई होती है।
• जैविक खेती द्वारा अनाज का उत्पादन कम हो जाता है। इसलिए किसान अपनी आय को कम नहीं करना चाहते। यदि उपज कम होती है तो कीमत अधिक रखनी पड़ती है जो कि लोग देना पसंद नहीं करेंगे।
• जैविक खेती से जो उपज पैदा होती है इसका उचित स्तर भारतीय किसानों द्वारा संभव नहीं है। लोग अधिकतर अनपढ़ होने के कारण इन बातों का ध्यान नहीं रख सकते।
• जैविक खेती द्वारा उपज के मण्डीकरण की समस्या उत्पन्न हो सकती है भारत में 90% लोगों की आय बहुत कम होने के कारण जैविक अनाज को खरीदना मुश्किल होगा। परन्तु आजकल जैविक खेती की तरफ रुझान बढ़ रहा है।

Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 24 कृषि उपज का मण्डीकरण Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 12 Economics Chapter 24 कृषि उपज का मण्डीकरण

PSEB 12th Class Economics कृषि उपज का मण्डीकरण Textbook Questions, and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
कृषि उत्पादन मण्डीकरण से क्या अभिप्राय है ?
उत्तर-
कृषि उत्पादन मण्डीकरण से अभिप्राय कृषि उत्पादन उपज की बिक्री तथा खरीददारों को एकत्रित करना होता है।

प्रश्न 2. नियमित मण्डी से क्या अभिप्राय है ?
उत्तर-
नियमित मण्डी कानून अधीन आरम्भ की जाती है, जोकि एक वस्तु अथवा वस्तुओं के समुच्चय के लिए बनाई जाती है। इसका संचालन मार्किट कमेटी द्वारा किया जाता है।

प्रश्न 3.
नियमित मण्डी का मुख्य उद्देश्य बताओ।
उत्तर-
नियमित मण्डी का उद्देश्य कृषि उपज की भ्रष्ट बुराइयों को दूर करके किसानों के हितों की रक्षा करना होता है। किसानों से प्राप्त किए अधिक व्ययों पर रोक लगाई जाती है।

प्रश्न 4.
भारत में नियमित मण्डियों की स्थिति का वर्णन करो।
उत्तर-
1951 में 200 नियमित मण्डियां स्थापित की गई थीं। 2020-21 में नियमित मण्डियों की संख्या 29000 हो गई है।

प्रश्न 5.
कृषि मण्डीकरण के सम्बन्ध में मॉडल एक्ट 2003 की कोई एक मुख्य विशेषता बताओ।
उत्तर-
किसानों, स्थानिक अधिकारियों तथा अन्य लोगों को नई मण्डियां स्थापित करने की आज्ञा दी गई है।

प्रश्न 6.
भारत में कृषि उत्पादन उपज के भण्डार की स्थिति पर प्रकाश डालें।
उत्तर-
सन् 2019 तक भारत में 211 मिलियन मीट्रिक टन अनाज के भण्डार की सुविधाएं उपलब्ध थीं।

प्रश्न 7.
जब कृषक अपनी आवश्यकताओं को पूरा करने के पश्चात् उपज को बाज़ार में बिक्री के लिए तैयार हो जाता है तो उसको ……………….. कहते हैं।
उत्तर-
बिक्री योग्य आधिक्य (Marketable Surplus)।

प्रश्न 8.
भारत में …………………….. मिलियन टन अनाज भण्डारण की योग्यता है।
उत्तर-
162 मिलियन मीट्रिक टन।

प्रश्न 9.
भारत में अनाज भण्डार के गोदाम ………….. हैं।
(a) अधिक
(b) सन्तोषजनक
(c) कम
(d) उपरोक्त में से कोई नहीं।
उत्तर-
(c) कम।

प्रश्न 10.
भारत में सन् 2019 में ………………… नियमित मण्डियां गांव तथा शहरों में काम करती हैं।
उत्तर-
शहरों में 8511 और गांवों में 20808 मण्डियां हैं।

प्रश्न 11.
भारत में कृषि उपज की न्यूनतम समर्थन कीमत कृषि लागत तथा कीमत कमीशन द्वारा निर्धारण होती है।
उत्तर-
सही।

प्रश्न 12.
सन्तोषजनक कृषि उपज की बिक्री के लिए उचित शर्त ………. है।
(a) साहूकार से छुटकारा
(b) सौदेबाज़ी की अधिक शक्ति
(c) मध्यस्थों का अन्त
(d) उपरोक्त सभी।
उत्तर-
(d) उपरोक्त सभी।

प्रश्न 13.
भारत में कृषि उपज की बिक्री की मुख्य समस्याएँ ………… हैं।
(a) संगठन की गैर-मौजूदगी
(b) बिचौलियों की अधिक संख्या
(c) ग्रेडिंग की गैर-मौजूदगी
(d) उपरोक्त सभी।
उत्तर-
(d) उपरोक्त सभी।

प्रश्न 14.
सहकारी मण्डीकरण से क्या अभिप्राय है ?
उत्तर-
सहकारी मण्डीकरण का अर्थ आपसी लाभ प्राप्ति और मण्डीकरण की समस्याओं का हल करने के लिए आपसी सहयोग देना है।

प्रश्न 15.
भारत में कृषि उपज की बिक्री के लिए उचित कदम उठाये गए हैं ?
उत्तर
-सही।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
भारत में कृषि उत्पादन उपज के मण्डीकरण की समस्याओं को स्पष्ट करो।
उत्तर –
भारत में कृषि उपज के मण्डीकरण की समस्याएं इस प्रकार हैं –

1. अपर्याप्त माल गोदाम-किसानों के पास माल गोदाम अपर्याप्त मात्रा में हैं। इसलिए किसानों की उपज का 10% से 20% हिस्सा नष्ट हो जाता है।
2. साख सुविधाओं की कमी-किसान को अपनी उपज बहुत कम कीमत पर बेचनी पड़ती है। किसानm ऋण में रहता है, इसलिए फसल की कटाई के तुरन्त पश्चात् वह अपनी उपज साहूकार के पास बेचने के लिए मजबूर हो जाता है।

प्रश्न 2.
भारत में नियमित मण्डियों की विशेषताएं बताओ।
उत्तर-
भारत में नियमित मण्डियों का उद्देश्य किसानों के साथ होने वाले शोषण को समाप्त करना है। भारत में नियमित मण्डियों की स्थापना कृषि उपज मण्डीकरण एक्ट 1951 के अनुसार की गई। 31 मार्च, 2019 तक भारत में 8511 मण्डियां थीं और 20868 मण्डियाँ फसल के आने पर काम करती हैं। नियमित मण्डियों की मुख्य विशेषताएं इस प्रकार हैं-

• नियमित मण्डियों का संचालन मार्किट कमेटियों द्वारा किया जाता है जिसमें राज्य सरकार के कर्मचारी, ज़िला बोर्ड, व्यापारी, कमीशन एजेन्ट तथा किसानों के प्रतिनिधि शामिल होते हैं।
• मार्किट कमेटी मण्डी में प्राप्त किए व्यय को निर्धारित करती है। यह भी निश्चित किया जाता है कि कितना व्यय खरीददार तथा कितना बेचने वाले को सहन करना पड़ेगा।

प्रश्न 3.
भारत में नियमित मण्डियों के लिए सरकार द्वारा उठाए कोई दो कदम बताएं।
उत्तर-
नियमित मण्डियों के लिए सरकार द्वारा उठाए गए पगभारत में सरकार ने नियमित मण्डियों सम्बन्धी निम्नलिखित पग उठाए हैं –
1. मण्डियों का सर्वेक्षण-देश में विभिन्न वस्तुओं की बिक्री के लिए भिन्न-भिन्न स्थानों पर मण्डियों का सर्वेक्षण किया गया है। सरकार इन मण्डियों में वस्तुओं की कीमतों को प्रकाशित करती है तथा प्रचार किया जाता है।

2. ग्रेडिंग तथा स्तरीकरण-भारत सरकार ने कृषि उत्पादन वस्तुओं की गुणवत्ता को बनाए रखने के लिए एगमार्क की मोहर लगाने का निर्णय किया। एगमार्क की वस्तुएं विश्वसनीय होती हैं, क्योंकि वस्तुओं की गुणवत्ता को परखकर मोहर लगाने का अधिकार दिया जाता है।

III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 1.
भारत में कृषि उत्पादन उपज के मण्डीकरण की समस्याओं को स्पष्ट करो।
उत्तर-
भारत में कृषि उपज के मण्डीकरण की समस्याएं इस प्रकार हैं –

1. अपर्याप्त माल गोदाम-किसानों के पास माल गोदाम अपर्याप्त मात्रा में हैं। इसलिए किसानों की उपज का 10% से 20% हिस्सा नष्ट हो जाता है।
2. साख सुविधाओं की कमी-किसान को अपनी उपज बहुत कम कीमत पर बेचनी पड़ती है। किसान ऋण में रहता है, इसलिए फसल की कटाई के तुरन्त पश्चात् वह अपनी उपज साहूकार के पास बेचने के लिए मजबूर हो जाता है।
3. यातायात की सुविधाओं की कमी-भारत में यातायात के साधन, रेलों की कमी के कारण, किसान को गांवों में से शहर तक उपज ले जाने में मुश्किल का सामना करना पड़ता है। उसको अधिक लागत सहन करनी पड़ती है तथा मार्ग में ही उसकी उपज का कुछ भाग नष्ट हो जाता है।
4. मण्डी में भ्रष्टाचार-भारत का किसान अनपढ़ तथा अज्ञानी है। मण्डी में उसका शोषण किया जाता है। किसान से अधिक कटौतियां प्राप्त की जाती हैं। नापतोल में हेरा-फेरी की जाती है।

प्रश्न 2.
कृषि मण्डियों में कौन-सी सुविधाओं की आवश्यकता है ?
उत्तर-
भारत में कृषि की उपज के मण्डीकरण में निम्नलिखित बुनियादी सुविधाओं की आवश्यकता है

• किसानों के पास माल गोदाम की उचित सुविधाएं होनी चाहिए।
• किसान के पास फसल को कुछ समय अपने पास रखने की समर्था होनी चाहिए अर्थात् फसल की कटाई के पश्चात् फसल बेचने की जगह पर कुछ समय के लिए किसान अपनी उपज को संभाल कर रख सकें तथा उचित मूल्य पर ही उसकी बिक्री करें।
• किसान को यातायात के लिए सुविधाएं प्रदान की जाएं ताकि वह अपनी उपज गांव में बेचने की जगह पर मण्डियों में उचित कीमत पर उपज बेच सकें।
• बाज़ार सम्बन्धी किसान को पूरी जानकारी प्रदान करनी चाहिए।
• बिचोलों की संख्या को घटाकर उनका कमीशन निर्धारण करना चाहिए।

प्रश्न 3.
भारत में नियमित मण्डियों की विशेषताएं बताओ।
उत्तर-
भारत में नियमित मण्डियों का उद्देश्य किसानों के साथ होने वाले शोषण को समाप्त करना है। भारत में नियमित मण्डियों की स्थापना कृषि उपज मण्डीकरण एक्ट 1951 के अनुसार की गई। 31 मार्च, 2009 तक भारत में 7139 मण्डियां थीं और 20868 मण्डियाँ फसल के आने पर काम करती हैं। नियमित मण्डियों की मुख्य विशेषताएं इस प्रकार हैं –

1. नियमित मण्डियों का संचालन मार्किट कमेटियों द्वारा किया जाता है, जिसमें राज्य सरकार के कर्मचारी, ज़िला बोर्ड, व्यापारी, कमीशन एजेन्ट तथा किसानों के प्रतिनिधि शामिल होते हैं।
2. मार्किट कमेटी मण्डी में प्राप्त किए व्यय को निर्धारण करती है। यह भी निश्चित किया जाता है कि कितना व्यय खरीददार तथा कितना बेचने वाले को सहन करना पड़ेगा।
3. नियमित मण्डियों द्वारा किसानों के साथ होने वाले छल-कपट पर नियन्त्रण करना है।
4. नियमित मण्डियों द्वारा किसानों को प्राप्त होने वाली आय तथा उपभोक्ताओं द्वारा किए गए व्यय में अन्तर को घटाना है।
5. मॉडल एक्ट 2003 अनुसार नियमित मण्डियों में नई सोच उत्पन्न की गई है, जिस द्वारा कई तरह के सुधार किए गए हैं। फसल की बिक्री के समय 20868 मण्डियां गांव में लगाई जाती है जिसके द्वारा किसान अपनी उपज गांव में ही बेच सकता है।

प्रश्न 4.
सहकारी मार्किट कमेटियों पर नोट लिखो।
उत्तर-
भारत में सहकारी मार्किट कमेटियों की स्थापना 1954 में की गई। सहकारी मार्किट कमेटियाँ किसानों की उपज का उचित मूल्य दिलवाने में सहायता करती हैं। इसके द्वारा किसानों को ऋण की सुविधाएं प्रदान की जाती हैं ताकि किसान अपनी उपज, कटाई के तुरन्त पश्चात् न बेचें तथा कुछ समय रुककर अच्छी कीमत पर फसल बेच सकें। मार्किट कमेटियों द्वारा किसान की उपज माल गोदाम में रखने की सुविधा प्रदान की जाती है।

किसान को सस्ते मूल्य पर यातायात के साधन उपलब्ध करवाए जाते हैं। किसानों को ग्रेडिंग तथा मयारीकरण की फसलें बेचने के लिए सहायता की जाती है। विचोलों की जगह पर फसल सीधी ग्राहकों के पास बेचने का प्रबन्ध किया जाता है। इस प्रकार सहकारी मार्किट कमेटियाँ किसानों के लाभ हेतू महत्त्वपूर्ण कार्य करती हैं। 2019-20 में 55885 करोड़ रु० की उपज की बिक्री की गई। इन कमेटियों के पास 4.4 मिलियन टन अनाज भण्डार करने के लिए गोदामों की व्यवस्था है।

प्रश्न 5.
भारत में कृषि उपज के मण्डीकरण सम्बन्धी सरकारी नीति पर टिप्पणी लिखो।
उत्तर-
भारत में कृषि उपज के मण्डीकरण सम्बन्धी सरकार ने निम्नलिखित महत्त्वपूर्ण पग उठाए हैं –

1. मार्किट कमेटियों की स्थापना-भारत में मण्डियों को नियमित करने के लिए मार्किट कमेटियों की स्थापना की गई है।
2. बाज़ार सम्बन्धी सूचना-भारत में बाज़ार सम्बन्धी सूचना प्रदान करने का महत्त्वपूर्ण कार्य सरकार द्वारा किया गया है। इस सम्बन्धी रोज़ाना मण्डियों के मूल्य तथा होने वाले परिवर्तन के बारे रेडियो, टी० वी० तथा अखबारों में सूचना दी जाती है।
3. वस्तुओं की ग्रेडिंग तथा मयारीकरण-वस्तुओं की ग्रेडिंग तथा मयारीकरण के लिए भी सरकार किसानों की सहायता करती है। सरकार द्वारा वस्तुओं की परख उपरान्त एगमार्क (AGMARK) का सर्टीफिकेट दिया जाता है। इससे अच्छी किस्म की वस्तुओं की बिक्री आसानी से हो जाती है।
4. गोदामों की सुविधा-कृषि उपज के भण्डार के लिए सरकार ने गोदामों की सुविधा में प्रशंसनीय वृद्धि की है। सन् 2012 में भारत में 751 लाख टन अनाज के भण्डार के लिए गोदाम थे।

प्रश्न 6.
भारत में अनाज की सरकारी खरीद पर प्रकाश डालें।
उत्तर-
भारत में 1965 में अनाज की कमी के पश्चात् सरकार ने अनाज का बफर स्टॉक स्थापित करने का निर्णय किया। इस उद्देश्य के लिए सरकार के पास 2006-07 में 358 लाख टन गेहूँ तथा चावल की खरीद की गई। 2017-20 तक भारत में गेहूँ तथा चावल की बफर कस्वटी (Buffer Norm) 311 लाख टन थी जबकि असल भण्डार 312 लाख टन था।

प्रश्न 7.
भारत में कृषि उपज की कम-से-कम समर्थन मूल्य पर प्रकाश डालें।
उत्तर-
भारत में कृषि उपज का कम-से-कम समर्थन मूल्य निश्चित किया जाता है, क्योंकि गेहूँ तथा चावल की फसल मण्डियों में आने से अनाज की पूर्ति बढ़ जाती है। इसलिए कीमतों के घटने का डर होता है। पिछले दस वर्षों से गेहूँ तथा चावल की कम-से-कम समर्थन कीमत में काफ़ी वृद्धि हुई है। भारत में एफ० सी० आई० (E.C.I.) द्वारा गेहूँ तथा चावल की खरीद की जाती है तथा इससे प्राकृतिक आपदाओं से बचने के लिए बफर स्टॉक स्थापित किया जाता है। 2006-07 में गेहूँ की कम-से-कम समर्थन कीमत (Minimum support price) 360 रु० प्रति क्विटल थी जोकि 2020-21 में 1658 रु० निश्चित की गई। चावल की कम-से-कम समर्थन कीमत 1994-95 में 340 रु० थी जोकि 2020-21 में बढ़ाकर 1868 रु० की गई।

प्रश्न 8.
भारत में कृषि उपज के माल गोदामों की भण्डार समर्था का वर्णन करो।
उत्तर-
भारत में अनाज की जो सरकार द्वारा खरीद की जाती है। इसको सम्भाल कर रखने के लिए माल गोदामों की समर्था इस प्रकार है-

1. फूड कार्पोरेशन ऑफ़ इंडिया (F.C.I.) भारत में फूड कार्पोरेशन गेहूँ तथा चावल की समर्थन कीमत पर खरीद करती है। 2018 में एफ० सी० आई० 362 लाख टन अनाज भण्डार की समर्था थी।
2. केन्द्रीय गोदाम कार्पोरेशन (C.W.C.)-केन्द्रीय गोदाम कार्पोरेशन भी अनाज के भण्डार की सुविधाएं प्रदान करती हैं। इस संस्था के पास 99 लाख टन अनाज भण्डार की समर्था है।
3. राज्य गोदाम कार्पोरेशन (S.W.C.)-भारत में 16 राज्यों में राज्य गोदाम कार्पोरेशन स्थापित किए गए हैं। इन गोदामों में 273 लाख टन अनाज भण्डार की समर्था है।
4. सहकारी गोदाम (Co-operative Warehouses)-राष्ट्रीय सहकारी विकास कार्पोरेशन (NCDC) की स्थापना 1963 में की गई। यह कार्पोरेशन सहकारी समितियों द्वारा भण्डार की सुविधाएं प्रदान करती हैं। 2012 में सहकारी गोदामों में 137.2 लाख टन अनाज की समर्था थी।
5. ग्रामीण विकास विभाग (Deptt. of Rural Development)-ग्रामीण विकास विभाग द्वारा भी गोदामों की सुविधा में वृद्धि की गई है। 2019 में ग्रामीण विकास विभाग द्वारा 25 लाख टन अनाज भण्डार करने की समर्था थी।
6. नाबार्ड अधीन विभिन्न एजेन्सियाँ (Various Agencies through NABARD)-भारत में कृषि तथा ग्रामीण विकास के लिए राष्ट्रीय बैंक (NABARD) द्वारा निजी क्षेत्र (Private Sector) में अनाज के भण्डार के लिए गोदाम स्थापित करने के लिए उत्साहित किया जाता है।

इस संस्था द्वारा विभिन्न एजेन्सियों द्वारा बनाए गए माल गोदामों की समर्था 2018 में 211 मिलियन थी। अन्य एजेन्सियों द्वारा भी 82.1 लाख टन अनाज भण्डार की सुविधा प्रदान की गई है। भारत में वर्ष 2019 में विभिन्न संगठनों द्वारा 751 लाख टन अनाज भण्डार के लिए माल गोदाम की सुविधा थी जो कि देश की ज़रूरतों से कहीं कम हैं। .

V. दीर्य उत्तरीय प्रश्न न मिलन (Long Answer Type Questions)

प्रश्न 1.
कृषि उत्पादन उपज के मण्डीकरण की समस्याओं का वर्णन करो। (Explain the problems of Agricultural selecting in India.)
उत्तर-
मण्डीकरण वह क्रिया है, जहां उत्पादक तथा खरीददारों को एक-दूसरे के सम्पर्क में लाया जाता है। उत्पादक, कृषि उपज पैदा करने वाले किसान होते हैं। खरीददारों में उपभोगी अथवा व्यापारी होते हैं। भारत में 70% लोग कृषि उत्पादन का कार्य करते हैं तथा गांवों में रहते हैं। कृषि उत्पादन उपज के मण्डीकरण में बहुत दोष हैं।

कृषि उत्पादन उपज के मण्डीकरण की समस्याएं (Problems of Agricultural Marketing)-
अथवा
कृषि उत्पादन उपज के मण्डीकरण की असंतोषजनक स्थिति (Unsatisfactory Condition of Agricultural Marketing) भारत में कृषि उत्पादन उपज के मण्डीकरण की स्थिति संतोषजनक नहीं है। इसकी मुख्य समस्याएं इस प्रकार हैं –

1. अपर्याप्त गोदाम सुविधाएं-भारत में कृषि उत्पादन उपज के भण्डार करने के लिए पर्याप्त गोदाम नहीं हैं। गांवों में कच्चे गोदाम हैं, जिनमें उपज का 10% से 20% भाग नष्ट हो जाता है। इसलिए किसान फसल की कटाई के पश्चात् इसको तुरन्त बेच देते हैं। किसानों को उपज का उचित मूल्य प्राप्त नहीं होता।
2. अपर्याप्त यातायात के साधन–भारत में यातायात के साधन भी अपर्याप्त मात्रा में उपलब्ध नहीं हैं। भारत के बहुत से भागों में रेल अथवा पक्की सड़क की सुविधा नहीं है। कुछ साधनों पर कच्ची सड़कें भी नहीं हैं । इसलिए कृषि उत्पादन उपज को घर से मण्डी तक ले जाने में कठिनाई का सामना करना पड़ता है। यातायात के साधनों पर अधिक व्यय करना पड़ता है तथा बहुत-सी उपज मार्ग में खराब हो जाती है।
3. अपर्याप्त साख सुविधाएं-भारत के किसान साख सुविधाओं की कमी के कारण अपनी उपज अनुचित समय, अनुचित लोगों को अनुचित कीमतों पर बेचनी पड़ती है। किसान पर ऋण होने के कारण, उसको अपनी उपज फसल की कटाई के पश्चात् तुरन्त बेचनी पड़ती है। साख सुविधाओं की कमी के कारण वह अपनी फसल को कुछ देर तक सम्भाल कर नहीं रख सकता।
4. ग्रेडिंग तथा मयारीकरण का अभाव-भारत में कृषि उत्पादन उपज के मण्डीकरण की एक समस्या यह है कि वस्तुओं की उचित ग्रेडिंग नहीं की जाती। इस कारण किसानों को उपज की उचित कीमत प्राप्त नहीं होती। खरीददार भी बिना मयारीकरण की वस्तुओं की खरीद करना पसन्द नहीं करते।
5. बाज़ार सम्बन्धी सूचना का अभाव-किसान को बाज़ार सम्बन्धी उचित सूचना भी प्राप्त नहीं होती। उनको विभिन्न स्थानों पर उपज की कीमतों, मांग, सरकारी नीति तथा अन्तर्राष्ट्रीय परिवर्तनों का ज्ञान प्राप्त नहीं होता। इसलिए जो सूचना साहूकारों से प्राप्त होती है, वह किसान के पक्ष में नहीं होती।
6. संस्थागत मंडियों का अभाव-भारत में कृषि उत्पादन उपज के मण्डीकरण का एक दोष यह है कि किसान अपनी उपज व्यक्तिगत तौर पर मण्डी में बेचता है। इसका मुख्य कारण यह है कि देश में सहकारी मण्डी समितियों की कमी पाई जाती है। सरकार द्वारा भी उपज खरीदने का उचित प्रबन्ध नहीं है। यदि देश में संस्थागत मण्डियाँ हों तो किसान को उपज का उचित मूल्य प्राप्त हो सकता है।
7. बिचोलों की अधिक संख्या-कृषि उपज किसान से लेकर अन्तिम उपभोगी तक पहुँचने के लिए बहुत से बिचोले होते हैं। प्रत्येक बिचोले का अपना कमीशन होता है। किसान को उपज की कम कीमत प्राप्त होती है, परन्तु जब वह उपज अन्तिम उपभोगी के पास पहुँचती है तो उसमें दलाल, परचून विक्रेता का कमीशन बढ़ने के कारण, उपज की कीमत बहुत बढ़ जाती है।
8. खरीद तथा बिक्री में भ्रष्टाचार-कृषि उत्पादन उपज की गुप्त खरीद तथा बेच, गलत मापतोल के पैमाने, फ़िजूल कटौतियाँ इत्यादि भी कृषि उत्पादन उपज के मण्डीकरण के कुछ अन्य दोष हैं। उपज खरीदने वाले गुप्त रूप में उपज की कीमत निश्चित कर लेते हैं।

इसलिए काश्तकार को अपनी उपज का ठीक मूल्य प्राप्त नहीं होता। कई स्थानों पर बाटों की जगह पर पत्थरों को बाटों के रूप में प्रयोग किया जाता है, जिनका भार साधारण बाटों से अधिक होता है। मण्डी फीस के रूप में बहुत सी फ़िजूल कटौतियाँ भी शामिल की जाती हैं। इस प्रकार किसानों का शोषण कई प्रकार से किया जाता है।

प्रश्न 2.
नियमित मण्डियों से क्या अभिप्राय है? भारत में नियमित मण्डियों के विकास के लिए सरकार द्वारा किए गए यत्नों को स्पष्ट करो।
(What do you mean by regulated Market ? Discuss the steps taken by the Government of India regarding Regulated Markets.)
उत्तर-
नियमित मण्डी किसी नियम को आधारित करके एक वस्तु अथवा वस्तुओं के समूह के लिए बनाई जाती है। ऐसी मण्डी का प्रबन्ध मार्किट कमेटी (Market Committee) द्वारा किया जाता है। मार्किट कमेटी में राज्य सरकार, जिला बोर्ड, व्यापारी कमीशन एजेन्ट तथा किसानों के प्रतिनिधि होते हैं। यह कमेटी सरकार द्वारा निश्चित समय के लिए नियुक्त की जाती है जोकि मण्डी का प्रबन्ध करती है। मार्किट कमेटी द्वारा कमीशन तथा कटौतियाँ निर्धारित की जाती हैं। नियमित मण्डी का मुख्य उद्देश्य बाजार में भ्रष्टाचार को दूर करके किसानों के हितों की रक्षा करना होता है। इस उद्देश्य के लिए सभी राज्यों में कानून पास किए गए हैं। 1951 में नियमित मण्डियों की संख्या 200 थी, जोकि 31 मार्च, 2012 को बढ़कर 7139 हो गई है। इनके बिना समय-समय पर गांवों में जो मण्डियां लगाई जाती हैं, उनकी संख्या 20868 है।

नियमित मण्डियों की विशेषताएँ–नियमित मण्डियों को सरकार ने स्वतन्त्रता के पश्चात् स्थापित किया है। नियमित मण्डी का मुख्य उद्देश्य किसानों को उपज का उचित मूल्य दिलवाना है। उत्पादक तथा उपभोगी में कीमत के अन्तर को घटाना है। व्यापारी तथा कमीशन एजेंटों द्वारा प्राप्त किए जाने वाले कमीशन को नियमित करना है। इस सम्बन्ध में केन्द्र सरकार ने 2003 में मॉडल एक्ट पास किया, जिसकी मुख्य विशेषताएं इस प्रकार हैं –

1. मॉडल एकट 2003 अनुसार किसानों तथा स्थानिक अधिकारियों को आज्ञा दी गई है कि वह किसी क्षेत्र में नई मण्डी स्थापित कर सकते हैं।
2. किसानों के लिए यह अनिवार्य नहीं है कि अपनी उपज निश्चित नियमित मण्डी में ही बेचें।
3. ऐसे खरीद केन्द्र स्थापित किए गए हैं, जहां पर किसान तथा उपभोगी प्रत्यक्ष तौर पर मण्डी में खरीद, बेच कर सकते हैं।
4. कृषि उत्पादन मण्डियों के विकास तथा प्रबन्ध के लिए सार्वजनिक क्षेत्र तथा निजी क्षेत्र में भ्रातृभाव को उत्साहित किया गया है।
5. नाशवान वस्तुएं जैसे कि सब्जियां, प्याज, फल तथा फूलों इत्यादि के लिए विशेष मण्डियां स्थापित की गई हैं।
6. ठेकेदारी काश्तकार के सम्बन्ध में नए नियम बनाए गए हैं।

सहकारी मण्डियाँ (Co-operative Marketing)-भारत में 1954 में सहकारी मण्डीकरण समितियों की स्थापना की गई। सहकारी मार्किटिंग समितियों में इसके सदस्य अपनी अधिक उपज सोसाइटी को बेचते हैं। यदि वह अपनी उपज नहीं बेचना चाहते तो सोसाइटी के पास रखकर उधार प्राप्त करते हैं, जब उनको उपज का उचित मूल्य प्राप्त होता है तो उस समय उपज बेची जा सकती है। सहकारी मार्किट समितियों की संख्या में निरन्तर वृद्धि हुई है। 1960-61 में इन समितियों द्वारा 169 करोड़ रु० कृषि उत्पादन उपज बेची गई, जोकि 2019-20 में 35 हज़ार करोड़ रु० हो गई। यह समितियां पंजाब, गुजरात, महाराष्ट्र तथा उत्तर प्रदेश में अधिक प्रचलित हैं। नियमित मण्डियों के लिए सरकार द्वारा उठाए गए पगभारत में सरकार ने नियमित मण्डियों सम्बन्धी निम्नलिखित पग उठाए हैं –

1. मण्डियों का सर्वेक्षण-देश में विभिन्न वस्तुओं की बिक्री के लिए भिन्न-भिन्न स्थानों पर मण्डियों का सर्वेक्षण किया गया है। सरकार इन मण्डियों में वस्तुओं की कीमतों को प्रकाशित करती है तथा प्रचार किया जाता है।
2. ग्रेडिंग तथा मयारीकरण-भारत सरकार ने कृषि उत्पादन वस्तुओं की गुणवत्ता को बनाए रखने के लिए एगमार्क की मोहर लगाने का निर्णय किया। एगमार्क की वस्तुएं विश्वसनीय होती हैं, क्योंकि वस्तुओं की गुणवत्ता को परखकर मोहर लगाने का अधिकार दिया जाता है।
3. नियमित मण्डियों की स्थापना-भारत सरकार ने 31 मार्च, 2020 तक 55885 कृषि उत्पादन मण्डियों की स्थापना की है, जोकि नियमों की पालना करके कृषि उत्पादन वस्तुओं की खरीद बेच करती हैं। इस समय कृषि उत्पादन उपज का 80% हिस्सा नियमित मण्डियों में बेचा जाता है। 20868 मण्डियाँ फसल आने के समय काम करती हैं।
4. गोदाम की सुविधाएं-किसानों की उपज को सम्भालने के लिए गोदाम स्थापित किए गए हैं। 1951 में केन्द्रीय वेयर हाऊसिंग कार्पोरेशन की स्थापना की गई, जिस द्वारा देश में 751 लाख टन अनाज रखने की व्यवस्था की गई है।
5. सहकारी मार्किटिंग समितियों की स्थापना-भारत में सहकारी मण्डीकरण समितियां स्थापित की गई हैं, जोकि कृषि उत्पादन उपज की बिक्री के साथ-साथ उधार की सुविधाएं भी प्रदान करती हैं।
6. कृषि उत्पादन वस्तुओं का निर्यात-सरकार ने कृषि उत्पादन वस्तुओं के निर्यात में वृद्धि करने के लिए विशेष बोर्डों की स्थापना की है। 2009-10 में 31500 करोड़ रु० की वस्तुओं का विदेशों को निर्यात किया गया। नई विदेशी नीति (2012-17) में कृषि उत्पादन उपज के निर्यात में वृद्धि करने के लिए कृषि निर्यात जोन बनाए गए हैं।
7. कृषि उत्पादन मण्डीकरण सुधार–भारत सरकार ने जोन 2002 में कृषि उत्पादन मण्डीकरण सुधार के लिए टास्क फोरस (Task Force) की स्थापना की जिसमें किसानों द्वारा उपज को प्रत्यक्ष तौर पर बेचना, भविष्य के लिए समझौते करने, गोदामों में माल रखने की सुविधा तथा आधुनिक तकनीकों की जानकारी प्रदान करना शामिल है।

प्रश्न 3.
भारत में सरकार द्वारा कृषि उत्पादन उपज की प्राप्ति तथा कीमत नीति को स्पष्ट करो। (Explain the Procurement and Price Policy of Agricultural Produce in India.)
उत्तर-
कृषि उत्पादन उपज की कीमत निर्धारण करना महत्त्वपूर्ण होता है, क्योंकि इस द्वारा किसानों की आय निश्चित होती है। अनाज खरीदने वाले भी उपज की कीमत से प्रभावित होते हैं। इसलिए कृषि उत्पादन उपज की कीमतें तथा प्राप्ति महत्त्वपूर्ण समस्या है। कृषि उत्पादन उपज की कीमत नीति-भारत जैसे देश में कृषि उत्पादन उपज की कीमत को निर्धारित करना महत्त्वपूर्ण समस्या है। कृषि उत्पादन आगतों (Inputs) की कीमतें निरन्तर बढ़ रही हैं। इसलिए कृषि उत्पादन उपज की कीमतों में वृद्धि करना अनिवार्य हो जाता है, परन्तु भारत में अधिक लोग निर्धन होने के कारण अनाज खरीदने की सामर्थ्य नहीं रखते, इसलिए अनाज की अधिक कीमतें निश्चित करना सम्भव नहीं।

अनाज की कीमतों में निरन्तर परिवर्तन होते हैं। इसलिए मुख्य तौर पर कीमतों में परिवर्तनों के दो कारण होते हैं-
1. मांग पक्ष-

• कृषि उत्पादन उपज की मांग में निरन्तर वृद्धि हो रही है, क्योंकि भारत में जनसंख्या तीव्रता से बढ़ रही है।
• उद्योगों का विकास होने के कारण कृषि उत्पादन उपज की मांग कच्चे माल के तौर पर अधिक रही है।
• कृषि उत्पादन उपज से वस्तुओं का निर्माण करके निर्यात किया जाता है। इसलिए मांग में वृद्धि हो रही है।

2. पूर्ति पक्ष-
कृषि उत्पादन के पूर्ति पक्ष में निरन्तर वृद्धि हो रही है। भारत में हरित क्रान्ति के पश्चात् वस्तुओं की उपज तथा उत्पादकता दोनों में ही वृद्धि हुई है। कुछ राज्यों पंजाब, हरियाणा तथा उत्तर प्रदेश में कृषि उत्पादन उपज में बहुत वृद्धि हुई है, जबकि बहुत से राज्यों में उत्पादकता कम है। कीमत स्थिरता की नीति-कृषि उत्पादन उपज की कीमतों को स्थिर रखा जाए अथवा दूसरी वस्तुओं की कीमतों के अनुसार बढ़ने दिया जाए, यह महत्त्वपूर्ण समस्या है।

यदि कीमतों में वृद्धि दूसरी उपभोगी वस्तुओं की कीमतों अनुसार की जाती है तो देश में लागत वृद्धि मुद्रा स्फीति उत्पन्न हो जाएगी। उपभोगी अपनी आवश्यकताओं की पूर्ति नहीं कर सकेंगे। यदि वस्तुओं को कम रखने का यत्न किया जाता है तो उत्पादक निरुत्साहित हो जाते हैं।

किसान अपनी लागत भी पूरी नहीं कर सकेंगे तो कृषि उत्पादन में उनकी रुचि कम हो जाती है। इसलिए उचित कीमत नीति निर्धारित करने के लिए तीन बातों का ध्यान रखना चाहिए –

1. कीमत स्तर इस प्रकार निश्चित किया जाए ताकि किसान उत्पादन करने के लिए उत्साहित हों। तकनीक तथा आधुनिक ढंगों का प्रयोग किया जा सके।
2. कृषि उत्पादन उपज की कीमतों का प्रभाव अर्थव्यवस्था के दूसरे क्षेत्रों पर देखना चाहिए । जब कृषि उत्पादन उपज को कच्चे माल के रूप में प्रयोग किया जाता है तो बाकी वस्तुओं की कीमतें बढ़ने की सम्भावना होगी, जिससे मुद्रा स्फीति उत्पन्न हो सकती है।
3. कृषि उत्पादन क्षेत्र तथा गैर-कृषि उत्पादन क्षेत्र में कीमतों के सन्तुलन रखने की आवश्यकता है। जैसे कि रासायनिक खादों, कीड़ेमार दवाइयों, बिजली, कपड़ा इत्यादि वस्तुओं की कीमतें बढ़ने से कृषि उत्पादन उपज की कीमतों में वृद्धि भी अनिवार्य होगी। इस उद्देश्य के लिए भारत सरकार ने देश में कृषि उत्पादन, लागत तथा कीमत कमीशन की स्थापना 1965 में की।

इस कमीशन को पहले कृषि उत्पादन कीमत कमीशन कहा जाता था। यह कमीशन कृषि उत्पादन में प्रयोग किए जाने वाले कच्चे माल की कीमतों को ध्यान में रखकर विभिन्न फसलों की कीमत निर्धारित करता है।

इसको न्यूनतम समर्थन कीमत (Minimum Support Price) कहा जाता है। इसको सरकारी प्राप्ति कीमत (Procurement Price) भी कहते हैं। प्राप्ति कीमत वह कीमत होती है, जिस पर देश की सरकार बाज़ार में आई उपज की खरीद करती है। इस कमीशन द्वारा डिपुओं पर दी जाने वाली चीनी, गेहूँ, चावल इत्यादि की कीमत भी निर्धारण की जाती है। कृषि उत्पादन उपज की सरकारी खरीद-भारत में कृषि मानसून हवाओं पर निर्भर है। इसलिए कृषि उत्पादन उपज अनिश्चित होने के कारण 1965-66 में अकाल की स्थिति उत्पन्न हो गई थी।

इसलिए सरकार ने अनाज भण्डार (Buffer stock) बनाने का निर्णय किया। इस नीति अधीन सरकार ने 1965 में कृषि उत्पादन लागतों तथा कीमतों कमीशन की स्थापना की, जोकि कृषि उत्पादन उपज की कम-से-कम समर्थन कीमत निश्चित करता है, जिसको प्राप्ति कीमत (Procurement Price) कहा जाता है । कम-से-कम समर्थन कीमत फसल को बीजते समय बताई जाती है ताकि किसान उस कीमत अनुसार फसल बीज सकें। देश में डिपुओं पर कम कीमत पर बेची जाने वाली वस्तुओं की कीमत भी कमीशन द्वारा निश्चित की जाती है। सरकार द्वारा कृषि उत्पादन उपज की खरीद करके अनाज का भण्डार बनाया जाता है ताकि मुश्किल समय प्रयोग किया जा सके।

भारत में फूड कार्पोरेशन ऑफ़ इंडिया द्वारा अनाज खरीदा जाता है। कृषि उपज की कीमतों में उचित वृद्धि की गई है, चाहे किसान को उपज का उचित मूल्य प्राप्त नहीं होता, परन्तु अनाज की पैदावार बढ़ने के कारण किसानों की आर्थिक स्थिति में सुधार हुआ है। उपभोक्ताओं को भी इस नीति का लाभ प्राप्त हुआ है। उनको अनाज उचित कीमतों पर प्राप्त हो जाता है। कृषि उत्पादन उपज की कीमतों को वैज्ञानिक बनाने की आवश्यकता है, इसलिए इस समस्या को मांग तथा लागत पक्ष से देखना आवश्यक है। समर्थन कीमत पर उचित वृद्धि करके किसान की आर्थिक स्थिति में सुधार करना चाहिए, जबकि देश के निर्धन लोगों तथा मजदूरों को वितरण प्रणाली द्वारा कम कीमतों पर अनाज खरीदने की सुविधा देनी चाहिए।

प्रश्न 4.
भारत में कृषि उत्पादन उपज के लिए माल गोदामों की सुविधा को स्पष्ट करो। (Explain the Warehousing facilities for Agriculture Produce in India.)
उत्तर-
भारत में कृषि उत्पादन उपज के भण्डार की समस्या बहुत समय से चली आ रही है। भण्डार सुविधाओं की कमी के कारण बहुत-सा अनाज नष्ट हो जाता है। इसलिए 1954 में सर्व भारतीय ग्रामीण ऋण सर्वेक्षण कमेटी (All India Rural Credit Survey Committee) की सिफारिशों के अनुसार

• केन्द्रीय स्तर
• राज्य स्तर
• ग्रामीण स्तर पर गोदाम की सुविधाएं प्रदान करने का कार्य आरम्भ किया गया।

इस उद्देश्य के लिए राष्ट्रीय सहकारी विकास तथा माल गोदाम बोर्ड (1956) तथा केन्द्रीय गोदाम कार्पोरेशन (1957) में स्थापित किए गए। इसके पश्चात् सभी राज्यों में राज्य गोदाम कार्पोरेशनों की स्थापना की गई।

इस समय सार्वजनिक क्षेत्र में तीन एजेन्सियाँ हैं, जोकि बड़े पैमाने पर गोदाम स्थापित करती हैं-

1. फूड कापैरेशन आँफ इंडिया (Food Corporation of India-F.C.I.)
2. केन्द्रीय गोदाम कार्पोरेशन (Central Warehousing Corporation-C.W.C.)
3. राज्य गोदाम कार्पोरेशन (State Warehousing Corporation-S.W.C.)

फूड कार्पोरेशन ऑफ़ इण्डिया (F.C.I.) के अपने गोदाम हैं तथा बाकी की सरकारी तथा निजी संस्थाओं से गोदाम किराए पर लेती हैं। इसकी कुल समर्था लगभग 32.05 मिलियन मीट्रिक टन है।

केन्द्रीय गोदाम कार्पोरेशन (C.W.C.) का मुख्य कार्य उचित स्थानों पर ज़मीन खरीद कर गोदामों का निर्माण करना है। इस कार्पोरेशन के पास 470 माल गोदाम हैं जिनकी समर्था 10.7 मिलियन मीट्रिक टन है। राज्य गोदाम कार्पोरेशन (S.W.C.) भी उचित स्थानों पर गोदाम निर्माण करके अनाज भण्डार की सुविधाएं प्रदान करती हैं। इसके पास लगभग 2000 गोदाम हैं, जिनकी भण्डार समर्था 21.29 मिलियन मीट्रिक टन है। इसके अतिरिक्त सहकारी समितियाँ ग्रामीण क्षेत्र (Rural Areas) में अनाज, खाद, बीज इत्यादि रखने की सुविधा प्रदान की जाती है। 2019-20 में सहकारी समितियों की भण्डार समर्था 154 लाख टन थी। इसके बिना देश में 3200 कोल्ड स्टोर बनाए गए हैं, जिनमें सब्जियां, फल, मीट, मछलियाँ रखने की सुविधा प्रदान की जाती हैं। कोल्ड स्टोरों की समर्था 80 लाख टन है।

केन्द्रीय क्षेत्र द्वारा ग्रामीण गोदाम निर्माण योजना-ग्रामीण क्षेत्रों में वैज्ञानिक ढंग से स्टोर बनाने के लिए 2001 में सरकार ने केन्द्रीय क्षेत्र योजना अधीन गांवों में गोदाम बनाने की योजना आरम्भ की है। इस योजना अधीन निजी तथा सहकारी क्षेत्र में गोदाम बनाने वालों को सहायता दी जाती है। 2019-20 में बैंकों द्वारा 4850 स्टोर बनाने के लिए 1300 करोड़ रु० के निवेश की मंजूरी दी गई। इस योजना का विस्तार 2013-14 तक किया गया है। इन गोदामों के गाँवों में स्थापित होने से किसान अपनी उपज गोदामों में रखकर बैंकों से उधार प्राप्त कर सकते हैं। इससे उनको अपनी उपज फसल की कटाई के तुरन्त पश्चात् बेचनी नहीं पड़ेगी। वह अपनी मर्जी से अच्छी कीमत पर उपज बेच सकेंगे।

भारत में माल गोदामों की वर्तमान स्थिति-भारत में ग्यारहवीं तथा बारहवीं योजना में ग्रामों में माल गोदामों के निर्माण पर अधिक जोर दिया गया। सहकारी क्षेत्र में 100 गोदाम बनाए गए। पश्चात् में ग्रामीण गोदाम योजना (Rural Godown Scheme) आरम्भ की गई, जिसमें 200 से 100 टन की समर्था के गोदाम गांवों में स्थापित करने का लक्ष्य रखा गया। क्षेत्रीय तथा राष्ट्रीय स्तर पर केन्द्रीय तथा राज्य गोदाम कार्पोरेशनें काम कर रही हैं। इनके बिना निजी क्षेत्र में 10 लाख टन समर्था के गोदामों का निर्माण किया गया है। कृषि उत्पादन तथा ग्रामीण विकास के लिए राष्ट्रीय बैंक (NABARD) भी विभिन्न एजेन्सियों द्वारा गोदामों के विस्तार का कार्य कर रहा है। भारत में 2019-20 में विभिन्न संस्थाओं द्वारा गोदामों में कुल समर्था 758.46 मिलियन मीट्रिक टन थी, जिसका विवरण अग्रलिखित है

देश में फूड कार्पोरेशन ऑफ़ इण्डिया द्वारा नियमित गोदामों की सपथ 74 35 मिलियन पाटेक : है। केन्द्रीय गोदाम कार्पोरेशन की समर्था, राज्य गोदाम कार्पोरेशन को समर्था तथा सहकारी सामों की समय 30.68 मीट्रिक टन है। निजी क्षेत्र की समर्था 2040 मीट्रिक टन है। इस प्रकार भारत में कुल समय 58 मिलियन मोट्रिक लाख टन है, जोकि संतोषजनक नहीं है। 2 फरवरी 2020 में वित्त मन्त्री निर्मला सीतारमण ने कहा कि वर्तमान में गोगों की माप 21 मिलियन sq.ft. से बढ़ाकर 2023 तक मिलियन sq.ft. करने का लक्ष्य है। इस उद्देश्य के लिए ₹ 2.99 करोड़ की राशि गोदामों के विस्तार के लिए मंजूर की गई है।

Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 23 ग्रामीण ऋण Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 12 Economics Chapter 23 ग्रामीण ऋण

PSEB 12th Class Economics ग्रामीण ऋण Textbook Questions, and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
भारत में ग्रामीण ऋणग्रस्तता का कोई एक उद्देश्य बताओ।
उत्तर-
उत्पादक व्यय-इस उद्देश्य के लिए ऋण जमीन खरीदने अथवा ज़मीन के सुधार के लिए प्राप्त किया जाता |

प्रश्न 2.
ग्रामीण ऋणग्रस्तता के कोई एक कारण बताओ।
उत्तर-
किसान निर्धन होने के कारण कृषि अथवा पारिवारिक व्यय के लिए ऋण लेता है।

प्रश्न 3.
ग्रामीण ऋणग्रस्तता का कोई एक प्रभाव बताओ।
उत्तर-
ऋण से किसान अपनी भूमि बेचकर ऋण तथा ब्याज का भार उतारता है। इसलिए वह भूमिरहित मज़दूर बन जाता है।

प्रश्न 4.
ग्रामीण ऋणग्रस्तता की समस्या के लिए कोई एक सुझाव दीजिए।
उत्तर-
भारत में किसानों पर चले आ रहे पुराने ऋण का निपटारा करना चाहिए। बहुत पुराने ऋण को समाप्त कर देना चाहिए।

प्रश्न 5.
श्री ………….. का यह कथन ठीक है, “भारतीय किसान कर्जे में जन्म लेता है, कर्ज़ में रहता है तथा कर्ज़ में मर जाता है।”
(a) एम० एल० डार्लिंग
(c) मनमोहन सिंह
(c) एस० एस० जोहल
(d) उपरोक्त में से कोई नहीं।
उत्तर-
(a) एम० एल० डार्लिंग।

प्रश्न 6.
अखिल भारतीय ग्रामीण ऋण तथा विनियोग सर्वेक्षण (1980-81) के अनुसार भारत में .. प्रतिशत कृषक परिवार ऋणग्रस्त हैं।
(a) 43%
(b) 53%
(c) 63%
(d) 73%.
उत्तर-
(a) 43%.

प्रश्न 7.
भारत में ग्रामीण ऋण का मुख्य कारण …… ……
(a) निर्धनता
(b) पैतृक ऋण
(c) मानसून की अनिश्चितता
(d) उपरोक्त सभी।
उत्तर-
(d) उपरोक्त सभी।

प्रश्न 8.
ऋणग्रस्तता के मुख्य प्रतिकूल प्रभाव …
(a) आर्थिक प्रभाव
(b) सामाजिक प्रभाव
(c) नैतिक प्रभाव
(d) उपरोक्त सभी।
उत्तर-
(d) उपरोक्त सभी।

प्रश्न 9.
भारत में ग्रामीण ऋणग्रस्तता सम्बन्धी अनुमान सबसे पहले किसने लगाया ?
उत्तर-
भारत में ग्राणीण ऋणग्रस्तता का अनुमान समय से पहले 1911 में श्री मैकलेगन ने लगाया।

प्रश्न 10.
भारत में उत्पादक व्यय के लिए 35.1% ऋण प्राप्त किया जाता है।
उत्तर-
सही।

प्रश्न 11.
भारत में किसान पारिवारिक व्यय के लिए 51% ऋण प्राप्त करते हैं।
उत्तर-
सही।

प्रश्न 12.
पारिवारिक व्यय के लिए भारत के किसान द्वारा ऋण का कितने प्रतिशत ऋण प्राप्त किया जाता
(a) 30%
(b) 51%
(c) 50%
(d) 60%.
उत्तर-
(b) 51%.

प्रश्न 13.
भारत में उत्पादन उद्देश्य के लिए सबसे कम ऋण प्राप्त किया जाता है।
उत्तर-
सही।

प्रश्न 14.
अल्पकाल के ग्रामीण ऋण के उद्देश्य बताओ।
उत्तर-
किसानों को 15 मास अथवा इससे कम समय के लिए ऋण अनिवार्य है। इस ऋण का उद्देश्य घरेलू व्ययों को पूरा करना होता है।

प्रश्न 15.
मध्यकालीन ऋण से क्या अभिप्राय है ?
उत्तर-
किसानों को कुछ ऋण मध्यम समय के लिए भी प्राप्त करना पड़ता है। यह ऋण 15 मास से 5 वर्ष के समय तक हो सकता है।

प्रश्न 16.
दीर्घकाल के ऋण को स्पष्ट करो।
उत्तर-
किसानों द्वारा 5 वर्ष से अधिक समय के लिए जो ऋण अनिवार्य है, उसको दीर्घकाल का ऋण कहा जाता है।

प्रश्न 17.
उत्पादक तथा अन-उत्पादक ऋण से क्या अभिप्राय है ?
उत्तर-
उत्पादक ऋण वह ऋण होता है, जोकि भूमि के विकास अथवा कृषि की आवश्यकताओं बीज, खाद, औज़ारों इत्यादि पर व्यय करने के लिए प्राप्त किया जाता है। अन-उत्पादक व्यय शादियों, जन्म, मृत्यु अथवा मुकद्दमेबाजी के लिए प्राप्त किया जाता है।

प्रश्न 18.
ग्रामीण उधार में व्यापारिक बैंकों का योगदान स्पष्ट करो।
उत्तर-
2016-17 में 4 लाख करोड़ रु० का उधार व्यापारिक बैंकों द्वारा दिया गया।

प्रश्न 19.
किसान उधार कार्ड योजना से क्या अभिप्राय है ?
उत्तर-
किसान उधार कार्ड योजना (Kishan Credit Card Scheme) भारत में 1998-99 में आरम्भ की गई। 2012-13 तक 82 लाख कार्ड दिए गए।

प्रश्न 20.
कृषि उत्पादन तथा ग्रामीण विकास के लिए राष्ट्रीय बैंक के योगदान पर नोट लिखो।
उत्तर-
कृषि उत्पादन तथा ग्रामीण विकास राष्ट्रीय बैंक (NABARD) की स्थापना जुलाई, 1982 में की गई। इस बैंक का उद्देश्य ग्रामों में सड़कों, सिंचाई, पुलों, पक्की गलियों इत्यादि की सुविधाओं के लिए उधार का प्रबन्ध करना है। इन उद्देश्यों की पूर्ति के लिए 2012-13 तक इस बैंक ने 42221 करोड़ रु० का ऋण प्रदान किया है।

प्रश्न 21.
जो ऋण किसान अपनी वर्तमान आवश्यकताओं को पूरा करने के लिए लेता है, जिसकी अवधि 15 महीने तक की होती है को अल्पकालीन साख कहते हैं।
उत्तर-
सही।

प्रश्न 22.
जो ऋण खेती के यन्त्र खरीदने, कुआं खुदवाने आदि कार्यों को पूरा करने के लिए 5 साल की अवधि के लिए लेता है को ……….. साख कहते हैं।
उत्तर-
मध्यकालीन साख (Medium Term Credit)।

प्रश्न 23.
जो ऋण पुराने कर्जे चुकाने, ट्रैक्टर खरीदने अथवा ज़मीन खरीदने के लिए 15 से 20 साल तक की अवधि के लिए लिए जाते हैं उनको … …. साख कहते हैं।
उत्तर-
दीर्घकालीन साख (Long Term Credit)।

प्रश्न 24.
जो कर्ज़ जन्म मृत्यु अथवा मुकद्दमेबाज़ी पर व्यय के लिए लिया जाता है को अन-उत्पादक कहते
उत्तर-
सही।

प्रश्न 25.
भारत में कृषि उत्पादन तथा ग्रामीण विकास राष्ट्रीय बैंक (NABARD) की स्थापना सन् …… में की गई।
(a) 1962
(b) 1972
(c) 1982
(d) 1992.
उत्तर-
(c) 1982.

प्रश्न 26.
भारत में कृषक को सबसे अधिक ऋण ………….. द्वारा दिया जाता है।
(a) साहूकार
(b) व्यापारी
(c) व्यापारिक और ग्रामीण बैंक
(d) सहकारी समितियां।
उत्तर-
(c) व्यापारिक और ग्रामीण बैंक।

प्रश्न 27.
भारत में आज भी कृषक साहूकार से ऋण प्राप्त करता है।
उत्तर-
सही।

प्रश्न 28.
भारत में 2012-13 में संस्थागत ग्रामीण ऋण …………. था।
(a) 59%
(b) 69%
(c) 79%
(d) 89%.
उत्तर-
(b) 69%.

प्रश्न 29.
भारत में गैर-संस्थागत ग्रामीण ऋण बढ़ रहा है ?
उत्तर-
ग़लत।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
भारत में ग्रामीण ऋणग्रस्तता के कारण बताओ।
उत्तर-
भारत में ग्रामीण ऋणग्रस्तता के मुख्य कारण निम्नलिखित हैं –

• निर्धनता-भारत का किसान निर्धन है। कृषि करने के लिए उसको कम समय तथा लंबे समय के ऋण की आवश्यकता पड़ती है।
• धार्मिक तथा सामाजिक रीति-रिवाज-भारतीय किसान सामाजिक तथा धार्मिक रीति-रिवाजों पर बहुत व्यय करता है। इस कारण जन्म, मृत्यु, शादी इत्यादि उद्देश्यों के लिए ऋण लेना पड़ता है।

प्रश्न 2.
भारत में ग्रामीण ऋणग्रस्तता के प्रभाव बताओ।
उत्तर-
भारत में ग्रामीण ऋणग्रस्तता के मुख्य प्रभाव इस प्रकार हैं –

1. आर्थिक प्रभाव-छोटे तथा सीमांत काश्तकारों को अपनी ज़मीन गिरवी रखकर ऋण लेना पड़ता है। ऋण तथा ब्याज वापिस करने के लिए उनको ज़मीन बेचनी पड़ती है तथा वह भूमिरहित मज़दूर बन जाता
2. सामाजिक प्रभाव-सामाजिक तौर पर ऋण काश्तकार, साहूकार को गुलाम बना देता है। इसके । परिणामस्वरूप साहूकार किसान का शोषण करता है।

प्रश्न 3.
ग्रामीण ऋणग्रस्तता की समस्या के लिए उपाय बताओ।
उत्तर-
ग्रामीण ऋणग्रस्तता की समस्या के लिए दो प्रकार के सुझाव दिए जाते हैं –
(A) पुराने ऋण का निपटारा-बहुत से राज्यों में कानून बनाए गए हैं ताकि पुराने ऋण का निपटारा किया जा सके।

• नए कानून अनुसार जहां किसान ने ऋण का ब्याज ऋण की राशि से बढ़कर दिया है, उस स्थिति में पुराना ऋण समाप्त किया जाए।
• पुराने ऋण की मूल राशि वापिस की जाए अथवा सरकारी एजेंसियों से कम ब्याज पर ऋण लेकर पुराने ऋण की वापसी की जाए।

(B) नए ऋण पर नियन्त्रण-पुराने ऋण के निपटारे से समस्या का हल नहीं किया जा सकता। इसलिए नए ऋण केवल उत्पादक उद्देश्यों के लिए दिए जाएं। ब्याज की दर कम की जाए। सामाजिक तथा धार्मिक उद्देश्यों के लिए ऋण को निरुत्साहित किया जाए।

प्रश्न 4.
उत्पादक तथा अन-उत्पादक उधार से क्या अभिप्राय है ?
उत्तर-
भारत में ग्रामीण कृषि उत्पादन वित्त की आवश्यकताओं का वर्गीकरण इस प्रकार है –

1. उत्पादक उधार-किसानों को बीज, रासायनिक खाद, पानी, औज़ार इत्यादि आवश्यकताओं की पूर्ति के लिए उधार लेना पड़ता है। इसको उत्पादक उधार कहा जाता है।
2. अन-उत्पादक उधार-शादियों, जन्म-मृत्यु, मुकद्दमेबाजी इत्यादि आवश्यकताओं के लिए प्राप्त किया – ऋण अन-उत्पादक होता है।

प्रश्न 5.
अल्प, मध्यम तथा दीर्घकालीन ऋण क्या होता है ?
उत्तर-
अल्प, मध्यम तथा दीर्घकालीन उधार-उधार को समय के आधार पर तीन भागों में विभाजित किया जाता है-
1. अल्पकाल उधार-किसानों को अल्पकाल के लिए अल्पकाल की आवश्यकता पड़ती है जोकि 15 महीनों के लिए होता है, घरेलू आवश्यकताओं के लिए प्राप्त किया जाता है। किसान को बीज, खाद, दवाइयों की खरीद करनी होती है। इस उद्देश्य के लिए जो ऋण प्राप्त किया जाता है, वह फसल की कटाई उपरान्त अदा किया जाता है।

2. मध्यमकालीन उधार-किसान को उधार की आवश्यकता मध्यमकाल के लिए भी पड़ती है। यह ऋण 15 महीने से 5 वर्ष के समय तक का होता है। ट्रैक्टर, ट्यूबवैल तथा अन्य कृषि उत्पादन औज़ारों की खरीद करने के लिए मध्यमकाल के ऋण की आवश्यकता होती है। इस ऋण की वापसी के लिए अधिक समय की आवश्यकता होती है।

3. दीर्घकालीन उधार-दीर्घकालीन ऋण 5 वर्ष से 20 वर्ष तक के समय के लिए प्राप्त किया जाता है। यह ऋण अन्य ज़मीन खरीदने के लिए अथवा पुराने ऋण का भुगतान करने के लिए लिया जाता है। इस ऋण की वापसी दीर्घकाल में की जाती है।

प्रश्न 6.
संस्थागत ऋण के कोई दो स्रोत बताएं।
उत्तर-

• सहकारी साख समितियां-सहकारी साख समितियां उधार का महत्त्वपूर्ण स्रोत हैं। 1950-51 में सहकारी समितियों द्वारा 23 करोड़ रु० का उधार दिया गया। 2016-17 में यह उधार 267 करोड़ रु० हो गया।
• सहकारी कृषि तथा ग्रामीण विकास बैंक-किसानों की दीर्घकाल की आवश्यकताओं की पर्ति के लिए सहकारी साख बैंक स्थापित किए गए हैं। सहकारी बैंक भी साख का महत्त्वपूर्ण स्रोत हैं। 1984-85 में सहकारी बैंकों द्वारा 3440 करोड़ रु० का ऋण दिया गया। 2016-17 में – 97321 हज़ार करोड़ रु० का ऋण दिया गया।

प्रश्न 7.
नाबार्ड पर टिप्पणी लिखें।
उत्तर-
कृषि उत्पादन तथा ग्रामीण विकास के लिए राष्ट्रीय बैंक (NABARD)-भारत के रिज़र्व बैंक ऑफ़ इण्डिया ने अल्पकाल तथा दीर्घकाल की कृषि उत्पादन ऋण आवश्यकताओं को पूरा करने के लिए 1982 में कृषि उत्पादन तथा ग्रामीण विकास के लिए राष्ट्रीय बैंक की स्थापना की। इसकी अधिकारित पूंजी 2000 करोड़ रु० है। इस बैंक ने 6280 करोड़ रु० की अधिक पूंजी 2001-02 में एकत्रित की। यह बैंक ग्रामीण क्षेत्र की अल्पकाल तथा दीर्घकाल की उधार आवश्यकताओं की पूर्ति के लिए स्थापित किया गया है। NABARD द्वारा 2016-17 में 51411 करोड़ रु० का ऋण अल्पकाल की आवश्यकताओं के लिए दिया गया, जिस पर रियायती ब्याज दर 3% निर्धारित की।

III. लघु उत्तरीय प्रश्न (Short Answer Typé Questions)

प्रश्न 1.
भारत में ग्रामीण ऋणग्रस्तता के अनुमान को स्पष्ट करो।
अथवा
भारत में रिज़र्व बैंक के सर्व-भारती ऋण सर्वेक्षण 1991-92 का उल्लेख करो।
उत्तर-
भारत में स्वतन्त्रता के पश्चात् 1991-92 में रिज़र्व बैंक इंडिया सर्वभारती ऋण सर्वेक्षण किया। इस सर्वेक्षण के अनुसार भारत में 42.8 प्रतिशत ग्रामीण परिवारों पर ऋण था। 1971 में ग्रामीण परिवारों पर 500 रु० का औसत ऋण था जोकि 1991 में बढ़कर 1906 रु० हो गया था। किए गए सर्वेक्षण में काश्तकारों तथा गैर- काश्तकारों पर ऋण का अनुमान लगाया गया। यह ऋण ग्रामीण परिवारों द्वारा दी गई सूचना पर आधारित था। इस ऋण में संस्थागत ऋण (बैंकों, सहकारी बैंकों अथवा अन्य सरकारी संस्थाओं से प्राप्त ऋण) तथा गैर-संस्थागत ऋण (साहूकार, जागीरदार, रिश्तेदारों, महाजनों तथा मित्रों से प्राप्त ऋण) को शामिल किया गया था।

प्रश्न 2.
भारत में ग्रामीण परिवारों द्वारा लिए ऋण के उद्देश्य बताओ।
उत्तर-
भारत में ग्रामीण परिवारों द्वारा प्राप्त ऋण का प्रतिशत विवरण इस प्रकार है –

1. उत्पादक व्यय-1971 से 1981 तक उत्पादक व्यय 50.1 से बढ़ाकर 69.2 प्रतिशत किया गया, परन्तु 1981 से 2019 तक उत्पादक व्यय घटकर 19% प्रतिशत रह गया है।
2. पारिवारिक व्यय-पारिवारिक व्यय में 1971 से 1981 तक कुछ कमी आई। परन्तु 1981 से 2020 तक यह फिर बढ़कर 38% हो गया।
3. अन्य व्यय-बीमारी, लड़ाई, मुकद्दमेबाज़ी, नशे इत्यादि उद्देश्यों के लिए ऋण में बहुत वृद्धि हुई है। 2020 में यह व्यय 22% था।

प्रश्न 3.
भारत में ग्रामीण ऋणग्रस्तता के कारण बताओ।
उत्तर-
भारत में ग्रामीण ऋणग्रस्तता के मुख्य कारण निम्नलिखित हैं –

1. निर्धनता-भारत का किसान निर्धन है। कृषि करने के लिए उसको कम समय तथा लंबे समय के ऋण की आवश्यकता पड़ती है।
2. धार्मिक तथा सामाजिक रीति-रिवाज-भारतीय किसान सामाजिक तथा धार्मिक रीति-रिवाजों पर बहुत व्यय करता है। इस कारण जन्म, मृत्यु, शादी इत्यादि उद्देश्यों के लिए ऋण लेना पड़ता है।
3. विरसे में ऋण-किसान को पिता की मृत्यु के पश्चात् जब ज़मीन-जायदाद प्राप्त होती है तो विरसे में ऋण भी चुकाना पड़ता है। पिता-पुरखी ऋण का भार भी किसान को सहन करना पड़ता है।
4. दोषपूर्ण ऋण प्रणाली-भारत में ऋण प्रणाली दोषपूर्ण है। किसान को अधिक ऋण महाजन, ज़मींदारों, रिश्तेदारों अथवा मित्रों से लेना पड़ता है। सरकारी एजेंसियों से प्राप्त ऋण की प्रणाली जटिल होने के कारण किसान साहूकार के ऋण के जाल में फंस जाता है।

प्रश्न 4.
भारत में ग्रामीण ऋणग्रस्तता के प्रभाव बताओ।
उत्तर-
भारत में ग्रामीण ऋणग्रस्तता के मुख्य प्रभाव इस प्रकार हैं –

• आर्थिक प्रभाव-छोटे तथा सीमांत काश्तकारों को अपनी ज़मीन गिरवी रखकर ऋण लेना पड़ता है। ऋण तथा ब्याज वापिस करने के लिए उसको ज़मीन बेचनी पड़ती है तथा वह भूमिरहित मज़दूर बन जाता है।
• सामाजिक प्रभाव-सामाजिक तौर पर ऋण काश्तकार, साहूकार को गुलाम बना देता है। इसके परिणामस्वरूप साहूकार किसान का शोषण करता है।
• राजनीतिक प्रभाव-आजकल के युग में लोकतंत्र है। काश्तकारों को अपनी वोट साहकार के कहने अनुसार ही डालनी पड़ती है। इस प्रकार उसकी राजनीतिक स्वतन्त्रता समाप्त हो जाती है।

प्रश्न 5.
ग्रामीण ऋणग्रस्तता की समस्या के लिए उपाय बताओ।
उत्तर-
ग्रामीण ऋणग्रस्तता की समस्या के लिए दो प्रकार के सुझाव दिए जाते हैं –
(A) पुराने ऋण का निपटारा-बहुत से राज्यों में कानून बनाए गए हैं ताकि पुराने ऋण का निपटारा किया जा सके।

• नए कानून अनुसार जहां किसान ने ऋण का ब्याज ऋण की राशि से बढ़कर दिया है, उस स्थिति में पुराना ऋण समाप्त किया जाए।
• पुराने ऋण की मूल राशि वापिस की जाए अथवा सरकारी एजेंसियों से कम ब्याज पर ऋण लेकर पुराने ऋण की वापसी की जाए।

(B) नए ऋण पर नियन्त्रण-पुराने ऋण के निपटारे से समस्या का हल नहीं किया जा सकता। इसलिए नए ऋण केवल उत्पादक उद्देश्यों के लिए दिए जाएं। ब्याज की दर कम की जाए। सामाजिक तथा धार्मिक उद्देश्यों के लिए ऋण को निरुत्साहित किया जाए।

प्रश्न 6.
कृषि उत्पादन वित्त का वर्गीकरण स्पष्ट करो।
उत्तर-
भारत में ग्रामीण कृषि उत्पादन वित्त की आवश्यकताओं का वर्गीकरण इस प्रकार है –

1. उत्पादक उधार-किसानों को बीज, रासायनिक खाद्य, पानी, औज़ार इत्यादि आवश्यकताओं की पूर्ति के लिए उधार लेना पड़ता है। इसको उत्पादक उधार कहा जाता है।
2. अन-उत्पादक उधार-शादियों, जन्म-मृत्यु, मुकद्दमेबाजी इत्यादि आवश्यकताओं के लिए प्राप्त किया ऋण अन-उत्पादक होता है।
3. अल्पकाल उधार-यह ऋण 15 माह तक के समय के लिए होता है, जो फसल की कटाई उपरान्त वापिस किया जाता है।
4. मध्यमकाल उधार-यह ऋण 15 माह से 5 वर्ष तक के समय के लिए प्राप्त किया जाता है। इसका उद्देश्य कृषि उत्पादन औज़ारों की खरीद करना होता है।
5. दीर्घकाल उधार-यह उधार 5 वर्ष से 20 वर्ष के समय के लिए प्राप्त किया जाता है। इसका उद्देश्य भूमि खरीदना अथवा ट्रैक्टर-ट्यूबवैल पर व्यय करना होता है।

प्रश्न 7.
ग्रामीण साख में सहकारी उधार समितियों के योगदान की व्याख्या करो।
उत्तर-
भारत में आर्थिक विकास के लिए ग्रामीण सहकारी उधार समितियों का योगदान महत्त्वपूर्ण है। ये समितियां अल्पकाल तथा दीर्घकाल के ऋण की आवश्यकताओं को पूरा करती हैं।
अल्पकाल की ग्रामीण सहकारी उधार संस्थाएं –

1. राज्य सहकारी बैंक
2. ज़िला केन्द्रीय सहकारी बैंक
3. प्राइमरी कृषि उत्पादन उधार समितियां।

दीर्घकाल की ग्रामीण सहकारी संस्थाएं-

• राज्य सहकारी कृषि उत्पादन तथा ग्रामीण विकास बैंक
• प्राइमरी सहकारी कृषि उत्पादन तथा ग्रामीण विकास बैंक इस प्रकार सहकारी उधार समितियों का संस्थागत ढांचा कार्य करता है, जिस द्वारा अल्पकाल तथा दीर्घकाल की उधार आवश्यकताओं की पूर्ति की जाती है।

भारत में 2012-13 में प्राइमरी सहकारी उधार समितियों ने 102592 करोड़ रु० का उधार दिया था। इस समय 369 जिलों में जिला केन्द्रीय सहकारी बैंक स्थापित हैं तथा 30 राज्यों में राज्य सहकारी बैंक स्थापित किए गए हैं। इन बैंकों द्वारा अल्पकाल तथा दीर्घकाल का उधार प्रदान किया जाता है। दिए गए उधार पर ब्याज की दर कम होती है। इन सहकारी समितियों की मुख्य समस्या दिए गए उधार की कम वापसी है। दिए गए उधार का 40% हिस्सा किसानों ने वापिस नहीं किया है।

प्रश्न 8.
भारत में क्षेत्रीय ग्रामीण बैंकों के योगदान को स्पष्ट करो।
उत्तर-
श्रीमती इन्दिरा गांधी ने 1975 में क्षेत्रीय ग्रामीण बैंक योजना आरम्भ की थी जोकि उत्तर प्रदेश में मुरादाबाद तथा गोरखपुर, हरियाणा में भिवानी, राजस्थान में जयपुर तथा पश्चिमी बंगाल में मालदा ज़िलों में आरम्भ की गई। यह योजना केन्द्र (50%), राज्य सरकारों (15%), व्यापारिक बैंक (35%), पूंजी के योगदान द्वारा आरम्भ की गई थी। क्षेत्रीय बैंक मुख्य तौर पर व्यापारिक बैंकों की तरह ही कार्य करते हैं, परन्तु इनमें मुख्य अन्तर यह है कि क्षेत्रीय बैंक एक अथवा दो जिलों में ही कार्य करते हैं, जिन द्वारा छोटे किसानों को उधार दिया जाता है तथा यह उधार केवल उत्पादक कार्यों के लिए होता है।

ब्याज की दर कम प्राप्त की जाती है। यह बैंक कृषि उत्पादन तथा ग्रामीण विकास के लिए राष्ट्रीय बैंक की सहायता से कार्य करते हैं। लोगों द्वारा जमा करवायी राशि पर व्यापारिक बैंकों से 1% अधिक ब्याज दिया जाता है। इस समय भारत के 23 राज्यों में 196 केन्द्रीय बैंक स्थापित हैं, जिनकी 14500 शाखाएं कार्य कर रही हैं। इन बैंकों ने 2012-13 में 57757 करोड़ रु० का ऋण प्रदान किया गया है।

इन बैंकों की मुख्य त्रुटि यह है कि उधार देते समय बहुत-सी पाबंदियां लगाई गई हैं। इसलिए साधारण निर्धन किसानों को उचित मात्रा में अनिवार्य ऋण प्राप्त नहीं होता। डॉ० ए० एस० खुसरो की प्रधानगी अधीन एक कमेटी की स्थापना की गई, जिसने क्षेत्रीय ग्रामीण बैंकों के दोष दूर करने के सुझाव दिए हैं। रिज़र्व बैंक ने ऐम० सी० भंडारी कमेटी की स्थापना की है, जिसने क्षेत्रीय ग्रामीण बैंकों के विस्तार के लिए कृषि उत्पादन तथा ग्रामीण विकास के लिए राष्ट्रीय बैंक के अधिक योगदान पर जोर दिया है।

प्रश्न 9.
ग्रामीण उधार में नबार्ड (NABARD) के योगदान को स्पष्ट करो।
उत्तर-
भारत के रिज़र्व बैंक ने ग्रामीण कृषि उत्पादन उधार की सुविधाओं पर आरम्भ से ध्यान दिया है। इस उद्देश्य के लिए जुलाई, 1982 में कृषि उत्पादन तथा ग्रामीण विकास के लिए राष्ट्रीय बैंक की स्थापना की गई। इस बैंक की अधिकारित पूंजी आरम्भ में 100 करोड़ रु० थी, जोकि बढ़ाकर 500 करोड़ रु० तथा फिर सन् 2000 में 2000 करोड़ रु० की गई है। इस बैंक द्वारा 6280 करोड़ रु. 2006-07 तथा 38489 करोड़ रु० 2019-20 में अन्य प्राप्त करके उधार की सुविधाओं में वृद्धि की है जोकि 60 हज़ार करोड़ रु० हो गया है। नाबार्ड द्वारा कृषि के विकास ग्रामों में छोटे पैमाने तथा घरेलू उद्योग स्थापित करने इत्यादि कार्य किए जाते हैं। यह बैंक ग्रामीण क्षेत्रीय बैंकों तथा क्षेत्रीय सेवा योजनाओं द्वारा गांवों में विकासवादी योजनाओं का संचालन करता है।

IV. दीर्य उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
भारत में ग्रामीण ऋणग्रस्तता के कारण तथा प्रभाव स्पष्ट करो। ग्रामीण ऋणग्रस्तता की समस्या के हल के लिए सुझाव दीजिए।
(Discuss the causes and effects of Rural Indebetedness in India. Suggest measures to solve the problem of Rural Indebtedness.)
उत्तर-
भारत में किसान पुराने समय से ऋणग्रस्तता की समस्या का शिकार रहा है। इसलिए श्री एम० एल० डार्लिंग ने यह ठीक कहा जाता है, “भारतीय किसान ऋण में जन्म लेता है, ऋण में जीवित रहता है तथा ऋण में मर जाता है।” (“‘The Indian Farmer is born in debt, lives in debt and dies in debt.” – M.L. Darling)

भारत में ग्रामीण ऋणग्रस्तता के अनुमान (Estimates of Indebtedness in India)-भारत में समय पर ग्रामीण ऋणग्रस्तता सम्बन्धी अनुमान लगाए गए हैं। 1924 में एम० एल० डारलिंग ने भारत के काश्तकारों पर 600 करोड़ रु० के ऋण का अनुमान लगाया था। भारत की स्वतन्त्रता के पश्चात् रिज़र्व बैंक ऑफ़ इंडिया ने 1951, 1961 तथा 1971 में ग्रामीण ऋणग्रस्तता सम्बन्धी सर्वेक्षण किए। राष्ट्रीय सैंपल सर्वे संगठन (N.S.S.O.) ने सर्व भारती ऋण तथा निवेश सर्वेक्षण 1981, 1982 तथा 1991, 1992, 2020 में किए। इन सर्वेक्षणों के आधार पर भारत में ग्रामीण परिवारों पर औसत ऋण का विवरण इस प्रकार दिया गया है।

Source: R.B.I. Bulletin, 2020.
भारत में रिज़र्व बैंक ऑफ़ इंडिया द्वारा किए गए सर्वेक्षण से यह ज्ञात होता है कि 1971 में 42.8% परिवारों पर औसत 500 रु० का ऋण था, जोकि 2020 में बढ़कर 200000 रु० का हो गया है। ऋण के बढ़ने का कारण कीमत स्तर में वृद्धि होना है। परन्तु परिवारों की संख्या 1981 में घटकर 20% रह गई तथा 2020 में लगभग 50% परिवारों पर ऋण का भार 2 लाख रु० था। इसमें संस्थागत संस्थाओं जैसे कि सहकारी समितियों तथा व्यापारिक बैंकों से प्राप्त किया जाने वाले ऋण तथा गैर-संस्थागत संस्थाओं साहूकार, ज़मींदार, व्यापारी अथवा रिश्तेदारों से प्राप्त किया ऋण शामिल है।

N.S.S.O. (National Sample Survey Organization) राष्ट्रीय सैंपल सर्वे संगठन ने 29th राऊंड सर्वे में ग्रामीण ऋणग्रस्तता के सम्बन्ध में यह कहा है –

1. भारत में 48.6% किसानों पर ऋण है।
2. जिन किसानों पर ऋण है उनमें से 61% के पास एक हेक्टर से कम भूमि है।
3. किसानों पर जो ऋण है उसमें 41.6% ऋण गैर-कार्यों के लिए, 30.6%, पूंजीगत तथा 27.8% खेती सम्बन्धी कार्यों के लिए लिया गया।
4. काश्तकारों पर जो ऋण है उसमें 57.7% सरकारी ऋण, संस्थाओं द्वारा तथा 42.3% गैर-सरकारी संस्थाओं द्वारा दिया जाता है।
5. गैर-सरकारी ऋण का अनुमान 48000 करोड़ रु० है जिस पर 30% ब्याज प्राप्त किया जाता है।

ग्रामीण परिवारों द्वारा प्राप्त ऋण का वर्गीकरण (Classification of Loans of All Rural Households)-
रिज़र्व बैंक ऑफ़ इंडिया (R.B.I.) के सर्वेक्षण 2011 में ग्रामीण परिवारों पर ऋण का वर्गीकरण अग्रलिखित अनुसार किया गया-
A. उत्पादक उद्देश्य-भारत में ज़मीन तथा काश्तकारी यन्त्र खरीदने के लिए ऋण लिया जाता है। कुल ऋण में से 35.1% हिस्सा उत्पादक उद्देश्यों के लिए होता है।
B. पारिवारिक व्यय-परिवार के व्यय के लिए भी ऋण प्राप्त किया जाता है, जोकि कुल ऋण का 51% हिस्सा होता है।
C. अन्य उद्देश्य-ऋण, बीमारी, लड़ाई-झगड़े, फ़िजूलखर्ची अथवा नशा करने के लिए भी प्राप्त किया जाता है जोकि कुल ऋण का 27.9% हिस्सा होता है।

ग्रामीण ऋणग्रस्तता के कारण (Causes of Rural Indebtedness)-भारत में ग्रामीण ऋणग्रस्तता के कारण इस प्रकार हैं-

1. निर्धनता-काश्तकारों पर ऋण का सबसे प्रमुख कारण काश्तकारों की निर्धनता है। काश्तकार निर्धन होने के कारण ऋण प्राप्त करते हैं, जोकि बीमारी, शराब, शादी के लिए प्राप्त किया जाता है। निर्धन होने के कारण ऋण की वापसी कठिन होती है।
2. पिता-पुरखीय ऋण-भारत के काश्तकारों पर ऋण का दूसरा महत्त्वपूर्ण कारण विरासत में मिला ऋण होता है। भारत के किसान को जहां विरासत में ज़मीन प्राप्त होती है, उसको ऋण भी प्राप्त होता है.। पितापुरखीय ऋण का भार अधिक होने के कारण किसान सारा जीवन ऋण उतारने के प्रयत्न में ही मर जाता
3. पिछड़ी हुई कृषि-भारत में कृषि का पिछड़ापन भी काश्तकारों के ऋण का कारण है। कृषि का उत्पादन कम होने के कारण किसान अच्छे यन्त्र, पशु, बीज, खाद्य इत्यादि आवश्यकताओं को पूरा करने के लिए ऋण लेता है।
4. सामाजिक तथा धार्मिक आवश्यकताएं-ग्रामों में सामाजिक रीति-रिवाजों तथा धार्मिक आवश्यकताओं को पूरा करने के लिए व्यय किया जाता है जैसे कि शादी, जन्म, मृत्यु इत्यादि समय किसानों को बहुत व्यय करना पड़ता है। इस उद्देश्य के लिए ऋण प्राप्त किया जाता है।
5. दोषपूर्वक ऋण प्रणाली-भारत में किसान आमतौर पर साहूकार से ऋण प्राप्त करता है। सरकारी एजेंसियों से आसानी से ऋण प्राप्त नहीं होता, जिस कारण काश्तकार गाँव में साहूकार से ऋण लेने के लिए मजबूर हो जाता है। एक बार साहूकार के जाल में फंसकर ऋण में से बाहर निकलना मुश्किल हो जाता है।

ग्रामीण ऋणग्रस्तता के परिणाम (Effects of Rural Indebtedness)-ग्रामीण ऋणग्रस्तता के परिणाम इस प्रकार हैं-

• आर्थिक परिणाम-छोटे किसान ऋण प्राप्त करते हैं, जिसको वापिस करना मुश्किल होता है। इसलिए अन्त में ज़मीन बेचकर ऋण उतारा जाता है। इस कारण काश्तकारों के पास जमीन नहीं रहती तथा वह मज़दूर बन जाते हैं।
• सामाजिक परिणाम-ग्रामों में ऋणग्रस्तता की समस्या से सामाजिक जीवन पर भी प्रभाव पड़ता है। ऋण प्राप्त करने के पश्चात् काश्तकार द्वारा साहूकारों को नफरत करने लगते हैं। इससे निर्धन तथा अमीर का अन्तर बढ़ जाता है। इसलिए समाज में किसानों की स्थिति कमजोर हो जाती है। यह समस्या बिहार, उडीसा, आन्ध्र प्रदेश में अधिक पाई जाती है, जहां पर किसानों का शोषण किया जाता है।
• राजनीतिक परिणाम साहूकार किसानों को अपनी इच्छानुसार वोट डालने के लिए मजबूर करते हैं। राजनीतिक शक्ति प्राप्त करने के उपरान्त साहूकार किसान विरोधी कानून बनाने में सफल होते हैं।

ग्रामीण ऋणग्रस्तता के हल के लिए उपाय (Measures of Solve the Rural Indebtedness)-ग्रामीण ऋणग्रस्तता सम्बन्धी दो प्रकार के सुझाव दिए जाते हैं-
A. वर्तमान ऋण का भार घटाना-किसानों पर वर्तमान ऋण के भार को घटाने की आवश्यकता है। इस उद्देश्य के लिए निम्नलिखित नीति का प्रयोग करना चाहिए –

• बहुत पुराने ऋण को समाप्त कर देना चाहिए, जहां काश्तकार प्राप्त की गई राशि से अधिक ब्याज दे चुके हैं।
• पिता-पुरखीय ऋण की मात्रा से अधिक ब्याज दे चुके हैं।
• पुराने ऋण की सिर्फ मूल राशि को सरकारी एजेंसियों द्वारा भुगतान करके पुराना ऋण समाप्त कर देना चाहिए।

B. भविष्य के लिए ऋण पर नियन्त्रण (Control over future Indebtedness)-
पुराने ऋण का भुगतान करने के उपरान्त भविष्य के लिए इस प्रकार की नीति बनानी चाहिए –

• निर्धन किसानों की आय में वृद्धि करने के यत्न करने चाहिएं।
• ग्रामों में फिजूलखर्ची को रोकने की आवश्यकता है। इसलिए पंचायतों को योगदान डालना चाहिए।
• किसानों को कम ब्याज पर ऋण सुविधाएं प्रदान करनी चाहिएं ताकि किसान अपनी आवश्यकताओं को पूरा कर सकें। इस प्रकार उत्पादक ऋण की सुविधाओं में वृद्धि करके ऋणग्रस्तता की समस्या का हल किया जा सकता है।

2006-07 में केन्द्र सरकार ने 71680 करोड़ रु० ऋण राहत योजना अधीन विभाजित किए थे। सहकारी ऋण संस्थाओं द्वारा सन् 2006 में 14000 करोड़ रु० ऋण राहत के रूप में विभाजित किए गए। किसानों को ऋण से राहत दिलवानी चाहिए ताकि वह आत्महत्या न करें। 2020 में 40 लाख करोड़ रु० का ऋण दिया गया। बजट 2016-17 में सीमान्त काश्तकारों के ऋण में से सरकारी ऋण 70,000 करोड़ रु० की माफी दी है। गैर-सरकारी ऋण से राहत दिलाने के लिए सरकार योजना बना रही है।

प्रश्न 2.
भारत में कृषि उत्पादन वित्त की आवश्यकता को स्पष्ट करो। कृषि उत्पादन उधार की विशेषताएं बताओ।
(Explain the need for Agriculture Finance in India. Discuss the main features of Agricultural Finance.)
उत्तर-
प्रत्येक उत्पादक क्रिया के लिए वित्त की आवश्यकता होती है। भारत में कृषि उत्पादन लोगों का मुख्य पेशा । है। इसलिए कृषि उत्पादन के लिए वित्त बहुत महत्त्वपूर्ण है।
कृषि उत्पादन वित्त की आवश्यकता (Need for Agricultural Finance)-

कृषि उत्पादन वित्त की आवश्यकता उत्पादक कार्यों के लिए होती है जैसे कि भूमि सुधार, कुएं तथा ट्यूबवैलों का निर्माण इत्यादि फसल को बीजने से लेकर मंडीकरण तक विभिन्न कार्यों के लिए वित्त अनिवार्य है। कृषि उत्पादन की आवश्यकताएं निम्नलिखित अनुसार हैं-
1. उत्पादक तथा अन-उत्पादक उधार-उत्पादन की विभिन्न क्रियाओं के लिए उधार की आवश्यकता होती है जैसे कि एक किसान ने बीज, रासायनिक खाद, पानी, औज़ार इत्यादि की खरीद करनी होती है। इसके बिना भूमि पर कुछ स्थायी सुधार करने की आवश्यकता होती है जैसे कि कुओं की खुदाई, खेत के इर्द-गिर्द बाड़ लगाना, भूमि को समतल करना। इन कार्यों के लिए उधार अथवा ऋण की आवश्यकता होती है, जिसको उत्पादक ऋण कहा जाता है। दूसरी ओर अन-उत्पादक ऋण वह ऋण होता है जो उपभोग के उद्देश्य के लिए प्राप्त किया जाता है।

जैसे कि शादियों पर किया गया व्यय, जन्म तथा मृत्यु के समय किया गया व्यय, मुकद्दमेबाजी पर भी व्यय करने के लिए उधार लिया जाता है। ऐसे ऋण की वापसी करनी मुश्किल होती है। अल्प, मध्यम तथा दीर्घकालीन उधार-उधार को समय के आधार पर तीन भागों में विभाजित किया जाता है –
(i) अल्पकाल उधार-किसानों को अल्पकाल के लिए अल्पकाल की आवश्यकता पड़ती है जोकि 15 महीनों के लिए होता है, घरेलू आवश्यकताओं के लिए प्राप्त किया जाता है। किसान को बीज, खाद, दवाइयों की खरीद करनी होती है। इस उद्देश्य के लिए जो ऋण प्राप्त किया जाता है, वह फसल की कटाई उपरान्त अदा किया जाता है।

(ii) मध्यमकालीन उधार-किसान को उधार की आवश्यकता मध्यमकाल के लिए भी पड़ती है। यह ऋण 15 महीने से 5 वर्ष के समय तक का होता है। ट्रैक्टर, ट्यूबवैल तथा अन्य कृषि उत्पादन औज़ारों की खरीद करने के लिए मध्यमकाल के ऋण की आवश्यकता होती है। इस ऋण की वापसी के लिए अधिक समय की आवश्यकता होती है।

(iii) दीर्घकालीन उधार-दीर्घकालीन ऋण 5 वर्ष से 20 वर्ष तक के समय के लिए प्राप्त किया जाता है। यह ऋण अन्य ज़मीन खरीदने के लिए अथवा पुराने ऋण का भुगतान करने के लिए लिया जाता है। इस ऋण की वापसी दीर्घकाल में की जाती है।

कृषि उत्पादन उधार की विशेषताएं (Main Features of Agricultural Finance)-

1. कृषि उत्पादन उधार की आवश्यकता स्थायी होती है।
2. कृषि उत्पादन प्रकृति पर निर्भर करता है। इसलिए कृषि उपज की निश्चितता न होने के कारण उधार की आवश्यकता होती है।
3. कृषि उत्पादकता में भूमि को गिरवी रखकर उधार प्राप्त किया जाता है। भूमि को जल्दी नकदी के रूप में परिवर्तित नहीं किया जा सकता। इसी कारण उधार लेने की मजबूरी होती है।
4. कृषि उत्पादन में उपज को बीमा नहीं करवाया जा सकता। इसलिए कृषि उत्पादन के जोखिम को किसान स्वयं सहन करता है। इसी कारण उसको ऋण की आवश्यकता होती है।
5. कृषि को मानसून पवनों के साथ जुआ कहा जाता है। इसलिए उपज की मात्रा तथा गुणवत्ता प्रकृति पर निर्भर करती है। इस कारण भी उधार लेना अनिवार्य होता है।
6. फसल बीजने से फसल की कटाई तक काफ़ी अधिक समय होता है। इस समय में किसान ने निजी उपभोग की आवश्यकताओं को पूरा करना होता है। इस कारण भी उसको उधार की आवश्यकता होती है।

प्रश्न 3.
ग्रामीण उधार के विभिन्न स्रोतों का वर्णन करो। (Explain the main sources of Agriculture finance in India.)
अथवा
भारत में ग्रामीण उधार के लिए विभिन्न वित्तीय संस्थाओं के योगदान को स्पष्ट करो।
(Explain the contribution of different financial Institutions regarding Agricultural finance in India.)
उत्तर-
भारत में ग्रामीण उधार देने के दो स्रोत हैं। संस्थागत स्रोत जिनमें सरकार, सहकारी बैंक, क्षेत्रीय ग्रामीण बैंक शामिल हैं तथा गैर-संस्थागत स्रोत जिनमें साहूकार, व्यापारी, रिश्तेदार तथा मित्रों को शामिल किया जाता है। इन स्रोतों से प्राप्त उधार का विवरण इस प्रकार है –

भारत में संस्थागत स्रोत से उधार में निरन्तर वृद्धि हो रही है। 1950-51 में 7% उधार संस्थागत स्रोतों द्वारा दिया जाता था। 2013-14 में यह बढ़कर 69% हो गया है। गैर-संस्थागत उधार 1950-51 में 93% था जोकि अब घटकर 31% रह गया है। साहूकारों द्वारा 2020-21 में 95000 करोड़ रु० का उधार दिया गया। भारत में संस्थागत उधार बहुतसी एजेंसियों द्वारा दिया जाता है।

संस्थागत साख (Institutional Finance)-भारत में संस्थागत साख में बहुत वृद्धि हुई है। 1984-85 में संस्थागत उधार 6230 करोड़ रु० दिया गया, जोकि 2020-21 में बढ़कर 195000 करोड़ रु० हो गया है। संस्थागत साख मुख्य तौर पर निम्नलिखित संस्थाओं द्वारा दिया जाता है।
1. सहकारी साख समितियां-सहकारी साख समितियां उधार का महत्त्वपूर्ण स्रोत हैं। 1950-51 में __ सहकारी समितियों द्वारा 23 करोड़ रु० का उधार दिया गया। 2020-21 में यह उधार 485 करोड़ रु० हो गया।

2. सहकारी कृषि तथा ग्रामीण विकास बैंक-किसानों की दीर्घकाल की आवश्यकताओं की पूर्ति के लिए सहकारी साख बैंक स्थापित किए गए हैं। सहकारी बैंक भी साख का महत्त्वपूर्ण स्रोत हैं। 1984-85 में सहकारी बैंकों द्वारा 3440 करोड़ रु० का ऋण दिया गया। 2020-21 में 95000 हज़ार करोड़ रु० का ऋण दिया गया।

3. व्यापारिक बैंक-भारत में व्यापारिक बैंकों का राष्ट्रीयकरण इस कारण किया गया, क्योंकि व्यापारिक बैंक कृषि उत्पादन की साख आवश्यकताओं की पूर्ति नहीं करते थे। व्यापारिक बैंक कृषि उत्पादन में अल्पकाल तथा मध्यम काल समय की आवश्यकताओं की पूर्ति के लिए उधार देते हैं। 2013-14 में व्यापारिक बैंकों में 368616 करोड़ रु० का उधार दिया गया, जोकि 2020-21 में बढ़कर 50,000 करोड़ रु० हो गया।

4. लीड बैंक योजना- भारत में बैंकों के राष्ट्रीयकरण के पश्चात् प्रो० डी० आर० गाडगिल की सिफ़ारिशों अनुसार लीड बैंक योजना आरम्भ की गई, जिसमें प्रत्येक जिले में एक बैंक को गांवों में साख प्रदान करने का कार्य सौंपा गया। इस योजना अधीन 1994-95 में 8255 करोड़ रु० कृषि उत्पादन कार्यों के लिए उधार दिए गए। 2020-21 में इन बैंकों द्वारा 15000 करोड़ रु० का उधार दिया गया।

5. ग्रामीण क्षेत्रीय बैंक-ग्रामीण क्षेत्रीय बैंक की योजना श्रीमती इंदिरा गांधी द्वारा आरम्भ की गई। यह योजना 1975 में उत्तर प्रदेश, हरियाणा, राजस्थान तथा पश्चिमी बंगाल में आरम्भ की गई थी। प्रत्येक ग्रामीण क्षेत्रीय बैंक की अधिकारित पूंजी एक करोड़ रु० निश्चित की गई, जिसमें 50% केन्द्र सरकार, 15% राज्य सरकारें तथा 35% व्यापारिक बैंकों द्वारा पूंजी का प्रबन्ध किया गया। इस योजना का मुख्य उद्देश्य विभिन्न क्षेत्रों की आवश्यकता को पूरा करना था। विशेषकर छोटे तथा सीमान्त किसानों की आवश्यकता की पूर्ति के लिए क्षेत्रीय बैंक स्थापित किए गए। इस समय 23 राज्यों में 196 क्षेत्रीय बैंक हैं, जिनकी 14500 ब्रांचे कार्य कर रही हैं। 2020-21 में क्षेत्रीय बैंकों ने 25000 हज़ार करोड़ रु० का ऋण दिया।

6. कृषि उत्पादन तथा ग्रामीण विकास के लिए राष्ट्रीय बैंक (NABARD) भारत के रिज़र्व बैंक ऑफ़ इण्डिया ने अल्पकाल तथा दीर्घकाल की कृषि उत्पादन ऋण आवश्यकताओं को पूरा करने के लिए 1982 में कृषि उत्पादन तथा ग्रामीण विकास के लिए राष्ट्रीय बैंक की स्थापना की। इसकी अधिकारित पूंजी 2000 करोड़ रु० है। इस बैंक द्वारा 6280 करोड़ रु० की अधिक पूंजी 2001-02 में एकत्रित की। यह बैंक ग्रामीण क्षेत्र की अल्पकाल तथा दीर्घकाल की उधार आवश्यकताओं की पूर्ति के लिए स्थापित किया गया है।

NABARD द्वारा 2010-11 में 1521 करोड़ रु० का ऋण अल्पकाल की आवश्यकताओं के लिए दिया गया, जिस पर रियायती ब्याज दर 3% निर्धारित की गई थी। यह संस्था सहकारी समितियों, सहकारी बैंकों तथा राज्य सरकारों द्वारा दीर्घकाल के ऋण की आवश्यकताओं की पूर्ति भी करती है। इस बैंक द्वारा ग्रामीण संरचनात्मक विकास फंड की स्थापना की गई है, जिस अनुसार भिन्न-भिन्न योजनाओं के लिए ऋण प्रदान किया जाता है।

1996 में 18300 करोड़ रु० का व्यय ग्रामीण विकास योजनाओं के लिए प्रदान किया गया जिसमें सड़कों, पुलों, सिंचाई योजनाओं का विस्तार किया गया। 2020-21 में इस उद्देश्य के लिए 25000 करोड़ रुपए का ऋण प्रदान किया गया है। वित्त मन्त्री निर्मला सीतरमण ने 2020-21 के बजट में कृषि उधार देने के लिए ₹ 15 लाख करोड़ रखे हैं।

Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 22 निर्धनता की समस्या Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 12 Economics Chapter 22 निर्धनता की समस्या

PSEB 12th Class Economics निर्धनता की समस्या Textbook Questions, and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
निर्धनता से क्या अभिप्राय है ?
उत्तर-
निर्धनता से अभिप्राय जीवन की न्यूनतम आवश्यकताओं रोटी, कपड़ा, मकान, शिक्षा, सेहत इत्यादि को पूरा करने की अयोग्यता होती है।

प्रश्न 2.
भारत में सापेक्ष निर्धनता से क्या अभिप्राय है ?
उत्तर-
सापेक्ष निर्धनता से अभिप्राय है तुलनात्मक निर्धनता।

प्रश्न 3.
निरपेक्ष निर्धनता से क्या अभिप्राय है ?
उत्तर-
निरपेक्ष निर्धनता से अभिप्राय उपभोग के विशेष बिन्दु को कम स्थिति में व्यय किया जाए, जिसको निर्धनता रेखा कहा जाता है।

प्रश्न 4.
भारत के किस राज्य में सबसे अधिक तथा किस राज्य में सबसे कम निर्धनता है ?
उत्तर-
भारत में सबसे अधिक निर्धनता बिहार में पाई जाती है। बिहार में 55 प्रतिशत लोग निर्धनता रेखा से नीचे जीवन बिता रहे हैं। पंजाब में सबसे कम निर्धनता है। 12 प्रतिशत लोग निर्धनता रेखा से नीचे जीवन व्यतीत कर रहे हैं।

प्रश्न 5.
जीवन स्वास्थ्य तथा कार्यकुशलता के लिए न्यूनतम उपभोग आवश्यकताओं की प्राप्ति की अयोग्यता को निर्धनता कहते हैं।
उत्तर-
सही।

प्रश्न 6.
भिखारी अथवा अनियमित मज़दूर जिनके पास कभी-कभी धन आ जाता है को ……… निर्धन कहते हैं।
उत्तर-
चिरकालिक निर्धन (Chronic Poor)।

प्रश्न 7.
वह व्यक्ति जिन के पास अधिकांश समय धन होता है परन्तु कभी-कभी अल्पकाल के लिए रोज़गार नहीं मिलता उनको ………… निर्धन कहते हैं।
उत्तर-
अल्पकालिक निर्धन (Transient Poor)।

प्रश्न 8.
वह व्यक्ति जो कभी भी निर्धन नहीं होते उनको ………….. निर्धन कहते हैं।
उत्तर-
और-निर्धन (Non-Poor)।

प्रश्न 9.
वह सीमा बिन्दू जो किसी देश में लोगों को निर्धन तथा अनिर्धन में विभाजित करता है को ……………. कहते हैं।
उत्तर-
निर्धनता रेखा (Poverty Line)।

प्रश्न 10.
निर्धनता रेखा के नीचे रहने वाले लोगों की संख्या के रूप में मापा जाता है को ………… अनुपात कहते हैं।
उत्तर-
व्यक्ति गणना अनुपात (Head Count Ratio)।

प्रश्न 11.
भारत में निर्धनता का सबसे महत्त्वपूर्ण कारण बढ़ती हुई जनसंख्या है।
उत्तर-
सही।

प्रश्न 12.
गरीबी रेखा की सीमा आय रूप में की जाए अथवा उपभोग रूप में की जाए ?
उत्तर-
उपभोग रूप में।

प्रश्न 13.
भारत में गरीबी रेखा की सीमा किस माप दण्ड में निर्धारण होती है ?
उत्तर-
आय द्वारा।

प्रश्न 14.
व्यक्तिगत गणना अनुपात से क्या अभिप्राय है ?
उत्तर-
व्यक्तिगत गणना अनुपात द्वारा गरीबों को गरीबी रेखा से नीचे रहने वाले लोगों की संख्या के रूप में माप करना होता है।

प्रश्न 15.
सन् 2012 में गरीबी रेखा को पुनः प्रभावित करने का आदेश किस संस्था ने दिया ?
उत्तर-
सुप्रीम कोर्ट ऑफ़ इण्डिया।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
सापेक्ष तथा निरपेक्ष निर्धनता से क्या अभिप्राय है ? ।
उत्तर-
सापेक्ष निर्धनता-जब विभिन्न देशों, क्षेत्रों अथवा वर्गों में तुलना की जाती है तथा तुलनात्मक आय कम होती है तो इसको सापेक्ष निर्धनता कहा जाता है, जैसे कि अमेरिका में प्रति व्यक्ति आय 58036 डालर है तथा भारत में प्रति व्यक्ति आय 6490 डालर है। इस प्रकार अमीर देशों की तुलना में भारत निर्धन देश है। निरपेक्ष निर्धनता-भारत में निरपेक्ष निर्धनता को निर्धन रेखा द्वारा मापते हैं। भारत के गाँवों में 1054 रु० प्रति माह तथा शहरों में 1984 रु० प्रति माह उपभोग व्यय करने वाले व्यक्तियों को निर्धन कहा जाता है, क्योंकि वह निर्धनता रेखा से नीचे जीवन व्यतीत करते हैं।

प्रश्न 2.
निर्धनता रेखा से क्या अभिप्राय है? क्या निर्धनता रेखा का आय अथवा उपभोग के रूप में निर्धारण करना चाहिए ?
उत्तर–
प्रति व्यक्ति व्यय से सम्बन्धित यह ऐसा बिन्दु है, जोकि किसी क्षेत्र के व्यक्तियों को निर्धन होने अथवा निर्धन न होने में विभाजित करता है। भारत में निर्धन होने के लिए ग्रामीण क्षेत्र में 816 रु० का व्यय तथा शहरी क्षेत्र के लिए 1000 रु० के व्यय को निर्धनता का बिन्दु मानकर निर्धनता रेखा को निश्चित किया गया है। निर्धनता रेखा को निर्धारण करने के लिए आय से उपभोग (consumption) को सूचक मानना चाहिए, क्योंकि आय द्वारा खरीद शक्ति का ज्ञान प्राप्त होता है जबकि उपभोग द्वारा यह पता लगता है कि मनुष्य कौन-सी वस्तुओं का प्रयोग करता है तथा कितनी मात्रा में प्रयोग किया जाता है। इस कारण उपभोग द्वारा निर्धनता रेखा को निर्धारित करना चाहिए। योजना आयोग ने निर्धनता रेखा की नई सीमा 67 रुपये प्रतिदिन करने की सिफ़ारिश की है।

प्रश्न 3.
भारत में निर्धनता के कोई दो कारण बताएं।
उत्तर-
भारत में निर्धनता के कारण (Causes of Poverty in India)—निर्धनता के कारण ही भारत की अर्थव्यवस्था कम विकसित है। भारत में निर्धनता के मुख्य कारण निम्नलिखित हैं-

1. विकास की कम दर-भारत की योजनाओं में आर्थिक विकास का लक्ष्य 5% वार्षिक रखा गया। परन्तु वास्तव में विकास दर 2.4% प्राप्त की गई। इस कारण निर्धनता की स्थिति पाई जाती है।
2. राष्ट्रीय उत्पाद का कम स्तर- भारत में राष्ट्रीय उत्पाद का स्तर यू०एन०ओ० की शर्तों अनुसार नीचा है। कम प्रति व्यक्ति आय भी निर्धनता का सूचक है। भारत की GDP 2020-21 में, 1.34 लाख करोड़ तथा P.C.I ₹ 1,38,000 थी।

प्रश्न 4.
भारत में निर्धनता को दूर करने हेतु कोई दो सुझाव दें।
उत्तर-
निर्धनता को दूर करने के लिए सुझाव (Suggestion to Remove Poverty)
1. विकास की दर में वृद्धि-भारत में विकास की दर में वृद्धि करनी चाहिए। यदि देश में कृषि, उद्योग, वाणिज्य, यातायात की वृद्धि की जाए तो रोज़गार के अधिक अवसर प्रदान करके निर्धनता को दूर किया जा सकता है।

2. जनसंख्या पर रोक-भारत में तीव्रता से बढ़ रही जनसंख्या पर रोक लगाने के लिए जन्म दर में कमी करने की आवश्यकता है। इससे निर्धनता को दूर किया जा सकता है।

III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 1.
भारत में निर्धनता रेखा का कैसे निर्धारण किया जाता है ?
उत्तर-
भारत में निर्धनता रेखा को निश्चित करने के लिए निम्नलिखित विधि को अपनाया जाता है –

1. उपभोग पर व्यय में सिर्फ निजी उपभोग व्यय को शामिल किया जाता है। सरकार द्वारा वस्तुओं पर किए व्यय को शामिल नहीं किया जाता।
2. निजी उपभोग व्यय में सिर्फ खाद्य पदार्थों पर व्यय को ही शामिल नहीं किया जाता, बल्कि गैर-खाद्य पदार्थों पर व्यय को भी शामिल किया जाता है।
3. खुराक पर व्यय की मदों से प्रति व्यक्ति भोजन में प्राप्त कैलोरियों द्वारा माप किया जाता है। अमीर तथा निर्धन वर्गों द्वारा उपभोग की कैलोरियों का विस्तार (Range) तथा स्तर (Level) मापा जाता है।
4. विभिन्न वर्ग के लोगों द्वारा किए गए उपभोग से प्राप्त कैलोरियों के आधार पर आवृत्ति वितरण तैयार की जाती है। इस प्रकार निर्धन लोग कम कैलोरी तथा अमीर लोग अधिक कैलोरी भोजन का उपभोग करते हैं।
5. आवृत्ति के आधार पर संख्या की जाती है। इससे ग्रामीण क्षेत्र के लिए विभिन्न तथा शहरी क्षेत्र के लिए विभिन्न निर्धनता रेखा निश्चित की जाती है। इस निर्धनता रेखा के बिन्दु से नीचे रहने वाले व्यक्तियों की संख्या की जाती है।

प्रश्न 2.
भारत में ग्रामीण तथा शहरी निर्धनता की स्थिति को स्पष्ट कीजिए।
उत्तर-
भारत में निर्धनता रेखा से नीचे जीवन व्यतीत करने वाले व्यक्तियों की कुल संख्या में निरन्तर कमी हो रही है। इसको सूची पत्र द्वारा स्पष्ट किया जा सकता है। विश्व बैंक ने 18 अप्रैल 2013 को रिपोर्ट में कहा है कि भारत में एक तिहाई जनसंख्या गरीब है।

Source: NITI Aayog (NSSO)

1. भारत में 1970-71 में 25 करोड़ गरीब थे, जिनकी संख्या 2019-20 में 22 करोड़ थी।
2. शहरी क्षेत्र में 1970-71 में निर्धनों की संख्या 42% थी जो कि 2019-20 में 14% हो गई है।
3. ग्रामीण क्षेत्र में 1970-71 में निर्धनता रेखा से नीचे रहने वाले लोगों की संख्या 54% थी, जोकि 2019-20 में घटकर 20% रह गई है।
4. भारत में निर्धनों की कुल संख्या 1970-71 में 51 प्रतिशत थी। 2019-20 में यह संख्या घटकर 17% रह गई है। 2022 तक गरीबों की संख्या 18% रहने का अनुमान है।

प्रश्न 3.
भारत में निर्धनता के मुख्य कारण बताओ।
उत्तर-
भारत में निर्धनता के मुख्य कारण निम्नलिखित हैं-

1. कम विकास दर-भारत में वार्षिक विकास दर 4 प्रतिशत हो रही है, परन्तु जनसंख्या में वृद्धि 2 प्रतिशत वार्षिक होने के कारण प्रति व्यक्ति आय में वृद्धि 2.4 प्रतिशत हुई। इसी कारण निर्धनता पाई जाती है।
2. जनसंख्या में वृद्धि- भारत में जनसंख्या में वृद्धि इतनी तीव्रता से हुई है, जिस कारण निर्धनों की संख्या में बहुत वृद्धि हुई है।
3. बेरोज़गारी- भारत में बेरोज़गारी तथा अल्पबेरोज़गारी ने निर्धनता में वृद्धि की है। देश में 2 करोड़ से – अधिक बेरोज़गार हैं।
4. संस्थागत ढांचे की कमी- भारत में बिजली, पानी, सड़कें, यातायात तथा संचार, शिक्षा, सेहत इत्यादि बुरी स्थिति में हैं। इसलिए उत्पादन में वृद्धि कम दर पर हुई है तथा निर्धनता पाई जाती है।

प्रश्न 4.
निर्धनता दूर करने के लिए सरकार द्वारा उठाए कोई दो पगों की व्याख्या करो।
अथवा
स्वर्ण जयंती ग्राम स्वयं रोज़गार योजना तथा स्वर्ण जयंती शहरी रोजगार योजना पर नोट लिखो।
उत्तर-
1. स्वर्ण जयंती ग्राम स्वयं रोजगार योजना निर्धनता दूर करने के लिए यह योजना अप्रैल 1999 में लागू की गई। यह योजना केन्द्र तथा राज्य सरकारों द्वारा 75:25 के अनुपात में व्यय के आधार पर बनाई जाती है। इस योजना द्वारा स्वयं रोज़गार के लिए ऋण की सुविधाओं का प्रबन्ध किया गया है। इस योजना पर जनवरी, 2019-20 तक 48000 करोड़ रु० व्यय किए गए।

2. स्वर्ण जयंती शहरी रोजगार योजना- यह योजना शहरी स्वयं रोज़गार तथा शहरी मज़दूरी रोज़गार प्रोग्राम को एकत्रित करके 1997 में आरम्भ की गई। यह योजना भी केन्द्र तथा राज्य सरकारों द्वारा 75:25 अनुपात अनुसार व्यय के आधार पर बनाई गई है। इस योजना पर जनवरी, 2019-20 में 5270 करोड़ रु० व्यय किए गए। इस राशि से 28 हज़ार शहरी गरीब परिवारों को रोजगार प्रदान किया गया।

IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
निर्धनता से क्या अभिप्राय है? भारत में निर्धनता के कारण बताओ। निर्धनता दूर करने के लिए सुझाव दीजिए।
(What is meant by Poverty ? Discuss the causes of Poverty in India ? Suggest measures to remove Poverty.)
उत्तर-
निर्धनता का अर्थ (Meaning of Poverty)-निर्धनता से अभिप्राय जीवन की न्यूनतम आवश्यकताओं रोटी, कपड़ा, मकान, शिक्षा, सेहत इत्यादि को पूरा करने की अयोग्यता होती है। निर्धनता को दो रूपों में प्रकट किया जाता है –
(A) सापेक्ष निर्धनता (Relative Poverty)-यू० एन० ओ० की रिपोर्ट अनुसार सापेक्ष निर्धनता का अर्थ तुलनात्मक निर्धनता से होता है, जब विभिन्न देशों, क्षेत्रों अथवा वर्गों की तुलना की जाती है तथा तुलनात्मक आय कम होती है अथवा इसको सापेक्ष निर्धनता कहा जाता है। जैसे कि भारत की प्रति व्यक्ति आय 6490डालर, अमेरिका की प्रति व्यक्ति आय 58030 डालर की तुलना में बहुत कम है। इसलिए भारत गरीब देश है। भारत में निर्धन व्यक्तियों की संख्या बिहार में 55% तथा पंजाब में 12% है। यह क्षेत्रीय निर्धनता है। इसी तरह कम आय 20% लोगों के पास राष्ट्रीय आय 7 प्रतिशत तथा अधिक आय वाले 20% लोगों के पास राष्ट्रीय आय 46 प्रतिशत है। यह वर्ग निर्धनता है।

(B) निरपेक्ष निर्धनता (Absolute Poverty)-भारत में निरपेक्ष निर्धनता को निर्धनता रेखा द्वारा मापते हैं। निर्धनता रेखा से अभिप्राय न्यूनतम आवश्यकताओं की पूर्ति के लिए प्रति माह औसत व्यय की रेखा होती है। भारत में 2004-05 की कीमतों के अनुसार ग्रामों में 816 रु० तथा शहरों में 1000 रु० प्रति माह व्यय करने वाले व्यक्तियों को निर्धनता रेखा से नीचे का जीवन व्यतीत करने वाले निर्धन व्यक्ति कहा जाता है।

भारत में निर्धनता का विस्तार (Extent of Poverty in India)-भारत में 2019-20 में 22 करोड़ व्यक्ति निर्धन थे अर्थात् इनमें से 20% लोग ग्रामों तथा 14% लोग शहरों में निर्धन थे। जनसंख्या में से 35% लोग निर्धनता रेखा से नीचे थे। बाहरवीं योजना अनुसार 2022 तक 18% प्रतिशत लोग निर्धनता रेखा से नीचे रह जाएंगे। भारत के विभिन्न राज्यों में से बिहार, उत्तर प्रदेश, मध्य प्रदेश, उड़ीसा में निर्धनों की संख्या अधिक है जबकि हिमाचल प्रदेश/हरियाणा तथा पंजाब में निर्धनों की संख्या कम है। बिहार में सबसे अधिक 55% लोग निर्धन हैं, जबकि पंजाब में सबसे कम 12% लोग निर्धन हैं।

भारत में निर्धनता के कारण (Causes of Poverty in India)-निर्धनता के कारण ही भारत की अर्थव्यवस्था कम विकसित है। भारत में निर्धनता के मुख्य कारण निम्नलिखित हैं-
1. विकास की कम दर- भारत की योजनाओं में आर्थिक विकास का लक्ष्य 10% वार्षिक रखा गया। परन्तु वास्तव में विकास दर 5.7% प्राप्त की गई। इस कारण निर्धनता की स्थिति पाई जाती है।

2. राष्ट्रीय उत्पाद का कम स्तर- भारत में राष्ट्रीय उत्पाद का स्तर यू० एन० ओ० की शर्तों अनुसार नीचा है। प्रचलित कीमतों पर 2019-20 में शुद्ध राष्ट्रीय उत्पाद 134 लाख करोड़ रु० तथा प्रति व्यक्ति आय 1,38,000 रु० थी। कम प्रति व्यक्ति आय भी निर्धनता का सूचक है।

3. अधिक जनसंख्या- भारत में निर्धनता का मुख्य तथा बड़ा कारण जनसंख्या का अधिक होना है। जनसंख्या की वृद्धि का कारण देश में जन्म दर से मृत्यु दर में बहुत अधिक कमी होना है। 1951 में भारत की जनसंख्या 36 करोड़ थी जोकि 2011 में 121 करोड़ हो गई है।

4. बढ़ती कीमतें-देश में उत्पादन की वृद्धि की कम दर तथा जनसंख्या की वृद्धि की अधिक दर के कारण कीमतों में वृद्धि तीव्रता से हो रही है। इससे निर्धन लोग अपनी आवश्यकताएं पूरी करने में असमर्थ हैं। 2019-20 में कीमतों में वृद्धि 5.2% रही।

5. पूंजी की कमी-भारत में प्राकृतिक साधन तो अधिक मात्रा में पाए जाते हैं परन्तु पूंजी की कमी के कारण साधनों का उचित प्रयोग नहीं हो रहा। इस कारण उत्पादकता कम है तथा निर्धनता पाई जाती है।

निर्धनता को दूर करने के लिए सुझाव (Suggestion to Remove Poverty)-

1. विकास की दर में वृद्धि-भारत में विकास की दर में वृद्धि करनी चाहिए । यदि देश में कृषि, उद्योग, वाणिज्य, यातायात की वृद्धि की जाए तो रोज़गार के अधिक अवसर प्रदान करके निर्धनता को दूर किया जा सकता है।
2. जनसंख्या पर रोक-भारत में तीव्रता से बढ़ रही जनसंख्या पर रोक लगाने के लिए जन्म दर में कमी करने की आवश्यकता है। इससे निर्धनता को दूर किया जा सकता है।
3. आय की असमानता में कमी-भारत में अमीर लोगों पर अधिक कर लगाकर प्राप्त हुई आय को निर्धनों की भलाई पर व्यय करना चाहिए। इससे आर्थिक असमानता आएगी तथा निर्धनता को दूर किया जा सकेगा।
4. निर्धनों की न्यूनतम आवश्यकताओं की पूर्ति- सरकार को निर्धन लोगों की न्यूनतम आवश्यकताओं की पूर्ति के लिए पग उठाने चाहिए । इस उद्देश्य के लिए निर्धनों के लिए अधिक रोज़गार तथा परिवार नियोजन पर ज़ोर देना चाहिए।
5. तकनीक में परिवर्तन- भारत में श्रम संघनी तकनीक द्वारा बेरोज़गारी को दूर किया जाए, कीमतों में स्थिरता द्वारा पिछड़े क्षेत्रों का विकास करके लोगों के लिए स्वयं रोज़गार के अवसर प्रदान करने की आवश्यकता है।

प्रश्न 2.
भारत में सरकार द्वारा निर्धनता को दूर करने के लिए किए गए उपायों का वर्णन करो। (Discuss the measures undertaken by Indian Government to remove poverty.)
अथवा
भारत में निर्धनता घटाओ प्रोग्रामों पर प्रकाश डालें। (Explain the main programmes to remove poverty in India.)
अथवा
भारत में रोजगार की वृद्धि के लिए बनाई योजनाओं को स्पष्ट करो। (Explain the programmes increase employment in India.)
उत्तर-
भारत में पंचवर्षीय योजनाओं में निर्धनता घटाने के लिए निम्नलिखित प्रोग्राम रखे हैं –
1. प्रधानमंत्री ग्राम सड़क योजना (PMGSY)-यह योजना दिसम्बर, 2000 में आरम्भ की गई। इस योजना का उद्देश्य सभी ग्रामों को जिनमें 1000 से अधिक लोग रहते हैं तथा पहाड़ी क्षेत्रों में 500 से अधिक जनसंख्या है, उनको 2009 तक सड़कों द्वारा शहरों से जोड़ा जाएगा। 2019-20 तक इस योजना पर 20,000 करोड़ रु० व्यय करके 2.42 लाख किलोमीटर लम्बी सड़क पूरी की गई है।

2. इन्दिरा आवास योजना (I.A.Y.)-इस योजना में अनुसूचित जातियों, जनजातियों तथा निर्धनता रेखा से नीचे रहने वाले लोगों को मुफ्त आवास का प्रबन्ध करना है। यह योजना केन्द्र तथा राज्य सरकारों द्वारा 75:25 की दर से लागत के आधार पर बनाई गई है। इस योजना अधीन मैदानी क्षेत्रों में 25,000 रु० तथा पहाड़ी क्षेत्रों में 27,500 रु० की सहायता दी जाती है। 2019-20 में इस योजना पर 15000 करोड़ रु० व्यय करके 35 लाख घरों का निर्माण किया जा चुका है।

3. स्वर्ण जयंती ग्राम स्वः रोज़गार योजना (SGSY)-गांवों में निर्धनता दूर करने के लिए ग्रामीण विकास के उद्देश्य के लिए यह योजना अप्रैल, 1999 में आरम्भ की गई। इस योजना में निर्धनता रेखा से ऊपर रहने वाले निर्धन लोगों को स्वयं रोज़गार के लिए ऋण दिया जाता है। यह योजना केन्द्र तथा राज्य सरकार द्वारा 75:25 की दर पर ऋण सुविधाएं प्रदान करती है जोकि बैंकों द्वारा दिया जाता है। इस योजना अधीन सरकार ने 2018-19 तक 10 हजार करोड़ रु० के ऋण प्रदान किए तथा 135.75 लाख लोगों को स्वयं रोज़गार प्रदान किया।

4. सम्पूर्ण ग्रामीण रोजगार योजना (S.G.RY.)-यह योजना 25 सितम्बर, 2001 को आरम्भ की गई। इस योजना का उद्देश्य ग्रामीण क्षेत्रों में नकद तथा अनाज के रूप में मजदूरी देकर रोज़गार प्रदान करना है। इस उद्देश्य के लिए केन्द्र सरकार अनाज का 75% हिस्सा तथा नकद मज़दूरी का 100% हिस्सा लगाती है। इस योजना में वर्ष 2019-20 में 0.90 लाख टन अनाज तथा 21,000 करोड़ रु० नकद व्यय किए गए।

5. राष्ट्रीय कार्य के बदले अनाज योजना (N.P.P.W.P.)-यह योजना नवम्बर, 2004 में आरम्भ की गई। इस योजना का उद्देश्य देश के 150 सबसे पिछड़े जिलों में जहां सूखा, बाढ़, सेम की स्थिति है, उनमें कार्य के बदले अनाज प्रदान करके लोगों की जीविका बनाए रखना है तथा नकद मज़दूरी भी दी जाती है। 2004-05 में इस योजना पर 2020 करोड़ रु० तथा 20 लाख टन अनाज देकर 7.85 करोड़ मानवीय दिन (8 घंटे) काम दिया गया। जनवरी, 2020 तक वर्ष पर 5000 करोड़ रु० तथा 42 लाख टन अनाज दिया जा चुका है।

6. सूखा, रेगिस्तान बेकार भूमि विकास प्रोग्राम-यह योजना 1973-74 में आरम्भ की गई। 2017-18 में इस योजना पर 1820 करोड़ रु० व्यय किए गए ताकि बेकार भूमि को कृषि योग्य बनाया जा सके।

7. स्वर्ण जयंती शहरी रोज़गार योजना (S.J.S.R.Y.)-शहरी क्षेत्र में रोजगार के लिए चल रही शहरी स्वयं रोज़गार प्रोग्राम तथा शहरी मज़दूरी रोज़गार प्रोग्राम इत्यादि को मिलाकर स्वर्ण जयंती शहरी रोजगार योजना केन्द्र तथा राज्य सरकारों के 75:25 अनुपात के सहयोग से चलाई गई। 2019-20 में 1900 करोड़ रु० व्यय किए गए जिस द्वारा 5 लाख शहरी गरीब लोगों को रोजगार प्रदान किया गया।

8. वाल्मीकि-अम्बेदकर आवास योजना (V.A.M.B.A.Y.)-यह योजना दिसम्बर, 2001 में आरम्भ की गई। इस योजना का उद्देश्य गंदी बस्तियों तथा शहरी निर्धन बस्तियों में शौचालय (Toilets) बनाना था। इस उद्देश्य के लिए केन्द्र तथा राज्य सरकारों द्वारा 50:50 की दर पर व्यय किया जाता है। इस योजना को निर्मल भारत अभियान का नाम दिया गया है। 2017-18 में इस योजना पर 1311 करोड़ रु० व्यय करने का लक्ष्य है।

9. महात्मा गांधी राष्ट्रीय ग्रामीण रोज़गार गारण्टी स्कीम (MGNREGS)-यह योजना आर्थिक तौर पर पिछड़े जिलों में आरम्भ की गई। इस योजना पर 2017-18 में 40 हज़ार करोड़ रुपए व्यय किये गए। जिस द्वारा 4.78 करोड़ परिवारों को इस स्कीम के अधीन रोज़गार प्रदान किए गये। इस स्कीम के अन्तर्गत प्रतिदिन मज़दूरी ₹ 132 निर्धारण की गई है।

10. आम आदमी बीमा योजना (AABY)—यह योजना 18 से 59 वर्ष के मज़दूरों पर लागू होगी जिसमें साधारण मृत पर 30,000 रु० दिये जाएंगे दुर्घटना की स्थिति में ₹ 75000 दिये जाएंगे। यदि अपाहज हो जाए तो ₹ 37500 दिये जाएंगे। इसके लिए ₹ 100 की किश्त देनी होती है। 30 अप्रैल, 2016 तक इस योजना के अन्तर्गत 5 करोड़ मजदूरों का बीमा हो चुका है।

11. कौशल विकास योजना (Skill Development Yojna)-गांवों में बच्चों के कौशल विकास के लिए 2019-20 में ₹ 4900 करोड़ खर्च किये जाएंगे।

Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 21 1991 से आर्थिक सुधार अथवा नई आर्थिक नीति Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 12 Economics Chapter 21 1991 से आर्थिक सुधार अथवा नई आर्थिक नीति

PSEB 12th Class Economics 1991 से आर्थिक सुधार अथवा नई आर्थिक नीति Textbook Questions, and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
आर्थिक सुधारों से क्या अभिप्राय है ?
अथवा
नई आर्थिक नीति का अर्थ बताओ।
उत्तर-
भारत में 1991 से किए गए आर्थिक सुधारों को नई आर्थिक नीति कहा जाता है।

प्रश्न 2.
उदारीकरण से क्या अभिप्राय है ?
उत्तर-
उदारीकरण का अर्थ है उद्योगों तथा व्यापार को परका की अनावश्यक पाबन्दियों से मुक्त करके अधिक प्रतियोगी बनाना।

प्रश्न 3.
निजीकरण से क्या अभिप्राय है ?
उत्तर-
सार्वजनिक क्षेत्र के उद्यमों का संचालन तथा मालकी निजी क्षेत्र को परिवर्तित करने की क्रिया को निजीकरण कहा जाता है।

प्रश्न 4.
विश्वीकरण से क्या अभिप्राय है ?
उत्तर-
विश्वीकरण का अर्थ है अर्थव्यवस्था का बाकी देशों से बिना रुकावट सम्बन्धी उत्पादन, व्यापार तथा वित्त सम्बन्धी आदान-प्रदान स्थापित करना।

प्रश्न 5.
नई आर्थिक नीति के पक्ष में कोई एक तर्क दें।
उत्तर-
नई आर्थिक नीति द्वारा प्रति व्यक्ति आय में वृद्धि करके विकसित देशों के समान आर्थिक विकास किया जा सकता है।

प्रश्न 6.
नई आर्थिक नीति के विपक्ष में कोई एक तर्क दीजिए।
उत्तर-
नई आर्थिक नीति से विदेशी पूंजी तथा तकनीक पर निर्भरता बढ़ जाएगी। इससे उन्नत देशों को अधिक लाभ होगा।

प्रश्न 7.
आर्थिक सुधारों की आवश्यकता क्यों है ?
उत्तर-
भारत में राजकोषीय घाटा निरन्तर बढ़ रहा है।

प्रश्न 8.
राजकोषीय घाटे से क्या अभिप्राय है ?
उत्तर-
राजकोषीय घाटा कुल व्यय तथा कुल आय मनफी ऋण का अन्तर होता है।

प्रश्न 9.
विश्व व्यापार संगठन (W.T.0.) से क्या अभिप्राय है ?
उत्तर-
विभिन्न अर्थव्यवस्थाओं में विश्वीकरण के विकास के लिए बनाई गई संस्था को विश्व व्यापार संगठन कहा जाता है।

प्रश्न 10.
भारत में आर्थिक सुधारों अथवा नई आर्थिक नीति की आवश्यकता क्यों थी ?
उत्तर-

• भारत में राजकोषीय घाटा अधिक हो गया था।
• भुगतान सन्तुलन प्रतिकूल हो गया था।
• विदेशी मुद्रा कोष कम हो गया था।

प्रश्न 11.
भारत में आर्थिक सुधारों की आवश्यकता थी क्योंकि
(a) भारत में राजकोषीय घाटा अधिक हो गया था।
(b) भुगतान सन्तुलन लगातार प्रतिकूल हो गया था।
(c) विदेशी मुद्रा कोष में बहुत कमी आ गई थी।
(d) उपरोक्त सभी।
उत्तर-
(d) उपरोक्त सभी।

प्रश्न 12.
नई आर्थिक नीति में उद्योग और व्यापार के लिए लाइसेंस के स्थान पर ……………. की नीति अपनाई है।
उत्तर-
उदारीकरण।

प्रश्न 13.
नई आर्थिक नीति में कोटा प्रणाली के स्थान पर . ………….. की नीति अपनाई गई।
उत्तर-
निजीकरण।

प्रश्न 14.
नई आर्थिक नीति में परमिट प्रणाली के स्थान पर ………….. नीति अपनाई गई।
उत्तर-
वैश्वीकरण।

प्रश्न 15.
नई आर्थिक नीति अथवा आर्थिक सुधारों में किस नीति को अपनाया गया ?
(a) उदारीकरण
(b) निजीकरण
(c) वैश्वीकरण
(d) उपरोक्त सभी।
उत्तर-
(d) उपरोक्त सभी।

प्रश्न 16.
पहली पीढ़ी (First Generation) के सुधारों से क्या अभिप्राय है ?
उत्तर-
वह सुधार जो प्रशासनिक मशीनरी द्वारा साधारण रूप में चलाए जाते हैं और इन सम्बन्धी विधानक कारवाई की ज़रूरत नहीं होती।

प्रश्न 17.
दूसरी पीढ़ी (Second Generation) के सुधारों से क्या अभिप्राय है ? .
उत्तर-
वह सुधार जिनके लिए विधानक (कानूनी) कारवाई की आवश्यकता होती है उनको दूसरी पीढ़ी के सुधार कहा जाता है।

प्रश्न 18.
आर्थिक सुधारों का ऋणात्मक प्रभाव बताएँ।
उत्तर-
आर्थिक सुधारों से विदेशी निवेश और तकनीक पर निर्भरता बढ़ जाती है। .

प्रश्न 19.
भारत में आर्थिक सुधारों का पहला चरण कब प्रारम्भ हुआ ?
(a) 1951
(b) 1971
(c) 1991
(d) 2011.
उत्तर-
(c) 1991.

प्रश्न 20.
भारत में आर्थिक सुधारों का दूसरा चरण कब प्रारम्भ हुआ ?
उत्तर-
1999 में।

प्रश्न 21.
विश्व व्यापार संगठन (WTO) गैट (GATT) का उत्तराधिकारी है।
उत्तर-
सही।

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
नई आर्थिक नीति (1991) क्यों आवश्यक हुई ?
उत्तर-
भारत में 1991 में आर्थिक सुधार की आवश्यकता इन कारणों से पड़ी-

1. भारत में भुगतान सन्तुलन प्रतिकूल था, जिस कारण विदेशी ऋण का भार बढ़ गया था।
2. भारत में आर्थिक संकट था। राजकोषीय घाटा बहुत बढ़ गया था।
3. इराक की जंग के कारण तेल की कीमतें तथा साधारण कीमत स्तर निरन्तर बढ़ गया था।
4. भारत में सार्वजनिक क्षेत्र असफल हो गया था। बहुत से सार्वजनिक उद्योगों में हानि हो रही थी।

प्रश्न 2.
निजीकरण पर नोट लिखो।
उत्तर-
नई आर्थिक नीति की एक विशेषता यह है कि निजीकरण का विस्तार किया गया है। सरकार द्वारा चलाए जाने वाले उद्योगों को निजी क्षेत्र में परिवर्तित किया जा रहा है। इस सम्बन्ध में निम्नलिखित उपाय किए गए –
(1) सार्वजनिक क्षेत्र में 17 उद्योगों की जगह पर 4 उद्योग

• सुरक्षा औज़ार
• एटोमिक शक्ति
• खाने
• रेलवे सुरक्षित किए गए हैं। शेष सभी उद्योग निजी क्षेत्र के लिए खुले हैं।

(2) सार्वजनिक क्षेत्र की वर्तमान इकाइयों के शेयर निजी क्षेत्र में बेचे जाएंगे।
(3) अब वित्तीय संस्थाओं तथा उद्योगों में निजी निवेश किया जा सकेगा। इससे निजी क्षेत्र की हिस्सेदारी 45% से बढ़कर 55% हो जाएगी।

प्रश्न 3.
विनिवेश से क्या अभिप्राय है?
उत्तर-
सार्वजनिक क्षेत्र के उद्योगों की बिक्री को विनिवेश कहा जाता है। आरम्भ में सरकार ने बीमार इकाइयां, जिन उद्योगों में हानि होती थी, उनको बेचने का निर्णय लिया। परन्तु धीरे-धीरे उद्योगों की कार्यकुशलता में वृद्धि करने के लिए बहुत-से अन्य उद्योगों का विनिवेश करना आरम्भ किया। इस प्रकार की प्रक्रिया आजकल चल रही है।

प्रश्न 4.
वैश्वीकरण पर नोट लिखो।
उत्तर-
नई आर्थिक नीति की एक विशेषता अर्थव्यवस्था का वैश्वीकरण है। वैश्वीकरण का अर्थ है एक अर्थव्यवस्था का शेष विश्व के देशों से उत्पादन, व्यापार तथा वित्तीय सम्बन्ध स्थापित करना तथा विदेशी व्यापार पर लगे प्रतिबन्ध हटाना। भारत में खुलेपन की नीति के लिए निम्नलिखित उपाय किए गए हैं-

1. विदेशी निवेशक अब भारतीय कम्पनियों में 51% से 100% तक निवेश कर सकते हैं।
2. व्यापार पर लगे प्रतिबन्ध 5 वर्षों में हटा दिए गए।
3. विदेशी निवेश को प्रोत्साहन देने के लिए, विदेशी निवेश प्रोत्साहन बोर्ड की स्थापना की गई है।

प्रश्न 5.
विश्व व्यापार संगठन (World Trade Organisation-W.T.O.) क्या है?
उत्तर-
विश्व व्यापार संगठन (W.T.O.) की स्थापना 1 जून, 1995 में की गई। यह संगठन अन्तर्राष्ट्रीय व्यापार में वृद्धि करने तथा वैश्वीकरण की प्रक्रिया को पूरा करने के लिए स्थापित किया गया है। इस संगठन का मुख्य उद्देश्य व्यापार पर लगाए जाने वाले करों में कमी तथा अन्य रुकावटों को दूर करके अन्तर्राष्ट्रीय व्यापार में मुकाबले की स्थिति उत्पन्न करना है जिससे विश्वभर के लोगों को लाभ प्राप्त हो सके। यह संस्था गैट (GATT) की उत्तराधिकारी है। विश्व व्यापार संगठन ने बौद्धिक सम्पत्ति अधिकार से सम्बन्धित व्यापार तथा निवेश को शामिल करके अपने कार्य क्षेत्र को विशाल किया है।

III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 1.
मुख्य आर्थिक सुधारों से क्या अभिप्राय है?
अथवा
नई आर्थिक नीति के अंश बताओ।
उत्तर-
भारत में जुलाई, 1991 से लागू किए विभिन्न नीति सम्बन्धों, उपायों तथा नीतियों से है, जिनका उद्देश्य अर्थव्यवस्था में उत्पादकता तथा कुशलता में वृद्धि करके प्रतियोगी वातावरण तैयार करना है। इस नीति के अंश निम्नलिखित हैं –

• देश में उद्योगों तथा व्यापार के लिए प्रचलित लाइसेंस नीति की जगह उदारीकरण की नीति को लागू करना।
• उद्योगों में कोटा प्रणाली की जगह पर निजीकरण की नीति को लागू करना।
• विदेशी नीति में परमिट की जगह पर वैश्वीकरण की नीति को लागू करना।

प्रश्न 2.
भारत में नई आर्थिक नीति उदारीकरण वाली है। इस सम्बन्ध में उठाए गए पग बताओ।
उत्तर-
भारत में नई आर्थिक नीति में अर्थव्यवस्था को सरकार के सीधे तथा भौतिक कन्ट्रोल से मुक्त किया गया है। इसको उदारीकरण (Liberalisation) वाली नीति कहा जाता है। इस सम्बन्धी निम्नलिखित पग उठाए गए हैं –

1. ‘नई औद्योगिक नीति’ में उदारवादी नीति को अपनाया गया है, जिसकी घोषणा जुलाई, 1991 में की गई। सिगरेट, सुरक्षा, औज़ार, खतरनाक रसायन, दवाइयां, औद्योगिक ऊर्जा तथा शराब, इन 6 उद्योगों को छोड़कर शेष किसी उद्योग के लिए लाइसेंस लेने की आवश्यकता नहीं।
2. अब एम० आर० टी० पी० (एकाधिकार तथा व्यापार रोक कानून) की धारणा को समाप्त किया गया है। अब किसी फ़र्म को निवेश सम्बन्धी निर्णय लेते समय सरकार की अनुमति लेने की आवश्यकता नहीं।
3. लघु पैमाने के उद्योगों की निवेश सीमा एक करोड़ रु० की गई।
4. मशीनों के आयात की स्वतन्त्रता दी गई।
5. उच्च तकनीक वाले कम्प्यूटर तथा उपकरण के आयात की छूट दी गई।

प्रश्न 3.
नई आर्थिक नीति के उद्देश्य लिखो।
उत्तर-

• आर्थिक विकास की दर में तीव्रता से वृद्धि।
• औद्योगिक क्षेत्र में प्रतियोगिता को प्रोत्साहित करना।
• निजी क्षेत्र द्वारा प्रतियोगिता से सार्वजनिक क्षेत्र की कार्यकुशलता में वृद्धि।
• राजकोषीय घाटे में कमी तथा मुद्रा स्फीति पर नियन्त्रण।
• आर्थिक समानता में कमी।

IV. दीर्य उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
भारत की नई आर्थिक नीति की विशेषताएं बताओ। (Explain the features of New Economic Policy of India.)
उत्तर-
नई आर्थिक नीति की मुख्य विशेषताएं अनलिखित हैं-
1. उदारीकरण (Liberalisation)-नई आर्थिक नीति की प्रथम विशेषता उदारीकरण की नीति का अपनाना है। उदारीकरण से अभिप्राय उद्योगों तथा व्यापार को सरकार की अनावश्यक पाबंदियों से मुक्त करवाना है, जिस व्यापार उदारीकरण से कोरिया, सिंगापुर इत्यादि अल्पविकसित देशों ने आर्थिक विकास किया है, उसी तरह भारत भी आर्थिक विकास कर सकता है। इस उद्देश्य के लिए 6 उद्योगों को छोड़कर शेष उद्योगों के लिए लाइसेंस लेने की नीति समाप्त की गई। नई नीति में पंजीकरण (Registration) योजनाएं समाप्त की गई हैं।

2. निजीकरण (Privatisation)-जो उद्योग प्रथम सार्वजनिक क्षेत्र के लिए आरक्षित थे, उनको निजी क्षेत्र के लिए छीनने की नीति को निजीकरण की नीति कहा जाता है। सार्वजनिक क्षेत्र की असफलता को देखते हुए सरकार ने निजीकरण को आंशिक अथवा पूर्ण रूप में अपनाया है, इस नीति को (U Turn) का नाम दिया गया है अर्थात् सार्वजनिक उद्योगों का निजीकरण करना।

3. वैश्वीकरण (Globalisation)-एक देश का दूसरे देशों से मुक्त व्यापार, पूंजी आदान-प्रदान तथा मनुष्यों की गतिशीलता को वैश्वीकरण कहा जाता है। इसका उद्देश्य विदेशी पूंजी का प्रयोग करके विश्व अर्थव्यवस्था को शक्तिशाली बनाना है। विदेशी व्यापार को उत्साहित करके विदेशी निवेश में वृद्धि करना तथा मानवीय पूंजी का एक देश से दूसरे देशों में प्रयोग करना, वैश्वीकरण मनुष्य का मुख्य उद्देश्य है।

4. राजकोषीय सुधार (Fiscal Reforms)-राजकोषीय सुधार भी नई आर्थिक नीति की विशेषता है। इस नीति में सरकार अपनी आय में वृद्धि करके व्यय में कमी करने का यत्न करेगी ताकि देश में उत्पादन तथा आर्थिक विकास पर बुरा प्रभाव न पड़े। इस उद्देश्य के लिए कर प्रणाली में सुधार किए गए हैं। आयातनिर्यात कर घटाए गए हैं। उत्पादन कर में कमी की गई है।

5. मौद्रिक सुधार (Monetary Reforms)-भारत में नई आर्थिक नीति अनुसार मौद्रिक नीति में परिवर्तन किया गया है। इसका मुख्य उद्देश्य कीमत स्तर को स्थिर रखना है। सरकार ने इस उद्देश्य के लिए नरसिंगम कमेटी ने मौद्रिक सुधारों के लिए सिफ़ारिशें कीं, जिनको लागू किया गया है। इस उद्देश्य के लिए नकद रिज़र्व अनुपात (C.R.R.) को घटाकर 5% किया गया है। ब्याज की दर, मांग तथा पूर्ति अनुसार निश्चित की जाएगी। बैंकों को कार्य करने की स्वतन्त्रता दी गई है।

6. सार्वजनिक क्षेत्र नीति (Public Sector Policy)-सार्वजनिक क्षेत्र को भारत की स्वतन्त्रता के समय आर्थिक विकास का महत्त्वपूर्ण साधन माना गया था। परन्तु सार्वजनिक क्षेत्र में असफलता के कारण अब सरकार ने 6 उद्योगों को इस क्षेत्र के लिए रिज़र्व रखा है, बाकी के उद्योग निजी क्षेत्र को बेच दिए जाएंगे। सार्वजनिक क्षेत्र के बहुत से उद्योगों का विनिवेश कर दिया जाएगा। इस क्षेत्र के शेयर वित्तीय संस्थाओं, साधारण लोगों तथा श्रमिकों को बेचे जाएंगे।

प्रश्न 2.
भारत की नई आर्थिक नीति के पक्ष में तर्क दो। (Give arguments in favour of New Economic Policy of India.)
उत्तर-
नई आर्थिक नीति में जो सुधार किए गए हैं, उसके पक्ष में निम्नलिखित तर्क दिए जा सकते हैं –
1. आर्थिक विकास की दर में वृद्धि-भारत में स्वतन्त्रता के पश्चात् 1951 से 1991 तक आर्थिक विकास की दर में वृद्धि 3.6% वार्षिक थी, जबकि प्रति व्यक्ति आय में वृद्धि 1.4% थी। 1991: 2009 तक विकास दर 7.2% वार्षिक हो गई। इससे स्पष्ट है कि आर्थिक सुधारों के कारण आर्थिक विकास में वृद्धि हुई है। 2017-18 में विकास दर 7.4% प्राप्त की गई।

2. औद्योगिक क्षेत्र की प्रतियोगिता में वृद्धि-औद्योगिक क्षेत्र की प्रतियोगिता में वृद्धि के लिए भी आर्थिक सुधार आवश्यक हैं। भारत के उद्योगों में उत्पादन लागत अधिक होने के कारण इनको सुरक्षा प्रदान की गई। इससे उद्योगों में मुकाबला करने की शक्ति बहुत घट गई। परिणामस्वरूप भारत का विदेशी व्यापार 1951 में विश्व व्यापार का 2% हिस्सा था, यह 1991 में घटकर 0.5 प्रतिशत रह गया। 2017-18 में भारत में विदेशी व्यापार 1.6% हो गया है। इसलिए आर्थिक सुधारों की आवश्यकता थी।

3. गरीबी तथा असमानता में कमी-भारत में गरीबी, असमानता तथा बेरोज़गारी की समस्या को योजनाओं द्वारा दूर नहीं किया जा सका। नई नीति द्वारा मानवीय साधनों का विकास करके रोज़गार तथा उत्पादन में वृद्धि करके लोगों की गरीबी को दूर करना भी इसका उद्देश्य है।

4. राजकोषीय घाटे तथा मुद्रास्फीति में कमी-भारत में राजकोषीय घाटा 1990-91 में 8.5% हो गया था। इससे देश में मुद्रा स्फीति की स्थिति उत्पन्न हो गई। सरकार को आन्तरिक तथा बाहरी ऋण लेना पड़ा। नई नीति द्वारा राजकोषीय घाटे पर काबू पाकर मुद्रा स्फीति में कमी सम्भव होगी।

5. सार्वजनिक उद्यमों की कार्यकुशलता में वृद्धि-सार्वजनिक क्षेत्र के उद्यमों में कार्यकुशलता तथा उत्पादकता में बहुत कमी है। नई आर्थिक नीति से सार्वजनिक क्षेत्र के दोष दूर करके इनकी कार्यकुशलता में वृद्धि की जाएगी। इसके परिणामस्वरूप सार्वजनिक उद्यमों की प्रतियोगिता शक्ति बढ़ जाएगी।

प्रश्न 3.
भारत की नई आर्थिक नीति के विपक्ष में तर्क दीजिए। (Give arguments Against New Economic Policy of India.)
उत्तर-
नई आर्थिक नीति के विपक्ष में निम्नलिखित तर्क देकर इसकी आलोचना की गई है –

1. कृषि को कम महत्त्व-भारत में नई आर्थिक नीति में उद्योगों के विकास की ओर अधिक ध्यान दिया गया है। कृषि उत्पादन क्षेत्र के विकास की ओर सरकार ने कोई ध्यान नहीं दिया। भारत में कृषि के विकास के बिना आर्थिक विकास प्राप्त नहीं किया जा सकता।
2. विश्व बैंक तथा अन्तर्राष्ट्रीय मुद्रा कोष का दबाव-भारत में खुले बाज़ार की नीति को अपनाने के लिए अन्तर्राष्ट्रीय संस्थाएं जैसे कि अन्तर्राष्ट्रीय मुद्रा कोष (I.M.F.) तथा विश्व बैंक (World Bank) ने उदारीकरण की नीति अपनाने के लिए दबाव पाया, जिस कारण यह नीति अपनाई गई। भारत को इन संस्थाओं से ऋण प्राप्त होता है। इसलिए नई आर्थिक नीति अपनाई गई।
3. विदेशी ऋण तथा तकनीक पर अधिक निर्भरता-नई आर्थिक नीति की आलोचना में कहा जाता है कि विदेशी ऋण पर भारत की निर्भरता बढ़ गई है। विदेशी तकनीक का आयात अनिवार्य हो गया है, क्योंकि भारत में उद्योगों की प्रतियोगिता शक्ति को आधुनिक तकनीकों के बगैर बढ़ाया नहीं जा सकता। विदेशी ऋण तथा तकनीकों पर निर्भरता देश के लिए घातक सिद्ध हो सकती है।
4. निजीकरण को अधिक महत्त्व-निजीकरण की नीति को नई आर्थिक नीति में आवश्यकता से अधिक महत्त्व दिया गया है। सार्वजनिक क्षेत्र में रोज़गार के अधिक अवसर प्रदान किए जाते थे। निजीकरण द्वारा एकाधिकारी शक्तियों का विकास होगा, जिस द्वारा लोगों का शोषण किया जाएगा। बेरोज़गारी, काला धन, भ्रष्टाचार, श्रमिक शोषण, धन असमानता इत्यादि की बुराइयां उत्पन्न हो जाएंगी।
5. अनिवार्य वस्तुओं की कमी-नई आर्थिक नीति द्वारा आरामदायक तथा विलास वस्तुओं के उत्पादन में वृद्धि होगी। स्कूटर, कारें, टेलीविज़न इत्यादि वस्तुओं की पैदावार बढ़ जाएगी, परन्तु अनिवार्य उपभोक्ता वस्तुएं तथा सामाजिक भलाई के लिए पैदावार में कमी आएगी। इससे गरीब लोगों के कष्ट में वृद्धि होगी।

प्रश्न 4.
भारत की नई आर्थिक नीति (1991) की विशेषताएं बताओ। (Explain the main features of New Economic Policy of India.)
उत्तर-
भारत में 1991 में नई आर्थिक नीति अनुसार उदारीकरण की नीति अपनाई गई। इस उद्देश्य के लिए भारत सरकार ने 24 जुलाई, 1991 को नई औद्योगिक नीति की घोषणा की। इस नीति की मुख्य विशेषताएं निम्नलिखित हैं-
1. लाइसेंस की समाप्ति-उद्योगों को राष्ट्रीय तथा अन्तर्राष्ट्रीय क्षेत्र में प्रतियोगी बनाने के लिए 6 उद्योगों को छोड़कर बाकी उद्योगों को स्थापित करने के लिए लाइसेंस समाप्त किया गया।
भारत में-

• • • शराब
    • सिगरेट
    • सुरक्षा उपकरण

(4) ख़तरनाक रसायन तथा (5) दवाइयों को छोड़कर शेष उद्योगों को लाइसेंस देने की आवश्यकता नहीं।

2. पंजीकरण की समाप्ति-नई औद्योगिक नीति के अनुसार नए उद्योग स्थापित करने अथवा उद्योगों में उत्पादन के विस्तार के लिए सरकारी आज्ञा की कोई आवश्यकता नहीं। सरकार को केवल सूचना ही देनी पड़ेगी।

3. सार्वजनिक क्षेत्र का संकुचन-सार्वजनिक क्षेत्र के लिए कुल 8 उद्योग सुरक्षित रखे गए हैं, जैसे कि परमाणु ऊर्जा, रेलवे, खानें, सैनिक साजो सामान इत्यादि, शेष सभी क्षेत्र में धीरे-धीरे निजी क्षेत्र को उत्पादन के अधिकार दिए जाएंगे। सार्वजनिक क्षेत्र के शेयर साधारण जनता तथा श्रमिकों में बेचकर इन उद्योगों की कार्यकुशलता में वृद्धि की जाएगी।

4. विदेशी पूंजी-नई नीति में विदेशी पूंजी निवेश सीमा 40% से बढ़ाकर 51% कर दी गई है। इस सम्बन्ध में विदेशी मुद्रा नियमन कानून (FERA) में आवश्यक संशोधन किया जाएगा। विदेशी पूंजी सम्बन्धी देश का केन्द्रीय बैंक, रिज़र्व बैंक ऑफ़ इंडिया, पूरी नज़र रखेगा।

5. बोर्डों का गठन-विदेशी पूंजी के सम्बन्ध में चुने हुए क्षेत्रों में निवेश करने के लिए विशेष अधिकार प्राप्त बोर्डों की स्थापना की गई है। यह बोर्ड बहुराष्ट्रीय कम्पनियों से बातचीत करके पूंजी लगाने के लिए अनिवार्य पग उठाएगा।

6. लघु उद्योगों को सुरक्षा-नई नीति में लघु उद्योगों की निवेश सीमा एक करोड़ रु० की गई है। इन उद्योगों द्वारा कुछ वस्तुओं के उत्पादन को सुरक्षित रखा जाएगा; जिनका उत्पादन बड़े उद्योग नहीं कर सकेंगे।

7. एकाधिकारी कानून से छूट- एकाधिकारी कानून के अधीन आने वाली कम्पनियों को भारी छूट दी गई है। अब निवेश की सीमा समाप्त की गई है। उद्यमी बिना परमिट नए उद्योग स्थापित कर सकेंगे। इस नीति में लाइसेंस की समाप्ति तथा एकाधिकारी कम्पनियों पर रोक हटा ली गई है। इसका मुख्य उद्देश्य विदेशी पूंजी को उत्साहित करके देश के उद्योगों का विकास करना है।

प्रश्न 5.
विश्व व्यापार संगठन (W.T.O.) पर नोट लिखो। भारतीय अर्थव्यवस्था पर विश्व व्यापार संगठन का प्रभाव स्पष्ट करो।
(Write a note on World Trade Organization (W.T.O.). Explain the effects of World Trade Organization on Indian Economy.)
उत्तर-
विश्व व्यापार संगठन (World Trade Organisation-W.T.O.) की स्थापना 1 जून, 1995 को हुई। यह अन्तर्राष्ट्रीय संगठन है, जोकि गैट (GATT) की बैठकों के परिणामस्वरूप अस्तित्व में आया है। इस संगठन का मुख्य उद्देश्य वस्तुओं तथा सेवाओं के आयात-निर्यात में आने वाली रुकावटों को दूर करके, विदेशी निवेश के अवसरों में वृद्धि करना, व्यापार सम्बन्धी बुद्धिजीवी संपदा अधिकार (TRIPS) तथा व्यापार सम्बन्धित निवेश उपायों (TRIMS) का विस्तार करना है। इस संगठन के मुख्य उद्देश्य हैं-

• वस्तुओं को मुक्त प्रवाह की आज्ञा देने के लिए रुकावटें दूर करना।
• पूंजी के मुक्त प्रवाह के लिए प्रेरक वातावरण तैयार करके निवेश में वृद्धि करना।
• अन्तर्राष्ट्रीय व्यापार में प्रतियोगिता की स्थिति उत्पन्न करके उपभोक्ताओं को कम लागत पर वस्तुएं उपलब्ध करवाना।
• विश्व के विभिन्न देशों को विश्व व्यापार में बुद्धिजीवी सम्पदा तथा व्यापार सम्बन्धित निवेश के लिए अधिक अवसर प्रदान करना।

विश्व व्यापार संगठन का भारतीय अर्थव्यवस्था पर प्रभाव-
(Effects of World Trade Organisation on Indian Economy)
A. अनुकूल प्रभाव (Favourable Effects)

1. निर्यात प्रोत्साहन-विश्व व्यापार संगठन भारतीय अर्थव्यवस्था के लिए निर्यात के अधिक अवसर प्रदान करेगा। इससे भारत का विदेशी व्यापार, अन्तर्राष्ट्रीय व्यापार में अधिक योगदान डाल सकेगा।
2. विकसित देशों की कोटा प्रणाली की समाप्ति-विश्व व्यापार संगठन द्वारा विकसित देशों द्वारा अपनाई जाने वाली कोटा प्रणाली को समाप्त किया जाएगा। इससे भारत के कपड़े के निर्यात में वृद्धि होगी।
3. कृषि को विकसित देशों द्वारा कम सहायता-विश्व व्यापार संगठन की शर्ते लागू होने से विकसित देश कृषि क्षेत्र को कम सहायता प्रदान कर सकेंगे। इससे भारत में से कृषि पदार्थों के निर्यात में वृद्धि होगी।

B. प्रतिकूल प्रभाव (Unfavourable Effects) –

1. श्रम बाज़ार प्रति पक्षपात-विश्व व्यापार संगठन द्वारा पूंजी बाज़ार की ओर अधिक ध्यान दिया जा रहा है, जबकि श्रम बाज़ार से पक्षपात की नीति अपनाई जा रही है। संगठन अनुसार पूंजी का निवेश एक देश द्वारा दूसरे देशों में बिना रुकावट किया जा सकता है। परन्तु श्रम बाज़ार में ऐसी स्वतन्त्रता नहीं होगी। इससे भारत जैसे कम विकसित देशों को हानि होगी।
2. लघु पैमाने के उद्योगों पर बुरा प्रभाव-विश्व व्यापार संगठन बड़े पैमाने के उद्योगों तथा लघु पैमाने के उद्योगों में भिन्नता नहीं करता। इस कारण लघु पैमाने के उद्योगों को न सिर्फ देश में बड़े पैमाने के उद्योगों द्वारा उत्पादित वस्तुओं से प्रतियोगिता करनी पड़ेगी, बल्कि विदेशी उद्योगों द्वारा उत्पादित वस्तुओं का मुकाबला भी करना पड़ेगा। इससे अगरबत्ती, आइसक्रीम, मिनरल वाटर इत्यादि उद्योग नष्ट हो जाएंगे।
3. विकसित देशों के दोहरे मापदण्ड-अमेरिका, ऑस्ट्रेलिया इत्यादि विकसित देशों द्वारा दोहरे मापदण्ड अपनाए जाते हैं। एक ओर अमेरिका अपने किसानों को बहुत अधिक सब्सिडी देता है। भारत से निर्यात कपड़ों पर बहुत अधिक कर लगाया जाता है। भारत से निर्यात दुशालें, रसायन, सिले-सिलाए कपड़े इत्यादि पर पाबंदी लगाई जाती है, क्योंकि ये वस्तुएं बच्चों द्वारा उत्पादित की जा सकती हैं। इसी तरह जापान से निर्यात किए जाने वाले लोहा तथा इस्पात पर पाबन्दी लगाई हुई है। इस प्रकार के दोहरे मापदण्डों पर बुरा प्रभाव पड़ता है।

Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 20 भारत में औद्योगिक विकास नीति तथा लाइसेसिंग Textbook Exercise Questions, and Answers.

PSEB Solutions for Class 12 Economics Chapter 20 भारत में औद्योगिक विकास नीति तथा लाइसेसिंग

PSEB 12th Class Economics भारत में औद्योगिक विकास नीति तथा लाइसेसिंग Textbook Questions, and Answers

I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)

प्रश्न 1.
घरेलू उद्योगों से क्या अभिप्राय है ?
उत्तर-
घरेलू उद्योग वह उद्योग होता है जो कि एक परिवार के सदस्यों द्वारा कम पूंजी से लगाया जाता है।

प्रश्न 2.
लघु उद्योग किसे कहते हैं ?
उत्तर-
लघु उद्योग वे उद्योग हैं जिनमें एक करोड़ रुपए तक की पूंजी निवेश की गई हो।

प्रश्न 3.
औद्योगीकरण की कोई एक समस्या का वर्णन करें।
उत्तर-
बड़े घरानों का विकास-भारत में औद्योगिक क्षेत्र में कुछ घराने तीव्रता से विकसित हो रहे हैं।

प्रश्न 4.
नई औद्योगिक नीति में उदारवादी नीति से क्या अभिप्राय है ?
उत्तर-
भारत की नई औद्योगिक नीति 1991 में सरकार ने उदारवादी नीति (Liberal Policy) अपनाई है।

प्रश्न 5.
औद्योगिक विकास के लिए कोई एक सुझाव दें।
उत्तर-
औद्योगिक विकास के लिए सरकार को आधारभूत सुविधाओं में वृद्धि करनी चाहिए।

प्रश्न 6.
भारत में घरेलू तथा छोटे उद्योगों के महत्त्व पर टिप्पणी लिखें।
उत्तर-
इन उद्योगों द्वारा रोज़गार के अधिक अवसर प्रदान किए जाते हैं।

प्रश्न 7.
छोटे पैमाने के उद्योगों की कठिनाइयां बताएं।
उत्तर-
घरेलू तथा छोटे उद्योगों में उत्पादन लागत अधिक आती है इसलिए बड़े उद्योगों से मुकाबला करना कठिन होता है।

प्रश्न 8.
भारत की 1991 की औद्योगिक नीति की कोई दो मुख्य विशेषताएं बताएं।
उत्तर-

• सार्वजनिक क्षेत्र में केवल चार उद्योग सुरक्षित रखे गए हैं।
• लाइसेंस प्राप्त करने की नीति का त्याग किया गया है।

प्रश्न 9.
किसी देश में उद्योगों की स्थापना में क्रान्तिकारी परिवर्तन को …………….. कहते हैं।
उत्तर-
औद्योगिक विकास।

प्रश्न 10.
परम्परागत वस्तुओं की पैदावार परम्परागत विधि से करने को ………………. उद्योग कहते हैं।
(a) छोटे उद्योग
(b) घरेलू उद्योग
(c) बड़े पैमाने के उद्योग
(d) उपरोक्त में से कोई नहीं।
उत्तर-
(b) घरेलू उद्योग।

प्रश्न 11.
भारत में नई औद्योगिक नीति 1991 को ………………. नीति कहा जाता है।
उत्तर-
उदारवादी नीति।

प्रश्न 12.
बारहवीं योजना में औद्योगिक विकास का वार्षिक टीचा …………… प्रतिशत रखा गया है।
(a) 8%
(b) 9%
(c) 12%
(d) 14%.
उत्तर-
(b) 9%.

प्रश्न 13. विभिन्न सिद्धान्त एवं क्रियाएं जो देश के औद्योगीकरण के लिए बनाए जाते हैं उनको ………… कहा जाता है।
(a) आर्थिक विकास
(b) औद्योगिक विकास
(c) औद्योगिक लाइसेंसिंग
(d) उपरोक्त में से कोई भी नहीं।
उत्तर-
(b) औद्योगिक विकास।

प्रश्न 14.
भारत में नई औद्योगिक नीति सन् …………………… में बनाई गई।
(a) 1956
(b) 1980
(c) 1991
(d) 2012.
उत्तर-
(c) 1991.

प्रश्न 15.
सन् 1991 में 6 उद्योगों को छोड़कर बाकी सभी उद्योगों के लिए लाइसेंस समाप्त कर दिया गया |
उत्तर-
सही।

प्रश्न 16.
नई औद्योगिक नीति अनुसार विदेशी पूंजी निवेश की सीमा बढ़ा कर 51 प्रतिशत कर दी गई है।
उत्तर-
सही।

प्रश्न 17.
भारत में औद्योगिक विकास के लिए पूंजी की कोई कमी नहीं है।
उत्तर-
ग़लत।

प्रश्न 18.
नई औद्योगिक नीति में निजी क्षेत्र को अधिक महत्त्व दिया गया है।
उत्तर-
सही।

प्रश्न 19.
भारत में औद्योगिक विकास की कोई एक समस्या बताएँ।
उत्तर-
भारत में आधारभूत उद्योगों का कम विकास हुआ है।

प्रश्न 20.
घरेलू तथा अल्प उद्योगों के महत्त्व को स्पष्ट करें।
उत्तर-
घरेलू तथा अल्प पैमाने के उद्योग श्रम के गहन होने के कारण इन द्वारा रोज़गार प्रदान किया जाता है।

प्रश्न 21.
भारत में नई औद्योगिक नीति कब बनाई गई ?
(a) 1971
(b) 1981
(c) 1991
(d) 2001.
उत्तर-
(c) 1991.

II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
भारत में उद्योगों के महत्त्व सम्बन्धी कोई दो बिन्दु बताएँ।
उत्तर-
भारत में औद्योगीकरण का विशेष महत्त्व है। उद्योगों के विकास द्वारा राष्ट्रीय आय, उत्पादन तथा रोजगार में वृद्धि कर भारतीय अर्थ-व्यवस्था की विकास दर को बढ़ाया जा सकता है। उद्योगों का महत्त्व इस प्रकार स्पष्ट किया जा सकता है-

1. रोज़गार में वृद्धि-औद्योगिक विकास द्वारा रोज़गार में वृद्धि की जा सकती है। भारत में भिन्न-भिन्न योजनाओं में रोज़गार की वृद्धि के लिए रखे गए लक्ष्य प्राप्त नहीं हुए इस कारण बेरोज़गारी में बहुत वृद्धि हुई है। 2019-20 में उद्योग द्वारा 125 मिलियन लोगों को रोज़गार प्रदान किया गया है। 2022 तक 200 मिलियन लोगों को रोजगार देने का अनुमान है।
2. आर्थिक विकास- भारत के आर्थिक विकास की दर तीव्र करने के लिए उद्योगों का विकास महत्त्वपूर्ण |

प्रश्न 2.
भारत की 12वीं योजना में भारत के औद्योगिक ढांचे का वर्णन करें।
उत्तर-
बारहवीं योजना में उद्योग (Industries in 12th Plan)-बारहवीं योजना (2012-17) में औद्योगिक विकास का लक्ष्य 12% से 14% रखा गया है। इस योजना में 200 मिलियन लोगों को रोजगार देने का लक्ष्य रखा गया है।

प्रश्न 3.
भारत की नई औद्योगिक नीति (1991) के गुण बताएं।
उत्तर-
नई औद्योगिक नीति के गुण (Merits)-

• नई नीति से उद्योगों की कुशलता में वृद्धि होगी।
• देश में विदेशी तकनीकों के प्रयोग के कारण उत्पादन में वृद्धि होगी।
• यह नीति उदारवादी नीति है जिसमें निजी क्षेत्र को प्राथमिकता दी गई है।
• भारतीय उद्योगों को विदेशी उद्योगों से प्रतियोगिता करने के समर्थ बनाने का यत्न किया गया है।
• घरेलू तथा छोटे उद्योगों को अधिक महत्त्व प्रदान किया गया है तथा मज़दूरों के कल्याण के लिए कार्यक्रम बनाए गए हैं।

प्रश्न 4.
भारतीय उद्योगों की कोई दो समस्याएं बताएं।
उत्तर-
1. कम प्राप्तियां (Less Achievements) भारत की भिन्न-भिन्न योजनाओं में विकास दर के लक्ष्य हमेशा अधिक रखे गए हैं। प्रत्येक योजना में 8% विकास दर प्राप्त करने का लक्ष्य रखा गया परन्तु वास्तव में 5.6% विकास दर प्राप्त की गई है। इसलिए निर्धारित लक्ष्यों तथा प्राप्तियों में बहुत अन्तर पाया जाता है।

2. बीमार उद्योग (Industrial Sickness)-भारत के रिज़र्व बैंक ने व्यापारिक बैंकों से जो सूचना प्राप्त की है उसके अनुसार 31 मार्च, 2020 तक 2,40,000 बीमार औद्योगिक इकाइयां थीं। 2020 में छोटे पैमाने के उद्योगों की बीमार इकाइयों की संख्या 1,00,000 थी। इस प्रकार बीमार इकाइयों की संख्या में वृद्धि होने के कारण औद्योगिक विकास नहीं हो रहा है।

प्रश्न 5.
भारत में औद्योगिक विकास के लिए कोई दो सुझाव दें।
उत्तर-

1. आधुनिकीकरण (Modernisation)-भारत में उद्योगों के आधुनिकीकरण की आवश्यकता है। इस लक्ष्य के लिए नई मशीनों तथा औज़ारों का निर्माण करना चाहिए ताकि उद्योगों में उत्पादन लागत कम हो सके।
2. मूलभूत सुविधाएं (Basic Facilities)- उद्योगों के विकास के लिए मूलभूत सुविधाएं जैसे कि कच्चा माल, साख सहूलियतें, करों में राहत तथा लघु उद्योगों को सुरक्षा प्रदान करनी चाहिए। इसके अतिरिक्त शक्ति, कोयला, यातायात के साधन, सड़कें, रेलों का विकास करने की आवश्यकता है।

प्रश्न 6.
भारत ने लाइसेंसिंग नीति से क्या अभिप्राय है ?
उत्तर-
औद्योगिक लाइसेंसिंग नीति (Industrial Lincensing Policy)-स्वतन्त्रता के बाद भारत सरकार ने सन् 1951 में एक एक्ट ‘औद्योगिक विकास एवं नियमन’ पास किया जिसके अनुसार प्रत्येक उद्योग को सरकार से अनुमति लेकर ही औद्योगिक उत्पादन करने का हक होता था। बिना सरकार की अनुमति और बिना लाइसेंस कोई भी व्यक्ति उद्योग स्थापित नहीं कर सकता था। उद्योग कहां स्थापित किया जाए, कौन-सी वस्तु का उत्पादन किया जाए और उस वस्तु का कितनी मात्रा में उत्पादन किया जाए, इन बातों के लिए लाइसेंस लेना ज़रूरी था। सरकार की इस नीति को औद्योगिक लाइसेंसिंग नीति कहा जाता है।

III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 1.
भारत में औद्योगीकरण के महत्त्व को स्पष्ट करें।
उत्तर-
भारत में औद्योगीकरण का विशेष महत्त्व है। उद्योगों के विकास द्वारा राष्ट्रीय आय, उत्पादन तथा रोजगार में वृद्धि कर भारतीय अर्थ-व्यवस्था की विकास दर को बढ़ाया जा सकता है। उद्योगों का महत्त्व इस प्रकार स्पष्ट किया जा सकता है-
1. रोज़गार में वृद्धि-औद्योगिक विकास द्वारा रोजगार में वृद्धि की जा सकती है। भारत में भिन्न-भिन्न योजनाओं में रोज़गार की वृद्धि के लिए रखे गए लक्ष्य प्राप्त नहीं हुए इस कारण बेरोजगारी में बहुत वृद्धि हुई है। 2019-20 में उद्योग द्वारा 160 मिलियन लोगों को रोजगार प्रदान किया गया है। 2022 तक 200 मिलियन लोगों को रोज़गार देने का अनुमान है।

2. आर्थिक विकास-भारत के आर्थिक विकास की दर तीव्र करने के लिए उद्योगों का विकास महत्त्वपूर्ण |

3. साधनों का उचित प्रयोग-भारत में प्राकृतिक साधन लोहा, कोयला, मैंगनीज़ तथा मानवीय साधन बहुत अधिक मात्रा में पाये जाते हैं। इसका उचित प्रयोग करने के लिए उद्योगों का विकास महत्त्वपूर्ण है।

4. विदेशी व्यापार-भारत द्वारा विदेशों को निर्यात कम मात्रा में किया जाता है तथा आयात अधिक होने के कारण भुगतान सन्तुलन भारत के प्रतिकूल रहता है। औद्योगीकरण द्वारा विदेशी व्यापार में वृद्धि करके भुगतान सन्तुलन को अनुकूल किया जा सकता है।

प्रश्न 2.
भारत की योजनाओं में औद्योगिक विकास दर पर टिप्पणी लिखें।
उत्तर-
भारत एक विकासशील देश है। इससे 1991 की औद्योगिक नीति से पूर्व सार्वजनिक क्षेत्र को अधिक महत्त्वपूर्ण स्थान दिया गया था परन्तु अब निजी क्षेत्र को अधिक महत्त्व दिया जा रहा है जिस कारण भारत में भिन्नभिन्न योजनाओं में विकास दर इस प्रकार रही है-

इससे ज्ञात होता है कि भारत में उद्योगों की विकास दर 10% से कम रही है। देश के आर्थिक विकास में वृद्धि करने के लिए विकास दर में और वृद्धि करने की आवश्यकता है। वर्ष 2012-17 में औद्योगिक विकास दर का लक्ष्य 9% रखा गया है। 2020-21 में 9.4% विकास दर प्राप्त करने का लक्ष्य है।

प्रश्न 3.
भारत में औद्योगिक विकास की मन्द गति के क्या कारण हैं ?
उत्तर-
भारत में औद्योगिक विकास की मन्द गति के मुख्य कारण निम्नलिखित हैं –

1. आधारभूत उद्योगों का कम विकास-प्रत्येक देश का आर्थिक विकास आधारभूत उद्योगों के विकास पर निर्भर करता है। यद्यपि भारत में मशीनें, लोहा तथा इस्पात, सीमेंट इत्यादि बनाने के उद्योग स्थापित किए गए हैं परन्तु देश की आवश्यकताओं को देखते हुए इनका कम विकास हुआ है।
2. पूंजी की कमी-उद्योगों के विकास के लिए पूंजी की आवश्यकता होती है। भारत में अधिक लोग निर्धन हैं इसलिए लोगों की बचत कम है। बचत द्वारा ही पूंजी निर्माण किया जाता है। पूंजी की कमी के कारण उद्योगों की गति मन्द है।
3. शक्ति की कमी-उद्योगों के विकास के लिए शक्ति साधनों की आवश्यकता होती है। भारत में शक्ति के तीन साधन विद्युत्, कोयला तथा तेल हैं। भारत में कोयला काफ़ी मात्रा में मिलता है परन्तु यह घटिया किस्म का होने के कारण आवश्यकताओं की पूर्ति नहीं करता। कोयले की खाने बिहार तथा बंगाल में केन्द्रित हैं इसलिए अन्य क्षेत्रों को कोयला भेजने की लागत बढ़ जाती है। इस कारण उद्योगों के विकास की गति मन्द है।
4. क्षेत्र असमानता-भारत में अधिकतर उद्योग कुछ क्षेत्रों जैसे कि महाराष्ट्र, गुजरात, तमिलनाडु में केन्द्रित हो गए हैं। कुछ राज्य जैसे कि पंजाब, उड़ीसा, मध्य प्रदेश, राजस्थान उद्योगों के पक्ष से पिछड़े हुए राज्य हैं। क्षेत्रीय असमानता होने के कारण भी उद्योगों के विकास की गति मन्द है।

प्रश्न 4.
भारत में औद्योगिक पिछड़ेपन को दूर करने के लिए चार सुझाव दें।
उत्तर-
भारत में उद्योग पिछड़ी हुई स्थिति में हैं। उद्योगों के पिछड़ेपन को दूर करने के लिए निम्नलिखित सुझाव दिए जा सकते हैं-

• निजी क्षेत्र का विकास- भारत में सार्वजनिक क्षेत्र असफल हो गया है। इसलिए निजी क्षेत्र को उत्साहित करने की आवश्यकता है। सरकार को निजी क्षेत्र के विकास के लिए अधिक सुविधाएं प्रदान करनी चाहिए। इससे निजी पूंजीपति अधिक उद्योग स्थापित करेंगे ताकि उद्योगों का विकास हो सके।
• साधनों का उचित प्रयोग-भारत में प्राकृतिक साधन काफ़ी मात्रा में पाए जाते हैं। देश के प्राकृतिक साधनों का उचित प्रयोग करके उद्योगों का विकास किया जा सकता है।
• आधुनिकीकरण तथा तकनीकी विकास-भारत में उत्पादन करने की विधियां पुरातन होने के कारण उद्योग पिछड़े हुए हैं। उद्योगों के विकास के लिए आवश्यक है कि आधुनिक युग में प्रयोग होने वाली मशीनों का प्रयोग किया जाए। तकनीकी तौर पर विकसित मशीनों के प्रयोग से न केवल उत्पादन लागत कम हो जाती है बल्कि उद्योग प्रतियोगिता करने में समर्थ हो जाते हैं।
• अवरोध दूर करना-औद्योगिक विकास के लिए आधारभूत ढांचे के मुख्य अवरोधों को दूर करना चाहिए अर्थात् देश में शक्ति, यातायात के साधन, संचार तथा कच्चे माल इत्यादि अवरोधों को दूर किया जाए तो इससे औद्योगिक पिछड़ापन दूर किया जा सकता है।

प्रश्न 5.
ग्यारहवीं योजना में औद्योगिक विकास पर टिप्पणी लिखें।
उत्तर-
भारत में बारहवीं पंचवर्षीय योजना 2012-17 तक बनाई गई। इस योजना में उद्योगों के विकास तथा खनिज पदार्थों पर 196000 करोड़ रुपए खर्च करने के लिए रखे गए थे। ग्यारहवीं योजना में चार क्षेत्रों को छोड़कर अन्य क्षेत्रों में लाइसेंस लेने की आवश्यकता नहीं है। विदेशी पूंजी 75% से 100% तक लगाई जा सकती है। पिछड़े क्षेत्रों में उद्योग स्थापित करने का लक्ष्य रखा गया था। इन उद्देश्यों की प्राप्ति के लिए निजी क्षेत्र को प्राथमिकता दी गई है। इस प्रकार भारतीय उद्योगों को प्रतियोगिता के योग्य बनाया जा रहा है। बारहवीं योजना (2012-17) में औद्योगिक विकास दर 12% का लक्ष्य रखा गया है।

IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 1.
भारत की अर्थ-व्यवस्था में उद्योगों के महत्त्व पर टिप्पणी लिखें। (Write a detailed note on the Importance of Industrialization in India.)
उत्तर-
भारत जैसे विकासशील देश के लिए औद्योगीकरण महत्त्वपूर्ण स्थान रखता है। इसके महत्त्व को निम्नलिखित अनुसार स्पष्ट किया जा सकता है-

1. रोज़गार में वृद्धि-भारत में जनसंख्या तीव्र गति से बढ़ रही है। बढ़ती हुई जनसंख्या के लिए रोजगार – के नए अवसर उत्पन्न करने के लिए औद्योगीकरण महत्त्वपूर्ण स्थान रखता है। कृषि से जनसंख्या का बोझ घटाने के लिए उद्योगों का विकास महत्त्वपूर्ण है।
2. राष्ट्रीय आय में वृद्धि-अगर हम विश्व के उन्नत देशों को देखते हैं तो आय में अधिक योगदान उद्योगों द्वारा दिया जाता है। भारत में 1950-51 में उद्योगों द्वारा 16% योगदान दिया गया था जो कि अब 2019-20 में बढ़ कर 25% हो गया है। आज भी उद्योगों से कृषि का योगदान महत्त्वपूर्ण है।
3. पूंजी निर्माण में वृद्धि-पूंजी निर्माण के अतिरिक्त कोई भी देश आर्थिक उन्नति नहीं कर सकता। प्रो० लुईस का विचार था कि कोई देश इतना निर्धन नहीं होता कि राष्ट्रीय आय का 12% भाग पूंजी निर्माण न कर सके। परन्तु उद्योगों के विकास के अतिरिक्त बचत में वृद्धि नहीं हो सकती इसलिए पूंजी निर्माण में वृद्धि करने के लिए औद्योगिक विकास आवश्यक है।
4. कृषि का विकास-कृषि का विकास औद्योगिक विकास के बिना सम्भव नहीं। उद्योगों में ऐसी मशीनें विकसित की जा सकती हैं जिनसे उत्पादन बढ़ाया जा सके। जब कृषि का उत्पादन बढ़ जाता है तो इससे उद्योगों का विकास होता है। इस प्रकार कृषि का विकास तथा औद्योगिक विकास एक-दूसरे पर निर्भर करते हैं।
5. विदेशी व्यापार का विकास-उद्योगों के विकास द्वारा विदेशी व्यापार में वृद्धि होती है। उद्योगों में जो वस्तुएं उत्पन्न की जाती हैं इनका निर्यात करके विदेशी पूंजी अर्जित की जा सकती है जो कि देश के आर्थिक विकास के लिए महत्त्वपूर्ण होती है।
6. सन्तुलित आर्थिक विकास- भारत में आर्थिक विकास तीव्र करने के लिए सन्तुलित आर्थिक विकास करने की आवश्यकता है। जब एक देश में कृषि तथा उद्योग एक साथ विकसित होते हैं तो इस को सन्तुलित विकास कहा जाता है। इसलिए भारत में सन्तुलित विकास करके आर्थिक विकास तीव्र गति से प्राप्त किया जा सकता है।
7. आत्म-निर्भरता- भारत में विदेशों से बहुत-सी वस्तुएं तथा मशीनें आयात की जाती हैं। इसलिए स्वतन्त्रता के पश्चात् भारत का भुगतान सन्तुलन भारत के प्रतिकूल रहा है। औद्योगिक विकास द्वारा वस्तुओं की अधिक आवश्यकता को पूर्ण किया जा सकता है।
8. सुरक्षा के लिए लाभदायक-देश की सुरक्षा के लिए औद्योगिक विकास लाभदायक होता है। देश में सुरक्षा सम्बन्धी उपकरणों का विकास करके विदेशों पर निर्भरता कम की जा सकती है।

प्रश्न 2.
स्वतन्त्रता के पश्चात् योजनाओं के दौरान भारत में औद्योगिक विकास के ढांचे का वर्णन करें। (Explain the Industrial development of India after Independence during plan period.)
उत्तर-
भारत की स्वतन्त्रता से पूर्व भारत के औद्योगिक विकास की तरफ ध्यान नहीं दिया गया था क्योंकि इंग्लैण्ड के उद्योगों में जो माल तैयार होता था वह भारत की मण्डियों में बेचा जाता था। भारत में से कच्चा माल इंग्लैण्ड को निर्यात किया जाता था। इसलिए स्वतन्त्रता से पूर्व भारत में औद्योगिक विकास नहीं हुआ, परन्तु स्वतन्त्रता के पश्चात् औद्योगिक विकास की तरफ ध्यान देना आरम्भ किया गया है। इसलिए भारतीय योजनाओं के दौरान उद्योगों को जिस प्रकार महत्त्व दिया गया है उसका विवरण इस प्रकार से है-
1. प्रथम योजना में उद्योग (Industries in First Plan)-प्रथम पंचवर्षीय योजना (1951-56) में कृषि के विकास की तरफ अधिक ध्यान दिया गया, परन्तु औद्योगिक विकास के लिए विशेष कार्य नहीं किया गया, परन्तु इस योजना में कुछ महत्त्वपूर्ण उद्योग जैसे कि सीमेंट, फैक्टरियां, टेलीफोन, इण्डस्ट्री, चितरंजन लोकोमोटिव वर्कस इत्यादि आरम्भ किए गए। इस योजना में उद्योगों के उत्पादन में 39% वृद्धि हुई है।

2. द्वितीय योजना में उद्योग (Industries in Second Plan)-द्वितीय योजना (1956-61) में उद्योगों के विकास की तरफ विशेष ध्यान दिया गया। यह योजना प्रो० पी० सी० महलानोबिस ने तैयार की थी। 1956 में औद्योगिक नीति की घोषणा की गई। इस योजना काल में सार्वजनिक क्षेत्र में आधारभूत उद्योग स्थापित करने को अधिक महत्त्व दिया गया। लोहा तथा इस्पात के उत्पादन के लिए दुर्गापुर, भिलाई तथा राऊरकेला के स्थान पर उद्योग स्थापित किए गए। नंगल में उर्वरक उद्योग स्थापित किया गया। इस योजना में औद्योगिक उत्पादन की विकास दर 6.6% वार्षिक रही।

3. तृतीय योजना में उद्योग (Industries in Third Plan)-भारत की तृतीय योजना (1961-66) में भारी उद्योग के विकास की तरफ विशेष ध्यान दिया गया। इसका मुख्य लक्ष्य औद्योगिक क्षेत्र में रोज़गार में वृद्धि करना रखा गया ताकि राष्ट्रीय आय में वृद्धि हो सके। इस योजना में जो उद्योग द्वितीय योजना में स्थापित किए गए थे उनकी योग्यता में वृद्धि की गई। भारत में मशीनों के पुर्जे, स्वास्थ्य से सम्बन्धित उपकरण तथा वैज्ञानिक औजार बनाने के कारखाने लगाए गए। इस योजना में औद्योगिक उत्पादन में 25% वृद्धि की गई।

4. चतुर्थ योजना में उद्योग (Industries in Fourth Plan)-चतुर्थ योजना (1969-74) से तीव्र गति से आत्मनिर्भरता प्राप्त करने के लिए औद्योगिक विकास की तरफ विशेष ध्यान दिया गया। भारत में पेट्रोल तथा रासायनिक पदार्थों के विकास के लिए निवेश में वृद्धि की गई। इस योजना काल में औद्योगिक उत्पादन को वार्षिक दर 5% रही।

5. पांचवीं योजना में उद्योग (Industries in Fifth Plan)-पांचवीं योजना (1974-78) में औद्योगिक विकास में. ६, वार्षिक विकास दर प्राप्त करने के लिए बनाई गई थी। इस योजना में उद्योगों के विकास के लिए सा जनिक क्षेत्र में 39,426 करोड़ रुपए का निवेश किया गया। योजना काल में इस्पात, उर्वरक, खनिज तेल, निर्यात, कपड़ा, चीनी इत्यादि उद्योगों के विकास की तरफ विशेष ध्यान दिया गया परन्तु औद्योगिक उत्पादन में विकास दर 5.3% रही।

6. छठी योजना में उद्योग (Industries in Sixth Plan)-छठी योजना (1980-85) में नए उद्योग स्थापित करने का लक्ष्य रखा गया। विशेषतया टेलीफोन तथा इलेक्ट्रोनिक्स उद्योगों की तरफ अधिक ध्यान. दिया गया। इस योजना में औसत वार्षिक विकास दर 5.5% वार्षिक रही।

7. सातवीं योजना में उद्योग (Industries in Seventh Plan)-सातवीं योजना (1985-90) में देश में औद्योगीकरण की नीति जारी रही। इस योजना में बड़े उद्योगों तथा खनिजों के उत्पादन की तरफ विशेष ध्यान दिया गया। उत्पादन में वृद्धि करने के लिए तकनीक को विकसित करने का कार्य आरम्भ किया गया। देश की आवश्यकताओं को ध्यान में रख कर उद्योगों को विकसित करने की योजना बनाई गई। विकास सम्भावना वाली सन्राइज इण्डस्ट्री (Sun Rise Industry) की स्थापना की गई। इस योजना काल में औद्योगिक विकास दर 8.5% वार्षिक रही।

8. आठवीं योजना में उद्योग (Industries in 8th Plan).- आठवीं योजना (1992-97) में उद्योगों पर कृषि से अधिक खर्च करने का कार्यक्रम बनाया गया। इस योजना में सार्वजनिक क्षेत्रों के उद्योगों के विकास के लिए 44.33 करोड़ रुपए खर्च किए गा ! इस निवेश का मुख्य लक्ष्य निजी उद्योगों की उत्पादन शक्ति में वृद्धि करना रखा गया।

9. नौवीं योजना में उद्योग (Industries in 9th Plan)-नौवीं योजना (1997-2002) में उदारीकरण की नीति को अपनाया गया है। नई औद्योगिक नीति के अनुसार उद्योगों में उत्पादन शक्ति को बढ़ाकर शेष विश्व की जस्तुओं से मुकाबला करने के योग्य बनाना है। इसके लिए सरकार ने सार्वजनिक क्षेत्र के स्थान पर निजी क्षेत्र को अधिक प्राथमिकता दी है। पूंजी बाज़ार को विशाल बनाया गया है। इस योजना में औद्योगिक विकास दर 5.5% रही।

10. दसवीं योजना में उद्योग (Industries in 10th Plan)-दसवीं पंचवर्षीय योजना 2002-07 में उदारीकरण व निजीकरण की नीति को अपनाया गया है। इस योजना काल में 8.2% वार्षिक विकास दर प्राप्त की गई है।

11. ग्यारहवीं योजना में उद्योग (Industries in 11th Plan)-ग्यारहवीं पंचवर्षीय योजना (2007-12) में औद्योगिक विकास का लक्ष्य 15% प्रति वर्ष रखा गया है। ग्यारहवीं योजना में औद्योगिक विकास पर 153600 करोड़ रुपए व्यय किया गया।

12. बारहवीं योजना में उद्योग (Industries in 12th Plan)-बारहवीं योजना (2012-17) में औद्योगिक विकास का लक्ष्य 9% रखा गया है। इस योजना काल में 292098 करोड़ रुपए व्यय किये जाएंगे।

प्रश्न 3.
भारत में घरेलू तथा लघु पैमाने के उद्योगों के महत्त्व की व्याख्या करें। (Explain the importance of cottage and small scale industries in India.)
उत्तर-
माईक्रो, लघु तथा मध्यम उद्योगों की परिभाषा (Definition of Micro, Small and Medium Industries)-भारत में माईक्रो, लघु तथा मध्यम उद्योगों के विकास एक्ट के अनुसार इन उद्योगों का वर्गीकरण इस प्रकार किया गया है-वित्त मन्त्री निर्मला सीतारमण ने 2 फरवरी 2020 को बजट में इन उद्योगों की परिभाषा बदल दी है-

निर्माण क्षेत्र (Manufacturing Sector)-

उद्यम श्रेणी	प्लांट तथा मशीनरी पर निवेश
माईक्रो उद्यम	₹ 1 करोड़ से अधिक निवेश नहीं होना चाहिए।
लघु उद्यम	₹10 करोड़ से अधिक परन्तु ₹ 50 करोड़ का उत्पादन नहीं होना चाहिए।
मध्यम उद्यम	₹ 10 करोड़ से अधिक परन्तु ₹ 50 करोड़ से अधिक निवेश नहीं होना चाहिए।

भारत में घरेलु तथा छोटे पैमाने के उद्योगों का महत्त्व बहुत अधिक है। यह उद्योग भारत के सकल घरेलू उत्पाद का 8% योगदान डालते हैं। इस उद्योगों द्वारा उत्पादन का 40% भाग निर्यात किया जाता है। भारत में इन उद्योगों की संख्या 26 मिलियन है जिसमें 60 मिलियन मज़दूरों को रोजगार दिया जाता है।

इन उद्योगों के महत्त्व को निम्नलिखित से ज्ञात किया जा सकता है –
1. रोज़गार (Employment)-घरेलू तथा छोटे पैमाने के उद्योग श्रम गहन होने के कारण रोज़गार में वृद्धि करते हैं। भारत में जनसंख्या बहुत अधिक है। इसलिए बेरोज़गारी की समस्या पाई जाती है। बेरोज़गारी को दूर करने के लिए घरेलू तथा छोटे पैमाने के उद्योग अधिक योगदान दे सकते हैं। लघु तथा मध्यम वर्ग के उद्योगों द्वारा 7.2 लाख लोगों को रोजगार प्रदान किया जाता है।

2. पूंजी की कम आवश्यकता (Need for Less Capital)-घरेलू तथा छोटे पैमाने के उद्योगों में पूंजी की कम आवश्यकता होती है। इसलिए भारत जैसे निर्धन देश में यह उद्योग विशेष महत्त्व रखते हैं।

3. विदेशी सहायता की आवश्यकता नहीं (No need of Foreign Help)-घरेलू तथा छोटे पैमाने के उद्योगों को स्थापित करने के लिए विदेशी मशीनों तथा आधुनिक तकनीकों की आवश्यकता नहीं होती। घरेलू तकनीक द्वारा ही उत्पादन में वृद्धि की जा सकती है।

4. कृषि पर जनसंख्या का कम बोझ (Less Pressure of Population on Agriculture)-भारत में कृषि पर 70% लोग निर्भर करते हैं। कृषि पर से जनसंख्या का बोझ हटाने के लिए घरेलू तथा छोटे पैमाने के उद्योगों का विकास आवश्यक है।

5. आय का समान विभाजन (Equal Distribution of Income)-भारत में आय का असमान विभाजन पाया जाता है। अमीर तथा निर्धन लोगों की आय में अन्तर बहुत अधिक है। आय के समान विभाजन के लिए भी घरेलू तथा छोटे पैमाने के उद्योगों का विकास आवश्यक है।

6. उद्योगों का विकेन्द्रीकरण (Decentralisation of Industries)-बड़े पैमाने के उद्योग एक स्थान पर केन्द्रित हो जाते हैं। उद्योगों में विकेन्द्रीकरण के लिए घरेलू तथा छोटे उद्योगों का विकास आवश्यक है।

7. बड़े पैमाने के उद्योगों के लिए सहायक (Helpful to Large Scale Industries)-छोटे पैमाने के उद्योगों में ऐसी वस्तुओं का उत्पादन किया जा सकता है जो कि बड़े पैमाने के उद्योगों के लिए सहायक हो सके जैसे कि साइकिल बनाने के उद्योगों के लिए छोटे पैमाने के उद्योगों द्वारा हैण्डल, स्टैण्ड, तारें इत्यादि नियमित किए जा सकते हैं।

8. कम औद्योगिक लड़ाई-झगड़े (Less Industrial Disputes)-बड़े पैमाने के उद्योगों से औद्योगिक लड़ाई-झगड़े आरम्भ हो जाते हैं परन्तु छोटे पैमाने पर उत्पादन करने से औद्योगिक झगड़ों की सम्भावना कम हो जाती है।

9. किसानों की आय में वृद्धि (Supplement to Farmer’s Income)-घरेलू उद्योग विशेषतया किसानों द्वारा आरम्भ किए जा सकते हैं। इससे किसानों की आय में वृद्धि हो सकती है।

प्रश्न 4.
भारत में स्वतन्त्रता के पश्चात् औद्योगिक नीति की आलोचना सहित व्याख्या करें। (Critically examines the Industrial Policy of India after Independence.)
अथवा
भारत में 1991 की औद्योगिक नीति की व्याख्या करें। (Explain the Industrial Policy of 1991 in India.)
अथवा
भारत की नई औद्योगिक नीति को स्पष्ट करें। (Explain the New Industrial Policy of India.)
उत्तर-
भारत की स्वतन्त्रता के पश्चात् औद्योगिक नीति का निर्माण किया गया। औद्योगिक नीति समय-समय पर परिवर्तित की गई है, जिसका विवरण इस प्रकार है-
1. औद्योगिक नीति 1948 (Industrial Policy of 1948)-भारत में स्वतन्त्रता के पश्चात् अर्थव्यवस्था (Mixed Economy) को अपनाया गया। इसमें औद्योगिक विकास के लिए सार्वजनिक क्षेत्र तथा निजी क्षेत्र के कार्य क्षेत्र निर्धारित किए गए। उद्योगों को चार क्षेत्रों में विभाजित करके स्पष्ट किया गया।

• सार्वजनिक क्षेत्र
• सरकारी तथा निजी क्षेत्र
• नियमित निजी क्षेत्र
• निजी तथा सहकारी क्षेत्र में बनाई गई।

2. इस नीति में-

• सार्वजनिक क्षेत्र में 17 उद्योगों का वर्णन किया गया।
• सरकारी तथा निजी क्षेत्र में साझे तौर पर चलाने के लिए 12 उद्योग रखे गए।
• निजी क्षेत्र में शेष उद्योगों को शामिल किया गया। घरेलू तथा छोटे पैमाने के उद्योगों की तरफ विशेष ध्यान दिया गया है।

इस औद्योगिक नीति में सार्वजनिक क्षेत्र को अधिक महत्त्व दिया गया तथा एकाधिकारी शक्तियों को नियन्त्रण में रखा गया।

3. औद्योगिक नीति 1997 (Industrial Policy of 1977)-1977 में जनता सरकार का राज्य स्थापित हुआ। इसलिए उन्होंने 1956 की औद्योगिक नीति में कुछ परिवर्तन किए परन्तु 1980 में कांग्रेस सरकार सत्ता में आई तो उन्होंने भी औद्योगिक नीति में परिवर्तन किए। नई औद्योगिक नीति 1991 (New Industrial Policy of 1991)–भारत सरकार ने 24 जुलाई, 1991 को नई औद्योगिक नीति की घोषणा की।

इस नीति की मुख्य विशेषताएं इस प्रकार हैं –

1. सरकारी क्षेत्र का संकुचन (Contraction of Public Sector)-नई नीति के अनुसार सरकारी क्षेत्र में सैन्य उपकरण, परमाणु, ऊर्जा, खनन तथा रेल यातायात के चार उद्योग रहेंगे जबकि शेष उद्योग निजी क्षेत्र के लिए आरक्षित किए गए।
2. लाइसेंस की समाप्ति (Delicensing)-नई औद्योगिक नीति में 18 उद्योग रखे गए जिनके लिए लाइसेंस लेने की आवश्यकता है जैसे कि कोयला, पेट्रोलियम, शराब, चीनी, मोटर, कारें, दवाइयां इत्यादि। इनके अतिरिक्त अन्य उद्योगों में लाइसेंस लेने की आवश्यकता नहीं है।
3. विदेशी पूंजी (Foreign Capital)-नई नीति के अनुसार विदेशी पूंजी निवेश की सीमा 40% से बढ़ा कर 51% की गई है।
4. बोर्डों का संगठन (Organisation of Boards)-नई नीति के अनुसार विदेशी पूंजी को उत्साहित करने के लिए विशेष बोर्डों का गठन किया जाएगा।
5. तकनीकी माहिर (Technical Experts)-नई नीति में तकनीकी माहिरों की सहायता लेकर औद्योगिक विकास किया जाएगा।
6. सरकारी निर्णय (Government Decision)-सरकार ने भारतीय औद्योगिक अर्थव्यवस्था को अफसरशाही नियन्त्रण के चंगुल से बाहर निकालने का फैसला किया विशेषतया सुरक्षा के क्षेत्र तथा अन्य आवश्यक क्षेत्र सार्वजनिक क्षेत्र में आरक्षित रखे जाएंगे जबकि अन्य क्षेत्रों में निजी पूंजीपतियों को निवेश करने की छूट दी जाएगी। भारत में सार्वजनिक क्षेत्र में लगातार हो रही हानि को ध्यान में रख कर नई औद्योगिक नीति उदारवादी नीति बनाई गई है। बारहवीं योजना में विकास दर 89% प्राप्त करने का लक्ष्य है।

नई नीति का मूल्यांकन (Evaluation of New Industrial Policy)गुण (Merits)-

1. नई नीति से उद्योगों की कुशलता में वृद्धि होगी।
2. देश में विदेशी तकनीकों के प्रयोग के कारण उत्पादन में वृद्धि होगी।
3. यह नीति उदारवादी नीति है जिसमें निजी क्षेत्र को प्राथमिकता दी गई है।
4. भारतीय उद्योगों को विदेशी उद्योगों से प्रतियोगिता करने के समर्थ बनाने का यत्न किया गया है।
5. घरेलू तथा छोटे उद्योगों को अधिक महत्त्व प्रदान किया गया है तथा मजदूरों के कल्याण के लिए कार्यक्रम बनाए गए हैं।

त्रुटियां (Shortcomings)-

• इससे सार्वजनिक क्षेत्र का महत्त्व कम हो गया है।
• सरकारी कर्मचारियों की निरन्तर छंटनी हो रही है।
• आर्थिक शक्ति कुछ हाथों में केन्द्रित हो जायेगी तथा एकाधिकारी शक्तियों का निर्माण होगा।
• विदेशी पूंजी से आर्थिक गुलामी की स्थिति उत्पन्न होगी।
• इस नीति से सामाजिक उद्देश्यों की पूर्ति नहीं की जा सकती तथा पिछड़े क्षेत्रों का विकास नहीं होगा।

प्रश्न 5.
भारत में औद्योगीकरण की मुख्य समस्याओं का वर्णन करें। उद्योगों के विकास के लिए सुझाव दें।
(Explain the main problems of Industrialization in India. Suggest measures for the Industrial development.)
उत्तर –
भारत में औद्योगिक विकास सन्तोषजनक नहीं हुआ। आज भी कृषि क्षेत्र का योगदान राष्ट्रीय आय में अधिक है। औद्योगिक विकास न होने के मुख्य कारण इस क्षेत्र की कुछ समस्याएं हैं जो कि इस प्रकार हैं-

कम प्राप्तियां (Less Achievements)-
भारत की भिन्न-भिन्न योजनाओं में विकास दर के लक्ष्य हमेशा अधिक रखे गए हैं। प्रत्येक योजना में 8% विकास दर प्राप्त करने का लक्ष्य रखा गया परन्तु वास्तव में 5.6% विकास दर प्राप्त की गई है। इसलिए निर्धारित लक्ष्यों तथा प्राप्तियों में बहुत अन्तर पाया जाता है।

1. बीमार उद्योग (Industrial Sickness)-भारत के रिज़र्व बैंक ने व्यापारिक बैंकों से जो सूचना प्राप्त की है उसके अनुसार 31 मार्च, 2019 तक 2,40,000 बीमार औद्योगिक इकाइयां थीं। 2019 में छोटे पैमाने के उद्योगों की बीमार इकाइयों की संख्या 1,13,178 थी। इस प्रकार बीमार इकाइयों की संख्या में वृद्धि होने के कारण औद्योगिक विकास नहीं हो रहा है।
2. बड़े घरानों का विकास (Growth of Big Houses)-भारत में टाटा, बिरला, डाल्मिया, श्री राम, मफतलाल जैसे बड़े घरानों के पास सम्पत्ति निरन्तर बढ़ रही है। इस प्रकार देश की आर्थिक शक्ति थोड़े से हाथों में केन्द्रित हो रही है।
3. विलास वस्तुओं का उत्पादन (Production of Luxury things)-भारत में औद्योगिक वस्तुओं के उत्पादन में अमीर लोगों द्वारा उपभोग की जाने वाली वस्तुओं का अधिक उत्पादन किया जाता है जबकि साधारण लोगों द्वारा प्रयोग की जाने वाली वस्तुओं में उत्पादन की तरफ ध्यान नहीं दिया गया।
4. क्षेत्रीय असन्तुलन (Regional Imbalance)-भारत में उद्योग थोड़े से राज्यों में केन्द्रित हो गए हैं जैसे कि महाराष्ट्र, गुजरात, तमिलनाडु राज्य औद्योगिक पक्ष से विकसित हैं जबकि बिहार, उड़ीसा, राजस्थान तथा मध्य प्रदेश औद्योगिक पक्ष से पिछड़े हुए राज्य हैं।
5. कम सुविधाएं (Less Facilities)-भारत के उद्योगों को बहुत-सी कठिनाइयों का सामना करना पड़ता है जैसे कि विदेशी प्रतियोगिता, विद्युत्, प्राकृतिक साधनों की कमी, प्रशिक्षण के माहिरों की कमी जिसके कारण औद्योगिक क्षेत्रों की उत्पादकता बहुत कम है। परिणामस्वरूप उद्योगों द्वारा लक्ष्यों की प्राप्ति नहीं की जा सकती।

औद्योगिक (Suggestion for Industrial Growth) –

• आधुनिकीकरण (Modernisation)-भारत में उद्योगों के आधुनिकीकरण की आवश्यकता है। इस लक्ष्य के लिए नई मशीनों तथा औज़ारों का निर्माण करना चाहिए ताकि उद्योगों में उत्पादन लागत कम हो सके।
• मूलभूत सुविधाएं (Basic Facilities) उद्योगों के विकास के लिए मूलभूत सुविधाएं जैसे कि कच्चा माल, साख सहूलियतें, करों में राहत तथा लघु उद्योगों को सुरक्षा प्रदान करनी चाहिए। इसके अतिरिक्त शक्ति, कोयला, यातायात के साधन, सड़कें, रेलों का विकास करने की आवश्यकता है।
• सरकारी सहायता (Government Assistance) सरकार को औद्योगिक विकास के लिए अनुकूल वातावरण निर्मित करना चाहिए। बीमार इकाइयों के सम्बन्ध में उचित नीति अपनानी चाहिए। उत्पादन करने की विधियों में परिवर्तन करके मांग में वृद्धि करनी चाहिए।
• वस्तुओं का मानकीकरण (Standardisation of Products)-भारत में वस्तुओं के मानकीकरण की आवश्यकता है ताकि विश्व स्तर पर वस्तुओं को प्रतियोगिता करने के योग्य बनाया जा सके। इसके लिए सरकार को नई मण्डियों की खोज करनी चाहिए। वस्तुओं का प्रचार करके मांग में वृद्धि करने की आवश्यकता है।
• औद्योगिक केन्द्र (Industrial Centres)-देश में कच्चे माल, विद्युत्, जल, मज़दूरों इत्यादि साधनों को ध्यान में रख कर औद्योगिक केन्द्र स्थापित करने चाहिए, विशेषतया कृषि उद्योगों को गांवों में स्थापित करने की आवश्यकता है। इस प्रकार सरकार को भिन्न-भिन्न प्रकार की सूचना प्रदान करके उद्योगों के विकास की तरफ ध्यान देना चाहिए।

प्रश्न 6.
औद्योगिक लाइसेंसिंग नीति से क्या अभिप्राय है ? भारत में लाइसेंस नीति के उद्देश्य तथा कार्य कुशलता का मूल्यांकन करें।
(What is meant by Industrial Licensing Policy? Discuss the objectives of this Policy. Evaluate the working of this Policy.)
उत्तर-
औद्योगिक लाइसेंसिंग नीति (Industrial Lincensing Policy) स्वतन्त्रता के बाद भारत सरकार ने सन् 1951 में एक एक्ट ‘औद्योगिक विकास एवं नियमन’ पास किया जिसके अनुसार प्रत्येक उद्योग को सरकार से अनुमति लेकर ही औद्योगिक उत्पादन करने का हक होता था। बिना सरकार की अनुमति और बिना लाइसेंस कोई भी व्यक्ति उद्योग स्थापित नहीं कर सकता था।

औद्योगिक कहां स्थापित किया जाए, कौन-सी वस्तु का उत्पादन किया जाए- और उस वस्तु का कितनी मात्रा में उत्पादन किया जाए, इन बातों के लिए लाइसेंस लेना ज़रूरी था। सरकार की इस नीति को औद्योगिक लाइसेंसिंग नीति कहा जाता है। औद्योगिक लाइसेंसिंग नीति के उद्देश्य (Objectives of Industrial Lincensing Policy)-औद्योगिक लाइसेंसिंग नीति के मुख्य उद्देश्य इस प्रकार हैं-

1. निवेश तथा उत्पादन पर नियन्त्रण-औद्योगिक नीति का उद्देश्य भारत में निवेश तथा उत्पादन पर नियन्त्रण रखना था। इस प्रकार विभिन्न योजनाओं में औद्योगिक विकास के लक्ष्यों की पूर्ति सम्भव है।
2. लघु उद्योगों का विकास-बड़े पैमाने के उद्योगों के विकास से लघु उद्योगों के विकास पर बुरा प्रभाव पड़ता है। लाइसेंसिंग नीति द्वारा सरकार उन उद्योगों को अनुमति नहीं देती थी जिनके विकास से लघु उद्योगों पर बुरा प्रभाव पड़े।
3. क्षेत्रीय सन्तुलन-भारत में सभी उद्योग एक स्थान पर केन्द्रित न हो जाए और देश के हर क्षेत्र का विकास हो इस लक्ष्य की पूर्ति के लिए भी लाइसेंसिंग नीति अनिवार्य भी है।
4. तकनीकी सुधार-औद्योगिक नीति का उद्देश्य तकनीकी सुधारों को बढ़ावा देना भी है।
5. विकेन्द्रीयकरण-उद्योगों के विकेन्द्रीयकरण के लिए भी लाइसेंसिंग नीति ज़रूरी थी। इस नीति का एक उद्देश्य उद्योगों का सन्तुलित विकास करना भी है। इसलिए नई औद्योगिक इकाइयां लाभ के लिए, वर्तमान में चल रही औद्योगिक ईकाइयों का पंजीकरण अनिवार्य है। नए उत्पादन बनाने के लिए और उत्पादन का विस्तार करने के लिए भी लाइसेंस लेना अनिवार्य है। यदि उद्यमी औद्योगिक इकाई के स्थान में परिवर्तन करता है तो इस के लिए भी सरकार की अनुमति अनिवार्य है।

लाइसेंसिंग नीति का मूल्यांकन (Evaluation of the Licensing Policy)-भारत में औद्योगिक नीति इस प्रकार रही है-
1. अनिवार्य लाइसेंसिंग-भारत में 1951 की नीति के अनुसार उन उद्योगों के लिए लाइसेंस लेना आवश्यक था जिनकी स्थाई पूंजी 10 लाख रुपए थी। इस सीमा में समय-समय पर परिवर्तन किया गया है। यह सीमा 1970 में एक करोड़, 1990 में 25 करोड़ कर दी गई। 1991 की नई औद्योगिक नीति में सुरक्षा से सम्बन्धित 14 उद्योगों को छोड़कर किसी उद्योग को लाइसेंस लेने की आवश्यकता नहीं है। 1999 में से 6 उद्योग हैं जिनके लिए लाइसेंस लेना अनिवार्य है। यह उद्योग है, तम्बाकू उत्पादन, सुरक्षा उपकरण, औद्योगिक विस्फोटक, दवाइयां, खतरनाक रसायन और एरोस्पेस । सरकार की इस नई औद्योगिक नीति को उदारवादी नीति कहा जाता है।

2. एकाधिकार एवं प्रतिबन्धात्मक व्यापार व्यवहार अधिनियम (M.R.T.P. Act)–भारत सरकार ने एकाधिकार पर नियन्त्रण पाने के लिए एकाधिकार एवं प्रतिबन्धात्मक व्यापार व्यवहार अधिनियम बनाया था जिसको 1969 में लागू किया गया। बड़े औद्योगिक गृहों पर नियन्त्रण पाने के लिए इस नियम को लागू किया गया ताकि बड़े घरानों पर प्रतिबन्ध लगाया जा सके। इस नियम को 2002 में समाप्त कर दिया गया है।

3. लघु उद्योगों को संरक्षण-लघु उद्योगों के लिए सरकार ने कई वस्तुओं के उत्पादन को सुरक्षित कर दिया है जिनका उत्पादन बड़े पैमाने के उद्योगों में नहीं किया जा सकता। 2016-17 में लघु उद्योगों के लिए 598 वस्तुएं सुरक्षित की गई हैं।

4. सार्वजनिक क्षेत्र के लिए संरक्षण-सार्वजनिक क्षेत्र को भारत में पहले अधिक महत्त्व दिया जाता था। अब सार्वजनिक क्षेत्र के स्थान पर निजी क्षेत्र को अधिक महत्त्व दिया जाता है। स्वतन्त्रता के पश्चात् सार्वजनिक क्षेत्र के लिए 17 उद्योग सुरक्षित रखे गए थे। इन उद्योगों की संख्या 1991 में कम करके 8 की गई तथा 2004-05 में केवल 3 उद्योग ही सार्वजनिक क्षेत्र के लिए सुरक्षित है। 31 मार्च, 2016 तक कुल 62 औद्योगिक इकाइयां काम कर रही थीं, जिनमें 5,28,951 करोड़ रुपए का निवेश किया गया था।

सरकार द्वारा सार्वजनिक उद्योगों के अध्ययन के लिए एक बोर्ड की स्थापना की गई। इस बोर्ड द्वारा अक्तूबर 2015 को 62 उद्योगों के पुनर्गठन की सिफ़ारिश की। बोर्ड ने 43 उद्योगों के पुनर्निर्माण (Revival) की मन्जूरी दी और 2 उद्योगों को बन्द करवा दिया। पुनर्निर्माण उद्योगों को 25104 करोड रुपए की सहायता दी। फलस्वरूप 13 उद्योगों द्वारा अधिक उत्पादन करके लाभ प्राप्त किया। भारत में लाइसेंसिंग नीति 1951 में लागू की गई इस नीति में सुधार के लिए समय-समय पर समितियों की स्थापना की गई। 1967 में हजारी समिति तथा 1969 में दत्त समिति में लाइसेंसिंग नीति में सुधार करने के लिए सुझाव दिये। इसके बाद औद्योगिक लाइसेंसिंग में 1991 तक बहुत तबदीली की गई। इन परिवर्तनों का मुख्य उद्देश्य लाइसेंसिंग नीति को सरल बनाना था।

इस प्रकार लाइसेंसिंग नीति में आए परिवर्तन के कारण अब यह नीति उदारवादी नीति में तबदील हो चुकी है। इस कारण देश में उद्योगों के विकास को बढ़ावा मिला है। नई सरकार ने ‘Make in India’ की नीति अपनाई है जिसमें नई क्रियाएं, नया आर्थिक ढांचा, नई मानसिक सोच तथा नए क्षेत्रों के विकास पर बल दिया गया है। वर्ष 2022 तक औद्योगिक क्षेत्र में 25% वृद्धि का लक्ष्य रखा गया है। अब सरकार सार्वजनिक उद्यमों में विनिवेश की नीति अपना रही है।