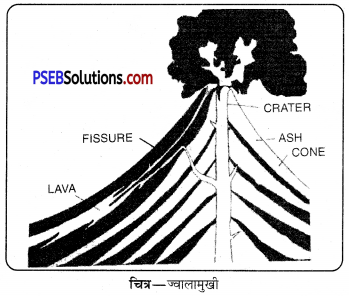
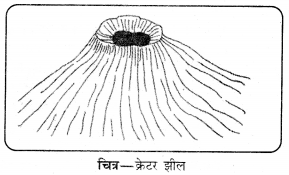
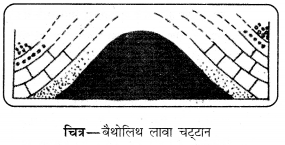
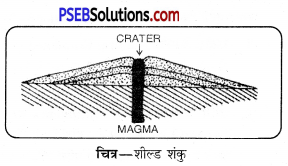
Punjab State Board PSEB 11th Class History Book Solutions Chapter 12 मुग़ल साम्राज्य की स्थापना Textbook Exercise Questions and Answers.
PSEB Solutions for Class 11 History Chapter 12 मुग़ल साम्राज्य की स्थापना
अध्याय का विस्तृत अध्ययन
(विषय सामग्री की पूर्ण जानकारी के लिए)
प्रश्न 1.
पानीपत के पहले दो युद्धों के बीच की राजनीतिक घटनाओं की रूप रेखा बताएं।
उत्तर-
पानीपत का प्रथम युद्ध 1526 ई० तथा दूसरा युद्ध 1556 ई० में हुआ। इन दो युद्धों के मध्य राजनीतिक घटनाएं चार व्यक्तियों के गिर्द घूमती हैं। ये व्यक्ति हैं-बाबर, हुमायूं, शेरशाह एवं उसके उत्तराधिकारी तथा अकबर। इन व्यक्तियों ने अपने-अपने ढंग से राजनीतिक घटनाओं को प्रभावित किया। संक्षेप में इनका वर्णन इस प्रकार है :
I. बाबर के अधीन राजनीतिक घटनाएं-
पानीपत की विजय (1526 ई०) द्वारा बहुत बड़ा प्रदेश बाबर के अधिकार में आ गया। बाबर ने दिल्ली के सिंहासन को काबुल के सिंहासन की अपेक्षा अधिक महत्त्व दिया और हिन्दुस्तान में ही रहने का निर्णय किया।
(i) राणा सांगा के साथ संघर्ष-बाबर के भारत में रहने के निर्णय के कारण उसका मेवाड़ के राणा संग्राम सिंह से संघर्ष होना अवश्यम्भावी था। राणा सांगा के अधीन मेवाड़ राजस्थान का सबसे शक्तिशाली राज्य बन गया था। जब बाबर ने सुल्तान इब्राहीम लोधी के इलाके से अफ़गानों को निकालना आरम्भ किया, तो उनमें से कुछ ने राणा सांगा से सहायता मांगी। राणा सांगा तो पहले ही उत्तरी भारत पर बाबर के अधिकार को अपनी महत्त्वाकांक्षाओं के लिए रोड़ा समझता था। बाबर के विरुद्ध राणा सांगा के साथ गठजोड़ करने वाले महत्त्वपूर्ण अफ़गानों में सुल्तान इब्राहीम लोधी का भाई महमूद लोधी और मेवात का शासक हसन खां थे। मार्च 1527 ई० में राणा सांगा ने आगरा की ओर कूच किया। बाबर की सेना से उसका सामना फतेहपुर सीकरी के निकट खनुआ के स्थान पर हुआ। दस घण्टों के घमासान युद्ध में बाबर को निर्णायक विजय प्राप्त हुई। इस युद्ध में बाबर ने उन्हीं युद्ध-चालों का प्रयोग किया जो उसने पानीपत के युद्ध में अपनाई थीं। खनुआ ने युद्ध से मेवाड़ की शक्ति और सम्मान को गहरा आघात पहुंचा और बाबर के लिए भारत विजय के द्वार खुल गए।
(ii) बाबर के अन्य सैनिक अभियान और मृत्यु-एक-एक कर बाबर ने अपने विरोधी अफ़गानों को समाप्त करना शुरू कर दिया। खनुआ की लड़ाई के शीघ्र ही बाद उसने हसन खां मेवाती की राजधानी अलवर पर अधिकार कर लिया। बाबर ने महमूद लोधी को बिहार से खदेड़ दिया। महमूद लोधी ने बंगाल के शासक नुरसत शाह की शरण ली। अफ़गानों ने महमूद लोधी के नेतृत्व में मई, 1529 ई० में बाबर के विरुद्ध घाघरा-गंगा संगम के निकट युद्ध किया। उस युद्ध में बाबर को ही विजय मिली। नुसरत शाह ने बाबर को दिल्ली का बादशाह स्वीकार कर लिया। उसने यह भी मान लिया कि वह अफ़गानों को शरण नहीं देगा। इस प्रकार लोधियों का सारा प्रदेश अब बाबर के अधिकार में आ गया। दिसम्बर, 1530 ई० में उसकी मृत्यु हो गई और उसका पुत्र हुमायूं राजगद्दी पर बैठ गया।
II. हुमायूं के अधीन राजनीतिक घटनाएं-
(i) राज्य का विभाजन-हुमायूं ने अपने पिता से मिले राज्य को अपने भाइयों में बांट दिया। उसने कामरान को काबुल और पंजाब का प्रदेश और अस्करी तथा हिन्दाल को क्रमशः सम्भल और मेवात के प्रदेश दिए।
(ii) आरम्भिक विजयें तथा विद्रोह-इसके उपरान्त हुमायूं ने कालिंजर के शासक पर आक्रमण किया और उसे नज़राना देने के लिए विवश किया। 1532 ई० में उसने जौनपुर की ओर बढ़ते हुए महमूद लोधी को पराजित किया। तत्पश्चात् उसने 1534 ई० में अपने रिश्तेदार मिर्जा मुहम्मद ज़मां और मुहम्मद सुल्तान के विद्रोह को कुचला।
(iii) मालवा और गुजरात पर अस्थायी अधिकार-हुमायूं ने अब अपना ध्यान गुजरात की ओर लगाया। उसके विरोधी अफ़गानों तथा मिर्जा मुहम्मद जमां को शरण देकर बहादुरशाह भी अब हुमायूं का शत्रु बन गया था। उसने मालवा को 1531 ई० में विजय करके अपनी शक्ति को और अधिक बढ़ा लिया था। उसने अगले दो वर्षों में राजस्थान के कई किलों पर अधिकार जमा लिया। हुमायूं ने शीघ्र बहादुरशाह के विरुद्ध कूच किया। बहादुरशाह को अपना राज्य छोड़ना पड़ा। हुमायूं ने अपने भाई अस्करी को गुजरात का सूबेदार नियुक्त किया। फरवरी 1532 ई० में हुमायूं मालवा लौटा। शीघ्र ही बहादुरशाह ने चम्पानेर और अहमदाबाद सहित गुजरात पर पुनः अधिकार कर लिया।
(iv) हुमायूं का भारत से निष्कासन-गुजरात से वापसी पर हुमायूं ने पूर्व में शेरशाह की ओर ध्यान दिया। अक्तूबर 1532 ई० में हुमायूं ने चुनार के किले को घेर लिया जो शेरखां के पुत्र कुतुब खां के अधिकार में था। यह मज़बूत किला बंगाल की ओर जाने वाले रास्ते पर था। इस पर अधिकार करने में छः माह लग गए । किला हुमायूं के अधिकार में आने के एक महीने बाद ही शेरखां ने बंगाल की राजधानी गौड़ पर अधिकार कर लिया। हुमायूं अब उसके विरुद्ध चल पड़ा। शेरखां ने स्थिति को समझते हुए हुमायूं से लड़ाई न की । हुमायूं ने आसानी से बंगाल पर अधिकार कर लिया किन्तु शेरखां ने बिहार पर आक्रमण करके हुमायूं की वापसी के रास्ते को रोक लिया। बंगाल से वापस लौटते समय शेरखां ने उसे पहले चौसा के स्थान पर तथा फिर कन्नौज के स्थान पर पराजित किया। अन्त में हुमायूं भारत छोड़कर भाग गया।
III. शेरशाह और उसके उत्तराधिकारियों की समकालीन राजनीतिक घटनाएं –
(i) शेरशाह द्वारा राज्य का विस्तार-शेरशाह ने कामरान को पंजाब से निकाल कर सिन्धु नदी तक के इलाके को अपने अधीन कर लिया। 1542 ई० में उसने मालवा को जीता। अगले वर्ष उसने मध्य भारत में स्थित रायसीन की चौहान रियासत को नष्ट कर दिया। 1543 में उसने मारवाड़ के मालदेव को पराजित किया। शेरशाह ने मेवाड़ तथा रणथम्भौर पर भी अधिकार कर लिया। उसने राजस्थान के अन्य इलाकों पर भी विजय प्राप्त की। इस प्रकार सारे राजस्थान पर शेरशाह का प्रभुत्व स्थापित हो गया। 1544 ई० के अन्तिम चरण में उसने कालिन्जर को घेर लिया तथा 22 मई, 1545 को उसने कालिन्जर को जीत लिया। उसी दिन धावा बोलते समय बारूद में आग लगने से उसकी मृत्यु हो गई। जब शेरशाह की मृत्यु हुई तब गुजरात को छोड़ कर लगभग सारा उत्तरी भारत उसके अधीन था।
(ii) शेरशाह के उत्ताधिकारियों की समकालीन राजनीतिक घटनाएं-शेरशाह की मृत्यु के बाद उसके छोटे पुत्र जलालखां ने इस्लामशाह की उपाधि धारण कर लगभग आठ वर्षों अर्थात् 1553 ई० तक शासन किया। उसने पूर्वी बंगाल को अपने राज्य में मिला लिया।
इस्लामशाह की मृत्यु (30 अक्तूबर, 1553) के बाद उसका बारह वर्षीय पुत्र फिरोज़ उत्तराधिकारी बना। किन्तु गद्दी पर बैठने के तीन दिन बाद ही उसके मामा मुबारिज़ खां ने उसका वध कर दिया। मुबारिज़ खां मुहम्मद आदिलशाह के नाम पर सिंहासन पर बैठा। उसे अफ़गान लोग अन्धा कहते थे। उसने पुराने अमीरों के विश्वास को जीतने का असफल प्रयत्न किया। किसी पठान की जगह आदिलशाह ने हेम को अपना वज़ीर बनाया जिससे अफ़गान अमीरों का रोष और भी बढ़ गया और वे स्वतन्त्र होने के बारे में सोचने लगे। शीघ्र ही शेरशाह द्वारा स्थापित राज्य पांच भागों में बंट गया।
(iii) हुमायूं का पुनः शक्ति में आना-हुमायूं ने स्थिति का लाभ उठाया। वह ईरान के शासक से सैनिक सहायता लेकर काबुल तक पहुंच चुका था। उसने 1554 के अन्त में पंजाब पर आक्रमण करने का निश्चय किया और छः महीनों के भीतर ही उसे हथिया लिया। सिकन्दरशाह सूर की सरहिन्द के निकट जून 1555 में पराजय हुई। हुमायूं ने दिल्ली पर और बाद में आगरा पर अधिकार कर लिया। किन्तु सात मास के पश्चात् हुमायूं की मृत्यु हो गई।
IV. अकबर के अधीन राजनीतिक घटनाएं हुमायूं की मृत्यु के समय अकबर की आयु 13 वर्ष थी। उसके संरक्षक बैरम खां ने उसका कलानौर में राजतिलक किया। उसके बाद वह दिल्ली की ओर चल दिया।
हुमायूं की मृत्यु के शीघ्र ही बाद हेमू ने आदिलशाह की ओर से आगरा पर अधिकार कर लिया और दिल्ली की तरफ चल पड़ा। मुग़ल सेनापति तारदी बेग पराजित हुआ। वह पंजाब की ओर भाग गया। बैरम खां ने तारदी बेग की पराजय के कारण उसका वध करवा दिया। उसके बाद अकबर ने पानीपत के युद्ध में नवम्बर 1556 ई० में हेमू को पराजित किया।
इस तरह पानीपत के प्रथम युद्ध की भान्ति पानीपत के दूसरे युद्ध ने भी मुग़लों के ही भाग्य को चमकाया। बाबर की विजय अस्थायी रही, परन्तु अकबर ने मुग़ल साम्राज्य की नींव को सुदृढ़ किया और एक विशाल राज्य की स्थापना की।

प्रश्न 2.
अकबर तथा उसके उत्तराधिकारियों के अधीन दक्कन में मुग़ल साम्राज्य के विस्तार से सम्बन्धित मुख्य घटनाएं क्या थी ?
उत्तर-
दक्कन का प्रदेश नर्मदा के पार स्थित था। अकबर से पूर्व किसी भी मुसलमान शासक ने दक्कन के किसी प्रदेश को अपने राज्य का भाग नहीं बनाया। अकबर पहला बादशाह था जिसके राज्य के तीन प्रान्त दक्षिण से सम्बन्धित थे। अकबर के बाद उसके उत्तराधिकारियों ने दक्कन में पूरी रुचि दिखाई। औरंगजेब ने तो अपना आधा शासनकाल दक्कन में ही व्यतीत कर दिया और उसकी मृत्यु भी वहीं हुई। संक्षेप में अकबर तथा उसके उत्तराधिकारियों की दक्कन में विस्तारवादी-नीति का वर्णन इस प्रकार है :
I. अकबर के अधीन दक्कन नीति 1591 ई० में अकबर ने अपने प्रतिनिधियों अर्थात वकीलों को दक्षिणी राज्यों (खानदेश, अहमदनगर, बीजापुर और गोलकुण्डा) भेजा ताकि उनके शासक उसके प्रभुत्व को स्वीकार कर लें। इनमें सबसे कम शक्तिशाली तथा उत्तरी भारत के सबसे निकट खानदेश का शासक राजा अली खां था। उसने तुरन्त अकबर के प्रभुत्व को स्वीकार कर लिया और आजीवन स्वामिभक्त रहा। परन्तु उसके पुत्र एवं उत्तराधिकारी मीरा बहादुरशाह ने मुग़लों की अधीनता को त्यागने का निश्चय किया। अकबर ने तुरन्त खानदेश की राजधानी बुरहानपुर को अपने अधिकार में ले लिया। उसने राज्य के महत्त्वपूर्ण किले आसीरगढ़ पर भी अधिकार कर लिया। इस प्रकार खानदेश 1601 ई० में मुग़ल साम्राज्य का एक प्रान्त बन गया। अहमदनगर, बीजापुर और गोलकुण्डा के सुल्तानों ने अकबर के वकीलों का परामर्श मानने से इन्कार कर दिया। परिणामस्वरूप कई सैनिक अभियान अहमदनगर के विरुद्ध भेजे गए। आखिर 1599 ई० में दौलताबाद पर अधिकार कर लिया गया। अहमदनगर सल्तनत की राजधानी अहमदनगर पर भी 1600 ई० में मुग़लों का अधिकार हो गया। अकबर ने अहमदनगर राज्य को समाप्त नहीं किया बल्कि उसने वहां के प्रदेशों का एक अलग प्रान्त बना दिया। अकबर की मृत्यु से पूर्व दक्कन अर्थात् विंध्य पर्वत और कृष्णा नदी के बीच के प्रदेश में तीन अधीनस्थ रियासतें बन चुकी थीं-खानदेश, बरार और अहमदनगर। इस तरह मुग़ल अपने साम्राज्य को नर्मदा के उस पार तक ले जाने में सफल हुए।
II. जहांगीर की दक्कन नीति-
जहांगीर ने दक्कन में प्रथम अभियान 1608 ई० में भेजा था। किन्तु उसे 1617 ई० में सफलता प्राप्त हुई जब शाहज़ादा खुर्रम ने अहमदनगर के सुल्तान को सन्धि करने के लिए बाध्य किया। सन्धि की शर्त यह थी कि सुल्तान विजित प्रदेश मुग़लों को सौंप दे। चार वर्षों के पश्चात् खुर्रम ने न केवल अहमदनगर के सुल्तान को अपितु बीजापुर और गोलकुण्डा के सुल्तानों को भी खिराज देने के लिए विवश कर दिया। उन्होंने क्रमशः बारह, अठारह और बीस लाख रुपए वार्षिक खिराज देना स्वीकार कर लिया। यह दक्कन में जहांगीर की सफलता का उत्कर्ष था। परन्तु 1627 ई० में उसकी मृत्यु के समय दक्कन में मुग़ल स्थिति बहुत अच्छी नहीं थी।
III. शाहजहां की दक्कन नीति –
(i) गोलकुण्डा के साथ शाहजहां की सन्धि-1636 ई० में शाहजहां ने गोलकुण्डा के सुल्तान को अपनी प्रभुसत्ता स्वीकार करने के लिए बाध्य कर दिया। सुल्तान को यह शर्त भी माननी पड़ी कि गोलकुण्डा के सिक्कों पर तथा खुतबे में शाहजहां के नाम के अतिरिक्त पहले चारों खलीफों के नाम भी हों। यह शर्त शाहजहां ने इसलिए रखी थी क्योंकि गोलकुण्डा का सुल्तान शिया होने के नाते केवल मुहम्मद साहिब के दामाद हज़रत अली को खलीफा मानता था। उसने 16 वर्षों के बकाया 128 लाख रुपया देना तो स्वीकार कर ही लिया, साथ में आठ लाख रुपए वार्षिक खिराज देना भी स्वीकार कर लिया। इसके बदले में मुग़ल सम्राट को गोलकुण्डा के सुल्तान की बीजापुर और मराठों से रक्षा करनी थी
(ii) बीजापुर के साथ शाहजहां की सन्धि-इसी समय मुग़ल सेना ने बीजापुर पर आक्रमण किया। बीजापुर का सुल्तान समझौते के लिए राजी हो गया। उसने मुग़ल सम्राट् की प्रभुसत्ता को स्वीकार कर लिया। उसने यह भी स्वीकार कर लिया कि वह गोलकुण्डा पर आक्रमण नहीं करेगा। उसने शाहजहां को 20 लाख रुपया देना और उसकी मध्यस्थता को भी स्वीकार कर लिया। बदले में मुग़ल सम्राट ने बीजापुर के जीते हुए कुछ प्रदेश उसे लौटा दिए। साथ में उसे अहमदनगर राज्य के कुछ नये प्रदेश भी दिए गए। इसके बाद बीस वर्षों तक मुग़ल बादशाह को बीजापुर तथा गोलकुण्डा के विरुद्ध अभियान नहीं भेजना पड़ा।
(iii) गोलकुण्डा तथा बीजापुर पर आक्रमण-1636 ई० को सन्धियों के पश्चात् गोलकुण्डा और बीजापुर के सुल्तानों ने अपनी-अपनी शक्ति और प्रदेश में वृद्धि कर ली। उन्होंने विजयनगर राज्य के प्रदेशों को हड़प कर अपने राज्य का विस्तार किया। शाहजहां ने दक्कन के तत्कालीन गवर्नर औरंगजेब को आज्ञा दी कि वह गोलकुण्डा और बीजापुर से बकाया खिराज वसूल करे। अत: औरंगज़ेब ने फरवरी 1656 ई० में गोलकुण्डा के किले को घेर लिया। औरंगजेब के डर से गोलकुण्डा का सुल्तान शाहजहां को पहले ही अपने एलची भेज चुका था। जब औरंगजेब की जीत होने वाली थी उसी समय उसे बादशाह की आज्ञा मिली कि वह गोलकुण्डा का घेरा उठा ले और वापस आ जाए। बादशाह ने गोलकुण्डा से स्वयं खिराज वसूल किया।
1656 ई० के बाद शाहजहां ने औरंगजेब को बीजापुर को विजय करने की आज्ञा दी। औरंगज़ेब ने तुरन्त ही बीदर और कल्याणी पर अधिकार कर लिया और बीजापुर पर आक्रमण कर दिया। 1657 ई० में बीजापुर के सुल्तान ने डेढ़ करोड़ रुपए देना और मांगे सभी प्रदेशों को वापस करना स्वीकार कर लिया। परन्तु तभी औरंगजेब को युद्ध बन्द कर देने और पीछे हटने का आदेश मिला। औरंगज़ेब निराश होकर 1658 ई० के आरम्भ में औरंगाबाद लौट आया। .
IV. औरंगजेब की दक्कन नीति-
औरंगज़ेब एक महत्त्वाकांक्षी सम्राट् था और वह सारे भारत पर मुग़ल पताका फहराना चाहता था। इसके अतिरिक्त उसे दक्षिण में शिया रियासतों का अस्तित्व भी पसन्द नहीं था। दक्षिण के मराठे भी काफ़ी शक्तिशाली होते जा रहे थे। वह उनकी शक्ति को कुचल देना चाहता था। इस उद्देश्य से उसने दक्षिण को विजय करने का निश्चय किया। उसने बीजापुर राज्य पर कई आक्रमण किए। कुछ असफल अभियानों के बाद 1686 ई० में वह इस पर विजय प्राप्त करने में सफल रहा। अगले ही वर्ष उसने रिश्वत और धोखेबाजी से बीजापुर राज्य को भी अपने अधीन कर लिया। परन्तु इन दो राज्यों की विजय उसकी निर्णायक सफलता नहीं थी बल्कि उसकी कठिनाइयों का आरम्भ थी। अब उसे शक्तिशाली मराठों से सीधी टक्कर लेनी पड़ी। इससे पूर्व उसने वीर मराठा सरदार शिवाजी को दबाने के अनेक प्रयत्न किए थे, परन्तु उसे कोई विशेष सफलता नहीं मिली थी। अब मराठों का नेतृत्व शिवाजी के पुत्र शंभू जी के हाथ में था। 1689 ई० में औरंगज़ेब ने उसे पकड़ लिया और उसका वध कर दिया। औरंगज़ेब की यह सफलता भी एक भ्रम मात्र थी। मराठे शीघ्र ही पुनः स्वतन्त्र हो गए। इसके विपरीत औरंगजेब का बहुत-सा धन और समय दक्षिण के अभियानों में व्यर्थ नष्ट हो गया। यहां तक कि 1707 ई० में दक्षिण में अहमदनगर के स्थान पर उसकी मृत्यु हो गई। इस प्रकार ‘दक्षिण’ औरंगजेब और मुग़ल साम्राज्य दोनों के लिए कब्र सिद्ध हुआ।
महत्त्वपूर्ण परीक्षा-शैली प्रश्न
I. वस्तुनिष्ठ प्रश्न
1. उत्तर एक शब्द से एक वाक्य तक
प्रश्न 1.
बाबर ने भारत का सर्वप्रथम अभियान कब किया?
उत्तर-
बाबर ने भारत का सर्वप्रथम अभियान 1519 ई० में किया।

प्रश्न 2.
बाबर के भारत आक्रमण के समय दिल्ली का शासक कौन था ?
उत्तर-
इब्राहीम लोधी।
प्रश्न 3.
पानीपत की पहली लड़ाई किस-किस के बीच हुई?
उत्तर-
पानीपत की पहली लड़ाई बाबर एवं इब्राहीम लोधी के बीच हुई।
प्रश्न 4.
बाबर के आक्रमण के समय पंजाब का गवर्नर कौन था?
उत्तर-
बाबर के आक्रमण के समय पंजाब का गवर्नर दौलत खां लोधी था।

प्रश्न 5.
हुमायूं की माता का क्या नाम था ?
उत्तर-
हुमायूं की माता का नाम महम बेगम था।
प्रश्न 6.
हुमायूं सिंहासन पर कब बैठा?
उत्तर-
हुमायूं 30 दिसम्बर, 1530 ई० में सिंहासन पर बैठा।
प्रश्न 7.
किस रानी ने हमायूं से बहादुरशाह के विरुद्ध सहायता मांगी थी?
उत्तर-
रानी कर्णवती ने हमायूं से बहादुरशाह के विरुद्ध सहायता मांगी थी।

प्रश्न 8.
शेर खां ने शिक्षा कहां प्राप्त की?
उत्तर-
शेर खां ने जौनपुर में शिक्षा प्राप्त की।
प्रश्न 9.
शेर खां ने कौन-कौन से ग्रन्थों का अध्ययन किया था?
उत्तर-
शेर खां ने गुलस्तां, बोस्ता, सिकन्दरनामा आदि ग्रन्थों का अध्ययन किया था।
प्रश्न 10.
फरीद को शेर खां की उपाधि किसने दी?
उत्तर-
फरीद को शेर खां की उपाधि बहार खां लोहानी ने दी।

प्रश्न 11.
शेर खां के सम्राट् बनने की भविष्यवाणी किस मुग़ल सम्राट् ने की थी?
उत्तर-
मुग़ल सम्राट् बाबर ने शेर खां के सम्राट बनने की भविष्यवाणी की थी।
प्रश्न 12.
अकबर के सिंहासनारोहण के समय दिल्ली का शासक कौन था?
उत्तर-
अकबर के सिंहासनारोहण के समय दिल्ली का शासक हेमू था।
प्रश्न 13.
बैरम खां का वध किसने किया?
उत्तर-
बैरम खां का वध मुबारक खां ने किया।

प्रश्न 14.
अकबर ने किस निर्णायक युद्ध द्वारा दिल्ली पर अधिकार किया था ?
उत्तर-
अकबर ने पानीपत की दूसरी लड़ाई द्वारा दिल्ली पर अधिकार किया था।
प्रश्न 15.
किस राजपूत राजा ने अकबर की अधीनता स्वीकार नहीं की थी?
उत्तर-
राजपूत राजा राणा प्रताप ने अकबर की अधीनता स्वीकार नहीं की थी।
प्रश्न 16.
शाहजहां का सिंहासनारोहण कब हुआ ?
उत्तर-
शाहजहां का सिंहासनारोहण 1627 ई० में हुआ।

प्रश्न 17.
शाहजहां ने किस बुंदेल नेता को संधि करने पर विवश किया ?
उत्तर-
शाहजहां ने जोझार सिंह ओरछा बुंदेल नेता को संधि करने पर विवश किया।
प्रश्न 18.
शाहजहां की सबसे प्रिय पत्नी कौन-सी थी?
उत्तर-
शाहजहां की सबसे प्रिय पत्नी मुमताज महल थी।
2. रिक्त स्थानों की पूर्ति करें
(i) बाबर के पिता का नाम
(ii) बाबर को भारत पर आक्रमण का निमंत्रण ………………… लोधी ने दिया।
(iii) हुमायूं की मृत्यु ………………… ई० में हुई।
(iv) शेरशाह सूरी का जन्म …………. ई० में हुआ।
(v) ………………… सूर साम्राज्य का संस्थापक था।
(vi) सूर साम्राज्य का अंतिम शासक …………… था।
(vii) ‘अकबरनामा’ का लेखक ……………. था।
(viii) ……………. अकबर का संरक्षक था।
(ix) जहाँगीर का वास्तविक नाम ………………… था।
(x) गुरु …………… की शहीदी के लिए जहाँगीर उत्तरदायी था।
(xi) शाहजहाँ के बचपन का नाम ……………… था।
(xii) औरंगजेब की मृत्यु ……………… ई० में अहमदनगर में हुई।
उत्तर-
(i) उमरशेख मिर्जा
(ii) दौलत खां
(iii) 1556
(iv) 1472
(v) शेरशाह सूरी
(vi) सिकंदर सूर
(vii) अबुल फज़ल
(viii) बैरम खां
(ix) मुहम्मद सलीम
(x) अर्जन देव जी
(xi) खुर्रम
(xii) 1707.

3. सही/गलत कथन
(i) बाबर के आक्रमण के समय उत्तरी भारत का मेवाड़ सबसे शक्तिशाली हिन्दू राज्य था। — (√)
(ii) इब्राहीम लोधी मेरठ का शासक था। — (×)
(iii) भारत में बाबर की अंतिम लड़ाई पानीपत की लड़ाई थी। — (×)
(iv) शेर खां का पिता हसन खां जमाल खां के पास नौकरी करता था। — (√)
(v) शेर खां ने हुमायूं को सूरजगढ़ के युद्ध में पराजित किया। — ()
(vi) शेरशाह का मकबरा सहसराम नामक स्थान पर स्थित है। — (√)
(vii) अकबर का सिंहासनारोहण अमरकोट में हुआ। — (×)
(viii) नूरजहाँ ने राजकुमार खुसरो का वध करवाया। — (×)
(xi) जहाँगीर के शासनकाल में सर टॉमस रो भारत आया। — (√)
(x) औरंगजेब के शासनकाल में गुरु अर्जन देव जी ने शहीदी दी। — (×)
4. बहुविकल्पीय प्रश्न
प्रश्न (i)
बाबर का पिता शासक था-
(A) कन्वाहा का
(B) फरगाना का
(C) काबुल का
(D) सिंध का
उत्तर-
(B) फरगाना का
प्रश्न (ii)
बाबर के आक्रमण के समय मेवाड़ का शासक था
(A) इब्राहीम लोधी
(B) दौलत खां लोधी
(C) राणा संग्राम सिंह
(D) आधम खां लोधी।
उत्तर-
(C) राणा संग्राम सिंह

प्रश्न (iii)
चन्देरी का युद्ध हुआ
(A) 1528 ई० में
(B) 1526 ई० में
(C) 1556 ई० में
(D) 1530 ई० में ।
उत्तर-
(A) 1528 ई० में
प्रश्न (iv)
‘तुजके बाबरी’ का लेखक है
(A) अकबर
(B) बाबर
(C) जहांगीर
(D) अबुल फज़ल ।
उत्तर-
(B) बाबर
प्रश्न (v)
हुमायूं तथा शेर खां के बीच चौसा का युद्ध हुआ
(A) 1526 ई० में
(B) 1530 ई० में
(C) 1556 ई० में।
(D) 1539 ई० में ।
उत्तर-
(D) 1539 ई० में ।

प्रश्न (vi)
शेर खां ने हुमायूं को हराया
(A) घाघरा के युद्ध में
(B) चंदेरी के युद्ध में
(C) चौसा के युद्ध में
(D) कालिंजर के युद्ध में ।
उत्तर-
(C) चौसा के युद्ध में
प्रश्न (vii)
शेरशाह की मृत्यु हुई
(A) घाघरा के युद्ध में
(B) चंदेरी के युद्ध में
(C) चौसा के युद्ध में
(D) कालिंजर के युद्ध में ।
उत्तर-
(D) कालिंजर के युद्ध में ।
प्रश्न (viii)
राजकुमार खुसरो का वध करवाया
(A) खुर्रम ने
(B) जहांगीर ने
(C) नूरजहां ने
(D) मुहम्मद सलीम ने ।
उत्तर-
(A) खुर्रम ने

प्रश्न (ix)
औरंगजेब अपनी निम्न नीति द्वारा मुग़ल साम्राज्य को पतन की ओर ले गया
(A) हिंदू नीति
(B) राजपूत नीति
(C) दक्षिण नीति
(D) उपरोक्त सभी ।
उत्तर-
(D) उपरोक्त सभी ।
II. अति छोटे उत्तर वाले प्रश्न
प्रश्न 1.
मुग़ल साम्राज्य के इतिहास के लिए चार प्रकार के स्त्रोतों के नाम बताएं।
उत्तर-
ऐतिहासिक स्त्रोत (अकबरनामा आदि), भवन, विदेशी यात्रियों के विवरण तथा मुग़लकालीन सिक्के मुग़ल इतिहास की जानकारी कराते हैं।
प्रश्न 2.
भारत में मुगल शासक अपने आपको किसका उत्तराधिकारी समझते थे और उसकी राजधानी कौनसी थी ?
उत्तर-
भारत के मुग़ल शासक अपने आपको तैमूर का उत्तराधिकारी मानते थे। उसकी राजधानी समरकन्द थी।

प्रश्न 3.
बाबर के पिता का क्या नाम था और वह किस रियासत का शासक था ?
उत्तर-
बाबर के पिता का नाम उमरशेख मिर्जा था। वह फरगाना का शासक था।
प्रश्न 4.
उज़बेक कौन थे तथा उनके नेता का नाम बताएं।
उत्तर-
उज़बेक एक.प्रकार की जाति थी जो तैमूर के उत्तराधिकारियों से लड़ते रहते थे। उनका नेता शैबानी खां था।
प्रश्न 5.
शैबानी खां को ईरान के किस राजवंश के कौन-से शासक ने कब हराया ?
उत्तर-
शैबानी खां को ईरान के सफवी राजवंश के संस्थापक शाह इस्माइल ने 1510 में हराया।

प्रश्न 6.
बाबर ने काबुल किस वर्ष जीता और समरकन्द पर उसने तीसरी बार किस वर्ष में अधिकार किया ?
उत्तर-
बाबर ने काबुल 1504 में जीता और समरकन्द पर उसने तीसरी बार 1511 में अधिकार किया।
प्रश्न 7.
बाबर को कौन-से वर्ष में बारूद के प्रयोग की सम्भवानाओं का पता चला और उसने अपने तोपखाने के लिए किसे नियुक्त किया ?
उत्तर-
बाबर को 1514 में बारूद के प्रयोग की सम्भावनाओं का पता चला और उसने तोपखाने के लिए अली नामक एक अनुभवी उस्ताद को नियुक्त किया।
प्रश्न 8.
16वीं सदी के आरम्भ में उत्तर भारत के चार प्रमुख राज्यों के नाम बताएं।
उत्तर-
16वीं सदी के आरम्भ में उत्तर भारत के चार प्रमुख राज्य-दिल्ली, लाहौर, मेवाड़ तथा बंगाल थे।

प्रश्न 9.
इब्राहीम लोधी के विरोधी दो लोधी सरदारों के नाम बताएं।
उत्तर-
इब्राहीम लोधी के विरोधी दो लोधी सरदारों में से एक दौलत खां लोधी और दूसरा आलम खां लोधी था।
प्रश्न 10.
इब्राहीम लोधी के साथ बाबर का युद्ध कहां और कब हुआ ?
उत्तर-
इब्राहीम लोधी के साथ बाबर का युद्ध पानीपत में 1526 ई० में हुआ।
प्रश्न 11.
इब्राहीम लोधी के विरुद्ध बाबर की विजय के दो मुख्य कारण बताएं।
उत्तर-
बाबर की विजय का मुख्य कारण उत्तम युद्धनीति तथा सामरिक चालों के साथ तोपखाने का प्रयोग था।

प्रश्न 12.
बाबर के समय राजस्थान का सबसे शक्तिशाली राज्य कौन-सा था और उसके शासक का नाम क्या था.?
उत्तर-
बाबर के समय राजस्थान का सबसे शक्तिशाली राज्य मेवाड़ था। उसके शासक का नाम राणा संग्राम सिंह था।
प्रश्न 13.
राणा सांगा के साथ गठजोड़ करने वाले दो अफ़गान सरदारों के नाम बताएं।
उत्तर-
राणा सांगा के साथ गठजोड़ करने वाले दो अफ़गान सरदार महमूद लोधी और हसन खां थे।
प्रश्न 14.
बाबर और राणा सांगा के बीच युद्ध कहां और कौन-से वर्ष में हुआ ?
उत्तर-
बाबर और राणा सांगा के बीच युद्ध 1527 ई० में फतेहपुर सीकरी के निकट खनुआ के स्थान पर हुआ।

प्रश्न 15.
बाबर ने महमूद लोधी से युद्ध कहां और कौन-से वर्ष में किया ?
उत्तर-
बाबर ने महमूद लोधी से मई 1529 ई० में घाघरा-गंगा संगम के निकट युद्ध किया।
प्रश्न 16.
बाबर ने पंजाब पर किस वर्ष में अधिकार किया और उसकी मृत्यु कब हुई ?
उत्तर-
बाबर ने पंजाब पर 1524 ई० में अधिकार किया। उसकी मृत्यु 1530 ई० में हुई।
प्रश्न 17.
बाबर के चार बेटों के नाम बताएं।
उत्तर-
बाबर के चार बेटे हुमायूं, कामरान, अस्करी तथा हिन्दाल थे।

प्रश्न 18.
हुमायूं ने कौन-से चार प्रदेश अपने भाइयों को सौंप दिए ?
उत्तर-
हुमायूं ने अपने भाइयों को-पंजाब, काबुल, सम्भल और मेवात के प्रदेश दिए।
प्रश्न 19.
हुमायूं के कौन-से दो रिश्तेदारों ने उसके विरुद्ध विद्रोह किया ?
उत्तर-
हुमायूं के दो रिश्तेदारों मिर्जा मुहम्मद जमां और मिर्ज़ा मुहम्मद सुल्तान ने उसके विरुद्ध विद्रोह किया।
प्रश्न 20.
हुमायूं ने गुजरात किस सुल्तान से जीता था और वहां का सूबेदार किसको नियुक्त किया ?
उत्तर-
हुमायूं ने गुजरात सुल्तान बहादुरशाह से जीता। उसने अपने भाई अस्करी को वहां का सूबेदार नियुक्त किया।

प्रश्न 21.
गुजरात के दो प्रधान नगरों के नाम बताओ।
उत्तर-
गुजरात के दो प्रधान नगर-चम्पानेर और अहमदाबाद थे।
प्रश्न 22.
पूर्व तथा पश्चिम में हुमायूं के दो प्रमुख प्रतिद्वन्द्वियों ने नाम बताएं।
उत्तर-
पूर्व में शेरखां और पश्चिम में बहादुरशाह हुमायूं के प्रमुख प्रतिद्वन्द्वी थे।
प्रश्न 23.
शेरखां किस कबीले से था और उसने आरम्भ में किस प्रदेश में अपनी शक्ति को संगठित किया ?
उत्तर-
शेरखां पठान कबीले से था। उसने दक्षिण बिहार में अपनी शक्ति को संगठित किया।

प्रश्न 24.
शेरशाह ने किन वर्षों में बंगाल के शासक को दो बार हराया ?
उत्तर-
उसने बंगाल के शासक को पहले 1534 ई० में और फिर 1536 ई० में पराजित किया।
प्रश्न 25.
हुमायूं ने बंगाल के रास्ते में किस किले पर घेरा डाला और यह किसके अधिकार में था ?
उत्तर-
हुमायूं ने बंगाल के रास्ते चुनार के किले पर घेरा डाला। यह किला शेरखां के पुत्र कुतुब खां के अधिकार में था।
प्रश्न 26.
हुमायूं तथा शेरखां के बीच दो निर्णायक युद्ध किन स्थानों पर तथा कब हुए ?
उत्तर-
हुमायूं तथा शेरखां के बीच पहला युद्ध चौसा के स्थान पर जून 1539 ई० में और दूसरा युद्ध कन्नौज में मई 1540 ई० में हुआ।

प्रश्न 27.
शेरखां ने शेरशाह की उपाधि कब धारण की और उसकी मृत्यु कब हुई ?
उत्तर-
चौसा के युद्ध के बाद शेरखां ने शेरशाह की उपाधि धारण की। उसकी मृत्यु 22 मई, 1545 ई० को हुई।
प्रश्न 28.
हुमायूं को हराने के बाद शेरशाह ने कौन-सी चार विजयें प्राप्त की ?
उत्तर-
हुमायूं को हराने के बाद शेरशाह ने पंजाब, मालवा, रायसिन तथा रणथम्भौर के प्रदेशों पर विजय प्राप्त की।
प्रश्न 29.
शेरशाह ने आवागमन की सुविधा के लिए कौन-से दो कार्य किए ?
उत्तर-
शेरशाह ने आवागमन की सुविधा के लिए सड़कें बनवाईं और उनके साथ-साथ थोड़ी-थोड़ी दूरी पर सरायें बनवाईं।

प्रश्न 30.
शेरशाह के लगान प्रबन्ध से किन्हें लाभ हुआ ?
उत्तर-
शेरशाह के लगान प्रबन्ध से राज्य तथा कृषकों को लाभ हुआ।
प्रश्न 31.
शेरशाह के बाद राज करने वाले चार सूर सुल्तानों के नाम बताएं।
उत्तर-
शेरशाह के बाद इस्लाम शाह, फिरोज, मुहम्मद आदिलशाह तथा सिकन्दर शाह सूर सुल्तान बने।
प्रश्न 32.
शेरशाह द्वारा स्थापित राज्य किन पांच भागों में बंट गया तथा इनके शासक कौन थे ?
उत्तर-
ये पांच भाग थे-पूर्वी उत्तर प्रदेश तथा बिहार, बंगाल, मालवा, दिल्ली तथा आगरा और पंजाब। इनके शासक क्रमशः आदिलशाह सूर, मुहम्मद शाह, बाज़बहादुर, इब्राहीम शाह सूर तथा सिकन्दरशाह सूर थे।

प्रश्न 33.
शेरशाह से हारने के बाद हुमायूं को किस देश के कौन-से शासक से सहायता मिली ?
उत्तर-
शेरशाह से हारने के बाद हुमायूं को ईरान के शाह ताहमस्प की सहायता मिली।
प्रश्न 34.
हुमायूं ने फिर से पंजाब कब जीता और उसकी मुत्यु कब हुई ?
उत्तर-
हुमायूं ने 1555 ई० में फिर से पंजाब जीता। उसकी 1556 ई० में मृत्यु हो गई।
प्रश्न 35.
अकबर का राज्याभिषेक कहां हुआ तथा उस समय उसकी आयु क्या थी ?
उत्तर-
अकबर का राज्याभिषेक कलानौर में हुआ। उस समय उसकी आयु 13 वर्ष थी।

प्रश्न 36.
अकबर के अभिभावक का नाम बताएं तथा कौन-से वर्षों में उसका प्रभाव रहा ?
उत्तर-
अकबर के अभिभावक का नाम बैरम खां था। उसका प्रभाव 1556 ई० से 1560 ई० तक रहा।
प्रश्न 37.
पानीपत का दूसरा युद्ध किस वर्ष में हुआ तथा इसमें अफ़गान सेनाओं का सेनापति कौन था ?
उत्तर-
पानीपत का दूसरा युद्ध 1556 ई० में हुआ। इस युद्ध में अफ़गान सेनाओं का नेतृत्व हेमू ने किया।
प्रश्न 38.
अकबर ने अपने राज्यकाल के आरम्भिक वर्षों में किन दो शक्तिशाली अमीरों से और कब छुटकारा प्राप्त किया ?
उत्तर-
अकबर ने आरम्भिक वर्षों में बैरम खां तथा आधम खां नामक अमीरों से क्रमशः 1560 ई० तथा 1562 ई० में छुटकारा प्राप्त किया।

प्रश्न 39.
अकबर के सौतेले भाई का क्या नाम था और वह किस प्रदेश का शासक था ?
उत्तर-
अकबर के सौतेले भाई का नाम मिर्जा हकीम था। वह काबुल का शासक था।
प्रश्न 40.
1560 ई० से 1570 ई० के बीच अकबर ने किन चार राज्यों को अपने साम्राज्य में मिलाया ?
उत्तर-
इस अवधि के दौरान अकबर ने मालवा, मारवाड़, मेड़ता तथा गढ़-कटंगा आदि प्रदेशों को अपने साम्राज्य में मिलाया।
प्रश्न 41.
अकबर की अधीनता स्वीकार करने वाली चार राजपूत रियासतों के नाम बताएं।
उत्तर-
अकबर की अधीनता स्वीकार करने वाली चार राजपूत रियासतें थीं : जयपुर, कालिन्जर, बीकानेर तथा रणथम्भौर।

प्रश्न 42.
अकबर ने गुजरात, बंगाल तथा उड़ीसा की विजयें कब प्राप्त की ?
उत्तर-
अकबर ने गुजरात को 1572-73, बंगाल को 1574-76 तथा उड़ीसा को 1591 ई० में विजय किया।
प्रश्न 43.
अकबर ने काबुल, कश्मीर, सिन्ध तथा बिलोचिस्तान की विजयें कौन-से वर्षों में प्राप्त की ?
उत्तर-
अकबर ने काबुल को 1581 ई०, कश्मीर को 1585 ई०, सिन्ध को 1591 ई० तथा बलुचिस्तान को 1595 ई० में विजय किया।
प्रश्न 44.
अकबर ने दक्षिण की कौन-सी चार सल्तनतों की ओर अपने वकील भेजे ?
उत्तर-
अकबर ने खानदेश, अहमदनगर, बीजापुर और गोलकुण्डा में अपने वकील भेजे।

प्रश्न 45.
सबसे पहले अकबर की अधीनता मानने वाला दक्षिण के किस राज्य का शासक था तथा उसका नाम क्या था ?
उत्तर-
सबसे पहले दक्षिण के खानदेश राज्य के शासक ने अकबर की अधीनता स्वीकार की। उसका नाम राजा अली खां था।
प्रश्न 46.
खानदेश की राजधानी कौन-सी थी और इसके किस महत्त्वपूर्ण किले पर अकबर ने अधिकार किया ?
उत्तर-
खानदेश की राजधानी बुरहानपुर थी। अकबर ने इसके असीरगढ़ नामक किले पर अधिकार किया।
प्रश्न 47.
अकबर ने किन वर्षों में बरार, दौलताबाद, अहमदनगर तथा खानदेश को जीत लिया ?
उत्तर-
अकबर ने बरार को 1596 ई०, दौलताबाद को 1599 ई०, अहमदनगर को 1600 ई० तथा खानदेश को 1601 ई० में जीता।

प्रश्न 48.
दक्कन में अकबर ने कौन-से दो प्रान्त बनाए ?
उत्तर-
अकबर ने वहां खानदेश तथा बरार नाम के दो प्रान्त बनाए।
प्रश्न 49.
जहांगीर का आरम्भिक नाम क्या था तथा वह कब गद्दी पर बैठा ?
उत्तर-
जहांगीर का आरम्भिक नाम सलीम था। वह 1605 ई० में गद्दी पर बैठा।
प्रश्न 50.
जहांगीर ने नूरजहां से कब विवाह किया तथा उसका आरम्भिक नाम क्या था ?
उत्तर-
जहांगीर ने नूरजहां से 1611 ई० में विवाह किया। उसका आरम्भिक नाम मेहरुन्निसा था।

प्रश्न 51.
नूरजहां के पिता और भाई के नाम बताएं ।
उत्तर-
नूरजहां के पिता का नाम ग्यासबेग तथा भाई का नाम आसफ खां था।
प्रश्न 52.
मेवाड़ के किस शासक ने और कब जहांगीर की अधीनता स्वीकार की ?
उत्तर-
मेवाड़ के राणा अमरसिंह ने 1615 ई० में जहांगीर की अधीनता स्वीकार की।
प्रश्न 53.
जहांगीर ने कांगड़ा का किला कब जीता और वहां कौन-सा अधिकारी नियुक्त किया ?
उत्तर-
जहांगीर ने कांगड़ा का किला 1620 ई० में जीता। उसने वहां अपना फौजदार नियुक्त किया।

प्रश्न 54.
जहांगीर के समय कन्धार मुग़लों से कब छिन गया तथा इस पर किसने अधिकार किया ?
उत्तर-
जहांगीर के समय कन्धार 1622 ई० में छिन गया। इस पर ईरान के शाह अब्बास ने अधिकार किया।
प्रश्न 55.
जहांगीर के समय दक्कन की किन सल्तनतों ने मुग़ल साम्राज्य को खिराज देना स्वीकार कर लिया ?
उत्तर-
जहांगीर के समय अहमदनगर, बीजापुर और गोलकुण्डा की सल्तनतों ने मुग़ल साम्राज्य को खिराज देना स्वीकार कर लिया।
प्रश्न 56.
अहमदनगर कौन-से बादशाह के समय और कब मुग़ल साम्राज्य में मिला लिया गया ?
उत्तर-
अहमदनगर को शाहजहां के समय 1633 ई० में मुग़ल साम्राज्य में मिला लिया गया।

प्रश्न 57.
गोलकुण्डा का सुल्तान इस्लाम के किस सम्प्रदाय से सम्बन्धित था तथा वह किसको पहला खलीफा मानता था ?
उत्तर-
गोलकुण्डा का सुल्तान इस्लाम के शिया सम्प्रदाय से सम्बन्धित था। वह मुहम्मद साहिब के दामाद हज़रत अली को पहला खलीफा मानता था।
प्रश्न 58.
शाहजहां ने कन्धार पर फिर से अधिकार कब किया गया तथा उस समय कन्धार का गवर्नर कौन था ?
उत्तर-
शाहजहां ने 1638 ई० में कन्धार पर फिर से अधिकार कर लिया गया। उस समय कन्धार का गवर्नर अली मर्दान खां था।
प्रश्न 59.
कन्धार मुगलों से हमेशा के लिए कब छिन गया और इस पर किस देश का अधिकार स्थापित हो गया ?
उत्तर-
कन्धार मुग़लों से 1649 ई० में छिन गया। इस पर ईरान का अधिकार स्थापित हो गया।

प्रश्न 60.
शाहजहां ने मध्य एशिया की विजय के लिए कौन-से शहजादों को और किन वर्षों में भेजा ?
उत्तर-
शाहजहां ने मध्य एशिया की विजय के लिए मुराद को 1644 ई० और औरंगज़ेब को 1647 ई० में भेजा।
प्रश्न 61.
शाहजहां के चार पुत्रों के नाम बताएं।
उत्तर-
शाहजहां के चार पुत्रों के नाम दारा, शुजा, मुराद और औरंगजेब थे।
प्रश्न 62.
उत्तराधिकार के युद्ध कब हुए और औरंगजेब ने दारा को किन दो लड़ाइयों में हराया ?
उत्तर-
उत्तराधिकार के युद्ध अप्रैल तथा मई, 1658 ई० में हुए। औरंगजेब ने दारा को धरमत तथा सामूगढ़ की लड़ाइयों में हराया।

प्रश्न 63.
शाहजहां का राज्य किस वर्ष जाता रहा और वह कब तक जीवित रहा ?
उत्तर-
शाहजहां का राज्य जून, 1658 ई० में जाता रहा। वह 1666 ई० तक जीवित रहा।
प्रश्न 64.
यूसुफजई पठानों ने किस वर्ष में तथा किन इलाकों में मुगलों के विरुद्ध सिर उठाया ?
उत्तर-
यूसुफजई पठानों ने 1667 ई० में पेशावर, अटक और हज़ारा नामक इलाकों में मुग़लों के विरुद्ध सिर उठाया।
प्रश्न 65.
अफरीदियों ने किस वर्ष मुगलों के विरुद्ध युद्ध की घोषणा की तथा इन्हें किस कवि का समर्थन प्राप्त था ?
उत्तर-
अफरीदियों ने 1672 ई० में मुग़लों के विरुद्ध युद्ध की घोषणा की। इन्हें कवि खुशाल खां का समर्थन प्राप्त था।

प्रश्न 66.
मारवाड़ की राजधानी कौन-सी थी और इसका राजा कौन था एवं उसकी मृत्यु किस वर्ष हुई ?
उत्तर-
मारवाड़ की राजधानी जोधपुर थी। इसका राजा जसवन्त सिंह था जिसकी मृत्यु 1678 ई० में हुई।
प्रश्न 67.
शहजादा अकबर ने औरंगजेब के विरुद्ध विद्रोह कब किया तथा उसे कौन-सी दो राजपूत रियासतों का समर्थन मिला ?
उत्तर-
शहजादा अकबर ने 1681 ई० में मेवाड़ और मारवाड़ के समर्थन से औरंगजेब के विरुद्ध विद्रोह किया।
प्रश्न 68.
औरंगजेब दक्कन में किस वर्ष से किस वर्ष तक रहा ?
उत्तर-
औरंगज़ेब दक्कन में 1682 ई० से 1707 ई० तक रहा।

प्रश्न 69.
औरंगजेब ने बीजापुर कब जीता और उस समय उसका सुल्तान कौन था ?
उत्तर-
औरंगजेब ने 1686 ई० में बीजापुर को जीता। उस समय इसका सुल्तान सिकन्दर आदिलशाह था।
प्रश्न 70.
औरंगजेब ने गोलकुण्डा कब जीता और उस समय उसका सुल्तान कौन था ?
उत्तर-
औरंगज़ेब ने 1687 ई० में गोलकुण्डा को जीता। उस समय इसका सुल्तान अबुल हसन था।
प्रश्न 71.
मुग़ल साम्राज्य के पतन के कारणों की जड़ क्या थी ?
उत्तर-
मुग़ल साम्राज्य के पतन के कारणों की जड़ औरंगजेब की दक्षिण नीति थी।

III. छोटे उत्तर वाले प्रश्न
प्रश्न 1.
बाबर तथा लोधी अफ़गानों के बीच संघर्ष के बारे में बताएं।
उत्तर-
बाबर और लोधी अफ़गानों के बीच पांच वर्ष तक संघर्ष चला। सर्वप्रथम बाबर ने सिकन्दर लोधी को 1525 ई० में पंजाब में पराजित किया। तत्पश्चात् उसने इब्राहीम लोधी के साथ पानीपत के ऐतिहासिक मैदान में 1526 ई० में टक्कर ली। इब्राहीम लोधी अपने कई हजार सैनिकों के साथ मारा गया। युद्ध में बाबर ने श्रेष्ठ युद्ध नीति का प्रदर्शन किया। इसके अतिरिक्त उसके तोपखाने ने भी शत्रुओं का साहस तोड़ दिया। बाबर ने शीघ्र ही दिल्ली और आगरा पर अधिकार कर लिया। उसने लोधी अफ़गानों को अपने प्रदेश से निकालना आरम्भ किया। अतः उन्होंने राणा संग्राम सिंह से सहायता मांगी। कनवाहा की लड़ाई (1527 ई०) में उन्होंने राणा सांगा का साथ दिया। इस युद्ध में बाबर की ही विजय हुई। 1529 ई० में अफगानों ने घाघरागंगा-संगम के निकट बाबर से युद्ध किया। इस बार भी बाबर विजयी रहा। इस तरह बाबर अफ़गानों की शक्ति कुचलने में सफल रहा।
प्रश्न 2.
बाबर तथा राणा सांगा के बीच युद्ध के बारे में बताएं।
उत्तर-
बाबर तथा राणा सांगा के बीच 1527 ई० में युद्ध हुआ। पानीपत की विजय के पश्चात् बाबर ने भारत में रहने का निश्चय किया। यह बात मेवाड़ के शासक राणा सांगा की महत्त्वाकांक्षाओं के मार्ग में बाधा थी। मेवाड़ राजस्थान का सबसे शक्तिशाली राज्य था। इसी बीच बाबर ने सुल्तान इब्राहीम लोधी के इलाकों से अफ़गानों को निकालना आरम्भ कर दिया। तंग आकर कुछ अफ़गान सरदारों ने राणा सांगा से सहायता मांगी। वह तुरन्त उनकी सहायता करने के लिए तैयार हो गया। मार्च 1527 ई० में राणा सांगा ने आगरा की ओर कूच किया। बाबर अपनी सेना को लेकर फतेहपुर सीकरी के निकट खनुआ आ पहुंचा। दोनों पक्षों में दस घण्टे तक युद्ध हुआ। बाबर को निर्णायक विजय प्राप्त हुई। राणा सांगा की प्रतिष्ठा को बड़ा आघात पहुंचा और एक वर्ष के भीतर ही उसकी मृत्यु हो गई। भारत में बाबर के लिए विजय द्वार खुल गए।

प्रश्न 3.
हुमायूं तथा बहादुरशाह के बीच संघर्ष के बारे में बताएं।
उत्तर-
गुजरात के शासक बहादुरशाह के साथ हुमायूं के सम्बन्ध आरम्भ से ही शत्रुतापूर्ण थे। बहादुरशाह उन अफ़गानों को आश्रय दे रहा था जिन पर मुग़ल साम्राज्य के प्रति विद्रोह का आरोप था। वह दिल्ली पर अधिकार करने का भी आकांक्षी था। हुमायूं पहले तो शान्त रहा, परन्तु जब बहादुरशाह सभी युद्धों से निपट चुका, तब हुमायूं ने उस पर आक्रमण किया। उसने बहादुरशाह की सेना को मन्दसौर के स्थान पर घेरा। बहादुरशाह अपने पांच साथियों सहित शिविर बन्द करके भाग निकला। हुमायूं ने उसका मांडू तथा चम्पानेर तक पीछा किया। बहादुरशाह खम्बात की ओर भागने को विवश हो गया। हुमायूं वापिस लौट आया और उसने चम्पानेर पर अधिकार कर लिया। यहां हुमायूं ने फिर भूल की। वह विजित प्रदेशों का प्रबन्ध किए बिना ही आगरा लौट आया। परिणामस्वरूप उसके जाते ही शत्रुओं ने अपने आपको स्वतन्त्र घोषित कर दिया।
प्रश्न 4.
हुमायूं तथा शेरशाह सूरी के बीच संघर्ष के बारे में बताएं। .
उत्तर-
शेर खां भारत के पूर्वी प्रदेशों में अपनी शक्ति बढ़ा रहा था। 1531 ई० में हुमायूं शेर खां के विरुद्ध बढ़ा। परन्तु उसने पहले मार्ग में स्थित चुनार के किले को जीतना उचित समझा। इस अवसर का लाभ उठाकर शेर खां ने अपनी शक्ति दृढ़ कर ली। उधर उसके सैनिकों ने हुमायूं को मार्ग में तेहरिया गढ़ी के स्थान पर रोक दिया और उसे बंगाल की राजधानी गौड़ की ओर न बढ़ने दिया। इसी बीच शेर खां ने गौड़ का कोष और अफ़गान परिवार रोहतासगढ़ भेज दिए। इसके बाद ही हुमायूं गौड़ को जीत सका। यहां वह रंगरलियों में डूब गया। हुमायूं जब वापिस चला तो चौसा के स्थान पर दोनों पक्षों में पुनः युद्ध हुआ, जिसमें हुमायूं बुरी तरह पराजित हुआ। शेर खां हुमायूं का पीछा करता हुआ कन्नौज तक बढ़ आया। हुमायूं के लिए यह संकट की घड़ी थी। उसने 1000 सैनिक इकट्ठे किए और एक बार फिर कन्नौज की ओर बढ़ा। दोनों पक्षों में युद्ध हुआ। चौसा की भान्ति यहां भी हुमायूं पराजित हुआ।

प्रश्न 5.
शेरशाह किन कार्यों के लिए प्रसिद्ध है ?
उत्तर-
शेरशाह सूरी ने 1540 ई० से 1545 ई० तक शासन किया। उसने मुग़ल राज्य (1540), मालवा (1542), मारवाड़ (1543) तथा रोहतासगढ़ तक के प्रदेश को विजय किया। इन महत्त्वपूर्ण विजयों के अतिरिक्त शेरशाह कई अन्य कार्यों के लिए भी प्रसिद्ध है। उसने अनेक सड़कें बनवाईं और सड़कों के किनारे थोड़ी-थोड़ी दूरी पर सराएं बनवाईं। उसके द्वारा बनवाई गई सबसे लम्बी सड़क शाही सड़क (जी० टी० रोड) थी जो बंगाल से सिन्ध नदी तक जाती थी। सड़कों के कारण सेनाओं, व्यापारियों तथा जनसाधारण को लाभ पहुंचा। शेरशाह सूरी ने अपने राज्य में शान्ति स्थापित की तथा एक उत्तम प्रकार की लगान व्यवस्था आरम्भ की। इस लगान व्यवस्था से राज्य तथा कृषकों को बड़ा लाभ पहुंचा। सच तो यह है कि शेरशाह एक सफल विजेता तथा उच्चकोटि का प्रबन्धक था।
प्रश्न 6.
पानीपत की पहली लड़ाई का वर्णन करो।
उत्तर-
पानीपत की पहली लड़ाई 1526 ई० में हुई। इस लड़ाई के परिणामस्वरूप भारत में सुल्तानों के राज्य का अन्त हुआ और मुगल वंश की स्थापना हुई। इस लड़ाई के कई कारण थे। मध्य-एशिया के युद्धों में बाबर को असफलता का मुंह देखना पड़ा था। फरगाना का राज्य भी उससे छिन गया था। भारत में दिल्ली सल्तनत बहुत कमजोर हो चुकी थी। इसी समय दौलत खां लोधी ने बाबर को भारत पर आक्रमण करने का निमन्त्रण दिया। इस प्रकार परिस्थितियां बाबर के लिए अनुकूल थीं। उसने इनका लाभ उठाया और अपनी सेनाओं सहित भारत आ पहुंचा। पानीपत के निकट आकर उसने बड़े अच्छे ढंग से मोर्चाबन्दी की और युद्ध की तैयारी करने लगा। 21 अप्रैल, 1526 ई० की प्रातः बाबर और इब्राहीम लोधी की सेनाओं में घमासान युद्ध हुआ। इब्राहीम लोधी बाबर जैसा योग्य सेनापति नहीं था। अतः वह युद्ध में हार गया और मारा गया। युद्ध में विजय पाने के बाद बाबर ने दिल्ली और आगरा पर अधिकार कर लिया।

प्रश्न 7.
बैरम खां के अधीन मुगल साम्राज्य का स्थिरीकरण किस प्रकार हुआ ?
उत्तर-
बैरम खां अकबर का संरक्षक था। उसी ने 1556 ई० में अकबर को कलानौर में हुमायूं का उत्तराधिकारी घोषित किया। इसीलिए शासन के आरम्भिक चार वर्षों में (1556 ई० से 1560 ई० तक) बैरम खां का मुग़ल दरबार में अत्यधिक प्रभाव रहा। हुमायूं की मृत्यु के शीघ्र बाद ही हेमू ने मुगल सेनापति तारदी बेग को पराजित कर दिया था। बैरम खां ने तारदी बेग की पराजय के कारण उसका वध करवा दिया। इसके बाद उसने अकबर को दिल्ली जाने का परामर्श दिया। 1556 ई० में पानीपत के मैदान में हेमू और मुग़ल सेनाओं में जम कर लड़ाई हुई। हेमू पराजित हुआ। इसी बीच उसके स्वामी आदिल शाह को बंगाल के खिज्र खां ने मार डाला। बैरम खां के प्रयत्नों के कारण सिकन्दर सूर ने आत्मसमर्पण कर दिया तथा बिहार में जागीर स्वीकार कर ली। बैरम खां ने ग्वालियर को भी जीता। इस प्रकार 1560 ई० तक बैरम खां ने काबुल से जौनपुर और पंजाब की पहाड़ियों से लेकर अजमेर तक फैले अकबर के राज्य को स्थिरता प्रदान की।
प्रश्न 8.
आपके विचार में भारत के मुसलमान शासकों में शेरशाह सूरी का क्या स्थान है ?
उत्तर-
शेरशाह सूरी को भारत के मुसलमान शासकों में एक बहुत ऊंचा स्थान प्राप्त है। एक साधारण जागीरदार के पुत्र की स्थिति से उठकर वह भारत का सम्राट बना। इस प्रकार उसने अपनी योग्यता, बल और उच्च कोटि के नेतृत्व का परिचय दिया। उसने केवल पांच वर्ष ही राज्य किया। इस थोड़े से समय में ही उसने शान्ति, सुरक्षा और सुव्यवस्था स्थापित करके देश को सुदृढ़ बनाया। वह प्रजा का हितैषी था। उसने अनुभव किया कि हिन्दू जनता का सहयोग प्राप्त किए बिना कोई भी राज्य स्थायी नहीं रह सकता। इसलिए उसने धार्मिक कट्टरता से मुक्त होकर हिन्दुओं के प्रति उदारता और सहनशीलता की नीति अपनाई। इस प्रकार शेरशाह ने अपने शासन सम्बन्धी सुधारों और धार्मिक उदारता की नीति से सम्राट अकबर के महान कार्य के लिए उचित वातावरण तैयार किया। यदि उसे राष्ट्र-निर्माता भी कहा जाए तो अतिशयोक्ति न होगी।

प्रश्न 9.
“शेरशाह सूरी अकबर का अग्रणी था” सिद्ध करो।
उत्तर-
निम्नलिखित चार बातों से यह स्पष्ट हो जाएगा कि शेरशाह सूरी अकबर का अग्रणी था :-
1. उच्च राजकीय आदर्श-शेरशाह सूरी कभी भी अपना समय नष्ट नहीं करता था। जनता की भलाई के लिए वह कठोर परिश्रम करता था। अकबर शेरशाह द्वारा दिखाई गई इसी राह पर चला।
2. प्रशासनिक विभाजन-शेरशाह ने शासन को सुचारू रूप से चलाने के लिए राज्य को ‘सरकारों’ तथा ‘परगनों’ में बांटा हुआ था। अकबर ने भी शेरशाह के समय की प्रशासकीय इकाइयों तथा नागरिक संस्थाओं को उनके नाम बदलकर अपनाया।
3. प्रजा-हितार्थ कार्य-शेरशाह ने अपने राज्य में सड़कें बनवाईं और सड़कों के दोनों किनारों पर छायादार वृक्ष लगवाए। यात्रियों की सुविधा के लिए उसने सराएं बनवाईं। अकबर ने भी राज्य में सड़कों का जाल बिछाया। उसने अनेक सरायें बनवाईं, अस्पताल खुलवाए और कुएं खुदवाए।
4. धार्मिक सहनशीलता-शेरशाह पहला मुस्लिम शासक था जिसने हिन्दुओं के प्रति उदारता दिखाई। अकबर ने भी इसी उदारता की नीति को अपनाया।
प्रश्न 10.
“अकबर एक राष्ट्रीय शासक था।” क्यों ?
उत्तर-
अकबर पहला मुस्लिम सम्राट् था जिसने किसी धर्म या सम्प्रदाय को उन्नत करने की बजाए राष्ट्रीय हितों को बढ़ावा दिया। उसने समस्त उत्तरी भारत को विजय करके एक सूत्र में बांधा। उसने समस्त राज्य में समान कानून तथा शासनप्रणाली लागू की। पहली बार हिन्दू-जनता को मुसलमानों के समान धार्मिक स्वतन्त्रता प्राप्त हुई। जज़िया समाप्त कर दिया गया। मुग़ल सम्राट अकबर ने न केवल राजपूत राजकुमारियों से विवाह ही किया बल्कि उन्हें पूरी तरह हिन्दू परम्पराओं के अनुसार पूजा-पाठ करने की अनुमति भी दे रखी थी। दीन-ए-इलाही अकबर की धार्मिक सहनशीलता की चरम सीमा थी। उसने यह धर्म हिन्दू तथा मुसलमानों में एकता स्थापित करने के लिए आरम्भ किया था। इन सभी कार्यों द्वारा अकबर देश में राष्ट्रीय राज्य स्थापित करने में सफल हुआ।

प्रश्न 11.
अकबर की धार्मिक नीति के विषय में आप क्या जानते हैं ?
उत्तर-
अकबर आरम्भ में परम्परावादी मुसलमान था परन्तु धीरे-धीरे उसके धार्मिक विचारों में उदारता आने लगी। उसने तीर्थ-कर और जजिया कर हटा दिये। उसने फतेहपुर सीकरी में इबादतखाना बनवाया जहां सभी धर्मों और सम्प्रदायों के लोग धार्मिक विषय पर चर्चा करते थे। इन सभी विचारों के सम्मिश्रण से अकबर ने एक नवीन धर्म का प्रारम्भ किया जिसे दीन ए-इलाही का नाम दिया जाता है। अकबर ने इस धर्म में अच्छे-अच्छे सिद्धान्तों का संग्रह किया। इसके अतिरिक्त अकबर ने राजपूत राजाओं से वैवाहिक सम्बन्ध स्थापित किए। सभी हिन्दू रानियों को हिन्दू परम्पराओं के अनुसार पूजा-पाठ करने की स्वतन्त्रता प्राप्त थी। अकबर ने नौकरियों के द्वार सभी धर्मों के लोगों के लिए समान रूप से खोल रखे थे। इस प्रकार मुस्लिम युग में पहली बार किसी मुसलमान शासक के अधीन धार्मिक सहनशीलता का वातावरण अस्तित्व में आया।
प्रश्न 12.
दीन-ए-इलाही से आप क्या समझते हैं ? उसके मुख्य सिद्धान्तों की विवेचना कीजिए।
उत्तर-
दीन-ए-इलाही अकबर की धार्मिक भावनाओं के विकास की चरम सीमा थी। उसने इबादतखाने में हुए वादविवादों से यह निष्कर्ष निकाला कि सभी धर्म मूल रूप से एक हैं। इस बात से प्रेरणा लेकर उसने 1582 ई० में दीन-ए-इलाही धर्म प्रचलित किया। उसने इसमें सभी धर्मों के मौलिक सिद्धान्तों का समावेश किया। देवी-देवताओं तथा पीर-पैगम्बरों का इस नए धर्म में कोई स्थान न था। इसके अनुसार ईश्वर एक है और अकबर उसका सबसे बड़ा पुजारी है। इस धर्म के अनुयायियों के लिए मांस खाने की मनाही थी। इसके मानने वाले “अल्लाह-हु-अकबर” कहकर एक-दूसरे का स्वागत करते थे। वे . सम्राट के लिए अपना सब कुछ न्योछावर करने के लिए भी तैयार रहते थे। परन्तु दीन-ए-इलाही अधिक लोकप्रिय न हो सका। अकबर ने इसके प्रचार के लिए भी कोई विशेष पग न उठाया। परिणामस्वरूप अकबर की मृत्यु के साथ ही इस धर्म का अन्त हो गया।

प्रश्न 13.
अकबर की राजपूतों के प्रति नीति का वर्णन करो।
उत्तर-
अकबर की राजपूत नीति उसकी राजनीतिक बुद्धिमता का प्रमाण थी। वह जानता था कि राजपूतों के सहयोग के बिना वह राष्ट्रीय शासक नहीं बन सकता। अतः उसने राजपूतों के प्रति मित्रता और सहनशीलता की नीति अपनाई। उसने राजपूत राजकुमारियों से विवाह किए, राजपूतों को उच्च पदों पर नियुक्त किया और उनको धार्मिक स्वतन्त्रता प्रदान की। उसने अम्बर (जयपुर) के राजा बिहारीमल, बीकानेर तथा जैसलमेर के राजपूत राजाओं से वैवाहिक सम्बन्ध स्थापित किए। भगवान् दास, मानसिंह, उदय सिंह आदि राजपूत अकबर के समय के उच्च सैनिक अधिकारी थे। उसने न तो राजपूतों के पवित्र मन्दिरों को तोड़ा और न ही अपने किसी युद्ध को जिहाद (धर्मयुद्ध) का नाम दिया। अकबर की राजपूत नीति का यह परिणाम हुआ कि राजपूत अकबर के मित्र बन गए। इस हिन्दू-मुस्लिम सहयोग के कारण ही अकबर आगे चलकर राष्ट्र-निर्माण के उद्देश्य में सफल हो सका।
प्रश्न 14.
एक शासक के रूप में जहांगीर के प्रमुख कार्यों का वर्णन करो।
उत्तर-
जहांगीर अपने पिता अकबर की मृत्यु के बाद 1605 ई० में मुग़ल सम्राट् बना। उसने मेवाड़ के साथ चले आ रहे लगभग 40 वर्षों के संघर्ष को समाप्त किया। उसने बंगाल में शान्ति स्थापित करने में भी सफलता प्राप्त की। 1622 ई० में उसका स्वास्थ्य गिर जाने के कारण राजनीति की बागडोर उसकी पत्नी नूरजहां के हाथ आ गई जिसके साथ उसने 1611 ई० में विवाह किया था। जहांगीर को अपने दूसरे पुत्र खुर्रम (शाहजहां) के विद्रोह के कारण कन्धार का किला भी खोना पड़ा। तत्पश्चात् उसे अपने एक सरदार महावत खां के विद्रोह में उलझना पड़ा जहां से उसे नूरजहां ने बचाया। उसने अकबर द्वारा स्थापित मनसबदारी प्रणाली में कुछ परिवर्तन किए। उदाहरण के लिए उसने सवार के औसत वेतन को घटा दिया और इस प्रणाली में दुअस्पाह-सिह-अस्पाह व्यवस्था का समावेश किया। इस नई व्यवस्था के अनुसार इस पदवी के मनसबदार को उसके सवार की पदवी के आधार पर निश्चित सैनिकों से दुगुने सैनिक रखने पड़ते थे। इसके लिए उसे वेतन भी दुगुना ही दिया जाता था। 1627 ई० में जहांगीर की मृत्यु हो गई।

प्रश्न 15.
नूरजहां पर एक संक्षिप्त नोट लिखो।
उत्तर-
नूरजहां का असली नाम मेहरून्निसा था। वह एक ईरानी सरदार ग्यासबेग की पुत्री थी। ग्यासबेग काम की तलाश में भारत आ रहा था। काफिले के सरदार मलिक मसऊद की सहायता से ग्यासबेग को अकबर के दरबार में छोटी-सी नौकरी मिल गई। 1595 ई० में मेहरून्निसा का विवाह एक ईरानी नवयुवक अली कुली खां से हो गया। अली कुली खां को सलीम से शेर अफ़गान की उपाधि भी प्राप्त हुई। सलीम जब राजा (जहांगीर) बना तो उसने शेर अफ़गान को बर्दवान का सूबेदार बना दिया। परन्तु 1607 ई० में शेर अफ़गान का वध कर दिया गया। इसके चार वर्ष बाद जहांगीर ने नूरजहां से स्वयं विवाह कर लिया। नूरजहां एक कुशल स्त्री थी। उसने शासन में काफ़ी अधिकार प्राप्त कर लिए। धीरे-धीरे शासन के सभी कार्य वह स्वयं करने लगी। प्रसिद्ध इतिहासकार एलफिंस्टन के मतानुसार, “नूरजहां बड़ी तीव्र बुद्धि की स्त्री थी जिसने फर्नीचर, आभूषणों तथा नवीन वेशभूषा का आविष्कार किया।”
प्रश्न 16.
शासक के रूप में शाहजहां के कार्यों की विवेचना कीजिए।
उत्तर-
शाहजहां अपने पिता जहांगीर की मृत्यु के बाद 1628 ई० में मुग़ल सम्राट् बना। अगले ही वर्ष उसने कन्धार पर फिर से मुगलों का अधिकार स्थापित किया, परन्तु लगभग 20 वर्ष बाद ईरानियों ने इस प्रदेश को पुनः अपने अधिकार में ले लिया। कन्धार के बाद शाहजहां ने मध्य एशिया में बल्ख और बदख्शां को विजय करने का प्रयत्न किया, परन्तु कन्धार की भान्ति ये प्रदेश भी मुग़ल राज्य का स्थायी अंग न बन सके। शाहजहां ने कला तथा प्रशासन के क्षेत्र में कुछ महत्त्वपूर्ण सफलताएं प्राप्त की। उसके द्वारा बनवाए गए आगरा तथा दिल्ली के भवन कला के सर्वोत्तम नमूने हैं। उसने मनसबदारी प्रथा में एक परिवर्तन किया। अब प्रत्येक सरकार को अपनी सवार पदवी के आधार पर निश्चित संख्या के एक-तिहाई सवारों को रखना पड़ता था। कुछ परिस्थितियों में यह संख्या एक-चौथाई अथवा पांचवां भाग भी होती थी। शाहजहां ने अपनी सेना को भी सुदृढ़ बनाया। 1666 ई० में उसकी मृत्यु हो गई।

प्रश्न 17.
औरंगजेब की धार्मिक नीति का वर्णन कीजिए।
उत्तर-
औरंगजेब एक कट्टर सुन्नी मुसलमान था और वह सुन्नी सम्प्रदाय के अतिरिक्त किसी भी धर्म को फलता-फूलता नहीं देख सकता था। अतः उसने सभी गैर-मुस्लिम सम्प्रदायों के विरुद्ध असहनशीलता की नीति अपनाई। उसने हिन्दुओं के अनेक मन्दिर नष्ट-भ्रष्ट कर दिए और उन पर लगे करों में वृद्धि कर दी। उसने हिन्दुओं से ‘जज़िया’ नामक धार्मिक कर भी फिर से लेना आरम्भ कर दिया। 1671 ई० में एक आदेश द्वारा उसने प्रशासन में नियुक्त सभी हिन्दुओं को उनके पदों से हटा दिया। उसने उनके उत्सवों पर भी रोक लगा दी और इस बात की मनाही कर दी कि कोई भी हिन्दू पालकी में बैठकर नहीं जा सकता। इतना ही नहीं, उसने हिन्दुओं को मुसलमान बनाने के लिए बल और प्रलोभन दोनों का प्रयोग किया। उसके इन कार्यों से सभी हिन्दू जातियां मुग़ल साम्राज्य के विरुद्ध हो गईं और स्थान-स्थान पर विद्रोह होने लगे। फलस्वरूप सारा प्रशासनिक ढांचा अस्त-व्यस्त हो गया।
प्रश्न 18.
औरंगजेब की राजपूत नीति क्या थी और इसके क्या परिणाम निकले ?
उत्तर-
राजपूतों के प्रति औरंगजेब की नीति अकबर की नीति के बिल्कुल विपरीत थी। अकबर ने उन्हें सीने से लगाया, परन्तु औरंगजेब ने उनकी पीठ में छुरा घोंपा। उसने अपने दो राजपूत सेनानायकों राजा जसवन्त सिंह तथा राजा जयसिंह के साथ बहुत बुरा व्यवहार किया। राजा जयसिंह को उसने विष दिलवा दिया और जसवन्त सिंह को अटक के पार भेज कर मौत के मुंह में धकेल दिया। 10 दिसम्बर, 1678 ई० को जसवन्त सिंह की जमरूद में मृत्यु हो गई और मुग़लों ने बड़ी सरलता से जोधपुर पर अधिकार कर लिया। वहां फौजदार, किलादार, कोतवाल तथा अमीन के पदों पर मुसलमानों को नियुक्त कर दिया गया। औरंगज़ेब राजा जसवन्त सिंह के पुत्र अजीत सिंह को अपने अधिकार में रखना चाहता था। इसलिए औरंगज़ेब और मारवाड़ में एक लम्बा युद्ध चला, जिसमें मेवाड़ का राजा भी सम्मिलित हो गया। औरंगज़ेब का अपना पुत्र अकबर भी राजपूतों से मिल गया। औरंगज़ेब की राजपूत नीति के कारण राजपूत मुग़ल साम्राज्य के कट्टर विरोधी हो गए थे। उनकी यह शत्रुता मुग़ल साम्राज्य के विनाश का कारण बनी।

प्रश्न 19.
औरंगजेब की दक्षिण नीति की विवेचना कीजिए।
उत्तर-
औरंगजेब को दक्षिण की शिया रिसायतों का अस्तित्व पसन्द नहीं था। वह मराठों की शक्ति को भी कुचल देना चाहता था। इस उद्देश्य से उसने दक्षिण को विजय करने का निश्चय किया। उसने गोलकुण्डा राज्य पर कई आक्रमण किए। कुछ असफल अभियानों के बाद 1687 ई० में वह इस राज्य पर विजय प्राप्त करने में सफल रहा। अगले ही वर्ष उसने रिश्वत और धोखेबाजी से बीजापुर राज्य को अपने अधीन कर लिया। दक्षिण में मराठों का नेतृत्व शिवाजी के पुत्र शम्भा जी के हाथ में था। 1689 ई० में औरंगज़ेब ने उसे पकड़ लिया और उसका वध कर दिया। औरंगज़ेब की यह सफलता एक भ्रम मात्र थी। मराठे शीघ्र ही पुनः स्वतन्त्र हो गए। 1707 ई० में दक्षिण में अहमदनगर के स्थान पर उसकी मृत्यु हो गई। इस प्रकार ‘दक्षिण’ औरंगज़ेब और मुग़ल साम्राज्य दोनों के लिए कब्र सिद्ध हुआ।
प्रश्न 20.
औरंगज़ेब भारत का राज्य लेने में किस तरह सफल हुआ ?
उत्तर-
1657 ई० में अपने पिता की बीमारी का समाचार सुन कर औरंगजेब ने बड़ी चालाकी से काम लिया। वह उस समय दक्षिण का सूबेदार था। उसने अपने भाई मुराद को, जो उस समय गुजरात का सूबेदार था, आधे राज्य का लालच देकर अपनी ओर मिला लिया। दोनों की संयुक्त सेनाएं आगरा की ओर बढ़ीं। मार्ग में उन्होंने राजा जसवन्त सिंह को हराया और फिर सामूगढ़ के मैदान में अपने बड़े भाई दारा को पराजित किया। तत्पश्चात् औरंगज़ेब ने अपने भाई मुराद को शराब पिला कर बन्दी बना लिया और ग्वालियर के किले में कैद कर लिया। बाद में उसे फांसी दे दी गई। उसने अपने पिता शाहजहां को भी कैद कर लिया। कुछ समय पश्चात् उसने दारा और उसके पुत्र सुलेमान शिकोह को मरवा दिया। इसी बीच उसके भाई शुजा का अराकान में वध हो चुका था। इस प्रकार अपने सभी शत्रुओं से मुक्त हो कर औरंगज़ेब भारत की राजगद्दी प्राप्त करने में सफल रहा।

IV. निबन्धात्मक प्रश्न
प्रश्न 1.
बाबर के प्रारम्भिक जीवन, उसकी विजयों और चरित्र का संक्षिप्त वर्णन कीजिए।
उत्तर-
प्रारम्भिक जीवन-बाबर का जन्म 1483 ई० को फरगाना की राजधानी अन्दीजन में हुआ। उसका पिता उमर शेख मिर्जा फरगाना का शासक था। जब बाबर 11 वर्ष का था तो उसके पिता का देहान्त हो गया। आरम्भ में बाबर ने तैमूर की राजधानी समरकन्द को जीतने का प्रयत्न किया, परन्तु वह इसमें असफल रहा। इस चक्कर में उसकी पैतृक सम्पत्ति फरगाना भी उनसे छिन गई। इतना होने पर भी बाबर ने साहस नहीं छोड़ा। 1504 ई० में उसने काबुल और गज़नी पर अधिकार कर लिया और अपने राज्य की स्थापना की।
बाबर की भारत-विजय-काबुल और गज़नी में राज्य स्थापित करने के पश्चात् बाबर ने भारत को विजय करने की योजना बनाई। आरम्भ में उसने कई भारतीय प्रदेशों पर आक्रमण किए, परन्तु उसकी सबसे महत्त्वपूर्ण लड़ाई दिल्ली के शासक इब्राहीम लोधी के विरुद्ध थी। यह लड़ाई 1526 ई० में पानीपत के मैदान में हुई। बाबर के तोपखाने के सामने इब्राहिम लोधी की सेना न टिक सकी। इस युद्ध में इब्राहीम लोधी मारा गया और बाबर विजयी हुआ। पानीपत की विजय के पश्चात् बाबर ने दिल्ली और आगरा पर भी अधिकार कर लिया।
दिल्ली विजय के पश्चात् बाबर को राजपूत शासक राणा सांगा से टक्कर लेनी पड़ी। 1527 ई० में आगरा के समीप कनवाहा नामक गांव में बाबर और राणा सांगा के बीच भयंकर युद्ध हुआ। राणा सांगा अन्त में मैदान छोड़कर भाग निकला और बाबर को विजय प्राप्त हुई। 1529 ई० में उसने घाघरा के युद्ध में अफ़गानों को परास्त किया। इस प्रकार भारत पर बाबर का अधिकार हो गया।
बाबर का चरित्र-बाबर एक सफल शासक तथा अनुभवी सैनिक था। वह विद्वान् और कला-प्रेमी था। इसके अतिरिक्त वह बड़ा साहसी और धैर्यवान था। कठिनाइयों में वह कभी नहीं घबराया। एक व्यक्ति के रूप में भी उसका चरित्र बड़ा प्रभावशाली था। वह एक अच्छा पिता, दयालु स्वामी तथा उदार मित्र था। वह हंसमुख और मिलनसार था। वह सदा अपने से बड़ों का आदर तथा छोटों से प्रेम करता था। इन गुणों के बावजूद बाबर में शराब तथा विषय-भोग जैसे अवगुण भी थे। परन्तु यह अवगुण उसके कर्त्तव्यपालन के मार्ग में कभी बाधा नहीं बन पाये। सच तो यह है कि भारतीय इतिहास में बाबर को एक बहुत उच्च स्थान प्राप्त है।
प्रश्न 2.
बाबर के पश्चात् हुमायूं के सामने कौन-कौन सी कठिनाइयां थीं ?
उत्तर-
1530 ई० में बाबर की मृत्यु के पश्चात् हुमायूं राजसिंहासन पर बैठा। परन्तु गद्दी पर बैठते ही उसे अनेक कठिनाइयों का सामना करना पड़ा। इन कठिनाइयों का वर्णन इस प्रकार है :
1. अस्थिर और अव्यवस्थित राज्य-हुमायूं को उत्तराधिकार में एक ऐसा राज्य मिला जो न तो सुदृढ़ था और न ही सुव्यवस्थित। बाबर ने न तो बंगाल को अपने अधीन किया था और न ही गुजरात को। राजपूत बाबर से पराजित अवश्य हुए थे, परन्तु उनकी शक्ति को पूर्णतः कुचला नहीं गया था। इस प्रकार हुमायूं चारों ओर से शत्रुओं से घिरा हुआ था।
2. विभाजित राज्य-राजगद्दी पर बैठते ही हुमायूं ने राज्य को अपने तीन भाइयों में बांट दिया। उसके तीनों भाई बड़े ही अयोग्य थे। उन्होंने हुमायूं की सहायता करने की बजाय उसके मार्ग में बाधाएं डालनी आरम्भ कर दी।
3. अफ़गानों का विरोध-पानीपत तथा घाघरा की लड़ाई में परास्त होकर भी अफ़गान शक्ति नष्ट नहीं हुई थी। बड़ेबड़े अफ़गान सरदार दिल्ली के सिंहासन को वापस लेना चाहते थे। प्रसिद्ध अफगान सरदार शेर खां तो हुमायूं के लिए एक बहुत बड़ा खतरा बन गया था।
4. खाली राजकोष-हुमायूँ के पिता बाबर ने अपनी उदारता के कारण अपना काफ़ी सारा धन व्यर्थ में व्यय कर दिया। फलस्वरूप हुमायूँ को एक ऐसा राजकोष मिला जो लगभग खाली हो चुका था। धन के अभाव में हुमायूँ के लिए शासन चलाना सरल नहीं था।
5. विश्वासपात्र सैनिकों का अभाव हुमायूं की सेना में किसी एक जाति के लोग नहीं थे। उसमें चुगताई, तुर्क, उजबेग, मुग़ल, अफ़गान और ईरानी सभी लोग शामिल थे। परिणामस्वरूप सेना में एकता का बड़ा अभाव था। सैनिक संगठन की कमी के कारण हुमायूं की कठिनाइयां और भी बढ़ गईं।
6. व्यक्तिगत दोष-हुमायूँ बड़ा ही विलासी व्यक्ति था। वह हर समय अफीम खाकर मस्त रहता था। शेर खां और बहादुरशाह जब उसके लिए खतरा बने हुए थे तो उसने अपना कीमती समय रंगरलियों में खो दिया। परिणामस्वरूप उसके शत्रुओं को शक्ति बढ़ाने को अवसर मिल गया।
इस प्रकार हुमांयू जीवन-भर इन कठिनाइयों से घिरा रहा। उसने अपनी भूलों से अपनी कठिनाइयों को और अधिक बढा दिया।

प्रश्न 3.
शासक के रूप में हुमायूं की असफलता के क्या कारण थे ?
अथवा
हुमायूँ की भूलों का वर्णन करो।
उत्तर-
हुमायूं अपनी निम्नलिखित भूलों के कारण शासक के रूप में असफल रहा :
1. हुमायूं द्वारा राज्य का मूर्खतापूर्ण विभाजन-गद्दी पर बैठते ही हुमायूं के कदम लड़खडा गये। उसने अपने भाइयों में राज्य का विभाजन राज्य के हितों को ध्यान में रखकर न किया, बल्कि अपने भाइयों की इच्छाओं को ध्यान में रखकर किया। उसने कामरान को काबुल तथा कन्धार, अस्करी को सम्भल और हिन्दाल को अलवर का शासक बना दिया। शीघ्र ही उसे अपनी भूल के परिणाम भुगतने पड़े। कामरान कुछ ही दिनों में अपने असली रूप में प्रकट हुआ। वह हुमायूं को राज्याभिषेक पर बधाई देने की आड़ में पंजाब की ओर बढ़ आया और वहां अपना अधिकार जमा लिया। इससे हुमायूं का आधा राज्य जाता रहा और उसकी सैनिक शक्ति काफ़ी दुर्बल हो गई। उसके अन्य भाइयों ने भी उसके लिए अनेक कठिनाइयां उत्पन्न की।
2. समय तथा धन की बर्बादी-हुमायूँ समय तथा धन के महत्त्व को नहीं समझता था। उसने अपने आरम्भिक वर्षों में दिल्ली तथा आगरा में धन को पानी की तरह बहाया। उसने राज्याधिकारियों को बहुमूल्य पुरस्कार दिए। “उसने अपना काफ़ी समय और धन दिल्ली में एक विशाल दुर्ग बनाने की योजना में नष्ट किया।” यह सब काम उसने उस समय किया जब गुजरात का बहादुरशाह उसके शत्रुओं को पनाह दे रहा था और अपनी शक्ति बढ़ाने में लगा हुआ था। समय और धन की यह बर्बादी हुमायूं की दूसरी बड़ी भूल थी।
3. गुजरात अभियान की भूलें-गुजरात अभियान में हुमायूं ने अनेक भूलें कीं। उसने रानी कर्णवती की पेशकश को ठुकरा कर राजपूतों की मित्रता से हाथ धो लिया। उसका समय पर बहादुरशाह पर आक्रमण न करना भी उसकी भूल थी। जब बहादुरशाह कर्णवती के विरुद्ध उलझा हुआ था तो हुमायूं रंगरलियों में डूब गया। फिर जब हुमायूं ने बहादुरशाह का पीछा किया तो उसका वध किए बिना ही वापस लौट आया। यह उसकी बड़ी भूल थी, क्योंकि कुछ समय के पश्चात् बहादुरशाह दियु से लौटकर हुमायूं के लिए समस्या बन गया। उसे गुजरात का शासन अस्करी को नहीं सौंपना चाहिए था। अस्करी न तो इतना योग्य था और न ही हुमायूँ का स्वामिभक्त । अतः उसके अधीन गुजरात की शासन-व्यवस्था बिगड़ गई और यह प्रान्त मुग़लों के हाथों से निकल गया।
4. शेर खां के विरुद्ध संघर्ष में उसकी भूल- शेर खां के विरुद्ध अभियान में भी हुमायूँ ने अनेक भूलें कीं। उसने चुनार पर घेरा डालकर गौड़ खो दिया। फिर गौड़ की रंगीनियों में डूबकर आगरा जाने वाला मार्ग छिनवा बैठा। गौड़ की वापसी पर भी उसने सुरक्षा का कोई प्रबन्ध नहीं किया। चौसा के मैदान में काफ़ी समय पड़ा रहना हुमायूं की भारी भूल थी। उसे शीघ्रातिशीघ्र आगरा पहुंचना चाहिए था। चौसा के मैदान में उसने पहरेदारी का काम एक विश्वासघाती को सौंप रखा था। शेर खां ने सोये हुए मुग़ल सैनिकों पर पौ फटने से पहले ही आक्रमण किया था। हुमायूं को इसकी कोई खबर तक न हुई। उसे तो स्वयं नदी में कूद कर अपनी जान बचानी पड़ी। हुमायूं की इन भूलों ने उसे भारत छोड़कर भागने के लिए विवश कर दिया।
प्रश्न 4.
“शेरशाह सूरी योग्यता तथा कूटनीति में अकबर का. अग्रगामी था।” कोई पांच तर्क देकर व्याख्या कीजिए।
अथवा
शेरशाह सूरी को अकबर का अग्रगामी कहना कहां तक उचित है ?
उत्तर-
शेरशाह तथा अकबर में वही सम्बन्ध था जो मार्गदर्शक तथा मार्ग पर चलने वालों में होता है। शेरशाह ने मार्ग तैयार किया। अकबर उस मार्ग पर चला भी और उसने वह मार्ग संवारा भी। निम्नलिखित तथ्यों से स्पष्ट हो जायेगा कि शेरशाह अकबर का अग्रगामी था :
1. उच्च राजकीय आदर्श-शेरशाह सूरी ने उच्च राजकीय आदर्श स्थापित किए। वह कभी भोग-विलास में अपना समय नष्ट नहीं करता था। जनता की भलाई के लिए वह कड़ा परिश्रम करता था। अकबर शेरशाह द्वारा दिखाई गई इसी राह पर चला।
2. प्रशासनिक विभाजन-शेरशाह ने शासन को सुचारु रूप से चलाने के लिए राज्य को ‘सरकारों’ तथा ‘परगनों’ में बाँटा हुआ था। अकबर ने भी शेरशाह के समय की प्रशासकीय इकाइयों तथा नागरिक संस्थाओं को अपनाया। अन्तर केवल दोनों के समय के अधिकारियों और प्रशासनिक इकाइयों के नामों में था।
3. भूमि-कर-प्रबन्ध-शेरशाह ने भूमि की पैमाइश करवाई, उपज को तीन श्रेणियों में बाँटा, एक-चौथाई भूमि-कर नियत किया तथा किसानों की सुविधा के लिए अनेक अन्य पग उठाये। अकबर ने भी शेरशाह की भूमि-प्रणाली को अपनाया, उसने भूमि को बाँसों के गजों से नपवाया और भूमि को चार भागों में बांटा। उसने किसानों को भी सुविधाएं प्रदान की।
4. धार्मिक सहनशीलता-धार्मिक सहनशीलता में भी शेरशाह सूरी ने अकबर का पथ-प्रदर्शन किया। शेरशाह पहला मुस्लिम शासक था जिसनें हिन्दुओं के प्रति उदारता दिखाई थी। अकबर ने तो क्षेत्र में एक नवीन आदर्श स्थापित किया। उसने हिन्दुओं से ‘जज़िया’ लेना बन्द कर दिया और उन्हें उच्च पदों पर भी नियुक्त किया।
5. सैनिक प्रबन्ध-सैनिक संगठन में भी शेरशाह सूरी अकबर का अग्रगामी था। अकबर ने शेरशाह की भान्ति स्थायी
6. मुद्रा-प्रणाली-शेरशाह ने मुद्रा-प्रणाली में प्रशासकीय सुधार किए। अकबर ने भी उसी द्वारा प्रचलित मुद्रा-प्रणाली को . अपनाया, परन्तु आवश्यकतानुसार उसका थोड़ा-सा रूप बदल दिया।
7. भवन-निर्माण कला-अकबर को भवन बनवाने का बड़ा चाव था, परन्तु इसकी प्रेरणा भी उसने शेरशाह सूरी से ही ली थी। शेरशाह ने सहसराम का मकबरा बनवाकर भवन-निर्माण में योगदान दिया था। अकबर ने भी अनेक सुन्दर भवन बनवाये। फतेहपुर सीकरी का बुलन्द दरवाज़ा, “जामा मस्जिद’, रानियों के महल तथा अन्य भवन उसने शेरशाह से प्रेरित होकर ही बनवाये थे।
8. प्रजा-हितार्थ कार्य-शेरशाह ने अनेक प्रजा-हितार्थ कार्य किये। उसने कई सड़कें बनवाईं। सड़कों के दोनों किनारों पर छायादार वृक्ष लगवाये और यात्रियों की सुविधा के लिए सरायों की व्यवस्था की। शेरशाह सूरी का अनुकरण करते हुए अकबर ने भी ये सभी प्रजा-हितार्थ कार्य किए। उसने कुछ सामाजिक सुधार भी किए।
9. सच तो यह है कि शेरशाह सूरी ने लगभग हर क्षेत्र में अकबर का मार्ग-दर्शन किया। डॉ० कानूनगो के शब्दों में, “शेरशाह ने अपने प्रशासकीय तथा आर्थिक सुधारों और सहनशील धार्मिक नीति द्वारा अकबर की महानता की नींव रखी।” (“Sher Shah laid the foundaitons of Akbar’s greatness by his administrative and economic reforms and the policy of religious toleration.”) अतः उसे अकबर का अग्रसर कहना उचित ही है।

प्रश्न 5.
“अकबर ने सारे उत्तरी भारत को एकता के सूत्र में बांध दिया।” सिद्ध कीजिए।
अथवा
अकबर की
(क) उत्तरी भारत तथा
(ख) दक्षिणी भारत की विजयों का वर्णन कीजिए।
उत्तर-
अकबर एक महान् विजेता था। वह 1556 ई० में राजगद्दी पर बैठा। अल्प आयु होने के कारण बैरम खां ने उसका संरक्षण किया और उसके लिए अनेक प्रदेश विजय किए। उसने पानीपत की दूसरी लड़ाई में हेमू को पराजित करके दिल्ली और आगरा पर अधिकार कर लिया। उसने मेवात को भी विजय किया। सिकन्दर सूरी की सेना ने उसके सामने आत्म-समर्पण कर दिया। तत्पश्चात् अकबर ने निम्नलिखित प्रदेश विजय किये :- .
(क) उत्तरी भारत की विजय-
1. मालवा की विजय-1560 ई० में अकबर ने मालवा पर विजय प्राप्त की और मालवा का प्रदेश पीर मुहम्मद को सौंप दिया गया। परन्तु पीर मुहम्मद शासन चलाने में असफल रहा और वहां के शासक बाज बहादुर ने मालवा को पुनः अपने अधिकार में ले लिया। 1562 ई० में अकबर ने उसके विरुद्ध एक बार फिर विशाल सेना भेजी। इस बार वह मालवा पर पूर्ण विजय प्राप्त करने में सफल रहा।
2. राजपूताना की विजय-1562 ई० में अकबर ने राजपूताना पर आक्रमण कर दिया। आमेर के राजा बिहारीमल ने शीघ्र ही अकबर की अधीनता स्वीकार कर ली तथा अपनी बेटी का विवाह भी अकबर से कर दिया। इसके साथ कई अन्य राजपूत शासकों ने भी अकबर की अधीनता स्वीकार कर ली, जैसे-कालिन्जर, मारवाड़, जैसलमेर, बीकानेर आदि।
3. मेवाड़ से संघर्ष-मेवाड़ का शासक अकबर की अधीनता स्वीकार नहीं करना चाहता था। 1568 ई० में अकबर ने मेवाड़ की राजधानी चित्तौड़ पर अधिकार कर लिया। परन्तु फिर भी महाराणा प्रताप ने उसकी अधीनता स्वीकार नहीं की। वह अन्त तक मुग़लों से संघर्ष करता रहा।
4. गुजरात पर विजय-1572-73 ई० में अकबर ने गुजरात पर विजय प्राप्त कर ली।
5. बिहार-बंगाल की विजय-1574-76 ई० में अकबर ने अफ़गानों को पराजित करके बिहार और बंगाल पर विजय प्राप्त कर ली।
6. अन्य विजयें-अकबर ने धीरे-धीरे कश्मीर, सिन्ध, उड़ीसा, बिलोचिस्तान तथा कन्धार पर भी विजय प्राप्त कर ली।
(ख) दक्षिणी भारत की विजयें उत्तरी भारत में अपनी शक्ति संगठित कर अकबर ने दक्षिणी भारत की ओर ध्यान दिया। दक्षिण में उसने निम्नलिखित विजयें प्राप्त की :
- बीजापुर तथा गोलकुण्डा की विजय-1591 ई० में अकबर ने बीजापुर तथा गोलकुण्डा पर विजय प्राप्त कर ली।
- खानदेश की विजय-1601 ई० में खानदेश के सुल्तान अली खां ने अकबर की अधीनता स्वीकार कर ली।
- अहमदनगर पर अधिकार-1600 ई० में अकबर की सेनाओं ने अहमदनगर की संरक्षिका चांद बीबी को परास्त कर दिया तथा अहमदनगर पर विजय पा ली।
- बरार पर अधिकार-अकबर ने दक्षिणी भारत के बरार प्रदेश पर भी अधिकार कर लिया। इस प्रकार अकबर ने एक विशाल साम्राज्य की स्थापना की।
प्रश्न 6.
“शाहजहां के राज्यकाल को मुगल साम्राज्य का उत्कर्ष काल अथवा स्वर्ण युग कहा जाता है।” आप इस विचार से कहां तक सहमत हैं ?
अथवा
मुगलकालीन इतिहास को शाहजहां की क्या देन थी ? किन्हीं पांच देनों की व्याख्या कीजिए।
उत्तर-
शाहजहां महान् मुग़ल शासकों में से एक था। उसके राज्य को मुग़ल साम्राज्य का उत्कर्ष काल अथवा स्वर्ण युग कहा जाता है। शाहजहां के काल में देश में चारों ओर शान्ति और समृद्धि थी तथा कला के हर क्षेत्र में अतुलनीय प्रगति हो रही थी। हिन्दू और मुसलमानों में एकता थी तथा व्यपार और वाणिज्य ने काफ़ी उन्नति की। इन सभी बातों के कारण शाहजहां के काल को स्वर्ण युग कहा जाता है। इसका विस्तारपूर्वक वर्णन इस प्रकार है :-
1. पूर्ण शान्ति-शाहजहां के शासन काल मे सब ओर शान्ति का वातावरण था। राजपूत राज्य के शुभचिन्तक थे। उत्तरपश्चिम में कन्धार को छोड़कर शेष सम्पूर्ण मुग़ल साम्राज्य पूरी तरह सुरक्षित था। दक्षिण की ओर से अब कोई भय न था। इस काल में अहमदनगर भी मुग़ल साम्राज्य में मिल चुका था। पुर्तगालियों की शक्ति का भी पतन हो रहा था परंतु उनका स्थान किसी अन्य शक्तिशाली यूरोपीय जाति ने अभी नहीं लिया था। तात्पर्य यह कि शाहजहां के राज्य में पूर्ण सुख-शान्ति थी और देश आन्तरिक विद्रोहों तथा विदेशी आक्रमणों से पूरी तरह सुरक्षित था। .
2. अच्छी आर्थिक अवस्था तथा समृद्धि-देश में सुख और शान्ति बने रहने के कारण लोग अपने-अपने व्यवसायों में जुटे हुए थे। इस प्रकार उनकी आर्थिक दशा बहुत सुदृढ़ हो रही थी। राज्य प्रबन्ध अकबर के समय से ही बहुत अच्छा था।
3. भवन-निर्माण कला के क्षेत्र में उन्नति-शाहजहां का शासनकाल भवन-निर्माण कला के क्षेत्र में अनुपम उन्नति के लिए विशेषकर प्रसिद्ध है। उसने आगरा, दिल्ली और कई अन्य स्थानों पर सुन्दर भवनों का निर्माण करवाया। ताजमहल इस काल की एक अनूठी कृति थी। यह प्रसिद्ध मकबरा सम्राट ने अपनी प्यारी मलिका मुमताज महल की याद में बनवाया था और यह अब भी विश्व में दाम्पत्य-प्रेम और अनुराग का एक अद्वितीय स्मारक है। ताज के अतिरिक्त आगरा में स्थित मोती मस्जिद और दिल्ली में जामा मस्जिद तथा दीवाने खास शाहजहां के कुछ अन्य शानदार भवन हैं। सम्राट् ने लगभग एक करोड़ की लागत से प्रसिद्ध तख्ते-ताऊस का निर्माण भी करवाया।
4. अन्य ललित कलाओं का विकास-चित्रकला तथा संगीत कला को शाहजहां के काल में काफ़ी प्रोत्साहन मिला। उसके शासनकाल का सबसे प्रसिद्ध चित्रकार मुहम्मद नादिर समरकन्दी था। उसके दरबार के सर्वप्रसिद्ध संगीतकार थे जगन्नाथ, महापतेर, राम दास. और लाल खां जो तानसेन का जमाता था। शाहजहां के काल में साहित्य भी किसी अन्य कला से पीछे नहीं था। उसके दरबार में काज़बीकी, अब्दुल हमीद लाहौरी, पीर अबुल कासिम ईरानी, मिर्जा जयाबुद्दीन, शेख बहलोल कादरी आदि बड़े-बड़े विद्वान् थे। इन मुसलमान विद्वानों के अतिरिक्त इस काल में बहुत से हिन्दू विद्वान् भी थे, जैसे सुन्दरदास, चिन्तामणि, कवीन्द्राचार्य और जगन्नाथ।
5. सबके लिए एस समान न्याय-शाहजहां बड़ा न्यायप्रिय शासक था। न्याय करते समय वह बड़े-बड़े अधिकारियों को भी दोषी होने पर क्षमा नहीं करता था। उसके काल में दण्ड बड़े कठोर थे। इसलिए अपराध करने का किसी को साहस नहीं होता था।”
6. व्यापार और वाणिज्य में उन्नति-शाहजहां के काल में व्यापार तथा वाणिज्य ने काफ़ी उन्नति की। विदेशों के साथ भारत का व्यापार काफ़ी उन्नति पर था। परिणामस्वरूप बहुत-सा विदेशी धन भारत में आने लगा।
7. प्रजा हितार्थ कार्य-शाहजहां ने प्रजा की भलाई के लिए बहुत से तालाब, नहरें, सड़कें, पुल तथा सराएं आदि बनवाईं। उसने लाहौर के निकट के खेतों की सिंचाई के लिए एक लाख रुपए के व्यय से रावी नदी से एक बड़ी नहर निकलवाई और फिरोजशाह तुग़लक द्वारा बनवाई गई पश्चिमी यमुना नहर की मुरम्मत करवाई। शाहजहां के राजकीय इतिहासकार अब्दुल हमीद के अनुसार शाहजहां ने अकाल पीड़ितों की खुले दिल से सहायता की, मुफ्त लंगर खुलवाये और लोगों के लगान माफ कर दिए। इन सब बातों को देखते हुए हम कह सकते हैं कि शाहजहां का काल वास्तव में ही मुग़ल इतिहास का स्वर्ण युग था।

प्रश्न 7.
औरंगजेब की राजपूत नीति तथा उसके परिणामों की व्याख्या कीजिए। उसकी यह नीति मुग़ल साम्राज्य के पतन के लिए कहां तक उत्तरदायी थी ?
अथवा
औरंगजेब ने राजपूतों के प्रति कैसी नीति अपनाई ? उसकी यह नीति मुगल साम्राज्य के लिए किस प्रकार घातक सिद्ध हुई ?
उत्तर-
औरंगजेब कट्टर सुन्नी मुसलमान था। उसके हृदय में राजपूतों के लिए कोई प्रेम नहीं था। वह राजपूतों को अपने दरबार मे उच्च पद देने के पक्ष में नहीं था। परन्तु जब तक दो वीर राजपूत-सरदार मिर्जा राजा जयसिंह तथा जसवन्त सिंह राठौर-जीवित रहे, उसने राजूपतों के विरुद्ध कोई कठोर पग न उठाया। उनकी मृत्यु के पश्चात् औरंगजेब ने राजपूतों के प्रति दमन की नीति अपनाई। औरंगज़ेब की राजपूतों के प्रति ऐसी नीति और उसके परिणामों का वर्णन इस प्रकार है :-
जसवन्त सिंह की मृत्यु-जसवन्त सिंह राठौर मारवाड़ का शासक था। वह शाहजहां के राज्यकाल में मुग़ल दरबार का मनसबदार था। 10 दिसम्बर, 1678 ई० को जमरूद में जसवन्त सिंह का देहान्त हो गया। उसकी मृत्यु के पश्चात औरंगजेब के लिए मारवाड़ पर अधिकार करना सरल हो गया। औरंगज़ेब ने जसवन्त सिंह के सिंहासन पर नागौड़ के राजपूत सरदार इन्द्र सिंह को बिठाया। उसे 36 लाख रुपए दिए गए और वह अपने यहां मुसलमान अधिकारी रखने के लिए राजी हो गया। परन्तु शीघ्र ही औरंगज़ेब के इस कार्य का विरोध होने लगा।
अजीत सिंह तथा दुर्गादास-औरंगज़ेब जसवन्त सिंह के नवाजात शिशु अजीत सिंह को मारवाड़ का शासक स्वीकार करने के लिए तैयार नहीं था। उसने अजीत सिंह को दिल्ली में ही कैद कर लिया। परन्तु दुर्गादास राठौर के प्रयत्नों से जसवन्त सिंह की दोनों रानियां और अजीत सिंह जोधपुर पहुंचने में सफल हुए।
मारवाड़ पर आक्रमण-मारवाड़ की जनता ने अजीत सिंह के पक्ष में विद्रोह कर दिया और इन्द्र सिंह को शासक मानने से इन्कार कर दिया। औरंगज़ेब ने अपने पुत्र अकबर को मेवाड़ पर अक्रमण करने का आदेश दिया। इस युद्ध में राजपूत पराजित हुए और इस प्रकार मारवाड़ फिर मुग़लों के अधिकार में आ गया। विवश होकर राजपूतों ने पर्वतों तथा वनों में आश्रय लिया और यहीं से उन्होंने गुरिल्ला युद्ध जारी रखा।
मेवाड़ तथा मारवाड़ का संगठन-मारवाड़ के पतन से मेवाड़ के राणा को बड़ा दुःख हुआ। उसने राठौरों और वीर सिसौदियों के साथ मुग़लों के विरुद्ध एक संयुक्त मोर्चा स्थापित किया, परन्तु औरंगजेब की विशाल सेना के समक्ष यह संयुक्त मोर्चा विफल साबित हुआ। राजपूतों ने अब मुग़लों के विरुद्ध गुरिल्ला युद्ध नीति अपनाई और काफ़ी सीमा तक सफल भी रहे।
अकबर का राजपूतों से गठजोड़ तथा विद्रोह-राजकुमार अकबर राजपूतों के सहयोग से दिल्ली का सिंहासन प्राप्त करना चाहता था। अतः उसने औरंगज़ेब के प्रति विद्रोह कर दिया। राजपूतों ने अकबर को हर सम्भव सहायता देने का वचन दिया। परन्तु यह मित्रता ज्यादा दिनों तक नहीं चली। औरंगज़ेब राजपूतों और अकबर के मध्य फूट डालने में सफल रहा।
उदयपुर की सन्धि-24 जून, 1681 ई० को औरंगज़ेब और मेवाड़ के राणा जयसिंह के बीच एक सन्धि हुई। इस सन्धि के अनुसार राजपूतों ने मुग़ल साम्राज्य के विरुद्ध कोई भी सहायता न करने का वचन दिया। जयसिंह को मेवाड़ का महाराणा मान लिया गया। उसे पांच हज़ारी मनसबदार भी नियुक्त किया गया।
उदयपुर की सन्धि के बाद भी राजपूतों ने मुग़लों के विरुद्ध संघर्ष जारी रखा। पहले दुर्गादास और फिर अजीत सिंह के नेतृत्व में उनका संघर्ष चलता रहा। 1707 ई० में औरंगजेब की मृत्यु के पश्चात् अजीत सिंह ने जोधपुर के मुग़ल सूबेदार को मार भगाया और स्वयं मारवाड़ का स्वतन्त्र शासक बना।
राजपूत नीति के परिणाम-
- राजभक्त राजपूत मुग़लों के शत्रु बन गए। उनकी शत्रुता मुग़ल साम्राज्य के लिए विनाशकारी सिद्ध हुई।
- राजस्थान की शासन व्यवस्था अस्त-व्यस्त हो गई। वहां की अव्यवस्था से पड़ोसी मुग़ल प्रदेश में अराजकता फैल गई।
- राजपूतों की मित्रता से वंचित होने के कारण सम्राट को अन्य अभियानों में अनेक कठिनाइयों का सामना करना पड़ा।
- साम्राज्य को जन और धन की अपार हानि उठानी पड़ी।
- शाही प्रतिष्ठा को भारी ठेस लगी। राजपूतों के आकस्मिक हमलों ने मुग़ल साम्राज्य की जड़ें खोखली करने का कार्य किया।
सच तो यह है कि औरंगजेब की राजपूत नीति महान् राजनीतिक आदर्शों से प्रेरित न थी। उनका सहयोग प्राप्त करके मुग़ल साम्राज्य को सुदृढ़ करने के स्थान पर उसने राजपूतों को अपना शत्रु बना लिया। राजपूतों की मित्रता के कारण मुग़ल साम्राज्य सशक्त बना था और उनकी शत्रुता के कारण मुग़ल साम्राज्य पतन की ओर अग्रसर हुआ।

प्रश्न 8.
शेरशाह सूरी के शासन-प्रबन्ध अथवा प्रशासनिक सुधारों का वर्णन करो।
अथवा
शेरशाह सूरी एक योग्य एवं प्रजाहितकारी शासक था ? स्पष्ट कीजिए।
उत्तर-
शेरशाह एक योग्य शासक था। उसने केवल पांच वर्ष राज्य किया। इतने कम समय में उसने इतना अच्छा राज्य प्रबन्ध किया कि इतिहास में उसका नाम अमर हो गया। उसके शासन-प्रबन्ध की मुख्य विशेषताएं निम्नलिखित है :-
1. केन्द्रीय शासन-केन्द्रीय शासन का मुखिया शेरशाह स्वयं था। सारे काम उसकी आज्ञा से होते थे। उसकी सहायता के लिए अनेक मन्त्री भी थे। वह लोगों की भलाई का ध्यान रखता था। वह राज्य का भ्रमण करके लोगों की शिकायतें सुनता था। प्रजा उससे बड़ी प्रसन्न थी।
2. प्रान्तीय शासन-शेरशाह ने अपने राज्य को अनेक प्रान्तों में बांटा हुआ था। प्रान्तों को सरकारों अथवा ज़िलों में विभक्त किया गया था। प्रत्येक सरकार परगनों में बंटी हुई थी। शासन की इन इकाइयों में शेरशाह ने बड़े योग्य अधिकारी नियुक्त किए हुए थे। गांव के प्रबन्ध के लिए पंचायतें थीं।

3. भूमि प्रबन्ध-शेरशाह ने सारे राज्य की भूमि की पैमाइश करवाई और उपज के आधार पर इसे तीन भागों में . बांटा-उत्तम, मध्यम तथा निम्न। उपज के आधार पर ही भूमिकर नियत किया गया जो उपज का एक-तिहाई भाग होता था।
4. कृषकों से अच्छा व्यवहार-शेरशाह सदा कृषकों की भलाई का ध्यान रखता था। उन्हें अकाल के दिनों में ऋण दिया जाता था। शेरशाह ने अपने सैनिकों को चेतावनी दी हुई थी कि वे चलते समय किसी कृषक की फसल को हानि न पहुँचाएं।
5. पुलिस-जनता के धन-माल तथा जीवन की रक्षा के लिए शेरशाह सूरी ने पुलिस की उत्तम-व्यवस्था की। अंपराधों के लिए स्थानीय अधिकारी स्वयं ज़िम्मेदार होते थे।
6. गुप्तचर विभाग-शेरशाह ने देश में गुप्तचर विभाग स्थापित किया। गुप्तचर राजा को सभी घटनाओं से सूचित करते रहते थे।
7. न्याय-शेरशाह एक प्रसिद्ध सम्राट् था। न्याय करते समय छोटे-बड़े या अमीर-ग़रीब का भेदभाव नहीं रखा जाता था। उसके दण्ड बड़े कठोर थे। दण्ड देते समय वह अपने सरदारों और निकट सम्बन्धियों को भी नहीं छोड़ता था।
8. सड़कों का निर्माण तथा डाक व्यवस्था-शेरशाह सूरी ने पुरानी सड़कों की मुरम्मत करवाई और नई सड़कों का निर्माण करवाया। उसकी बनवाई हुई सड़कों में से पहली सड़क पेशावर से सुनार गांव तक जाती है। दूसरी आगरा से बुरहानपुर तक जाती थी। तीसरी सड़क आगरा से जोधपुर तक और चौथी सड़क लाहौर से मुल्तान तक चली गई थी। शेरशाह सूरी ने डाक लाने और ले जाने के लिए सड़कों पर डाक चौकियों की स्थापना भी की।
9. प्रजा की भलाई के कार्य-शेरशाह सूरी ने प्रजा की भलाई के लिए अनेक कार्य किए। उसने यात्रियों की सुविधा के लिए कुएँ खुदवाए और सड़कों के किनारे छायादार वृक्ष लगवाये। रात को ठहरने के लिए थोड़-थोड़ी दूरी पर सराएं भी बनवाई गईं।
सच तो यह है कि शेरशाह सूरी एक महान् शासन-प्रबन्धक था। उसके शासन-प्रबन्ध की प्रशंसा करते हुए कीन ने ठीक ही कहा है, “किसी भी सरकार ने, यहां तक कि अंग्रेजी सरकार ने भी, इस पठान, (शेरशाह) जैसी योग्यता नहीं दिखाई।”
![]()
![]()