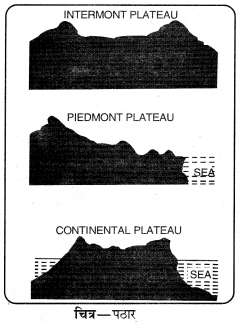
Punjab State Board PSEB 11th Class Sociology Book Solutions Chapter 12 पश्चिमी समाजशास्त्री विचारक Textbook Exercise Questions and Answers.
PSEB Solutions for Class 11 Sociology Chapter 12 पश्चिमी समाजशास्त्री विचारक
पाठ्य-पुस्तक के प्रश्न (Textual Questions)
I. निम्नलिखित प्रश्नों के उत्तर 1-15 शब्दों में दीजिए :
प्रश्न 1.
एक अकादमिक अनुशासन के रूप में समाज का औपचारिक अध्ययन किस देश में तथा किस शताब्दी में प्रारम्भ हुआ ?
उत्तर-
एक विषय के रूप में समाज का औपचारिक अध्ययन फ्राँस (यूरोप) में 19वीं शताब्दी में शुरू हुआ।
प्रश्न 2.
उन तीन कारकों के नाम बताइये जो एक स्वतन्त्र अनुशासन के रूप में समाजशास्त्र के विकास के लिए उत्तरदायी है।
उत्तर-
औद्योगिक क्रान्ति, फ्रांसीसी क्रान्ति तथा नवजागरण के विचारों के फैलाव से समाजशास्त्र का विकास एवं स्वतन्त्र विषय के रूप में हुआ।
प्रश्न 3.
नवजागरण से सम्बद्ध दो विचारकों के नाम बताइए।
उत्तर-
चार्ल्स मान्टेस्कयू (Charles Montesquieu) तथा जीन जैक्स रूसो (Jean Jacques Rousseau)।
प्रश्न 4.
फ्रांसीसी क्रान्ति किस वर्ष अस्तित्व में आयी ?
उत्तर-
फ्रॉसीसी क्रान्ति सन् 1789 में हुई थी।

प्रश्न 5.
प्रत्यक्षवाद शब्द से क्या अभिप्राय है ?
उत्तर-
यह माना जाता है कि समाज कुछ स्थिर नियमों के अनुसार कार्य करता है, जिन्हें ढूंढा जा सकता है। इसे ही सकारात्मकवाद कहते हैं।
प्रश्न 6.
किसने समाजशास्त्र की दो शाखाओं सामाजिक स्थितिकी तथा सामाजिक गतिकी की चर्चा की ?
उत्तर-
अगस्ते काम्ते ने यह नाम दिया।
प्रश्न 7.
अगस्ते कोंत के तीन चरणों के नियम को चार्ट द्वारा प्रस्तुत कीजिए।
उत्तर-
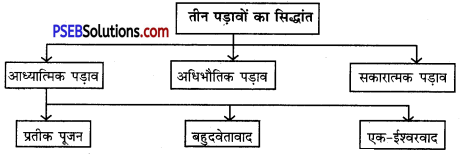
प्रश्न 8.
कार्ल मार्क्स का वर्ग का सिद्धांत किस निर्धारणवाद पर आधारित है ?
उत्तर-
कार्ल मार्क्स का वर्ग का सिद्धांत उत्पादन के साधनों की मल्कियत पर आधारित है कि एक समूह के पास उत्पादन के साधन होते हैं तथा एक के पास नहीं होते हैं।

प्रश्न 9.
‘कम्युनिस्ट मैनिफैस्टो’ पुस्तक किसने लिखी है ?
उत्तर-
पुस्तक ‘कम्युनिस्ट मैनिफैस्टो’ कार्ल मार्क्स ने लिखी है।
प्रश्न 10.
कार्ल मार्क्स द्वारा प्रस्तुत सामाजिक परिवर्तन के चरण कौन-से हैं ?
उत्तर-
मार्क्स के अनुसार सामाजिक परिर्वतन के चार मुख्य स्तर हैं–आदिम समुदाय समाज, दासमूलक समाज, सामन्ती समाज तथा पूँजीवादी समाज।
प्रश्न 11.
किसने समाज में उपस्थित एकता की प्रकृति के आधार पर समाज को वर्गीकृत है ?
उत्तर-
एमिल दुर्शीम ने समाज में मौजूद एकता की प्रकृति के आधार पर समाज को बाँटा है।
प्रश्न 12.
एमिल दुर्थीम द्वारा प्रस्तुत एकता के दो प्रकार बताइये।
उत्तर-
यान्त्रिक एकता (Mechnical Solidarity) तथा सावयवी एकता (Organic Solidarity)।

प्रश्न 13.
मैक्स वैबर द्वारा प्रस्तुत सामाजिक क्रिया के प्रकारों की सूची बताइये।
उत्तर-
मैक्स वैबर ने चार प्रकार की सामाजिक क्रिया के बारे में बताया है- Zweekrational, Wertnational, Affeective क्रिया तथा Traditional क्रिया।
प्रश्न 14.
मैक्स वैबर द्वारा प्रस्तुत सत्ता के प्रकार बताइये।
उत्तर-
मैक्स वैबर ने सत्ता के तीन प्रकार दिए हैं-परंपरागत सत्ता, वैधानिक सत्ता तथा करिश्मई सत्ता।
II. निम्नलिखित प्रश्नों के उत्तर 30-35 शब्दों में दीजिए :
प्रश्न 1.
नवजागरण किसे कहते हैं ?
उत्तर-
नवजागरण वह समय था जब काफ़ी अधिक बौद्धिक विकास हुआ तथा दार्शनिक विचारों में बहुत परिवर्तन आए। यह समय 17वीं-18वीं शताब्दी के बीच था। इस समय के मशहूर विचारक मान्टेस्क्यू तथा रूसो थे। यह विचारक विज्ञान की सर्वोच्चता तथा विश्वास के ऊपर तर्क को ऊँचा मानते थे। इन विचारों के कारण ही सामाजिक प्रकटन में वैज्ञानिक विधि के प्रयोग पर बल दिया।
प्रश्न 2.
धर्मशास्त्रीय तथा तत्वशास्त्रीय चरणों पर संक्षिप्त टिप्पणी लिखिए।
उत्तर-
कोंत के अनुसार आध्यात्मिक पड़ाव में मनुष्य के विचार काल्पनिक थे। वह सभी चीज़ों को परमात्मा के रूप में समझता था। धारणा यह थी कि चाहे सभी चीज़े निर्जीव हैं परन्तु उनमें सर्वशक्ति व्यापक है। अधिभौतिक पड़ाव 14वीं से 16वीं शताब्दी तक चला। इस समय बेरोक निरीक्षण का अधिकार सामने आया जिसकी कोई सीमा नहीं थी। इस कारण आत्मिकता का पतन हुआ जिसका सांसारिक पक्ष पर भी प्रभाव पड़ा।

प्रश्न 3.
जीववाद (Animism) से आप क्या समझते हैं ?
उत्तर-
जीववाद एक विचारधारा है जिनमें लोग विश्वास करते हैं कि परमात्मा केवल चलने वाली या जीने वाली वस्तुओं में मौजूद है। शब्द Anima का अर्थ है आत्मा (Soul) या चाल (Movement)। लोगों ने जानवरों, पंक्षियों, पृथ्वी तथा हवा की भी पूजा करनी शुरू कर दी।
प्रश्न 4.
कार्ल मार्क्स की वर्ग की परिभाषा दीजिए।
उत्तर-
मार्क्स के अनुसार, “वर्ग लोगों के ऐसे बड़े-बड़े समूहों को कहते हैं जो सामाजिक उत्पादन की इतिहास की तरफ से निर्धारित किसी पद्धति में, अपने-अपने स्थान की दृष्टि से, उत्पादन के साधनों के साथ अपने संबंध की दृष्टि से, परिश्रम के सामाजिक संगठन में अपनी भूमिका की दृष्टि से तथा परिणामस्वरूप सामाजिक सम्पत्ति के जितने हिस्से के वह मालिक होते हैं, उसके परिणाम तथा उसे प्राप्त करने के तौर-तरीके की दृष्टि से एक-दूसरे से अलग होते हैं।
प्रश्न 5.
वर्ग चेतना से आप क्या समझते हैं ?
उत्तर-
प्रत्येक वर्ग अपने सदस्यों, उनकी सामाजिक स्थिति, रुतबें इत्यादि के बारे में चेतन होता है। इस प्रकार की चेतना को ही वर्ग चेतना कहा जाता है। सभी वर्गों के लोग अपने समूह के प्रति चेतन होते हैं जिस कारण वह साधारण तथा अपने वर्ग के सदस्यों के साथ ही संबंध रखना पसंद करते हैं।
प्रश्न 6.
ऐतिहासिक भौतिकवाद को परिभाषित कीजिए।
उत्तर-
ऐतिहासिक भौतिकवाद वह दार्शनिक विद्या है जो एक अखण्ड व्यवस्था के रूप में समाज का तथा उस व्यवस्था के कार्य तथा विकास को शामिल करने वाले मुख्य नियमों का अध्ययन करती है। संक्षेप में ऐतिहासिक भौतिकवाद सामाजिक विकास का दार्शनिक सिद्धांत है। इस प्रकार यह मार्क्स का सामाजिक तथा ऐसिहासिक सिद्धांत है।

प्रश्न 7.
सामाजिक तथ्य पर एक संक्षिप्त टिप्पणी लिखिए।
उत्तर-
दुर्थीम ने सामाजिक तथ्य का सिद्धांत दिया था तथा अपनी पुस्तक के प्रथम अध्याय के अंत में इसकी परिभाषा दी। दुर्थीम के अनुसार, “एक सामाजिक तथ्य क्रिया करने का प्रत्येक स्थायी, अस्थायी तरीका है जो व्यक्ति के ऊपर बाहरी दबाव डालने में समर्थ होता है अथवा दोबारा क्रिया करने का प्रत्येक तरीका है जो किसी समाज में आम रूप से पाया जाता है परन्तु साथ ही व्यक्तिगत विचारों से स्वतन्त्र अस्तित्व रखता है।
प्रश्न 8.
सावयवी एकता (Organic Solidarity) पर चर्चा कीजिए।
उत्तर-
सावयवी एकता आधुनिक समाजों में पाई जाती है तथा यह स्तर सदस्यों के बीच मौजूद अंतरों पर आधारित है। यह अधिक जनसंख्या वाले समाजों में पाई जाती है जहाँ पर लोगों के बीच अव्यक्तिगत सामाजिक संबंध पाए जाते हैं। इन समाजों में प्रतिकारी कानून पाए जाते हैं।
प्रश्न 9.
ज्वैकरेशनल क्रिया से आप क्या समझते हैं ?
उत्तर-
Zweckrational क्रिया का अर्थ ऐसे सामाजिक व्यवहार से होता है जो उपयोगिता को ध्यान में रखते हुए कई उद्देश्यों की अधिक-से-अधिक प्राप्ति के लिए तार्किक रूप से निर्देशित हो। इसमें साधनों के चुनाव केवल उनकी विशेष कार्यकुशलता की तरफ ही ध्यान नहीं दिया जाता बल्कि मूल्य में की तरफ भी ध्यान जाता है।
प्रश्न 10.
भावनात्मक क्रिया किसे कहते हैं ?
उत्तर-
यह वह क्रियाएं हैं जो मानवीय भावनाओं, संवेगों तथा स्थायी अर्थों के कारण होती हैं। समाज में रहते हुए, प्रेम, नफरत, गुस्सा इत्यादि जैसी भावनाओं का सामना करना पड़ता है। इस कारण ही समाज में शान्ति या अशान्ति की अवस्था उत्पन्न हो जाती है। इन व्यवहारों के कारण परंपरा तथा तर्क का थोड़ा सा भी सहारा नहीं लिया जाता।

प्रश्न 11.
सत्ता को परिभाषित कीजिए।
उत्तर-
वैबर के अनुसार प्रत्येक संगठित समूह में सत्ता में तत्त्व मूल रूप में मौजूद होते हैं। संगठित समूह में कुछ तो साधारण सदस्य होते हैं तथा कुछ व्यक्ति ऐसे होते हैं जिनके पास ज़िम्मेदारी होती है तथा वह अन्य लोगों से वैधानिक तौर पर आदेश देकर अपनी बात मनवाते हैं। इस बात मनवाने की व्यवस्था को ही सत्ता कहते हैं।
III. निम्नलिखित प्रश्नों के उत्तर 75-85 शब्दों में दीजिए :
प्रश्न 1.
अगस्त कोंत द्वारा प्रतिपादित तीन चरणों के नियम की विवेचना कीजिए।
उत्तर-
अगस्त कोंत ने समाज के उद्विकास का सिद्धांत दिया तथा कहा कि समाज के विकास के तीन पड़ाव हैं-आध्यात्मिक पड़ाव, अधिभौतिक पड़ाव तथा सकारात्मक पड़ाव। आध्यात्मिक पड़ाव में मनुष्य के सभी विचार काल्पनिक थे तथा वह सभी वस्तुओं को किसी आलौकिक जीव की क्रियाओं के परिणाम के रूप में मानता था। धारणा यह थी कि चाहे सभी वस्तुएं निर्जीव हैं परन्तु उनमें वह शक्ति व्यापक है। दूसरा पड़ाव अधिभौतिकं पडाव था जो 14वीं शताब्दी से 19वीं शताब्दी तक चला। इस पड़ाव में क्रान्तिक आंदोलन शुरू हुआ तथा प्रोटैस्टैंटवाद सामने आया। 16वीं शताब्दी में नकारात्मक सिद्धांत सामने आया जिसका मुख्य उद्देश्य सामाजिक परिवर्तन था। इसमें बेरोक निरीक्षण का अधिकार था तथा निरीक्षण की कोई सीमा नहीं थी। सकारात्मक पड़ाव में औद्योगिक समाज शुरू हुआ तथा विज्ञान सामने आया। इसमें सामाजिक व्यवस्था तथा प्रगति में कोई द्वन्द नहीं होता है।
प्रश्न 2.
यान्त्रिक एकता की विशेषताओं की चर्चा कीजिए।
उत्तर-
- यान्त्रिक एकता वाले समाज के सदस्यों के व्यवहारों में समरूपता मिलती है तथा उनके व्यवहार एक जैसे होते हैं।
- समान विश्वास तथा भावनाएं यान्त्रिक एकता के प्रतीक हैं। इस समाज के सदस्यों में सामूहिक चेतना मौजूद होती है।
- यान्त्रिक समाजों में दमनकारी कानून मिलते हैं जहाँ पर अपराधी को पूर्ण दण्ड देने की व्यवस्था होती है।
- नैतिकता यान्त्रिक समाजों का मूल आधार होती है जिस कारण समाज में एकता बनी रहती है।
- धर्म यान्त्रिक समाज में एकता का महत्त्वपूर्ण आधार है तथा धर्म के अनुसार ही आचरण तथा व्यवहार किया जाता है।

प्रश्न 3.
सावयवी एकता की विशेषताओं की चर्चा कीजिए।
उत्तर-
- आंगिक अथवा सावयवी एकता वाले समाजों में विभेदीकरण तथा विशेषीकरण पाया जाता है। समाज में बहत से वर्ग मिलते हैं।
- इन समाजों में श्रम विभाजन का बोलबाला होता है तथा लोग अपनी आवश्यकताओं की पूर्ति के लिए एक दूसरे पर निर्भर होते हैं।
- इन समाजों में बहुत से संगठन तथा समूह मिलते हैं जिस कारण इनमें प्रतिकारी कानूनों की प्रधानता होती
- सावयवी समाजों में समझौतों पर आधारित संबंध सामाजिक एकता का स्रोत होते हैं तथा नौकरियों में व्यक्तियों को अनुबंध पर रखा जाता है।
- सावयवी एकता वाले समाजों में धर्म का प्रभाव काफ़ी कम होता है।
- इस प्रकार के समाज आधुनिक समाज होते हैं।
प्रश्न 4.
धर्मशास्त्रीय एवं तत्वशास्त्रीय चरणों में अंतर कीजिए।
उत्तर-
1. धर्मशास्त्रीय पड़ाव-यह पड़ाव मानवता के शुरू होने के समय शुरू होता है जब मनुष्य प्राकृतिक शक्तियों से डरता था। वह सभी चीजों को किसी आलौकिक शक्ति की क्रियाओं के परिणाम के रूप में देखता था। वह सोचता था कि चाहे सभी वस्तुएं निर्जीव हैं परन्तु सब में परमात्मा मौजूद है। यह पड़ाव आगे तीन उप-पड़ावों प्रतीक पूजन, बहु-देवतावाद तथा एक-ईश्वरवाद में विभाजित है।
2. तत्वशास्त्रीय पड़ाव-इस पड़ाव को काम्ते आधुनिक समाज का क्रान्तिक समय भी कहता है। यह पड़ाव 5 शताब्दियों तक 14वीं से 19वीं तक चला। इसे दो भागों में विभाजित किया गया है। प्रथम भाग में क्रान्तिक आंदोलन स्वयं ही चल पड़ा तथा क्रान्तिक फिलास्फी 16वीं शताब्दी में प्रोटैस्टैंटवाद में आने से शुरू हुई। दूसरा भाग 16वीं शताब्दी से शुरू हुआ। इसमें नकारात्मक सिद्धांत शुरू हुआ जिसका मुख्य उद्देश्य सामाजिक परिवर्तन था। इसमें बेरोक निरीक्षण का अधिकार था।
प्रश्न 5.
क्या आप सोचते हैं कि निकट भविष्य में साम्यवादी समाजों द्वारा पूँजीवाद को विस्थापित कर दिया जायेगा ?
उत्तर-
जी नहीं, हम नहीं सोचते कि आने वाले भविष्य में पूँजीवादी व्यवस्था को कम्युनिस्ट व्यवस्था बदल देगी। वास्तव में पूँजीवादी व्यवस्था स्वतन्त्र मार्कीट के सिद्धांत पर आधारित है जबकि कम्युनिस्ट अर्थव्यवस्था सरकारी नियन्त्रण के अन्तर्गत होती है तथा आजकल के समय में कोई भी सरकारी नियन्त्रण को पसन्द नहीं करता। 1917 में रूस में राजशाही को कम्युनिस्ट व्यवस्था ने बदल दिया था परन्तु वहां की अर्थव्यवस्था का कुछ ही समय में बुरा हाल हो गया था। इस कारण ही सन् 1990 में U.S.S.R. के टुकड़े हो गए थे तथा वह कई देशों में विभाजित हो गया था। इस प्रकार हम कह सकते हैं कि कम्युनिस्ट पूँजीवादी व्यवस्था को नहीं बदल सकती।

IV. निम्नलिखित प्रश्नों के उत्तर 250-300 शब्दों में दें:
प्रश्न 1.
क्या समाजशास्त्र एक पूर्ण विज्ञान के रूप में विकसित हुआ है जिसकी कल्पना अगस्ते कोंत ने की थी ?
उत्तर-
शब्द समाजशास्त्र (Sociology) का प्रथम बार प्रयोग अगस्ते काम्ते ने 1839 में किया था। काम्ते ने एक पुस्तक लिखी ‘The Course on Positive Philosophy’ जो कि 6 भागों में छपी थी। इस पुस्तक में उन्होंने कहा था कि समाज में अलग-अलग भागों का अध्ययन अलग-अलग सामाजिक विज्ञान करते हैं, उदाहरण के लिए समाज के राजनीतिक हिस्से का अध्ययन राजनीति विज्ञान करता है, आर्थिक हिस्से का अध्ययन अर्थशास्त्र करता है। उस प्रकार एक ऐसा विज्ञान भी होना चाहिए जो समाज का अध्ययन करे। इस प्रकार उन्होंने समाज, सामाजिक संबंधों के अध्ययन की कल्पना की तथा उनकी कल्पना के अनुसार एक नया विज्ञान सामने आया जिसे समाजशास्त्र का नाम दिया गया।
काम्ते के पश्चात् हरबर्ट स्पैंसर ने भी कई संकल्प दिए जिससे समाजशास्त्र का दायरा बढ़ना शुरू हुआ। इमाईल दुर्थीम प्रथम समाज शास्त्री था जिसने समाजशास्त्र को एक विज्ञान के रूप में स्थापित करने का प्रयास किया। उन्होंने अपने अध्ययनों में वैज्ञानिक विधि का प्रयोग किया तथा कहा कि समाज का वैज्ञानिक विधियों, जैसे कि निरीक्षण की सहायता से अध्ययन किया जा सकता है। उनके द्वारा दिए संकल्पों, जैसे कि सामाजिक तथ्य, आत्महत्या का सिद्धांत, श्रम विभाजन का सिद्धांत, धर्म का सिद्धांत इत्यादि में वैज्ञानिक विधियों का प्रयोग साफ झलकता है। समाजशास्त्र के इतिहास में दुर्थीम पहले प्रोफैसर थे।
समाजशास्त्र को विज्ञान के रूप में स्थापित करने में कार्ल मार्क्स तथा मैक्स वैबर ने भी बहुत बड़ा योगदान दिया। कार्ल मार्क्स ने संघर्ष का सिद्धांत दिया तथा सम्पूर्ण समाजशास्त्र संघर्ष सिद्धांत में इर्द-गिर्द घूमता है।
मार्क्स ने समाज का आर्थिक पक्ष से अध्ययन किया तथा बताया कि समाज का इतिहास वर्ग संघर्ष का इतिहास है। उन्होंने दो प्रकार के वर्गों तथा उनके बीच हमेशा चलने वाले संघर्ष का विस्तृत वर्णन किया। उन्होंने ऐतिहासिक भौतिकवाद, वर्ग तथा वर्ग संघर्ष का सिद्धांत, अलगाव का सिद्धांत जैसे संकल्प समाजशास्त्र को दिए। मैक्स वैबर ने भी समाजशास्त्र को विज्ञान के रूप में स्थापित करने का प्रयास किया तथा सामाजिक क्रिया का सिद्धांत दिया। उन्होंने समाजशास्त्र की व्याख्या दी, सामाजिक क्रिया का सिद्धांत दिया, सत्ता तथा प्रभुत्ता का सिद्धांत दिया, धर्म की व्याख्या दी तथा कर्मचारीतन्त्र का सिद्धांत दिया।
इन सभी समाजशास्त्र के संस्थापकों के पश्चात् बहुत से समाजशास्त्री हुए तथा समाजशास्त्र को विज्ञान के रूप में स्थापित करने में उनके योगदान को नकारा नहीं जा सकता। टालक्ट पारसन्ज़, जे० एस० मिल, राबर्ट मर्टन, मैलिनोवस्की, गिलिन व गिलिन, जी० एस० घूर्ये इत्यादि जैसे समाजशास्त्री इनमें से प्रमुख हैं।
अब पिछले कुछ समय से समाजशास्त्र में वैज्ञानिक विधियों का प्रयोग काफ़ी हद तक किया जा रहा है ताकि अध्ययन को अधिक-से-अधिक वस्तुनिष्ठ तथा निष्पक्ष रखा जा सके। इससे एक क्षेत्र में किए अध्ययनों को दूसरे क्षेत्रों में भी लागू किया जा सकेगा। उपकल्पना, निरीक्षण, सैंपल विधि, साक्षात्कार, अनुसूची प्रश्नावली, केस स्टडी, वर्गीकरण, सारणीकरण, आँकड़ों के प्रयोग से समाजशास्त्र निश्चित रूप से एक विज्ञान के रूप में स्थापित हो गया है।
प्रश्न 2.
मार्क्स का वर्ग संघर्ष का सिद्धांत बताइये।
उत्तर-
मार्क्स की उन्नत ‘वैज्ञानिक प्रस्थापना’ में यह बात भी शामिल है कि उन्होंने अलग सामाजिक समूहों पर सर्वप्रथम वर्गों के अस्तित्व की व्याख्या की थी। सबसे महत्त्वपूर्ण बात यह है कि मार्क्स ने वर्गों की व्याख्या बहुत अच्छे प्रकार से की है। मार्क्स की विचारक खोज का मुख्य उद्देश्य यह पता करना था कि यह मानव समाज जिसमें हम सभी रहते हैं, और इसका जो रूप या स्वरूप हमें दिखाई देता है वह इस तरह क्यों है ? और इस समाज में परिवर्तन क्यों और किन शक्तियों के द्वारा आते हैं ? इसके साथ ही मार्क्स ने इसकी स्पष्ट व्याख्या और विवेचना की थी और लिखा था कि आने वाले समय में समाज में किस तरह और कैसे परिवर्तन आयेंगे ? अपनी खोजों के द्वारा मार्क्स और उसके निकट सहयोगी ‘ऐंजलस’ इस निष्कर्ष पर पहुंचे कि इस समाज में काफ़ी अमानवीय शोषण फैला हुआ है। इसलिये उन्होंने अपनी खोज का दूसरा उद्देश्य उस समाज का निर्माण करना या स्थापना करनी है जो कि शोषण रहित हो बताया है ।
वर्ग किसे कहते हैं (What is Class) मार्क्स के वर्ग संघर्ष को समझने के लिये यह अति आवश्यक है कि पहले यह जाने कि वर्ग क्या है ? कार्ल मार्क्स ने इतिहास का अध्ययन करने के लिये इस बात की विशेष वकालत की कि हमें यह अध्ययन उस दृष्टिकोण से करना चाहिये जिसके साथ हम उन प्राकृतिक नियमों का पता लगा सकें जो पूरे मानव इतिहास का संचालन करते हैं और ऐसा करने के लिए हमें कुछ विशेष व्यक्तियों के कार्यों और आम व्यक्तियों के कार्यों और व्यवहारों की तरफ ध्यान देना चाहिये। प्रत्येक समाज लगभग कई जनसमूहों में बंटे हुए होते हैं। इस प्रकार भिन्न-भिन्न वर्ग एक विशेष सामाजिक आर्थिक इकाई का निर्माण करते थे। इस इकाई विशेष को हम वर्ग के नाम से जानते हैं।
मार्क्स ने अपने कम्युनिस्ट मैनीफैस्टो किस्से के पहले अध्याय की शुरुआत भी इन्हीं शब्दों से की है कि अभी तक समाज का इतिहास वर्ग संघर्ष का इतिहास रहा है और इतिहास में वर्णित समाजों में हर समाज में विभिन्न प्रकार की श्रेणियां पाई जाती हैं। सामाजिक श्रेणियों की बहरूपी दर्जाबंदी, प्राचीन रोम में पैट्रोशियन, नाई पलेबियन और दास मिलते थे। मध्यकाल में हमें सामन्तवादी अधीन जागीरदारी, उस्ताद, कारीगर, मज़दूर कारीगर, ज़मीनी दास इत्यादि दिखाई पड़ते हैं और लगभग इन सभी में द्वितीय श्रेणियां या वर्ग पाए जाते हैं।
मार्क्स की वर्ग व्यवस्था के आधार पर ही लेनिन ने वर्गों की व्याख्या और परिभाषा पेश की है। लेनिन ने लिखा है कि, “वर्ग लोगों के ऐसे बडे-बडे समूहों को कहते हैं जो सामाजिक उत्पादन की इतिहास की तरफ से निर्धारित किसी पद्धति में अपनी-अपनी जगह की नज़र से उत्पादन के साधनों के साथ अपने सम्बन्धों जो कि अधिकतर मामलों में कानून के द्वारा निश्चित और निरूपित होते हैं की नज़रों से, मेहनत के सामाजिक संगठन में अपनी भूमिका को नज़र से और फलस्वरूप सामाजिक सम्पत्ति के जितने भाग के वह मालिक होते हैं, उसके परिमाण और उसको प्राप्त करने के तौर-तरीकों की नज़र से एक दूसरे से अलग होते हैं।”
मार्क्स के अनुसार, “इतिहास की भौतिकवादी धारणा में यह कहा गया है कि मानव जीवन के विकास के लिये आवश्यक साधनों का उत्पादन और उत्पादन के उपरान्त बनी वस्तुओं का लेन-देन (Exchange) प्रत्येक सामाजिक व्यवस्था का आधार है। इतिहास में जितनी भी सामाजिक व्यवस्थाएं बनी हैं इसमें जिस तरह धन का बंटवारा हुआ है और समाज का वर्गों और श्रेणियों में बंटवारा हुआ है वह इस बात पर निर्भर है कि इस समाज में क्या उत्पादन हुआ है ? और कैसे हुआ है ? और फिर उपज की Exchange कैसे हुई ? मार्क्स के अनुसार, “किसी भी युग में परिश्रम का बंटवारा और जीवन जीने के साधनों की प्राप्ति के अलग-अलग साधनों के होने के कारण मनुष्य अलग-अलग वर्गों में बंट जाता है और प्रत्येक वर्ग की विशेष वर्ग चेतनता होती है।”
वर्ग से मार्क्स का अर्थ भारत की जातीय व्यवस्था से सम्बन्धित नहीं है बल्कि वर्ग से उनका अर्थ उस जातीय समूह व्यवस्था से है जिसकी परिभाषा उत्पादन की उस प्रक्रिया में उनकी भूमिका के साथ की जा सकती है। आम शब्दों में कहा जाये तो वर्ग लोगों के ऐसे समूहों को कहा जाता है, जो अपनी जीविका केवल एक ही ढंग से कमाते हैं, वर्ग का जन्म उत्पादन के तौर-तरीकों पर आधारित होता है। जैसे किसी उत्पादन व्यवस्था में परिवर्तन आता है, तो पुराने वर्गों के स्थान पर नये स्थान ले लेते हैं।
वर्ग संघर्ष (Class Struggle)-
इस तरह कार्ल मार्क्स ने प्रत्येक समाज में दो-दो वर्गों की विवेचना की है। मार्क्स की वर्ग की धारणाओं को प्रत्येक समाज में ध्यान से समझने के पश्चात् हम अब इस स्थिति में है कि उसकी वर्ग संघर्ष की धारणा को समझें। मार्क्स ने बताया कि समाज के प्रत्येक वर्ग में दो प्रकार के परस्पर विरोधी वर्ग रहे हैं। एक शोषण करने वाला व दूसरा जो शोषण को सहन करता है। इनमें आपस में संघर्ष होता है। इसे मार्क्स ने ‘वर्ग संघर्ष’ का नाम दिया है। कम्युनिस्ट घोषणा-पत्र में वह कहते हैं कि समाज के अस्तित्व के साथ-साथ ही वर्ग संघर्ष का भी जन्म हो जाता है। मार्क्स का यह वर्ग संघर्ष का सिद्धान्त उसके विचारों से और संसार में भी बहुत महत्त्वपूर्ण है।
उनके प्रभाव के कारण ही ‘स्माल थास्टरीन बैवलीन’ और ‘कूले’ इत्यादि ने भी वर्ग संघर्ष को अपने चिन्तन का एक अंग रूप माना है।
मार्क्स के अनुसार, “उत्पादन की प्रक्रियाओं में अलग-अलग वर्गों की अलग-अलग भूमिकाएं होती हैं। अब वर्गों की आवश्यकताओं और हितों पर संघर्ष की स्थिति पैदा होना आवश्यक है। वही संघर्ष विरोधी विचारधारा में एक ‘आधार’ (Base) पैदा करता है। विकासशील उत्पादित शक्तियों और प्रकृतिवादी स्थिर सम्पत्ति के सम्बन्धों में टकराव पैदा होता है। इससे संघर्ष की गति भी तेजी से बढ़ती है। इतिहास की गति वर्गों की भूमिका के द्वारा ही निर्धारित होती है और सामाजिक एवं आर्थिक वर्ग उन सभी समाजों में पाए जाते हैं जहां श्रम विभाजन का आम सिद्धान्त लागू होता है।
मार्क्स के अनुसार वर्ग संघर्ष एक ऐसी उत्पादित व्यवस्था से जन्म लेता है, जो समाज को भिन्न-भिन्न वर्गों में बांट देती है। इसमें एक वर्ग तो काफ़ी कठोर परिश्रम करके उत्पादन करता है, जैसे दास, अर्द्धदास, किसान और मज़दूर इत्यादि और दूसरा वर्ग ऐसा है जो उत्पादन के लिये कोई परिश्रम किये बिना, बिना कोई काम किये उत्पादन के बड़े-बड़े भाग का उपयोग करता है, जैसे दासों के स्वामी, जागीरदार, ज़मींदार और पूंजीपति इत्यादि। मार्क्स के अनुसार, “इस वर्ग संघर्ष को मनुष्य के उत्पादन की पहली और ऊंची अवस्था तक पहुंचने में मदद करता है। वह मानते हैं कि कोई भी क्रान्ति जब सफल होती है तो उनके साथ नयी आर्थिक सामाजिक व्यवस्था का जन्म होता है।”
इस आधार पर ही मार्क्स ने अब तक के मानवीय इतिहास को चार युगों में विभाजित किया है-
1. पहला युग-इतिहास का पहला युग आदिम साम्यवादी समाज था। इस युग में उत्पादन के साधन अविकसित थे। उत्पादन के साधनों को आवश्यक वस्तुओं को उत्पन्न करने के लिए प्रयोग किया जाता था तथा संयुक्त परिश्रम के साथ इन्हें प्रयोग किया जाता था। इस प्रकार उत्पादन पर सभी का समान अधिकार होता था। आर्थिक शोषण तथा वर्ग भेद नाम की कोई चीज़ मौजूद नहीं थी।
2. दूसरा युग-दूसरा युग दास मूलक समाज का था। कृषि, पशुपालन तथा धातु के औज़ारों के विकसित होने से उत्पादन व्यवस्था के सम्बन्ध बदल गए तथा दास प्रथा शुरू हो गयी। विकसित उत्पादन के साधनों के कारण व्यक्तिगत संपत्ति का संकल्प सामने आया। इस समय दास स्वामी तथा दासों के अलग-अलग वर्ग बन गए तथा वर्ग संघर्ष शुरू हो गया। मार्क्स का कहना था कि इस समाज से ही वर्ग संघर्ष की शुरुआत हुई क्योंकि मालिकों ने अपने दासों का शोषण करना शुरू कर दिया था।
3. तीसरा युग-सामन्ती समाज तीसरा युग था। इस युग में उत्पादन के साधनों पर कुछ सामन्तों तथा भूपतियों का अधिकार हो गया। इस युग में निजी सम्पत्ति की धारणा और सुद्रढ़ हो गई। कई विकासशील तथा अर्द्ध विकसित देशों में इस युग के अवशेष देखने को मिल जाएंगे। इस युग में सामन्तों तथा किसानों के दो वर्ग बन गए तथा वर्ग संघर्ष और तेज़ हो गया।
4. चौथा युग-चौथा युग पूँजीपति समाज था। 15वीं शताब्दी के अंत में विज्ञान का विकास होना शुरू हुआ। इससे उत्पादन व्यवस्था के सम्बन्धों तथा उत्पादन के नए साधनों में विरोध उत्पन्न हो गए। मशीनों का आविष्कार हुआ। बड़े-बड़े उद्योग स्थापित हुए जिससे पूँजीवादी युग शुरू हो गया तथा यह आज भी चल रहा है। इस व्यवस्था में एक तरफ तो उद्योगों के मालिक थे तथा दूसरी तरफ उन उद्योगों में कार्य करने वाले श्रमिक थे। इस प्रकार दो वर्ग पूँजीपति तथा श्रमिक बन गए। इस युग में विज्ञान की प्रगति से, शिक्षा के बढ़ने, बड़े उद्योगों में श्रमिकों के इकट्ठे रहने के कारण आसानी से संगठित होने से वर्ग चेतना का काफ़ी विकास हो गया है। आज का शोषित वर्ग अब शोषण तथा वर्ग विरोधों को और सहन करने को तैयार नहीं हैं। अब वर्ग संघर्ष अपनी चरम सीमा पर पहुँच गया है। मार्क्स का कहना है कि पूँजीवादी युग का खात्मा आवश्यक है। शोषण पर आधारित यह अन्तिम व्यवस्था होगी। आज पूँजीवाद का खात्मा शुरू हो गया है। मनुष्यों का समाज तेज़ी से समाजवाद की तरफ बढ़ रहा है। रूस तथा चीन की समाजवादी सरकारों की स्थापना इसका प्रमाण है।
मार्क्स के अनुसार, “निजी सम्पत्ति ही शोषण की जड़ है। इसी के कारण ही मूल रूप से आर्थिक उत्पादन के क्षेत्र में समाज में दो मुख्य वर्ग हैं। इनमें एक वर्ग के हाथ में आर्थिक उत्पादन के सभी साधन केन्द्रित हो जाते हैं जिसके आधार पर यह वर्ग शोषित और कमजोर वर्ग का शोषण करता है।” इन वर्गों में आपस में समाज की हर युग (केवल आदिमयुग छोड़कर) में आपस में वर्ग संघर्ष चलता आया है। मार्क्स की मान्यता के अनुसार, सभी उत्पादन साधनों पर अधिकार करके शोषक वर्ग बल के साथ अपने सैद्धान्तिक विचारों एवं जीवन प्रणाली को सारे समाज पर थोपता है। मार्क्स के अनुसार, “वह वर्ग जो समाज की शोषक भौतिक शक्ति होता है, साथ ही समाज की शासक भौतिक शक्ति भी होता है। वह वर्ग जिसके पास भौतिक उत्पादन के साधन मौजूद होते हैं वह सामाजिक उत्पादन के साधनों पर भी नियन्त्रण रखता है। इस प्रकार के नियन्त्रण के लिए शोषक वर्ग बल प्रयोग भी करता है। उसके द्वारा समाज के ऊपर थोपे गये धर्म, दर्शन, राजनीति, अर्थशास्त्र और नैतिकता के विचार उसके इस प्रभाव को मज़बूत करने के लिये शोषण वर्ग के दास बन जाते हैं। शोषण की इस स्थिति को बरकरार रखने के लिए नये उभरते हुए शोषित वर्ग को बलपूर्वक दबाना आवश्यक हो जाता है। इसलिये मार्क्स ने कहा है बल नये समाज को अपने गर्भ में धारण करने वाले प्रत्येक पुराने समाज की ‘दाई’ (Midwife) है।
समाज का विकास अलग-अलग अवस्थाओं की देन हैं। किसी भी सामाजिक व्यवस्था अथवा ऐतिहासिक युग का मूल्यांकन हालातों, देश तथा काल के ऊपर निर्भर करता है। कोई भी सामाजिक व्यवस्था स्थायी नहीं है। सभी प्रक्रियाएँ द्वन्दात्मक होती है। उत्पादन की नई तथा पुरानी प्रक्रिया में जो अन्दरूनी संघर्ष होता है वह ही इसकी प्रेरक शक्ति होती है। पुरानी के स्थान पर नई पद्धति को अपनाना आवश्यक होता है। धीरे-धीरे होने वाले परिमाणात्मक परिवर्तन तेज़ी से अचानक होने वाले गुणात्मक परिवर्तन में बदल जाते है। इसलिए विकास के नियम के अनुसार क्रान्तिकारी परिवर्तन आवश्यक तथा स्वाभाविक होते हैं।
यह परिवर्तन बल (Force) पर आधारित होते हैं। विकास के रास्ते में उभरने वाली असंगतियों के आधार पर विरोधी शक्तियों में टकराव होता है। अंत में वर्ग संघर्ष तेज़ होता है जिसमें शोषित वर्ग अर्थात् मज़दूर वर्ग का अन्तिम रूप में जीतना आवश्यक है। मार्क्स के अनुसार इन विरोधों के कारण पूंजीवाद स्वयं विनाश की तरफ बढ़ता है।
पूँजीवादी व्यवस्था में दिन प्रतिदिन निर्धनता, बेरोज़गारी, भूखमरी बढ़ जाएगी। सहन करने की एक सीमा के पश्चात श्रमिक वर्ग क्रान्ति शुरू कर देगा। मार्क्स के अनुसार पूंजीवाद शोषण पर आधारित अन्तिम व्यवस्था होगी। अपने स्वार्थों के साथ घिरे पूंजीवाद संसदीय नियमों के साथ अपने एकाधिकार का कभी भी त्याग नहीं करेंगे। जैसे कि महात्मा गांधी ने अपने ट्रस्टीशिप सिद्धान्त की व्याख्या में कहा था। शांतिपूर्ण तरीके से शोषण को खत्म नहीं किया जा सकता था। इसके लिये क्रान्ति ज़रूरी है। समाज का एक बहुत बड़ा भाग (सर्वहारा) मजबूर हो जायेगा और यही क्रान्तिकारी हरियाली को दर्शायेगा।”
सर्वहारा (मज़दूर) वर्ग की लीडरशिप में वर्ग संघर्ष के द्वारा राज्य के यन्त्र पर अधिकार हो जाने के बाद समाजवाद के युग का आरम्भ होगा। मार्क्स के अनुसार राज्य शोषक वर्ग के हाथ में होने के कारण दमन की नीति एक बहुत बड़ा हथियार होता है। क्रान्ति के बाद भी सामन्तवाद और पूंजीवाद के दलाल प्रति क्रान्ति की कोशिश करते हैं। इसलिए पूंजीवाद के समाजवाद के बीच जाने के समय मज़दूर की सत्ता की अस्थाई अवस्था होगी। समाजवाद की स्थापना के बाद शोषण का अन्त हो जायेगा। इससे वर्ग समाप्त हो जाएंगे। इससे प्रत्येक व्यक्ति को अपनी मेहनत का पूर्ण भाग मिल सकेगा। समाजवाद की अधिक उन्नतावस्था में प्रत्येक व्यक्ति को उसकी आवश्यकता अनुसार मिलेगा। धीरे-धीरे राज्य जो शोषक वर्ग का हथियार रहा है, टूट जायेगा और इसके स्थान पर आपसी सहयोग और सहकारिता के आधार पर बनी संस्थाएं ले लेंगी। वर्गों और वर्ग संघर्ष का अन्त हो जायेगा।
सर्वहारा (मज़दूर) और पूंजीपति के बीच चले वर्ग संघर्ष का अन्त पूंजीवाद के अन्त के साथ ही होगा। उत्पादन के साधनों पर समाज का अधिकार हो जाने के साथ उत्पादन पर लगे प्रतिबन्ध हट जायेंगे। उत्पादन की शक्तियां और समय की बर्बादी भी खत्म हो जायेगी। वर्ग संघर्ष के द्वारा वर्गों का अन्त आज केवल एक दुःस्वप्न मात्र बन कर नहीं रह गया। संसार बड़ी तेज़ी से वर्गहीन समाजवादी समाज की स्थापना की तरफ बढ़ रहा है। ‘ऐंजलस’ ने काफ़ी समय पहले ही कहा था “आज इतिहास में पहली बार यह सम्भावना पैदा हो गई है कि सामाजिक उत्पादन के द्वारा समाज के प्रत्येक सदस्य को ऐसा जीवन मिल सके जो भौतिक दृष्टि से अच्छा हो जाये और दिन प्रतिदिन अधिक सुख सम्पन्न हो जाये, ऐसा नहीं एक ऐसे जीवन का निर्माण हो जिसमें व्यक्ति की शारीरिक एवं मानसिक शक्तियों का उन्मुख विकास संभावित हो। इस बात की सम्भावना पहली बार बनी है परन्तु बनी ज़रूर है।
श्रमिकों की क्रांति के द्वारा इन विरोधों तथा अन्य विरोधों का हल होगा। श्रमिकों की मुक्ति के इस कार्य को पूर्ण करना आधुनिक श्रमिक वर्ग का ऐतिहासिक फर्ज हैं। इसके बाद मनुष्य स्वयं श्रमिक के रूप में अपने इतिहास का निर्माण करेगा।
मार्क्स की एक दृढ़ विचारधारा है इस अन्तिम वर्ग संघर्ष के बाद होने वाले नये सामाजिक आर्थिक ढांचे में वर्ग संरचना में काफ़ी परिवर्तन की स्थिति होती है। जिन देशों में समाजवाद की विजय होती है वहां पर शोषक वर्ग समाप्त हो जाता है। वहां केवल मेहनतकश वर्ग ही रह जाता है। तब समाज का शासन शोषक वर्ग नहीं चलाता। जैसा कि पिछले सभी सामाजिक वर्गों में हुआ करता था, जिसमें भिन्न-भिन्न वर्ग होते थे बल्कि इसे मज़दूर वर्ग चलाता है। ये वर्ग समाज का नेतृत्व स्वतः अपने हाथों में ले लेता है और नये उत्पादन सम्बन्ध पैदा करता है। मजदूर वर्ग सभी मेहनतकश (उद्यमी) लोगों और मेहनतकश किसानों के साथ मिलकर अपना काम चलाते हैं । भिन्न-भिन्न वर्गों में नफरत भरे सम्बन्धों की जगह मित्रता, दोस्ती और आपसी भाईचारा ले लेता है। अन्ततः अमूल परिवर्तन उसको कहा जाता है जबकि समाज का मज़दूर वर्ग एक सहयोग पूर्ण वर्गहीन संरचना की तरफ बढ़ता है। इस तरह मज़दूर वर्ग की नीति का निशाना होता है वर्तमान सामाजिक समूहों के बीच के अन्तर को कम या समाप्त करना और एक वर्गहीन समाज का निर्माण करना।

प्रश्न 3.
रूस तथा चीन की साम्यवादी क्रांतियों पर एक टिप्पणी लिखिए।
उत्तर-
(i) रूसी क्रान्ति (Russian Revolution)-रूस पर रोमानोव (Romanov) परिवार का राज्य था। प्रथम विश्व युद्ध (1914) के शुरू होने के समय ज़ार निकोलस II का रूस पर राज्य था। मास्को के इर्द-गिर्द के क्षेत्र के अतिरिक्त उस समय के रूसी साम्राज्य में आज के मौजूदा देश फिनलैंड, लाटवीया, लिथुआनिया, ऐसटोनिया, पोलैंड का हिस्सा, यूक्रेन तथा बैलारूस भी शामिल थे। जार्जिया, आर्मीनिया तथा अज़रबाईजान भी इसका हिस्सा थे।
1914 से पहले रूस में राजनीतिक दलों की मनाही थी। 1898 में समाजवादियों ने रूसी लोकतान्त्रिक वर्कज़ पार्टी शुरू की तथा वह कार्ल मार्क्स के विचारों का समर्थन करते थे। परन्तु सरकारी नीतियों के अनुसार, इसे गैरकानूनी ढंग से कार्य शुरू करना पड़ा। इसने अपना अखबार शुरू किया, मज़दूरों को इकट्ठा करना शुरू किया तथा हड़तालें करनी शुरू की।
रूस में तानाशाही शासक था। अन्य यूरोपियन देशों के विपरीत, ज़ार वहाँ की संसद् के प्रति जबावदेह नहीं था। उदारवादियों ने एक आन्दोलन चलाया ताकि इस गलत प्रथा को खत्म किया जा सके। उदारवादियों ने समाजवादी लोकतन्त्रीय तथा सामाजिक क्रान्तिकारियों के साथ मिलकर किसानों तथा मजदूरों को इकट्ठा किया। 1905 की क्रान्ति के दौरान संविधान की मांग की गई। उनके प्रयासों से प्रभावित होकर रूस के वर्कर चेतन हो गए तथा उन्होंने कार्य के घण्टे कम करने तथा तनख्वाह बढ़ाने की मांग की। जब वह क्रान्ति की तैयारी कर रहे थे, पुलिस ने उन पर हमला कर दिया। 100 से अधिक वर्कर मारे गए तथा 300 से अधिक जख्मी हो गए। क्योंकि यह घटना इतवार को हुई थी, इसलिए इसे Bloody Sunday के नाम से जाना जाता है।
1914 में प्रथम विश्व युद्ध शुरू हुआ तथा ज़ार ने रूस को लड़ाई में धकेल दिया। रूस की स्थिति, जोकि पहले ही खराब चल रही थी, और भी खराब हो गई। रूस लड़ाई में बुरी तरह उलझ गया था। एक तरफ ज़ार संसद् (डुमा) को भंग करने का प्रयास कर रहा था तथा दूसरी तरफ संसद् के सदस्य इस स्थिति से बचने का प्रयास कर रहे थे। इस स्थिति में पेट्रोग्राड में 22 फरवरी, 1917 को एक फैक्ट्री बंद हो गई तथा सभी वर्कर बेरोज़गार हो गए। हमदर्दी के कारण वहां की 50 फैक्ट्रियों के वर्करों ने भी हड़ताल कर दी। इस समय तक कोई भी राजनीतिक दल इस आन्दोलन की अगुवाही नहीं कर रहा था। सरकारी इमारतों को वर्करों ने घेर लिया तथा सरकार ने कयूं लगा दिया। शाम तक वर्कर भाग गए परन्तु 24 व 25 तारीख तक वह फिर इकट्ठे हो गए। सरकार ने सेना को बुला लिया तथा पुलिस को उनकी निगरानी के लिए कहा गया।
25 फरवरी इतवार को सरकार ने संसद् (डुमा) को भंग कर दिया। नेताओं ने इसके विरुद्ध बोलना शुरू कर दिया। प्रदर्शनकारी पूरी शक्ति से 26 तारीख को सड़कों पर वापिस आ गए। 27 तारीख को पुलिस का हैडक्वाटर तबाह कर दिया गया। सड़कों पर लोग बाहर आ गए तथा उन्होंने ब्रैड, तनख्वाह, कार्य में कम घण्टे तथा लोकतन्त्र के नारे लगाने शुरू कर दिए। सरकार ने सेना को वापिस बुला लिया परन्तु सेना ने लोगों पर गोली चलाने से मना कर दिया। जिस अफसर ने गोली चलाने का आदेश दिया था, उसे भी मार दिया गया। सेना के लोग भी आम जनता से मिल गए तथा सोवियत को बनाने के लिए उस इमारत में एकत्र हो गए जहाँ डुमा पिछली बार एकत्र हुई थी।
अगले दिन वर्करों का प्रतिनिधिमण्डल ज़ार को मिलने के लिए गया। सेना के बड़े अधिकारियों ने ज़ार को प्रदर्शनकारियों की बात मानने की सलाह दी। अंत 2 मार्च को ज़ार ने उनकी बात मान ली तथा ज़ार का शासन खत्म हो गया। अक्तूबर में लेनिन (Lenin) ने रूस का शासन संभाल लिया तथा रूसी क्रान्ति पूर्ण हो गई।
(ii) चीनी क्रान्ति (Chinese Revolution)-1 अक्तूबर, 1949 को चीनी कम्यूनिस्ट नेता माओ-त्से-तुंग ने People’s Republic of China को बनाने की घोषणा की। इस घोषणा से चीनी कम्यूनिस्ट पार्टी तथा राष्ट्रवादी पार्टी के बीच चल रही लड़ाई खत्म हो गई जो दूसरे विश्व युद्ध के बाद शुरू हुई थी। PRC के बनने के साथ ही चीन में लंबे समय से (1911 की चीनी क्रान्ति) चला आ रहा सरकारी उथल-पुथल का कार्य भी खत्म हो गया। राष्ट्रवादी पार्टी के हारने से अमेरिका ने चीन से सभी राजनीतिक संबंध खत्म कर दिए।
चीनी कम्युनिस्ट पार्टी की स्थापना 1921 में शंघाई में हुई थी। चीनी कम्यूनिस्टों ने 1926-27 के उत्तरी हमले के समय राष्ट्रवादी पार्टी का समर्थन किया। यह समर्थन 1927 के White Terror तक चला जब राष्ट्रवादियों ने कम्यूनिस्टों को मारना शुरू कर दिया।
1931 में जापान ने मंचुरिया पर कब्जा कर लिया। इस समय Republic of China की सरकार को तीन तरफ से हमले का डर था तथा वह थे जापानी हमला, कम्यूनिस्ट विद्रोह तथा उत्तर वाले लोगों के हमले का डर। चीन की सेना के कुछ उच्चाधिकारी Chiang-Kai-Shek के इस व्यवहार से दुखी हो गए कि वह आन्तरिक खतरों पर अधिक ध्यान दे रहा था न कि जापानी हमले पर। उन्होंने Shek को पकड़ लिया उसे कम्यूनिस्ट सेना से सहयोग करने के लिए कहा। यह राष्ट्रवादी सरकार तथा चीनी कम्यूनिस्ट पार्टी (CCP) में सहयोग करने की पहली कोशिश थी परन्तु यह कोशिश कम समय के लिए ही थी। राष्ट्रवादियों ने जापान के ऊपर ध्यान करने की बजाए कम्यूनिस्टों को दबाने की तरफ ध्यान दिया जबकि कम्यूनस्टि ग्रामीण क्षेत्रों में अपना प्रभाव बढ़ाने में लगे रहे।
द्वितीय विश्व युद्ध के दौरान कम्यूनिस्टों के लिए समर्थन काफ़ी बढ़ गया। चीन में अमेरिकी अधिकारियों राष्ट्रवादियों के क्षेत्र में लोगों के समर्थन को दबाने के प्रयास किए। इन अलोकतान्त्रिक नातियों तथा युद्ध के दौरान हो रहे भ्रष्टाचार ने चीन की सरकार को कम्यूनिस्टों के विरुद्ध काफ़ी कमज़ोर कर दिया। कम्यूनिस्ट पार्टी ने ग्रामीण क्षेत्रों में भूमि सुधार करने शुरू किए जिससे उनका समर्थन बढ़ गया।
1945 में जापान युद्ध हार गया जिससे चीन में गृह युद्ध का खतरा बढ़ गया। Chiang Kai-Shek की सरकार को अमेरिकी समर्थन मिलना जारी रहा क्योंकि कम्यूनिस्टों के बढ़ते खतरे को चीन में केवल वह ही रोक सकता था। 1945 में Chiang-Kai-Shek तथा माओ-त्से-तुंग मिले ताकि लड़ाई के बाद की सरकार के गठन के ऊपर चर्चा की जा सके। दोनों लोकतन्त्र की बहाली, इकट्ठी सेना, चीन के राजनीतिक दलों की स्वतन्त्रता पर हामी भर चुके थे। सन्धि होने वाली थी परन्तु अमेरिका के दखल के कारण वह न हो सकी तथा 1946 में गृह युद्ध शुरू हो गए।
गृह युद्ध में 1947 से 1949 में कम्यूनिस्टों की जीत पक्की लग रही थी क्योंकि उन्हें जनसमर्थन प्राप्त था, उच्च दर्जे की सेना थी तथा मंचुरिया में जापानियों से छीने हुए हथियार भी थे। अक्तूबर 1949 में कई स्थान जीतने के पश्चात् माओ-त्से-तुंग ने People’s Republic of China के गठन की घोषणा की। Chiang-Kai-Shek अपनी सेना के पुनर्गठन के लिए ताईवान भाग गया। इस प्रकार 1949 में चीनी क्रान्ति पूर्ण हो गई।

प्रश्न 4.
समाजशास्त्र में दुर्थीम का योगदान बताइये।
उत्तर-
प्रसिद्ध समाज शास्त्री और दार्शनिक इमाइल दुर्थीम का जन्म 15 अप्रैल 1858 को उत्तरी-पूर्वी फ्रांस के लॉरेन (Lorraine) क्षेत्र में स्थित एपीनल (Epinal) नामक स्थान में हुआ था। दुर्थीम की आरम्भिक शिक्षा एपीनल की एक संस्था में हुई थी। बचपन से ही दुर्थीम एक मेधावी, प्रतिभाशाली तथा होनहार छात्र के रूप मे जाने जाते थे। दुर्थीम के पूर्वज ‘रेबी शास्त्रकार’ के रूप में प्रसिद्ध हुए थे। इसीलिए प्रतिभा तो दुर्थीम को विरासत से प्राप्त हुई थी। एपीनल में ही ग्रेजुएट तक की शिक्षा प्राप्त करने के बाद उच्च शिक्षा के लिए दुर्थीम फ्रांस की राजधानी पैरिस में चले गए।
पैरिस में दुर्थीम की उच्च शिक्षा का आरम्भ हुआ। यहां पर उन्होंने विश्व प्रसिद्ध संस्था इकोल नारमेल अकादमी (Ecol Normale Superieure) में दाखिला लेने की कोशिश की। यहां यह बताना ज़रूरी है कि इस संस्था में बहुत बढ़िया विद्यार्थियों को ही दाखिला मिलता था। दो असफल प्रयासों के बाद 1879 में दुर्थीम को इस संस्था में दाखिला मिल ही गया। यह संस्था फ्रांसीसी, लातिनी और ग्रीक दर्शन विषयों पर शिक्षा प्रदान करती थी और वहां के पूरे पाठ्यक्रम में यही विषय शामिल थे। लेकिन प्रत्यक्षवादी और वैज्ञानिक प्रवृत्ति वाले दुीम इन विषयों में ज्यादा रुचि न ले सकें क्योंकि वो तो समाज की असली, राजनीतिक, बौद्धिक और सामाजिक इत्यादि दिशाओं के अध्ययन में रुचि रखते थे।
दुर्थीम का यह पूर्ण विश्वास था कि ज्ञान में प्रत्यक्षवाद (Positivism) ज़रूर होना चाहिए। उनका मानना था कि अगर किसी भी ज्ञान अथवा दर्शन का अध्ययन करते समय वर्तमान, बौद्धिक और सामाजिक समस्याओं का अध्ययन नहीं किया जाता तो उस ज्ञान का कोई फायदा नहीं हैं। अपने इन विचारों के कारण दुर्थीम इस विश्व प्रसिद्ध संस्था के वातावरण से इतने असंतुष्ट थे कि वह कभी-कभी तो अपने अध्यापकों के विरुद्ध भी हो जाते थे। लेकिन फिर भी दुर्थीम ने इकोल नारमेल को अपने अंदर इतना बसा लिया कि उन्होंने अपने पुत्र आंद्रे को यहां दाखिल करवाया।
प्रसिद्ध प्रत्यक्षवादी और महान् इतिहासकार प्रोफैसर कुलांज (Prof. Fustel de Coulanges) 1880 में इस संस्था के निदेशक बने। वह दुीम के उन अध्यापकों में से एक थे जिनका दुीम से विशेष प्यार था। कुलांज ने वहां के पाठ्यक्रम में बदलाव किया जिससे दुर्थीम बहुत खुश हुए। दुीम कुलांज का इतना आदर करते थे कि लातिनी भाषा में उन्होंने मान्टेस्क्यू (Montesquieu) नामक किताब लिखी जो उन्होने कुलांज को समर्पित किया। वहां ही दुर्थीम इमाइल बोटरोकस (Emile Boutrocus) को भी मिले। यहीं पर ही दुर्थीम और विश्व प्रसिद्ध विद्वानों को मिले और उन प्रतिभावान विद्यार्थियों को मिले जो बाद में प्रमुख समाजशास्त्री बने। इन प्रसिद्ध विद्वानों के सम्पर्क में आने से दुर्थीम के बौद्धिक और मानसिक चिंतन में काफ़ी बढ़ोत्तरी हुई।
1882 में वह इकोल नार्मेल को छोड़ कर 5 वर्षों तक पैरिस के पास स्थित हाई स्कूलों सेनस, सेंट क्युटिंन और ट्राईज़ में दर्शन शास्त्र पढ़ाते रहे। साथ ही साथ अपने प्रभाव से इन स्कूलों में समाजशास्त्र का नया पाठ्यक्रम भी शुरू किया। दुर्थीम बहुत बढ़िया अध्यापक के रूप में प्रसिद्ध हुए। इसके बाद भी दुर्थीम का मन यहां न लगा। 1885-86 में वह उच्च अध्ययन के लिए नौकरी से एक वर्ष की छुट्टी लेकर वर्ष के अंत में जर्मनी चले गए।
जर्मनी में दुर्शीम ने अर्थशास्त्र, लोक मनोविज्ञान, सांस्कृतिक मनोविज्ञान इत्यादि का काफ़ी गहराई से अध्ययन किया । यहाँ दुीम ने काम्ते (Comte) के लेखों का बारीकी से अध्ययन किया और शायद उससे प्रभावित होकर समाजशास्त्रीय प्रत्यक्षवाद (Sociological Positivism) को जन्म दिया।
1887 में दुर्थीम जर्मनी आ गए और बोर्डिक्स विश्वविद्यालय में प्रवेश रूप से सामाजिक शास्त्र का एक नया अलग विभाग स्थापित किया और आप को यहां अध्ययन के लिए बुलाया गया। लगभग 9 वर्षा के निरन्तर अध्ययन के पश्चात् वह 1896 में इसी विभाग के प्रोफेसर बन गए। इस दौरान पैरिस विश्वविद्यालय द्वारा दुर्थीम को 1893 में उनके फ्रांसीसी भाषा में लिखे शोध ग्रंथ Dela Divsion du Travail Social (Division of Labour in Society) पर उनको बहुत डाक्टरेट की उपाधी दी। उनके इस ग्रंथ के छपने के बाद उनको बहुत प्रसिद्धि मिली। 1895 में दुर्शीम ने अपने दूसरे महत्त्वपूर्ण ग्रंथ Les Regles de ea Methode Sociologique (The rules of Sociological Method) की रचना की। इसकी दो वर्षों के बाद 1897 में दुर्थीम ने तीसरे महान् ग्रंथ Le Suicide : Etude de Sociologie (Suicide A Study of Sociology) की रचना की। इन महान् ग्रंथों की रचना के बाद दुखीम का नाम विश्व के प्रमुख दार्शनिक समाज शास्त्री और महान् लेखक के रूप में जाना जाने लगा।
वर्ष 1898 में दुर्शीम ने ‘L’ Annee Sociologique नाम से समाजशास्त्र सम्बन्धी मैगज़ीन की शुरुआत की और 1910 तक आप इस मैगजीन के सम्पादक रहे। दुर्थीम के इस मैगजीन ने फ्रांस के बौद्धिक वातावरण को बहुत नाम कमाया। इसमें बहुत सारे उच्च कोटि के विचार को जार्जस, डेवी, लेवी स्टार्स, साईमन इत्यादि ने अपने पत्र छपवाए।
इस विश्वविद्यालय में दुर्थीम ने बहुत प्रसिद्धि प्राप्त की और उसके बाद 1902 में पैरिस विश्वविद्यालय में दुर्थीम को शिक्षा शास्त्र के प्रोफैसर पद पर नियुक्त किया गया। यहां एक महत्त्वपूर्ण बात थी कि उस समय तक विश्व में समाज शास्त्र का कोई अलग विभाग नहीं होता था। यह दुर्थीम की कोशिशों का ही नतीजा था कि 1913 में शिक्षा शास्त्र विभाग का नाम बदल कर शिक्षा शास्त्र और समाजशास्त्र रख दिया गया। यहां दुर्थीम ने और विषयों के साथ-साथ विकास और परिवार की शुरुआत, नैतिक शिक्षा, धर्म की उत्पत्ति, काम्ते और सेंट साईमन के सामाजिक दर्शन को बहुत लगन के साथ पढ़ाया। जिन विद्यार्थियों ने दुीम से शिक्षा प्राप्त की वह उनसे बहुत प्रभावित हुए। दुर्शीम ने एक और पुस्तक Les Farmes Elementains delavie Religieuse (Elementary forms of Religious Life) की रचना की।
र्बोडिक्स विश्वविद्यालय में नियुक्त होने के पश्चात् ही उन्होंने विवाह करवा लिए। उनकी पत्नी का नाम लुईस डरेफू (Louise Drefus) था और उनके दो बच्चे थे। उनकी लड़की का नाम मैंरी (Marie) और लड़के का नाम आंद्रे (Andre) था। दुर्शीम की पत्नी सम्पादन के काम से लेकर चैक करना, उसको संशोधित करना, पत्र व्यवहार करने जैसे सभी कार्य को बहुत मेहनत से करके दुर्थीम की सहायता करती थी।
दुर्शीम ने 1914 के पहले विश्व युद्ध में अपने पुत्र आंद्रे को समाज सेवा के लिए पेश किया और स्वयं अपने लेखों और भाषणों से जनता का मनोबल बना रखने के लिए जुट गए। युद्ध ने दुर्शीम जी को मानसिक तौर से काफ़ी कमज़ोर कर दिया क्योंकि वह शांति के समर्थक थे। जब दुर्थीम युद्ध में महत्त्वपूर्ण भूमिका निभा रहे थे तो उनको अपने पुत्र की मौत का समाचार मिला जिसकी मृत्यु लड़ाई के बुरी तरह जख्मी होने के कारण बुलगारीया के अस्पताल में हुई थी। आंद्रे उनका केवल पुत्र ही नहीं बल्कि सबसे अच्छा विद्यार्थी भी था इसी कारण उसकी मृत्यु ने दुर्थीम को अन्दर से तोड़ दिया।
दुर्थीम 1916 के अंत में एकदम बीमार हो गए लेकिन इसके पश्चात् भी वह 1917 में नीतिशास्त्र पर किताब लिखने के लिए फाऊंट नबलियु स्थान पर गए। 15 नवंबर, 1917 को असाधारण प्रतिभा वाले इस समाजशास्त्री की 59 वर्ष की आयु में मृत्यु हो गई।
दुर्शीम की रचनाएं (Writings of Durkheim) –
दुर्शीम ने अपने जीवनकाल के समय कई महान् ग्रंथों की रचना की जिनके नाम निम्नलिखित हैं-
1. The Division of Labour in Society – 1893
2. The Rules of Sociological Method – 1895
3. Suicide – 1897
4. Elementary Forms of Religious Life – 1912
5. Education and Sociology (After Death) – 1922
6. Sociology and Philosophy (After Death) – 1924
7. Moral Education (After Death) – 1925
8. Sociology and Saint Simon(After Death) – 1924
9. Pragmatism and Sociology (After Death) – 1925

प्रश्न 5.
वैबर द्वारा प्रस्तुत सामाजिक क्रिया के प्रकारों की चर्चा कीजिए।
उत्तर-
सामाजिक व्यवहार की पूरी व्याख्या करते हुए वैबर ने चार प्रकार के सामाजिक कार्यों की व्याख्या की है।
1. तार्किक उद्देश्यपूर्ण व्यवहार (Zweckrational)-वैबर ने बताया है कि तार्किक उद्देश्यपूर्ण सामाजिक व्यवहार का अर्थ ऐसे सामाजिक व्यवहार से होता है जो उपयोगिता को ध्यान में रखते हुए अनेक उद्देश्यों की अधिक-से-अधिक प्राप्ति के लिए तार्किक रूप में निर्देशित हो, इसमें साधनों के चुनाव में केवल उनके विशेष प्रकार की कार्यकुशलता की तरफ ध्यान ही नहीं दिया जाता बल्कि भूल पर भी ध्यान दिया जाता है। साध्य और साधनों की अच्छी तरह जांच की जाती है और उसके आधार पर ही क्रिया सम्पादित होती है।
2. मूल्यात्मक व्यवहार (Wertrational)-मूल्यात्मक व्यवहार में किसी विशेष और स्पष्ट मूल को बहुत अधिक प्रभावशाली उपलब्ध साधनों के द्वारा स्थान दिया जाता है। दूसरे मूल्यों की कीमतों पर कुछ ध्यान नहीं दिया जाता है। इसमें तार्किक आधार नहीं हो सकता, बल्कि नैतिकता, धार्मिक या सुन्दरता के आधार पर ही मान ली गई है। नैतिक और धार्मिक मान्यताओं को बनाये रखने के लिए मूल्यात्मक क्रियाएं की जाती हैं। इन क्रियाओं को मानने में किसी भी प्रकार के तर्क की सहायता नहीं ली जाती है। वह इसी तरह ही मान ली जाती है क्योंकि इसके कारण सामाजिक सम्मान भी बढ़ता है और आत्मिक सन्तोष भी बढ़ता है।
3. संवेदात्मक व्यवहार (Assectual Behaviour)-ऐसी क्रियाएं मानवीय भावनाओं, संवेगों और स्थायी भावों के कारण होती हैं। समाज में रहते हुए हमें प्रेम, नफरत, गुस्सा इत्यादि भावनाओं का शिकार होना पड़ता है। इसके कारण ही समाज में शान्ति या अशान्ति की अवस्था पैदा हो जाती है। इन व्यवहारों के कारण परम्परा और तर्क का थोड़ा सा भी सहारा नहीं लिया जाता है।
4. परम्परागत व्यवहार (Traditional Behaviour)-परम्परागत क्रियाएं पहले से निश्चित प्रतिमानों के आधार पर की जाती हैं । सामाजिक जीवन को सरल और शांतमय रखने के लिए परम्परागत क्रियाएं महत्त्वपूर्ण मानी जाती हैं। सम्भव है कभी वह स्थिति पैदा हो जाये, कि इन क्रियाओं द्वारा समाज में संघर्ष पैदा हो जाये कि इन क्रियाओं द्वारा तर्क, कार्यकुशलता और किसी और प्रकार का सहारा लेने की आवश्यकता ही नहीं पड़ती। सामाजिक प्रथाएं ही इन क्रियाओं को संचालित करती हैं ।।
वैबर ने बताया है कि सामाजिक क्रियाएं तीन प्रकार से निर्देशित होती हैं ।
प्रश्न 6.
वैबर किस प्रकार धर्म को आर्थिक क्रियाओं से जोड़ते हैं ?
उत्तर-
पूंजीवाद का सार (Essence of Capitalism)-वैबर का आरम्भिक अध्ययन एक ऐसी प्रवृत्ति पर केन्द्रित है जो आधुनिक समाज में विशेष रूप में दिखाई देती है। आर्थिक व्यवहारों पर धार्मिक प्रभावों को स्पष्ट करने के लिए 1904 से 1905 में जो लेख लिखे हैं उनके आधार पर उसकी सबसे प्रसिद्ध किताब The Protestant Ethic and the Spirit of Capitalism के नाम से छपी। इस किताब के अधिकतर भाग में वैबर ने इस समस्या पर प्रकाश डाला है कि प्रोटैस्टैंट धर्म के विचारों या नीतियों ने किस प्रकार पूंजीवाद के विकास को प्रभावित किया है। यह विचार मार्क्स के इस सिद्धान्त के लिए एक खुली चुनौती थी कि मानव की सामाजिक व धार्मिक चेतना उसके सामाजिक वर्ग द्वारा निर्धारित होती है।
वैबर के विचारों से आधुनिक औद्योगिक जगत् के मानव की एकता स्पष्ट है कि उसको सख्त मेहनत करनी चाहिए। वैबर के अनुसार, “कठोर काम एक कर्तव्य है व इसका नतीजा इसी के बीच शामिल है।” यह विचार वैबर के दृष्टिकोण से आधुनिक औद्योगिक जगत् के मानव का विशेष गुण है। मानव अपने काम में अच्छी तरह काम इसलिए नहीं करना चाहता क्योंकि उसको काम करना पड़ेगा बल्कि इसलिए कि वह ऐसा करना चाहता है। वैबर के अनुसार यह उसकी व्यक्तिक संतुष्टि का आधार है। वैबर ने स्वयं लिखा है कि एक व्यक्ति से अपनी आजीविका के मूल्य के प्रति होने वाले कर्त्तव्य का अनुभव करने की आशा की जाती है व वह ऐसा करता भी है चाहे वह किसी भी क्षेत्र में क्यों न हो। अमरीका की एक कहावत है कि, “यदि कोई व्यक्ति काम करने के योग्य है तो उसे सबसे बढ़िया ढंग से पूरा करना चाहिए।” यह कहावत वैबर के अनुसार पूंजीवाद का सार भी है क्योंकि इस धारणा का सम्बन्ध किसी आलौकिक उद्देश्य से नहीं बल्कि आर्थिक जीवन में व्यक्ति को प्राप्त होने वाली सफलता से है। चाहे किसी विशेष समय में यह धारणा धार्मिक नैतिकता से सम्बन्धित रही है। पूंजीवाद के सार को स्पष्ट करने के लिए वैबर ने उसकी तुलना एक अन्य आर्थिक क्रिया से की है जिसका नाम उन्होंने परम्परावाद रखा है। आर्थिक क्रियाओं में परम्परावाद वह स्थिति है जिसमें व्यक्ति अधिक लाभ के बाद भी कम-से-कम काम करना चाहता है।
वह काम के दौरान अधिक-से-अधिक आराम करना पसन्द करता है व काम के नये तरीके से अनुकूलन करने की इच्छा नहीं करते हैं। वह जीवन जीने के लिए साधारण तरीकों से ही खुश हो जाते हैं व एकदम लाभ प्राप्त करने की कोशिश करते हैं। सिद्धान्तहीन रूप से धन का इकट्ठा करना आर्थिक परम्परावाद का ही एक हिस्सा है तथा ये सारी विशेषताएं पूंजीवाद के सार से पूरी तरह उलट हैं । असल में आधुनिक पूंजीवाद अन्तर्सम्बन्धित संस्थाओं का एक ऐसा बड़ा एकत्र (Complex) है, जिसका आधार आर्थिक कोशिशें हैं न कि स्टोरियों की कोशिशें। पूंजीवाद के अन्तर्गत व्यापारी निगमों का कानूनी रूप, संगठित लेन-देन का केन्द्र, सरकारी कर्जा पत्रों के रूप में सार्वजनिक कर्जा देने की प्रणाली व ऐसे उद्योगों के संगठनों का समूह है जिनका उद्देश्य वस्तुओं के तार्किक आधार पर उत्पादन करना होता है न कि उनका व्यापार करना। वैबर का विचार था कि दक्षिणी यूरोप, रोम अभिजात वर्ग व ओलबी नदी के पूर्व के ज़मींदारों की आर्थिक क्रियाएं अचानक लाभ प्राप्त करने के लिए की गईं जिनमें उन्होंने सारे नैतिक विचारों का त्याग कर दिया। उनकी क्रियाओं में आर्थिक लाभ की तार्किक कोशिशों की कमी थी जिस कारण उन्हें पूंजीवाद के बराबर नहीं रखा जा सकता।
वैबर के अनुसार पूंजीवाद के सार का गुण केवल पश्चिमी समाज का ही गुण नहीं है। अनेकों समाजों में ऐसे व्यक्ति हुए हैं जिन्होंने अपने व्यापार को बढ़िया ढंग से चलाया, जो नौकरों से भी अधिक मेहनत करते हैं, जिनका जीवन सादा था व जो अपनी बचत को भी व्यापार में ही लगा देते थे पर इसके बाद भी इन पंजीवादी विशेषताओं का प्रभाव पश्चिमी समाजों में कहीं ज्यादा मिलता रहा है, इसका कारण यह था कि पश्चिम में यह गुण एक व्यक्तिगत गुण न रहकर जीवन जीने के आम तरीके के रूप में विकसित हुआ। इस तरह लोगों में फैली कठोर मेहनत, व्यापारिक व्यवहार, सार्वजनिक कर्जा व्यवस्था, पूंजी का लगातार व्यापार में लगाते रहना व मेहनत के प्रति इच्छा ही पूंजीवाद का सार है। इसके विपरीत एकदम लाभ पाने की कोशिश, मेहनत को बोझ व श्राप समझकर उसको न करना, धन को इकट्ठा करना व जीवन जीने के साधारण स्तर से ही सन्तुष्ट हो जाना आम आर्थिक आदतें हैं।
प्रोटैस्टैंट नीति (Protestant Ethic) यह स्पष्ट करने के बाद कि उनके अध्ययन का उद्देश्य पूंजीवाद का सार है वैबर ने ऐसे अनेकों कारण बताए हैं जिनके आधार पर सुधार आन्दोलन के धार्मिक विचारों में इसकी उत्पत्ति को ढूंढना है। वैबर ने अपने एक विद्यार्थी बाडेन (Baden) को राज्य में धार्मिक सम्बन्धों व शिक्षा को चयन का अध्ययन करने के लिए कहा। बाडेन ने एक परिणाम यह पेश किया कि कैथोलिक विद्यार्थियों की तुलना में प्रोटैस्टैंट विद्यार्थी उन शिक्षा संस्थाओं में अधिक दाखिला लेते हैं जो औद्योगिक जीवन से सम्बन्धित हैं। एक और कारण यह भी था कि यूरोप में समय-समय पर कम गणना समूहों ने अपनी सामाजिक व राजनीतिक हानि को कठोर आर्थिक मेहनत से पूरा कर लिया जबकि कैथोलिक ऐसा न कर सके। इन हालातों के प्रभाव से वैबर की इस धारणा को बल मिला कि धार्मिक नीति व आर्थिक क्रियाओं में कोई सम्बन्ध ज़रूर है। इसके बाद वैबर ने यह भी देखा कि 16वीं सदी में बहुत सारे अमीर प्रदेशों व शहरों में प्रोटैस्टैंट धर्म स्वीकार कर लिया क्योंकि प्रोटैस्टैंट धर्म अपनी अनेकों नीतियों के कारण आर्थिक लाभ की कोशिशों को आगे बढ़ा रहा है। इसी आधार पर वैबर ने यह पता करने की कोशिश की कि प्रोटैस्टैंट धर्म का प्रचार आर्थिक दृष्टि से पिछड़े हुए देशों में हुआ व अंतः पूंजीवादी अर्थव्यवस्था के बाद भी किसी क्षेत्र में कैथोलिक धर्म प्रभावशाली बना रहा।
The Protestant Ethic and the Spirit of Capitalism लिखने में वैबर का उद्देश्य बहुत कुछ इस विरोध की व्याख्या के कारण आर्थिक जीवन पर धार्मिक नीतियों के प्रभाव को स्पष्ट करना था। वैबर यह स्पष्ट करना चाहते हैं कि प्रोटैस्टैंट धर्म की नीतियां किस तरह उन लोगों के लिए प्रेरणा का स्रोत बन गईं जो आर्थिक लाभों को तार्किक दृष्टि से प्राप्त करने के हक में थीं। इस तरह वैबर के अनुसार किसी भी धर्म के साथ सम्बन्धित सिद्धान्तों पर इस नज़र से विचार करना चाहिए कि यह सिद्धान्त अपने शिष्यों को किस तरह के व्यवहारों का प्रोत्साहन देता है। इस प्रश्न को ध्यान में रखते हुए वैबर ने प्रोटैस्टैंट धर्म के शुद्ध विचारवादी पादरियों के लेखों को परखा व उनके द्वारा बनाए कालविनवादी सिद्धान्तों का समुदाय के दैनिक व्यवहार पर प्रभाव स्पष्ट किया।
प्रोटैस्टैंट धर्म के नीति के रूप में सेंट पाल के इस आदेश को व्यापक रूप से ग्रहण किया जाने लगा कि, “जो व्यक्ति काम नहीं करेगा वह रोटी नहीं खाएगा व ग़रीब की तरह अमीर भी भगवान के गौरव को बढ़ाने के लिए किसी न किसी समय पर व्यापार को ज़रूर करे।” इस तरह मेहनती जीवन ही प्रोटैस्टैंट धर्म शुद्ध विचारवादी धार्मिक भक्ति के अनुसार है।
रिचर्ड बैक्सटर (Richard Baxter) ने कहा कि, “केवल धर्म के लिए ही भगवान् हमारी क्रियाओं की रक्षा करता है। मेहनत ही शक्ति का नैतिक व प्राकृतिक उद्देश्य है, केवल मेहनत से ही भगवान् की सबसे ज्यादा सेवा हो सकती है।” एक अन्य सन्त जॉन बयिन ने कहा था कि, “यह नहीं कहा जाएगा कि आप क्यों विश्वास करते थे, केवल ये कहा जाएगा कि आप कुछ मेहनत भी करते थे या केवल बातें ही करते थे।” इस तरह प्रोटैस्टैंट धर्म की नीति में काम करते जीवन को ही खुदा की भक्ति के रूप में मान लिया गया। प्रोटैस्टैंट धर्म में मेहनत की प्रशंसा ने नये नियमों को जन्म दिया। इसके अनुसार समय को व्यर्थ नष्ट करना पाप है। जीवन छोटा व मूल्यवान् है, इसलिए मानव को हर समय भगवान् का गौरव बढ़ाने के लिए अपना समय अपने उपयोगी काम में लगाना चाहिए। व्यर्थ की बातचीत, लोगों को ज्यादा मिलना, ज़रूरत से ज्यादा सोना व दैनिक कार्यों को हानि पहुंचा कर धार्मिक कार्यों में लगे रहना पाप है क्योंकि इनके कारण भगवान् के द्वारा दिए आजीविका काम को भगवान् की इच्छा के अनुसार पूरा नहीं किया जा सकता। इस दृष्टिकोण से प्रोटैस्टैंट धर्म की नीतियां व्यक्तिगत नीति के इस आदर्श के विरुद्ध हैं, “अमीर व्यक्ति कोई काम न करे या यह कि धार्मिक ध्यान सांसारिक कार्यों से ज्यादा मूल्यवान् है। यही प्रोटैस्टैंट नीति है।”
पूंजीवाद व प्रोटैस्टैंट नीति का सम्बन्ध (Relationship of Capitalism and Protestant Ethic)पूंजीवाद के सार व प्रोटैस्टैंट नीतियों के अध्ययन से वैबर को इनके अनेकों आधारों में समानता मिलती है। इन समानताओं ने वैबर को इस तथ्य पर विचार करने से प्रेरणा दी है कि आर्थिक व्यवहारों व धार्मिक नीतियों में समानताएं किन परिस्थितियों के कारण समानताओं का वर्णन परिस्थितियों के परिणाम से है। वैबर ने पहले 16वीं व 17वीं सदी में धर्म संघों व उनकी मान्यताओं में होने वाले परिवर्तनों का मानवीय व्यवहारों पर प्रभावों का अध्ययन किया। शुरू में अनेकों धर्म संघों ने भौतिक चीजों की प्राप्ति व उनके इकट्ठा करने पर जोर दिया व कुछ समय के बाद धन के एकत्र को अधार्मिकता की श्रेणी में रखा जाने लगा जिसमें मेहनत के सामने सारी इच्छाओं को समाप्त कर लेना ठीक था। इस धर्म संघ ने इच्छाओं के दमन करने की निष्पक्षता को खत्म करने के रूप में न लेकर श्रम के रास्ते में आने वाली रुकावट को इच्छा खत्म करने के रूप में स्पष्ट किया। वैबर के अनुसार, “जब इच्छा ख़त्म कर लेने की धारणा धर्म केन्द्रों की सीमा से बाहर निकल कर सांसारिक नैतिकता को प्रभावित करने लगी तो इसने आधुनिक अर्थव्यवस्था (पूंजीवाद) की रचना में ही अपना योगदान शुरू कर दिया।” इस परिवर्तन ने वैबर को अध्ययन की एक दिशा प्रदान की। धर्म की नीतियां ही वे मूल कारण हैं जो व्यक्ति के आर्थिक वे धर्म-निरपेक्ष व्यवहारों को प्रभावित करती हैं।
इस तरह वैबर ने अत्यधिक परिणामों द्वारा यह स्पष्ट किया कि किस तरह प्रोटैस्टैंट धर्म की नीतियां योग के अनेकों देशों में आरम्भिक पूंजीवाद के विकास के लिए ठीक हैं। प्रोटैस्टैंट धर्म के सुधार आन्दोलन के शुरू से ही धार्मिक समारोहों में प्रवेश करने का अधिकार उन लोगों को दिया जिनकी इन धर्म की नीतियों में बहुत ज्यादा श्रद्धा थी। धार्मिक परिषदों के सदस्यों को यह सिद्ध करना पड़ता था कि उनमें अपने धर्म की नीतियों को व्यावहारिक रूप देने की पूरी समर्था है। यह परम्परा वैबर के अनुसार साधनों से सम्बन्ध आजीविका को महत्त्व देकर आधुनिक पूंजीवाद के विकास में बहत ज्यादा सहायक सिद्ध हई। धीरे-धीरे प्रोटैस्टैंट धर्म की नैतिक शिक्षाओं को मानने वालों के जीवन की शैली एक व्यवस्थित शैली में बदल गई। वैबर ने इस स्थिति को एक ऐसी घटना के रूप में स्वीकार किया कि जिससे पश्चिमी जीवन के भिन्न-भिन्न पहलुओं में तर्कवाद बढ़ा। यह तर्कवाद पश्चिमी सभ्यता के भिन्नभिन्न रूपों में स्पष्ट हुआ व पूंजीवाद के विकास से इसका प्रत्यक्ष सम्बन्ध है। इस तरह पूंजीवाद के सार व प्रोटैस्टैंट नीति के सम्बन्ध की व्याख्या के आधार पर धर्म को समझाया है।

वस्तुनिष्ठ प्रश्न
I. बहुविकल्पीय प्रश्न (Multiple Choice Questions):
प्रश्न 1.
मार्क्स के अनुसार समाज में कितने वर्ग होते हैं ?
(A) दो
(B) तीन
(C) चार
(D) पाँच।
उत्तर-
(A) दो।
प्रश्न 2.
इनमें से कौन-सा वर्ग का प्रकार मार्क्स ने दिया था जो हरेक समाज में मौजूद होता है ?
(A) पूंजीपति वर्ग
(B) श्रमिक वर्ग
(C) दोनों (A + B)
(D) कोई नहीं।
उत्तर-
(C) दोनों (A + B)।
प्रश्न 3.
कार्ल मार्क्स ने समाज में वर्ग संघर्ष का कौन-सा कारण दिया है ?
(A) पूंजीपति वर्ग द्वारा श्रमिक वर्ग का शोषण
(B) श्रमिक वर्ग द्वारा पूंजीपति वर्ग का शोषण
(C) दोनों वर्गों में ऐतिहासिक दुश्मनी
(D) उपर्युक्त सभी।
उत्तर-
(A) पूंजीपति वर्ग द्वारा श्रमिक वर्ग का शोषण।
प्रश्न 4.
इनमें से कौन-सा संकल्प मार्क्स ने समाजशास्त्र को दिया था ?
(A) वर्ग संघर्ष
(B) ऐतिहासिक भौतिकवाद
(C) अतिरिक्त मूल्य का सिद्धांत
(D) उपर्युक्त सभी।
उत्तर-
(D) उपर्युक्त सभी।

प्रश्न 5.
दुर्खीम का जन्म कब हुआ था ?
(A) 1870
(B) 1858
(C) 1864
(D) 1868.
उत्तर-
(B) 1858.
प्रश्न 6.
फ्रांस में समाजशास्त्र में काम्ते का उत्तराधिकारी किसे कहा जाता है ?
(A) वैबर
(B) मार्क्स
(C) दुखीम
(D) स्पैंसर।
उत्तर-
(C) दुर्खीम।
प्रश्न 7.
इनमें से कौन-सी पुस्तक दुर्खीम ने लिखी थी ?
(A) Division of Labour in Society
(B) Suicide-A Study of Sociology
(C) The Rules of Sociological Method
(D) All of these.
उत्तर-
(D) All of these.
प्रश्न 8.
इनमें से कौन-सा सिद्धान्त दुर्खीम ने दिया था ?
(A) श्रम विभाजन
(B) सामाजिक तथ्य
(C) आत्महत्या का सिद्धांत
(D) उपर्युक्त सभी।
उत्तर-
(D) उपर्युक्त सभी।

प्रश्न 9.
दुर्खीम ने सामाजिक तथ्य के कितने प्रकार दिए हैं ?
(A) दो
(B) तीन
(C) चार
(D) पाँच।
उत्तर-
(B) तीन।
प्रश्न 10.
दुर्खीम ने इनमें से सामाजिक तथ्य का कौन-सा प्रकार दिया था ?
(A) बाध्यता
(B) बाहरीपन
(C) सर्वव्यापकता
(D) उपर्युक्त सभी।
उत्तर-
(D) उपर्युक्त सभी।
प्रश्न 11.
इनमें से कौन-सा संकल्प वैबर ने समाजशास्त्र को दिया है ?
(A) सत्ता
(B) आदर्श प्रारूप
(C) सामाजिक क्रिया
(D) उपर्युक्त सभी।
उत्तर-
(D) उपर्युक्त सभी।
II. रिक्त स्थान भरें (Fill in the blanks) :
1. कार्ल मार्क्स …………… दार्शनिक थे।
2. मैक्स वैबर ने सामाजिक …………. का सिद्धांत दिया था।
3. श्रम विभाजन का सिद्धांत …………. ने दिया था।
4. ऐतिहासिक योगदान का संकल्प …………… ने दिया था।
5. कार्ल मार्क्स ने वर्ग ………….. का सिद्धांत दिया था।
6. वैबर अनुसार ………….. धर्म पूँजीवाद को सामने लाने के लिए उत्तरदायी है।
7. आत्महत्या का सिद्धांत ………….. ने दिया था।
उत्तर-
- जर्मन,
- क्रिया,
- दुर्खीम,
- कार्ल मार्क्स,
- संघर्ष,
- प्रोटैस्टैंट,
- दुर्खीम।

III. सही/गलत (True/False) :
1. दुर्खीम फ्रांस में पैदा हुआ था।
2. दुर्खीम ने तीन प्रकार की आत्महत्या के बारे में बताया था।
3. वैबर ने चार प्रकार की सत्ता का वर्णन किया था।
4. मार्क्स के अनुसार समाज में तीन प्रकार के वर्ग होते हैं।’
5. मजदूर वर्ग पूँजीपति वर्ग का शोषण करता है।
6. सामाजिक एकता का सिद्धांत दुर्खीम ने दिया था।
उत्तर-
- सही,
- सही,
- गलत,
- गलत,
- गलत,
- सही।
IV. एक शब्द/पंक्ति वाले प्रश्न उत्तर (One Wordline Question Answers) :
प्रश्न 1.
समाजशास्त्र का जन्मदाता किसे कहा जाता है ?
उत्तर-
अगस्ते काम्ते को समाजशास्त्र का जन्मदाता कहा जाता है।

प्रश्न 2.
समाजशास्त्र शब्द का प्रयोग पहली बार कब किया गया था ?
उत्तर-
समाजशास्त्र शब्द का प्रयोग पहली बार 1839 में किया गया था।
प्रश्न 3.
कार्ल मार्क्स कब तथा कहाँ पैदा हुए थे ?
उत्तर-
कार्ल मार्क्स 5 मई, 1818 को प्रशिया के राईन प्रांत के ट्रियर शहर में पैदा हुए थे।
प्रश्न 4.
कार्ल मार्क्स को कब तथा कहां डाक्टरेट की उपाधि प्राप्त हुई थी ?
उत्तर-
कार्ल मार्क्स को 1841 को जेना विश्वविद्यालय से डाक्टरेट की उपाधि मिली थी।
प्रश्न 5.
Communist Menifesto कब तथा किसने लिखी थी ?
उत्तर-
Communist Menifesto सन् 1848 को मार्क्स तथा ऐंजल्स ने लिखा था।

प्रश्न 6.
कार्ल मार्क्स की मृत्यु कब हुई थी ?
उत्तर-
कार्ल मार्क्स की मृत्यु 14 मार्च,1883 को हुई थी।
प्रश्न 7.
मार्क्स के अनुसार समाज में कितने वर्ग होते हैं ?
उत्तर-
मार्क्स के अनुसार समाज में दो प्रमुख वर्ग होते हैं-पूँजीपति वर्ग तथा श्रमिक वर्ग।
प्रश्न 8.
मार्क्स ने समाजशास्त्र को कौन-से संकल्प दिए हैं ?
उत्तर-
मार्क्स ने समाजशास्त्र को वर्ग संघर्ष, ऐतिहासिक भौतिकवाद, सामाजिक परिवर्तन, अलगाव एवं अतिरिक्त मूल्य के सिद्धांत दिए हैं।
प्रश्न 9.
दुीम को फ्रांस में तथा समाजशास्त्र में किसका उत्तराधिकारी माना जाता है ?
उत्तर-
दुर्खीम को समाजशास्त्र में काम्ते का उत्तराधिकारी माना जाता है।

प्रश्न 10.
दुखीम किस विश्वविद्यालय में प्रोफैसर नियुक्त हए थे ?
उत्तर-
दुर्खीम पैरिस विश्वविद्यालय में प्रोफैसर नियुक्त हुए थे।
प्रश्न 11.
दुर्जीम ने समाजशास्त्र को कौन-से सिद्धांत दिए थे ?
उत्तर-
दुर्खीम ने समाजशास्त्र को सामाजिक तथ्य, आत्महत्या, धर्म, श्रम विभाजन इत्यादि जैसे सिद्धांत दिए थे।
प्रश्न 12.
वैबर के अनुसार सत्ता के कितने प्रकार हैं ?
उत्तर-
वैबर के अनुसार सत्ता के तीन प्रकार होते हैं-परंपरागत, वैधानिक व करिश्मई।
प्रश्न 13.
वैबर के अनुसार कौन-सा धर्म विकास के लिए उत्तरदायी है ?
उत्तर-
वैबर के अनुसार पूँजीवाद के विकास के लिए प्रोटैस्टैंट धर्म उत्तरदायी है।

प्रश्न 14.
वैबर ने समाजशास्त्र को क्या योगदान दिया है ?
उत्तर-
वैबर ने सत्ता के प्रकार, आदर्श प्रारूप, सामाजिक क्रिया, पूँजीवाद, प्रोटैस्टैंट धर्म की व्याख्या इत्यादि जैसे संकल्पों का योगदान दिया है।
अति लघु उत्तरात्मक प्रश्न
प्रश्न 1.
पूँजीवादी वर्ग क्या होता है ?
उत्तर-
मार्क्स के अनुसार पूँजीवादी वर्ग ऐसा वर्ग होता है जिसके पास उत्पादन के सभी साधन होते हैं तथा वह सभी उत्पादन के साधनों का मालिक होता है जिनकी सहायता से वह अन्य वर्गों का शोषण करता है। अपने साधनों की सहायता से वह पैसे कमाता है तथा आराम का जीवन व्यतीत करता है। मार्क्स ने अनुसार एक दिन मज़दूर वर्ग इस वर्ग की सत्ता उखाड़ फेंकेगा।
प्रश्न 2.
मज़दूर वर्ग क्या होता है ?
उत्तर-
मार्क्स के अनुसार मज़दूर वर्ग के पास उत्पादन के साधनों की मल्कियत नहीं होती। उसके पास कोई पूँजी या पैसा नहीं होता। उसके पास रोटी कमाने के लिए अपना परिश्रम बेचने के अतिरिक्त और कुछ भी नहीं होता। वह हमेशा पूँजपति वर्ग के हाथों शोषित होता रहता है। इस शोषण के कारण वह निर्धन होता जाता है।

प्रश्न 3.
पूँजीवाद क्या होता है ?
उत्तर-
पूँजीवाद एक आर्थिक व्यवस्था है जिसमें निजी सम्पत्ति की प्रधानता होती है तथा बाजार पर सरकारी नियन्त्रण न के बराबर होता है। प्रत्येक व्यक्ति को अपनी इच्छा तथा योग्यता के अनुसार कमाने का अधिकार होता है। पूँजीवाद में पूँजीपति अपने पैसे से और पैसा कमाता है तथा मजदूर वर्ग का शोषण करता है।
प्रश्न 4.
सामाजिक एकता क्या है ?
उत्तर-
दुर्खीम के अनुसार प्रत्येक समाज के कुछ मूल्य, आदर्श, विश्वास, व्यवहार के तरीके, संस्थाएं तथा कानून प्रचलित होते हैं जो समाज को बाँध कर रखते हैं। ऐसे तत्त्वों के कारण समाज में एकता बनी रहती है। इनके कारण समाज में संबंध बने रहते हैं तथा यह समाज में एकता उत्पन्न करते हैं जिसे हम सामाजिक एकता कहते हैं।
प्रश्न 5.
श्रम विभाजन क्या है ?
उत्तर-
दुर्खीम के अनुसार श्रम विभाजन का अर्थ अलग-अलग लोगों अथवा वर्गों में उनके सामर्थ्य तथा योग्यता के अनुसार कार्य का विभाजन करना है ताकि कार्य संगठित तरीके से पूर्ण किया जा सके। इसे ही श्रम विभाजन कहा जाता है। यह प्रत्येक समाज में पाया जाता है। इसकी उत्पत्ति नहीं बल्कि विकास होता है।
लघु उत्तरात्मक प्रश्न
प्रश्न 1.
आध्यात्मिक पड़ाव।
उत्तर-
काम्ते की सैद्धान्तिक स्कीम में आध्यात्मिक पड़ाव बहुत महत्ता रखता है। उसके अनुसार इस अवस्था में मानव के विचार काल्पनिक थे। मानव सब वस्तुओं को परमात्मा के रूप में या किसी आलौकिक जीव की उस समय की क्रियाओं के परिणामस्वरूप में देवता मानता व समझता था। धारणा यह होती थी कि सभी वस्तुएं चाहे निर्जीव हो व सजीव हैं या कार्यरूप अलौकिक शक्तियां हैं अर्थात् सब वस्तुओं में वही शक्ति व्यापक है। धार्मिक पड़ाव में मानव के बारे चर्चा करते काम्ते कहते हैं कि इस अवस्था में सृष्टि के ज़रूरी स्वभाव की खोज करना या प्राकृतिक घटनाओं के होने के अन्तिम कारणों को जानने के यत्न में मानव का दिमाग यह मान लेता है कि सब घटनाएं अलौकिक प्राणियों की तत्कालीन घटनाओं का प्रमाण है। यह आगे तीन उप पड़ावों-प्रतीक पूजन, बहुदेवतावाद व ऐकेश्वरवाद में बांटा है।
प्रश्न 2.
अधिभौतिक पड़ाव।
उत्तर-
इस पड़ाव को काम्ते आधुनिक समाज का क्रान्तिकाल भी कहते हैं। यह पड़ाव पांच शताब्दियों तक 14वीं से 19वीं तक चला। इसे दो भागों में बाँट सकते हैं। प्रथम भाग में क्रान्तिक आन्दोलन स्वयं ही चल पड़ा। क्रान्तिक फिलासफी 16वीं सदी में प्रोटैस्टैंटवाद के आने से आरम्भ हुई। यहां ध्यान रखने योग्य बात यह है कि रोमन कैथोलिक वाद में आत्मिक व दुनियावी ताकतों के बिछड़ने से आध्यात्मिक सवालों के सामाजिक हालतों पर भी विचार करने का हौसला दिलाया। दूसरा भाग 16वीं सदी से आरम्भ हुआ। इस समय में नकारात्मक सिद्धान्त शुरू हुआ जिसका मुख्य उद्देश्य सामाजिक परिवर्तन था। इसमें प्रोटैस्टैन्टवाद हमारे सामने आया। इसमें बेरोक निरीक्षण का अधिकार था और यह विचार दिया कि निरीक्षण की कोई सीमा नहीं है जिस कारण आत्मिकता का पतन हुआ जिसका दुनियावी पक्ष पर भी असर हुआ।

प्रश्न 3.
सकारात्मक पड़ाव।
उत्तर-
इस पड़ाव को काम्ते औद्योगिक समाज के तौर पर देखता है तथा वे इसकी शुरुआत भी 14वीं सदी से ही मानते हैं। इस पड़ाव में सिद्धान्त व उसके प्रयोग में एक अन्तर पैदा हुआ। बौद्धिक कल्पना तीन अवस्थाओं में बांटी गई। ये है औद्योगिक या असली, एस्थैटिक या शाब्दिक व वैज्ञानिक या फिलास्फीकल। यह तीन अवस्थाएं प्रत्येक विषय के प्रत्येक पक्ष से मेल खाती हैं। औद्योगिक योजना का विशेष गुण राजनीतिक आजादी का होना है व इन्कलाबी पात्र का होना है। काम्ते सबसे ज्यादा महत्ता फिलास्फी व विज्ञान को देता है। उसका विचार है कि सकारात्मक पड़ाव में इन दोनों की बढ़त होती है इस पड़ाव की प्रमुख विशेषता यह है कि इसमें सामाजिक व्यवस्था व विकास में कोई द्वन्द नहीं होता है।
प्रश्न 4.
सकारात्मकवाद।
उत्तर-
काम्ते के अनुसार सकारात्मकवाद का अर्थ वैज्ञानिक विधि है वैज्ञानिक विधि वह विधि है, जिसमें किसी विषय वस्तु के समझने व परिभाषित करने के लिए कल्पना या अनुमान का कोई स्थान नहीं होता। यह तो परीक्षण अनुभव वर्गीकरण व तुलना व ऐतिहासिक विधि की एक व्यवस्थित कार्य प्रणाली होती है। इस तरह परीक्षण, अनुभव, वर्गीकरण तुलना व ऐतिहासिक विधि द्वारा किसी विषय के बारे में सब कुछ समझना व उसके द्वारा ज्ञान प्राप्त करना सकारात्मकवाद है। सकारात्मकवाद का सम्बन्ध वास्तविकता से है कल्पना से नहीं। इसका सम्बन्ध उन निश्चित तथ्यों से है न कि अस्पष्ट विचारों से जिनका पूर्व ध्यान सम्भव है। सकारात्मकवाद वह प्रणाली है जो कि सर्वव्यापक रूप में सब को मान्य है।
प्रश्न 5.
सामाजिक स्थैतिकी।
उत्तर-
काम्ते ने समाज शास्त्र की इस शाखा की परिभाषा देकर लिखा है, समाज शास्त्र के स्थैतिकी अध्ययन से मेरा अभिप्राय सामाजिक प्रणाली के विभिन्न भागों में होने वाली क्रियाओं व प्रतिक्रियाओं से सम्बन्धित नियमों की खोज करने से है। काम्ते अनुसार सामाजिक स्थैतिकी में हम विभिन्न संस्थाओं व उनके बीच सम्बन्धों की चर्चा करते हैं। कृषि समाज को केवल उसकी विभिन्न संस्थाओं के अन्तर्सम्बन्धों की व्यवस्था के रूप में समझा जा सकता है।

प्रश्न 6.
सामाजिक गतियात्मकता।
उत्तर-
काम्ते के अनुसार समाज शास्त्र की दूसरी शाखा सामाजिक गतिशीलता में समाज की विभिन्न इकाइयों के विकास व उनमें होने वाले परिवर्तनों का अध्ययन किया जाता है। काम्ते के विचार में सामाजिक गति आत्मिकता के नियम केवल बड़े समाज में ही स्पष्ट रूप में देखे जा सकते हैं। इस सम्बन्ध में काम्ते का निश्चित विचार था कि सामाजिक परिवर्तन के कुछ निश्चित पड़ावों में से निकलते हैं व उनमें लगातार प्रगति होती है।
प्रश्न 7.
वर्ग संघर्ष।
उत्तर-
कार्ल मार्क्स ने प्रत्येक समाज में दो वर्गों की विवेचना की है। उसके अनुसार प्रत्येक समाज में दो विरोधी वर्ग एक शोषण करने वाला व दूसरा शोषित होने वाला वर्ग होते हैं, जिनमें संघर्ष होता है इसी को मार्क्स वर्ग संघर्ष कहते हैं । शोषण करने वाला वर्ग जिसको वह पूंजीपति वर्ग या Bourgouisses का नाम देता है उसके पास उत्पादन के साधन होते हैं और वह इन उत्पादन के साधनों से अन्य वर्गों को दबाता है। दूसरा वर्ग जिसके वह मजदूर वर्ग या Proletariats का नाम देता है। उसके पास उत्पादन के कोई साधन नहीं होते। उसके पास रोजी कमाने के लिए केवल अपनी मेहनत बेचने के अलावा कुछ नहीं होता। वह पूंजीपति वर्ग से हमेशा शोषित होता है। इन दोनों में हमेशा एक संघर्ष चलता रहता है। इसी को मार्क्स ने वर्ग संघर्ष का नाम दिया है।
प्रश्न 8.
मार्क्स के अनुसार किस समय वर्ग एवं वर्ग संघर्ष का अन्त हो जाएगा?
उत्तर-
मजदूर वर्ग के नेतृत्व में वर्ग संघर्ष के द्वारा राज्य पर अधिकार हो जाने के पश्चात् समाजवाद के युग का आरम्भ होगा। मार्क्स के अनुसार, राज्य शोषक ‘वर्ग के हाथों’ में दमन का बहुत बड़ा हाथ होता है। क्रान्ति के बाद भी सामन्तवाद व पूंजीवाद के दलाल प्रति क्रान्ति की कोशिश करते हैं। इसलिए पूंजीवाद के समाजवाद में जान कर संक्रमण काल में मजदूर की सत्ता की अस्थायी अवस्था होगी। समाजवाद की स्थापना के बाद शोषण का अन्त हो जाने पर वर्ग खत्म हो जाएगा व प्रत्येक व्यक्ति को अपने श्रम के अनुसार उत्पादन का लाभ मिलेगा। पर साम्यवाद की अधिक उन्नत अवस्था में प्रत्येक को उसकी ज़रूरत के अनुसार ही मिलने लग जाएगा। धीरे-धीरे राज्य जो शोषक वर्ग का हथियार रहा है, बिखर जाएगा व इसकी जगह आपसी सहयोग व सहकारिता के अनुसार पर आधारित संस्थाएं ले लेंगी। वर्गों व वर्ग संघर्ष का अन्त हो जाएगा।
प्रश्न 9.
पूंजीवादी वर्ग।
उत्तर-
मार्क्स ने पूंजीवादी वर्ग की धारणा दी है। उस अनुसार, समाज में एक वर्ग ऐसा होता है जिसके पास उत्पादन के साधन होते हैं वह जो सभी उत्पादन के साधनों का मालिक होता है। वह अपने उत्पादन के साधनों की मदद से और वर्गों का शोषण करता है। इन साधनों की मदद से वे और पैसे कमाते हैं और अमीर हुए जाते हैं। इस पैसे व उत्पादन के साधनों की मलकीयत करके आराम की ज़िन्दगी व्यतीत करता है। यह एक प्रगतिशील वर्ग होता है। जो थोड़े समय में ही शक्तिशाली उत्पादन शक्ति का मालिक हो गया है, वह यहां आकर यदि उन्नति को रोकते हैं व मजदूर वर्ग का शोषण करते हैं एक दिन आएगा जब मज़दूर वर्ग, इस वर्ग की सत्ता उखाड़ फेंकेगे व समाजवादी समाज की स्थापना करेंगे।

प्रश्न 10.
मज़दूर वर्ग।
उत्तर-
मार्क्स के अनुसार, समाज में दो वर्ग होते हैं। पूंजीपति वर्ग व मज़दूर वर्ग। इस मज़दूर वर्ग के पास उत्पादन के साधनों की मलकियत नहीं होती। उसके पास कोई पूंजी (पैसा) नहीं होती। उसके पास अपनी रोजी कमाने के लिए अपनी मेहनत बेचने के अलावा और कोई तरीका नहीं होता। वह हमेशा पूंजीपति वर्ग के हाथों शोषित होता रहता है। पूंजीपति वर्ग हमेशा उनसे अधिक-से-अधिक काम लेता रहता है व कम-से-कम पैसा देता है। उसकी मेहनत ही अतिरिक्त मूल्य का उत्पादन करती है तथा उसको पूंजीपति वर्ग ही रखता है। इस शोषण के कारण ही मज़दूर वर्ग और ग़रीब होता जाता है। एक दिन दोनों में संघर्ष छिड़ जाएगा अन्त में मजदूर वर्ग पूंजीपति वर्ग को उखाड़ गिराएगा व समाजवादी समाज की स्थापना करेगा।
प्रश्न 11.
वैधानिक सत्ता।
उत्तर-
जहां कहीं भी नियमों की ऐसी प्रणाली है जो निश्चित सिद्धान्तों के अनुसार न्यायिक व प्रशासनिक रूप से की जाती है व जो एक नियमित समूह के सभी सदस्यों के लिए सही व मानने योग्य होती है, वहां व्यापक सत्ता है। जो व्यक्ति आदर्श की शक्ति को चलाते हैं वह विशेष रूप से श्रेष्ठ होते हैं। वह कानून द्वारा सारी विधि के अनुसार नियुक्त होते हैं या चुने जाते हैं और वे वैधानिक व्यवस्था को चलाने के लिए आप निर्देशित रहते हैं।
जो व्यक्ति बिना आदेशों के अधीन हैं वह वैधानिक रूप से समान हैं वह विधान का पालन करते हैं न कि उस विधान में काम करने वालों का। यह नियम उस उपकरण के लिए उपयोग किए जाते हैं जो वैधानिक सत्ता की प्रणाली का उपयोग करते हैं। यह संगठन स्वयं अबाध्य होते हैं। इसके अधिकारी उन नियमों के अधीन होते हैं जो इसकी सत्ता की सीमा निर्धारित करते हैं।
प्रश्न 12.
परम्परागत सत्ता।
उत्तर-
इस प्रकार की सत्ता में एक व्यक्ति की वैधानिक नियमों के अन्तर्गत एक पद पर बैठे होने के कारण नहीं बल्कि परम्परा के द्वारा माने हुए पदों पर बैठे होने के कारण प्राप्त होती है। चाहे इस पद को परम्परागत व्यवस्था के अनुसार परिभाषित किया जाता है। इस कारण ऐसे पद पर बैठे होने के कारण व्यक्ति को कुछ विशेष सत्ता मिल जाती है। उस प्रकार की सत्ता परम्परागत विश्वासों पर टिकी होने के कारण परम्परागत सत्ता कहलाती है। जैसे क्षेत्रीय युग में भारतीय गाँवों में मिलने वाली पंचायत में पंचों की सत्ता को ही ले लो। इन पंचों की सत्ता की तुलना भगवान् की सत्ता की तुलना से की जाती थी जैसे कि पंच परमेश्वर की धारणा में दिखाई देता था। उसी प्रकार पितृसत्तात्मक परिवार में पिता को परिवार से सम्बन्धित सभी विषयों में जो अधिकार पर सत्ता प्राप्त होती है उसका भी आधार वैधानिक न होकर परम्परा होता है।

प्रश्न 13.
चमत्कारी सत्ता।
उत्तर-
व्यक्तिगत सत्ता का स्रोत परम्परा से बिल्कुल भिन्न भी हो सकता है। आदेश की शक्ति एक नेता भी प्रयोग कर सकता है चाहे वह एक पैगम्बर हो, नायक हो, या अवसरवादी नेता हो पर ऐसा व्यक्ति तो ही चमत्कारी नेता हो सकता है जब वह सिद्ध कर दे कि तान्त्रिक शक्तियां देवी शक्तियां नायकत्व या अन्य अभूतपूर्व गुणों के कारण उसके पास चमत्कार है।
इस प्रकार यह सत्ता न तो वैधानिक नियमों पर व न ही परम्परा पर बल्कि कुछ करिश्मा या चमत्कार पर आधारित होती हैं। इस प्रकार की शक्ति केवल उन व्यक्तियों के पास सीमित होती है जिनके पास चमत्कारी शक्तियां होती हैं इस प्रकार की सत्ता प्राप्त करने में व्यक्ति को काफ़ी समय लग जाता है व पर्याप्त यानी पूरे साधनों, कोशिशों के बाद ही लोगों द्वारा यह सत्ता स्वीकार की जाती है। दूसरे शब्दों में एक व्यक्ति के द्वारा अपने व्यक्तित्व का विकास इस प्रकार किया जाता है कि लोग यह समझने लगें कि उसने अपने व्यक्तित्व में कोई चमत्कारी शक्ति का विश्वास कर लिया है। इसके बल पर ही वह और लोगों को अपने सामने झुका लेता है। व्यक्तियों द्वारा सत्ता स्वीकार कर ली जाती है। इस तरह करिश्माई नेता अपने प्रति या अपने लक्ष्य या आदर्श के प्रतिनिष्ठा के नाम पर दूसरों से आज्ञापालन करने की माँग करता है। जादूगर, पीर, पैगम्बर, अवतार, धार्मिक नेता, सैनिक योद्धा, दल के नेता इसी तरह की सत्ता सम्पन्न व्यक्ति होते हैं। लोग इसी कारण ऐसे लोगों की सत्ता स्वीकार कर लेते हैं।
प्रश्न 14.
सामाजिक क्रिया।
उत्तर-
वैबर अनुसार सामाजिक क्रिया व्यक्तिगत क्रिया से भिन्न है। इसकी परिभाषा देते हुए वैबर ने लिखा है कि, “किसी भी क्रिया को करने वाले व्यक्ति या व्यक्तियों द्वारा लिए गए Subjective अर्थ के अनुसार उस क्रिया में दूसरे व्यक्तियों के मन के भावों पर क्रियाओं का समावेश हो तथा उसी के अनुसार गतिविधि निर्धारित हो।” वैबर के अनुसार सामाजिक क्रिया और व्यक्तियों के भूत, वर्तमान या होने वाले व्यवहार द्वारा प्रभावित हो सकती है व हर प्रकार की बाहरी क्रिया सामाजिक क्रिया नहीं हो सकती।
प्रश्न 15.
पूंजीवाद के मुख्य लक्षण बताओ।
उत्तर-
- पूजीवाद में पूंजीपति का कमाए हुए लाभ पर पूरा अधिकार होता है।
- पूंजीवाद में ज्यादा से ज्यादा उत्पादन करने की कोशिश की जाती है ताकि अधिक-से-अधिक लाभ उठाया जा सके।
- व्यापार को वैज्ञानिक तरीके से किया या चलाया जाना चाहिए।
- उत्पादन हमेशा बाज़ार के सामने रखकर या बेचने के लिए किया जाता है।
- लेखा-जोखा रखने की उन्नत विधि अपनाई जाती है।

प्रश्न 16.
सामाजिक तथ्य क्या है?
उत्तर-
विभिन्न प्रकार के समाजों में कुछ ऐसे तथ्य होते हैं, जो भौतिक प्राणीशास्त्री व मनोवैज्ञानिक तथ्यों से अलग होते हैं। दुर्खीम इस प्रकार के तथ्यों को सामाजिक तथ्य मानते हैं। दुर्खीम ने सामाजिक तथ्यों की कुछ परिभाषा दी है। एक जगह दुर्खीम लिखते हैं, “सामाजिक तथ्य काम करने, सोचने व अनुभव करने के वे तरीके हैं जिस में व्यक्तिगत चेतना से बाहर भी अस्तित्व को बनाए रखने की उल्लेखनीय विशेषता होती है।”
एक अन्य स्थान पर दुर्खीम ने लिखा है, “सामाजिक तथ्यों में काम करने, सोचने, अनुभव करने के तरीके शामिल है, जो व्यक्ति के लिए बाहरी होते हैं व जो अपनी दबाव शक्ति के मध्यम से व्यक्ति को निर्धारित करते अपनी किताब के प्रथम Chapter की आखिरी पंक्तियों में इसकी विस्तार सहित परिभाषा पेश करते हुए लिखा है, “एक सामाजिक तथ्य क्रिया करने का प्रत्येक स्थायी, अस्थायी तरीका है, जो आदमी पर बाहरी दबाव डालने में समर्थ होता है या दोबारा क्रिया करने का प्रत्येक तरीका जो किसी समाज में आम रूप से पाया जाता है पर साथ ही साथ व्यक्तिगत विचारों से स्वतन्त्र भिन्न अस्तित्व रखता है।”
प्रश्न 17.
बाह्यता।
उत्तर-
बाह्यता (Exteriority)—सामाजिक तत्त्व की सबसे पहली व महत्त्वपूर्ण विशेषता उसका बाहरीपन है। बाह्यता का अर्थ है सामाजिक तथ्य का निर्माण तो समाज के सदस्यों की ओर से ही होता है परन्तु सामाजिक तथ्य एक बार विकसित होने के पश्चात् फिर किसी व्यक्ति विशेष के नहीं रहते व वह उस अर्थ में कि इसको एक स्वतन्त्र वास्तविक रूप में अनुभव किया जाता है। वैज्ञानिक का उससे कोई आन्तरिक सम्बन्ध नहीं होता और न ही सामाजिक तथ्यों का व्यक्ति विशेष पर कोई प्रभाव पड़ता है।
इस प्रकार बाह्यता का अर्थ है कि सामाजिक तथ्य व्यक्ति के लिए बाहरी होते हैं। वह किसी व्यक्ति विशेष के नहीं होते बल्कि सम्पूर्ण समाज के होते हैं।
प्रश्न 18.
(विवशता) बाध्यता।
उत्तर-
बाध्यता या विवशता (Constraint) सामाजिक तथ्यों की दूसरी प्रमुख व महत्त्वपूर्ण विशेषता उसकी विवशता है। दूसरे शब्दों में व्यक्ति पर सामाजिक तथ्यों का एक दबाव या विवशता का प्रभाव पड़ता है। वस्तुतः सामाजिक तथ्यों का निर्माण एक व्यक्ति या कुछ व्यक्तियों द्वारा नहीं होता बल्कि अनेकों व्यक्तियों द्वारा होता है। अतः यह बहुत शक्तिशाली होते हैं व किसी व्यक्ति पर इनकी विवशता के कारण प्रभाव पड़ता है।
दुर्खीम का मानना है कि सामाजिक तथ्य केवल व्यक्ति के व्यवहार को नहीं बल्कि उसके सोचने विचारने आदि के तरीके को प्रभावित करते हैं। दुर्खीम बताते हैं कि हम सामाजिक तथ्यों की यह विशेषता इस रूप में देख सकते हैं कि यह सामाजिक तथ्य आदमी की अभिरुचि के अनुरूप नहीं बल्कि व्यक्ति के व्यवहार उनके अनुरूप होता है।

प्रश्न 19.
व्यापकता।
उत्तर-
सामाजिक तथ्यों की तीसरी विशेषता यह है कि समाज विशेष में यह तथ्य आदि से अन्त तक फैले होते हैं। यह सब के साझे होते हैं। यह किसी व्यक्ति विशेष की व्यक्तिगत विशेषताएं नहीं होती। लेकिन व्यापकता अनेकों वैयक्तिक तथ्यों की केवल एक मात्र परिणाम ही नहीं होती। यह तो शुद्ध रूप में अपने स्वभाव से ही सामूहिक होती है। व्यक्तियों पर इनका प्रभाव इनकी सामूहिक विशेषता का परिणाम होता है।
प्रश्न 20.
सामाजिक तथ्य के प्रकार।
उत्तर-
दुर्खीम ने दो प्रकार के सामाजिक तथ्यों का वर्णन किया है। साधारण तथ्य (Normal) तथ्य तथा यह वह सामाजिक तथ्य होते हैं, जो पूरी मानव जाति के क्षेत्र में फैले होते हैं, व यदि वह सभी व्यक्तियों में नहीं तो उनमें से अधिकतर में पाए जाते हैं। व्याधिकीय या Pathological सामाजिक तथ्य वह होते हैं जो पूरी मानव जाति में न मिलकर कहीं-कहीं ही फैले होते हैं।
प्रश्न 21.
दमनकारी कानून क्या होते हैं ?
उत्तर-
दमनकारी कानून (Repressive Law)-दमनकारी कानूनों को एक प्रकार से सार्वजनिक कानून (Public Law) कहा जा सकता है। दुर्खीम के अनुसार, यह दो प्रकार के होते हैं –
(i) दण्ड सम्बन्धी कानून (Penal Laws)-जिनका सम्बन्ध कष्ट देने, हानि पहुंचाने, हत्या करने या स्वतन्त्रता न देने के साथ है। इन्हें संगठित दमनकारी कानून (Organized Repressive Law) कहा जा सकता है।
(ii) व्याप्त कानून (Diffused Laws)-कुछ दमनकारी कानून ऐसे होते हैं जो पूरे समूह में नैतिकता के आधार पर फैले होते हैं। इसलिए दुर्खीम इन्हें व्याप्त कानून कहते हैं। दुर्खीम के अनुसार, दमनकारी कानून का सम्बन्ध आपराधिक कार्यों से होता है। यह कानून अपराध व दण्ड की व्याख्या करते हैं। यह कानून समाज की सामूहिक जीवन की मौलिक दशाओं का वर्णन करते हैं। प्रत्येक समाज के अपने मौलिक हालात होते हैं इसलिए भिन्न-भिन्न समाजों में दमनकारी कानून भिन्न-भिन्न होते हैं। इन दमनकारी कानूनों की शक्ति सामूहिक दमन में होती है, व सामूहिक मन समानताओं से शक्ति प्राप्त करता है।
प्रश्न 22.
प्रतिकारी कानून।
उत्तर-
प्रतिकारी कानून (Restitutive Laws) कानून का दूसरा प्रकार प्रतिकारी कानून व्यवस्था है। यह कानून व्यक्तियों के सम्बन्धों में पैदा होने वाले असन्तुलन को साधारण स्थिति प्रदान करते हैं। इस वर्ग के अन्तर्गत व्यापारिक कानून, नागरिक कानून, संवैधानिक कानून, प्रशासनिक कानून इत्यादि आ जाते हैं। इनका सम्बन्ध पूरे समाज के सामूहिक स्वरूप से न होकर व्यक्तियों से होता है। यह कानून समाज के सदस्यों के व्यक्तिगत सम्बन्धों में पैदा होने वाले असन्तुलन को दोबारा सन्तुलित व व्यवस्थित करते हैं। दुर्खीम कहते हैं कि प्रतिकारी कानून व्यक्तियों व समाज को कुछ मध्य संस्थाओं से जोड़ता है।

प्रश्न 23.
यान्त्रिक एकता क्या होती है?
उत्तर-
यान्त्रिक एकता (Mechanical Solidarity)-दुर्खीम के अनुसार, यान्त्रिक एकता समाज की दण्ड संहिता में अर्थात् दमनकारी कानूनों के कारण होती है। समूह के सदस्यों में मिलने वाली समानताएं इस एकता का आधार हैं जिस समाज के सदस्यों में समानताओं से भरपूर जीवन होता है जहां विचारों, विश्वासों, कार्यों व जीवन शैली के साधारण प्रतिमान व आदर्श प्रचलित होते हैं व जो समाज इन समानताओं के परिणामस्वरूप एक सामूहिक इकाई के रूप में सोचता व क्रिया करता है वह यान्त्रिक एकता दिखलाता है। उसके सदस्य मशीन की तरह के भिन्न-भिन्न पुओं की भांति संगठित रहते हैं। दुर्खीम ने आपराधिक कार्यों को दमनकारी कानून व यान्त्रिक एकता की अनुरूपता का माध्यम बताया है।
प्रश्न 24.
आंगिक एकता क्या होती है?
उत्तर-
आंगिक एकता (Organic Solidarity)-दुर्खीम के अनुसार दूसरी एकता आंगिक एकता है। दमनकारी कानून की शक्ति सामूहिक चेतना में होती है। सामूहिक चेतना समानताओं से शक्ति प्राप्त करती है। आदिम समाज में दमनकारी कानूनों की प्रधानता होती है, क्योंकि उनमें समानताएं सामाजिक जीवन का आधार हैं। दुर्खीम के अनुसार, आधुनिक समाज श्रम विभाजन व विशेषीकरण से प्रभावित है जिसमें समानता की जगह विभिन्नताएं प्रमुख हैं। सामूहिक जीवन की यह विभिन्नता व्यक्तिगत चेतना को प्रमुखता देती है।
आधुनिक समाज में व्यक्ति प्रत्यक्ष रूप से समूह से बन्धा नहीं रहता। इस सम्बन्ध में मानवों के आपसी सम्बन्धों का महत्त्व ज्यादा होता है। यही कारण है कि दुर्खीम ने आधुनिक समाजों में दमनकारी कानून की जगह प्रतिकारी कानून की प्रधानता बताई है। विभिन्नता पूर्ण जीवन में मानवों को एक-दूसरे पर निर्भर रहना पड़ता है। प्रत्येक व्यक्ति केवल एक काम में विशेष योग्यता प्राप्त कर सकता है व बाकी सारे कामों के लिए उसको दूसरों पर निर्भर रहना पड़ता है। समूह के मैम्बरों की यह आपसी निर्भरता उनकी व्यक्तिगत असमानता उन्हें एक-दूसरे के नज़दीक आने के लिए मजबूर करती है। जिसके आधार पर समाज में एकता की स्थापना होती है। इस एकता को दुर्खीम ने आंगिक एकता (Organic Solidarity) कहा है। यह प्रतिकारी कानून व्यवस्था में दिखाई देता है।
प्रश्न 25.
सामाजिक एकता क्या है?
उत्तर-
दुखीम कहते हैं कि प्रत्येक समाज में कुछ मूल आदर्श, विश्वास, व्यवहार के तरीके, संस्थाएं व कानून प्रचलित होते हैं जो कि समाज को एक सूत्र में बांध कर रखते हैं। ऐसे तत्त्वों के कारण समाज में सम्बद्धता बनी रहती है व एकता भी बनी रहती है। यह कारक समाज में सर्वसम्मत्ति पैदा करते हैं व एकता को बढ़ाते हैं। इस प्रकार की एकता को सामाजिक एकता कहते हैं। इन कारणों के नष्ट होने या बिखरने से सामाजिक एकता खतरे में पड़ जाती है। जिस कारण समाज विघटन की ओर जाने लगता है।

बड़े उत्तरों वाले प्रश्न
प्रश्न 1.
काम्ते के तीन पड़ावों के सिद्धान्त का वर्णन करो।
उत्तर-
समाजशास्त्रीय क्षेत्र में काम्ते का एक महत्त्वपूर्ण योगदान उसके द्वारा पेश किया तीन पड़ावों का नियम है। उसने अपनी प्रसिद्ध किताब पाज़ीटिव फिलोस्फी (Positive Philosophy) में इस सिद्धान्त के बारे में बताया। इस सिद्धान्त का निर्माण काम्ते ने 1822 में किया जब कि उसकी उम्र केवल 24 साल की थी। काम्ते ने इस नियम का विचार कोन्डरसेट (Conderect), टुरर्गेट (Turoget) तथा सेन्ट साईमन (Saint Simon) से प्राप्त किया।
काम्ते का कहना है कि मानव के ज्ञान या चिन्तन प्रक्रियाओं का विकास नहीं हुआ है। वह तो कुछ निश्चित पड़ावों में से ही निकला है काम्ते लिखते हैं, “सारे समाजों में व सारे युगों में मानव के बौद्धिक विकास का अध्ययन करने से उस महान् आधार, मौलिक नियम का पता चलता है जिसके अधीन मानव का चिन्तन आवश्यक रूप से होता है व जिसका ठोस परिणाम संगठन के तथ्यों व हमारे ऐतिहासिक अनुभवों, दोनों में शामिल है। यह नियम इस प्रकार है, हमारा प्रत्येक प्रमुख संकल्प हमारे ज्ञान की प्रत्येक शाखा एक के बाद एक तीन भिन्न-भिन्न सैद्धान्तिक अवस्थाओं (Theoretical Conditions) में से होकर निकलती है तथा वह हैं आध्यात्मिक या काल्पनिक (Theological or fictious) अवस्था, अर्द्धभौतिक या अमूर्त (Metaphysical or abstract) अवस्था व वैज्ञानिक या सकारात्मक (Scientific or positive) अवस्था। सरल शब्दों में उपस्थित नियम का अर्थ है कि मानवीय जीवन के आरम्भ में जब लोगों ने किसी विषय के सम्बन्ध में बोध करना या ज्ञान प्राप्त करना होता था, तो वह आध्यात्मिक आधार पर सोच विचार करते थे। समय व्यतीत होने के साथ लोगों ने आध्यात्मिक आधार की जगह अर्द्धभौतिकी आधार के किसी भी विषय के बारे में ज्ञान प्राप्त करना शुरू किया पर समय कुछ आगे बढ़ा तो मानव ने उपरोक्त दोनों आधारों की बजाय किसी प्रपंच के सकारात्मक आधार पर समझना आरम्भ किया। प्रथम अवस्था में कल्पना, दूसरी में भावना व तीसरी में तर्क प्रधान रहता है।
काम्ते ने इस नियम को मानवीय स्वभाव के पहलुओं पर आधारित किया। मानवीय स्वभाव के तीन महत्त्वपूर्ण पहलू निम्नलिखित हैं-
1. भावनाएं (Feelings)—मानव की भावनाएं उसे काम करने के लिए उत्साहित करती हैं तथा इन्हीं कामों की सेवा करता रहता है।
2. सोचशक्ति या विचार (Thought)-मानव इन भावनाओं की तृप्ति करने के बारे में सोचता है और विचार बनाता है। यह विचार इन भावनाओं की तृप्ति करने की ज़िम्मेदारी लेते हैं तथा इन्हें संचालित करने में मदद लेते
3. कार्य (Action)-भावनाओं की तृप्ति या उन्हें पूरा करने के लिए मानव कार्य करता है।
काम्ते का कहना था कि व्यक्ति जीवन तो ही जी सकता है, यदि उसके स्वभाव के इन तीन पहलुओं में तालमेल हो। यदि व्यक्ति की भावनाएं कुछ और हों, सोच कुछ व कार्य कुछ और करे तो ऐसा व्यक्ति साधारण जीवन नहीं जी सकता। इसी प्रकार सामाजिक व्यक्तियों के बीच सांझे व संचालित व्यवहारों की प्रणाली का होना व निरन्तरता के लिए संस्थाएं, ज्ञान कीमतें व विश्वासों की किसी प्रणाली का होना ज़रूरी है जो कि सफलतापूर्वक ढंग से समाज के सदस्यों की भावनाएं, विचारों व कार्यों में सम्बन्ध स्थापित करें।
काम्ते ने मानवता के इतिहास का निरीक्षण किया और कहा कि उपरोक्त समस्या के हल के लिए तीन सामाजिक प्रणालियां विकसित हुई हैं जिनमें उपरोक्त तालमेल था। वह इस प्रकार हैं-
- आध्यात्मिक पड़ाव (Theological Stage)
- अधिभौतिक पड़ाव (Metaphysical Stage)
- सकारात्मक पड़ाव (Positive Stage)
1. आध्यात्मिक पड़ाव (Theological Stage)-काम्ते की सैद्धान्तिक योजना में आध्यात्मिक पड़ाव बहुत महत्त्व रखता है। हमारा विचार है कि इसके अनुसार सामाजिक क्रम विकास का आरम्भ समझने के लिए पहले पड़ाव का अच्छी तरह निरीक्षण करना अनिवार्य है। उसके अनुसार आध्यात्मिक पड़ाव में मानव के विचार काल्पनिक थे। मानव सब वस्तुओं को परमात्मा के रूप में या किसी अलौकिक जीव की उस समय की क्रियाओं के परिणाम के रूप में देखता था, मानता व समझता था। धारणा यह होती थी कि सब वस्तुएं चाहे निर्जीव हैं चाहे सजीव का कार्य रूप, अलौकिक शक्तियां हैं। अर्थात् सब वस्तुओं में वही शक्ति व्यापक है। धार्मिक पड़ाव में मानव के विचारों के बारे में चर्चा करते हुए काम्ते लिखते हैं कि आध्यात्मिक अवस्था में सृष्टि के आवश्यक स्वभाव की ख़ोज करने या प्राकृतिक घटनाओं के होने के अन्तिम कारण को जानने के यत्न में मानव का दिमाग यह मान लेता है कि सब घटनाएं आलौकिक प्राणियों को तत्कालीन घटनाओं का सबूत हैं । काम्ते के अनुसार इस स्तर को नीचे तीन उप-स्तरों में बांटा जा सकता है।
(i) प्रतीक पूजन (Festishism) सामाजिक गतिशीलता में काम्ते अपनी फ़िलास्फी के मल तत्त्व को स्थापित करके उसका मानव इतिहास के विश्लेषण में उपयोग करता है। उसकी धारणा है कि उसका मूल तत्त्व, सामाजिक विज्ञानों को फिर सजीव करेगा। आध्यात्मिक पड़ाव काम्ते के विचार अनुसार प्रतीक पूजन या फैटिशवाद के सिवाय अन्य किसी तरह भी शुरू नहीं हो सकता था। मानवीय सोच में यह विचार बनना प्राकृतिक था कि सभी बाहरी वस्तुओं में उनकी तरह से ही जीवन है। इस स्थिति में बौद्धिक जीवन से जज्बात अधिक हावी थे। प्रतीक पूजन की फिलास्फी का मूल तत्त्व यह विश्वास है कि लोगों के जीवन पर कई किस्म के अनजाने असर कुछ वस्तुओं के कार्यों के कारण सामने आते हैं जिनको वह जीवित समझते हैं। प्रतीक पूजन आध्यात्मिकता का बिगड़ा स्वरूप नहीं बल्कि इसका स्रोत है।
प्रतीक पूजन का सदाचार, भाषा, बोध व समाज से एक विशेष किस्म का सम्बन्ध था। मानव जाति की आरम्भिक अवस्था में भावुकता हावी थी। जिससे सदाचार व नैतिकता पर अधिक दबाव डाला जाता था। भाषा का चिन्तनात्मक आधार नहीं है। काम्ते का विचार है कि मानवीय भाषा का एक रूपीय आकार है। बौद्धिक स्तर पर फैटिशवाद बहुत जबरदस्त प्रणाली थी। इस अवस्था में मानव केवल आध्यात्मिक संकल्प देख व जान सकता है। बहुत ही कम प्राकृतिक प्रघटन होंगे जिनका उसे निजी अनुभव था जिनमें उसका ज्ञान बढ़ा था। परिणामस्वरूप इस उप-पड़ाव की सभ्यता का सार बहुत ही निम्न था। सामाजिक स्तर पर फैटिशवाद ने एक विशेष प्रकार के पादरीवाद को जन्म दिया। इसमें भविष्य बताने वाले व जादू-टोना करने वाले पादरी पैदा हुए क्योंकि प्रतीक पूजन अवस्था में प्रत्येक वस्तु का मानव से सीधा सम्बन्ध था इसलिए पादरीवाद एक संगठित रूप में विकसित नहीं हुआ। फिर आदमी की ज़िन्दगी पर यह फैटिश देवता बहुत प्रभाव नहीं डालते थे। परिणामस्वरूप चिन्तनशील श्रेणी के जन्म का इस उप-पड़ाव में कोई मौका नहीं था।
यहां ध्यान देने योग्य बात यह है कि मानव की प्रकृति पर विजय इस उप-पडाव से आरम्भ होती है। सबसे विशेष पक्ष इस अवस्था में मानव का पशुओं को अपने बस करके पालतू बनाना है। काम्ते का ख्याल है कि बहुदेवतावाद, जोकि अगला उप-पड़ाव है का आरम्भ प्रतीक पूजन में ही ढूंढ़ा जा सकता है। एक प्रकार से वह इस बात को ऐतिहासिक ज़रूरत के स्तर पर ले जाते हैं। आध्यात्मिक पड़ाव के दूसरे उप-पड़ाव पर पहुँचने के लिए सबसे महत्त्वपूर्ण बौद्धिक बदलाव मानव के तारों के बारे में विचार बदलने से शुरू हुए। तारों की पूजा फैटिशवाद में भी होती थी पर उनको देवताओं के दर्जे पर पहुँचने में एक अमूर्त स्थिति ने ठोस रूप दे दिया।
(ii) बहु देवतावाद-बहु देवतावाद की अवस्था सबसे अधिक सजीव रही है। इस उप-पड़ाव को समझने के लिए काम्ते सबसे पहले अपनी विश्लेषण विधि के बारे में प्रकाश डालते हैं। उसका कहना है कि हमारी विधि को बहु-देवतावाद के ज़रूरी गुणों का अमूर्त अध्ययन करना चाहिए। उसके बाद बह देवतावाद का उन गुणों के सन्दर्भ में निरीक्षण करना चाहिए। मानवीय बोध के विकास के आरम्भ में बहुत सी घटनाओं से सुमेल रखते देवताओं की आवश्यकता थी। बहु देवतावाद बुनियादी तौर से हर किस्म की वैज्ञानिक व्याख्या के खिलाफ थे, पर विज्ञान का आरम्भ इसी पड़ाव से हुआ। वास्तव में मानवीय बौद्ध का फैटिशवाद से बहु देवतावाद तक पहुँचना एक महान् प्राप्ति है। बहु देवतावाद की सामाजिक सोच दो पक्षों से कही जा सकती है यह है राजनीतिक व नैतिक।
(क) राजनीतिक आकार-राजनीति के बीज शुरू से ही मानव जाति में कई तरीकों से बीजे गए थे। शुरू में सियासत में सैनिक गुण जैसे कि हिम्मत व हौंसला सबसे महत्त्वपूर्ण तत्त्व थे। बाद में समझदारी व कूटनीति ताकत का आधार बने। काम्ते के अनुसार बहु-देवतावाद की अवस्था में राजनीतिक आकार के कई पक्ष थे जैसे कि धर्म युद्ध व सैनिक प्रणाली। इसी उप-पड़ाव में धर्म ने सामाजिक महत्ता ग्रहण की। यूनानी सभ्यता में धार्मिक मेले व अन्य कई घटनाएं इस पक्ष को उजागर करते हैं। इसके सिवा इस अवस्था में सेना का विकास एक आवश्यकता थी। इस सैनिक सभ्याचार के विकास का मुख्य कारण यह था कि इस के बिना राजनीतिक आकार व उसकी तरक्की असम्भव थी। बहु-देवतावाद ने सैनिक अनुशासन को न केवल स्थापित ही किया बल्कि पूरी दृढ़ता से कायम भी रखा। राजनीतिक आकार के बहु देवतावाद के इस उप-पड़ाव में दो विशेष गुण हैं। यह हैं गुलाम प्रथा व आत्मिक व दुनियावी ताकत का केन्द्रीयकरण ।
(ख) नैतिकता-ऊपर दिए राजनीतिक आकार पर दिए वर्णन से स्पष्ट है कि नैतिकता की स्थिति बहुत बढ़िया नहीं थी। काम्ते के अनुसार गुलाम प्रथा में निजी पारिवारिक व सामाजिक सम्बन्ध बुरी तरह भ्रष्ट हो जाते हैं। इसके सिवा नैतिकता राजनीतिक आकार के मुकाबले निम्न स्थिति में होती है। काम्ते के अनुसार बहु-देवतावाद की तीन अवस्थाएं हैं
(1) प्रथम अवस्था को काम्ते ने मिस्त्री या दैव शासकीय अवस्था का नाम दिया है। मध्य अवस्था के बौद्धिक व सामाजिक तत्त्व केवल पुरोहित पक्षों के हाथों में सम्पूर्ण सत्ता आ जाने से ही विकसित हो सकते हैं। इसका व्यापक स्तर पर क्रियाओं व पद्धतियों के योग बनाना व मानना एक महत्त्वपूर्ण कार्य है। परिणामस्वरूप इस प्रकार की बहु देवतावाद की अवस्था में एक विशेष किस्म की संस्था ने जन्म लिया जिनको जाति कहते हैं। सबसे पहले जाति-प्रथा एशिया के देशों में विकसित हुई। यह जाति-प्रथा चाहे सैनिक सभ्याचार में से निकली थी पर इस ने युद्ध की रुचियों पर काबू पाया व पुरोहितवाद को सत्ता दी। पश्चिमी सभ्यता में जाति-प्रथा विकसित नहीं हुई।
कामते के अनुसार इस सभ्यता में सामाजिक समतावाद मुख्य कीमत रही है। वह मार्क्स से बहुत सहमत लगता है जब वह कहता है कि उपनिवेशवाद इन्हीं एशियाई देशों के लिए बढ़ा है, क्योंकि पश्चिमी देशों के समतावाद ने जाति-प्रथा को तोड़ने में महत्त्वपूर्ण भूमिका निभाई है। पर जाति-प्रथा प्राचीन सभ्यता का व्यापक स्तर पर एक आधार है। इसकी व्यापकता इसकी मानवीय ज़रूरतों के लिए क्रियाशील होने का बहुत बड़ा सबूत है। जाति-प्रथा का बौद्धिक विकास में सब से बड़ी भूमिका इसका सिद्धान्त व अमल को भिन्न करना है। राजनीतिक तौर से इस की महत्ता समाज में शांति व व्यवस्था रखने में भी थी। पर इन सब गुणों के बावजूद दैवी शासकीय अवस्था उन्नति विरोधी थी।
(2) दूसरी अवस्था यूनानी या बौद्धिक थी जिसमें पहली बार बौद्धिक व सामाजिक तरक्की में अन्तर उत्पन्न किया गया। इस अवस्था के दौरान एक ऐसी चिन्तनशील कक्षा ने जन्म लिया जो सैद्धान्तिक सृजनों के अलावा कोई धन्धा नहीं करती थी इसलिए वह पुरोहित या पादरी समाज के विकल्प के रूप में उभर कर सामने आई। इसका असर विज्ञान की तरक्की पर पड़ा। इसमें सबसे विशेष रेखा गणित में हुआ क्रांतिकारी विकास है। विज्ञान के विकास को काम्ते बौद्धिक अवस्था में खोज के लिए तर्कशील स्वीकारात्मक को उपयोग से जोड़ते हैं। फिलासफी की प्रगति सबसे पहले विज्ञान के विकास के प्रभाव से शुरू हुई।
(3) तीसरी अवस्था को काम्ते ने रोमन या सैनिक का नाम दिया है। रोम की बहुत बड़ी प्राप्ति इसका अपने आप को दैवीय शासन से आजाद करवाना था जिसकी वजह से यहां राज्य प्रथा की जगह सीनेट का राज्य स्थापित हुआ। रोमन अवस्था का केन्द्रीय गुण इसकी युद्ध नीति थी। युद्ध का मुख्य उद्देश्य उपनिवेश इलाके स्थापित करना था। आदमी की चरित्र का विकास भी इस युद्ध सभ्याचार पर निर्भर था। उसको शुरू से ही सैनिक अनुशासन में पाला जाता था। अपनी जीत को बढ़ाने की लगातार बढ़ाने की नीति में ही रोम के पतन के कारण ढूंढ़े जा सकते हैं।
बहु-देवतावाद की इन तीन अवस्थाओं की एक व्यापक भूमिका है। काम्ते उन्हें मिस्त्र, यूनान व रोम के नमूनों के तौर पर देखता था। उसका मुख्य उद्देश्य तीन प्रकार के बहु देवतावाद को दर्शाना ही है।
(iii) एक ईश्वरवाद (Monotheism)-जब रोम ने सारे सभ्य जगत को इकट्ठा किया तो सामाजिक जीवन को ऊँचा करने के लिए एक ईश्वरवाद को बौद्धिक स्तर पर काम करने का मौका मिला। आध्यात्मिक फ़िलासफी का बौद्धिक पतन भी ज़रूरी होना था। काम्ते एक ईश्वरवाद की अवस्था की व्याख्या करने के लिए रोमन कैथोलिकवाद को उदाहरण के तौर पर पेश करता है। एक ईश्वरवाद मूलतयाः से एक विश्वास प्रणाली है जिसकी स्थापना राजनीतिक प्रणाली से स्वतन्त्र है। धर्म व राजनीतिक शक्ति में भिन्नता आना आधुनिक काल की महान् प्राप्ति है। रोमन कैथोलिकवाद की एक प्राप्ति नैतिकता को अपने अधिकार में लाना था। इससे पहले सदाचार सियासी ज़रूरतों द्वारा नियन्त्रत किया जाता था। इससे उप-पड़ाव में चिन्तनशील कक्षा का एक आज़ाद व प्रभावशाली अस्तित्व स्थापित हुआ। इसके परिणामस्वरूप सिद्धान्त व उसके अमल में पृथक्कता आई। अब सिद्धान्त बनाने के लिए अनुभव पर आधारित सन्दर्भ की आवश्यकता नहीं थी। राजनीति प्रणाली के बीच सुधार लाने के लिए अमूर्त सिद्धान्त बनाए जा सकते थे। इसी तरह समाज की भविष्य की ज़रूरतों के बारे में एक बात की जा सकती थी।
एक ईश्वरीवाद उप-पड़ाव में जागीरदारी प्रणाली को आधुनिक समाज की आधारशिला माना जा सकता है। नैतिक क्षेत्र में रोमन कैथोलिकवाद एक व्यापक नैतिकता कायम रखने में काफ़ी सफल रहा। नैतिकता की राजनीति से आज़ादी ने इसके विभिन्न स्तरों पर अलग-अलग प्रकारों में पैदा होने में सहायता दी। जैसे निजी नैतिकता, पारिवारिक व सामाजिक नैतिकता परन्तु बौद्धिक गिरावट आई। इसके मुकाबले बहु-देवतावाद बौद्धिक विकास के लिए ज्यादा उचित था।
2. अधिभौतिक पड़ाव (Metaphysical Stage)-इस पड़ाव को काम्ते आधुनिक समाज क्रांति काल भी कहा जाता है। यह पड़ाव पांच सदियों तक चला। यह 14वीं से 19वीं सदी तक चला। इस समय को हम दो भागों में बांट सकते हैं। प्रथम भाग में क्रांतिक आन्दोलन अपने आप व अनजाने में ही शुरू हो गया। दूसरा भाग सोलहवीं सदी से आरम्भ हुआ। इसमें नकारात्मक सिद्धान्त शुरू हुआ, जिसका मुख्य उद्देश्य सामाजिक बदलाव था। क्रांतिक पड़ाव का आरम्भ एक ईश्वरीवाद का आत्मिक व दुनियावी शक्तियों को भिन्न करने के वक्त से ही माना जा सकता है। क्रान्तिक फिलासफी 16वीं सदी में प्रोटैस्टैंटवाद के आने से शुरू हुआ था। यहां ध्यान देने योग्य यह है कि रोमन कैथोलिकवाद में आत्मिक व दुनियावी शक्तियों में विभिन्नता ने आध्यात्मिक सवालों को सामाजिक मामलों पर ही विचार करने की शक्ति दी है। अधिभौतिक पड़ाव के द्वितीय भाग को हम तीन अवस्थाओं में बांट सकते हैं। प्रथम अवस्था में पुरानी प्रणाली का 15वीं सदी के अन्त तक अपने आप अन्त हो गया था। द्वितीय अवस्था में प्रोटैस्टैंट वाद हमारे सामने आया।
इसमें चाहे काफी निरीक्षण का अधिकार था पर यह ईसाई धर्मशास्त्र तक ही सीमित रहा। तृतीय अवस्था में देववाद (Deism) 18वीं सदी में आगे आया। इस ने निरीक्षण की सीमित सीमाओं को तोड़ कर यह विचार दिया कि इसकी कोई सीमा नहीं है। एक तरह से इस पड़ाव में मध्यकालीन दर्शन व कानूनी विशेषताओं का काल आया। इन्हीं दोनों ने कैथोलिक व्यवस्था को आघात दिया। परिणामस्वरूप आत्मिकता का पतन हुआ जिसका दुनियावी पक्ष पर भी सहजता से असर हुआ। जागीरदार समाज व उच्च श्रेणी का भी पतन हुआ। प्रोटैस्टैंट वाद ने व्यापक आज़ादी का रूझान पैदा किया, जिसके परिणाम से लोग पुरानी व्यवस्था के सामाजिक व बौद्धिक तत्त्वों को नष्ट करने के लिए तैयार हो गए। इस पड़ाव में नकारात्मक फिलासफी स्थापित हुई।
3. सकारात्मक पड़ाव (Positivism Stage)-सकारात्मक पड़ाव का आरम्भ समझने के लिए दो बातें ध्यान देने योग्य हैं। पहली बात यह कि काम्ते इसको औद्योगिक समाज के तौर पर देखते थे। दूसरी बात यह है कि वह इसका आरम्भ भी 14वीं सदी से ही मानते हैं जिसका अर्थ यह है कि आध्यात्मिक या क्रांतिक पड़ाव के साथसाथ ही सकारात्मक पड़ाव का आरम्भ हुआ, पर यह 19वीं सदी में आकर हावी होना प्रारम्भ हुआ। – सकारात्मक पड़ाव में सिद्धान्त व उसके प्रयोग में एक अन्तर पैदा हुआ। बौद्धिक कल्पना तीन अवस्थाओं में बांटी गई। ये थीं औद्योगिक या अमली, एस्थैटिक या काविक तथा वैज्ञानिक या फिलास्फीकल। यह तीन अवस्थाएं हर विषय के तीन पक्षों से मेल खाती हैं जैसे कि अच्छा या फायदेमन्द, सुन्दर और सच्चा। इनमें से सबसे महत्त्वपूर्ण औद्योगिक पक्ष है जिसके आधार पर हम प्राचीन समाज से आधुनिक अवस्था की तुलना कर सकते हैं। औद्योगिक पक्ष में महत्त्वपूर्ण गुण राजनीतिक आज़ादी का पैदा होना है।
अन्त में काम्ते सबसे अधिक महत्ता फिलासफी व विज्ञान को देता है। उसका विचार है कि सकारात्मक पड़ाव में इन दोनों की सब से अधिक प्रभाव होता है। इस पड़ाव की प्रमुख विशेषता यह है कि इसमें सामाजिक व्यवस्था व उन्नति में कोई द्वन्द्व नहीं होता।

प्रश्न 2.
काम्ते के सकारात्मक (Positivism) के सिद्धान्त का वर्णन करो।
उत्तर-
काम्ते ने अपनी पुस्तक ‘पॉजटिव फिलास्फी’ में जिस प्रकार संकल्प ‘सकारात्मक’ का उपयोग किया है, स्पष्ट रूप में विवादात्मक है। इसने सही में इस संकल्प का उपयोग विचारधारक हथियार के तौर से क्रान्ति के साथ-साथ संघर्ष करने के लिए किया।
काम्ते का मुख्य उद्देश्य सामाजिक प्रपंच के समझने के लिए नकारात्मक फिलास्फी के आलोचनात्मक व विनाशकारी सिद्धान्तों को रद्द करना व उनकी जगह सकारात्मक फिलास्फी के रचनात्मक तथा उजागर सिद्धान्तों को स्थापित करना था। दूसरे शब्दों में काम्ते का मुख्य आदर्श सामाजिक अध्ययन व खोज के वैज्ञानिक स्तर पर लाना था। सकारात्मकवाद प्राकृतिक विज्ञानों की विधि को सामाजिक अध्ययन में उपयोग के सामाजिक विज्ञान को भी उन्होंने यथार्थ बनाता है जितना कि भौतिकवाद रासायनिक विज्ञान आदि हैं। उसका विश्वास था कि सकारात्मकवाद द्वारा वास्तविक व सकारात्मक विधि द्वारा ज्ञान प्राप्त होगा व उसकी व्यवहारिक उपयोग द्वारा सामाजिक उन्नति को सम्भव बनाया जा सकेगा। वास्तविक या सकारात्मक ज्ञान सामाजिक पुनर्संगठन की भी ठोस बुनियाद होगी। सकारात्मकवाद का अन्तिम उद्देश्य सामाजिक पुनर्निर्माण या पुनर्संगठन है।
अब प्रश्न उठता है कि संकल्प सकारात्मकवाद से काम्ते का क्या अर्थ था।
संक्षेप शब्दों में सामाजिक प्रपंच का अध्ययन करने के लिए काम्ते द्वारा प्रयोग की गई वैज्ञानिक विधि ही सकारात्मकवाद है। काम्ते ने यह विधि ह्युम, कान्त व गाल से अध्ययन विधि के रूप में ग्रहण की। इसने अपने सिद्धान्तों का निर्माण करते हुए सकारात्मकवाद का उपयोग किया परन्तु अपनी पुस्तकों में सकारात्मकवाद की स्पष्ट व्याख्या नहीं की व न ही इसके नियमों की उचितता को सबित करने का यत्न किया। ऐसा काम्ते ने जानबूझ कर किया क्योंकि उसका विश्वास था कि विद्या की चर्चा उस प्रपंच के अध्ययन से भिन्न करके नहीं की जा सकती, जिसकी इस विद्या द्वारा खोज की जाए।
काम्ते का सकारात्मकवाद से क्या अर्थ था। यह जानने का एक ही तरीका है कि हम उसके इस संक्षेप सम्बन्धी कथनों को एकत्र करें जो उसकी लेखनी में बिखरे हुए हैं।
काम्ते के सकारात्मकवाद के बारे में कथनों के विश्लेषणात्मक अध्ययन के आधार पर यह कहा जा सकता है कि काम्ते अनुसार सकारात्मकवाद का अर्थ वैज्ञानिक विधि है। वैज्ञानिक विधि वह विधि है जिस में किसी विषयवस्तु को समझने व प्रभावित करने के लिए कल्पना या अनुमान का कोई स्थान नहीं होता। यह तो (1) परीक्षण (2) तर्जुबा (3) वर्गीकरण, तुलना तथा ऐतिहासिक विधि की एक व्यवस्थित कार्य प्रणाली होती है। इस तरह परीक्षण, तजुर्बे, वर्गीकरण, तुलना व ऐतिहासिक विधि पर आधारित वैज्ञानिक विधि द्वारा किसी विषय के बारे में सब कुछ समझना और उसके द्वारा ज्ञान प्राप्त करना सकारात्मकवाद है।
चैम्बलिन ने काम्ते के सकारात्मकवाद के अर्थों को इन शब्दों में स्पष्ट किया है कि काम्ते ने यह अस्वीकार किया था कि सकारात्मकवाद अनीश्वरवादी है क्योंकि वह किसी भी रूप में पर्याप्त श्रमिकता से सम्बन्ध नहीं है। उसका यह भी दावा था कि सकारात्मकवाद किस्मतवादी नहीं है क्योंकि वह यह स्वीकार करता है कि बाहरी अवस्था में परिवर्तन हो सकता है। वह आशावादी भी नहीं है क्योंकि इसमें आशावाद के आध्यात्मिक आधार का अभाव है। यह भौतिकवादी भी नहीं क्योंकि यह भौतिक शक्तियों को बौद्धिक शक्तियों के अधीन करता है। सकारात्मकवाद का सम्बन्ध वास्तविकता से है कल्पना से नहीं, उपयोगी ज्ञान से है नाकि पूर्ण ज्ञान से, इसका सम्बन्ध उन निश्चित तथ्यों से है जिसका कि पूर्व-ध्यान सम्भव है। इसका सम्बन्ध यथार्थ ज्ञान से है न कि अस्पष्ट विचारों से आंगिक सच्चाई से है न कि दैवी सच्चाई से, सापेक्ष से है न कि निष्पक्ष से। अन्त में सकारात्मकवाद इस अर्थ में हमदर्दीपूर्ण है कि यह उन सब लोगों को एक भाईचारे में बांध देता है जो कि इसके मूल सिद्धान्तों तथा अध्ययन प्रणालियों पर विश्वास करते हैं। संक्षेप में सकारात्मकवाद विचार की वह प्रणाली है जो कि सर्वव्यापक रूप में सब को मान्य है।
उपरोक्त चर्चा से स्पष्ट है कि सकारात्मकवाद परीक्षण, निरीक्षण वर्णन, वर्गीकरण, तुलना, तजुर्बे व ऐतिहासिक विधि पर आधारित वैज्ञानिक विधि है जिससे किसी भी विषय-सम्बन्धी वास्तविक व सकारात्मक ज्ञान प्राप्त किया जाता है।
कान्त व ह्यूम के विचारों का अनुसरण करते हुए काम्ते इस बात को स्पष्ट थे कि विज्ञान को क्या प्राप्त करना चाहिए तथा इसको प्राप्त करने के लिए यत्न करना चाहिए। वैज्ञानिक ज्ञान का अध्ययन-क्षेत्र सीमित है। वैज्ञानिक ज्ञान में ऐसे तर्क-वाक्य शामिल हैं जोकि परम्परा में सम्बन्धों के बारे में व जिनकी जांच की जा सकती है। यह तर्कवाद दो किस्मों के हैं-
- सहयोग की समानताएं (Uniformities of co-existence) अध्ययन किए जा रहे प्रपंच बीच भागों की अन्तर्निर्भरता के बारे में।
- अनुक्रमण की समानताएं (Uniformities of succession)
काम्ते के समय प्रकृति विज्ञान जैसे कि गणित, तारा विज्ञान, भौतिक विज्ञान, रासायन विज्ञान व जीव विज्ञान विकसित हो चुके थे और इनके विषय-वस्तु का अध्ययन वैज्ञानिक विधि द्वारा किया जाता था। काम्ते अपने समय की प्रचलित तात्विक तथा धार्मिक विधियों द्वारा सामाजिक प्रपंचों की अध्ययन प्रणाली से सन्तुष्ट नहीं थे। इसने तो वैज्ञानिक विधि को सर्वोच्च प्रधानता प्रदान की थी इसलिए यह सामाजिक अध्ययन कार्य को भी परीक्षण, निरीक्षण व वर्गीकरण को वैज्ञानिक कार्य प्रणाली के घेरे में लाने के पक्ष में हैं। काम्ते का कहना था कि अनुभव, निरीक्षण, तजुर्बा वर्गीकरण की व्यवस्थित कार्य प्रणालियों द्वारा न केवल प्राकृतिक प्रपंचों का ही अध्ययन सम्भव है बल्कि समाज का भी क्योंकि समाज भी प्रकृति का अंग है।
जिस प्रकार प्राकृतिक प्रपंच कुछ निश्चित नियमों पर आधारित होते हैं उसी तरह प्रकृति के अंग के रूप में सामाजिक प्रपंच भी कुछ निश्चित नियमों के अनुसार प्रतीत होते हैं। जैसे धरती की गति, सूर्य व चांद का उदय होना व छिपना आदि प्राकृतिक प्रपंच अवास्तविक नहीं हैं उसी तरह सामाजिक प्रपंच भी अवास्तविक नहीं होते, बल्कि पूर्व निश्चित नियमों अनुसार प्रतीत होते हैं। वैसे सामाजिक प्रपंच कैसे प्रतीत होते हैं ? इनकी गति व कर्म क्या हैं ? अर्थात् सामूहिक जीवन उस से सम्बन्धित मौलिक नियमों का अध्ययन यथार्थ रूप में सम्भव है। यह भी सकारात्मकवाद का बुनियादी सिद्धान्त है। स्पष्ट है कि काम्ते का सकारात्मकवाद कल्पना के आधार पर नहीं बल्कि निरीक्षण, परीक्षण, तजुर्बे, तुलना, ऐतिहासिक विधि को व्यवस्थित कार्य प्रणाली के आधार पर सामाजिक प्रपंचों की व्याख्या करता है। पहले कारण ढूंढ़ने की जगह कारण सम्बन्धों की खोज पर अधिक दबाव देता है।
उपरोक्त चर्चा से स्पष्ट है कि काम्ते अनुसार सकारात्मवादी प्रणाली के अन्तर्गत सब से पहले हम अध्ययन विषय को चुनते हैं फिर परीक्षण द्वारा उस विषय से सम्बन्धित प्रकट होने वाले सब तथ्यों को एकत्र करते हैं। उसके किसी भी विषय के बारे, चाहे वह भौतिक है या सामाजिक, तथ्यों या सामग्री एकत्र करने के लिए प्रमुख विधि परीक्षण है। इसके बाद उसका वर्णन किया जाता है। फिर विश्लेषण करके सामान्य विशेषताओं के आधार पर इनका वर्गीकरण किया जाता है। अन्त में उस विषय से सम्बन्धित परिणाम निकाला जाता है फिर उसकी प्रामाणिकता की जांच तथा तुलना ऐतिहासिक विधि के उपयोग से की जाती है।

प्रश्न 3.
मैक्स वैबर द्वारा दिये गये सत्ता के प्रकारों का वर्णन करो ।
उत्तर-
मनुष्य की क्रियाएं मानवीय संरचना के अनुसार ही होती हैं। प्रत्येक संगठित समूह में सत्ता के तत्त्व मूल रूप में विद्यमान रहते हैं। संगठित संग्रह में कुछ तो आम (साधारण) सदस्य होते हैं और कुछ ऐसे व्यक्ति या सदस्य होते हैं जिनके पास जिम्मेवारी होती है। उन्हीं के पास ही सत्ता भी होती है। कुछ लोग प्रधान प्रशासक के रूप में होते हैं, सत्ता की दृष्टि से समूह की रचना इसी प्रकार की होती है और उसमें सत्ता के तत्त्व मौजूद रहते हैं।
मैक्स वैबर के अनुसार, “समाज में सत्ता विशेष रूप से आर्थिक आधारों पर ही आधारित होती है। यद्यपि आर्थिक कारक सत्ता के निर्माण में एक मात्र कारक नहीं कहा जाता है। आर्थिक जीवन में यह आसानी से स्पष्ट है कि एक तरफ मालिक वर्ग, उत्पादन के साधनों एवं मजदूरों की सेवाओं के ऊपर अधिकार डालने की कोशिश करते हैं और दूसरी तरफ मज़दूर वर्ग अपनी मज़दूरी (सेवाओं) के एवज़ में मजदूरों के लिए अधिक-से-अधिक अधिकार प्राप्त करने की कोशिश करते हैं। सत्ता का केन्द्र उनके हाथ में रहता है जिनकी सम्पत्ति के ऊपर उत्पादन के साधन केन्द्रित हैं । इसी सत्ता के आधार पर ही मज़दूरों की आजादी खरीद ली जाती है और मालिकों को मजदूरों के ऊपर एक विशेष अधिकार प्राप्त हो जाता है।”
यद्यपि इस प्रकार की सत्ता अब कम होती जा रही है और काफ़ी कम भी हो गयी है। परन्तु फिर भी आर्थिक क्षेत्रों में निजी सम्पत्ति और उत्पादन के साधन किसी भी वर्ग के लिए सत्ता के निर्धारण में कारक सिद्ध होते हैं। संक्षेप में आर्थिक जीवन में एक स्थिर या संस्थागत अर्थव्यवस्था समाज के कुछ विशेष वर्गों को अधिकार या सत्ता प्रदान करती है। यह वर्ग अपनी उस सत्ता के बल पर दूसरे वर्ग के ऊपर काबू (Control) रखते हैं या उनसे ऊंची स्थिति पर विराजमान रहते हैं। संत्ता के संस्थागत होने के विषय में वैबर का विश्लेषण बहुत कुछ इसी दिशा में ही है। फिर भी वैबर ने तीन मुख्य सत्ताओं का वर्णन किया है, ये तीन प्रकार की सत्ता निम्नलिखित हैं-
- वैधानिक सत्ता (Legal Authority)
- परम्परागत सत्ता (Traditional Authority)
- करिश्माई सत्ता (Charismatic Authority)
1. वैधानिक सत्ता (Legal Authority)-जहां कहीं भी नियमों की ऐसी व्यवस्था है जो निश्चित सिद्धान्तों के अनुसार न्यायिक व प्रशासनिक रूप से प्रयोग की जाती है और जोकि एक निश्चित समूह के सभी सदस्यों के लिए सही व मानने योग्य हो वह वैधानिक सत्ता है। जो व्यक्ति आदर्श रूपी शक्ति को चलाते हैं वह निश्चित रूप से श्रेष्ठ होते हैं। वह व्यक्ति कानून की सभी विधियों के अनुसार ही नियुक्त होते हैं या चुने जाते हैं और वह स्वयं वैधानिक व्यवस्था को चलाने के लिए निर्देशित रहते हैं। जो व्यक्ति इन आदेशों के अधीन हैं वे विधान के रूप में समान होते हैं। वह विधान का पालन करते हैं न कि विधान के काम करने वालों का ये नियम के लिए उनके द्वारा प्रयोग किये जाते हैं जो विधान की सत्ता की व्यवस्था का प्रयोग करते हैं। इस संगठन के अपने नियम होते हैं । इसके अधिकारी उन नियमों के अधीन होते हैं जो इसकी सत्ता की सीमा को निर्धारित करते हैं।
यह नियम सत्ता का कार्य करने वालों के ऊपर प्रतिबन्ध लगाते हैं, अधिकारी के व्यक्तिक रूप को उसके अधिकारी के रूप में करने वाले कार्य के सम्पादन से अलग करते हैं और यह आशा रखते हैं कि सम्पूर्ण कार्यवाही वैध होने के लिए लिखित में होनी चाहिए। इस प्रकार राज्य की ओर से बनाए कुछ साधारण नियमों के अनुसार पैदा अनेकों पद ऐसे हैं जिनके साथ एक विशेष प्रकार की सत्ता जुड़ी होती है। इस कारण जो भी व्यक्ति उन पदों पर बैठ जाता है उनके हाथों में उन पदों से सम्बन्धित सत्ता भी चली जाती है।
इसमें सत्ता का स्रोत किसी व्यक्ति की निजी प्रसिद्धि नहीं होता बल्कि जिन नियमों के अन्तर्गत वह इस विशेष पद पर बैठा है वह उन नियमों की सत्ता के अन्दर रहता है। इसलिए उसका कार्य क्षेत्र वहां तक सीमित है जहां तक विधान से सम्बन्धित नियम उसे विशेष अधिकार प्रदान करते हैं। एक व्यक्ति को विधान के नियमों के अनुसार जितना अधिकार प्राप्त हुआ है वह उससे बाहर जाकर या उसके अधिक सत्ता का प्रयोग नहीं कर सकता। इस तरह व्यक्ति को वैधानिक सत्ता के क्षेत्र और उससे बाहर के क्षेत्र में आधारभूत अन्तर होता है। जैसे जो व्यक्ति किसी अधिकारी पद पर कार्य कर रहा है वह अपने दफ्तर में जिन अधिकारों का अधिकारी है वह उसके घर के क्षेत्र से बिल्कुल भिन्न होता है। घर में वह कोई अधिकारी न होकर बल्कि पिता या पति के रूप में सत्ता में है। एक जटिल समाज में सत्ता प्रत्येक व्यक्ति के हाथों में समान नहीं होती बल्कि इसमें एक ऊंच-नीच का भेदभाव भी होता है अर्थात् वैधानिक अधिकार के समाज में उच्च-निम्न सताएं विराजमान हैं।।
2. परम्परागत सत्ता (Traditional Authority)-परम्परागत सत्ता उस सत्ता की वैधता के विश्वास पर आधारित है, जो हमेशा बनी रहती है। आदेश की शक्ति को पूर्ण करने वाले व्यक्ति आम रूप से प्रभु के समान होते हैं। वह अपनी स्थिति के कारण व्यक्तिगत सत्ता का उपयोग करते हैं और उनके पास स्वतन्त्र रूप से व्यक्तिगत निर्णयों के विशेषाधिकार भी प्राप्त होते हैं। इस प्रथा की नकल और व्यक्तिगत निरंकुशता ही तो ऐसे नियमों की विशेषताएं होती हैं। जो व्यक्ति इस प्रभु के आदेशों के अधीन होते हैं वह शाब्दिक अर्थों में उसके शिष्य होते हैं। वह प्रभु के लिए व्यक्तिगत रूप से शिष्य होने के कारण उसकी आज्ञा का पालन करते हैं। भूतकाल से बने हुए पद के लिए उनकी पवित्र श्रद्धा होती है। इसलिए वह उसकी आज्ञा का पालन करते हैं। इस प्रकार की व्यवस्था या प्रथा के लिए दो प्रकार के उदाहरण हैं। पैतृक (Ancestral) शासन में इस उपकर्म में व्यक्तिगत अनुगामी होते हैं।
जैसे कि घर का अधिकारी, सम्बन्धी या कृपा पात्र व्यक्ति। एक सामन्तवादी समाज में इस उपकर्म के अन्तर्गत व्यक्तिगत रूप से शिष्य मित्र होते हैं जिसके अधीन जगीरदार या करदाता सरकार होती है। यह व्यक्तिगत नीचे वाले अधिकारी ही अपने प्रभु सत्ता के निरंकुश आदेशों या परम्परागत आदेशों के अधीन होते हैं तथा उनकी क्रियाओं का क्षेत्र या आदेश की शक्ति एक निम्न स्तर पर उसके प्रभु की Mirror Image होती है। इसके विपरीत एक सामन्तवादी समाज के पदाधिकारी व्यक्तिगत रूप से निर्भर नहीं होते। बल्कि सामाजिक रूप से प्रमुख मित्र होते हैं। जिन्होंने प्रभु भक्ति की कसमें खाई होती हैं और Grant या Contract के आधार पर जिनका स्वतन्त्र रूप से क्षेत्र होता है। सामन्तवादी और पितृनामी शासन का भेद और दोनों व्यवस्थाओं में परम्परात्मक और निरंकुश आदेशों की निकटता सभी प्रकार की परम्परात्मक प्रभुता में छाई रहती है।
इस प्रकार की सत्ता में एक व्यक्ति को विधि के नियमों के अनुसार एक पद पर बैठे होने के कारण नहीं बल्कि परम्परा के कारण बने हुए पदों पर बैठने के कारण प्राप्त होती है। यद्यपि इस पद को परम्परानुसार परिभाषित किया जाता है। इस कारण ऐसे पदों पर बैठे होने के कारण व्यक्ति को कुछ विशेष प्रकार की सत्ता प्राप्त हो जाती है। इस प्रकार की सत्ता परम्परात्मक विश्वासों पर टिकी होती है। इसलिए यह परम्परात्मक सत्ता कहलाती है। जिस तरह खेती-बाड़ी युग में भारतीय गांवों में मिलने वाली पंचायतों में पंचों की सत्ता को ही ले लीजिए। पहले इन पंचों की सत्ता विधिनुसार नहीं आती थी बल्कि परम्परागत रूप में ही उन्हें सत्ता प्राप्त हो जाती थी। यहां तक कि पंचों की सत्ता को ईश्वरीय सत्ता के समान तक समझा जाता था।
जैसे कि ‘पंच परमेश्वर’ की धारणा में दिखता था। उसी प्रकार पितृसत्तात्मक परिवार में पिता को ही परिवार के साथ सम्बन्धित सभी विषयों में जो अधिकार और सत्ता प्राप्त होती है, उसका भी आधार वैधानिक न होकर परम्परा होती है। पिता के आदेश का पालन हम इसलिए नहीं करते कि उनको कोई वैधानिक सत्ता प्राप्त होती है बल्कि इसलिए करते हैं कि परम्परागत रूप में ऐसा होता रहा है। वैधानिक सत्ता वैधानिक नियमों के अनुसार निश्चित और सीमित होती है क्योंकि वैधानिक नियम निश्चित और स्पष्ट रूप से परिभाषित होते हैं। लेकिन परम्परा और सामाजिक नियमों में इतनी स्पष्टता और निश्चितता नहीं होती। इस कारण परम्परागत सत्ता की वैधानिक सत्ता की तरह कोई निश्चित सीमा नहीं होती है। उदाहरण के लिए किसी अधिकारी की सत्ता कहाँ से शुरू होकर कहां पर खत्म होती है, के बारे में कुछ सीमा तक निश्चित तौर पर कहा जा सकता है लेकिन उस व्यक्ति के घर में पति तथा पिता के रूप में सत्ता की क्या सीमाएँ हैं कहना कठिन है।
3. करिश्माई सत्ता (Charismatic Authority)—व्यक्तिगत सत्ता का स्रोत परम्परा से सर्वथा भिन्न भी हो सकता है। आदेश की शक्ति एक नेता भी प्रयोग कर सकता है। चाहे वह कोई पैगम्बर हो, या नायक हो, या अवसरवादी नेता हो परन्तु ऐसा नेता तभी चमत्कारी नेता हो सकता है, जब वह सिद्ध कर दे कि तान्त्रिक शक्तियां, दैवी शक्तियां या अन्य अभूतपूर्व गुणों के कारण उसके पास चमत्कार है। जो व्यक्ति इस प्रकार के नेता की आज्ञा का पालन करते हैं, वह शिष्य होते हैं। जो निश्चित नियमों या परम्परा से पवित्र पद की गरिमा की जगह उसके अभूतपूर्व गुणों में एक चमत्कारी नेता के अन्तर्गत पदाधिकारियों को उनके चमत्कार एवं व्यक्तिगत निर्भरता के आधार पर विश्वास करते हैं। उन शिष्य पदाधिकारियों को बड़ी मुश्किल से ही एक संगठन के रूप में माना जाता है और उनकी क्रियाओं का क्षेत्र और आदेश की शक्ति एवं दैवी सन्देश नकल करने वाले के आचरण पर निर्भर करती है। पदाधिकारियों का चुनाव इनमें से किसी एक आधार पर हो सकता है। परन्तु इनमें से कोई भी पदाधिकारी न तो नियमों से बंधा हुआ है न ही परम्परा के साथ बल्कि केवल नेता के निर्णय के साथ ही बंधा हुआ है।
इस प्रकार यह सत्ता न तो वैधानिक नियमों पर और न ही परम्परा पर, बल्कि करिश्मा या चमत्कार पर निर्भर करती है। इस प्रकार की शक्ति केवल उन व्यक्तियों तक सीमित होती है (आधारित होती), जिनके पास केवल चमत्कारी शक्तियां होती हैं। इस प्रकार की सत्ता प्राप्त करने में व्यक्ति को काफ़ी समय लग जाता है और पर्याप्त यानि पूरे साधनों के विचार के बाद लोगों द्वारा इस प्रकार की सत्ता स्वीकार की जाती है। दूसरे शब्दों में एक व्यक्ति के द्वारा अपने व्यक्तित्व का विकास इस तरह किया जाता है कि लोग ये समझने लगे कि उसने अपने व्यक्तित्व में कोई चमत्कारी शक्ति का विकास कर लिया है। इसी के बल पर ही वह लोगों को अपनी तरफ झुका लेता है और लोगों द्वारा उसकी सत्ता स्वीकार कर ली जाती है। इस तरह करिश्माई नेता अपने प्रति या अपने लक्ष्य के प्रति या आदर्शों के प्रति दूसरों से आज्ञा का पालन करवाने के लिए मांग करता है। जादूगर, पीर, पैगम्बर, अवतार, धार्मिक नेता, सैनिक, यौद्धा या किसी दल के नेता, इसी प्रकार की सत्ता सम्पन्न व्यक्ति माने जाते हैं।
लोग इस कारण ऐसे लोगों की सत्ता स्वीकार कर लेते हैं क्योंकि उनमें कुछ चमत्कारी गुण होते हैं जो साधारण व्यक्तियों में देखने को नहीं मिलते। इसी कारण प्रत्येक व्यक्ति के दिल में इन विशेष गुणों के प्रति श्रद्धा स्वाभाविक होती है। इन गुणों को ज्यादातर दैवीय गुणों के समान अथवा उनके अंश के रूप में माना जाता है। इस कारण इस प्रकार की सत्ता से सम्पन्न व्यक्ति की आज्ञा लोग श्रद्धा और भक्ति के साथ पूर्ण करते हैं। इस सत्ता की भी परम्परात्मक सत्ता के जैसी कोई निश्चित सीमा नहीं होती। इस सत्ता की एक विशेषता यह है कि हालात के अनुसार यह सत्ता वैधानिक अथवा परम्परात्मक सत्ता में बदल जाती है।

प्रश्न 4.
वैबर की सामाजिक क्रिया के सिद्धान्त के बारे आप क्या जानते हैं ? व्याख्या करो।
उत्तर-
मैक्स वैबर की सामाजिक क्रिया (Max Weber’s Social-Action)-सामाजिक क्रिया के सिद्धान्त की स्थापना में मैक्स वैबर का नाम काफ़ी महत्त्वपूर्ण है। वैबर ने सामाजिक क्रिया के सिद्धान्त की बड़ी ही खुली और वैज्ञानिक दृष्टिकोण से भी व्याख्या की है। मैक्स वैबर सामाजिक क्रिया के सिद्धान्त के द्वारा ही समाजशास्त्र की वैज्ञानिक प्रकृति को स्पष्ट करता है। अनेक समाजशास्त्री रेमण्ड, इरविंग, जैटलिन, बोगार्डस और रैक्स इत्यादि ने वैबर की आलोचना का काम उसके इस सामाज शास्त्र से ही आरम्भ किया है। इससे पहले कि हम वैबर के सामाजिक क्रिया के सिद्धान्त को समझने की कोशिश करें हम यह जान लें कि क्रिया और व्यवहार में कोई तकनीकी अन्तर नहीं मानना चाहिए।
समाज के सदस्यों के लिए यह ज़रूरी है कि वह सम्बन्धों के निर्माण के लिए अन्तर क्रिया करे। इन अन्तर क्रियाओं के आधार पर ही सामाजिक सम्बन्धों का जन्म होता है और व्यक्ति का जीवन इन सम्बन्धों के साथ ही बंधा हुआ होता है। व्यक्ति की प्रत्येक प्रकार की क्रिया के पीछे कोई न कोई उद्देश्य अवश्य होता है। इस उद्देश्य पूर्ति हेतु उसे क्रिया करनी पड़ती है। समाजशास्त्रीय रूप में सभी क्रियाएं सामाजिक क्रियाओं के दायरे में नहीं आती हैं बल्कि वही क्रियाएं सामाजिक क्रियाएं कही जाती हैं जिनको कर्ता अर्थात् क्रिया करने वाला कोई न कोई अर्थ देता है। व्यक्तियों की यह क्रिया बाहरी, अन्दरूनी, मानसिक एवं भौतिक हो सकती है। साथ ही काल या समय के नजरिये से क्रिया का सम्बन्ध वर्तमान, भूत, भविष्य तीनों में से किसी के साथ भी हो सकता है अर्थात् इसका सम्बन्ध किसी एक काल के साथ भी हो सकता है।
सामाजिक क्रिया के सिद्धान्त को पेश करने का सेहरा सबसे पहले ‘अल्फ्रेड मार्शल’ को जाता है। मार्शल ने उपयोगितावादी धारणा की विवेचना करके ‘गतिविधि’ की धारणा को विकसित किया। गतिविधि को मार्शल ने मूल्य की एक विशेष श्रेणी माना है। इसी श्रेणी में दुर्खीम ने ‘सामाजिक तथ्य’ को प्रकट किया।
आधुनिक काल में सामाजिक क्रिया धारणा के प्रमुख प्रवर्तक मैक्स वैबर थे, जिन्होंने अर्थपूर्ण सिद्धान्त को सामने रखा। इस तरह वैबलीन, मैकाइवर, कार्ल मैनहाईम, पारसंस और मर्टन के नाम महत्त्वपूर्ण हैं। हम इसी श्रेणी में विलियम वैट, डेविड काईजमैन और सी० राईट मिल्स को भी रख सकते हैं। मैक्स वैबर ने अपनी ‘सामाजिक क्रिया’ की धारणा को अपनी पुस्तक “The Theory of Social & Economic Organisation” में पेश (प्रस्तुत) किया।
मैक्स वैबर के अनुसार, “सामाजिक क्रिया व्यक्तिक क्रिया से अलग है। वैबर ने इसको परिभाषित करते हुए लिखा है कि किसी भी क्रिया को हम तभी ही सामाजिक क्रिया मान सकते हैं, जब उस क्रिया को करने वाले व्यक्ति या व्यक्तियों द्वारा लाये गये Subjective अर्थ के अनुसार उस क्रिया में दूसरे व्यक्तियों के सम्मान और भावों पर क्रियाएं इकट्ठी हों और उसी के अनुसार गतिविधि निर्धारित हो।”
मैक्स वैबर ने अपनी सामाजिक क्रिया की धारणा को समझाने के लिए इसको चार भागों में बांट कर समझाया है। वैबर ने लिखा है कि क्रियाओं का यह वर्गीकरण वस्तुओं के साथ सम्बन्धों पर आधारित है। पारसंस ने इसकी अभिमुखता का प्रारूप माना है। गरथ और मिल्स इसको प्रेरणा की दिशा कहते हैं।
वैबर के क्रिया के वर्गीकरण को समझने से पहले हम सामाजिक क्रिया की धारणा को पूरी तरह समझ लें। वैबर के अनुसार किसी भी क्रिया को सामाजिक क्रिया मानने से पहले हमें चार बातों का ध्यान रखना चाहिए।
(1) मैक्स वैबर का मानना है कि सामाजिक क्रिया दूसरे या अन्य व्यक्तियों के भूत, वर्तमान या होने वाले व्यवहार द्वारा प्रभावित हो सकती है। यदि हम अपने पहले किये हुए किसी काम के लिए क्रिया करते हैं, तो वह भूतकालीन क्रिया होगी। यदि वर्तमान समय में कोई क्रिया करते हैं तो वह वर्तमान और यदि भविष्य को ध्यान में रखते हुए कोई क्रिया करते हैं तो वह भविष्य वाली क्रिया कहलायेगी।
(2) वैबर का कहना है कि हर प्रकार की बाहरी क्रिया सामाजिक क्रिया नहीं हो सकती। बाहरी क्रिया असामाजिक है जो पूरी तरह जड़ और बेज़ानदार वस्तुओं द्वारा प्रभावित और उसकी क्रिया स्वरूप की जाती है। उदाहरण के लिए ईश्वर की अराधना, नमाज पढ़ना या अकेले ही समाधि लगाना, सामाजिक क्रिया नहीं है, परन्तु ब्राह्मणों के कहने पर पूजा अर्चना करना, मुल्लाओं के कहने पर नमाज पढ़ना इत्यादि सामाजिक क्रिया है।
(3) मनुष्य के कुछ सम्पर्क उस सीमा तक सामाजिक क्रिया में आते हैं जहां तक वह दूसरों के व्यवहार के साथ अर्थपूर्ण ढंग के साथ सम्बन्धित और प्रभावित होते हैं। हर प्रकार के सम्पर्क सामाजिक नहीं कहे जा सकते।
उदाहरण के लिए अगर सिनेमा की सीढ़ियां उतरते समय दो व्यक्ति आपस में टकरा जाएं तो यह सामाजिक क्रिया नहीं होगी, अगर वह आपस में संघर्ष पर उतर आए अथवा माफी मांगने लगे तो यह सामाजिक क्रिया होगी क्योंकि ऐसा करने से दोनों के व्यवहार आपस में सम्बन्धित और प्रभावित होते हैं।
(4) सामाजिक क्रिया न तो अनेक व्यक्तियों द्वारा की जाने वाली एक जैसी क्रिया को कहा जाता है और न ही उस क्रिया को कहा जाता है जो कि केवल दूसरे व्यक्तियों द्वारा प्रभावित होती है।
उदाहरण के लिए बारिश होने पर सड़क पर अनेकों व्यक्तियों द्वारा छाता खोल लेने की क्रिया सामाजिक क्रिया नहीं होती क्योंकि प्रत्येक व्यक्ति की क्रिया का दूसरे अथवा और व्यक्तियों से कोई सम्बन्ध नहीं होता। वैबर कहते हैं कि दूसरे की क्रिया की नकल करना सामाजिक क्रिया नहीं है, जब तक कि वह और व्यक्ति जिसकी कि नकल की जा रही है, की क्रिया साथ अर्थपूर्ण सम्बन्ध न रखता हो अथवा उसकी क्रिया द्वारा अर्थपूर्ण रूप से प्रभावित न होता हो।
मैक्स वैबर के अनुसार सामाजिक क्रिया को समझने के लिए उसकी अर्थ मूलक व्याख्या की आवश्यकता होती है। इस व्याख्या को दो भागों में विभक्त करके समझाया जा सकता है।
- औसत प्रकार की अर्थ मूलक व्याख्या
- विशुद्ध प्रकार की अर्थ मूलक व्याख्या
वैबर ने इस बात पर विशेष जोर दिया कि सामाजिक क्रिया का अध्ययन विशुद्ध अर्थ मूलक की व्याख्या के लिए करना चाहिए परन्तु इनको समझने के लिए कुछ महत्त्वपूर्ण विधियों का भी वर्णन किया गया है जिनके आधार पर समाज की धारणाओं को सही तरह समझा गया है। इसमें वैबर ने तर्कपूर्ण और अर्थपूर्ण व्याख्या पर जोर दिया है।
इस सम्बन्ध में वैबर ने यह बताया है कि सभी सामाजिक क्रियाओं के कुछ निश्चित अर्थ होते हैं और एक प्रेरक शक्ति भी होती है। यह दोनों ही दूसरे व्यक्तियों की प्रेरक शक्तियों और क्रियाओं में बदलते रहते हैं।
यहाँ एक बात बहुत महत्त्व की है कि समाज शास्त्री किसी सामाजिक क्रिया की व्याख्या उसके अर्थ के आधार पर करता है जो कि दूसरे की क्रियाओं द्वारा निर्देशित होता है। इस प्रकार समाज शास्त्र प्राकृतिक विज्ञानों से पूरी तरह अलग हो जाता है।
सामाजिक क्रिया के प्रकार (Types of Social Action)-देखें पाठ्य-पुस्तक के प्रश्न IV (5)
वैबर ने बताया है कि सामाजिक क्रियाएं तीन प्रकार से निर्देशित होती हैं-
- परम्परागत प्रयोग-इसका अर्थ यह है कि जो क्रियाएं परम्परा के आधार पर सम्पादित की जायें। सामाजिक प्रथाएं मनुष्य की क्रियाओं को प्रभावित करती हैं। इसका परिणाम यह होता है कि लोगों की क्रियाएं परम्परा से हटकर बाहर नहीं जाती हैं और सामाजिक मर्यादा पूरी तरह बनी रहती है।
- हित-हित का अर्थ उन समरूपताओं से है जिसमें क्रियाओं को विवेकपूर्ण निर्देशन के रूप में समझा जा सके।
- न्यायसंगत व्याख्या-इससे सम्बन्धित व्यवहार क्रियाएं, कर्ता के किसी आदर्श के निश्चित होने की नज़र से निर्देशित होती हैं। ये ऐसे आदर्शों से भी निर्देशित होती हैं जोकि किसी विशेष निर्देश को पाने के लिए तार्किक समझे जाये।
सामाजिक क्रिया के सम्बन्ध में वैबर ने बताया कि सामाजिक सम्बन्धों के आधार पर ही क्रिया निश्चित होती है।
वैबर ने आगे कहा है कि सामाजिक सम्बन्धों की पहली और आवश्यक कसौटी यह है कि उसमें प्रत्येक व्यक्ति की क्रिया का दूसरे की कोशिश की तरह परस्पर रूप से निर्देशन हो। इसके Contents की प्रकृति चाहे अलगअलग प्रकार की क्यों न हो जैसे कि संघर्ष विरोध, यौन आकर्षण, मित्रता, अनुराग या आर्थिक लेन-देन इत्यादि।
इस सम्बन्ध में अर्थ का बड़ा ही महत्त्व है, अर्थ का मतलब उस अर्थ से है जो किसी विशेष दशा में लिया जाता है। यह अर्थ औसत रूप या सैद्धान्तिक रूप से बनाकर, विशुद्ध रूप में लाया जाता है।
वैबर ने यह भी बताया कि सामाजिक सम्बन्धों में पारम्परिक रूप के साथ निर्देशित बल के Subjective अर्थ एक समान ही है।
“सामाजिक क्रिया को अभिमुखता की प्राकृतिक के आधार पर दोबारा विवेक अभिमुख, अविवेक अभिमुख, सहानुभूति अभिमुख और आपसी अभिमुख क्रिया के रूप में रखा जा सकता है।” मानव के ज्ञान पर ही कुछ व्यवहार आधारित होते हैं तथा यह ज्ञान ही साधन के लक्ष्य का आधार होता है, लेकिन साथ ही कुछ ऐसे व्यवहार भी होते हैं जिसमें ज्ञान की प्रधानता ना होकर सामाजिक मूल्यों को प्रधानता दी जाती है। इन व्यवहारों को विवेकपूर्ण माना जाता है। कुछ व्यवहार उस श्रेणी में आते हैं जहां अपनापन और हमदर्दी को मानव द्वारा महत्त्व दिया जाता है। चाहे वह व्यवहार अविवेकपूर्ण हो और कुछ व्यवहार विवेकपूर्ण इसलिए भी हो जाते हैं क्योंकि मानव परम्परा को महत्त्व दे बैठता है। मानव सम्बन्धी तथ्य प्रत्यक्षवादी परिप्रेक्ष्य से विवेकपूर्ण क्रिया के अन्तर्गत परिभाषित किए जाते हैं।
इस स्थिति में पैरेटो और वैबर के एक-दूसरे के विचारों में भिन्नता आ जाती है कि अविवेकपूर्ण क्रिया, विवेकपूर्ण क्रिया से सही अलग क्रिया है। आपसी क्रिया ऐसी क्रिया है जिसमें परम्परागत तथ्य प्रधानता रखते हैं, औसत श्रेणी में संवेगात्मक अथवा हमदर्दी अभिमुख क्रिया को लेते हैं। मानवीय क्रियाओं की अभिमुखता, प्रचलन रुचि और सही आज्ञा से भी हो सकती है। विद्वानों की राय है कि वैबर की क्रिया के सिद्धान्त को अपनी इच्छा तथा आधारित क्रिया के सिद्धान्त से कुछ हद तक जाना जा सकता है। पारसंस के क्रिया के सिद्धान्त पर वैबर का प्रभाव देखा जा सकता है। विवेक की धारणा को वैबर ने 6 प्रकार से प्रयोग में लिया है।
मैक्स वैबर ने जिस क्रिया के सिद्धान्त को दिया है वह मार्क्स के सिद्धान्त से बिल्कुल अलग है। साधनयुक्त विवेक को वैबर ने अपने विचारों में प्रमुख स्थान दिया है। कर्ता की तरफ से उद्देश्य की प्राप्ति के मूल्य और उद्देश्य दोनों का मूल्यांकन इस प्रकार के व्यवहार में किया जाता है। कर्ता के द्वारा एक उद्देश्य की प्राप्ति से दूसरे उद्देश्य की प्राप्ति के लिए साधन के बारे में कल्पना की जाती है। इस तरह की भावना वैबर के विचारों में थी। विवेक शब्द का प्रयोग वैबर ने व्यवहार और विश्वास दोनों के लिए किया है। यानि विवेकपूर्ण व्यवहार वही है जिसमें कर्ता के द्वारा विवेक को स्थान दिया जाता है और उसी के अनुरूप विश्वास के स्तर पर भी विवेक को महत्त्व दिया गया है। सामाजिक व्यवहार के रूप में अनेक विद्वानों ने ऊपरलिखित विवेचनाओं से नतीजा निकाला है कि जिसमें संवेगात्मक और सहानुभूति के तत्त्व मौजूद होते हैं ऐसे व्यवहारों को विवेकपूर्ण व्यवहार कहा गया है।
विवेक वैबर के लिए एक आदर्श रहा है। आपसी सामाजिक रचना के टूटने का एक मुख्य कारण वो बढ़ता हुआ विवेकीकरण है। विशेष तौर पर हम विवेकीकरण की बढ़ती हुई मात्रा को बाज़ार के सम्बन्धों में देख सकते हैं।

प्रश्न 5.
दुर्खीम के सामाजिक तथ्य की विवेचना करो।
अथवा
दुर्खीम के सामाजिक तथ्य के बारे में चर्चा करो।
उत्तर-
इमाइल दुर्खीम द्वारा दी गई “सामाजिक तथ्य” की विवेचना बहुत महत्त्वपूर्ण है। दुर्खीम के सामाजिक तथ्यों सम्बन्धी विचार उसकी दूसरी प्रमुख पुस्तक “दि रूलस ऑफ़ सोशोलोजीकल मैथड’ में दिखाई पड़ते हैं। दुर्खीम की 1895 में प्रकाशित ये पुस्तक समाजशास्त्र के शास्त्रीय ग्रन्थ के रूप में पहचानी जाती है।
दुर्खीम ने यह अनुभव किया कि समाज शास्त्र को एक स्वतन्त्र विज्ञान के रूप में तब तक स्थापित नहीं किया जा सकता जब तक कि उसका अध्ययन वस्तु की विशेषता स्पष्ट न हो और इसकी खोज के लिये एक व्यवस्थित पद्धति शास्त्र का विकास न हो। इन दो उद्देश्यों के लिये दुर्खीम ने The Rules of Sociological Method की रचना की।
दुर्खीम ने काम्ते, स्पैंसर, मिल इत्यादि समाजशास्त्रियों की खामियों का अनुभव किया, और स्पष्ट लिखा है कि, “यह समाजशास्त्री जिनकी चर्चा हमने अभी की है, वह समाजों की प्रवृत्ति और समाजिक जैविकीय क्षेत्रों के मध्य सम्बन्धों के विषय में अस्पष्ट समाजीकरण से बहुत आगे चले गए थे।”
दुर्खीम ने अपने उद्देश्य के अनुरूप इस पुस्तक में दो प्रमुख कठिनाइयों का वर्णन किया।
- उन्होंने समाज शास्त्र के अध्ययन के लिये विद्यार्थियों के लिए सारी विषय सामग्री का निर्धारण किया। इस तरह करने के साथ उसने समाज-शास्त्र को मनोवैज्ञानिक और जीव संसार से मुक्त करवा कर उसे एक अलग स्वतन्त्र अस्तित्व प्रदान किया।
- प्राकृतिक विज्ञान की प्रत्यक्षयवादी, तथ्यात्मक अध्ययन पद्धति के रूप में देखा और इस पद्धति के सफल प्रयोग के लिये पालने योग्य नियमों का निर्माण किया।
दुर्खीम ने अपनी पुस्तक में सामाजिक तथ्य की विवेचना के लिए 6 मुख्य बातों की विवेचना की जिसको उसने 6 मुख्य (chapters) में पेश किया, जो कि निम्नलिखित हैं-
- सामाजिक तथ्य क्या है?
- सामाजिक तथ्यों के निरीक्षण और नियम।
- Normal और Pathological तथ्यों में भेद करने के नियम
- सामाजिक रूपों के वर्गीकरण के नियम
- सामाजिक तथ्यों की व्याख्या के नियम
- समाज शास्त्रीय प्रमाणों की स्थापना के साथ सम्बन्धित नियम।
सामाजिक तथ्य क्या हैं ?
(What are Social Facts ?)
दुर्खीम ने विषय सामग्री और अध्ययन पद्धति दोनों ही नज़रियों से समाज-शास्त्र को एक स्वतन्त्र सामाजिक विज्ञान के रूप में स्थापित करने की कोशिश की है। दुर्खीम ने समाज-शास्त्र की विषय सामग्री के रूप में सामाजिक तथ्यों को पेश किया है। दुर्खीम का स्पष्ट मानना है कि समाज-शास्त्र सभी मानवीय गतिविधियों का अध्ययन नहीं करता बल्कि अपने आपको केवल सामाजिक तथ्यों के अध्ययन तक ही सीमित रखता है।
दुर्खीम ने अपने इस अध्याय में यह बात स्पष्ट करने की कोशिश की है कि वास्तव में किन तथ्यों को सामाजिक तथ्य कहा जायेगा? सामाजिक तथ्यों की क्या विशेषताएं हैं और उनका अध्ययन किस प्रकार किया जायेगा? सामाजिक तथ्यों के अर्थ स्पष्ट करते हुए दुर्खीम कहते हैं कि सामाजिक तथ्यों के बारे में अनेक प्रकार की शंकाएं प्रचलित हैं और यही कारण है कि मनोविज्ञान, प्राणी शास्त्र और समाज शास्त्र के विषय वस्तु के सम्बन्धों में कई प्रकार की भ्रान्तियां भी मन में पड़ जाती हैं। स्वयं दुर्खीम ने लिखा है सामाजिक तथ्यों की पद्धति के बारे में जानने से पूर्व यह जानना ज़रूरी है कि कब तथ्यों को आमतौर पर ‘सामाजिक’ कहा जाता है। यह सूचना और भी अधिक आवश्यक है, क्योंकि ‘सामाजिक’ शब्द का प्रयोग अधिक अनिश्चित रूप में होता है। वर्तमान में इस शब्द का प्रयोग समाज में होने वाली किसी भी घटना के लिए किया जाता है चाहे उसकी सामाजिक रुचि कितनी ही कम क्यों न हो। परन्तु ऐसी कोई भी मानवीय घटना नहीं है जिसको सामाजिक न कहा जा सके। प्रत्येक व्यक्ति सोता है, खाता है, पीता है और विचार करता है और यह सामाजिक हित में होता है कि यह सभी कार्य सही व्यवस्थित ढंग से हों। यदि इन सबको सामाजिक तथ्य मान लिया जाये तो समाज शास्त्र की भिन्न रूप से कोई विषय वस्तु नहीं होगी। इससे समाज-शास्त्र, प्राणी शास्त्र और मनोविज्ञान शास्त्र में भ्रम की स्थिति उत्पन्न हो जाती है।
सामाजिक तथ्य के अर्थ की विवेचना करते हुए दुर्खीम ने सर्वप्रथम यह कहा कि सामाजिक तथ्यों को वस्तुओं के समान समझना चाहिए। यद्यपि दुर्खीम ने वस्तु शब्द का वास्तविक अर्थ कहीं भी स्पष्ट नहीं किया। दुर्खीम ने वस्तु शब्द को चार अलग-अलग अर्थों में प्रयोग किया है। यह हैं-
(1) सामाजिक तथ्य एक ऐसी वस्तु है, जिसमें कुछ विशेष गुण होते हैं जिसको बाहरी रूप में देखा जा सकता
है।
(2) सामाजिक तथ्य एक ऐसी वस्तु है, जिसको केवल अनुभव द्वारा ही जाना जा सकता है।
(3) सामाजिक तथ्य एक ऐसी वस्तु है, जिसका अस्तित्व मनुष्य के ऊपर बिल्कुल निर्भर नहीं।
(4) सामाजिक तथ्य एक ऐसी वस्तु है, जिसको केवल बाहरी तौर पर देखते हुए जाना जा सकता है। परन्तु क्योंकि सामाजिक तथ्य वस्तु के समान है, अतः यह कोई स्थिर धारणाएं नहीं हैं बल्कि गतिशील धारणा के रूप में जानने योग्य है। इस तरह हम देखते हैं कि समाज में कुछ ऐसे तथ्य होते हैं जो कि भौतिक प्राणी शास्त्र और मनोवैज्ञानिक तथ्यों से अलग होते हैं। दुर्खीम इस प्रकार के तथ्यों को सामाजिक तथ्य मानते हैं। दुर्खीम ने सामाजिक तथ्यों की कुछ परिभाषाएं पेश की हैं, एक स्थान पर दुर्खीम लिखते हैं, “सामाजिक तथ्य कार्य करने, सोचने और अनुभव करने के वह तरीके हैं, जिसमें व्यक्तिगत चेतना से बाहर ही अस्तित्व को बनाये रखने की उल्लेखनीय विशेषता होती है।”
एक अन्य स्थान पर दुर्खीम ने लिखा है कि, “सामाजिक तथ्यों में कार्य करने सोचने, अनुभव करने के वह तरीके हैं जिसमें व्यक्तिगत चेतना से बाहर भी अस्तित्व को बनाये रखने को उल्लेखनीय विशेषता होती है।” अपनी पुस्तक के पहले chapter की अन्तिम पंक्तियों में इसकी विस्तार के साथ परिभाषा पेश करते हुए लिखा है, “एक सामाजिक तथ्य क्रिया करने का हर स्थायी और अस्थायी तरीका है जो व्यक्ति पर बाहरी दबाव डालने में समर्थ होता है या फिर कृपा करने का हर तरीका जो किसी समाज में आम रूप में पाया जाता है परन्तु साथ ही साथ व्यक्तिगत विचारों से स्वतन्त्र अलग अस्तित्व रखता है।”
दुर्खीम की उपरोक्त परिभाषाओं से स्पष्ट है कि “क्रिया करने के तरीके” सामाजिक तथ्य हैं। क्रिया करने के तरीकों में मानवीय व्यवहार के सभी पहलू शामिल हैं, जो उसके विचार, अनुभव और क्रिया के साथ सम्बन्ध रखते हैं। यह सामाजिक वास्तविकता के अंग हैं। ऐसी सामाजिक घटना स्थायी भी हो सकती है, और अस्थायी भी हो सकती है। उदाहरणार्थ किसी समाज में आत्महत्याओं की, विवाहों की, मृत व्यक्तियों की संख्या में बहुत कम अन्तर होता है। अर्थात् इनकी वार्षिक दर आमतौर पर स्थित रहती है। अतः इसको सामाजिक तथ्य कहा जाता है।
इस तरह ‘भगवान्’ को सामाजिक तथ्य नहीं कहा जाता है क्योंकि वह वास्तविक निरीक्षण से दूर है। इस तरह मनही-मन सोचा गया, कोई विचार भी सामाजिक तथ्य की श्रेणी में नहीं आयेगा क्योंकि उनका कोई स्पष्ट रूप नहीं है। परन्तु किसी विद्वान् द्वारा दिया गया कोई भी सिद्धान्त, या नियम या ईश्वरीय सम्बन्धी पूजा, प्रार्थना या आराधना, जिसमें टोटमवाद भी शामिल है, को सामाजिक तथ्य माना जायेगा क्योंकि उनका साफ निरीक्षण सम्भव है। भाषा, लोक कथा, धार्मिक विश्वास, क्रियाएं, Business के नियम, नैतिक नियम इत्यादि सामाजिक तथ्यों की कितनी ही अनुपम उदाहरणे हैं क्योंकि इन सभी का निरीक्षण एवं परीक्षण सम्भव है और यह व्यक्ति के साथ जुड़े होते हैं। यह व्यक्ति के ऊपर दबाव डालने की शक्ति रखते हैं।
इस प्रकार दुर्खीम ने सामाजिक तथ्यों की विवेचना दो प्रमुख यथार्थक मापदंडों के माध्यम से बहुत ही स्पष्ट रूप से हमारे सामने पेश की है, वह मापदंड है
- वह वैज्ञानिक के दिमाग से बाहर होने चाहिए और
- उसका वैज्ञानिक पर ज़रूरी अथवा मजबूरी का प्रभाव होना चाहिए।
सामाजिक तथ्यों की विशेषताएं (Characteristics of Social Facts) –
दुर्खीम की विवेचना के आधार पर हम देखते हैं कि दुर्खीम ने सामाजिक तथ्यों की धारणा को समझने के लिए दो शब्दों बाहरीपन (Exteriority) और बाध्यता (Constraint) का सहारा लिया गया है। इन दोनों को सामाजिक तथ्यों की विशेषता के रूप में पेश किया जा सकता है।
1. बाहरीपन (Exteriority)-सामाजिक तथ्य की सबसे पहली और महत्त्वपूर्ण विशेषता उसका बाहरीपन है। बाहरीपन का अर्थ है सामाजिक तत्त्वों का निर्माण लो समाज के सदस्यों के द्वारा ही होता है। परन्तु सामाजिक तथ्य एक बार विकसित होने के बाद फिर किसी व्यक्ति विशेष के नहीं रहते हैं और वह इस अर्थ में कि इसको एक स्वतन्त्र वास्तविकता के रूप में अनुभव किया जा सकता है अर्थात् विज्ञान का उसके साथ अन्दरूनी सम्बन्ध नहीं होता है और न ही सामाजिक तथ्यों का व्यक्ति विशेष पर कोई प्रभाव पड़ता है।
सामाजिक तथ्यों के बाहरीपन को स्पष्ट करने के लिए दुर्खीम ने इसको व्यक्तिगत चेतना,सामूहिक चेतना के अन्तर अथवा भेद के आधार पर स्पष्ट किया है। दुर्खीम ने व्यक्तिगत चेतना के स्वरूप और संगठन के अध्ययन से यह स्पष्ट किया है कि व्यक्तिगत चेतनाओं का मूल आधार भावनाएँ हैं। संवेदनाएं अलग-अलग सैलों की अंतर क्रियाओं का प्रतिफल है लेकिन अलग-अलग सैलों द्वारा पैदा होने वाली संवेदनाओं की अपनी खास विशेषता होती है, जो संगठन अथवा उत्पत्ति से पहले सोलां सैलों में से किसी में भी मौजूद नहीं थी। Synthesis and Suigeneris के इस सिद्धांत में दुर्खीम ने यह बताया है कि इकट्ठा होने से एक नई वस्तु का जन्म होता है। अर्थात् प्रसार और संयोग की क्रिया द्वारा तथ्य का रूप ही बदल जाता है। जैसे व्यक्तिगत विचारों का आधार स्नायुमंडल के अलग है। उसी प्रकार दुर्खीम कहते हैं कि सामाजिक विचारों का मूल आधार समाज के सदस्य होते हैं। सामूहिक चेतना का विकास व्यक्तिगत चेतना में मिलने से संगठन के विकास से होता है। इसी प्रकार दुर्खीम के शब्दों में, “यह व्यक्तिगत चेतना से बाहर रहने वाले विशेष तथ्यों को पेश करता है।”
एक उदाहरण से इसे और भी स्पष्ट किया जा सकता है। ऑक्सीजन और हाइड्रोजन के एक निश्चित योग के साथ पानी बनता है। पानी की अपनी कुछ विशेषताएं हैं। ये विशेषताएं न ऑक्सीजन की हैं और न ही हाइड्रोजन की हैं। पानी को अलग करके फिर पुनः ऑक्सीजन और हाइड्रोजन को नहीं बनाया जा सकता। इस तरह व्यक्ति चेतनाओं के योग के साथ सामूहिक चेतना का निर्माण होता है। जो व्यक्तिगत तथ्यों से अलग अपना स्वतन्त्र अस्तित्व रखता है। अतः वह प्रत्येक व्यक्ति के लिए बाहरी होती है।
2. विवशता (Constraint)-सामाजिक तथ्यों की दूसरी प्रमुख और महत्त्वपूर्ण विशेषता उसकी विवशता है। दूसरे शब्दों में व्यक्ति के ऊपर सामाजिक तथ्यों का एक दबाव या विवशता का एक प्रभाव पड़ता है। वस्तुतः सामाजिक तथ्यों का निर्माण एक व्यक्ति या कुछ व्यक्तियों के द्वारा नहीं होता बल्कि अनेकों व्यक्तियों के द्वारा होता है। अतः ये बहुत शक्तिशाली होते हैं और किसी व्यक्ति के ऊपर इस विवशता के कारण प्रभाव पड़ता है।
दुर्खीम का मानना है कि सामाजिक तथ्य केवल व्यक्ति के व्यवहार को नहीं बल्कि उसके सोचने, विचार करने इत्यादि के तरीकों को भी प्रभावित करते हैं। दुर्खीम बताते हैं कि इन सामाजिक तथ्यों की यह विशेषता इस रूप में देख सकते हैं कि ये सामाजिक तथ्य व्यक्ति की अनुभूति के अनुरूप नहीं, बल्कि व्यक्ति का व्यवहार उनके
अनुरूप होता है।
दुर्खीम सामाजिक तथ्यों की इस विशेषता के विवेचन में अनेक उदाहरण पेश करते हैं। आपके अनुसार समाज में प्रचलित अनेक सामाजिक तथ्य जैसे कि नैतिक नियम, धार्मिक विश्वास, वित्तीय व्यवस्था, आदि सभी मनुष्य के व्यवहार और तरीकों को प्रभावित करते हैं। स्वयं दुर्खीम लिखते हैं कि यदि यह दबाव इन तथ्यों की अन्दरूनी विशेषताएं होती हैं और इसका सबूत यह है कि जब मैं इनका विरोध करने की कोशिश करता हूं तो यह और भी अधिक दबाव डाल देते हैं। वह आगे लिखते हैं” यदि मैं समाज के नियमों को नहीं मानता हूं तो जिस हंसी का पात्र मुझे बनाया जाता है और जिस तरह मुझे समाज से अलग रखा जाता है, और यह असली अर्थों में एक प्रकार के दण्ड या सज़ा की तरह प्रभाव डालने वाला होता है। यद्यपि ये विवशता तथा दबाव अप्रत्यक्ष होते हुए भी प्रभावकारी होते हैं।”
विवशता की एक और उदाहरण में दुर्खीम इसको स्पष्ट करते हैं, “मेरे लिए यह जरूरी नहीं कि मैं अपने देशवासियों से फ्रांसीसी अथवा किसी और भाषा में ही बात करूँ और प्रचलित मुद्रा का प्रयोग करूँ, लेकिन ये सब इससे विपरीत कार्य करना मेरे लिए संभव नहीं होगा। एक उद्योगपति के रूप में मैं बीत गई सदियों की तकनीकी विधियों को अपनाने में पूरी तरह स्वतन्त्र हैं लेकिन ऐसा करने से मैं अपने आपकी बरबादी को बुलावा दूंगा। लेकिन अगर मैं ज़रूरी तथ्यों से बचने की कोशिश करूंगा तो पूरी तरह असफल रह जाऊंगा। अगर मैं इन नियमों से अपने आप को स्वतन्त्र कर लेता हूँ तो सफलता से उनका विरोध करता हूँ तो भी मुझे हमेशा इनसे संघर्ष करने के लिए मज़बूर किया जाता है, और अंत में वह अपने बदले द्वारा अपने दबाव का अनुभव हमें करा देते हैं।”
दुर्खीम कहते हैं कि “कभी-कभी इस विवशता को प्रत्यक्ष रूप से नहीं देख सकते। वह समाजीकरण की एक उदाहरण दे कर इसको स्पष्ट करते हैं कि जीवन के आरम्भिक काल में हमें बच्चे को खाने, पीने, व सोने के लिए विवश करते हैं। हम उसे सफ़ाई, शान्ति और कहना मानने के लिए भी विवश करते हैं। बाद में हम उसे दूसरों के प्रति उचित भाव, प्रथा, रीति रिवाजों, प्रति सम्मान करना और काम करने की आवश्यकता आदि के बारे में सिखाते हैं। विवशता अनुभव न होने के कारण यह होता है कि धीरे-धीरे यह विवशता आदतों में तबदील हो जाती है।”
सामूहिक चेतना व्यक्तिगत चेतना से उत्तम रूप है क्योंकि सामूहिक चेतना व्यक्तिगत चेतनाओं के अस्तित्व से विशेषताओं की संगठित (मिली-जुली) हुई चेतना है। दुर्खीम लिखते है, “एक सामाजिक तथ्य ‘विश्व दबाव’ की शक्ति से पहचाना जाता है जो कि व्यक्ति पर प्रयोग किया जाता है अथवा व्यक्ति पर प्रयोग करने योग्य हो।” दुर्खीम के अनुसार सामाजिक तथ्य ‘सामूहिक चेतना’ की श्रेणी में आते है इसीलिए यह चेतनाओं की चेतना है।
3. व्यापकता (Generality)—यह समाज विशेष में सांझे और आदि अंत तक फैले होते हैं। लेकिन यह विलक्षण विशेषता नहीं हो तो और न ही व्यापकता अनेकों व्यक्तिगत तथ्यों के केवल जोड़फल मात्र का परिणाम नहीं होते बल्कि यह तो शुद्ध रूप में अपने स्वभाव से ही सामूहिक होते हैं और व्यक्तियों पर इनका प्रभाव इनकी सामूहिक विशेषता का ही नतीजा है। इसीलिए इसको सामाजिक तथ्यों की तीसरी विशेषता कहा जाता है।
दुर्खीम के ऊपर लिखे सामाजिक तथ्यों के विश्लेषण से यह स्पष्ट होता है कि सामाजिक तथ्यों की दो महत्त्वपूर्ण विशेषताएं होती हैं।
- सामाजिक तथ्य व्यक्तिगत विचारों से स्वतन्त्र अपना अलग स्वतन्त्र अस्तित्व रखते हैं। अर्थ यह कि व्यक्ति से अलग होते हैं।
- सामाजिक तथ्यों का व्यक्ति पर एक मज़बूरी का प्रभाव पड़ता है अर्थात् यह व्यक्ति पर दबाव डालने की शक्ति से भरे होते हैं।
ऊपर दी गई विवेचना के आधार पर दुर्खीम ने अपने पहले अध्याय की अंतिम लाईनों में सामाजिक तथ्य को पेश करते हुए लिखा है कि, “एक सामाजिक तथ्य काम करने का वह तरीका है, जो चाहे निश्चित हो अथवा नहीं, जो कि व्यक्ति पर बाहरी दबाव डालने की शक्ति रखता है अथवा काम करने का वह हर तरीका जो एक दिए हुए समाज में सभी तरफ सामान्य है और साथ ही व्यक्तिगत विचारों से स्वतन्त्र उसकी अपनी अलग स्थिति बनी रहती संक्षेप में दुर्खीम के अनुसार सामाजिक तथ्य कार्य करने का वह तरीका है, जो व्यक्तियों से बाहर है तथा व्यक्ति पर दबाव डालने की शक्ति रखता है।

प्रश्न 6.
दुर्खीम के श्रम विभाजन के सिद्धान्त की व्याख्या करो और इसके उत्तरदायक कारकों का स्पष्टीकरण करो।
अथवा
दुर्खीम के श्रम विभाजन के सिद्धान्त की विवेचना करो।
उत्तर-
दुर्खीम ने 1893 में फ्रैंच भाषा में अपनी पहली किताब De la Division du Trovail social के नाम से प्रकाशित की। चाहे यह दुर्खीम का पहला ग्रन्थ था पर उसकी प्रसिद्धि की यह एक आधार-शिला थी। इसी ग्रन्थ पर दुर्खीम को 1893 में पैरिस विश्वविद्यालय में डॉक्टरेट की उपाधि प्रदान की गई थी। इस महान् ग्रन्थ में दुर्खीम ने सामाजिक श्रम विभाजन का प्रत्यक्ष सिद्धान्त पेश किया है। दुर्खीम की यह किताब तीन भागों में बांटी हुई है हर भाग में दुर्खीम ने श्रम विभाजन के भिन्न-भिन्न पक्षों की विवेचना की है। ये तीन खण्ड हैं-
- श्रम विभाजन के प्रकार्य (The functions of Division of Labour)
- कारण व दशाएं (Causes and Conditions)
- श्रम विभाजन के असाधारण स्वरूप (Abnormal forms of Division of Labour)
दुर्खीम ने अपनी किताब के पहले भाग ‘श्रम विभाजन के प्रकार्य’ में श्रम विभाजन को सामाजिक एकता (Social solidarity) का आधार सिद्ध करने की कोशिश की है। साथ ही उसके वैज्ञानिक अध्ययन की नज़र से कानूनों के स्वरूप, एकता के रूप, मानवीय सम्बन्धों के स्वरूप, अपराध, दण्ड, सामाजिक विकास आदि अनेकों मुश्किलों व धारणाओं की व्याख्या पेश की है। दूसरे हिस्से में श्रम विभाजन के कारणों व परिणामों का विस्तृत विश्लेषण पेश किया है। तीसरे खण्ड में दुर्खीम ने श्रम विभाजन के असाधारण स्वरूपों की विवेचना दी है।
अब हम दुर्खीम के पहले दोनों भागों की विवेचना की मदद से सामाजिक श्रम-विभाजन के सिद्धान्त की विवेचना करेंगे।
श्रम विभाजन के प्रकार्य (Functions of Division of Labour) –
दुर्खीम प्रत्येक सामाजिक तथ्य को एक नैतिक तथ्य के रूप में स्वीकार करते हैं। कोई भी सामाजिक प्रतिमान नैतिक आधार पर ही सुरक्षित रहता है। एक कार्यवादी के रूप में सबसे पहले दुीम ने श्रम विभाजन के कार्य की खोज की है। दुर्खीम ने सबसे पहले ‘प्रकार्य’ शब्द का अर्थ स्पष्ट किया है प्रकार्य के उन्होंने दो अर्थ बताए हैं।
(1) प्रकार्य का मतलब गति व्यवस्था से है अर्थात् क्रिया से है।
क्रिया के द्वारा पूरी होने वाली ज़रूरत से है।
दुर्खीम ‘प्रकार्य’ का प्रयोग दूसरे शब्दों में करते हैं इस प्रकार श्रम विभाजन के प्रकार्य से उनका अर्थ यह है कि श्रम विभाजन की प्रक्रिया समाज के अस्तित्व के लिए कौन-सी मौलिक ज़रूरत को पूरा करती है। प्रकार्य तो वह है जिसकी अनावश्यकता में उसके तत्त्वों की मौलिक ज़रूरत की पूर्ति नहीं हो सकती।
आमतौर से यह कहा जाता है कि श्रम विभाजन का प्रकार्य सभ्यता का विकास करना है क्योंकि यह स्पष्ट सच है कि श्रम विभाजन के विकास के साथ-साथ विशेषीकरण के नतीजे के तौर पर समाज में सभ्यता बढ़ती है। श्रम विभाजन के परिणाम के तौर पर उत्पादन शक्ति में बढ़ावा होता है, भौतिक व बौधिक विकास होता है व साधारण जीवन में सुख के उपभोग व ज्ञान का प्रसार होता है इसलिए आमतौर पर श्रम विभाजन को सभ्यता का स्रोत कहा जाता है।
मुश्किलों व धारणाओं की व्याख्या पेश की है। दूसरे हिस्से में श्रम विभाजन के कारणों व परिणामों का विस्तृत विश्लेषण पेश किया है। तीसरे खण्ड में दुर्थीम ने श्रम विभाजन के असाधारण स्वरूपों की विवेचना दी है।
अब हम दुर्थीम के पहले दोनों भागों की विवेचना की मदद से सामाजिक श्रम-विभाजन के सिद्धान्त की विवेचना करेंगे।
श्रम विभाजन के प्रकार्य
(Functions of Division of Labour)
दुर्थीम प्रत्येक सामाजिक तथ्य को एक नैतिक तथ्य के रूप में स्वीकार करते हैं। कोई भी सामाजिक प्रतिमान नैतिक आधार पर ही सुरक्षित रहता है। एक कार्यवादी के रूप में सबसे पहले दुीम ने श्रम विभाजन के कार्य की खोज की है। दुर्थीम ने सबसे पहले ‘प्रकार्य’ शब्द का अर्थ स्पष्ट किया है प्रकार्य के उन्होंने दो अर्थ बताए हैं।
- प्रकार्य का मतलब गति व्यवस्था से है अर्थात् क्रिया से है।
- प्रकार्य का दूसरा अर्थ इस क्रिया या गति और उसके अनुरूप ज़रूरतों के आपसी सम्बन्धों से है अर्थात् क्रिया के द्वारा पूरी होने वाली ज़रूरत से है।
दुर्थीम ‘प्रकार्य’ का प्रयोग दूसरे शब्दों में करते हैं इस प्रकार श्रम विभाजन के प्रकार्य से उनका अर्थ यह है कि श्रम विभाजन की प्रक्रिया समाज के अस्तित्व के लिए कौन-सी मौलिक ज़रूरत को पूरा करती है। प्रकार्य तो वह है जिसकी अनावश्यकता में उसके तत्त्वों की मौलिक ज़रूरत की पूर्ति नहीं हो सकती।
आमतौर से यह कहा जाता है कि श्रम विभाजन का प्रकार्य सभ्यता का विकास करना है क्योंकि यह स्पष्ट सच है कि श्रम विभाजन के विकास के साथ-साथ विशेषीकरण के नतीजे के तौर पर समाज में सभ्यता बढ़ती है। श्रम विभाजन के परिणाम के तौर पर उत्पादन शक्ति में बढ़ावा होता है, भौतिक व बौधिक विकास होता है व साधारण जीवन में सुख के उपभोग व ज्ञान का प्रसार होता है इसलिए आमतौर पर श्रम विभाजन को सभ्यता का स्रोत कहा जाता है।
दुर्शीम ने विरोध किया है। उसने सभ्यता के विकास को श्रम विभाजन का प्रकार्य नहीं माना है। दुर्थीम के अनुसार स्रोत का काम नहीं है। सुखों में बढ़ोत्तरी या बौद्धिक व भौतिक विकास प्रकार्य विभाजन के परिणाम से उत्पन्न होते हैं। इसलिए यह इस प्रक्रिया के परिणाम हैं, काम नहीं। काम का अर्थ परिणाम नहीं होता।
सभ्यता के विकास में तीन प्रकार के विकास शामिल हैं और यह तीन प्रकार निम्नलिखित हैं-
- औद्योगिक अथवा आर्थिक पक्ष
- कलात्मक पक्ष
- वैज्ञानिक पक्ष।
दुर्शीम ने सभ्यता के इन तीनों ही पक्षों के विकास को नैतिक तत्त्वों से विहीन बताया है। उसके विचार में औद्योगिक, कलात्मक तथा वैज्ञानिक विकास के साथ-साथ समाजों में अपराध, आत्महत्या इत्यादि अनैतिक घटनाओं में बढ़ोत्तरी होती है। अंत दुर्थीम के श्रम विभाजन का कार्य सभ्यता का विकास नहीं है।
परन्तु दुर्थीम के अनुसार श्रम विभाजन का प्रकार्य क्या है ? दुर्थीम के अनुसार नये समूहों का निर्माण व उनकी एकता ही श्रम विभाजन के काम हैं। दुर्थीम ने समाज के अस्तित्व से सम्बन्धित किसी नैतिक ज़रूरत को ही श्रम विभाजन के काम के रूप में खोजने की कोशिश की है। उसके विचार अनुसार समाज के सदस्यों की गणना व उनके आपसी सम्बन्धों में अधिकता होने से धीरे-धीरे श्रम विभाजन की प्रक्रिया का विकास हुआ है। इस प्रक्रिया में बहुत सारे नए-नए व्यावसायिक व सामाजिक समूहों का निर्माण हुआ। इन भिन्न-भिन्न समूहों की एकता का प्रश्न समाज के अस्तित्व के लिए अनिवार्य है। इनकी आपसी एकता की अनावश्यकता में सामाजिक व्यवस्था न सन्तुलन की कल्पना नहीं की जा सकती। इसलिए इन भिन्न-भिन्न समूहों में एकता एक नैतिक ज़रूरत है।
अनुसार स्रोत का काम नहीं है। सुखों में बढ़ोत्तरी या बौद्धिक व भौतिक विकास प्रकार्य विभाजन के परिणाम से उत्पन्न होते हैं। इसलिए यह इस प्रक्रिया के परिणाम हैं, काम नहीं। काम का अर्थ परिणाम नहीं होता।
सभ्यता के विकास में तीन प्रकार के विकास शामिल हैं और यह तीन प्रकार निम्नलिखित हैं-
- औद्योगिक अथवा आर्थिक पक्ष
- कलात्मक पक्ष
- वैज्ञानिक पक्ष।
दुर्खीम ने सभ्यता के इन तीनों ही पक्षों के विकास को नैतिक तत्त्वों से विहीन बताया है। उसके विचार में औद्योगिक, कलात्मक तथा वैज्ञानिक विकास के साथ-साथ समाजों में अपराध, आत्महत्या इत्यादि अनैतिक घटनाओं में बढ़ोत्तरी होती है। अंत दुर्खीम के श्रम विभाजन का कार्य सभ्यता का विकास नहीं है।
परन्तु दुर्खीम के अनुसार श्रम विभाजन का प्रकार्य क्या है ? दुर्खीम के अनुसार नये समूहों का निर्माण व उनकी एकता ही श्रम विभाजन के काम हैं। दुर्खीम ने समाज के अस्तित्व से सम्बन्धित किसी नैतिक ज़रूरत को ही श्रम विभाजन के काम के रूप में खोजने की कोशिश की है। उसके विचार अनुसार समाज के सदस्यों की गणना व उनके आपसी सम्बन्धों में अधिकता होने से धीरे-धीरे श्रम विभाजन की प्रक्रिया का विकास हुआ है। इस प्रक्रिया में बहुत सारे नए-नए व्यावसायिक व सामाजिक समूहों का निर्माण हुआ। इन भिन्न-भिन्न समूहों की एकता का प्रश्न समाज के अस्तित्व के लिए अनिवार्य है। इनकी आपसी एकता की अनावश्यकता में सामाजिक व्यवस्था न सन्तुलन की कल्पना नहीं की जा सकती। इसलिए इन भिन्न-भिन्न समूहों में एकता एक नैतिक ज़रूरत है।
दुर्खीम के अनुसार समाज की इसी ज़रूरत की पूर्ति श्रम-विभाजन की ओर से की जाती है। जहां एक ओर श्रम विभाजन से नए सामाजिक समूहों का निर्माण होता है, वहां दूसरी ओर इन समूहों की आपसी एकता व सामूहिकता बनी रहती है।
अन्त दुीम के अनुसार श्रम विभाजन का काम समाज में एकता स्थापित करना है। श्रम-विभाजन मानवों की क्रियाओं की भिन्नता से सम्बन्धित है पर यह भिन्नता भी समाज की एकता का आधार है। इस सामाजिक तथ्य के बारे दुर्खीम ने तथ्यात्मक आधार पर बताया है। उन्होंने कहा कि आपसी आकर्षण के दो विरोधी आधार हो सकते हैं। हम उन व्यक्तियों के प्रति ही नज़दीकी अनुभव करते हैं जो हमारी तरह हैं व उनकी ओर ही खिंचे जा सकते हैं। जो हमसे भिन्न हैं पर पूरी तरह की भिन्नता एक-दूसरे को अपनी ओर नहीं खींचती। ईमानदार बेइमानों को व खर्चीले कंजूसों को पसन्द नहीं करते। केवल यह भिन्नता इन दोनों को एक दूसरे के नज़दीक लाती है जो एक दूसरे की पूरक हैं। एक दोस्त में कोई कमी होती है, व वही चीज़ दूसरे में होती है जिस कारण दोनों के सम्बन्ध बनते हैं व एक दूसरे की ओर खिंचे जाते हैं।
दुर्खीम कहते हैं श्रम-विभाजन का सबसे महत्त्वपूर्ण परिणाम यह नहीं कि यह बांटे हुए काम से उत्पादन में बढ़ोत्तरी करता है बल्कि यह है कि यह उनको संगठित करता है। अतः दुर्खीम के अनुसार श्रम-विभाजन समूहों का निर्माण करता है व उनमें एकता पैदा करता है।
कानून और एकता (Law and Solidarity) -दुर्खीम ने श्रम-विभाजन का काम समाज में एकता पैदा करना बताया है। सामाजिक एकता एक नैतिक तथ्य है। दुर्खीम श्रम-विभाजन से पैदा सामाजिक एकता को स्पष्ट करने के लिए कानून का वर्गीकरण करते हैं। किसी कानून के वर्गीकरण के अनुरूप उन्होंने सामाजिक एकता के प्रकार निर्धारित करते हैं। दुर्जीम ने दो प्रकारों के कानूनों के बारे में बताया है वे हैं-
(a) दमनकारी कानून (Repressive Law)
(b) प्रतिकारी कानून (Restitutive Law)
(a) दमनकारी कानून (Repressive Law)-दमनकारी कानूनों को एक प्रकार से सार्वजनिक कानून (Public Law) कहा जा सकता है। दुर्खीम के अनुसार यह दो प्रकार के होते हैं
(i) दण्ड सम्बन्धी कानून (Penal Law)-जिनका सम्बन्ध कष्ट देने, हानि पहुंचाने, हत्या करने या स्वतन्त्रता न देने से है। इनको संगठित दमनकारी कानून (Organized Repressive Law) कहा जाता है।
(ii) व्याप्त कानून (Diffused Law)-कुछ दमनकारी कानून ऐसे होते हैं जो पूरे समूह में नैतिकता के आधार पर फैले होते हैं। इसलिए दुर्खीम इनको व्याप्त कानून कहते हैं। दुर्खीम के अनुसार दमनकारी कानून का सम्बन्ध आपराधिक कार्यों से होता है। यह कानून अपराध व दण्ड की व्याख्या करते हैं। यह कानून समाज के सामूहिक जीवन की मौलिक दशाओं का वर्णन करते हैं। प्रत्येक समाज के अपने मौलिक हालात होते हैं। इसलिए भिन्नभिन्न समाजों में दमनकारी कानून भिन्न-भिन्न होते हैं। इन दमनकारी कानूनों की शक्ति सामूहिक दमन में होती है व सामूहिक मन समानताओं से शक्ति प्राप्त करता है।
(b) प्रतिकारी कानून (Restitutive Law) कानून का दूसरा भाग प्रतिकारी कानून व्यवस्था है। यह कानून व्यक्तियों के सम्बन्धों में पैदा होने वाले असन्तुलन को साधारण स्थिति प्रदान करते हैं। इस वर्ग के अन्तर्गत दीवानी (civil) कानून, व्यापारिक कानून, संवैधानिक कानून, प्रशासनिक कानून आदि आ जाते हैं। इनका सम्बन्ध पूरे समाज के सामूहिक स्वरूप से न होकर व्यक्तियों से होता है। यह कानून समाज के सदस्यों के व्यक्तिगत सम्बन्धों से पैदा होने वाले असन्तुलन के द्वारा सन्तुलित व व्यवस्थित होते हैं। दुर्खीम कहते हैं कि प्रतिकारी कानून व्यक्तियों व समाज के कुछ बीच की संस्थाओं से जोड़ते हैं।
कानून के उपरोक्त दो प्रकार के आधार पर दुर्खीम के अनुसार दो भिन्न-भिन्न प्रकार की सामाजिक एकताओं (Social Solidarity) का निर्माण होता है। यह दो प्रकार समाज की दो भिन्न-भिन्न जीवन-शैलियों के परिणाम हैं। दमनकारी-कानून का सम्बन्ध व्यक्तियों की साधारण प्रवृत्ति से है, समानताओं से है, जबकि प्रतिकारी कानून का सम्बन्ध विभिन्नताओं से या श्रम-विभाजन से है। दमनकारी कानून के द्वारा जिस प्रकार की सामाजिक एकता बनती है उसको दुर्खीम यान्त्रिक एकता (Mechanical Solidarity) कहते हैं। प्रतिकारी कानून आंगिक एकता (Organic Solidarity) के प्रतीक है जिसका आधार श्रम-विभाजन है। अतः दुर्खीम के अनुसार समाज में दो प्रकार की सामाजिक एकता मिलती है।
(i) यान्त्रिक एकता (Mechanical Solidarity)-दुर्खीम के अनुसार यान्त्रिक एकता समाज की दण्ड संहिता में अर्थात् दमनकारी कानूनों के कारण होती है। समूह के सदस्यों में मिलने वाली समानताएं इस एकता का आधार हैं। जिस समाज के सदस्यों में समानताओं से भरपूर जीवन होता है, जहां विचारों, विश्वासों, कार्यों व जीवन इकाई के रूप में सोचता व क्रिया करता है, वह यान्त्रिक एकता दिखाता है अर्थात् उसके सदस्य मशीन के औज़ार भिन्न पुों की तरह संगठित रहते हैं। दुर्खीम ने अपराधी कार्यों के दमनकारी एकता कानून व यान्त्रिक एकता की अनुरूपता का माध्यम बताया है।
(ii) आंगिक एकता (Organic Solidarity)-दुर्खीम के अनुसार दूसरी एकता आंगिक एकता है। दमनकारी कानून की शक्ति सामूहिक चेतना में होती है। सामूहिक चेतना समानताओं से शक्ति प्राप्त करती है। आदिम समाज में दमनकारी कानूनों की प्रधानता होती है क्योंकि उनमें समानताएं सामाजिक जीवन का आधार हैं। दुर्खीम के अनुसार आधुनिक समाज श्रम-विभाजन व विशेषीकरण से प्रभावित है जिसमें समानता की जगह विभिन्नताएं प्रमुख हैं। सामूहिक जीवन को यह विभिन्नता व्यक्तिगत चेतना को प्रमुखता देती है।
आधुनिक समाज में व्यक्ति प्रत्यक्ष रूप से समूह से बंधा नहीं रहता। इस समाज में मानवों के आपसी सम्बन्धों का महत्त्व अधिक होता है। यही कारण है कि दुर्खीम ने आधुनिक समाजों में दमनकारी कानून की जगह प्रतिकारी कानून की प्रधानता बताई है। विभिन्नतापूर्ण जीवन में मानवों को एक-दूसरे पर निर्भर रहना पड़ता है। प्रत्येक व्यक्ति केवल एक काम में विशेष योग्यता प्राप्त कर सकता है व बाकी सभी कामों के लिए उसके अन्य लोगों पर निर्भर रहना पड़ता है। समूह के सदस्यों को यह आपसी निर्भरता, उनकी व्यक्तिगत असमानता, उनके एक-दूसरे के नज़दीक आने के लिए मजबूर करती है जिसके आधार पर समाज में एकता की स्थापना होती है। इस एकता को दुर्खीम ने आंगिक एकता (Organic Solidarity) कहा है। यह प्रतिकारी कानून व्यवस्था में दिखाई देता है।
दुर्खीम के अनुसार यह एकता शारीरिक एकता के समान है। हाथ, पैर, नाक, कान, आँख आदि अपने-अपने विशेष कामों के आधार पर स्वतन्त्र अंगों के रूप में हाजिर रहते हैं पर उनके काम तो ही सम्भव हैं जब तक एकदूसरे से मिले (जुड़े) हुए हैं, हाथ शरीर से भिन्न होकर कोई काम नहीं कर सकता। दूसरे शब्दों में शरीर के भिन्नभिन्न अंगों में एकता तो है पर वह आपसी निर्भरता पर टिकी हुई है।
दुीम के अनुसार जनसंख्या के बढ़ने से समाज की ज़रूरतें भी बढ़ती जाती है। इन बढ़ती हुई ज़रुरतों को पूरा करने के लिए श्रम विभाजन तथा विशेषीकरण हो जाता है। इसी कारण ही आधुनिक समाजों में आंगिक एकता दिखाई देती है। हम दुर्खीम के कानून, सामूहिक चेतना, एकता तथा समाजों को निम्न बने चित्र में से समझ सकते है। समाज को बनाए रखने के लिए सामाजिक एकता का होना बहुत ज़रूरी है। आदिम समाजों में समूह के सदस्यों में पूरी समानता होती है जिस कारण उनमें सामूहिक चेतना अधिक प्रबल होती है। वह एक-दूसरे पर कार्यात्मक दृष्टि से ही निर्भर नहीं होते बल्कि इतने जुड़े होते हैं कि उनमें हमेशा स्वाभाविक एकता बनी रहती है। यह एकता दुर्खीम के शब्दों में ठीक वैसी ही होती है जैसी कि किसी यन्त्र की एकता होती है। जिस प्रकार यन्त्र के किसी एक भाग को हिलाने से पूरा यन्त्र हरकत में आता है ठीक उसी प्रकार समानताओं पर आधारित इस एकता को दुर्खीम यान्त्रिक एकता कहते हैं।
दूसरी तरफ आधुनिक समाजों में विशेषीकरण बढ़ने से कार्यों का विभाजन हो गया है जिसके परिणामस्वरूप सामाजिक विभिन्नताएं बढ़ गई है। इस श्रम विभाजन के नतीजे के कारण समूह के सभी एक-दूसरे पर निर्भर हो गए हैं। किसी प्राणी की शारीरिक एकता की तरह, सामाजिक एकता के भिन्न-भिन्न अंगों में कार्यात्मक से उत्पन्न ज़रूरी सहयोग इस पूरी एकता की क्रियाशीलता का आधार है। इसीलिए दुर्खीम श्रम विभाजन से उत्पन्न जो एकता समाज को मिलती है उसे आंगिक एकता कहते हैं।
(iii) संविदात्मक एकता (Contractual Solildarity)-आंगिक व यान्त्रिक एकता के अध्ययन के बाद दुर्खीम ने एक और एकता के बारे में बताया है, जिसको उसने संविदात्मक एकता (Contractual Solidarity) या समझौते वाली एकता कहा है।
दुर्खीम के अनुसार श्रम-विभाजन की प्रक्रिया समझौते पर आधारित सम्बन्धों को जन्म देती है। समूह के लोग आपसी समझौते के आधार पर एक-दूसरे की सेवाओं को प्राप्त करते हैं व परस्पर सहयोग करते हैं। यह सच है कि आधुनिक समाजों में समझौतों के आधार पर लोगों में सहयोग व एकता स्थापित होती है पर श्रम-विभाजन का काम संविदात्मक एकता की उत्पत्ति करना ही नहीं है। दुर्खीम के विचार से संविदात्मक एकता एक व्यक्तिगत तथ्य है चाहे यह समाज द्वारा ही चलती है।
कारण तथा दशाएं (Causes and Conditions)-दुर्खीम की पुस्तक The division of Labour in Society का दूसरा भाग श्रम विभाजन के कारणों, दशाओं तथा परिणामों से सम्बन्धित है। दुर्खीम श्रम विभाजन के कारणों तथा दिशाओं की व्याख्या पेश करते हुए लिखते हैं कि श्रम विभाजन के विकास के प्रेरक तथा सुख में बढ़ौत्तरी की इच्छा अथवा ‘आनन्द प्राप्ति’ नहीं है क्योंकि सुख में व्यक्तिगत तथ्य मौजूद हैं तथा सुख की इच्छा मनोवैज्ञोनिक का विषय है। समाजशास्त्रीय विवेचना का नहीं चाहे श्रम विभाजन को दुर्खीम ने सामाजिक तथ्य माना है।
श्रम-विभाजन के कारण (Causes of Division of Labour)-दुीम ने श्रम-विभाजन की व्याख्या समाजशास्त्रीय आधार पर की है। उसने श्रम विभाजन के कारणों की खोज सामाजिक जीवन की दशाओं व उनसे पैदा सामाजिक ज़रूरतों से की है। इस नज़र से उसने श्रम-विभाजन के कारणों को दो भागों में बांटा है। पहला है प्राथमिक कारक व दूसरा है द्वितीय कारक। प्राथमिक कारक के रूप में दुर्खीम ने जनसंख्या में बढ़ोत्तरी व उससे उत्पन्न परिणामों को माना है। जबकिं द्वितीय कारकों को वह दो भागों में रखता है। वह है आम चेतना की बढ़ती हुई अस्पष्टता व पैतृकता का घटता हुआ प्रभाव।
अब हम इनके कारकों की विस्तार से व्याख्या करेंगे-
(i) जनसंख्या के आकार व घनत्व में बढ़ोत्तरी (Increase in Density and size of Population)दुर्खीम के अनुसार जनसंख्या के आकार व घनत्व में बढ़ोत्तरी ही श्रम-विभाजन का केन्द्रीय व प्राथमिक कारक है। दुर्खीम के अनुसार, “श्रम-विभाजन समाज में जटिलता व घनत्व के साथ सीधे अनुपात में रहता है व यदि सामाजिक विकास के दौरान यह लगातार बढ़ता है तो इसका कारण यह है कि समाज लगातार अधिक घनत्व व अधिक जटिल हो जाते हैं।” दुर्खीम के अनुसार जनसंख्या में बढ़ोत्तरी के दो पक्ष हैं-जनसंख्या के आकार में अधिकता व जनसंख्या के घनत्व में अधिकता। यह दोनों पक्ष श्रम-विभाजन को जन्म देते हैं। जनसंख्या में बढ़ोत्तरी होने से सरल समाज समाप्त हो जाते हैं और मिश्रित समाज बनने लग जाते हैं। जनसंख्या विशेष केन्द्रों पर एकत्र होने लगती है। जनसंख्या के घनत्व को भी दुर्खीम ने दो भागों में बांटा है-
(a) भौतिक घनत्व (Material Density)-शारीरिक नज़र से लोगों का एक ही स्थान पर एकत्र होना घनत्व है।
(b) नैतिक घनत्व (Moral Density)-भौतिक घनत्व के परिणाम से लोगों के आपसी सम्बन्ध बढ़ते हैं जिससे उनकी क्रियाओं व प्रतिक्रियाओं में बढ़ोत्तरी होती है। इन आपसी सम्बन्धों व अन्तर क्रियाओं में बढ़ोत्तरी से उत्पन्न जटिलता को दुर्खीम ने नैतिक घनत्व कहा है।
(ii) सामूहिक चेतना का कम होना या पतन-दुर्खीम ने श्रम-विभाजन को द्वितीय कारकों के बारे में बताया है। इसमें उसने सामूहिक चेतना के पतन को सबसे पहले रखा है। समानताओं पर आधारित समाज में सामूहिक चेतना प्रबल या ताकतवर होती है जिस कारण समूह के सदस्य व्यक्तिगत भावनाओं से प्रेरित होते हैं। सामूहिक भावना ही उनको रास्ता दिखाती है। दुर्खीम के अनुसार श्रम-विभाजन तब ही सम्भव है जब सामूहिक दृष्टिकोण की जगह व्यक्तिगत दृष्टिकोण का विकास हो जाए व व्यक्तिगत चेतना सामूहिक चेतना को नष्ट कर दे। अतः दुर्खीम के अनुसार, “चेतना निश्चित व मज़बूत होगी इसके विपरीत यह उतनी ही अधिक तेज़ होगी, जितना व्यक्ति अपने व्यक्तिगत वातावरण से समझौता करने में असमर्थ होगा।
(iii) पैतृकता व श्रम-विभाजन-दुीम ने द्वितीय कारक के दूसरे प्रकार को पैतृकता के घटते प्रभाव को कारण माना है। चाहे दुर्खीम ने सामाजिक घटनाओं की व्याख्या के लिए सामाजिक कारकों को ही प्राथमिकता दी है पर श्रम-विभाजन के विकास में पैतृकता का प्रभाव जितना अधिक होता है परिवर्तन के मौके उतने ही कम होते हैं।
अन्य शब्दों में श्रम विभाजन के विकास के लिए यह ज़रूरी है कि पैतृक गुणों को महत्त्व न दिया जाए। श्रम विभाजन का विकास तभी सम्भव है जब लोगों में प्रकृति तथा स्वभाव में भिन्नता हो, पैतृकता से प्राप्त योग्यताओं के आधार पर व्यक्तियों का वर्गीकरण करके उनको विशेष जातियों से सम्बन्धित करके, उनके पूर्वजों तथा अतीत से कठोरता से बांध देने की प्रक्रिया के फलस्वरूप यह होता है कि हम अपनी विशेष रुचिओं का विकास नहीं कर सकते तथा परिवर्तन नहीं कर सकते। इस प्रकार कहा जा सकता है कि पैतृकता के आधार पर कार्यों का विभाजन भी श्रम विभाजन में रुकावट है। दुर्खीम के अनुसार समय की गति तथा सामाजिक विकास के साथ लगातार होने वाले परिवर्तन पैतृकता में लचकीला पन पैदा करते हैं अर्थात् पैतृकता के गुण कमजोर होने लग जाते हैं। परिणामस्वरूप व्यक्तियों की विभिन्नताएं विकसित हो जाती है तथा श्रम विभाजन में बढ़ोत्तरी होती है।
इस प्रकार हम देखते हैं कि दुर्खीम ने जनसंख्या में बढ़ोत्तरी, सामूहिक चेतना का पतन तथा पैतृकता के घटते प्रभाव को श्रम विभाजन का कारक माना है।
श्रम-विभाजन के परिणाम (Consequences of Division of Labour)-श्रम-विभाजन के प्राथमिक व द्वितीय कारणों के पश्चात् दुर्खीम इसके विकास के परिणामस्वरूप होने वाले परिणामों पर रोशनी डालते हैं। हमें यह ध्यान रखना चाहिए कि ‘कार्य’ व ‘परिणाम’ दो भिन्न-भिन्न शब्द हैं। ऐसे बहत से तथ्य जो आम आदमी की नज़र से श्रम-विभाजन से कार्य दिखाई देते हैं। वह सच्चाई में उसके परिणाम है। दुर्खीम ने श्रम-विभाजन के बहुत सारे परिणामों की ओर हमारा ध्यान केन्द्रित किया है। उनमें से कुछ निम्नलिखित हैं
1. कार्यात्मक स्वतन्त्रता व विशेषीकरण-दुर्खीम ने शारीरिक श्रम-विभाजन व सामाजिक श्रम-विभाजन में अन्तर बताया है व सामाजिक श्रम-विभाजन के परिणाम बताए हैं। दुीम के अनुसार श्रम-विभाजन का एक परिणाम यह होता है कि जैसे ही काम अधिक बांटा जाता है उसी प्रकार काम करने की स्वतन्त्रता व गतिशीलता में बढ़ोत्तरी होती है। श्रम-विभाजन के कारण मानव अपनी कुछ विशेष योग्यताओं को विशेष काम में लगा देता है। दुीम के अनुसार श्रम-विभाजन के विकास का एक परिणाम यह भी होता है कि व्यक्तियों के काम उनके शारीरिक लक्षणों से स्वतन्त्र हो जाते हैं। दूसरे शब्दों में मानव की संरचनात्मक विशेषताएं उनकी कार्यात्मक प्रवृत्तियों को अधिक प्रभावित नहीं करतीं।
2. सभ्यता का विकास-दुर्खीम ने शुरू में ही यह स्पष्ट किया है कि सभ्यता का विकास करना श्रम-विभाजन का काम नहीं है क्योंकि श्रम-विभाजन एक नैतिक तथ्य है व सभ्यता के तीन अंग, औद्योगिक या आर्थिक, कलात्मक व वैज्ञानिक विकास नैतिक विकास से सम्बन्ध नहीं रखते।
दुर्खीम ने श्रम-विभाजन के परिणाम के रूप में सभ्यता के विकास की व्याख्या की है। आपका कहना था कि जनसंख्या के आकार व घनता में अधिकता होने के साथ सभ्यता का विकास भी ज़रूरी हो जाता है। श्रम-विभाजन व सभ्यता दोनों साथ-साथ प्रगति करते हैं। परन्तु श्रम-विभाजन का विकास पहले होता है व उसके परिणामस्वरूप सभ्यता विकसित होती है। इसलिए दुर्खीम का मानना है कि सभ्यता न तो श्रम-विभाजन का लक्ष्य है व न ही उसका कार्य है बल्कि एक ज़रूरी परिणाम है।
3. सामाजिक प्रगति-प्रगति परिवर्तन का परिणाम है। श्रम-विभाजन भी परिवर्तन को जन्म देता है। परिवर्तन समाज में एक निरन्तर प्रक्रिया है। इसलिए प्रगति भी समाज में निरन्तर होती रहती है। दुर्खीम के अनुसार इस परिवर्तन का मुख्य कारण श्रम-विभाजन है। श्रम-विभाजन के कारण परिवर्तन होता है व परिवर्तन के कारण प्रगति होती है। इस तरह सामाजिक प्रगति श्रम-विभाजन का एक परिणाम है। दुर्खीम के विचार से प्रगति का प्रमुख कारक समाज है। हम इसलिए बदल जाते हैं क्योंकि समाज बदल जाता है। प्रगति तो रुक ही सकती है जब समाज रुक जाए पर वैज्ञानिक नज़र से यह सम्भव नहीं है। इसलिए दुर्खीम के अनुसार प्रगति भी सामाजिक जीवन का परिणाम है।
4. सामाजिक परिवर्तन व व्यक्तिगत परिवर्तन-दुर्खीम ने सामाजिक परिवर्तन की व्याख्या श्रम-विभाजन के आधार पर की है। व्यक्तियों में होने वाले परिवर्तन समाज में होने वाले परिवर्तन का परिणाम हैं। दुर्खीम का मानना है कि समाज में होने वाले परिवर्तन मूल कारक हैं। जनसंख्या के आकार, वितरण व घनत्व में होने वाला परिवर्तन है जो मानवों में श्रम-विभाजन कर देता है व सारे व्यक्तिगत परिवर्तन इसी सामाजिक परिवर्तन के परिणामस्वरूप होते हैं।
5. नवीन समूहों की उत्पत्ति व अन्तर्निर्भरता-दुर्खीम के अनुसार श्रम-विभाजन का एक परिणाम यह होता है कि विशेष कार्यों में लगे व्यक्तियों के विशेष हितों का विकास हो जाता है। इस प्रकार जितना अधिक श्रमविभाजन होता है उतनी ही अधिक अन्तर्निर्भरता बढ़ती है। अन्तर्निर्भरता सहयोग को जन्म देती है। इसलिए श्रमविभाजन सहयोग की प्रक्रिया को सामाजिक जीवन के लिए ज़रूरी बना देता है।
6. व्यक्तिवादी विचारधारा-दुर्खीम के अनुसार श्रम-विभाजन के परिणामस्वरूप व्यक्तिगत चेतना बढ़ती है। सामूहिक चेतना का नियन्त्रण कम हो जाता है। व्यक्तिगत स्वतन्त्रता व विशेषता व्यक्तिवादी विचारधारा को जन्म देती है। इस तरह श्रम-विभाजन के परिणामस्वरूप व्यक्तिवादी विचारधारा को बल मिलता है।
7. प्रतिकारी कानून व नैतिक दबाव-दुर्खीम के अनुसार श्रम-विभाजन कानूनी व्यवस्था में ही बदलाव कर देता है। श्रम-विभाजन के परिणामस्वरूप आपसी सम्बन्धों का विस्तार होता है व जटिलता व कार्यात्मक सम्बन्धों के कारण व्यक्तिगत समझौते का महत्त्व कम हो जाता है। मानवों के संविदात्मक या समझौते वाले सम्बन्धों को सन्तुलित करने के लिए प्रतिकारी या सहकारी कानूनों का विकास हो जाता है। श्रम-विभाजन जहां एक ओर व्यक्तिवाद को प्रोत्साहन देता है, वहां दूसरी ओर यह व्यक्तियों में विशेष आचरण से सम्बन्धित व सामूहिक कल्याण से सम्बन्धित नैतिक जागरूकता का भी निर्माण करता है। दुर्खीम के विचार से व्यक्तिवाद मानवों की इच्छा पर फल नहीं बल्कि श्रम-विभाजन से उत्पन्न सामाजिक परिस्थिति का आवश्यक परिणाम है।

पश्चिमी समाजशास्त्री विचारक PSEB 11th Class Sociology Notes
- 19वीं तथा 20वीं शताब्दी के दौरान यूरोप के समाज में बहुत से परिवर्तन आए तथा यह कहा जाता है कि इन परिवर्तनों के अध्ययन के लिए ही समाजशास्त्र का जन्म हुआ।
- 17वीं, 18वीं तथा 19वीं शताब्दी में बहुत से विचारकों ने पुस्तकें लिखीं जिन्होंने समाजशास्त्र के उद्भव में काफ़ी महत्त्वपूर्ण योगदान दिया तथा इनमें मान्टेस्कयू (Montesquieu), रूसो (Rousseau) इत्यादि प्रमुख
- अगस्ते कोंत, जोकि एक फ्रांसीसी दार्शनिक थे, को समाजशास्त्र का पितामह माना जाता है। उसने अपनी पुस्तक ‘The Course on Postitive Philosophy’ लिखी जिसमें उन्होंने 1839 में पहली बार शब्द Sociology का प्रयोग किया तथा इसे समाजशास्त्र का नाम दिया।
- कोंत ने सकारात्मकवाद का सिद्धांत दिया तथा कहा कि सामाजिक घटनाओं को भी वैज्ञानिक व्याख्या से समझा जा सकता है तथा सकारात्मकवाद वह विधि है। इस प्रकार सकारात्मकवाद प्रेक्षण, तजुर्बे, तुलना तथा ऐतिहासिक विधि की एक व्यवस्थित कार्य प्रणाली है जिससे समाज का वैज्ञानिक अध्ययन किया जा सकता है।
- कोंत ने अलग-अलग समाजों का अध्ययन किया तथा कहा कि वर्तमान अवस्था में पहुँचने के लिए समाज को तीन पड़ावों से गुजरना पड़ता है तथा वह पड़ाव हैं-आध्यात्मिक पड़ाव, अधिभौतिक पड़ाव तथा सकारात्मक पड़ाव। यह ही कोंत का तीन पड़ावों का सिद्धांत है।
- कार्ल मार्क्स एक जर्मन दार्शनिक थे जिन्हें संसार में उनके वर्ग तथा वर्ग संघर्ष पर दिए विचारों के लिए जाना जाता है। समाजवाद तथा साम्यवाद की धारणा भी मार्क्स ने ही दी है।
- मार्क्स के अनुसार शुरू से लेकर अब तक का इतिहास वर्ग संघर्ष का इतिहास रहा है। सभी समाजों में दो प्रकार के वर्ग होते हैं। प्रथम है पूँजीपति वर्ग जिसके पास उत्पादन के सभी साधन मौजूद हैं तथा दूसरा है मज़दूर वर्ग जिसके पास अपना श्रम बेचने के अतिरिक्त और कुछ भी नहीं है। दोनों के बीच अधिक प्राप्त करने के लिए संघर्ष चलता रहता है तथा इसको ही वर्ग संघर्ष कहते हैं।
- इमाईल दुर्थीम भी समाजशास्त्र के संस्थापकों में से एक है। उन्होंने समाजशास्त्र को एक विज्ञापन के रूप में स्थापित करने का प्रयास किया। वह समाजशास्त्र के प्रथम प्रोफेसर भी थे।
- वैसे तो समाजशास्त्र को दुर्थीम का काफ़ी योगदान है परन्तु उनके कुछ महत्त्वपूर्ण सिद्धांत हैं-सामाजिक तथ्य का सिद्धांत, आत्महत्या का सिद्धांत, श्रम विभाजन का सिद्धांत, धर्म का सिद्धांत इत्यादि।
- दुर्थीम के अनुसार श्रम विभाजन का सिद्धांत हमारे समाज में प्राचीन समय से ही मौजूद है। श्रम विभाजन के कारण ही समाज की प्रवृत्ति निश्चित होती है तथा इसमें मौजूद कानूनों की प्रकृति भी निश्चित होती है।
- मैक्स वैबर भी एक प्रमुख समाजशास्त्री थे। मार्क्स की तरह वह भी जर्मनी के दाशनिक थे। उन्होंने भी समाजशास्त्र को बहत से सिद्धांत दिए जिनमें से प्रमुख हैं-सामजिक क्रिया का सिद्धांत, सत्ता तथा उसके प्रकार, प्रोटैस्टैंट एथिक्स तथा पूँजीवाद की आत्मा इत्यादि।
- वर्ग (Class)–लोगों का समूह जिनके उत्पादन के साधन समान होते हैं।
- सत्ता (Authority)-शक्ति का वह विशेष रूप जिसे सामाजिक व्यवस्था के नियमों, परिमापों का समर्थन प्राप्त होता है तथा साधारणतया इसे उन सभी की तरफ से वैध माना जाता है जो इसमें भाग लेते हैं।
- सामाजिक क्रिया (Social Action)—वह क्रिया जिसमें अन्य व्यक्तियों की क्रियाओं तथा प्रतिक्रियाओं को सामने रखा जाता है। इसे सामाजिक उस समय कहा जाता है जब क्रिया करने वाला व्यक्ति अन्य व्यक्तियों के व्यवहारों को सामने रखता है।
- वर्ग चेतना (Class Consciousness)-एक वर्ग के सदस्यों के बीच अपने समूह के साधारण हितों की चेतना की मौजूदगी।
- वर्ग संघर्ष (Class Struggle)-पूँजीपति तथा मजदूर वर्ग के बीच हमेशा हितों का संघर्ष होता है। यह हितों का संघर्ष दोनों वर्ग के बीच संघर्ष का कारण बनता है। जब लोगों में वर्ग चेतना बढ़ जाती है तो वर्ग संघर्ष भी बढ़ जाता है।
- सकारात्मवाद (Positivism)-सकारात्मकवाद में माना जाता है कि समाज कुछ नियमों के अनुसार कार्य करता है जिन्हें ढूंढ़ा जा सकता है।
- यान्त्रिक एकता (Mechanical Solidarity)-समानताओं पर आधारित समाजों के सदस्यों के बीच एकता की एकता को यान्त्रिक एकता कहते हैं।
- सावयवी एकता (Organic Solidarity)-कई समाजों में लोगों के बीच अंतर होते हैं जिस कारण वह एक दूसरे पर निर्भर होते हैं। इन समाजों में लोगों के बीच मौजूद एकता को सावयवी एकता कहते हैं।
![]()
![]()
![]()
![]()