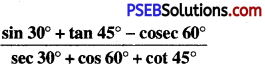Class 10

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.4

Question 1.
Express the trigonometric ratios of sin A, sec A and tan A in terms of cot A.
Solution:
By using Identity,
cosec² A – cot² A = 1
⇒ cosec² A = 1 + cot² A
⇒ (cosec A)² = cot² A + 1
⇒ \(\left(\frac{1}{\sin A}\right)^{2}\) = cot² A + 1
⇒ (sin A)² = \(\frac{1}{\cot ^{2} \mathrm{~A}+1}\)
⇒ sin A = ± \(\frac{1}{\sqrt{\cot ^{2} \mathrm{~A}+1}}\)
We reject negative values of sin A for acute angle A.
Therefore, sin A = \(\frac{1}{\sqrt{\cot ^{2} A+1}}\)
By using identity,
sec² A – tan² A = 1
⇒ sec² A = 1 + tan² A
= 1 + \(\frac{1}{\cot ^{2} A}\)
= \(\frac{\cot ^{2} A+1}{\cot ^{2} A}\)

⇒ sec A = \(\sqrt{\frac{\cot ^{2} A+1}{\cot ^{2} A}}\)

tan A = \(\frac{1}{\cot A}\).

Question 2.
Write all the other trigonometric ratios of ∠A in terms of sec A.
Solution:
By using Identity
sin² A + cos² A = 1
⇒ sin² A = 1 – cos² A
= 1 – \(\frac{1}{\sec ^{2} \cdot A}\) = \(\frac{\sec ^{2} A-1}{\sec ^{2} A}\)

⇒ (sin A)² = \(\frac{\sec ^{2} A-1}{\sec ^{2} A}\)

⇒ sin A = ± \(\sqrt{\frac{\sec ^{2} A-1}{\sec ^{2} A}}\)

[Reject – ve sign for acute angle A]
⇒ sin A = ± \(\sqrt{\frac{\sec ^{2} A-1}{\sec ^{2} A}}\)
cos A = \(\frac{1}{\sec A}\)
1 + tan² A = sec² A
tan² A = sec² A – 1
(tan A)² = sec² A – 1
⇒ tan A = ± \(\sqrt{\sec ^{2} A-1}\)
[Reject – ve sign for acute angle A]
i.e., tan A = \(\sqrt{\sec ^{2} A-1}\)
cosec A = \(\frac{1}{\sin A}=\frac{1}{\sqrt{\sec ^{2} A-1}}\)

= \(\frac{\sec A}{\sqrt{\sec ^{2} A-1}}\)

cot A = \(\frac{1}{\tan A}=\frac{1}{\sqrt{\sec ^{2} A-1}}\).

Question 3.
Evaluate:
(i) \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)

(ii) sin 25° cos 65° + cos 25° sin 65°.
Solution:
(i) \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\cos ^{2} 73^{\circ}}\)

= \(\frac{\left\{\sin \left(90^{\circ}-27^{\circ}\right)+\sin ^{2} 27^{\circ}\right\}}{\cos ^{2} 17^{\circ}+\left\{\cos \left(90^{\circ}-17^{\circ}\right)\right\}^{2}}\)
[∵ sin(90 – θ) = cos θ and cos (90 – θ) = sin θ]

= \(\frac{\left\{\cos 27^{\circ}\right\}^{2}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\left\{\sin 17^{\circ}\right\}^{2}}\)

= \(\frac{\cos ^{2} 27^{\circ}+\sin ^{2} 27^{\circ}}{\cos ^{2} 17^{\circ}+\sin ^{2} 17^{\circ}}\)
= \(\frac{1}{1}\) = 1.

(ii) sin 25° cos 65° + cos 25° sin 65°
= sin 25° × cos (90° – 25°)
+ cos 25° × sin (90° – 25°)
[∵ cos (90° – θ) = sin θ
sin(90° – θ) = cos θ].
= sin 25° × sin 25° + cos 25° × cos 25°
= sin² 25° + cos² 25° = 1.

Question 4.
Choose the correct option. Justify your choice:
(i) 9 sec² A – 9 tan² A =
(A) 1
(B) 9
(C) 8
(D) 0.

(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) =
(A) θ
(B) 1
(C) 2
(D) – 1.

(iii) (sec A + tan A) (1 – sin A) =
(A) sec A
(B) sin A
(C) cosec A
(D) cos A.

(iv) \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\) =
(A) sec²A
(B) – 1
(C) cot² A
(D) tan² A.

Solution:
(i) Consider, 9 sec² A – 9 tan² A
= 9 (sec² A – tan² A)
= 9 × 1 = 9.
Option (B) is correct.

(ii) Consider, (1 + tan θ + sec θ) (1 + cot θ – cosec θ)
= \(\left\{1+\frac{\sin \theta}{\cos \theta}+\frac{1}{\cos \theta}\right\} \times\left\{1+\frac{\cos \theta}{\sin \theta}-\frac{1}{\sin \theta}\right\}\)

= \(\left\{\frac{\cos \theta+\sin \theta+1}{\cos \theta}\right\} \times\left\{\frac{\sin \theta+\cos \theta+1}{\sin \theta}\right\}\)

= \(\begin{array}{r}
\{(\cos \theta+\sin \theta)+1\} \\
\times\{(\cos \theta+\sin \theta)-1\} \\
\hline \cos \theta \times \sin \theta
\end{array}\)

= \(\frac{(\cos \theta+\sin \theta)^{2}-(1)^{2}}{\cos \theta \times \sin \theta}\)

[∵ (a + b) (a – b) = a² – b²]

= \(\frac{\cos ^{2} \theta+\sin ^{2} \theta+2 \cos \theta \sin \theta-1}{\cos \theta \times \sin \theta}\)

= \(\frac{1+2 \cos \theta \sin \theta-1}{\cos \theta \sin \theta}\) = 2.

Option (C) is correct.

(iii) Consider, (sec A + tan A) (1 – sin A)
= \(\left(\frac{1}{\cos A}+\frac{\sin A}{\cos A}\right)\) × (1 – sin A)

= \(\frac{(1+\sin A)}{\cos A}\) × (1 – sin A)

= \(\frac{(1+\sin A)(1-\sin A)}{\cos A}\)

= \(\frac{(1)^{2}-(\sin A)^{2}}{\cos A}=\frac{1-\sin ^{2} A}{\cos A}=\frac{\cos ^{2} A}{\cos A}\)
[∵ cos² A = 1 – sin² A]
= cos A.
Option (D) is correct.

(iv) Consider, \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\)

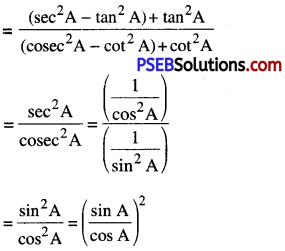
= tan² A.
Option (D) is correct.

Question 5.
Prove the following Identities, where the angles involved are acute angles for which the expressions are defined.
(i) (cosec θ – cot θ) = \(\frac{1-\cos \theta}{1+\cos \theta}\)

(ii) \(\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}\) = 2 sec A.

(iii) \(\frac{\tan \theta}{1+\cot \theta}+\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ
[Hint : Write the expression in terms of sin θ and cos θ]

(iv) \(\frac{1+\sec A}{\sec A}=\frac{\sin ^{2} A}{1-\cos A}\)
[Hint: Simplify L.H.S. and R.H.S. separately]

(v) \(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\) using the identity cosec² A = 1 + cot² A.

(vi) \(\sqrt{\frac{1+\sin A}{1-\sin A}}\) = sec A + tan A

(vii) \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\) = tan θ

(viii) (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A.

(ix) (cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\)
[Hint : Simplify L.H.S. and R.H.S. separately]

(x) \(\left(\frac{1+\tan ^{2} A}{1+\cot A^{2}}\right)=\left(\frac{1-\tan A}{1-\cot A}\right)^{2}\) = tan² A.

Solution:
(i) L.H.S. = (cosec θ – cot θ)²
= \(\left\{\frac{1}{\sin \theta}-\frac{\cos \theta}{\sin \theta}\right\}^{2}\)

= \(\left(\frac{1-\cos \theta}{\sin \theta}\right)^{2}=\frac{(1-\cos \theta)^{2}}{\sin ^{2} \theta}\)
Using identity, sin² θ + cos² θ = 1
⇒ sin² θ = 1 – cos² θ
= \(\frac{(1-\cos \theta)^{2}}{1-\cos ^{2} \theta}\)
= \(\)
[∵ a² – b² = (a + b) (a – b)]

= \(\)

∴ L.H.S. = R.H.S.
Hence, (cosec θ – cot θ)² = \(\frac{1-\cos \theta}{1+\cos \theta}\)

(ii) L.H.S. = \(\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}\)

= \(\frac{2}{\cos A}\) = cos A
∴L.H.S. = R.H.S.
Hence, \(\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}\) = 2 sec A.

(iii) L.H.S. = \(\frac{\tan \theta}{1+\cot \theta}+\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ

= \(\frac{\left(\frac{\sin \theta}{\cos \theta}\right)}{\left(1-\frac{\cos \theta}{\sin \theta}\right)}+\frac{\left(\frac{\cos \theta}{\sin \theta}\right)}{\left(1-\frac{\sin \theta}{\cos \theta}\right)}\)

= \(\frac{1+\sin \theta \cos \theta}{\cos \theta \sin \theta}=\frac{1}{\cos \theta \sin \theta}+1\)

= 1 + \(\left(\frac{1}{\cos \theta}\right)\left(\frac{1}{\sin \theta}\right)\) = 1 + sec θ cosec θ
∴L.H.S. = R.H.S.
Hence, \(\frac{\tan \theta}{1+\cot \theta}+\frac{\cot \theta}{1-\tan \theta}\) = 1 + sec θ cosec θ

(iv) L.H.S. = \(\frac{1+\sec A}{\sec A}=\frac{\sin ^{2} A}{1-\cos A}\)
= \(\frac{1+\frac{1}{\cos A}}{\frac{1}{\cos A}}\)
= 1 + cos A …………….(1)
R.H.S = \(\frac{\sin ^{2} A}{1-\cos A}\)
(∵ 1 – cos² A = sin² A.)
= \(\frac{1-\cos ^{2} A}{1-\cos A}\)

= \(\frac{(1+\cos A)(1-\cos A)}{(1-\cos A)}\)

= 1 + cos A. …………….(2)
From (1) and (2) it is clear that
∴ L.H.S. = R.H.S.
Hence, \(\frac{1+\sec A}{\sec A}=\frac{\sin ^{2} A}{1-\cos A}\).

(v) L.H.S. = \(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\) using the identity cosec² A

= cosec A + cot A
= R.H.S
∴ L.H.S. = R.H.S.
Hence, \(\frac{\cos A-\sin A+1}{\cos A+\sin A-1}\) using the identity cosec² A = 1 + cot² A.

(vi) L.H.S. = \(\sqrt{\frac{1+\sin A}{1-\sin A}}\)

= \(\sqrt{\frac{(1+\sin A)(1+\sin A)}{(1-\sin A)(1+\sin A)}}\)

= \(\sqrt{\frac{(1+\sin A)^{2}}{(1)^{2}-(\sin A)^{2}}}\)

= \(\sqrt{\frac{(1+\sin A)^{2}}{1-\sin ^{2} A}}=\sqrt{\frac{(1+\sin A)^{2}}{\cos ^{2} A}}\)

= \(\frac{1+\sin A}{\cos A}=\frac{1}{\cos A}+\frac{\sin A}{\cos A}\)
= sec A + tan A
∴ L.H.S. = R.H.S.
Hence, \(\sqrt{\frac{1+\sin A}{1-\sin A}}\) = sec A + tan A.

(vii) L.H.S. = \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\)

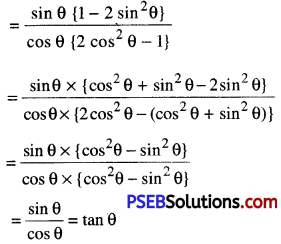
∴ L.H.S. = R.H.S.
Hence, \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\) = tan θ

(viii) L.H.S. = (sin A + cosec A)² + (cos A + sec A)²
= (sin² A + cosec² A + 2 sin A × cosec A) + {cos² A + sec² A
+ 2 cos A × sec A)
= [sin² A + co² A + 2sin A × \(\frac{1}{\sin A}\)] + [cos² A + sec² A + 2 cosA × \(\frac{1}{\cos A}\)]
= (sin² A + cosec² A + 2) + (cos² A + sec² A + 2)
= 2 + 2 + (sin² A + cos² A) + sec² A + cosec² A
= 2 + 2 + 1 + 1 + tan² A + 1 + cot² A
= 7 tan² A + cot² A
∴ L.H.S. = R.H.S.
Hence, (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot² A.

(ix) L.H.S. = (cosec A – sin A) (sec A – cos A)

From (1) and (2), it is clear that
L.H.S. = R.H.S.
Hence, (cosec A – sin A) (sec A – cos A) = \(\frac{1}{\tan A+\cot A}\)

(x) \(\left(\frac{1+\tan ^{2} A}{1+\cot A^{2}}\right)\)
(∵ 1 + tan² A = sec² A
and 1 + cot² A = cosec² A)

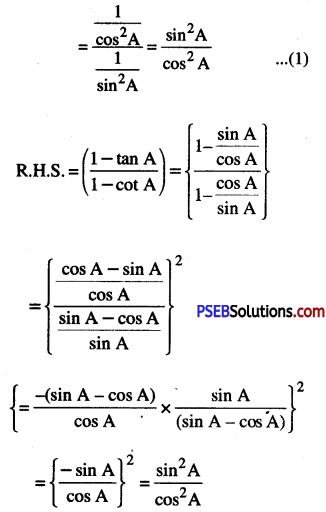
From (1) and (2), it is clear that
LH.S. = R.H.S.
Hence, \(\left(\frac{1+\tan ^{2} A}{1+\cot A^{2}}\right)=\left(\frac{1-\tan A}{1-\cot A}\right)^{2}\) = tan² A.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.3

Question 1.
Evaluate:
(i) \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\)
(ii) \(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}\)
(iii) cos 48° – sin 42°
(iv) cosec 31° – sec 59°.
Solution.
(i) \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\)
= \(\frac{\sin 18^{\circ}}{\cos \left(90^{\circ}-18^{\circ}\right)}\)
= \(\frac{\sin 18^{\circ}}{\sin 18^{\circ}}\) = 1
[∵ cos (90° – θ) = sin θ]

(ii) \(\frac{\tan 26^{\circ}}{\cos 64^{\circ}}=\frac{\tan 26^{\circ}}{\cot \left(90^{\circ}-26^{\circ}\right)}\)
= \(\frac{\tan 26^{\circ}}{\tan 26^{\circ}}\) = 1
[∵ cot (90°- θ) = tan θ]

(iii) cos 48° – sin 42°
= cos (90° – 42°) – sin 42°
[∵ cos (90° – 0) = sin O]
= sin 42° – sin 42° = 0.

(iv) cosec 31° – sec 59°
=cosec 31° – sec (90° – 31°)
= cosec 31° – cosec 31°
[∵ sec (90° – θ) = cosec θ].

Question 2.
Show that:
(i) tan 4 tan 230 tan 42° tan 67° = 1
(ii) cos 38° cos 52° – sin 38° sin 52° = 0
Solution:
(i) L.H.S.
= tan 48° tan 23° tan 42° tan 67°
= tan 48° × tan 23° × tan (90° – 48°) × tan (90° – 23°)
= tan48° × tan 23° × cot48° × cot 23°
= tan 48C × tan 23° × \(\frac{1}{\tan 48^{\circ}}\) × \(\frac{1}{\tan 23^{\circ}}\) = 1
∴ L.H.S. = R.H.S.

(ii) L.H.S.= cos 38° cos 52° – sin 38° sin 52°
= cos 38° × cos (90 – 38°) – sin 38° × sin (90° – 38°)
= cos 38° × sin 38° – sin 38° × cos 38
= 0.
∴ L.H.S. = RH.S.

Question 3.
If tan 2A = cot (A – 18°) where 2A is an acute angle, find the value of A.
Solution:
Given: tan 2A = cot (A – 18°)
⇒ cot (90° – 2A) = cot (A – 18°)
[cot (90° – θ) = tan θ]
⇒ 90°- 2A = A – 18°
⇒ 3A = 108°
⇒A = 36°.

Question 4.
If tan A = cot B, prove that A + B = 90°.
Solution:
Given that: tan A = cot B
⇒ tan A = tan(90° – B)
[∵ tan (90° – θ) = cot θ]
⇒ A = 90° – B.
⇒ A + B = 90°..

Question 5.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution:
Given that: sec 4A = cosec (A – 20°)
⇒ cosec (90° – 4A) = cosec (A — 20°)
[∵ cosec (90° – θ) = sec θ]
⇒ 90° – 4A = A – 20°
⇒ 5A = 110°
⇒ A = 22°.

Question 6.
If A, B and C interior angles of a triangle ABC, then show that: \(\sin \left(\frac{B+C}{2}\right)=\cos \left(\frac{A}{2}\right)\)
Solution:
Since, A, B and C are interior angles of a triangle
∴ A + B + C = 180°
[Sum of three angles of a triangle is 180°]
⇒ B + C = 180° – A
⇒ \(\frac{\mathrm{B}+\mathrm{C}}{2}=\frac{180^{\circ}-\mathrm{A}}{2}\)
⇒ \(\frac{\mathrm{B}+\mathrm{C}}{2}=\left(90^{\circ}-\frac{\mathrm{A}}{2}\right)\)
Taking sin on both sides, we get
⇒ \(\sin \left(\frac{\mathrm{B}+\mathrm{C}}{2}\right)=\sin \left(90^{\circ}-\frac{\mathrm{A}}{2}\right)\)
[∵ sin (90° – θ) = cos θ].

Question 7.
Express sin 67° + cos 75° in terms of Trigonometric ratios of angles between 0° and 45°.
Solution:
Given that: sin 67° + cos 75°
= sin (90° – 23°) + cos (90° – 15°)
= cos 23° + sin 15°
[∵ sin(90° – θ) = cos θ and cos (90° – θ) = sin θ].

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.2

Question 1.
Evaluate the following:
(i) sin 60° cos 30° + sin 30° cos 60°

(ii) 2 tan² 45° + cos² 30° – sin² 60°

(iii)

(iv)

(v) \(\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)
Solution:
(i) sin 60° cos 30° + sin 30° cos 60°
= \(\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)+\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\)

= \(\left(\frac{\sqrt{3}}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}\)
= \(\frac{3}{4}+\frac{1}{4}\) = 1.

(ii) 2 tan² 45° + cos² 30° – sin² 60° = 2 (tan 45°)² + (cos 30°)² – (sin 60°)²
= 2 (1)² + (\(\frac{\sqrt{3}}{2}\))² – (\(\frac{\sqrt{3}}{2}\))² = 2.

(iii)
= \(\frac{\frac{1}{\sqrt{2}}}{\left(\frac{2}{\sqrt{3}}\right)+(2)}=\frac{\frac{1}{\sqrt{2}}}{\frac{2+2 \sqrt{3}}{\sqrt{3}}}\)

= \(\frac{1}{\sqrt{2}}: \frac{\sqrt{3}}{2+2 \sqrt{3}}=\frac{\sqrt{3}}{2 \sqrt{2}(\sqrt{3}+1)}\)

= \(\frac{\sqrt{3}(\sqrt{3}-1)}{2 \sqrt{2}(\sqrt{3}+1)(\sqrt{3}-1)}\)

= \(\frac{\sqrt{2} \times \sqrt{3} \times(\sqrt{3}-1)}{4(3-1)}=\frac{3 \sqrt{2}-\sqrt{6}}{8}\).

(iv)

= \(\frac{\frac{1}{2}+1-\frac{2}{\sqrt{3}}}{\frac{2}{\sqrt{3}}+\frac{1}{2}+1}=\frac{\frac{3}{2}-\frac{2}{\sqrt{3}}}{\frac{2}{\sqrt{3}}+\frac{3}{2}}\)

= \(\frac{3 \sqrt{3}-4}{4+3 \sqrt{3}}\)

= \(\frac{(3 \sqrt{3}-4)(3 \sqrt{3}-4)}{(3 \sqrt{3}+4)(3 \sqrt{3}-4)}\)

= \(\frac{27+16-24 \sqrt{3}}{27-16}\)

= \(\frac{43-24 \sqrt{3}}{11}\)

(v) \(\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}\)

= \(\begin{array}{r}
5\left(\cos 60^{\circ}\right)^{2}+4\left(\sec 30^{\circ}\right)^{2} \\
\frac{-\left(\tan 45^{\circ}\right)^{2}}{\left(\sin 30^{\circ}\right)^{2}+\left(\cos 30^{\circ}\right)^{2}}
\end{array}\)

= \(\frac{5\left(\frac{1}{2}\right)^{2}+4\left(\frac{2}{\sqrt{3}}\right)^{2}-(1)^{2}}{\left(\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}}\)

= \(\frac{\frac{5}{4}+4 \times \frac{4}{3}-1}{\frac{1}{4}+\frac{3}{4}}=\frac{\frac{5}{4}+\frac{1}{3}-1}{\frac{1}{4}+\frac{3}{4}}\)

= \(\frac{5}{4}+\frac{16}{3}-1=\frac{15+64-12}{12}=\frac{67}{12}\).

Question 2.
Choose the correct option and justify your choice.

(i) \(\frac{2 \tan 30^{\circ}}{1+\tan 30^{\circ}}\)
(A) sin 60°
(B) cos 60°
(C) tan 60°
(D) sin 30°

(ii) \(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan 45^{\circ}}\)
(A) tan 90°
(B) 1
(C) sin 45°
(D) 0.

(iii) sin 2A = 2 sin A is true when
(A) 0°
(B) 30°
(C) 45°
(D) 60°

(iv) \(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}\)
(A) cos 60°
(B) sin 60°
(C) tan 60°
(D) sin 30°.

Solution:
(i) \(\frac{2 \tan 30^{\circ}}{1+\tan 30^{\circ}}=\frac{2\left(\frac{1}{\sqrt{3}}\right)}{1+\left(\frac{1}{\sqrt{3}}\right)^{2}}\)

\(\frac{\frac{2}{\sqrt{3}}}{1+\frac{1}{3}}=\frac{2}{\sqrt{3}} \times \frac{3}{4}=\frac{\sqrt{3}}{2}\) = sin 60°.
So, correct anwer is (A).

(ii) \(\frac{1-\tan ^{2} 45^{\circ}}{1+\tan ^{2} 45^{\circ}}=\frac{1-(1)^{2}}{1+(1)^{2}}\) = 0
So, correct anwer is (D).

(iii) Here when A = 0°
L.H.S. = sin 2A = sin 0° = 0
and R.H.S. = 2 sin A = 2 sin 0°
= 2 × 0 = 0
∴ Option (A) is correct.

(iv) \(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}=\frac{2\left(\frac{1}{\sqrt{3}}\right)}{1-\left(\frac{1}{\sqrt{3}}\right)^{2}}\)

= \(\frac{\frac{2}{\sqrt{3}}}{1-\frac{1}{3}}=\frac{2}{\sqrt{3}} \times \frac{3}{2}=\sqrt{3}\)

= tan 60°
∴ Option (C) is correct.

Question 3.
If tan (A + B) = \(\sqrt{3}\) and tan (A – B) = \(\frac{1}{\sqrt{3}}\); 0° ∠A + B ≤ 90°; A > B. find A and B.
Solution:
tan (A + B) = \(\sqrt{3}\). Given
tan (A + B) = tan 60°
⇒ A + B = 60° ……………..(1)
tan (A – B) = \(\frac{1}{\sqrt{3}}\) (Given)
or tan (A – B) = tan 30°
⇒ A – B = 30° …………….(2)
On adding (1) and (2),

A = 45°

Pu value of A = 45° in (1)
45° + B = 60°
B = 60° – 45°
B = 15°
Hence A = 45° and B = 15°.

Question 4.
State whether the following are true or false. Justify your answer.
(i) sin (A + B) = sin A + sin B.
(ii) The value of sin q increases as q increases.
(iii) The value of cos q Increases as q increases
(iv) sin q = cos q for all value of q.
(v) cot A is not defined for A = 0°.
Solution:
(i) False.
When A = 60°, B = 30°
L.H.S. = sin (A + B) = sin (60° + 30°) = sin 90° = 1
R.H.S. = sin A + sin B
= sin 60° + sin 30°
= \(\frac{\sqrt{3}}{2}+\frac{1}{2}\) ≠ 1
i.e., L.H.S. ≠ R.H.S.

(ii) True, sin 30° = \(\frac{1}{2}\) = 0.5,
Note that sin 0° = 0,
sin 45° = \(\frac{1}{\sqrt{2}}\) = 0.7 (approx.)
sin 60° = \(\frac{\sqrt{3}}{2}\) = 0.87 (approx.)
and sin 90° = 1
i.e., value of sin θ increases as θ increases from 0° to 90°.

(iii) False.
Note that cos 0° = 1,
cos 30° = \(\frac{\sqrt{3}}{2}\) = 0.87(approx.)
cos 45° = \(\frac{1}{\sqrt{2}}\) = 0.7.(approx.)
cos 60° = \(\frac{1}{2}\) = 0.5
and cos 90° = 0.
Hence, value of θ decreases as θ increases from 0° to 90°.

(iv) False
Since sin 30° = \(\frac{1}{2}\)
and cos 30° = \(\frac{\sqrt{3}}{2}\)
or sin 30° ≠ cos 30°
Only we have: sin 45° = cos 45°.
\(\frac{1}{\sqrt{2}}\) = \(\frac{1}{\sqrt{2}}\)

(v) True.
cot 0° = \(\frac{1}{\tan 0^{\circ}}=\frac{1}{0}\), or not defined.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 8 Introduction to Trigonometry Ex 8.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry Ex 8.1

Question 1.
In ∆ABC, right angled at B, AB = 24 cm; BC = 7 cm. Determine
(i) sin A, cos A
(ii) sin C, cos C.
Solution:
(i) We are to find sin A .cos A AB = 24 cm; BC = 7 cm
By using Pythagoras Theorem,

AC² = AB² + BC²
AC² = (24)² + (7)²
AC² = 576 + 49
AC² = 625
AC = \(\sqrt{625}\)
AC = 25 cm.
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)

sin A = \(\frac{7 \mathrm{~cm}}{25 \mathrm{~cm}}=\frac{7}{25}\)

cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{24 \mathrm{~cm}}{25 \mathrm{~cm}}\)

cos A = \(\frac{24}{25}\)

Hence sin A = \([latex]\frac{7}{25}\)[/latex] and cos A = \([latex]\frac{24}{25}\)[/latex].

(ii) sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{24 \mathrm{~cm}}{25 \mathrm{~cm}}\)

sin C = \(\frac{24}{25}\)

cos C = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7 \mathrm{~cm}}{25 \mathrm{~cm}}\)

cos C = \(\frac{7}{25}\)

Hence sin C = \(\frac{24}{25}\) and cos C = \(\frac{7}{25}\).

Question 2
In fig., find tan P – cot R.

Solution:
Hyp. PR = 13 cm

By using Pythagoras Theorem,
PR² = PQ² + QR²
or (13)² = (12)² + QR²
or 169 = 144 + (QR)²
or 169 – 144 = (QR)²
or 25 = (QR)²
or QR = ± \(\sqrt{25}\)
or QR = 5, – 5.
But QR = 5 cm.
[QR ≠ – 5, because side cannot be negative]
tan P = \(\frac{R Q}{Q P}=\frac{5}{12}\)

cot R = \(\frac{R Q}{P Q}=\frac{5}{12}\)

∴ tan P – cot R = \(\frac{5}{12}-\frac{5}{12}\) = 0
Hence tan P – cot R = 0.

Question 3.
If sin A = \(\frac{3}{4}\) calculate cos A and tan A.
Solution:
Let ABC be any triangle with right angle at B.

sin A = \(\frac{3}{4}\)
But sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) [From figure]
∴ \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3}{4}\)
But \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3}{4}\) = K
where K, is constant of proportionality.
⇒ BC = 3K, AC = 4K
By using Pythagoras Theorem,
AC² = AB² + BC²
or (4K)² = (AB)² + (3K)²
or 16K² = AB² + 9K²
or 16K² – 9K² = AB²
or 7K² = AB²
or AB = ± \(\sqrt{7 K^{2}}\)
or AB = ± \(\sqrt{7} \mathrm{~K}\)
[AB ≠ \(\sqrt{7 K}\) because side of a triangle cannot be negative]

⇒ AB = \(\sqrt{7} \mathrm{~K}\)
cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
cos A = \(\frac{\sqrt{7} K}{4 K}=\frac{\sqrt{7}}{4}\)
tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{3 \mathrm{~K}}{\sqrt{7} \mathrm{~K}}=\frac{3}{\sqrt{7}}\)

Hence cos A = \(\frac{\sqrt{7}}{4}\) and tan A = \(\frac{3}{\sqrt{7}}\).

Question 4.
Given 15 cot A = 8, find sin A and sec A.
Solution:
Let ABC be any right angled triangle where A is an acute angle with right angle at B.

15 cot A = 8
cot A = \(\frac{8}{15}\)
But cot A = \(\frac{A B}{B C}\) (fromfig.)
⇒ \(\frac{A B}{B C}=\frac{8}{15}\) = K
where K is constant of proportionality.
AB = 8 K, BC = 15 K
By using Pythagoras Theorem.
AC² = (AB)² + (BC)²
(AC)² = (8 K)² + (15 K)²
(AC)² = 64K² + 225 K²
(AC)² = 289 K²
AC = ± \(\sqrt{289 K^{2}}\)
AC = ± 17 K
⇒ AC = 17K
[AC = – 17 K, Because side cannot be negative]
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{15 \mathrm{~K}}{17 \mathrm{~K}}=\frac{15}{17}\)

sin A = \(\frac{15}{17}\)

sec A = \(\frac{\mathrm{AC}}{\mathrm{AB}}\)

sec A = \(\frac{17 \mathrm{~K}}{8 \mathrm{~K}}=\frac{17}{8}\)

sec A = \(\frac{17}{8}\)

Hence, sin A = \(\frac{15}{17}\) and sec A = \(\frac{17}{8}\).

Question 5.
Given sec θ = \(\frac{13}{2}\), calculate all other trigonometric ratios.
Solution:
Let ABC be any right angled triangle with right angle at B.
Let ∠BAC = θ

sec θ = \(\frac{13}{12}\)

But sec θ = \(\frac{\mathrm{AC}}{\mathrm{AB}}\) ……….[from fig.]

\(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{13}{12}\)

But \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{13}{12}\) = k where k is constant of proportionality.
AC = 13 k and AB = 12 k
By using Pythagoras Theorem,
AC² = (AB)² + (BC)²
or (13k)² = (12k)² + (BC)²
or 169k² = 144k² + (BC)²
or 169k² – 144k² = (BC)
or (BC)² = 25k²
or BC = ± \(\sqrt{25 k^{2}}\)
or BC = ± 5k
or BC = 5k.
[BC ≠ – 5k because side cannot be negative]

sin θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{5 k}{13 k}=\frac{5}{13}\)
cos θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{12 k}{13 k}=\frac{12}{13}\)
tan θ = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{5 k}{12 k}=\frac{5}{12}\)
cosec θ = \(\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{13 k}{5 k}=\frac{13}{5}\)
cot θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{12 k}{5 k}=\frac{12}{5}\).

Question 6.
If ∠A and ∠B are acute angles such that cos A = cos B, show that LA = LB.
Solution:
Let ABC be any triangle, where ∠A and ∠B are acute angles. To find cos A and cos B.

Draw CM ⊥ AB
∠AMC = ∠BMC = 90°
In right angled ∆AMC,
\(\frac{\mathrm{AM}}{\mathrm{AC}}\) = cos A ……………(1)
In right angled ∆BMC,
\(\frac{\mathrm{BM}}{\mathrm{BC}}\) = cos B ……………(2)
But cos A = cos B [given] ………..(3)
From (1), (2) and (3),
\(\frac{\mathrm{AM}}{\mathrm{AC}}=\frac{\mathrm{BM}}{\mathrm{BC}}\)
\(\frac{\mathrm{AM}}{\mathrm{BM}}=\frac{\mathrm{AC}}{\mathrm{BC}}=\frac{\mathrm{CM}}{\mathrm{CM}}\)
∴ ∆AMC = ∆BMC [By SSS similarity]
⇒ ∠A = ∠B [∵ Corresponding angles of two similar triangles are equal].

Question 7.
If cot θ = \(\frac{7}{8}\) evaluate
(i) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
(ii) cot² θ.
Solution:
(i) ∠ABC = θ.
In right angled triangle ABC with right angle at C.

Given that, cot θ = \(\frac{7}{8}\)
But cot θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) [From fig.]
⇒ \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{8}\)
Let \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{8}\) = k
where k is constant of proportionality.
⇒ BC = 7k, AC = 8k
By using Pythagoras Theorem,
AB² = (BC)² + (AC)²
or (AB)² = (7k)² + (8k)²
or (AB)² = 49k² + 64k²
or (AB)² = 113 k²
or AB = ± \(\)
AB = \(\sqrt{113 k^{2}}\) k
AB = \(\sqrt{113}\) k
[AB ≠ \(\sqrt{113}\) k because side cannot be negative]

sin θ = \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{8 k}{\sqrt{113} k}\)
sin θ = \(\frac{8}{\sqrt{113}}\)
cos θ = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{7 k}{\sqrt{113} k}=\frac{7}{\sqrt{113}}\)
cos θ = \(\frac{7}{\sqrt{113}}\)

(1 + sin θ) (1 – sin θ) = (1 + \(\frac{8}{\sqrt{113}}\)) (1 – \(\frac{8}{\sqrt{113}}\))
= (1)² – (\(\frac{8}{\sqrt{113}}\))²
[By using formula (a + b) (a – b) = a² – b²]
= 1 – \(\frac{64}{113}\)
(1 + sin θ) (1 – sin θ) = \(\frac{113-64}{113}=\frac{49}{113}\)
(1 + sin θ)(1 – sin θ) = \(\frac{49}{113}\) ……………..(1)

(1 + cos θ) (1 – cos θ) = (1 + \(\frac{8}{\sqrt{113}}\)) (1 – \(\frac{8}{\sqrt{113}}\))
(1)² – (\(\frac{7}{\sqrt{113}}\))²
[By using formula(a + b) (a – b) = a² – b²]
= 1 – \(\frac{49}{113}\) = \(\frac{113-49}{113}\)
(1 + cos θ) (1 – cos θ) = \(\frac{64}{113}\) ……….(2)

Consider, \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}=\frac{\frac{49}{113}}{\frac{64}{113}}\) [From (1) and (2)]

Hence \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}=\frac{49}{64}\)

(ii) cot θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{7}{8}\)
cot² θ = (cot θ)²
cot² θ= (\(\frac{7}{8}\))²
⇒ cot² θ = \(\frac{49}{64}\).

Question 8.
If 3 cot A = 4 check whether \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\) = cos² A – sin² A or not.
Solution:
Let ABC be a right angled triangle with right angled at B.

It is given that 3 cot A = 4
cot A = \(\frac{4}{3}\)
But cot A = \(\frac{\mathrm{AB}}{\mathrm{BC}}\) [From fig.]
⇒ \(\frac{A B}{B C}=\frac{4}{3}\)
But \(\frac{A B}{B C}=\frac{4}{3}\) = k
⇒ AB = 4k, BC = 3k
By using Pythagoras Theorem,
(AC)² = (AB)² + (BC)²
(AC)² = (4k)² + (3k)²
(AC)² = 16 k² + 9 k²
(AC)² = 25 k²
AC=± \(\sqrt{25 k^{2}}\)
AC = ± 5k

But AC = 5k.
[AC ≠ – 5k. because side cannot be negative]
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{3 k}{5 k}=\frac{3}{5}\)

tan A = \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{3 k}{4 k}=\frac{3}{4}\)

cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{4 k}{5 k}=\frac{4}{5}\)

L.H.S. = \(\frac{1-\tan ^{2} \mathrm{~A}}{1+\tan ^{2} \mathrm{~A}}\)

∴ cos² A – sin² A = \(\frac{7}{25}\) ………..(2)

From (1) and (2),
L.H.S = R.H.S
Hence, \(\frac{1-\tan ^{2} \mathrm{~A}}{1+\tan ^{2} \mathrm{~A}}\) = cos² A – sin² A.

Question 9.
In triangle ABC, right angled at B, if tan A = \(\frac{1}{\sqrt{3}}\). Find the value of:
(i) sin A cos C + cos A sin C
(ii) cos A cos C – sin A sin C.
Solution:
(i) Given: ABC with right angled at B

tan A = \(\frac{1}{\sqrt{3}}\) ……………..(1)
But tan A = \(\frac{B C}{A B}\) ……………(2)
From (1) and (2),
\(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{3}}\)
Let \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{1}{\sqrt{3}}\) = k
BC = k, AB = k
where k is constant of proportionality.
In right angled triangle ABC,
By using Pythagoras Theorem,
(AC)² = (AB)² + (BC)²
or (AC)² = (Jk)² + (k)²
or AC² = 3k² + k²
or AC² = 4k²
or AC = ± \(\sqrt{4 k^{2}}\)
AC = ± 2k.
where AC = 2k
[AC ≠ – 2k side cannot be negative]

[sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{k}{2 k}=\frac{1}{2}\)

cos C = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{k}{2 k}=\frac{1}{2}\)

cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}\)

sin C = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\sqrt{3} k}{2 k}=\frac{\sqrt{3}}{2}\)] …………….(3)

sin A cos C = \(\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)=\frac{1}{4}\)
cos A sin C = \(\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)=\frac{3}{4}\)
sin A cos C + cos A sin C = \(\frac{1}{4}+\frac{3}{4}\)
= \(\frac{1+3}{4}\)
= \(\frac{4}{4}\) = 1
∴ sin A cos C + cos A sin C = 1.

(ii) cos A cos C = \(\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{2}\right)=\frac{\sqrt{3}}{4}\) [From (3)]
sin A sin C = \(\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right)=\frac{\sqrt{3}}{4}\) [From (3)]

cos A cos C – sin A sin C = \(\left(\frac{\sqrt{3}}{4}\right)-\left(\frac{\sqrt{3}}{4}\right)\) = 0.

Question 10.
In ∆PQR, right angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P.
Solution:
Given: ∆PQR, right angled at Q

PR + QR = 25 cm
PQ = 5 cm
In right angled triangle PQR
By using Pythagoras Theorem,
(PR)² = (PQ)² + (RQ)²
or (PR)² = (5)² + (RQ)²
[∴ PR + QR = 25, QR = 25 – PR]
or (PR)² = 25 + [25 – PR]²
or (PR)² = 25 + (25)² + (PR)² – 2 × 25 × PR
or (PR)² = 25 + 625 + (PR)² – 50
or (PR)² – (PR)² + 50 PR = 650
or 50 PR = 650
or PR = \(\frac{650}{50}\)
or PR = 13 cm
QR = 25 – PR
QR = (25 – 13) cm
or QR = 12 cm.

sin P = \(\frac{Q R}{P R}=\frac{12}{13}\)

cos P = \(\frac{P Q}{P R}=\frac{5}{13}\)

tan P = \(\frac{Q R}{P Q}=\frac{12}{5}\)

Question 11.
State whether the following are true or false. Justify your answer.
(i) The value of tan A is always less than 1
(ii) sec A = \(\frac{12}{5}\) for some value of angle A.
(iii) cos A is abbreviation used for cosecant of angle A.
(iv) cot A is product of cot and A.
(v) sin θ = \(\frac{4}{3}\) for some angle θ.
Solution:
(i) False
∵ tan 60° = √3 = 1.732 > 1.

(ii) True; sec A = \(\frac{12}{5}\) = 240 > 1
∵ Sec A is always greater than 1.

(iii) False.
Because cos A is used for cosine A.

(iv) False.
Because cot A is cotangent of the angle A not the product of cot and A.

(v) False; sin θ = \(\frac{4}{3}\) = 1.666 > 1
Because sin θ is always less than 1.

Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 7 Coordinate Geometry Ex 7.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 10 Maths Chapter 7 Coordinate Geometry Ex 7.4

Question 1.
Determine the ratio in which the line it + y – 4 = 0 divides the line segment joining the points A (2, – 2) and B (3, 7).
Solution:
Let line 2x + y – 4 = 0 divides the line segment joining the points A (2,- 2) and B(3, 7) at C (x, y) in the ratio k : 1

∴ Coordinates of C are x = \(\frac{3 k+2 \times 1}{k+1}=\frac{3 k+2}{k+1}\) and y = \(\frac{7 k+(-2) \times 1}{k+1}=\frac{7 k-2}{k+1}\)
∴ C \(\left[\frac{3 k+2}{k+1}, \frac{7 k-2}{k+1}\right]\). must lie on the line 2x + y – 4 = 0

i.e., 2\(\left(\frac{3 k+2}{k+1}\right)+\left(\frac{7 k-2}{k+1}\right)\) – 4 = 0
or \(\frac{6 k+4+7 k-2-4 k-4}{k+1}\) = 0
or 9k – 2 = 0
or 9k = 2
or k = \(\frac{2}{9}\).
∴ ratio k : 1 = \(\frac{2}{9}\) : 1 = 2 : 9.
Hence required ratio is 2 : 9.

Question 2.
Find a relation between x and y if (x, y) ; (1, 2) and (7, 0) are collinear.
Solution:
Let given points are A (x, y); B (1, 2) and C (7, 0).
Here x₁ = x, x₂ = 1, x₃ = 7
y₁ = y, y₂ = 2, y₃ = 0
∵ Three points are collinear
iff \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)] = 0
or \(\frac{1}{2}\) x (2 – 0) + 1 (0 – y) + 7 (y – 2)] = 0
or 2x – y + 7y – 14 = 0
or 2x + 6y – 14 = 0
or x + 3y – 7 = 0 is the required relation.

Question 3.
Find the centre of a cirçle passing through the points (6, —6); (3, —7) and (3,3).
Solution:
Let O (x, y) be the required centre of the circle which passes through points P(6, – 6); Q(3, – 7) and R (3, 3).
∴ radii of circle are equal.

∴ OP = OQ = OR
or (OP)² = (OQ)² = (OR)²
Now, (OP)² = (OQ)²
(x – 6)² + (y + 6)² = (x – 3)² + (y + 7)²
or x² + 36 – 12x + y² + 36 + 12y = x² + 9 – 6x + y² + 49 + 14y
or – 12x + 12y + 72 = – 6x + 14y + 58
or – 6x – 2y + 14 = 0
or 3x + y – 7 = 0 ………………(1)
Also, (OQ)² = (OR)²
or (x – 3)² + (y + 7)² = (x – 3)² + (y – 3)²
or (y + 7)² = (y – 3)²
or y² + 49 + 14y = y² + 9 – 6y
or 20y = – 40
y = \(\frac{-40}{20}\) = – 2
Substitute this value of)’ in (1), we get
3x – 2 – 7 = 0
or 3x – 9 = 0
or 3x = 9
or x = \(\frac{9}{3}\) = 3
∴ Required centre is (3, – 2).

Question 4.
The two opposite vertices of a square are (- 1, 2) and (3, 2). Find the coordinates of other two vertices.
Solution:
Let two opposite vertices of a square ACBD are A (- 1, 2) and B (3, 2) and coordinates of C are (x, y)
∵ Length of each sides of square are equal.
∴ AC = BC
or (AC)² = (BC)²
or (x + 1)² + (y – 2)² = (x – 3)² + (y – 2)²

or (x + 1)² = (x – 3)²
or x² + 1 + 2x = x² + 9 – 6x
or 8x = 8
or x = \(\frac{8}{8}\) = 1
Now, in rt ∠d ∆ACB,
Using Pythagoras Theorem,
(AC)² + (BC)² = (AB)²
(x + 1)² + (y – 2)² + (x – 3)² + (y – 2)² = (3 + 1)² + (2 – 2)²
or x² + 1 + 2x + y² + 4 – 4y + x² + 9 – 6x + y² + 4 – 4y = 16
or 2x² + 2y² – 4x – 8y + 2 = 0
or x² + y² – 2x – 4y + 1 = 0
Putting the value of x = 1 in (1), we get
(1)² + y² – 2 (1) – 4y + 1 = 0
or y² – 4y = 0
or y (y – 4) = 0
Either y = 0 or y – 4 = 0
Either y = 0 or y = 4
∴ y = 0, 4
∴ Required points are (1. 0) and (1.4).

Question 5.
The Class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar are planted on the boundary at a distance of 1m from each other. There ¡s a triangular grassy lawn in the plot as shown in the Fig. The students are to sow seeds of flowering plants on the remaining area of the plot.

(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of A PQR if C is the origin? Also calculate the areas of the triangles In these cases. What do you observe?
Solution:
Case I:
When taking A as origin then AD is X-axis and AB is Y-axis.
∴ Coordinates of triangular grassy Lawn
PQR are P (4, 6); Q (3, 2) and R(6, 5).
Here x₁ = 4, x₂ = 3, x₃ = 6
y₁ = 6, y₂ = 2, y₃ = 50
Now, area of ∆PQR = \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]
= \(\frac{1}{2}\) [4 (2 – 5) + 3 (5 – 6) + 6 (6 – 2)]
= \(\frac{1}{2}\) [- 12 – 3 + 24] = \(\frac{9}{2}\)
= 4.5 sq. units.

Case II: When taking C as origin then CB is X – axis and CD is Y – axis.
∴ Coordinates of triangular grassy lawn PQR
are P(12, 2); Q (13,6) and R (10, 3)
Here x₁ = 12, x₂ = 13, x₃ = 10
y₁ = 2, y₂ = 6, y₃ = 3
Now, area of ∆PQR = \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]
= \(\frac{1}{2}\) [12 (6 – 3) + 13 (3 – 2) + 10 (2 – 6)]
= \(\frac{1}{2}\) [36 + 13 – 40]
= \(\frac{9}{2}\) = 4.5 sq. units.
From above two cases, it is clear that area of triangular grassy lawn is same.

Question 6.
The vertices of a ∆ABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{1}{4}\) Calculate the area of the ∆ADE and compare it with the area of ∆ABC. (Recall Theorem 6.2 and Theorem 6.6).
Solution:
The vertices of ∆ABC are A (4, 6); B (1, 5) and C (7, 2)

A line is drawn to intersect sides AB and AC at D (x₁, y₁) and E (x₂, y₂) respectively such that \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{AC}}=\frac{1}{4}\).

∴ D and E divides AB and AC in the ratio 1 : 3.
∴ Coordinates of D are
x₁ = \(\frac{1(1)+3(4)}{1+3}=\frac{1+12}{4}=\frac{13}{4}\) and y₁ = \(\frac{1(5)+3(6)}{1+3}=\frac{5+18}{4}=\frac{23}{4}\)

∴ Coordinates of D are (\(\frac{13}{4}\), \(\frac{23}{4}\))
Now, coordinates of E are
x₂ = \(\frac{1(7)+3(4)}{1+3}=\frac{7+12}{4}=\frac{19}{4}\) and y₂ = \(\frac{1(2)+3(6)}{1+3}=\frac{2+18}{4}=\frac{20}{4}=5\)

∴ Coordinates of E are (\(\frac{19}{4}\), 5).

In ∆ADE
x₁ = 4, x₂ = \(\frac{13}{4}\), x₃ = \(\frac{19}{4}\)
y₂ = 6, y₂ = \(\frac{23}{4}\), y₃ = 5
area of ∆ADE = \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]

= \(\frac{1}{2}\left[4\left(\frac{23}{4}-5\right)+\frac{13}{4}(5-6)+\frac{19}{4}\left(6-\frac{23}{4}\right)\right]\)

= \(\frac{1}{2}\left[4\left(\frac{23-20}{4}\right)+\frac{13}{4}(-1)+\frac{19}{4}\left(\frac{24-23}{4}\right)\right]\)

= \(\frac{1}{2}\left[3-\frac{13}{4}+\frac{19}{16}\right]\)

= \(\frac{1}{2}\left[\frac{48-52+19}{16}=\frac{15}{16}\right]\)
= \(\frac{15}{32}\) sq. units.

In ∆ABC
x₁ = 4, x₂ = 1, x₃ = 7
y₂ = 6, y₂ = 5, y₃ = 2
Area of ∆ABC = \(\frac{1}{2}\) [x₁ (y₂ – y₃) + x₂ (y₃ – y₁) + x₃ (y₁ – y₂)]

= \(\frac{1}{2}\) [4 (5 – 2) + 1 (2 – 6) + 7 (6 – 5)]
= \(\frac{1}{2}\) [12 – 4 + 7] = \(\frac{15}{2}\) sq.units.

Now, \(\frac{\text { area of } \Delta \mathrm{ADE}}{\text { area of } \Delta \mathrm{ABC}}=\frac{\frac{15}{32}}{\frac{15}{2}}=\frac{15}{32} \times \frac{2^{1}}{16_{1}}\)

= \(\frac{1}{16}=\left(\frac{1}{4}\right)^{2}\)

= \(\left(\frac{A D}{A B}\right)^{2} \text { or }\left(\frac{A E}{A C}\right)^{2}\).

Question 7.
Let (4, 2), B (6, 5) and C (1, 4) be the vertices of ∆ABC.
(i) The median from A meets BC at D. Find the coordinates of the point D.
(ii) Find the coordinates of the potnt P on AD such that AP : PD = 2 : 1
(iii) Find the coordinates of points Q and R on medians BE and CF respectively such that BQ : QE = 2 : 1 and CR : RF = 2 : 1.
(iv) What do you observe?
[Note : The point which is common to all the three medians ¡s called centroid and this point divides each median in the ratio 2: 1]
(v) if A (x₁, y₁), B (x₂, y₂) and C (x₃, y₃) are the vertices of ∆ABC, find the coordinates of the centroid of the triangle.
Solution:
Given that vertices of ∆ABC are A (4, 2); B (6, 5) and C (1, 4).
(i) AD is the median from the vertex A.
∴ D is the mid point of BC.

then x = \(\frac{6+1}{2}=\frac{7}{2}\) and y = \(\frac{5+4}{2}=\frac{9}{2}\)
Hence, coordinates of D is (\(\frac{7}{2}\), \(\frac{9}{2}\)).

(ii) Let P(x, y) be point on AD such that AP : PD = 2 : 1

then x = \(\frac{2\left(\frac{7}{2}\right)+1(4)}{2+1}\)
= \(\frac{7+4}{3}=\frac{11}{3}\)

and y = \(\frac{2\left(\frac{9}{2}\right)+1(2)}{2+1}\)
= \(\frac{9+2}{3}=\frac{11}{3}\)

Hence, Coordinates of P is (\(\frac{11}{3}\), \(\frac{11}{3}\)).

(iii) Le BE and CF are the medians of ∆ABC to AC and AB respectively.
∴ E and F are mid points of AC and AB respectively.

Coordinate of E are
x₁ = \(\frac{4+1}{2}=\frac{5}{2}\)
and y₁ = \(\frac{4+2}{2}=\frac{6}{2}\) = 3
Coordinate of E are (\(\frac{5}{2}\), 3)
Coordinate of F are
x₂ = \(\frac{4+6}{2}=\frac{10}{2}\) = 5
and y₂ = \(\frac{5+2}{2}=\frac{7}{2}\)
∴ Coordinate of F are (5, \(\frac{7}{2}\))
Now, Q divides BE such that BQ : QE = 2: 1

∴ Coordinate of Q are \(\left(\frac{2\left(\frac{5}{2}\right)+6(1)}{2+1}, \frac{2(3)+1(5)}{2+1}\right)\)

= \(\left(\frac{5+6}{3}, \frac{6+5}{3}\right)\) = \(\left(\frac{11}{3}, \frac{11}{3}\right)\)

Also, R divides CF such that CR : RF = 2 : 1

∴ Coordinate of R are = \(\left(\frac{2(5)+1(1)}{2+1}, \frac{2\left(\frac{7}{2}\right)+(4)}{2+1}\right)\)

= \(\left(\frac{10+1}{3}, \frac{7+4}{3}\right)\)

= \(\left(\frac{11}{3}, \frac{11}{3}\right)\)

(iv) From above discussion, it is clear that coordinates of P, Q and R are same and coincide at a point, is known as centroid of triangle, which divides each median in the ratio 2: 1.

(v) The vertices of given ∆ABC are
A (x₁, y₁); B (x₂, y₂) and C (x₃, y₃).

Let AD is median of E, ∆ABC.
∴ D is the mid point of BC then coordinates of D are \(\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)\)

Now, G be the centroid of ABC, which divides the median AD in the ratio 2: 1
∴ Coordinates of G are [using (iv)]

= \(\left[\frac{2\left(\frac{x_{2}+x_{3}}{2}\right)+1\left(x_{1}\right)}{2+1}, \frac{2\left(\frac{y_{2}+y_{3}}{2}\right)+1\left(y_{1}\right)}{2+1}\right]\)

= \(\left[\frac{x_{2}+x_{3}+x_{1}}{3}, \frac{y_{2}+y_{3}+y_{1}}{3}\right]\)

= \(\left[\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right]\).

Question 8.
ABCD is a rectangle formed by the points A (- 1, – 1), B (- 1, 4), C (5, 4) and D (5, – 1). P, Q R and S are the mid points
of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square ? a rectangle? or a rhombus ? Justify your answer.
Solution:
Given: The vertices ot’ given rectangle ABCD are
A(- 1, – 1); B(- 1, 4); C(5, 4) and D (5, – 1).

∵ P is the mid point of AB.
∴ Coordinates of P are \(\left(\frac{-1-1}{2}, \frac{-1+4}{2}\right)=\left(-1, \frac{3}{2}\right)\)
∵ Q is the mid point of BC.
∴ Co-ordinates of Q are \(\left(\frac{-5+5}{2}, \frac{4+4}{2}\right)\) = (2, 4)
∵ R is the mid point of CD.
∴ Coordinates of R are \(\left(\frac{5+5}{2}, \frac{4+1}{2}\right)=\left(5, \frac{3}{2}\right)\)

∵ S is the mid point of AD.
∴ Co-ordinates of S are \(\left(\frac{5-1}{2}, \frac{-1-1}{2}\right)\) = (2, -1)

PQ = \(\sqrt{(2+1)^{2}+\left(4-\frac{3}{2}\right)^{2}}\)

= \(\sqrt{9 \times \frac{25}{4}}=\sqrt{\frac{36+25}{4}}\)

PQ = \(\sqrt{\frac{61}{4}}\)

QR = \(\sqrt{(5-2)^{2}+\left(\frac{3}{2}-4\right)^{2}}\)

= \(\sqrt{(3)^{2}+\left(\frac{3-8}{2}\right)^{2}}\)

= \(\sqrt{9+\frac{25}{4}}=\sqrt{\frac{36+25}{4}}\)

QR = \(\sqrt{\frac{61}{4}}\)

RS = \(\sqrt{(2-5)^{2}+\left(-1-\frac{3}{2}\right)^{2}}\)

= \(\sqrt{9+\frac{25}{4}}=\sqrt{\frac{36+25}{4}}\)

RS = \(\sqrt{\frac{61}{4}}\)

and SP = \(\sqrt{(-1-2)^{2}+\left(\frac{3}{2}+1\right)^{2}}\)

SP = \(\sqrt{9+\frac{25}{4}}=\sqrt{\frac{61}{4}}\)

Also PR = \(\sqrt{(5+1)^{2}+\left(\frac{3}{2}-\frac{3}{2}\right)^{2}}\)
PR = \(\sqrt{36+0}=\sqrt{36}\) = 6
QS = \(\sqrt{(2-2)^{2}+(4+1)^{2}}\)
= \(\sqrt{0+25}=\sqrt{25}\) = 5.

Form above discussion it is clear that PQ = QR = RS = SP.
Also, PR ≠ QS.
⇒ All sides of quad. PQRS are equal but their diagonals are not equal.
Quad. PQRS is a rhombus.