Punjab State Board PSEB 10th Class Agriculture Book Solutions Chapter 5 ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਦੀ ਕਾਸ਼ਤ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Agriculture Chapter 5 ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਦੀ ਕਾਸ਼ਤ
Agriculture Guide for Class 10 PSEB ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਦੀ ਕਾਸ਼ਤ Textbook Questions and Answers
ਅਭਿਆਸ
(ੳ) ਇੱਕ-ਦੋ ਸ਼ਬਦਾਂ ਵਿੱਚ ਉੱਤਰ ਦਿਓ :-
ਪ੍ਰਸ਼ਨ 1.
ਪੰਜਾਬ ਵਿੱਚ ਫ਼ਲਾਂ ਹੇਠ ਕਿੰਨਾ ਰਕਬਾ ਹੈ ?
ਉੱਤਰ-
78000 ਹੈਕਟੇਅਰ ।
ਪ੍ਰਸ਼ਨ 2.
ਬੂਟਿਆਂ ਨੂੰ ਸਿਊਂਕ ਤੋਂ ਬਚਾਉਣ ਲਈ ਕਿਹੜੀ ਦਵਾਈ ਪਾਉਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
30 ਗ੍ਰਾਮ ਲਿੰਡੇਨ ਜਾਂ 15 ਮਿਲੀ ਲੀਟਰ ਕਲੋਰੋਪਾਈਰੀਫਾਸ 20 ਤਾਕਤ ਨੂੰ 2.5 ਕਿਲੋ ਮਿੱਟੀ ਵਿੱਚ ਰਲਾ ਕੇ ਪ੍ਰਤੀ ਟੋਏ ਦੇ ਹਿਸਾਬ ਨਾਲ ਪਾਓ ।
ਪ੍ਰਸ਼ਨ 3.
ਆਤੂ ਦੀਆਂ ਦੋ ਉੱਨਤ ਕਿਸਮਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਫਲੋਰਿਡਾ ਪਰਿੰਸ, ਪਰਤਾਪ ।
![]()
ਪ੍ਰਸ਼ਨ 4.
ਬਾਗ ਲਗਾਉਣ ਦੇ ਕਿੰਨੇ ਢੰਗ ਹਨ ?
ਉੱਤਰ-
ਤਿੰਨ ਢੰਗ ਹਨ-ਵਰਗਾਕਾਰ, ਛਿੱਲਰ, ਛੇ ਕੋਨਾ ਢੰਗ ।
ਪ੍ਰਸ਼ਨ 5.
ਪੱਤਝੜੀ ਫ਼ਲਦਾਰ ਬੂਟੇ ਕਿਹੜੇ ਮਹੀਨੇ ਵਿੱਚ ਲਗਾਏ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
ਅੱਧ ਜਨਵਰੀ ਤੋਂ ਅੱਧ ਫਰਵਰੀ ।
ਪ੍ਰਸ਼ਨ 6.
ਅੰਬ ਅਤੇ ਲੀਚੀ ਦੇ ਬੂਟੇ ਲਗਾਉਣ ਦਾ ਸਹੀ ਸਮਾਂ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਸਤੰਬਰ-ਅਕਤੂਬਰ ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 7.
ਬਾਗਾਂ ਵਿੱਚ ਦੇਸੀ ਰੂੜੀ ਕਦੋਂ ਪਾਉਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਜਾਂ
ਫ਼ਲਦਾਰ ਪੌਦਿਆਂ ਨੂੰ ਰੂੜੀ ਦੀ ਖਾਦ ਕਿਹੜੇ ਮਹੀਨੇ ਵਿੱਚ ਪਾਉਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਫੁਟਾਰਾ ਆਉਣ ਤੋਂ 2-3 ਮਹੀਨੇ ਪਹਿਲਾਂ, ਆਮ ਕਰਕੇ ਦਸੰਬਰ ਮਹੀਨੇ ਵਿਚ ।
ਪ੍ਰਸ਼ਨ 8.
ਆਂਵਲੇ ਦੀਆਂ ਦੋ ਉੱਨਤ ਕਿਸਮਾਂ ਦੇ ਨਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਬਲਵੰਤ, ਨੀਲਮ, ਕੰਚਨ ।
![]()
ਪ੍ਰਸ਼ਨ 9.
ਫ਼ਲਦਾਰ ਬੂਟੇ ਲਗਾਉਣ ਲਈ ਟੋਆ ਕਿੰਨਾ ਡੂੰਘਾ ਪੁੱਟਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਇੱਕ ਮੀਟਰ ਡੂੰਘਾ ।
ਪ੍ਰਸ਼ਨ 10.
ਅੰਮ੍ਰਿਤਸਰ ਜ਼ਿਲ੍ਹੇ ਵਿੱਚ ਕਿਹੜੇ ਫ਼ਲ ਲਗਾਏ ਜਾ ਸਕਦੇ ਹਨ ?
ਉੱਤਰ-
ਨਾਸ਼ਪਾਤੀ, ਅੰਗੂਰ, ਅੰਬ, ਅਮਰੂਦ, ਆਤੂ, ਕਿਨੂੰ, ਹੋਰ ਸੰਗਤਰੇ, ਨਿੰਬੂ ਆਦਿ ।
(ਅ) ਇਕ-ਦੋ ਵਾਕਾਂ ਵਿੱਚ ਉੱਤਰ ਦਿਓ :-
ਪ੍ਰਸ਼ਨ 1.
ਫ਼ਲਦਾਰ ਬੂਟੇ ਲਗਾਉਣ ਲਈ ਕਿਸ ਤਰ੍ਹਾਂ ਦੀ ਮਿੱਟੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਫ਼ਲਦਾਰ ਬੂਟੇ ਲਗਾਉਣ ਲਈ ਚੰਗੇ ਜਲ ਨਿਕਾਸ ਵਾਲੀ, ਭਲ ਵਾਲੀ, ਡੂੰਘੀ ਤੇ ਉਪਜਾਊ ਜ਼ਮੀਨ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਜ਼ਮੀਨ ਦੀ ਦੋ ਮੀਟਰ ਤੱਕ ਦੀ ਡੂੰਘਾਈ ਵਿੱਚ ਕੋਈ ਸਖ਼ਤ ਤਹਿ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ ।
ਪ੍ਰਸ਼ਨ 2.
ਨੀਮ ਪਹਾੜੀ ਇਲਾਕੇ ਵਿੱਚ ਕਿਹੜੇ ਫ਼ਲਦਾਰ ਬੂਟੇ ਲਗਾਏ ਜਾ ਸਕਦੇ ਹਨ ?
ਉੱਤਰ-
ਅਮਰੂਦ, ਅੰਬ, ਲੀਚੀ, ਨਾਸ਼ਪਾਤੀ, ਕਿੰਨੂ ਅਤੇ ਹੋਰ ਸੰਗਤਰੇ, ਨਿੰਬੂ, ਆੜੂ, ਅਲੂਚਾ, ਚੀਕੂ, ਆਮਲਾ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 3.
ਸੇਂਜੂ ਅਤੇ ਖੁਸ਼ਕ ਇਲਾਕੇ ਦੇ ਢੁੱਕਵੇਂ ਫ਼ਲ ਕਿਹੜੇ ਹਨ ?
ਉੱਤਰ-
ਮਾਲਟਾ, ਨਿੰਬੂ, ਕਿਨੂੰ ਅਤੇ ਹੋਰ ਸੰਗਤਰੇ, ਬੋਰ, ਅੰਗੂਰ, ਅਮਰੂਦ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 4.
ਸਦਾਬਹਾਰ ਫ਼ਲਦਾਰ ਬੂਟੇ ਕਿਹੜੇ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਲੁਕਾਠ, ਅਮਰੂਦ, ਅੰਬ, ਲੀਚੀ, ਕਿੰਨੂ ਅਤੇ ਹੋਰ ਸੰਗਤਰੇ, ਮਾਲਟਾ, ਨਿੰਬੂ, ਚੀਕੂ ਆਦਿ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਪੱਤਝੜੀ ਫ਼ਲਦਾਰ ਬੂਟੇ ਕਿਹੜੇ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਨਾਸ਼ਪਾਤੀ, ਅੰਗੂਰ, ਆੜੂ, ਅਲੂਚਾ ।
ਪ੍ਰਸ਼ਨ 6.
ਵਰਗਾਕਾਰ ਢੰਗ ਤੋਂ ਤੁਹਾਡਾ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
ਇਹ ਬਾਗ਼ ਲਾਉਣ ਦਾ ਇੱਕ ਢੰਗ ਹੈ ਜਿਸ ਵਿੱਚ ਬੁਟਿਆਂ ਅਤੇ ਕਤਾਰਾਂ ਵਿਚ ਫ਼ਾਸਲਾ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਆਮਣੇ-ਸਾਹਮਣੇ ਲਗਾਏ ਚਾਰ ਬੂਟੇ ਇੱਕ ਵਰਗਾਕਾਰ ਬਣਾਉਂਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 7.
ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਨੂੰ ਪਾਣੀ ਕਿੰਨੀ ਦੇਰ ਬਾਅਦ ਦੇਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਛੋਟੇ ਬੂਟਿਆਂ ਨੂੰ 3-4 ਸਾਲ ਤੱਕ ਮਾਰਚ ਤੋਂ ਜੂਨ ਤੱਕ ਹਫ਼ਤੇ-ਹਫ਼ਤੇ ਮਗਰੋਂ, ਨਵੰਬਰ ਤੋਂ ਫ਼ਰਵਰੀ ਤੱਕ 2-3 ਹਫ਼ਤਿਆਂ ਬਾਅਦ ਅਤੇ ਜੁਲਾਈ ਤੋਂ ਨਵੰਬਰ ਤੱਕ ਵਰਖਾ ਅਤੇ ਮਿੱਟੀ ਦੀ ਕਿਸਮ ਅਨੁਸਾਰ ਪਾਣੀ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਬਾਗਾਂ ਲਈ ਪਾਣੀ ਦਾ ਪੱਧਰ ਕਿੰਨਾ ਡੂੰਘਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਬਾਗਾਂ ਲਈ ਪਾਣੀ ਦਾ ਪੱਧਰ ਤਿੰਨ ਮੀਟਰ ਤੋਂ ਥੱਲੇ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ਅਤੇ ਇਸ ਵਿੱਚ ਕੋਈ ਉਤਰਾਅ-ਚੜ੍ਹਾਅ ਨਹੀਂ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 9.
ਬਾਗ ਲਗਾਉਣ ਦੇ ਛਿੱਲਰ ਢੰਗ ਬਾਰੇ ਜਾਣਕਾਰੀ ਦਿਓ ।
ਉੱਤਰ-
ਕੁੱਝ ਫ਼ਲਦਾਰ ਬੂਟੇ, ਜਿਵੇਂ, ਲੀਚੀ, ਅੰਬ, ਨਾਸ਼ਪਾਤੀ ਬਹੁਤ ਲੰਬੇ ਸਮੇਂ ਬਾਅਦ ਫਲ ਦੇਣਾ ਸ਼ੁਰੂ ਕਰਦੇ ਹਨ । ਇਹਨਾਂ ਬਾਗਾਂ ਵਿੱਚ ਪਹਿਲਾਂ ਕੁੱਝ ਅਸਥਾਈ ਬੂਟੇ ਲਗਾਏ ਜਾ ਸਕਦੇ ਹਨ, ਜੋ ਜਲਦੀ ਫ਼ਲ ਦੇਣ ਵਾਲੇ ਹੋਣ । ਇਹ ਛਿੱਲਰ ਦਾ ਕੰਮ ਕਰਦੇ ਹਨ । ਜਦੋਂ ਮੁੱਖ ਬਾਗ਼ ਫਲ ਦੇਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੰਦੇ ਹਨ ਤੇ ਇਹਨਾਂ ਅਸਥਾਈ ਪੌਦਿਆਂ ਨੂੰ ਪੁੱਟ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 10.
ਬਾਗ ਲਗਾਉਣ ਲਈ ਬੂਟੇ ਕਿੱਥੋਂ ਲੈਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਬਾਗ਼ ਲਗਾਉਣ ਲਈ ਚੰਗੀ ਕਿਸਮ ਦੇ, ਕੀੜਿਆਂ ਅਤੇ ਰੋਗਾਂ ਤੋਂ ਰਹਿਤ, ਸਿਹਤਮੰਦ ਬੁਟੇ ਕਿਸੇ ਭਰੋਸੇਮੰਦ ਨਰਸਰੀ, ਹੋ ਸਕੇ ਤਾਂ ਪੀ.ਏ.ਯੂ. ਲੁਧਿਆਣਾ, ਬਾਗ਼ਬਾਨੀ ਵਿਭਾਗ ਅਤੇ ਸਰਕਾਰੀ ਮਨਜੂਰਸ਼ੁਦਾ ਨਰਸਰੀਆਂ ਤੋਂ ਲੈਣੇ ਚਾਹੀਦੇ ਹਨ ।
![]()
(ੲ) ਪੰਜ-ਛੇ ਵਾਕਾਂ ਵਿੱਚ ਉੱਤਰ ਦਿਓ :-
ਪ੍ਰਸ਼ਨ 1.
ਨਰਸਰੀ ਤੋਂ ਫ਼ਲਦਾਰ ਬੂਟੇ ਖ਼ਰੀਦਣ ਸਮੇਂ ਕਿਹੜੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
- ਬੂਟੇ ਚੰਗੀ ਕਿਸਮ ਦੇ, ਕੀੜਿਆਂ ਅਤੇ ਰੋਗਾਂ ਤੋਂ ਮੁਕਤ, ਸਿਹਤਮੰਦ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ !
- ਬੁਟੇ ਨਰੋਏ ਅਤੇ ਦਰਮਿਆਨੀ ਉਚਾਈ ਦੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
- ਸਦਾ ਬਹਾਰ ਬੂਟਿਆਂ ਨੂੰ ਪੁੱਟਣ ਲੱਗੇ ਧਿਆਨ ਰੱਖੋ ਕਿ ਜੜਾਂ ਤੇ ਮਿੱਟੀ ਕਾਫ਼ੀ ਮਾਤਰਾ ਵਿੱਚ ਹੋਵੇ ।
- ਪਿਉਂਦੀ ਬੂਟੇ ਦੀ ਪਿਉਂਦ ਮੁੱਢਲੇ ਬੂਟੇ ਤੇ ਕੀਤੀ ਗਈ ਹੋਵੇ ਅਤੇ ਇਸਦਾ ਜੋੜ ਪੱਧਰਾ ਹੋਵੇ ।
- ਬੂਟੇ ਖਰੀਦਣ ਸਮੇਂ ਲੋੜ ਤੋਂ 10% ਬੂਟੇ ਵੱਧ ਖਰੀਦਣੇ ਚਾਹੀਦੇ ਹਨ ਤਾਂ ਕਿ ਮਰਨ ਵਾਲੇ ਬੂਟਿਆਂ ਦੀ ਜਗ੍ਹਾ ਤੇ ਲਾਇਆ ਜਾ ਸਕੇ ।
ਪ੍ਰਸ਼ਨ 2.
ਬਾਗ਼ ਲਗਾਉਣ ਦੇ ਕਿਹੜੇ-ਕਿਹੜੇ ਢੰਗ ਹਨ ? ਵਿਸਥਾਰ ਸਹਿਤ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਬਾਗ ਲਗਾਉਣ ਦੇ ਤਿੰਨ ਢੰਗ ਹਨ-
(i) ਵਰਗਾਕਾਰ ਢੰਗ,
(ii) ਛਿੱਲਰ ਢੰਗ,
(iii) ਛੇ ਕੋਨਾ ਢੰਗ ।
(i) ਵਰਗਾਕਾਰ ਢੰਗ – ਇਸ ਢੰਗ ਵਿਚ ਲਗਾਏ ਬੂਟਿਆਂ ਅਤੇ ਕਤਾਰਾਂ ਦਾ ਫ਼ਾਸਲਾ ਇੱਕ-ਦੂਸਰੇ ਤੋਂ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਆਹਮਣੇ-ਸਾਹਮਣੇ ਲੱਗੇ ਚਾਰ ਬੂਟੇ ਵਰਗਾਕਾਰ ਬਣਾਉਂਦੇ ਹਨ । ਇਸ ਢੰਗ ਨੂੰ ਪੰਜਾਬ ਵਿਚ ਕਾਫ਼ੀ ਪਸੰਦ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਇਸ ਢੰਗ ਨਾਲ ਲੱਗੇ ਬੂਟੇ ਲੰਬੇ ਸਮੇਂ ਤੱਕ ਫ਼ਲ ਦਿੰਦੇ ਰਹਿੰਦੇ ਹਨ ਅਤੇ ਸ਼ੁਰੂਆਤੀ ਸਾਲਾਂ ਵਿੱਚ ਜਦੋਂ ਬਾਗ਼ ਤੋਂ ਆਮਦਨ ਨਹੀਂ ਹੁੰਦੀ ਤਾਂ ਇਸ ਵਿੱਚ ਅੰਤਰ ਫ਼ਸਲਾਂ ਉਗਾ ਕੇ ਲਾਭ ਲਿਆ ਜਾ ਸਕਦਾ ਹੈ ।
(ii) ਛਿੱਲਰ ਢੰਗ – ਕੁੱਝ ਫ਼ਲਦਾਰ ਬੂਟੇ, ਜਿਵੇਂ, ਲੀਚੀ, ਅੰਬ, ਨਾਸ਼ਪਾਤੀ ਬਹੁਤ ਲੰਬੇ ਸਮੇਂ ਬਾਅਦ ਫ਼ਲ ਦੇਣਾ ਸ਼ੁਰੂ ਕਰਦੇ ਹਨ । ਇਹਨਾਂ ਬਾਗਾਂ ਵਿੱਚ ਪਹਿਲਾਂ ਕੁੱਝ ਅਸਥਾਈ ਬੂਟੇ ਲਗਾਏ ਜਾਂਦੇ ਹਨ, ਜੋ ਜਲਦੀ ਫ਼ਲ ਦੇਣ ਵਾਲੇ ਹੋਣ, ਲਗਾਉਣੇ ਚਾਹੀਦੇ ਹਨ । ਇਹ ਛਿੱਲਰ ਦਾ ਕੰਮ ਕਰਦੇ ਹਨ । ਜਦੋਂ ਮੁੱਖ ਬਾਗ਼ ਫ਼ਲ ਦੇਣਾ ਸ਼ੁਰੂ ਕਰ ਦਿੰਦੇ ਹਨ ਤਾਂ ਇਹਨਾਂ ਅਸਥਾਈ ਪੌਦਿਆਂ ਨੂੰ ਪੁੱਟ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ।
(iii) ਛੇ ਕੋਨਾ ਢੰਗ – ਇਸ ਢੰਗ ਵਿਚ ਕਤਾਰਾਂ ਦਾ ਫ਼ਾਸਲਾ ਬੁਟਿਆਂ ਵਿਚਲੇ ਫ਼ਾਸਲੇ ਨਾਲੋਂ ਘੱਟ ਹੁੰਦਾ ਹੈ ਪਰ ਬੂਟੇ ਤੋਂ ਬੂਟੇ ਦਾ ਫ਼ਾਸਲਾ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ । ਇਸ ਢੰਗ ਦੀ ਵਰਤੋਂ ਕਰਕੇ 15 ਤੋਂ 20 ਫੀਸਦੀ ਵੱਧ ਬੂਟੇ ਲਗਾਏ ਜਾ ਸਕਦੇ ਹਨ । ਇਸ ਢੰਗ ਵਿਚ ਬੁਟਿਆਂ ਨੂੰ ਆਪਸ ਵਿੱਚ ਫਸਣ ਤੋਂ ਬਚਾਉਣ ਲਈ ਕਾਂਟ-ਛਾਂਟ ਵਧੀਆ ਢੰਗ ਨਾਲ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 3.
ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਦੀ ਸੁਧਾਈ ਅਤੇ ਕਾਂਟ-ਛਾਂਟ ਕਰਨੀ ਕਿਉਂ ਜ਼ਰੂਰੀ ਹੈ ?
ਉੱਤਰ-
ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਨੂੰ ਛੋਟੀ ਉਮਰ ਵਿਚ ਹੀ ਸਹੀ ਆਕਾਰ ਤੇ ਢਾਂਚਾ ਦੇਣ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਇਹ ਕੰਮ ਇਹਨਾਂ ਦੀ ਸੁਧਾਈ ਕਰਕੇ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਸਹੀ ਆਕਾਰ ਅਤੇ ਢਾਂਚਾ ਇਸ ਲਈ ਜ਼ਰੂਰੀ ਹੈ ਤਾਂ ਕਿ ਪੌਦਿਆਂ ਵਿੱਚ ਸੂਰਜੀ ਪ੍ਰਕਾਸ਼ ਅਤੇ ਹਵਾ ਦਾ ਨਿਕਾਸ ਵਧੀਆ ਢੰਗ ਨਾਲ ਹੋ ਸਕੇ । ਇਸ ਨਾਲ ਫ਼ਲ ਦੀ ਗੁਣਵੱਤਾ ਵੀ ਵੱਧਦੀ ਹੈ ਤੇ ਬੂਟੇ ਦੀ ਉਮਰ ਵਿਚ ਵੀ ਵਾਧਾ ਹੁੰਦਾ ਹੈ । ਪੰਜਾਬ ਵਿੱਚ ਕਾਸ਼ਤ ਕੀਤੇ ਜਾਣ ਵਾਲੇ ਪੱਤਝੜ ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਜਿਹਨਾਂ ਵਿਚ ਪ੍ਰਮੁੱਖ ਤੌਰ ‘ਤੇ ਅੰਗੂਰ, ਨਾਖ, ਆਤੂ ਅਤੇ ਅਲੂਚਾ ਹਨ, ਦੀ ਸੁਧਾਈ ਪਹਿਲੇ ਚਾਰ ਤੋਂ ਪੰਜ ਸਾਲਾਂ ਤੱਕ ਕੀਤੀ ਜਾਂਦੀ ਹੈ । ਜਦੋਂ ਪੌਦਿਆਂ ਨੂੰ ਫ਼ਲ ਲੱਗਣਾ ਸ਼ੁਰੂ ਹੋ ਜਾਂਦਾ ਹੈ ਤਾਂ ਉਤਪਾਦਕਤਾ ਵਿਚ ਕਮੀ ਨਾ ਆਵੇ ਤੇ ਇਹ ਸਿਖਰਾਂ ਛੂਹੇ ਅਤੇ ਫ਼ਲ ਵੀ ਮਿਆਰੀ ਮਿਲੇ । ਇਸ ਲਈ ਪੌਦਿਆਂ ਦੀ ਕਾਂਟ-ਛਾਂਟ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ਜੋ ਕਿ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਫ਼ਲ ਤੋੜਨ ਸਮੇਂ ਕਿਹੜੀਆਂ ਗੱਲਾਂ ਦਾ ਧਿਆਨ ਰੱਖਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
- ਫ਼ਲਾਂ ਦੀ ਤੁੜਾਈ ਲਈ ਕੁੱਝ ਮਾਪਦੰਡ ਨਿਰਧਾਰਿਤ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ ; ਜਿਵੇਂ, ਕੁੱਝ ਫ਼ਲਾਂ ਨੂੰ ਤੋੜਨ ਤੋਂ ਬਾਅਦ ਵੀ ਪਕਾਇਆ ਜਾ ਸਕਦਾ ਹੈ; ਜਿਵੇਂ-ਅੰਬ, ਕੇਲਾ, ਅਲੂਚਾ ਆਦਿ । ਪਰ ਅੰਗੂਰ, ਲੀਚੀ ਆਦਿ ਨੂੰ ਤੋੜ ਕੇ ਨਹੀਂ ਪਕਾਇਆ ਜਾ ਸਕਦਾ ।
ਇਸ ਲਈ ਫ਼ਲ ਅਨੁਸਾਰ ਹੀ ਮਾਪ-ਦੰਡ ਨਿਰਧਾਰਿਤ ਕਰਨੇ ਚਾਹੀਦੇ ਹਨ । - ਫ਼ਲਾਂ ਨੂੰ ਕਦੇ ਵੀ ਟਹਿਣੀ ਨਾਲੋਂ ਖਿੱਚ ਕੇ ਨਹੀਂ ਤੋੜਨਾ ਚਾਹੀਦਾ | ਇਸ ਤਰ੍ਹਾਂ ਟਹਿਣੀ ਨੂੰ ਵੀ ਨੁਕਸਾਨ ਹੋ ਸਕਦਾ ਹੈ ਤੇ ਫ਼ਲ ਦੀ ਛਿੱਲ ਵੀ ਲਹਿ ਸਕਦੀ ਹੈ ।
- ਤੋੜੇ ਫ਼ਲਾਂ ਦੀ 34 ਵਰਗਾਂ ਵਿੱਚ ਦਰਜ਼ਾਬੰਦੀ ਕਰ ਲੈਣੀ ਚਾਹੀਦੀ ਹੈ ਅਤੇ ਦਰਜ਼ਾਬੰਦੀ ਤੋਂ ਬਾਅਦ ਇਹਨਾਂ ਨੂੰ ਗੱਤੇ ਦੇ ਡੱਬਿਆਂ, ਪੋਲੀ ਨੈਟ, ਪਲਾਸਟਿਕ ਦੇ ਕਰੇਟਾਂ ਵਿੱਚ ਪਾ ਕੇ ਪੈਕ ਕਰਨਾ ਚਾਹੀਦਾ ਹੈ ।
- ਕੱਚੇ, ਵੱਧ ਪੱਕੇ, ਛੋਟੇ, ਬਦਸ਼ਕਲ, ਗਲੇ-ਸੜੇ ਅਤੇ ਦਾਗੀ ਫ਼ਲਾਂ ਨੂੰ ਡੱਬਾ ਬੰਦ ਨਹੀਂ ਕਰਨਾ ਚਾਹੀਦਾ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਬਾਗਾਂ ਵਿਚ ਖਾਦਾਂ ਦੀ ਵਰਤੋਂ ਬਾਰੇ ਇੱਕ ਪੈਰਾ ਲਿਖੋ ।
ਉੱਤਰ-
ਜਦੋਂ ਫ਼ਲਦਾਰ ਪੌਦੇ ਲਾਉਣ ਲਈ ਟੋਇਆ ਪੁੱਟਿਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਇਸ ਦੀ ਉੱਪਰਲੀ ਅੱਧੀ ਮਿੱਟੀ ਵਿੱਚ ਬਰਾਬਰ ਰੂੜੀ ਖਾਦ ਮਿਲਾਈ ਜਾਂਦੀ ਹੈ ।
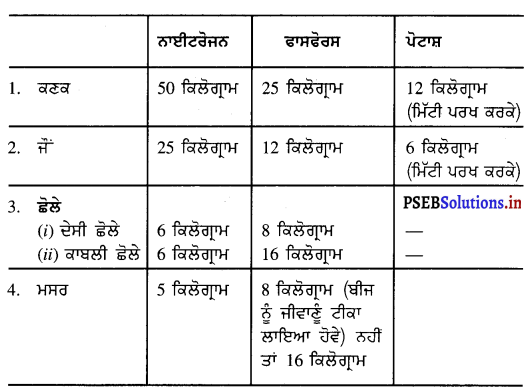
ਇਸ ਤੋਂ ਬਾਅਦ ਪੌਦੇ ਲਗਾਉਣ ਤੋਂ ਬਾਅਦ ਫ਼ਰਵਰੀ ਤੋਂ ਅਪਰੈਲ ਮਹੀਨੇ ਵਿਚ ਬੁਟਿਆਂ ਦਾ ਵਾਧਾ ਹੁੰਦਾ ਹੈ । ਵਾਧੇ ਪਏ ਬੂਟਿਆਂ ਨੂੰ ਸਾਰੇ ਤੱਤ ਮਿਲਣੇ ਚਾਹੀਦੇ ਹਨ । ਇਸ ਲਈ ਦੇਸੀ ਖਾਦ , ਜਿਵੇਂ ਗਲੀ-ਸੜੀ ਰੂੜੀ ਦੀ ਖਾਦ ਨੂੰ ਫੁਟਾਰਾ ਆਉਣ ਤੋਂ 2-3 ਮਹੀਨੇ ਪਹਿਲਾਂ ਪਾਉਣਾ ਚਾਹੀਦਾ ਹੈ । ਗਲੀ-ਸੜੀ ਰੂੜੀ ਨੂੰ ਆਮ ਕਰਕੇ ਦਸੰਬਰ ਮਹੀਨੇ ਵਿਚ ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਨਾਈਟਰੋਜਨ ਤੱਤ ਬੂਟਿਆਂ ਨੂੰ ਦੋ ਭਾਗਾਂ ਵਿੱਚ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਇੱਕ ਫੁਟਾਰਾ ਪੈਣ ਤੇ ਅਤੇ ਇੱਕ ਫ਼ਲ ਲੱਗਣ ਤੋਂ ਬਾਅਦ 1 ਫਾਸਫੋਰਸ ਖਾਦ ਨਾਈਟਰੋਜਨ ਖਾਦ ਦੇ ਪਹਿਲੇ ਭਾਗ ਨਾਲ ਪਾਉਣੀ ਚਾਹੀਦੀ ਹੈ । ਪੋਟਾਸ਼ ਖਾਦ ਨੂੰ ਫ਼ਲ ਪੱਕਣ ਤੋਂ ਪਹਿਲਾਂ ਪਾਉਣਾ ਚਾਹੀਦਾ ਹੈ ਤਾਂ ਕਿ ਫ਼ਲ ਦੀ ਗੁਣਵੱਤਾ ਵਧੀਆ ਰਹੇ । ਮੁੱਖ ਤੱਤ ਵਾਲੀਆਂ ਖਾਦਾਂ ਨੂੰ ਛੱਟਾ ਦੇ ਕੇ ਪਾਇਆ ਜਾਂਦਾ ਹੈ । ਛੋਟੇ ਤੱਤਾਂ ਵਾਲੀਆਂ ਖਾਦਾਂ ; ਜਿਵੇਂ ਜ਼ਿਮਕ, ਲੋਹਾ, ਮੈਗਨੀਜ਼ ਆਦਿ ਦੀ ਵਰਤੋਂ ਇਹਨਾਂ ਦੀ ਘਾਟ ਹੋਣ ਤੇ ਹੀ ਕਰਨੀ ਚਾਹੀਦੀ ਹੈ ।
PSEB 10th Class Agriculture Guide ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਦੀ ਕਾਸ਼ਤ Important Questions and Answers
ਬਹੁਤ ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਫ਼ਲਾਂ ਵਿੱਚ ਕਿਹੜੇ ਤੱਤ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਫ਼ਲਾਂ ਵਿੱਚ ਪ੍ਰੋਟੀਨ, ਖਣਿਜ, ਵਿਟਾਮਿਨਜ਼ ਆਦਿ ਹੁੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 2.
ਪੰਜਾਬ ਨੂੰ ਜਲਵਾਯੂ ਦੇ ਆਧਾਰ ਤੇ ਕਿੰਨੇ ਇਲਾਕਿਆਂ ਵਿਚ ਵੰਡਿਆ ਗਿਆ ਹੈ ?
ਉੱਤਰ-
ਤਿੰਨ ।
ਪ੍ਰਸ਼ਨ 3.
ਬਾਗ਼ ਲਗਾਉਣ ਦੇ ਸਮੇਂ ਅਨੁਸਾਰ ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਨੂੰ ਕਿੰਨੀਆਂ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ਵੰਡਿਆ ਹੈ ?
ਉੱਤਰ-
ਦੋ ਸ਼੍ਰੇਣੀਆਂ ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 4.
ਸਦਾਬਹਾਰ ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਦੀ ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਅੰਬ, ਲੀਚੀ, ਨਿੰਬੂ, ਕਿੰਨੂ, ਚੀਕੂ ਆਦਿ ।
![]()
ਪ੍ਰਸ਼ਨ 5.
ਪੱਤਝੜੀ ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਦੀ ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਨਾਸ਼ਪਾਤੀ, ਅੰਗੂਰ, ਆੜੂ, ਅਲੂਚਾ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 6.
ਸਦਾਬਹਾਰ ਫ਼ਲਦਾਰ ਬੂਟੇ ਲਗਾਉਣ ਦਾ ਸਹੀ ਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਫ਼ਰਵਰੀ-ਮਾਰਚ, ਸਤੰਬਰ-ਅਕਤੂਬਰ ਦਾ ਮਹੀਨਾ ।
ਪ੍ਰਸ਼ਨ 7.
ਅੰਬ ਅਤੇ ਲੀਚੀ ਦੇ ਬਾਗ਼ ਕਦੋਂ ਲਗਾਉਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਸਤੰਬਰ-ਅਕਤੂਬਰ ਵਿੱਚ ।
ਪ੍ਰਸ਼ਨ 8.
ਪੱਤਝੜੀ ਫ਼ਲਦਾਰ ਬੂਟੇ ਕਦੋਂ ਲਗਾਉਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਸਰਦੀਆਂ ਵਿੱਚ ਜਦੋਂ ਇਹ ਸਥਿੱਲ ਅਵਸਥਾ ਵਿੱਚ ਹੁੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 9.
ਆੜੂ, ਅਲੂਚਾ ਦੇ ਬੂਟੇ ਕਦੋਂ ਲਗਾਉਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਅੱਧ ਜਨਵਰੀ ।
ਪ੍ਰਸ਼ਨ 10.
ਨਾਸ਼ਪਾਤੀ, ਅੰਗੂਰ ਦੇ ਬੂਟੇ ਕਦੋਂ ਲਗਾਉਣੇ ਚਾਹੀਦੇ ਹਨ ?
ਉੱਤਰ-
ਅੱਧ ਫ਼ਰਵਰੀ ।
![]()
ਪ੍ਰਸ਼ਨ 11.
ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਦੀ ਕਾਸ਼ਤ ਲਈ ਪਾਣੀ ਦਾ ਪੱਧਰ ਕਿਹੋ ਜਿਹਾ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ?
ਉੱਤਰ-
ਪਾਣੀ ਦਾ ਪੱਧਰ ਤਿੰਨ ਮੀਟਰ ਤੋਂ ਹੇਠਾਂ ਹੋਣਾ ਚਾਹੀਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 12.
ਸੰਤਰੇ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਕਿਨੁ, ਦੇਸੀ, ਡੇਜ਼ੀ, ਡਬਲਿਯੂ ਮਰਕਟ ।
ਪ੍ਰਸ਼ਨ 13.
ਮਾਲਵੇ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਮੁਸੰਮੀ, ਜਾਫ਼ਾ, ਬਲੱਡ ਪ੍ਰੈੱਡ, ਵਲੈਨਸੀਆ ।
ਪ੍ਰਸ਼ਨ 14.
ਨਿੰਬੂ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਕਾਗ਼ਜ਼ੀ, ਬਾਰਾਮਾਸੀ ਨਿੰਬੂ, ਗਲਗਲ ।
ਪ੍ਰਸ਼ਨ 15.
ਅੰਬ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਦੁਸਹਿਰੀ, ਲੰਗੜਾ, ਅਲਫੌਂਜੋ ।
ਪ੍ਰਸ਼ਨ 16.
ਨਾਸ਼ਪਾਤੀ ਦੀਆਂ ਦੋ ਉੱਨਤ ਕਿਸਮਾਂ ਦੇ ਨਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਪੰਜਾਬ ਨਾਖ, ਪੱਥਰ ਨਾਖ (ਸਖ਼ਤ), ਪੰਜਾਬ ਨੈਕਟਰ, ਪੰਜਾਬ ਗੋਲਡ, ਬੱਗੂਗੋਸ਼ਾ ਅਤੇ ਲਿਕੋਟ ਆਦਿ ।
![]()
ਪ੍ਰਸ਼ਨ 17.
ਆਤੂ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਅਰਲੀ ਰੈੱਡ, ਸ਼ਾਨੇ ਪੰਜਾਬ, ਪਰਭਾਤ ।
ਪ੍ਰਸ਼ਨ 18.
ਅਲੂਚੇ ਦੀਆਂ ਕਿਸਮਾਂ ਲਿਖੋ ।
ਉੱਤਰ-
ਸਤਲੁਜ ਪਰਪਲ, ਕਾਲਾ ਅੰਮ੍ਰਿਤਸਰੀ ।
ਪ੍ਰਸ਼ਨ 19.
ਅਮਰੂਦ ਦੀਆਂ ਉੱਨਤ ਕਿਸਮਾਂ ਦੇ ਨਾਮ ਲਿਖੋ ।
ਉੱਤਰ-
ਸਰਦਾਰ, ਅਲਾਹਾਬਾਦ, ਸਫ਼ੈਦਾ, ਅਰਕਾ ਅਮੁਲਿਆ, ਪੰਜਾਬ ਪਿੰਕ ।
ਪ੍ਰਸ਼ਨ 20.
ਅੰਗੂਰ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਪਰਲਿਟ, ਬਿਊਟੀ ਸੀਡਲੈਸ, ਫਲੇਮ ਸੀਡਲੈਸ, ਪੰਜਾਬ ਪਰਪਲ, ਸ਼ਵੇਤਾ ।
ਪ੍ਰਸ਼ਨ 21.
ਬੇਰ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਉਮਰਾਨ, ਸਨੌਰ-2, ਵਲੈਤੀ ।
![]()
ਪ੍ਰਸ਼ਨ 22.
ਲੀਚੀ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਦੇਹਰਾਦੂਨ, ਕਲਕੱਤੀਆ ।
ਪ੍ਰਸ਼ਨ 23.
ਚੀਕੂ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਕਾਲੀ ਪੱਤੀ, ਕ੍ਰਿਕਟ ਬਾਲ ।
ਪ੍ਰਸ਼ਨ 24.
ਅਨਾਰ ਦੀਆਂ ਕਿਸਮਾਂ ਦੱਸੋ ।
ਉੱਤਰ-
ਭਗਵਾ, ਗਨੇਸ਼, ਕੰਧਾਰੀ ।
ਪ੍ਰਸ਼ਨ 25.
ਬਾਗ਼ ਲਾਉਣ ਦੇ ਛੇ ਕੋਨਾ ਢੰਗ ਨਾਲ ਕਿੰਨੇ ਬੂਟੇ ਵੱਧ ਲੱਗ ਜਾਂਦੇ ਹਨ ?
ਉੱਤਰ-
15-20%.
ਪ੍ਰਸ਼ਨ 26.
ਨਰਸਰੀ ਤੋਂ ਲਏ ਬੂਟਿਆਂ ਦੀ ਉੱਚਾਈ ਬਾਰੇ ਦੱਸੋ ।
ਉੱਤਰ-
ਬੂਟੇ ਦਰਮਿਆਨੀ ਉਚਾਈ ਦੇ ਹੋਣੇ ਚਾਹੀਦੇ ਹਨ ।
![]()
ਪ੍ਰਸ਼ਨ 27.
ਬਾਗ਼ ਵਿਚ ਮੁੱਖ ਤੱਤ ਵਾਲੀਆਂ ਖਾਦਾਂ ਕਿਸ ਵਿਧੀ ਨਾਲ ਪਾਈਆਂ ਜਾਂਦੀਆਂ
ਹਨ ?
ਉੱਤਰ-
ਛੱਟਾ ਵਿਧੀ ਨਾਲ ।
ਪ੍ਰਸ਼ਨ 28.
ਫ਼ਲ ਨੂੰ ਟਹਿਣੀ ਨਾਲੋਂ ਖਿੱਚ ਕੇ ਕਿਉਂ ਨਹੀਂ ਤੋੜਨਾ ਚਾਹੀਦਾ ?
ਉੱਤਰ-
ਫ਼ਲ ਦੀ ਛਿੱਲ ਲਹਿ ਸਕਦੀ ਹੈ ਤੇ ਟਹਿਣੀ ਟੁੱਟ ਸਕਦੀ ਹੈ ।
ਛੋਟੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਪੰਜਾਬ ਨੂੰ ਜਲਵਾਯੂ ਦੇ ਆਧਾਰ ਤੇ ਕਿੰਨੇ ਇਲਾਕਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਹੈ ਤੇ ਕਿਹੜੇ ?
ਉੱਤਰ-
ਪੰਜਾਬ ਨੂੰ ਜਲਵਾਯੂ ਦੇ ਆਧਾਰ ‘ਤੇ ਤਿੰਨ ਇਲਾਕਿਆਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਹੈ ਜੋ ਹਨ-
- ਨੀਮ ਪਹਾੜੀ ਇਲਾਕੇ
- ਕੇਂਦਰੀ ਇਲਾਕਾ ।
- ਸੇਂਜੂ ਅਤੇ ਖ਼ੁਸ਼ਕ ਇਲਾਕਾ ।
ਪ੍ਰਸ਼ਨ 2.
ਨੀਮ ਪਹਾੜੀ ਇਲਾਕੇ ਵਿੱਚ ਕਿਹੜੇ ਜ਼ਿਲ੍ਹੇ ਹਨ ?
ਉੱਤਰ-
ਰੂਪਨਗਰ, ਹੁਸ਼ਿਆਰਪੁਰ, ਪਠਾਨਕੋਟ, ਸਾਹਿਬਜ਼ਾਦਾ ਅਜੀਤ ਸਿੰਘ ਨਗਰ, ਸ਼ਹੀਦ ਭਗਤ ਸਿੰਘ ਨਗਰ, ਕੇਂਦਰੀ ਸ਼ਾਸ਼ਤ ਪ੍ਰਦੇਸ਼ ਚੰਡੀਗੜ੍ਹ ।
ਪ੍ਰਸ਼ਨ 3.
ਨੀਮ ਪਹਾੜੀ ਇਲਾਕੇ ਵਿੱਚ ਕਿਹੜੇ ਮੁੱਖ ਫ਼ਲਾਂ ਦੀ ਕਾਸ਼ਤ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਅੰਬ, ਨਿੰਬੂ, ਨਾਸ਼ਪਾਤੀ, ਕਿੰਨੂ, ਸੰਗਤਰੇ, ਲੀਚੀ, ਆੜੂ, ਅਲੂਚਾ, ਚੀਕੂ, ਆਮਲਾ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 4.
ਕੇਂਦਰੀ ਇਲਾਕੇ ਵਿੱਚ ਕਿਹੜੇ ਜ਼ਿਲ੍ਹੇ ਹਨ ?
ਉੱਤਰ-
ਅੰਮ੍ਰਿਤਸਰ, ਤਰਨਤਾਰਨ, ਕਪੂਰਥਲਾ, ਬਰਨਾਲਾ, ਪਟਿਆਲਾ, ਜਲੰਧਰ, ਸੰਗਰੂਰ, ਲੁਧਿਆਣਾ, ਮੋਗਾ, ਫਤਹਿਗੜ੍ਹ ਸਾਹਿਬ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 5.
ਕੇਂਦਰੀ ਇਲਾਕੇ ਵਿੱਚ ਕਿਹੜੇ ਫ਼ਲਾਂ ਦੀ ਕਾਸ਼ਤ ਕੀਤੀ ਜਾਂਦੀ ਹੈ ?
ਉੱਤਰ-
ਨਾਸ਼ਪਾਤੀ, ਅਮਰੂਦ, ਆੜੂ, ਅੰਬ, ਕਿੰਨੂ, ਸੰਗਤਰੇ, ਨਿੰਬੂ, ਅੰਗੂਰ ਆਦਿ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਸੇਂਜੂ ਤੇ ਖ਼ੁਸ਼ਕ ਇਲਾਕੇ ਵਿੱਚ ਕਿਹੜੇ ਜ਼ਿਲ੍ਹੇ ਹਨ ?
ਉੱਤਰ-
ਬਠਿੰਡਾ, ਮਾਨਸਾ, ਸ੍ਰੀ ਮੁਕਤਸਰ ਸਾਹਿਬ, ਫਰੀਦਕੋਟ, ਫ਼ਿਰੋਜ਼ਪੁਰ, ਫਾਜ਼ਿਲਕਾ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 7.
ਸੇਂਜੂ ਅਤੇ ਖ਼ੁਸ਼ਕ ਇਲਾਕਿਆਂ ਦੇ ਫ਼ਲ ਦੱਸੋ 1
ਉੱਤਰ-
ਕਿੰਨੂ ਤੇ ਹੋਰ ਸੰਗਤਰੇ, ਨਿੰਬੂ, ਅੰਗੂਰ, ਬੇਰ, ਅਮਰੂਦ ਆਦਿ ।
ਪ੍ਰਸ਼ਨ 8.
ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਦੀ ਕਾਸ਼ਤ ਲਈ ਮਿੱਟੀ ਕਿਹੋ ਜਿਹੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ ?
ਉੱਤਰ-
ਫ਼ਲਦਾਰ ਬੂਟੇ ਲਗਾਉਣ ਲਈ ਚੰਗੇ ਜਲ ਨਿਕਾਸ ਵਾਲੀ, ਡੂੰਘੀ, ਭਲ ਵਾਲੀ ਤੇ ਉਪਜਾਊ ਮਿੱਟੀ ਹੋਣੀ ਚਾਹੀਦੀ ਹੈ । ਜ਼ਮੀਨ ਦੀ ਦੋ ਮੀਟਰ ਤੱਕ ਦੀ ਡੂੰਘਾਈ ਤੇ ਕੋਈ ਸਖ਼ਤ ਤਹਿ ਨਹੀਂ ਹੋਣੀ ਚਾਹੀਦੀ ।
ਪ੍ਰਸ਼ਨ 9.
ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਲਈ ਕਿਹੋ ਜਿਹੀ ਮਿੱਟੀ ਠੀਕ ਨਹੀਂ ਰਹਿੰਦੀ ?
ਉੱਤਰ-
ਫ਼ਲਦਾਰ ਬੂਟੇ ਸੇਮ ਵਾਲੀਆਂ, ਤੇਜ਼ਾਬੀ ਅਤੇ ਲੁਣੀਆਂ ਜ਼ਮੀਨਾਂ ਵਿੱਚ ਨਹੀਂ ਲਗਾਉਣੇ ਚਾਹੀਦੇ ।
ਪ੍ਰਸ਼ਨ 10.
ਕਿਹੜੇ ਫ਼ਲ ਤੋੜਣ ਤੋਂ ਬਾਅਦ ਵੱਧ ਪੱਕ ਸਕਦੇ ਹਨ ਤੇ ਕਿਹੜੇ ਨਹੀਂ ? ਉਦਾਹਰਨ ਦਿਓ ।
ਉੱਤਰ-
ਕੇਲਾ, ਅੰਬ, ਅਲੂਚਾ ਆਦਿ ਤੋੜਨ ਤੋਂ ਬਾਅਦ ਵੱਧ ਪੱਕ ਸਕਦੇ ਹਨ ਪਰ ਅੰਗੂਰ, ਲੀਚੀ ਆਦਿ ਤੋੜਨ ਤੋਂ ਬਾਅਦ ਪੱਕ ਨਹੀਂ ਸਕਦੇ ।
![]()
ਵੱਡੇ ਉੱਤਰਾਂ ਵਾਲੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਫ਼ਲਦਾਰ ਬੂਟਿਆਂ ਦੀ ਸਿੰਚਾਈ ਅਤੇ ਖਾਦਾਂ ਦਾ ਵੇਰਵਾ ਦਿਓ ।
ਉੱਤਰ-
ਦੇਖੋ ਉਪਰੋਕਤ ਪ੍ਰਸ਼ਨਾਂ ਵਿਚ (ਖਾਦਾਂ ਲਈ) ।
ਸਿੰਚਾਈ-ਛੋਟੇ ਬੂਟਿਆਂ ਨੂੰ 3-4 ਸਾਲ ਤੱਕ ਮਾਰਚ ਤੋਂ ਜੂਨ ਤੱਕ ਹਫ਼ਤੇ-ਹਫ਼ਤੇ ਮਗਰੋਂ, ਨਵੰਬਰ ਤੋਂ ਫ਼ਰਵਰੀ ਤੱਕ 2-3 ਹਫ਼ਤਿਆਂ ਬਾਅਦ ਅਤੇ ਜੁਲਾਈ ਤੋਂ ਨਵੰਬਰ ਤੱਕ ਵਰਖਾ ਅਤੇ ਮਿੱਟੀ ਦੀ ਕਿਸਮ ਅਨੁਸਾਰ ਪਾਣੀ ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ।
ਬਾਗ਼ ਫ਼ਲ ਦੇਣ ਲੱਗ ਜਾਣ ਤਾਂ ਕਰੂੰਬਲਾਂ ਫੁੱਟਣ ਤੋਂ ਪਹਿਲਾਂ, ਫ਼ਲ ਪੈਣ ਤੇ ਅਤੇ ਵਧੇਰੇ ਗਰਮੀ ਵਿਚ ਪਾਣੀ ਦੇਣਾ ਬਹੁਤ ਜ਼ਰੂਰੀ ਹੋ ਜਾਂਦਾ ਹੈ । ਗਰਮੀਆਂ ਵਿਚ ਪਾਣੀ ਦੀ ਘਾਟ ਨਾਲ ਫੁੱਲ ਦੀ ਕੋਰ ਵੱਧ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਹੇਠ ਲਿਖੇ ਫ਼ਲਾਂ ਦੀਆਂ ਉੱਨਤ ਕਿਸਮਾਂ ਦੱਸੋ । ਅੰਬ, ਆੜੂ, ਅਲੂਚਾ, ਅਮਰੂਦ, ਅੰਗੂਰ, ਆਂਵਲਾ, ਅਨਾਰ ।
ਉੱਤਰ-
ਅੰਬ – ਲੰਗੜਾ, ਅਲਫੈਂਜ਼ੋ, ਦੁਸਹਿਰੀ, ਚੁਪਣ ਵਾਲੇ ਅੰਬ ।
ਆੜੂ – ਪਰਤਾਪ, ਸ਼ਾਨੇ ਪੰਜਾਬ, ਫਲੋਰਿਡਾ ਪਰਿੰਸ, ਅਰਲੀ ਰੈੱਡ, ਪਰਭਾਤ ।
ਅਲੂਚਾ – ਕਾਲਾ ਅੰਮ੍ਰਿਤਸਰੀ, ਸਤਲੁਜ ਪਰਪਲੇ ।
ਅਮਰੂਦ – ਅਰਕਾ ਅਮੁਲਿਆ, ਸਫੈਦਾ, ਪੰਜਾਬ ਪਿੰਕ, ਅਲਾਹਾਬਾਦ, ਸਰਦਾਰ ।
ਅੰਗੂਰ – ਬਿਉਟੀ ਸੀਡਲੈਸ, ਪੰਜਾਬ ਪਰਪਲ, ਫਲੇਮ ਸੀਡਲੈਸ, ਪਲਿਟ, ਸ਼ਵੇਤਾ ।
ਆਂਵਲਾ – ਨੀਲਮ, ਕੰਚਨ, ਬਲਵੰਤ ।
ਅਨਾਰ – ਕੰਧਾਰੀ, ਗਨੇਸ਼, ਭਗਵਾ ।
ਬਹੁ-ਵਿਕਲਪੀ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਫ਼ਲਾਂ ਵਿਚ ਹੇਠਲੇ ਖ਼ੁਰਾਕੀ ਤੱਤ ਹੁੰਦੇ ਹਨ-
(ਉ) ਵਿਟਾਮਿਨ
(ਅ) ਖਣਿਜ
(ੲ) ਪ੍ਰੋਟੀਨ
(ਸ) ਸਾਰੇ ।
ਉੱਤਰ-
(ਸ) ਸਾਰੇ ।
ਪ੍ਰਸ਼ਨ 2.
ਸਦਾਬਹਾਰ ਫ਼ਲਦਾਰ ਬੂਟੇ ਕਦੋਂ ਲਾਉਣੇ ਚਾਹੀਦੇ ਹਨ ?
(ਉ) ਫ਼ਰਵਰੀ-ਮਾਰਚ
(ਅ) ਸਤੰਬਰ-ਅਕਤੂਬਰ
(ੲ) ਦੋਨੋਂ ਠੀਕ
(ਸ) ਕੋਈ ਨਹੀਂ ।
ਉੱਤਰ-
(ੲ) ਦੋਨੋਂ ਠੀਕ
ਪ੍ਰਸ਼ਨ 3.
ਬਾਗ਼ ਲਾਉਣ ਦੇ ਢੰਗ ਹਨ-
(ਉ) ਵਰਗਾਕਾਰ
(ਅ) ਛਿੱਲਰ ਢੰਗ
(ੲ) ਛੇ ਕੋਨਾ ਢੰਗ
(ਸ) ਸਾਰੇ ।
ਉੱਤਰ-
(ਸ) ਸਾਰੇ ।
![]()
ਪ੍ਰਸ਼ਨ 4.
ਸਦਾਬਹਾਰ ਫ਼ਲਦਾਰ ਬੂਟਾ ਨਹੀਂ ਹੈ-
(ਉ) ਨਾਸ਼ਪਾਤੀ
(ਅ) ਲੁਕਾਠ
(ੲ) ਅੰਬ
(ਸ) ਲੀਚੀ ।
ਉੱਤਰ-
(ਉ) ਨਾਸ਼ਪਾਤੀ
ਪ੍ਰਸ਼ਨ 5.
ਪੱਤਝੜੀ ਫ਼ਲਦਾਰ ਬੂਟੇ ਹਨ-
(ਉ) ਅੰਗੂਰ
(ਅ) ਆੜੂ
(ੲ) ਅਲੂਚਾ
(ਸ) ਸਾਰੇ ।
ਉੱਤਰ-
(ਸ) ਸਾਰੇ ।
ਪ੍ਰਸ਼ਨ 6.
ਸਦਾਬਹਾਰ ਫ਼ਲਦਾਰ ਬੂਟੇ ਹਨ-
(ਉ) ਅੰਬ
(ਅ) ਲੀਚੀ
(ੲ) ਨਿੰਬੂ
(ਸ) ਸਾਰੇ ।
ਉੱਤਰ-
(ਸ) ਸਾਰੇ ।
ਪ੍ਰਸ਼ਨ 7.
ਪੱਤਝੜੀ ਫ਼ਲਦਾਰ ਬੂਟੇ ਕਿਹੜੇ ਮਹੀਨੇ ਵਿਚ ਲਗਾਏ ਜਾਂਦੇ ਹਨ ?
(ਉ) ਅਪ੍ਰੈਲ-ਮਈ
(ਅ) ਜਨਵਰੀ-ਫ਼ਰਵਰੀ
(ੲ) ਜੂਨ-ਜੁਲਾਈ
(ਸ) ਮਈ-ਜੂਨ ।
ਉੱਤਰ-
(ਅ) ਜਨਵਰੀ-ਫ਼ਰਵਰੀ
ਠੀਕ/ਗਲਤ ਦੱਸ-
1. ਪਰਤਾਪ ਆੜੂ ਦੀ ਕਿਸਮ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ
![]()
2. ਕੰਚਨ ਆਂਵਲੇ ਦੀ ਉੱਨਤ ਕਿਸਮ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ
3. ਫਲਾਂ ਨੂੰ ਟਹਿਣੀਆਂ ਨਾਲੋਂ ਖਿੱਚ ਕੇ ਤੋੜਨਾ ਚਾਹੀਦਾ ਹੈ ।
ਉੱਤਰ-
ਗਲਤ
4. ਫਲਦਾਰ ਬੂਟਿਆਂ ਦਾ ਜੀਵਨ ਚੱਕਰ ਕਈ ਸਾਲਾਂ ਦਾ ਹੁੰਦਾ ਹੈ ।
ਉੱਤਰ-
ਠੀਕ
5. ਬਾਗ ਲਗਾਉਣ ਦੇ ਤਿੰਨ ਢੰਗ ਹਨ ।
ਉੱਤਰ-
ਠੀਕ
ਖਾਲੀ ਥਾਂ ਭਰੋ-
1. ……………………… ਫਲਦਾਰ ਬੂਟੇ ਅੱਧ ਜਨਵਰੀ ਤੋਂ ਅੱਧ ਫ਼ਰਵਰੀ ਵਿਚ ਲਗਾਏ ਜਾਂਦੇ ਹਨ ।
ਉੱਤਰ-
ਪੱਤਝੜੀ
2. ਡਬਲਿਉ ਮਰਕਟ …………………….. ਦੀ ਕਿਸਮ ਹੈ ।
ਉੱਤਰ-
ਸੰਤਰੇ
3. ਕ੍ਰਿਕੁਟ ਬਾਲ ……………………………….. ਦੀ ਕਿਸਮ ਹੈ ।
ਉੱਤਰ-
ਚੀਕੂ
![]()
4. ਗਨੇਸ਼ ………………………. ਦੀ ਇੱਕ ਕਿਸਮ ਹੈ ।
ਉੱਤਰ-
ਅਨਾਰ
5. ਅਰਲੀ ਗੈਂਡ ………………………. ਦੀ ਕਿਸਮ ਹੈ ।
ਉੱਤਰ-
ਆਤੂ ।