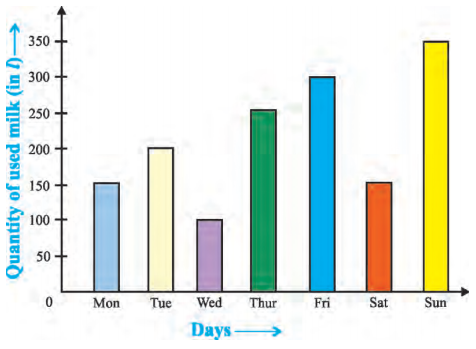
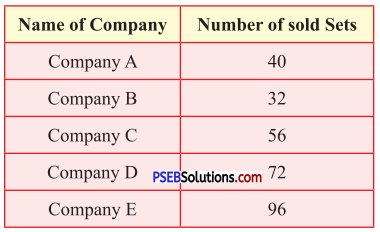
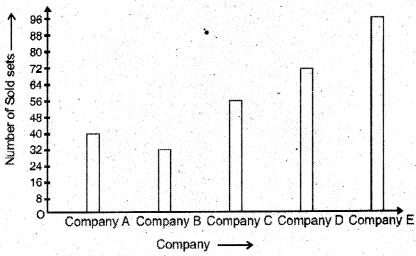
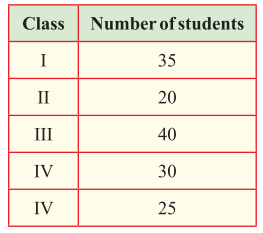
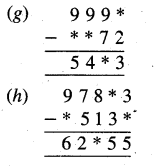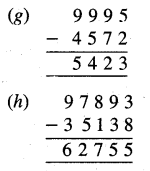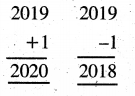Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 2 Fundamental Operations on Numbers Ex 2.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 5 Maths Chapter 2 Fundamental Operations on Numbers Ex 2.3
Think and Do :
Question 1.
(a) Find the sum of 60498,31292 and 7132.
(b) Find the difference of 70123 and 40268.
Solution:

Question 2.
27020 bricks are required for constructing a kitchen and 31275 bricks are required for constructing a room. How many bricks in total are required for construction of both ?
Solution:
No. of bricks required for the construction of a kitchen = 27020
No. of bricks required for the construction of a room = + 31275
Total no. of bricks required for the construction of the both = 58295.
![]()
Question 3.
Surjit had ₹ 20000 with him. He bought clothes costing ₹ 13750. How much amount was left with him ?
Solution:

Question 4.
In a library, there are 30155 Punjabi books, 28653 Maths books and 12376 English books. How many books are there in the library ?
Solution:

Question 5.
The sum of two numbers is 89000. If one number is 25450 then find the other number.
Solution:
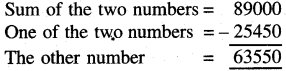
Question 6.
What number must be added to 70429 to get 100000 ?
Solution:

![]()
Question 7.
Find the number which is :
(a) 7976 more than 36798
(b) 12967 less than 30067.
Solution:

Question 8.
If the price of a computer is ₹ 15560 and price of a laptop is ₹ 9050 more than price of the computer then find :
(a) Price of the laptop
(b) Total price of both the items.
Solution:

Question 9.
Find the greatest and smallest 5 digit numbers using digits 9, 3, 4, 0, 7. Also find their difference.
Solution:

Question 10.
Find the sum of greatest 2 digits, 3 digits and 4 digits numbers.
Solution:

Question 11.
Find the difference of place values of 6 and 7 in number 96074.
Solution:
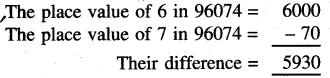
Question 12.
Subtract 45555 from 6 digit smallest number.
Solution:

![]()
Question 13.
Satnam had ₹ 8765 with him. His uncle gave him ₹ 2500. Satnam gave ₹ 4770 to his sister out of his total money. How much money was left with him ?
Solution:

Question 14.
Mandeep had 110000. He bought a pair of shoes for ₹ 1050 and a suit for ₹ 3600. How much money was left with him ?
Solution:

Question 15.
Sandeep has t 78500 in his bank account. How much more amount should he deposit in the account so that he has ? 100000 in his account ?
Solution:

Question 16.
A person travels 165 km by car from Pathankot to Kashmir. Next day, he drives 138 km from Kashmir to Leh. How much distance did he cover ?
Solution: