Bhagya

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 6 Measurement MCQ Questions and Answers.

PSEB 5th Class Maths Chapter 6 Measurement MCQ Questions

Multiple Choice Questions

Tick (✓) the right answer :

Question 1.
Convert 8 m into centimetres,
(a) 80 cm
(b) 800 cm
(c) 8000 cm
(d) 8 cm.
ans:
(b) 800 cm

Question 2.
Convert 16 kl into litres.
(a) 160 l
(b) 1600 l
(c) 16000 l
(d) 160000 l
Ans:
(c) 16000 l

Question 3.
Convert 10 da.g.into grams.
(a) 100 g
(b) 1000 g
(c) 10 g
(d) 10000 g.
Ans:
(c) 10 g

Question 4.
How many kg are there in 1000 g?
(a) 100 kg
(b) 10 kg
(c) 20 kg
(d) 1 kg.
Ans:
(d) 1 kg.

Question 5.
Decimal formation of 3 l 175 ml.
(a) 31.75 l
(b) 317.5 l
(c) 3.175 l
(d) 0.3175 l
ans:
(c) 3.175 l

Question 6.
3.5 km = …………… m
(a) 350 m
(b) 3500 m
(c) 35 m
(d) 0.350 m.
Ans:
(b) 3500 m

Question 7.
Which unit is used by a shopkeeper to weigh vegetables ?
(a) litre and kl
(b) metre and km
(c) gram and kg
(d) none.
Ans:
(c) gram and kg

Question 8.
Which unit is used to measure liquids ?
(a) litre
(b) kilometre
(c) metre
(d) none.
Ans:
(a) litre

Question 9.
Kanwal bought 6 kg potatoes, 3 kg 500 g onions and 500 g tomatoes from the market How many kg of vegetables had he bought ?
(a) 10 kg
(b) 6 kg
(c) 3 kg
(d) 11 kg.
ans:
(a) 10 kg

Question 10.
Harpreet has bought 10 m cloth, he uses 6 m 50 cm cloth for her suit. How much cloth is left ?
(a) 2 m 50 cm
(b) 4 m
(c) 4 m 50 cm
(d) 3 m 50 cm.
ans:
(d) 3 m 50 cm

Question 11.
How many metre are in one milimetre ?
(a) \(\frac{1}{100}\)
(b) \(\frac{1}{1000}\)
(c) \(\frac{1}{10}\)
(d) 100.
Ans:
(b) \(\frac{1}{1000}\)

Question 12.
How many centimetres are in one hectometres ?
(a) 1000
(b) 10,000
(c) 100
(d) \(\frac{1}{1000}\)
Ans:
(b) 10,000

Question 13.
How many hectogram are in one kilogram ?
(a) 100
(b) \(\frac{1}{100}\)
(c) 10
(d) \(\frac{1}{10}\)
Ans.
(c) 10

Question 14.
How many decalitres are in one kilolitre ?
(a) 1000
(b) 500
(c) 200
(d) 100
Ans.
(d) 100

Question 15.
How many mililitres are in one decilitre ?
(a) 10
(b) 100000
(c) 100
(d) 1000
Ans:
(c) 100

Question 16.
How many days are in a leap year ?
(a) 364
(b) 366
(c) 365
(d) 363
Ans:
(b) 366

Question 17.
How many days are there in the month of February in a leap year ?
(a) 28
(b) 30
(c) 29
(d) 31.
Ans:
(c) 29

Question 18.
Write 3:10 pm according to 24 hour clock ?
(a) 23:10
(b) 25:10
(c) 15:10
(d) 13:10.
Ans:
(c) 15:10

Question 19.
Write 22:25 according to 12 hour clock.
(a) 10:25 PM
(b) 12:25 AM
(c) 12:25 PM
(d) 9: 25 PM.
Ans:
(a) 10:25 PM

Question 20.
How many seconds make one hour ?
(a) 60
(b) 3600
(c) 360
(d) 300.
Ans:
(b) 3600

Question 21.
The distance of your village dispensary from your school is 2 km, village community hall 955 m and distance of guruduara is 1500 m. Which of these is at a maximum distance from your school ?
(a) Dispensary
(b) Community centre
(c) Guruduara
(d) All are at equal distances.
Ans:
(a) Dispensary

Question 22.
See Carefully and tell :


(a) less than 500 ml
(b) In-between 500 ml and 1 litre
(c) In between 1 l and 2 l
(d) More than 2 l
Ans:
(c) In between 1 l and 2 l

Question 23.
How many metres are there in 3.5 kilometres ?
Ans:
3.5 kilometres = 3.5 × 1000 metre
= 3500 metre.

Question 24.
How many seconds are there in a day ?
Ans:
1 day = 24 hours = 24 × 60 minutes
= 24 × 60 × 60 seconds = 86400 seconds.

Question 25.
The map of a village which is at a distance from a city is given. Simran is moving in the village on his cycle.

Find the distance covered by Simran :
(a) From D to A (passing through B)
(b) From A to D (passing through B and C)
Ans:
(a) Distance covered by Simran from D to A (passing through B) = DB + BA.
= 1335 m + 1580 m
= 2915 m

(b) Distance covered by Simran from A to D (passing through B and C)
= AB + BC + CD
= 1580m + 1200m + 1315 m
= 4095m

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 6 Measurement Ex 6.7 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 6 Measurement Ex 6.7

1. Find the difference :

Question 1.
8 hours 30 min and 2 hours 10 min
Solution:

Question 2.
10 hours 30 min 20 sec and 8 hours 20 min 15 sec
Solution:

Question 3.
11 years 5 months and 6 years
Solution:

Question 4.
7 years 2 months and 3 years
Solution:

Note, ∵ 1 year = 12 months
∴ 12 months + 2 months = 14 months

2. Find the Time :

Question 1.
4 hours before 5:30 pm
Solution:
4 hours before 5:30 pm
4 hours = 30 minutes + 3 hours + 30 minutes
30 minutres before 5:30 pm = 5.00 pm
3 hours before 5:00 pm = 2:00 pm
30 minutes before 2:00 pm = 1:30 pm

Question 2.
2 hours after 11:00 am
Solution:
2 hours after 11:00 am
1 hour after 11:00 am = 12:00 noon
1 hour after 12:00 noon =1:00 pm
Second method :
2 hours after 11:00 am

i.e. 12:00 +1:00
= 1:00 pm

Question 3.
6 hours before 4:30 am
Solution:
6 hours before 4:30 am
6 hours = 30 minutes + 4 hours + 1 hour + 30 minutes
30 minutes before 4:30 am = 4:00 am
4 hours before 4:00 am = 12:00 mid night
1 hour before 12:00 mid night = 11:00 pm

Question 4.
1 hour 45 min after 8:30 am
Solution:
1 hour 45 min after 8:30 am
1 hour 45 minutes = 30 minutes + 1 hour + 15 minutes
30 minutes after 8:30 am = 9:00 am
1 hour after 9:00 am = 10: 00 am
15 minutes after 10:00 am = 10:15 am

3. Find the Time Gap :

Question 1.
From 3:00 am to 10:00 am
Solution:
Time gap from 3:00 am to 10:00 am = 7 hour

Question 2.
From 6:00 am to 1:30 pm
Solution:
Time gap from 6:00 am to 1:30 pm
Time gap between 6:00 am to 12:00 noon = 6 hours
Time gap from 12:00 noon to 1:00 pm = 1 hour
Time gap from 1:00 pm to 1:30 pm = 30 minutes
Hence, time gap from 6:00 am to 1:30 pm = 7 hours 30 minutes

Second Method :
1:30 pm = 1:30 + 12:00 = 13:30 o’clock
Time gap from 6:00 am to 1:30 pm

Question 3.
From 5:00 am to 10:45 pm
Solution:
Time gap from 5:00 pm to 10:45 pm
Time gap from 5:00 pm to 10:00 pm = 5 hours
Time gap from 10:00 pm to 10:45 pm = 45 minutes
Hence, time gap from 5:00 to 10:45 pm = 5 hours 45 minutes

Question 4.
From 9:00 am to 2:30 am (next morning)
Solution:
Time gap from 9:00 pm to 2:30 am (next morning)
Time gap from 9:00 pm to 12:00 mid night = 3 hours
Time gap from 12:00 mid night to 2:00 am = 2 hours
Time gap from 2:00 am to 2:30 am = 30 minutes
Hence, time gap from 9:00 pm to 2:30 am (next morning) = 5 hours 30 minutes

Question 4.
A bank opens at 9:30 am and closes at 5:00 pm. How many working hours are there ?
Solution:
Time gap from 9:30 am to 10:00 am
= 30 minutes Time gap from 10:00 am to 12:00 noon = 2 hours
Time gap from 12:00 noon to 5:00 pm = 5 hours
Hence, time gap from 9:00 am to 5:00 pm = 7 hours 30 minutes
Therefore, working hours of the bank = 7 hours 30 minutes

Question 5.
A bus starts from Chandigarh at 7:30 am and reaches Shimla at 10:50 am. How much time is taken by the bus to reach Shimla ?
Solution:
Time gap from 7:30 am to 8:00 am = 30 minutes
Time gap from 8:00 am to 10:00 am = 2 hours
Time gap from 10:00 am to 10:50 am = 50 minutes
Time gap from 7:30 am to 10:50 am
= 30 minutes + 2 hours + 50 minutes
= 2 hours + 80 minutes
= 2 hours + 60 minutes + 20 minutes
= 2 hours + 1 hour + 20 minutes
= 3 hours 20 minutes
Therefore, time taken by the bus to reach Shimla = 3 hours 20 minutes

Second Method :
The time at which the bus reaches Shimla = 10:50 am
The time at which the bus starts from Chandigarh = 7:30 am
= 3:20 hours
The time taken by bus to reach Shimla = 3 hours 20 min.

Question 6.
A boy goes to school at 7:30 am and returns back from school at 2:45 pm. How much time does he spend in the school ?
Solution:
The time when the boy goes to school = 7:30 am
The time when the boy returns back = 2.45 am
The time gap from 7:30 am to 8:00 am = 30 minutes
The time gap from 8:00 am to 12:00 noon = 4 hours
The time gap from 12:00 noon to 2:00 pm = 2 hours
The time gap from 2:00 pm to 2:45 pm = 45 minutes
Total time
= 30 minutes + 6 hours + 45 minutes
= 6 hours + 75 minutes = 6 hours + 60 minutes + 15 minutes
= 6 hours + 1 hour + 15 minutes
= 7 hours 15 minutes
Therefore, time spent in the school = 7 hours 15 minutes

Second Method :
2:45 pm = 2:45 + 12:00 = 14:45 o’clock
The time when the boy returns back = 14:45 o’clock
The time when the boy goes to school = 7:30 o’clock
The time spent in the school by boy

= 7 hours 15 minutes

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 4 Fractions Ex 4.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 4 Fractions Ex 4.1

Question 1.
Out of the following group of stars:

(a) Write the fraction of coloured stars. ____
Solution:
\(\frac{4}{9}\)

(b) Write fraction of stars without colour. ____
Solution:
\(\frac{5}{9}\)

Question 2.
In the following diagram

(a) Write fraction of coloured ice creams ____
Solution:
\(\frac{2}{5}\)

(b) Write fraction of ice creams without colour
Solution:
\(\frac{3}{5}\)

Question 3.
In the following diagram:

(a) Write fraction of coloured balls. ____
Solution:
\(\frac{6}{11}\)

(b) Write fraction of balls without colour.
Solution:
\(\frac{5}{11}\)

Question 4.
There are 12 balls in each of the following box. Colour the balls according to given fraction in the box and write number of coloured balls in blank box :

Solution:

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 6 Measurement Ex 6.6 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 6 Measurement Ex 6.6

1. Addition :

Question 1.
2 hours 10 min and 1 hour 20 min.
Solution:

Question 2.
4 hours 35 min and 3 hours 40 min.
Solution:

= 7 hours + 75 min
= 7 hours + 60 min + 15 min
= 7 hours + 1 hours + 15 min
= 8 hours 15 min

2. Add the following :

Question 1.
1 hour 10 min 20 sec and 3 hours 20 min
Solution:

Question 2.
2 hours 50 min 30 sec and 1 hour 10 min 30 sec
Solution:

3 hours + 60 min + 60 sec
= 3 hours + 1 hour + 1 min + 0 sec
= 4 hours + 1 min + 0 sec
= 4 hours 1 min

3. Add :

Question 1.
7 months and 2 years 3 months
Solution:

Question 2.
4 years 5 months and 1 year 8 months.
Solution:

= 5 years + 13 months
= 5 years + 12 months + 1 month
= 5 years + 1 year + 1 month
= 6 years 1 month

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 4 Fractions InText Questions and Answers.

PSEB 5th Class Maths Solutions Chapter 4 Fractions InText Questions

Try These : (Textbook Page No.86)

Question 1.
Write the fraction of coloured stars.

Solution:
\(\frac{1}{2}\)

Solution:
\(\frac{3}{4}\)

Solution:
\(\frac{5}{8}\)

Question 2.
Colour the diagram according to given fraction :

(a) \(\frac{2}{3}\)



Solution:

Question 3.
In fraction \(\frac{2}{3}\), numerator is and denominator is .
Solution:
In fraction \(\frac{2}{3}\), numerator is and denominator is .

Question 4.
In fraction \(\frac{1}{2}\), numerator is and denominator is .
Solution:
In fraction \(\frac{1}{2}\), numerator is and denominator is .

Question 5.
Write the fraction with numerator 4 and denominator 5:
Solution:
Write the fraction with numerator 4 and denominator 5:

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 6 Measurement Ex 6.5 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 6 Measurement Ex 6.5

Question 1.
The cost of 1 m cloth for pants is ₹ 265.50 and there is 24 m cloth in a roll. Find the cost of one bundle.
Solution:
Cost of 1 m cloth for pants = ₹ 265,50
Cost of 24 m cloth in a roll
= ₹ 265.50 × 24
= ₹ 6372.00
= ₹ 6372

Question 2.
The weight of a box of mangoes is 32.4 kg. A shopkeeper wants to make 6 packets from this. How many kilograms of mangoes will be there in each packet?
Solution:
The weight of the box of mangoes = 32.4 kg
Number of packets = 6
Weight of mangoes in each box = 32.4 kg ÷ 6

= 5.4 kg

Question 3.
A vessel contains 28.5 7 oil. It is poured into. 5 small containers. How much milk will be there in one small container?
Solution:
Quantity of milk in the given vessel = 28.5 l
Number of small containers = 5
Quantity of milk in each of small container = 28.5 ÷ 5

= 5.7 l

Question 4.
1 bundle of copies weighs 9.8 kgs. Find the weight of 14 such bundles.
Solution:
Weight of 1 bundle of copies = 9.8 kg
Weight of 14 bundles of copies
= 9.8 × 14 kg
= 137.2 kg.

Question 5.
The length of a stick is 12.7 cm. Find the length of 7 such sticks.
Solution:
The length of 1 stick = 12.7 cm
The length of 7 sticks = 12.7 × 7 cm
= 88.9 cm

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 3 HCF and LCM MCQ Questions and Answers.

PSEB 5th Class Maths Chapter 3 HCF and LCM MCQ Questions

Tick (✓) the right answer :

Question 1.
Which number is the smallest even Prime number ? ………
(a) 0
(b) 1
(c) 2
(d) 4
Answer:
(c) 2

Question 2.
Which number is neither Prime nor Composite ?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(a) 1

Question 3.
Which numbers are Prime numbers between 70 and 80 ?
(a) 71, 72, 73
(b) 71, 75, 79
(c) 71, 80
(d) 71, 73, 79.
Answer:
(d) 71, 73, 79.

Question 4.
HCF of 75 and 90 = ……
(a) 5
(b) 10
(c) 15
(d) 20.
Answer:
(c) 15

Question 5.
LCM of 12, 18 and 24 = …….
(a) 72
(b) 36
(c) 48
(d) 24
Answer:
(a) 72

Question 6.
If HCF of any two numbers is 8 then out of following which can not be LCM of that numbers ?
(a) 48
(b) 60
(c) 24
(d) 56
Answer:
(b) 60

Question 7.
What is length of the largest tape which can measure the lengths of 24 m and 30 m ?
(a) 4 m
(b) 5 m
(c) 6 m
(d) 7 m.
Answer:
(c) 6 m

Question 8.
What is the smallest number which is divisible by 8 and 12 ?
(a) 16
(b) 48
(c) 72
(d) 24
Answer:
(d) 24

Question 9.
LCM of 26 and 39 = ……
(a) 13
(b) 78
(c) 39
(d) 26
Answer:

Question 10.

(a) 5
(b) 65
(c) 12
(d) 13.
Answer:
(d) 13.

Question 11.
Which number is composite number in the following?
(a) 43
(b) 23
(c) 21
(d) 37.
Answer:
(c) 21

Question 12.
Out of following, which number is multiple of 19?
(a) 171
(b) 172
(c) 173
(d) 174.
Answer:
(a) 171

Question 13.
HCF of 15, 45 and 105 = ………
(a) 15
(b) 5
(c) 30
(d) 45.
Answer:
(a) 15

Question 14.
What is the HCF of two prime numbers ?
(a) 1
(b) 2
(c) 3
(d) 4
Answer:
(a) 1

Question 15.
Three bells ring with the time gap of 10 min, 15 min and 20 min respectively in a school. If all bells are rung together at 9:00 am then after how long the bells would ring together again ?
(a) 11:00 o’clock
(b) 08:00 o’clock
(c) 10:00 o’clock
(d) 12:00 o’clock
Answer:
(c) 10:00 o’clock

Read this pattern carefully and answer questions (16 – 20)

Question 16.
Read the above pattern and find the sum of first 6 Odd numbers.
(a) 30
(b) 12
(c) 25
(d) 36.
Answer:
(d) 36.

Question 17.
Read the above pattern and find the sum of first 10 Odd numbers.
(a) 20
(b) 50
(c) 100
(d) 40.
Answer:
(c) 100

Question 18.
Read the above pattern and find the sum of first 8 Even numbers.
(a) 16
(b) 24
(c) 72
(d) 64.
Answer:
(c) 72

Question 19.
Read the above pattern and find sum of first 9 even numbers.
(a) 19
(b) 18
(c) 45
(d) 90.
Answer:
(d) 90.

Question 20.
On a given road, the poles are erected at a distance of 24 m each and piles of stones are lying at a distance of 30 m each. If the 1st pile of stones is lying adjacent to the first pole, at what distance will the pole and the pile of stones be together again ?
(a) 100 m
(b) 110 m
(c) 150 m
(d) 120 m.
Answer:
(d) 120 m.

Question 21.
What is the length of the largest inchitape which can measure the lengths of 24 m and 30 m completely:
(a) 4 m
(b) 5 m
(c) 6 m
(d) 7 m.
Answer:
(c) 6 m

Question.
Write the smallest number which is divisible by 8 and 12.
Solution:
The smallest number which is divisible by 8 and 12 = LCM of 8 and 12.

= 2 × 2 × 2 × 3 = 24

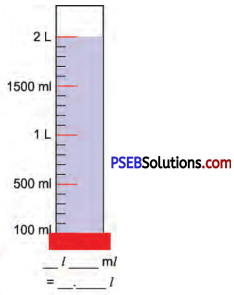
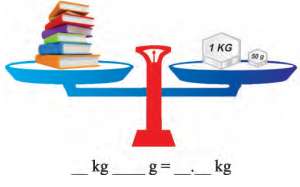
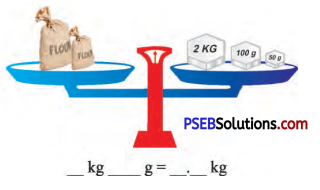
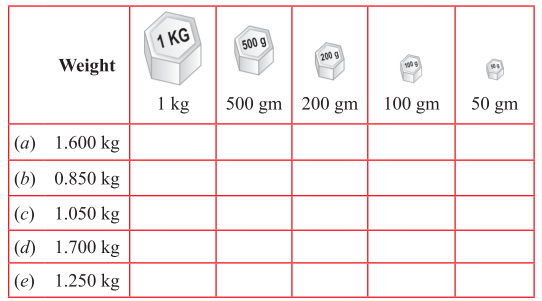
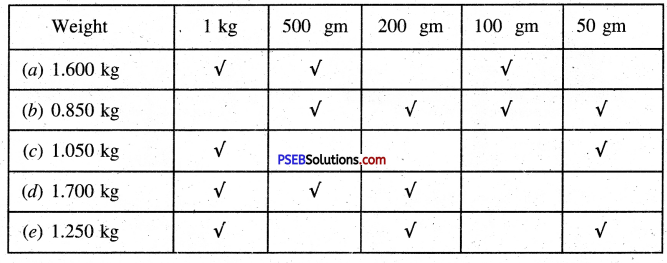
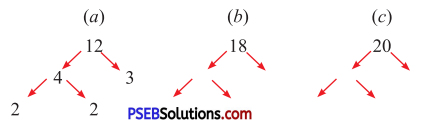
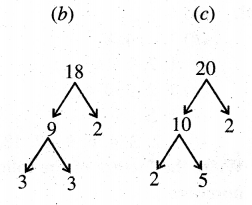
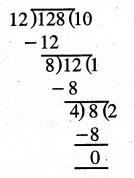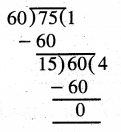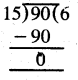Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 3 HCF and LCM Ex 3.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 3 HCF and LCM Ex 3.3

Question 1.
Find LCM of the following :
(a) 5, 10
(b) 6,18
(c) 25, 50
(d) 9, 24
Solution:
(a) Multiples of 5 = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, …….
Multiples of 10 = 10, 20, 30, 40, 50, ……..
Common multiples of 5 and 10 = 10, 20, 30, 40, 50, ……….
The lowest common multiple = 10
So, LCM of 5 and 10 = 10

(b) Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, …….
Multiples of 18 = 18, 36, 54, ……….
Common multiples of 6 and 18 = 18, 36, 54, ………
The lowest common multiple = 18
So, LCM of 6 and 18= 18

(c) Multiples of 25 = 25, 50, 75, 100, 125, 150, …….., …….
Multiples of 50 = 50, 100, 150, 200, ……, ……, ……..
Common multiples of 25 and 50= 50, 100, 150, ………..
The lowest common multiple = 50
So, LCM of 25 and 50 = 50

(d) Multiples of 9 = 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, ………
Multiples of 24 = 24, 48, 72, 96, …., ….., …….
Common multiples of 9 and 24 = 72,
So, LCM of 9 and 24 = 72

Question 2.
Find LCM of the follówing:
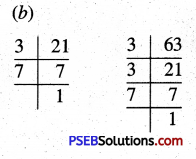
(a) 4, 8 and 12
(b) 6, 12 and 24
(e) 15, 18 and 27
(d) 24, 36 and 40
Solution:
(a) Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36,. 40, 44, 48,
Multiples of 8 = 8, 16, 24, 32, 40, 48, …….
Multiples of 12 = 12, 24, 36, 48, 60, ……..
Common multiples of 4, 8 and 12 = 24, 48
The lowest common multiple = 24
So, LCM of 4, 8, 12 = 24

(b) Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ……
Multiples of 12 = 12, 24, 36, 48, 60, 72, …….
Multiples of 24 = 24, 48, 72, 96, ……..
Common multiples of 6, 12 and 24 = 24, 48, 72, …..
The lowest common multiple = 24
So, LCM of 6, 12, 24 = 24

LCM of 15, 18 and 27 = 3 × 3 × 5 × 2 × 3 = 270

LCM of 24, 36 and 40 = 2 × 2 × 2 × 3 × 3 × 5 = 360

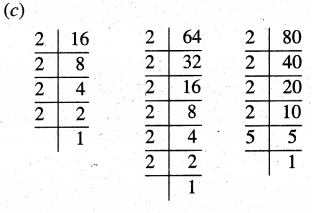
Question 3.
Find LCM of following using Prime factorisation :
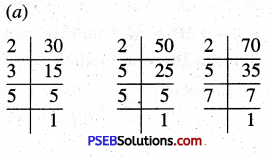
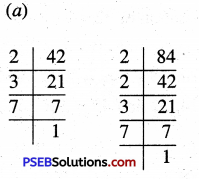
(a) 32,40
(b) 24, 36
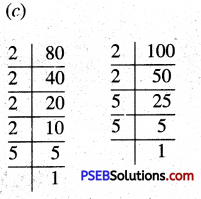
(c) 15, 30 and 45
(d) 40, 44 and 48
Solution:
(a)

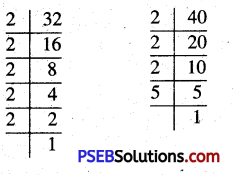
32 = 2 × 2 × 2 × 2 × 2
40 = 2 × 2 × 2 × 5
Common factors = 2 × 2 × 2
Remaining factors = 2 × 2 × 5
So, LCM = 2 × 2 × 2 × 2 × 2 × 5 = 160

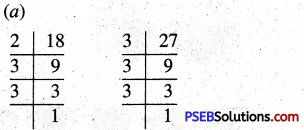
(b) 24 = 2 × 2 × 2 × 3
36 = 2 × 2 × 3×3

Common factors = 2 × 2 × 3
Remaining factors = 2 × 3
So, LCM = 2 × 2 × 2 × 3 × 3 = 72

(c) 15 = 3 × 5
30 = 2 × 3 × 5
45 = 3 × 3 × 5

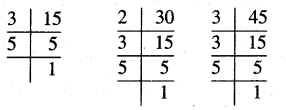
Common factors = 3 × 5
Remaining factors = 2 × 3
So, LCM = 3 × 5 × 2 × 3 = 90

(d) 40 = 2 × 2 × 2 × 5
44 = 2 × 2 × 11
48 = 2 × 2 × 2 × 2 × 3

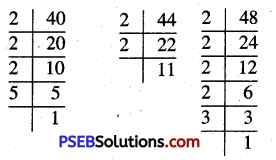
Common factors = 2 × 2
Remaining factors = 5 × 11 × 2 × 2 × 3
So, LCM = 2 × 2 × 2 × 2 × 5 × 3 × 11
= 2640

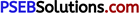
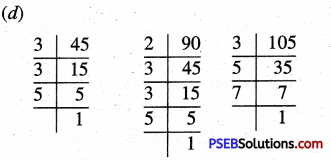
Question 4.
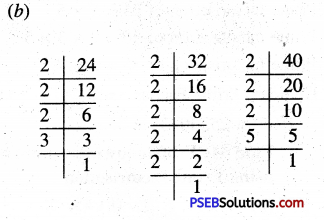
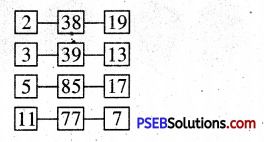
Find LCM of following using Division method :
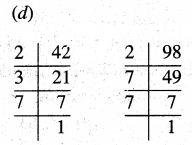
(a) 15, 20
(b) 12, 38
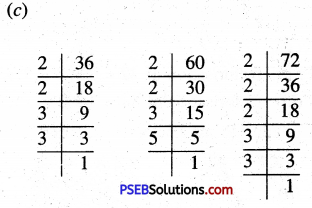
(c) 30, 45 and 50
(d) 40, 68 and 60
Solution:
(a)

LCM of 15 and 20 = 2 × 2 × 5 × 3 = 60
(b)

LCM of 12 and 38 = 2 × 2 × 3 × 19 = 228

(c)

LCM of 30, 45 and 50 = 2 × 3 × 3 × 5 × 5 = 450

(d)

LCM of 40, 68 and 60 = 2 × 2 × 2 × 3 × 5 × 17 = 2040

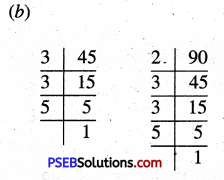
Question 5.
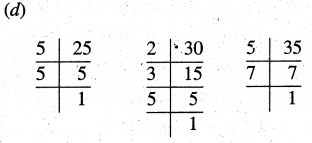
Find the smallest number which is divisible by 12, 15 and 20 completely ?
Solution:
LCM of 12, 15 and 20
LCM = 2 × 2 × 3 × 5 = 60
Smallest number which is divisible by 12, 15 and 20 = 60

Question 6.
One child jumps 3 feet high and another jumps 4 feet high. If both the children continue jumping together in same direction then after how many feet they will be together again ?
Solution:
We are to find the LCM of 3 and 4
LCM = 3 × 4 = 12
They will be together again after 12 feet.

Question 7.
How many minimum number of students are required from a class to make groups of 4 each and 5 each so that no student is left ?
Solution:
We are to find the LCM of 4 and 5
LCM = 4 × 5 = 20
Number of students required = 20

Question 8.
Three bells ring with a time gap of 10 min, 20 min and 30 min respectively in a school. If all bells are rung together at 8:00 am then after how long the beUs would ring together again ?
Solution:
We are to find the LCM of 10, 20 and 30
LCM = 2 × 5 × 2 × 3 = 60

The bells will ring together after 60 min. i.e. 1 hours.
Thus, the bells will ring together at 9:00 am

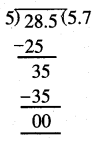
Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 6 Measurement Ex 6.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 6 Measurement Ex 6.4

1. Add the following :

Question 1.
7 km 7.50 m and 2 km 575 m
Solution:

= 10 km 325 m

Question 2.
4 kg 500 g and 9 kg 825 g
Solution:

= 14 kg 325 kg

Question 3.
5 l 925 ml and 7 l 650 ml
Solution:

= 13 l 575 ml

Question 4.
10 m, 3 m 85 cm and 6 m 25 cm
Solution:

= 20 m 10 cm

Question 5.
8 kg 700 g, 975 g and 2 kg 350 g
Solution:

= 12 kg 25 g

2. Subtract:

Question 1.
7 km 625 m from 12 km 300 m
Solution:

= 4 km 675 m

Question 2.
3 kg 650 g from 8 kg
Solution:

= 4 kg 350 g

Question 3.
5 l 850 ml from 10 l 350 ml
Solution:

= 4 l 500 ml

Question 4.
9m 60 cm from 15 m
Solution:

= 5 m 40 cm

Question 5.
13 l from 25 l 765 ml
Solution:

= 12 l 765 ml

Question 3.
Anand has bought 2 kg 350 g onions. 1 kg 750 g potatoes. How many kilograms of vegetables has he bought?
Solution:
Quantity of onions bought by Anand = 2 kg 350 g
Quartity of potatoes bought by Anand = 1 kg 750 g
Total quantity of vegetables bought = 4 kg 100 g

Question 4.
Ajay has travelled 150 km 400 m distancebybus, 120 km 650 m by taxi. How much distance has he covered?
Solution:
Distance travelled by bus = 150 km 400 m
Distance travelled by taxi = 120 km 650 m
Total distance travelled by him = 271 km 50 m

Question 5.
Three containers contained 10 l 350 ml, 9 l 850 ml and 11 l oil respectively. Find the total quantity of oil contained in three containers.
Solution:
First container contains oil = 10 l 350 ml
Second container contains oil = 9 l 850 ml
Third container contains oil = 11 l 000 ml
The total quantity of oil contained in three containers = 31 l 200 ml

Question 6.
Anita bought 7 m 30 cm cloth. She used 2 m 50 cm cloth for her suit. Find the remaining length of the cloth.
Solution:
Length of cloth bought by Anita = 7 m 30 cm
Length of cloth used for suit = 2 m 50 cm
Remaining length of cloth = 4 m 80 cm

Question 7.
A family consumes 10 kg 750 g wheat and 4 kg 500 g rice in a month. Find the difference of consumption of rice and wheat.
Solution:
Quantity of wheat consumed = 10 kg 750 g
Quantity of rice consumed = 4 kg 500 g
Difference of consumption of rice and wheat = 6 kg 250 g

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 6 Measurement Ex 6.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 6 Measurement Ex 6.3

1. Find the amount of liquid in the following:

Question 1.

Question 2.

Solution:
1l 800 ml = 1.800 l

Question 3.

Solution:
1 l 500 ml= 1.500 l

Question 4.

Solution:
1 l 100 ml 1.100 l

Question 5.

Solution:
2 l 0 ml = 2.000 l

2. Colour the following scales vessels according to the given quantity:

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

3. Fill in the blanks:

Question 1.
3.125 l = ………………. l …………………. ml
Solution:
3.125 l = 3 l 125 ml

Question 2.
8.720 kl = …………… kl …………….. l
Solution:
8.720 kl = 8 kl 720 l

Question 3.
…………….., l = 4 l 948 ml
Solution:
4.498 l = 4 l = 948 ml

Question 4.
………………….. kl = 15 kl 650 l
Solution:
15.650 kl = 15 kl 650 l

Question 5.
18.045 l = …………….. l …………….. ml
Solution:
18.045 l = 18 l 45 ml

4. Convert:

Question 1.
7.6 l into mililitres
Solution:
7.6 l = 7.6 × 1000 ml
= 7600 ml

Question 2.
250 ml into litres
Solution:
250 ml = \(\frac{250}{1000}\) l
= 0.250 l

Question 3.
4.25 kl into litres
Solution:
4.25 kl = 4.25 × 1000 l
= 4250 l

Question 4.
0.845 l into mililitres
Solution:
0.845 l = 0.845 × 1000 ml
= 845 ml

Question 5.
92 l into kilolitres
Solution:
92 l = \(\frac{92}{1000}\) kl
= 0.092 kl