Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 3 HCF and LCM Ex 3.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 5 Maths Chapter 3 HCF and LCM Ex 3.3
Question 1.
Find LCM of the following :
(a) 5, 10
(b) 6,18
(c) 25, 50
(d) 9, 24
Solution:
(a) Multiples of 5 = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, …….
Multiples of 10 = 10, 20, 30, 40, 50, ……..
Common multiples of 5 and 10 = 10, 20, 30, 40, 50, ……….
The lowest common multiple = 10
So, LCM of 5 and 10 = 10
(b) Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, …….
Multiples of 18 = 18, 36, 54, ……….
Common multiples of 6 and 18 = 18, 36, 54, ………
The lowest common multiple = 18
So, LCM of 6 and 18= 18
(c) Multiples of 25 = 25, 50, 75, 100, 125, 150, …….., …….
Multiples of 50 = 50, 100, 150, 200, ……, ……, ……..
Common multiples of 25 and 50= 50, 100, 150, ………..
The lowest common multiple = 50
So, LCM of 25 and 50 = 50
(d) Multiples of 9 = 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, ………
Multiples of 24 = 24, 48, 72, 96, …., ….., …….
Common multiples of 9 and 24 = 72,
So, LCM of 9 and 24 = 72
![]()
Question 2.
Find LCM of the follówing:
(a) 4, 8 and 12
(b) 6, 12 and 24
(e) 15, 18 and 27
(d) 24, 36 and 40
Solution:
(a) Multiples of 4 = 4, 8, 12, 16, 20, 24, 28, 32, 36,. 40, 44, 48,
Multiples of 8 = 8, 16, 24, 32, 40, 48, …….
Multiples of 12 = 12, 24, 36, 48, 60, ……..
Common multiples of 4, 8 and 12 = 24, 48
The lowest common multiple = 24
So, LCM of 4, 8, 12 = 24
(b) Multiples of 6 = 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ……
Multiples of 12 = 12, 24, 36, 48, 60, 72, …….
Multiples of 24 = 24, 48, 72, 96, ……..
Common multiples of 6, 12 and 24 = 24, 48, 72, …..
The lowest common multiple = 24
So, LCM of 6, 12, 24 = 24

LCM of 15, 18 and 27 = 3 × 3 × 5 × 2 × 3 = 270

LCM of 24, 36 and 40 = 2 × 2 × 2 × 3 × 3 × 5 = 360
Question 3.
Find LCM of following using Prime factorisation :
(a) 32,40
(b) 24, 36
(c) 15, 30 and 45
(d) 40, 44 and 48
Solution:
(a)
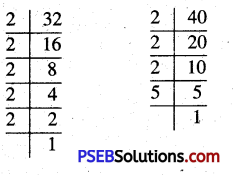
32 = 2 × 2 × 2 × 2 × 2
40 = 2 × 2 × 2 × 5
Common factors = 2 × 2 × 2
Remaining factors = 2 × 2 × 5
So, LCM = 2 × 2 × 2 × 2 × 2 × 5 = 160
(b) 24 = 2 × 2 × 2 × 3
36 = 2 × 2 × 3×3

Common factors = 2 × 2 × 3
Remaining factors = 2 × 3
So, LCM = 2 × 2 × 2 × 3 × 3 = 72
(c) 15 = 3 × 5
30 = 2 × 3 × 5
45 = 3 × 3 × 5
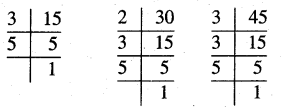
Common factors = 3 × 5
Remaining factors = 2 × 3
So, LCM = 3 × 5 × 2 × 3 = 90
(d) 40 = 2 × 2 × 2 × 5
44 = 2 × 2 × 11
48 = 2 × 2 × 2 × 2 × 3
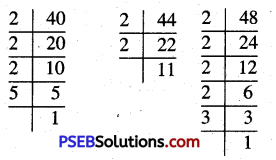
Common factors = 2 × 2
Remaining factors = 5 × 11 × 2 × 2 × 3
So, LCM = 2 × 2 × 2 × 2 × 5 × 3 × 11
= 2640
![]()
Question 4.
Find LCM of following using Division method :
(a) 15, 20
(b) 12, 38
(c) 30, 45 and 50
(d) 40, 68 and 60
Solution:
(a)

LCM of 15 and 20 = 2 × 2 × 5 × 3 = 60
(b)

LCM of 12 and 38 = 2 × 2 × 3 × 19 = 228
(c)

LCM of 30, 45 and 50 = 2 × 3 × 3 × 5 × 5 = 450
(d)

LCM of 40, 68 and 60 = 2 × 2 × 2 × 3 × 5 × 17 = 2040
Question 5.
Find the smallest number which is divisible by 12, 15 and 20 completely ?
Solution:
LCM of 12, 15 and 20
LCM = 2 × 2 × 3 × 5 = 60
Smallest number which is divisible by 12, 15 and 20 = 60

Question 6.
One child jumps 3 feet high and another jumps 4 feet high. If both the children continue jumping together in same direction then after how many feet they will be together again ?
Solution:
We are to find the LCM of 3 and 4
LCM = 3 × 4 = 12
They will be together again after 12 feet.
Question 7.
How many minimum number of students are required from a class to make groups of 4 each and 5 each so that no student is left ?
Solution:
We are to find the LCM of 4 and 5
LCM = 4 × 5 = 20
Number of students required = 20
Question 8.
Three bells ring with a time gap of 10 min, 20 min and 30 min respectively in a school. If all bells are rung together at 8:00 am then after how long the beUs would ring together again ?
Solution:
We are to find the LCM of 10, 20 and 30
LCM = 2 × 5 × 2 × 3 = 60

The bells will ring together after 60 min. i.e. 1 hours.
Thus, the bells will ring together at 9:00 am