Bhagya

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 2 ਸੰਖਿਆਵਾਂ ਉੱਪਰ ਮੁੱਢਲੀਆਂ ਕਿਰਿਆਵਾਂ Ex 2.4 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 2 ਸੰਖਿਆਵਾਂ ਉੱਪਰ ਮੁੱਢਲੀਆਂ ਕਿਰਿਆਵਾਂ Ex 2.4

ਪ੍ਰਸ਼ਨ 1.
ਹੱਲ ਕਰੋ :
(a) 450 × 6
ਹੱਲ:

(b) 963 × 9
ਹੱਲ:

(c) 529 × 23
ਹੱਲ:

(d) 988 × 38
ਹੱਲ:

(e) 912 × 56
ਹੱਲ:

(f) 806 × 56
ਹੱਲ:

(g) 252 × 54
ਹੱਲ:

(h) 1888 × 19
ਹੱਲ:

(i) 2005 × 34
ਹੱਲ:

(j) 1560 × 64
ਹੱਲ:

(k) 10569 × 8
ਹੱਲ:

(l) 102109 × 9
ਹੱਲ:

(m) 230 × 150
ਹੱਲ:

(n) 400 × 225.
ਹੱਲ:

ਪ੍ਰਸ਼ਨ 2.
ਹੇਠ ਲਿਖਿਆਂ ਦਾ ਗੁਣਨਫਲ ਪਤਾ ਕਰੋ :
(a) 4045 × 23
ਹੱਲ:

(b) 1609 × 30
ਹੱਲ:

(c) 363 × 134
ਹੱਲ:

(d) 455 × 208
ਹੱਲ:

(e) 105 × 120
ਹੱਲ:

(f) 1440 × 25
ਹੱਲ:

(g) 1530 × 61
ਹੱਲ:

(h) 3817 × 12
ਹੱਲ:

(i) 1908 × 35
ਹੱਲ:

(j) 1000 × 29
ਹੱਲ:

ਪ੍ਰਸ਼ਨ 3.
* ਦੀ ਥਾਂ ਅੰਕ ਭਰੋ :

ਹੱਲ:

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 2 ਸੰਖਿਆਵਾਂ ਉੱਪਰ ਮੁੱਢਲੀਆਂ ਕਿਰਿਆਵਾਂ Ex 2.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 2 ਸੰਖਿਆਵਾਂ ਉੱਪਰ ਮੁੱਢਲੀਆਂ ਕਿਰਿਆਵਾਂ Ex 2.3

ਸਮਝੋ ਅਤੇ ਕਰੋ-

ਪ੍ਰਸ਼ਨ 1.
(a) 60498,31292 ਅਤੇ 7132 ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:

(b) 70123 ਅਤੇ 40268 ਦਾ ਅੰਤਰ ਪੱਤਾ ਕਰੋ ।
ਹੱਲ:

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਘਰ ਦੀ ਰਸੋਈ ਬਣਾਉਣ ਲਈ 27020 ਇੱਟਾਂ ਦੀ ਅਤੇ ਕਮਰਾਂ ਬਣਾਉਣ ਲਈ 31275 ਇੱਟਾਂ ਦੀ ਲੋੜ ਹੈ ਘਰ ਦੀ ਰਸੋਈ ਅਤੇ ਕਮਰਾ ਬਣਾਉਣ ਲਈ ਕੁੱਲ ਕਿੰਨੀਆਂ ਇੱਟਾਂ ਦੀ ਲੋੜ ਹੋਵੇਗੀ ?
ਹੱਲ:
ਰਸੋਈ ਬਣਾਉਣ ਲਈ ਇੱਟਾਂ ਦੀ ਲੋੜ = 27020
ਕਮਰਾ ਬਣਾਉਣ ਲਈ ਇੱਟਾਂ ਦੀ ਲੋੜ = +31275
ਰਸੋਈ ਅਤੇ ਕਮਰਾ ਬਣਾਉਣ ਲਈ ਜਿੰਨੀਆਂ ਇੱਟਾਂ ਦੀ ਲੋੜ ਹੈ = 58295

ਪ੍ਰਸ਼ਨ 3.
ਸੁਰਜੀਤ ਕੋਲ ₹ 20000 ਸਨ । ਉਸਨੇ ₹ 13750 ਦੇ ਕੱਪੜੇ ਖਰੀਦ ਲਏ । ਉਸ ਕੋਲ ਕਿੰਨੀ ਰਕਮ ਬਾਕੀ ਰਹਿ ਗਈ ?
ਹੱਲ:
ਸੁਰਜੀਤ ਕੋਲ ਕੁੱਲ ਰਕਮ ਸੀ = ₹ 20000
ਕੱਪੜਿਆਂ ਤੇ ਕੀਤੇ ਖ਼ਰਚ = – ₹ 13750
ਬਾਕੀ ਬਚੀ ਰਕਮ = ₹ 6250

ਪ੍ਰਸ਼ਨ 4.
ਇੱਕ ਲਾਇਬਰੇਰੀ ਵਿੱਚ 30155 ਪੁਸਤਕਾਂ ਪੰਜਾਬੀ ਦੀਆਂ, 28653 ਪੁਸਤਕਾਂ ਗਣਿਤ ਦੀਆਂ ਅਤੇ 12376 ਪੁਸਤਕਾਂ ਅੰਗਰੇਜ਼ੀ ਦੀਆਂ ਹਨ । ਲਾਇਬਰੇਰੀ ਵਿੱਚ ਕੁੱਲ ਕਿੰਨੀਆਂ ਪੁਸਤਕਾਂ ਹਨ ?
ਹੱਲ :
ਪੰਜਾਬੀ ਦੀਆਂ ਪੁਸਤਕਾਂ = 30155
ਗਣਿਤ ਦੀਆਂ ਪੁਸਤਕਾਂ = + 28653
ਅੰਗਰੇਜ਼ੀ ਦੀਆਂ ਪੁਸਤਕਾਂ = + 12376
ਲਾਇਬਰੇਰੀ ਵਿਚ ਕੁੱਲ ਪੁਸਤਕਾਂ = 71184

ਪ੍ਰਸ਼ਨ 5.
ਦੋ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜ 89000 ਹੈ । ਜੇਕਰ ਇੱਕ ਸੰਖਿਆ 25450 ਹੋਵੇ ਤਾਂ ਦੂਜੀ ਸੰਖਿਆ ਦਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਦੋ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜ = 89000
ਇੱਕ ਸੰਖਿਆ = – 25450
ਦੂਜੀ ਸੰਖਿਆ = 63550

ਪ੍ਰਸ਼ਨ 6.
ਸੰਖਿਆ 70429 ਵਿੱਚ ਕੀ ਜੋੜੀਏ ਕਿ ਜੋੜਫਲ 100000 ਪ੍ਰਾਪਤ ਹੋਵੇ ?
ਹੱਲ :
ਜੋੜਫਲ = 100000
ਦਿੱਤੀ ਸੰਖਿਆ = – 70429
ਜੋ ਜੋੜਿਆ ਜਾਏ = 29571

ਪ੍ਰਸ਼ਨ 7.
ਉਹ ਸੰਖਿਆ ਪਤਾ ਕਰੋ ਜਿਹੜੀ :
(a) 36798 ਤੋਂ 1976 ਵੱਧ ਹੋਵੇ
ਹੱਲ:
ਲੋੜੀਂਦੀ ਸੰਖਿਆ

(b) 30067 ਤੋਂ 12967 ਘੱਟ ਹੋਵੇ ।
ਹੱਲ:
ਲੋੜੀਂਦੀ ਸੰਖਿਆ

ਪ੍ਰਸ਼ਨ 8.
ਜੇਕਰ ਕੰਪਿਊਟਰ ਦਾ ਮੁੱਲ ਤੋਂ 15560 ਹੈ ਅਤੇ ਲੈਪਟਾਪ ਦਾ ਮੁੱਲ ਕੰਪਿਊਟਰ ਦੇ ਮੁੱਲ ਤੋਂ ₹ 9050 ਵੱਧ ਹੈ ਤਾਂ :
(a) ਲੈਪਟਾਪ ਦਾ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਕੰਪਿਊਟਰ ਦਾ ਮੁੱਲ = ₹ 15560
ਲੈਪਟਾਪ ਦਾ ਮੁੱਲ ਜਿੰਨਾ ਵੱਧ ਹੈ = + ₹ 9050
ਲੈਪਟਾਪ ਦਾ ਮੁੱਲ = ₹ 24610

(b) ਕੰਪਿਊਟਰ ਅਤੇ ਲੈਪਟਾਪ ਦਾ ਕੁੱਲ ਮੁੱਲ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਕੰਪਿਊਟਰ ਦਾ ਮੁੱਲ = ₹ 15560
ਲੈਪਟਾਪ ਦਾ ਮੁੱਲ = + ₹ 24610
ਕੰਪਿਊਟਰ ਅਤੇ ਲੈਪਟਾਪ ਦਾ ਕੁੱਲ ਮੁੱਲ = ₹ 40170

ਪ੍ਰਸ਼ਨ 9.
ਅੰਕਾਂ 9, 3, 4, 0, 7 ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹੋਏ 5 ਅੰਕਾਂ ਦੀ ਵੱਡੀ ਤੋਂ ਵੱਡੀ ਅਤੇ ਛੋਟੀ ਤੋਂ ਛੋਟੀ । ਸੰਖਿਆ ਪਤਾ ਕਰੋ । ਇਹਨਾਂ ਦਾ ਅੰਤਰ ਵੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
5 ਅੰਕਾਂ ਦੀ ਵੱਡੀ ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ = 97430
5 ਅੰਕਾਂ ਦੀ ਛੋਟੀ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ = – 30479
ਇਹਨਾਂ ਦਾ ਅੰਤਰ = 6695

ਪ੍ਰਸ਼ਨ 10.
4 ਅੰਕਾਂ ਦੀ, 3 ਅੰਕਾਂ ਦੀ ਅਤੇ 2 ਅੰਕਾਂ ਦੀਆਂ ਵੱਡੀ ਤੋਂ ਵੱਡੀ ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜਫਲ ਪਤਾ ਕਰੋ
ਹੱਲ:
4 ਅੰਕਾਂ ਦੀ ਵੱਡੀ ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ = 9999
3 ਅੰਕਾਂ ਦੀ ਵੱਡੀ ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ = + 999
2 ਅੰਕਾਂ ਦੀ ਵੱਡੀ ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ = + 99
ਸੰਖਿਆਵਾਂ ਦਾ ਜੋੜਫਲ = 11097

ਪ੍ਰਸ਼ਨ 11.
ਸੰਖਿਆ 96074 ਵਿੱਚ, 6 ਦੇ ਸਥਾਨਕ ਮੱਲ ਅਤੇ 7 ਦੇ ਸਥਾਨਕ ਮੁੱਲ ਦਾ ਅੰਤਰ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
6 ਦਾ ਸਥਾਨਕ ਮੁੱਲ = 6000
7 ਦਾ ਸਥਾਨਕ ਮੁੱਲ = – 70
ਅੰਤਰ = 5930

ਪ੍ਰਸ਼ਨ 12.
6 ਅੰਕਾਂ ਦੀ ਛੋਟੀ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ ਵਿੱਚੋਂ 45555 ਨੂੰ ਘਟਾਓ ।
ਹੱਲ:
6 ਅੰਕਾਂ ਦੀ ਛੋਟੀ ਤੋਂ ਛੋਟੀ ਸੰਖਿਆ = 100000
ਜਿਹੜੀ ਸੰਖਿਆ ਘਟਾਉਣੀ ਹੈ = – 45555
ਅੰਤਰ = 54445

ਪ੍ਰਸ਼ਨ 13.
ਸਤਨਾਮ ਕੋਲ ਤੇ 8765 ਸਨ । ਉਸ ਦੇ ਮਾਮਾ ਜੀ ਨੇ ਉਸਨੂੰ ਵੀ 2500 ਹੋਰ ਦਿੱਤੇ । ਫਿਰ ਸਤਨਾਮ ਨੇ ਆਪਣੇ ਕੁੱਲ ਰੁਪਇਆਂ ਵਿੱਚੋਂ ਆਪਣੀ ਭੈਣ ਨੂੰ 4770 ਦੇ ਦਿੱਤੇ । ਹੁਣ ਉਸ ਕੋਲ ਕਿੰਨੇ ਰੁਪਏ ਬਾਕੀ ਬਚੇ ? [From Board M.Q.P. 2021]
ਹੱਲ:
ਸਤਨਾਮ ਕੋਲ ਰਕਮ ਸੀ = ₹ 8765
ਉਸ ਦੇ ਮਾਮਾ ਜੀ ਨੇ ਦਿੱਤੇ = + ₹ 2500
ਸਤਨਾਮ ਕੋਲ ਕੁੱਲ ਰਕਮ = ₹ 11265

ਸਤਨਾਮ ਕੋਲ ਕੁੱਲ ਰਕਮ = ₹ 11265
ਸਤਨਾਮ ਨੇ ਆਪਣੀ ਭੈਣ ਨੂੰ ਦਿੱਤੇ = – ₹ 4770
ਉਸ ਕੋਲ ਬਾਕੀ ਬਚੇ ਰੁਪਏ = ₹ 6495

ਪ੍ਰਸ਼ਨ 14.
ਮਨਦੀਪ ਕੋਲ ਤੋਂ 10000 ਸਨ । ਉਸਨੇ ਬਜ਼ਾਰ ਵਿੱਚੋਂ ₹ 1050 ਦਾ ਬੁਟਾਂ ਦਾ ਜੋੜਾ ਅਤੇ ₹ 3600 ਦਾ ਇੱਕ ਕੋਟ-ਪੈਂਟ ਖਰੀਦਿਆ । ਉਸ ਕੋਲ ਕਿੰਨੇ ਰੁਪਏ ਬਾਕੀ ਬਚੇ ?
ਹੱਲ:
ਬੁਟਾਂ ਦੇ ਜੋੜੇ ਦਾ ਮੁੱਲ = ₹ 1050
ਕੋਟ ਪੈਂਟ ਦਾ ਮੁੱਲ = + ₹ 3600
ਦੋਵਾਂ ਦਾ ਕੁੱਲ ਮੁੱਲ = 4650

ਮਨਦੀਪ ਕੋਲ ਕੁੱਲ ਰਕਮ = ₹ 10000
ਖ਼ਰਚ ਕੀਤੀ ਰਕਮ = – ₹ 4650
ਬਾਕੀ ਬਚੇ ਰੁਪਏ = ₹ 5350

ਪ੍ਰਸ਼ਨ 15.
ਸੰਦੀਪ ਦੇ ਬੈਂਕ ਖਾਤੇ ਵਿੱਚ ਤੋਂ 7800 ਹਨ । ਉਹ ਆਪਣੇ ਬੈਂਕ ਖਾਤੇ ਵਿੱਚ ਕਿੰਨੇ ਰੁਪਏ ਹੋਰ ਜਮਾਂ ਕਰਵਾਏ ਕਿ ਉਸਦੇ ਖਾਤੇ ਵਿੱਚ ਤੋਂ 100000 ਪੂਰੇ ਹੋ ਜਾਣ ?
ਹੱਲ:
ਕੁੱਲ ਰਕਮ = ₹ 100000
ਬੈਂਕ ਖਾਤੇ ਵਿਚ ਜਮ੍ਹਾਂ ਰਕਮ = – ₹ 78500
ਜਿੰਨੇ ਰੁਪਏ ਹੋਰ ਜਮਾਂ ਕਰਵਾਏ = ₹ 21500

ਪ੍ਰਸ਼ਨ 16.
ਇੱਕ ਆਦਮੀ ਪਹਿਲੇ ਦਿਨ ਪਠਾਨਕੋਟ ਤੋਂ ਕਸ਼ਮੀਰ ਤੱਕ 165 ਕਿ.ਮੀ. ਕਾਰ ਚਲਾਉਂਦਾ ਹੈ । ਅਗਲੇ ਦਿਨ ਉਹ ਆਦਮੀ ਕਸ਼ਮੀਰ ਤੋਂ ਲੇਹ ਤੱਕ 138 ਕਿ. ਮੀ. ਕਾਰ ਚਲਾਉਂਦਾ ਹੈ ਉਸ ਆਦਮੀ ਨੇ ਦੋ ਦਿਨਾਂ ਵਿੱਚ ਕਿੰਨੀ ਦੂਰੀ ਤੈਅ ਕੀਤੀ ?
ਹੱਲ:
ਪਹਿਲੇ ਦਿਨ ਤੈਅ ਕੀਤੀ ਦੁਰੀ = 165 ਕਿ.ਮੀ.
ਦੂਜੇ ਦਿਨ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = 138 ਕਿ.ਮੀ.
ਦੋ ਦਿਨਾਂ ਵਿਚ ਤੈਅ ਕੀਤੀ ਦੂਰੀ = 303 ਕਿ.ਮੀ.

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 9 ਆਇਤਨ MCQ Questions and Answers.

PSEB 5th Class Maths Chapter 9 ਆਇਤਨ MCQ Questions

ਬਹੁ-ਵਿਕਲਪਿਕ ਪ੍ਰਸ਼ਨ

1. ਸਹੀ ਉੱਤਰ ਦੇ ਸਾਹਮਣੇ ਠੀਕ (✓) ਦਾ ਨਿਸ਼ਾਨ ਲਗਾਓ :

ਪ੍ਰਸ਼ਨ 1.
9 ਸਮ ਭੁਜਾ ਵਾਲੇ ਘਣ ਦਾ ਆਇਤਨ ਹੋਵੇਗਾ :
(a) 8 ਘਣ ਸੈਂ.ਮੀ.
(b) 90 ਘਣ ਸੈਂ.ਮੀ.
(c) 729 ਘਣ ਸੈਂ.ਮੀ.
(d) 8 ਘਣ ਸੈਂ.ਮੀ. 1
ਹੱਲ:
(c) 729 ਘਣ ਸੈਂ.ਮੀ.

ਪ੍ਰਸ਼ਨ 2.
ਇੱਕ ਘਣਾਵ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ ਜਿਸ ਦੀ ਲੰਬਾਈ 6 ਸੈਂ.ਮੀ., ਚੌੜਾਈ 4 ਸੈਂ.ਮੀ. ਅਤੇ ਉੱਚਾਈ 2 ਸੈਂ.ਮੀ. ਹੈ :
(a) 24 ਘਣ ਸੈਂ.ਮੀ.
(b) 28 ਘਣ ਸੈਂ.ਮੀ.
(c) 64 ਘਣ ਸੈਂ.ਮੀ.
(d) 48 ਘਣ ਸੈਂ.ਮੀ.
ਹੱਲ:
(d) 48 ਘਣ ਸੈਂ.ਮੀ.

ਪ੍ਰਸ਼ਨ 3.
ਆਇਤਨ ਦੀ ਮੂਲ ਇਕਾਈ ਕਿਹੜੀ ਨਹੀਂ ਹੈ ?
(a) ਘਣ ਸੈਂ.ਮੀ.
(b) ਵਰਗ ਮੀ.
(c) ਘਣ ਮਿ.ਮੀ.
(d) ਘਣ ਮੀ.
ਹੱਲ:
(b) ਵਰਗ ਮੀ.

ਪ੍ਰਸ਼ਨ 4.
ਜਿਸ ਘਣਾਵ ਦੇ ਸਾਰੇ ਕਿਨਾਰੇ ਬਰਾਬਰ ਹੋਣ ਉਸ ਨੂੰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ :
(a) ਵਰਗ
(b) ਘਣ
(c) ਘਣਾਵ
(d) ਆਇਤ
ਹੱਲ:
(b) ਘਣ

ਪ੍ਰਸ਼ਨ 5.
ਘਣਾਂ ਦੀ ਗਿਣਤੀ ਕਰਕੇ ਘਣਾਵ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ :

ਹੱਲ:
ਘਣਾਵ ਦਾ ਆਇਤਨ = 8 ਘਣ ਸੈਂਟੀਮੀਟਰ ।

ਪ੍ਰਸ਼ਨ 6.
ਇੱਕ ਟਰਾਲੀ ਇੱਟਾਂ ਨਾਲ ਪੂਰੀ ਭਰੀ ਹੋਈ ਹੈ । ਇਸ ਟਰਾਲੀ ਦੀ ਲੰਬਾਈ 40 ਸੈਂਟੀਮੀਟਰ, ਚੌੜਾਈ 200 ਸੈਂਟੀਮੀਟਰ ਅਤੇ ਡੂੰਘਾਈ 100 ਸੈਂਟੀਮੀਟਰ ਹੈ । ਇੱਕ ਇੱਟ ਦੀ ਲੰਬਾਈ 20 ਸੈਂਟੀਮੀਟਰ, ਚੌੜਾਈ 10 ਸੈਂਟੀਮੀਟਰ ਅਤੇ ਉੱਚਾਈ 6 ਸੈਂਟੀਮੀਟਰ ਹੈ | ਟਰਾਲੀ ਵਿੱਚ ਕਿੰਨੀਆਂ ਇੱਟਾਂ ਹੋਣਗੀਆਂ ?
ਹੱਲ:
ਟਰਾਲੀ ਦੀ ਲੰਬਾਈ = 400 ਸੈਂਟੀਮੀਟਰ
ਟਰਾਲੀ ਦੀ ਚੌੜਾਈ = 200 ਸੈਂਟੀਮੀਟਰ
ਟਰਾਲੀ ਦੀ ਉੱਚਾਈ = 100 ਸੈਂਟੀਮੀਟਰ
ਟਰਾਲੀ ਦਾ ਆਇਤਨ = ਲੰ. × ਚੌ. × ਉ.
= 400 ਸਮ × 200 ਸਮ × 100 ਸਮ
ਇੱਟ ਦੀ ਲੰਬਾਈ = 20 ਸਮ
ਇੱਟ ਦੀ ਚੌੜਾਈ = 10 ਸਮ
ਇੱਟ ਦੀ ਉੱਚਾਈ = 6 ਸਮ
1 ਇੱਟ ਦੀ ਆਇਤਨ = ਲੰ. × ਚੌ. × ਉ.
= 20 ਸਮ × 10 ਸਮ × 6 ਸਮ

= \(\frac{400 \times 200 \times 100}{20 \times 10 \times 6}\)
= \(\frac{20 \times 10 \times 100}{3}\) = \(\frac{2000}{3}\)
= 6666

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 9 ਆਇਤਨ Intext Questions and Answers.

PSEB 5th Class Maths Solutions Chapter 9 ਆਇਤਨ Intext Questions

ਦੁਹਰਾਈ

(a) ਵੱਧ ਥਾਂ ਘੇਰਨ ਵਾਲੀ ਵਸਤੂ ਦੇ ਸਾਹਮਣੇ ਸਹੀ (✓) ਦਾ ਨਿਸ਼ਾਨ ਲਗਾਓ :

ਪ੍ਰਸ਼ਨ 1.

ਹੱਲ:

ਪ੍ਰਸ਼ਨ 2.

ਹੱਲ:

ਪ੍ਰਸ਼ਨ 3.

ਹੱਲ:

ਪ੍ਰਸ਼ਨ 4.

ਹੱਲ:

ਪ੍ਰਸ਼ਨ 5.

ਹੱਲ:

(ਅ) ਵਸਤੂਆਂ ਨੂੰ ਉਨ੍ਹਾਂ ਦੇ ਥਾਂ ਘੇਰਨ ਅਨੁਸਾਰ ਵੱਧਦੇ ਕ੍ਰਮ ਵਿੱਚ ਲਿਖੋ :

ਹੱਲ:

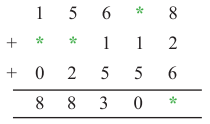
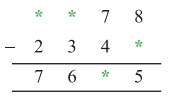
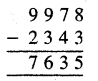
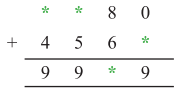
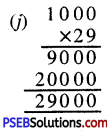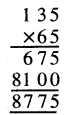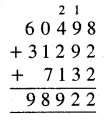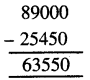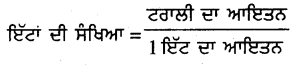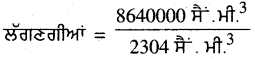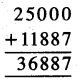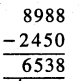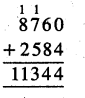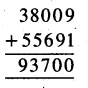Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 9 ਆਇਤਨ Ex 9.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 9 ਆਇਤਨ Ex 9.1

1. ਹੇਠਾਂ ਦਿੱਤੇ ਘਣਾਵ ਵਿਚਲੇ ਘਣਾਂ ਨੂੰ ਗਿਣ ਕੇ ਆਇਤਨ ਪਤਾ ਕਰੋ ।

ਪ੍ਰਸ਼ਨ 1.
ਆਇਤਨ = …………

ਹੱਲ:
ਆਇਤਨ = 3 ਸੈਂ.ਮੀ³

ਪ੍ਰਸ਼ਨ 2.
ਆਇਤਨ = …………

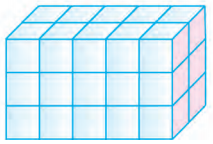
ਹੱਲ:
ਆਇਤਨ = 30 ਸੈਂ.ਮੀ³

ਪ੍ਰਸ਼ਨ 3.
ਆਇਤਨ = …………

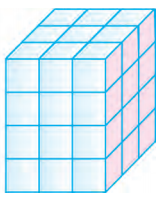
ਹੱਲ:
ਆਇਤਨ = 36 ਸੈਂ.ਮੀ³

ਪ੍ਰਸ਼ਨ 2.
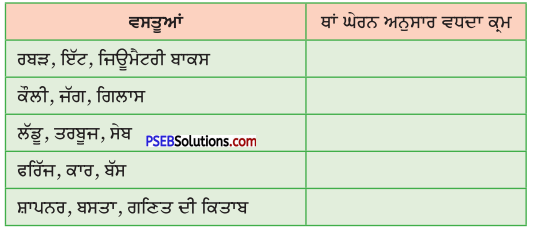
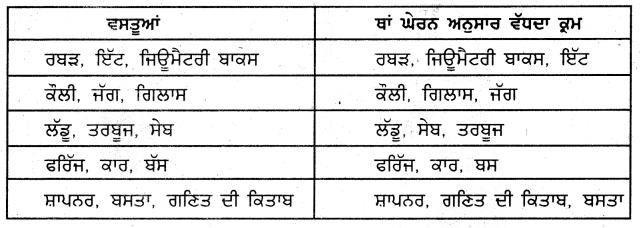
ਸਾਰਨੀ ਪੂਰੀ ਕਰੋ :

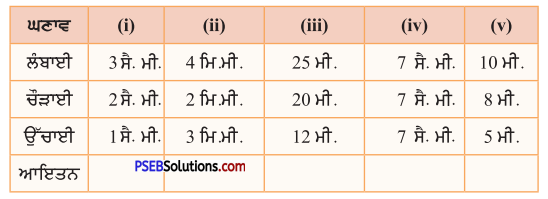
ਹੱਲ :
(i) 6 ਸੈਂ.ਮੀ.³
(ii) 24 ਮਿ.ਮੀ³
(iii) 6000
(iv) 343 ਸੈਂ.ਮੀ.³
(v) 400 ਮੀ.³ .

3. ਹੇਠਾਂ ਕੁੱਝ ਘਣਾਂ ਦੇ ਕਿਨਾਰਿਆਂ ਦੀ ਲੰਬਾਈ ਦਿੱਤੀ ਗਈ ਹੈ । ਹਰੇਕ ਘਣ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
6 ਸਮ
ਹੱਲ:
ਕਿਨਾਰੇ ਦੀ ਲੰਬਾਈ = 6 ਸਮ
ਘਣ ਦਾ ਆਇਤਨ = ਭੁਜਾ × ਭੁਜਾ × ਭੁਜਾ
= 6 ਸਮ × 6 ਸਮ × 6 ਸਮ
= 216 ਸਮ³

ਪ੍ਰਸ਼ਨ 2.
8 ਮੀ.
ਹੱਲ:
ਕਿਨਾਰੇ ਦੀ ਲੰਬਾਈ = 8 ਮੀ.
ਘਣ ਦਾ ਆਇਤਨ = ਭੁਜਾ × ਭੁਜਾ × ਭੁਜਾ
= 8. ਮੀ. × 8 ਮੀ. ×8 ਮੀ.
= 512 ਮੀ.³

ਪ੍ਰਸ਼ਨ 3.
15 ਮਿ.ਮੀ.
ਹੱਲ:
ਕਿਨਾਰੇ ਦੀ ਲੰਬਾਈ = 15 ਮਿ.ਮੀ.
ਘਣ ਦਾ ਆਇਤਨ = ਭੁਜਾ × ਭੁਜਾ × ਭੁਜਾ
= 15 ਮਿ. ਮੀ. × 15 ਮਿ. ਮੀ. × 15 ਮਿ.ਮੀ.
= 3375 ਮਿ.ਮੀ.³ .

ਪ੍ਰਸ਼ਨ 4.
21 ਮੀ.
ਹੱਲ :
ਕਿਨਾਰੇ ਦੀ ਲੰਬਾਈ = 21 ਮੀ.
ਘਣ ਦਾ ਆਇਤਨ = ਭੁਜਾ × ਭੁਜਾ × ਭੁਜਾ
= 21 ਮੀ. × 21 ਮੀ. × 21 ਮੀ.
= 9261 ਮੀ.³

4. ਉਸ ਘਣਾਵ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ ਜਿਸ ਦੀ ਲੰਬਾਈ, ਚੌੜਾਈ ਅਤੇ ਉੱਚਾਈ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ :

ਪ੍ਰਸ਼ਨ 1.
9 ਸੈਂ.ਮੀ., 6 ਸੈਂ.ਮੀ., 3 ਸੈਂ.ਮੀ.
ਹੱਲ:
ਘਣਾਵ ਦੀ ਲੰਬਾਈ = 9 ਸੈਂ.ਮੀ.
ਘਣਾਵ ਦੀ ਚੌੜਾਈ = 6 ਸੈਂ.ਮੀ.
ਘਣਾਵ ਦੀ ਉੱਚਾਈ = 3 ਸੈਂ.ਮੀ.
ਘਣਾਵ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 9 ਸੈਂ.ਮੀ. × 6 ਸੈਂ.ਮੀ. × 3 ਸੈਂ.ਮੀ.
= 162 ਸੈਂ.ਮੀ.³.

ਪ੍ਰਸ਼ਨ 2.
12 ਮਿ.ਮੀ., 9 ਮਿ.ਮੀ., 4 ਮਿ. ਮੀ.
ਹੱਲ:
ਘਣਾਵ ਦੀ ਲੰਬਾਈ = 12 ਮਿ.ਮੀ.
ਘਣਾਵ ਦੀ ਚੌੜਾਈ = 9 ਮਿ.ਮੀ.
ਘਣਾਵ ਦੀ ਉੱਚਾਈ = 4 ਮਿ.ਮੀ.
ਘਣਾਵ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 12 ਮਿ.ਮੀ. × 9 ਮਿ.ਮੀ. × 4 ਮਿ.ਮੀ.
= 432 ਮਿ.ਮੀ.³

ਪ੍ਰਸ਼ਨ 3.
15 ਮੀ., 13 ਮੀ., 12 ਮੀ.
ਹੱਲ:
ਘਣਾਵ ਦੀ ਲੰਬਾਈ = 15 ਮੀ.
ਘਣਾਵ ਦੀ ਚੌੜਾਈ = 13 ਮੀ.
ਘਣਾਵ ਦੀ ਉੱਚਾਈ = 12 ਮੀ.
ਘਣਾਵ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 15 ਮੀ. × 13 ਮੀ. × 12 ਮੀ.
= 2340 ਮੀ.³.

ਪ੍ਰਸ਼ਨ 4.
22 ਮਿ. ਮੀ., 16 ਮਿ. ਮੀ., 12 ਮਿ.ਮੀ.
ਹੱਲ:
ਘਣਾਵ ਦੀ ਲੰਬਾਈ = 22 ਮਿ.ਮੀ.
ਘਣਾਵ ਦੀ ਚੌੜਾਈ = 16 ਮਿ.ਮੀ.
ਘਣਾਵ ਦੀ ਉੱਚਾਈ = 12 ਮਿ.ਮੀ.
ਘਣਾਵ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 22 ਮਿ.ਮੀ. × 16 ਮਿ.ਮੀ. × 12 ਮਿ.ਮੀ.
= 4224 ਮਿ.ਮੀ.³

ਪ੍ਰਸ਼ਨ 5.
25 ਮੀ., 23 ਮੀ., 21 ਮੀ.
ਹੱਲ:
ਘਣਾਵ ਦੀ ਲੰਬਾਈ = 25 ਮੀ.
ਘਣਾਵ ਦੀ ਚੌੜਾਈ = 23 ਮੀ.
ਘਣਾਵ ਦੀ ਉੱਚਾਈ = 21 ਮੀ.
ਘਣਾਵ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 25 ਮੀ. × 23 ਮੀ. × 21 ਮੀ.
= 12075 ਮੀ.³

ਪ੍ਰਸ਼ਨ 5.
ਚਾਕਾਂ ਦਾ ਇੱਕ ਡੱਬਾ 8 ਸੈਂ. ਮੀ. ਲੰਬਾ, 6 ਸੈਂ. ਮੀ. ਚੌੜਾ ਅਤੇ 10 ਸੈਂ.ਮੀ. ਉੱਚਾ ਹੈ । ਇਸ ਦਾ ਆਇਤਨ ਕਿੰਨਾ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਚਾਕ ਦੇ ਡੱਬੇ ਦੀ ਲੰਬਾਈ = 8 ਸੈਂ.ਮੀ.
ਚਾਕ ਦੇ ਡੱਬੇ ਦੀ ਚੌੜਾਈ = 6 ਸੈਂ.ਮੀ.
ਚਾਕ ਦੇ ਡੱਬੇ ਦੀ ਉੱਚਾਈ 10 ਸੈਂ.ਮੀ.
ਚਾਕ ਦੇ ਡੱਬੇ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 8 ਸੈਂ.ਮੀ. × 6 ਸੈਂ.ਮੀ. × 10 ਸੈਂ.ਮੀ.
= 480 ਸੈਂ.ਮੀ.³

ਪ੍ਰਸ਼ਨ 6.
ਗੱਤੇ ਦੀ ਇੱਕ ਪੇਟੀ ਜਿਸ ਦੀ ਲੰਬਾਈ 50 ਸੈਂ.ਮੀ., ਚੌੜਾਈ 40 ਸੈਂ. ਮੀ. ਅਤੇ ਉੱਚਾਈ 24 ਸਮ ਹੈ । ਇਸ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਗੱਤੇ ਦੀ ਇਕ ਪੇਟੀ ਦੀ ਲੰਬਾਈ = 50 ਸੈਂ.ਮੀ.
ਗੱਤੇ ਦੀ ਇਕ ਪੇਟੀ ਦੀ ਚੌੜਾਈ =40 ਸੈਂ.ਮੀ.
ਗੱਤੇ ਦੀ ਇਕ ਪੇਟੀ ਦੀ ਉੱਚਾਈ = 24 ਸੈਂ.ਮੀ.
ਗੱਤੇ ਦੀ ਇਕ ਪੇਟੀ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 50 ਸੈਂ.ਮੀ. × 40 ਸੈਂ.ਮੀ. × 24 ਸੈਂ.ਮੀ.
= 48000 ਸੈਂ.ਮੀ.³

ਪ੍ਰਸ਼ਨ 7.
ਜਸ਼ਨ ਦੇ ਟਿਫਨ ਬਾਕਸ ਦੀ ਲੰਬਾਈ 15 ਸੈਂ.ਮੀ. , ਚੌੜਾਈ 10 ਸੈਂ.ਮੀ. ਅਤੇ ਉੱਚਾਈ 8 ਸੈਂ.ਮੀ. ਹੈ ਅਤੇ ਗੁਰਵਿੰਦਰ ਦੇ ਟਿਫਨ ਬਾਕਸ ਦੀ ਲੰਬਾਈ 12 ਸੈਂ.ਮੀ., ਚੌੜਾਈ 10 ਸੈਂ. ਮੀ. ਅਤੇ ਉੱਚਾਈ 10 ਸੈਂ. ਮੀ. ਹੈ । ਇਹਨਾਂ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ । ਕਿਸ ਦੇ ਟਿਫਨ ਬਾਕਸ ਦਾ ਆਇਤਨ ਜ਼ਿਆਦਾ ਹੈ ?
ਹੱਲ:
ਜਸ਼ਨ ਦੇ ਟਿਫਨ ਬਾਕਸ ਦੀ ਲੰਬਾਈ = 15 ਸੈਂ.ਮੀ.
ਜਸ਼ਨ ਦੇ ਟਿਫਨ ਬਾਕਸ ਦੀ ਚੌੜਾਈ = 10 ਸੈਂ.ਮੀ.
ਜਸ਼ਨ ਦੇ ਟਿਫਨ ਬਾਕਸ ਦੀ ਉੱਚਾਈ = 8 ਸੈਂ.ਮੀ.
ਜਸ਼ਨ ਦੇ ਟਿਫਨ ਬਾਕਸੇ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 15 ਸੈਂ.ਮੀ. × 10 ਸੈਂ.ਮੀ. × 8 ਸੈਂ.ਮੀ.
= 1200 ਸੈਂ.ਮੀ.³
ਗੁਰਵਿੰਦਰ ਦੇ ਟਿਫਨ ਬਾਕਸ ਦੀ ਲੰਬਾਈ = 12 ਸੈਂ.ਮੀ.
ਗੁਰਵਿੰਦਰ ਦੇ ਟਿਫਨ ਬਾਕਸ ਦੀ ਚੌੜਾਈ = 10 ਸੈਂ.ਮੀ.
ਗੁਰਵਿੰਦਰ ਦੇ ਟਿਫਨ ਬਾਕਸ ਦੀ ਉੱਚਾਈ = 10 ਸੈਂ.ਮੀ.
ਗੁਰਵਿੰਦਰ ਦੇ ਟਿਫਨ ਬਾਕਸ ਦਾ ਆਇਤਨ
= ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 12 ਸੈਂ.ਮੀ. × 10 ਸੈਂ.ਮੀ. × 10 ਸੈਂ.ਮੀ.
= 1200 ਸੈਂ.ਮੀ.³
ਦੋਨਾਂ ਦੇ ਟਿਫਨ ਬਾਕਸ ਦਾ ਆਇਤਨ ਬਰਾਬਰ ਹੈ ।

ਪ੍ਰਸ਼ਨ 8.
12 ਸੈਂ.ਮੀ. ਲੰਬਾਈ, 9 ਸੈਂ.ਮੀ. ਚੌੜਾਈ ਅਤੇ 6 ਸੈਂ. ਮੀ. ਉੱਚਾਈ ਵਾਲੇ 25 ਘਣਾਵਕਾਰੀ ਡੱਬਿਆਂ ਦਾ ਕੁੱਲ ਆਇਤਨ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਡੱਬੇ ਦੀ ਲੰਬਾਈ = 12 ਸੈਂ.ਮੀ.
ਡੱਬੇ ਦੀ ਚੌੜਾਈ = 9 ਸੈਂ.ਮੀ.
ਡੱਬੇ ਦੀ ਉੱਚਾਈ = 6 ਸੈਂ.ਮੀ.
ਡੱਬੇ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 12 ਸੈਂ.ਮੀ. × 9 ਸੈਂ.ਮੀ. × 6 ਸੈਂ.ਮੀ.
= 648 ਸੈਂ.ਮੀ.³
25 ਘਣਾਵਕਾਰੀ ਡੱਬਿਆਂ ਦਾ ਕੁੱਲ ਆਇਤਨ
= 648 × 25 ਸੈਂ.ਮੀ.³
= 16200 ਸੈਂ.ਮੀ.³

ਪ੍ਰਸ਼ਨ 9.
ਬਜ਼ਾਰ ਵਿੱਚ ਦੋ ਪ੍ਰਕਾਰ ਦੇ ਪਾਊਡਰ ਦੇ ਡੱਬੇ ਮਿਲਦੇ ਹਨ, ਇੱਕ 8 ਸੈਂ.ਮੀ. ਕਿਨਾਰੇ ਵਾਲਾ ਘਣ ਆਕਾਰ ਅਤੇ ਦੂਜਾ 15 ਸੈਂ. ਮੀ. ਲੰਬਾ, 8 ਸੈਂ. ਮੀ. ਚੌੜਾ ਅਤੇ 4 ਸੈਂ.ਮੀ. ਉੱਚਾਈ ਵਾਲਾ ਘਣਾਵਕਾਰ ਡੱਬਾ ਹੈ । ਦੱਸੋ ਕਿਸ ਡੱਬੇ ਵਿੱਚ ਵੱਧ ਪਾਊਡਰ ਆਵੇਗਾ ਅਤੇ ਕਿੰਨਾ ? ਜੇਕਰ ਦੋਹਾਂ ਦੀ ਕੀਮਤ ਇੱਕ ਸਮਾਨ ਹੋਵੇ ਤਾਂ ਤੁਸੀਂ ਕਿਹੜਾ ਡੱਬਾ ਲੈਣਾ ਪਸੰਦ ਕਰੋਗੇ ?
ਹੱਲ:
ਘਣਾਕਾਰ ਡੱਬੇ ਦੇ ਕਿਨਾਰੇ ਦੀ ਭੁਜਾ = 8 ਸੈਂ.ਮੀ.
ਘਣਾਕਾਰ ਡੱਬੇ ਵਿੱਚ ਪਾਉਡਰ ਦਾ ਆਇਤਨ = ਭੁਜਾ × ਭੁਜਾ × ਭੁਜਾ
= 8 ਸੈਂ.ਮੀ. × 8 ਸੈਂ.ਮੀ. × 8 ਸੈਂ.ਮੀ. .
= 512 ਸੈਂ.ਮੀ.³
ਦੁਜੇ ਘਣਾਵਕਾਰ ਡੱਬੇ ਦੀ ਲੰਬਾਈ = 15 ਸੈਂ.ਮੀ.
ਦੁਜੇ ਘਣਾਵਕਾਰ ਡੱਬੇ ਦੀ ਚੌੜਾਈ = 8 ਸੈਂ.ਮੀ.
ਦੂਜੇ ਘਣਾਵਕਾਰ ਡੱਬੇ ਦੀ ਉੱਚਾਈ = 4 ਸੈਂ.ਮੀ.
ਦੂਜੇ ਘਣਾਵਕਾਰ ਡੱਬੇ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 15 ਸੈਂ.ਮੀ. × 8 ਸੈਂ.ਮੀ. × 4 ਸੈਂ.ਮੀ.
= 480 ਸੈਂ.ਮੀ.³
ਘਣਾਕਾਰ ਡੱਬੇ ਵਿਚ 512-480 ਸੈਂ.ਮੀ.³ = 32 ਸੈਂ.ਮੀ.³ ਵੱਧ ਪਾਉਡਰ ਆਵੇਗਾ । ਜੇਕਰ ਦੋਹਾਂ ਦੀ ਕੀਮਤ ਇਕ ਸਮਾਨ ਹੋਵੇ ਤਾਂ ਅਸੀਂ ਘਣਾਕਾਰ ਡੱਬਾ ਲੈਣਾ ਪਸੰਦ ਕਰਾਂਗੇ ।

ਪ੍ਰਸ਼ਨ 10.
ਇੱਕ 12 ਮੀ. ਲੰਬੀ, 3 ਮੀ. ਉੱਚੀ ਅਤੇ 24 ਸੈਂ.ਮੀ. ਮੋਟੀ ਕੰਧ ਨੂੰ ਬਣਾਉਣ ਲਈ 24 ਸੈਂ.ਮੀ. ਲੰਬਾਈ, 12 ਸੈਂ.ਮੀ. ਚੌੜਾਈ ਅਤੇ 8 ਸੈਂ.ਮੀ. ਮੋਟਾਈ ਵਾਲੀਆਂ ਕਿੰਨੀਆਂ ਇੱਟਾਂ ਲੱਗਣਗੀਆਂ ?
ਹੱਲ:
ਕੰਧ ਦੀ ਲੰਬਾਈ = 12 ਮੀ. = 12 × 100
ਸੈਂ.ਮੀ. = 1200 ਸੈਂ.ਮੀ.
ਕੰਧ ਦੀ ਉਚਾਈ = 3 ਮੀ. = 3 × 100
ਸੈਂ.ਮੀ. = 300 ਸੈਂ.ਮੀ.
ਕੰਧ ਦੀ ਮੋਟਾਈ – 24 ਸੈਂ.ਮੀ.
ਕੰਧ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਮੋਟਾਈ
= 1200 ਸੈਂ.ਮੀ. × 300 ਸੈਂ.ਮੀ. ×24 ਸੈਂ.ਮੀ.
= 8640000 ਸੈਂ.ਮੀ.³
ਇੱਕ ਇੱਟ ਦੀ ਲੰਬਾਈ = 24 ਸੈਂ.ਮੀ.
ਇੱਕ ਇੱਟ ਦੀ ਚੌੜਾਈ = 12 ਸੈਂ.ਮੀ.
ਇੱਕ ਇੱਟ ਦੀ ਮੋਟਾਈ ” – 8 ਸੈਂ.ਮੀ.
ਇੱਕ ਇੱਟ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਮੋਟਾਈ
= 24 ਸੈਂ.ਮੀ. × 12 ਸੈਂ.ਮੀ. × 8 ਸੈਂ.ਮੀ.
= 2304 ਸੈਂ.ਮੀ.³
2304 ਸੈਂ.ਮੀ.³ ਵਾਲੀਆਂ ਜਿੰਨੀਆਂ ਇੱਟਾਂ

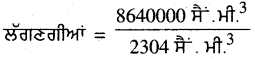
= 3750 ਇੱਟਾਂ

ਪ੍ਰਸ਼ਨ 11.
ਬਿਸਕੁਟਾਂ ਦੇ ਇੱਕ ਪੈਕਟ ਦੀ ਲੰਬਾਈ 15 ਸੈਂ. ਮੀ., ਚੌੜਾਈ 9 ਸੈਂ.ਮੀ. ਅਤੇ ਉੱਚਾਈ 6 ਸੈਂ.ਮੀ. ਹੈ । ਜੇਕਰ ਇੱਕ ਪੈਕਟ ਵਿੱਚ ਕੁੱਲ 30 ਬਿਸਕੁਟ ਹੋਣ ਤਾਂ ਹਰੇਕ ਬਿਸਕੁਟ ਦਾ ਆਇਤਨ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਬਿਸਕੁਟ ਦੇ ਇਕ ਪੈਕਟ ਦੀ ਲੰਬਾਈ = 15 ਸੈਂ.ਮੀ.
ਬਿਸਕੁਟ ਦੇ ਇਕ ਪੈਕਟ ਦੀ ਚੌੜਾਈ = 9 ਸੈਂ.ਮੀ.
ਬਿਸਕੁਟ ਦੇ ਇਕ ਪੈਕਟ ਦੀ ਉੱਚਾਈ = 6 ਸੈਂ.ਮੀ.
ਬਿਸਕੁਟ ਦੇ ਇਕ ਪੈਕਟ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 15 ਸੈਂ.ਮੀ. × 9 ਸੈਂ.ਮੀ. × 6 ਸੈਂ.ਮੀ.
= 810 ਸੈਂ.ਮੀ.³
ਇੱਕ ਪੈਕਟ ਵਿਚ ਕੁੱਲ ਬਿਸਕੁਟ = 30

= 27 ਸੈਂ.ਮੀ³

ਪ੍ਰਸ਼ਨ 12.
ਇੱਕ ਟਰਾਲੀ ਇੱਟਾਂ ਨਾਲ ਪੂਰੀ ਭਰੀ ਹੋਈ ਹੈ । ਇਸ ਟਰਾਲੀ ਦੀ ਲੰਬਾਈ 4 ਮੀ. , ਚੌੜਾਈ 2 ਮੀ. ਅਤੇ ਡੂੰਘਾਈ 60 ਸੈਂ.ਮੀ. ਹੈ। ਇੱਕ ਇੱਟ ਦੀ ਲੰਬਾਈ 20 ਸੈਂ.ਮੀ., ਚੌੜਾਈ 10 ਸੈਂ.ਮੀ. ਅਤੇ ਉੱਚਾਈ 6 ਸੈਂ.ਮੀ. ਹੈ । ਟਰਾਲੀ ਵਿੱਚ ਕਿੰਨੀਆਂ ਇੱਟਾਂ ਹੋਣਗੀਆਂ ?
ਹੱਲ:
ਟਰਾਲੀ ਦੀ ਲੰਬਾਈ = 4 ਮੀ.
= 4 × 100 ਸੈਂ.ਮੀ. = 400 ਸੈਂ.ਮੀ.
ਟਰਾਲੀ ਦੀ ਚੌੜਾਈ = 2 ਮੀ.
= 2 × 100 ਸੈਂ.ਮੀ. = 200 ਸੈਂ.ਮੀ.
ਟਰਾਲੀ ਦੀ ਡੂੰਘਾਈ = 60 ਸੈਂ.ਮੀ.
ਟਰਾਲੀ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਡੂੰਘਾਈ
= 400 ਸੈਂ.ਮੀ. × 200 ਸੈਂ.ਮੀ. × 60 ਸੈਂ.ਮੀ.
= 4800000 ਸੈਂ.ਮੀ.³
ਇੱਕ ਇੱਟ ਦੀ ਲੰਬਾਈ = 20 ਸੈਂ.ਮੀ.
ਇੱਕ ਇੱਟ ਦੀ ਚੌੜਾਈ = 10 ਸੈਂ.ਮੀ.
ਇੱਕ ਇੱਟ ਦੀ ਉੱਚਾਈ = 6 ਸੈਂ.ਮੀ.
ਇੱਕ ਇੱਟ ਦਾ ਆਇਤਨ = ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ
= 20 ਸੈਂ.ਮੀ. × 10 ਸੈਂ.ਮੀ. × 6 ਸੈਂ.ਮੀ.
= 1200 ਸੈਂ.ਮੀ.³
ਟਰਾਲੀ ਵਿੱਚ ਜਿੰਨੀਆਂ ਇੱਟਾਂ ਹੋਣਗੀਆਂ
= \(\frac{4800000}{1200}\) ਸੈਂ.ਮੀ.³
= 4000

13. ਖਾਲੀ ਥਾਂਵਾਂ ਭਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਘਣ ਦਾ ਆਇਤਨ = …………. × ……….. × ………….
ਹੱਲ:
ਭੁਜਾ × ਭੁਜਾ × ਭੁਜਾ

ਪ੍ਰਸ਼ਨ 2.
ਘਣਾਵ ਦਾ ਆਇਤਨ = ……………. × …………….. × ……………
ਹੱਲ:
ਲੰਬਾਈ × ਚੌੜਾਈ × ਉੱਚਾਈ

ਪ੍ਰਸ਼ਨ 3.
ਕਿਸੇ ਠੋਸ ਦੁਆਰਾ ਘੇਰੀ ਗਈ ਥਾਂ ਨੂੰ ਉਸ ਠੋਸ ਦਾ …………. ਆਖਦੇ ਹਨ ।
ਹੱਲ:
ਆਇਤਨ

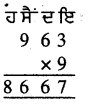
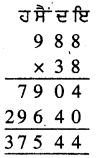
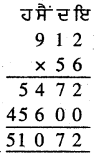
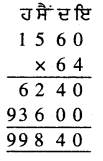
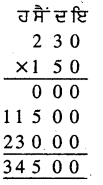
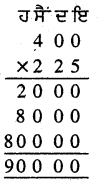
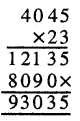
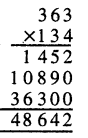
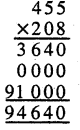
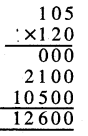
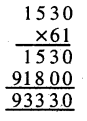
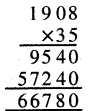
Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 2 ਸੰਖਿਆਵਾਂ ਉੱਪਰ ਮੁੱਢਲੀਆਂ ਕਿਰਿਆਵਾਂ Ex 2.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 2 ਸੰਖਿਆਵਾਂ ਉੱਪਰ ਮੁੱਢਲੀਆਂ ਕਿਰਿਆਵਾਂ Ex 2.2

ਸਮਝੋ ਅਤੇ ਕਰੋ-

Question 1.
* ਦੀ ਥਾਂ ‘ਤੇ ਸੰਖਿਆ ਕਰੋ :

(a)

ਹੱਲ:

(b)

ਹੱਲ:

(c)

ਹੱਲ:

(d)

ਹੱਲ:

(e)

ਹੱਲ:

(f)

ਹੱਲ:

(g)

ਹੱਲ:

(h)

ਹੱਲ:

ਹੈਲ ਕਰੋ :

(a) 1238 – 1025 + 5018
ਹੱਲ:

(b) 9386 – 2535 – 1002
ਹੱਲ:

(c) 6307 – 4052 + 2115
ਹੱਲ:

(d) 8107 + 2437 – 6089
ਹੱਲ:

(e) 18337 + 30947 – 34413
ਹੱਲ:

(f) 91206 – 70413 + 30824
ਹੱਲ:

(g) 10003 – 5911 – 3284
ਹੱਲ:

(h) 92319 – 65424 – 12105
ਹੱਲ:

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 2 ਸੰਖਿਆਵਾਂ ਉੱਪਰ ਮੁੱਢਲੀਆਂ ਕਿਰਿਆਵਾਂ Ex 2.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 2 ਸੰਖਿਆਵਾਂ ਉੱਪਰ ਮੁੱਢਲੀਆਂ ਕਿਰਿਆਵਾਂ Ex 2.1

ਸੰਮਝੋ ਅਤੇ ਕਰੋ-

ਪ੍ਰਸ਼ਨ 1.
ਹੱਲ ਕਰੋ :
(a) 6574 + 5502
ਹੱਲ:

(b) 5350 +4102
ਹੱਲ:

(c) 56754 + 25740
Solution:

(d) 25000 + 11887
Solution:

(e) 8988 – 2450
Solution:

(f) 8990 – 1034
Solution:

(g) 80029 – 21200
Solution:

(h) 56789 – 1234
ਹੱਲ:

ਪ੍ਰਸ਼ਨ 2.
ਹੱਲ ਕਰੋ :
(a) 8760 + 2584
ਹੱਲ:

(b) 9649 + 5161
ਹੱਲ:

(c) 38009 + 55691
ਹੱਲ:

(d) 25347 + 74040
ਹੱਲ:

(e) 8761+ 5584 + 4320
ਹੱਲ:

(f) 4687 + 1000 + 1130
ਹੱਲ:

(g) 28740 + 54938 + 12338
ਹੱਲ:

(h) 72624+ 3106 + 10234
ਹੱਲ:

(i) 8849 – 4118
ਹੱਲ:

(j) 51307 – 42158
ਹੱਲ:

(k) 80003 – 19219
ਹੱਲ:

(l) 70000 – 12345
ਹੱਲ:

ਪ੍ਰਸ਼ਨ 3.
ਘਟਾਓ ਅਤੇ ਪੜਤਾਲ ਕਰੋ :
(a) 98920 – 12334
ਹੱਲ:

(b) 40013 – 18167
ਹੱਲ:

(c) 78901 – 52214
ਹੱਲ:

(d) 40467 – 10239
ਹੱਲ:

(e) 79571 – 48678
ਹੱਲ:

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 10 ਅੰਕੜਾ ਵਿਗਿਆਨ MCQ Questions and Answers.

PSEB 5th Class Maths Chapter 10 ਅੰਕੜਾ ਵਿਗਿਆਨ MCQ Questions

ਬਹੁ-ਵਿਕਲਪਿਕ ਪ੍ਰਸ਼ਨ

1. ਕਿਸੇ ਸ਼ਹਿਰ ਦੇ ਸੱਤ ਦਿਨਾਂ ਦੇ ਵੱਧ ਤੋਂ ਵੱਧ ਤਾਪਮਾਨ ਦੇ ਅੰਕੜੇ ਇਸ ਤਰ੍ਹਾਂ ਹਨ :

ਪ੍ਰਸ਼ਨ 1.
ਸਭ ਤੋਂ ਜ਼ਿਆਦਾ ਗਰਮ ਦਿਨ ਕਿਹੜਾ ਹੈ ?
(a) ਮੰਗਲਵਾਰ
(b) ਵੀਰਵਾਰ
(c) ਐਤਵਾਰ
(d) ਸੋਮਵਾਰ
ਹੱਲ:
c) ਐਤਵਾਰ

ਪ੍ਰਸ਼ਨ 2.
ਕਿਹੜਾ ਦਿਨ ਸਭ ਤੋਂ ਠੰਡਾ ਰਿਹਾ ?
(a) ਬੁੱਧਵਾਰ
(b) ਮੰਗਲਵਾਰ
(c) ਸ਼ਨੀਵਾਰ
(d) ਸ਼ੁੱਕਰਵਾਰ
ਹੱਲ:
(b) ਮੰਗਲਵਾਰ

ਪ੍ਰਸ਼ਨ 3.
ਸਭ ਤੋਂ ਵੱਧ ਅਤੇ ਘੱਟ ਤਾਪਮਾਨ ਵਿੱਚ ਕਿੰਨਾ ਅੰਤਰ ਹੈ ?
(a) 6°C
(b 8°C
(c) 5°C
(d) 7°C.
ਹੱਲ :
(d) 7°C

ਪ੍ਰਸ਼ਨ 4.
ਕਿਹੜੇ ਦੋ ਦਿਨ ਬਰਾਬਰ ਗਰਮ ਰਹੇ ?
(a) ਵੀਰਵਾਰ ਅਤੇ ਸ਼ਨੀਵਾਰ
(b) ਐਤਵਾਰ ਅਤੇ ਸੋਮਵਾਰ ,
(c) ਮੰਗਲਵਾਰ, ਅਤੇ ਬੁੱਧਵਾਰ
(d) ਵੀਰਵਾਰ ਅਤੇ ਸ਼ੁੱਕਰਵਾਰ ।
ਹੱਲ:
(a) ਵੀਰਵਾਰ ਅਤੇ ਸ਼ਨੀਵਾਰ ।

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ ਕ੍ਰਿਕੇਟ ਦੇ ਖਿਡਾਰੀ ਦੁਆਰਾ ਲਗਾਤਾਰ ਚਾਰ ਸਾਲਾਂ ਵਿੱਚ ਬਣਾਈਆਂ ਗਈਆਂ ਦੌੜਾਂ ਇਸ ਤਰ੍ਹਾਂ ਹਨ ।

ਪ੍ਰਸ਼ਨ 1.
ਖਿਡਾਰੀ ਨੇ 2016 ਵਿੱਚ ਕਿੰਨੀਆਂ ਦੌੜਾਂ ਬਣਾਈਆਂ ?
(a) 300
(b) 400
(c) 350
d) 200
ਹੱਲ:
(b) 400

ਪ੍ਰਸ਼ਨ 2.
ਖਿਡਾਰੀ ਨੇ ਸਭ ਤੋਂ ਘੱਟ ਦੌੜਾਂ ਕਿਹੜੇ ਸਾਲ ਦੌਰਾਨ ਬਣਾਈਆਂ ?
(a) 2017
(b) 2016
(c) 2015
(d) 2014.
ਹੱਲ:
(c) 2015

ਪ੍ਰਸ਼ਨ 3.
ਖਿਡਾਰੀ ਦੁਆਰਾ ਸਭ ਤੋਂ ਵੱਧ ਅਤੇ ਸਭ ਤੋਂ ਘੱਟ ਬਣਾਈਆਂ ਗਈਆਂ ਦੌੜਾਂ ਦਾ ਅੰਤਰ ਕਿੰਨਾ ਹੈ ?
(a) 150
(b) 50
(c) 200
(d) 100
ਹੱਲ:
(a) 150

ਪ੍ਰਸ਼ਨ 4.
ਖਿਡਾਰੀ ਦੁਆਰਾ ਲਗਾਤਾਰ ਚਾਰ ਸਾਲਾਂ ਵਿੱਚ ਬਣਾਈਆਂ ਗਈਆਂ ਕੁੱਲ ਦੌੜਾਂ ਕਿੰਨੀਆਂ ਹਨ ?
(a) 1100
(b) 1000
(c) 1300
(d) 1200
ਹੱਲ:
(c) 1300.

ਪ੍ਰਸ਼ਨ 3.
ਚਿੱਤਰ ਨੂੰ ਦੇਖ ਕੇ ਦੱਸੋ ਕਿ ਖੇਡ-3 ਵਿਚ ਕਿੰਨੇ ਪ੍ਰਾਪਤ ਕੀਤੇ ਅੰਕ ਬਣਾਏ ਗਏ ਹਨ ?

(a) 35
(b) 30
(c) 40
(d) 25
ਹੱਲ:
(c) 40

ਪ੍ਰਸ਼ਨ 4.
ਚਿੱਤਰਗ੍ਰਾਫ ਅਨੁਸਾਰ ਸ਼ਹਿਰ ਖੰਨਾ ਵਿਚ ਕਿੰਨੀਆਂ ਕਾਰਾਂ ਵਿਕੀਆਂ ?

(a) 6
(b) 600
(c) 300
(d) 400
ਹੱਲ:
(b) 600

ਪ੍ਰਸ਼ਨ 5.
ਦਿੱਤੇ ਗਏ ਪਾਈ ਚਾਰਟ (ਗੋਲ ਨਕਸ਼ਾ) ਵਿੱਚ ਜਮਾਤ ਪੰਜਵੀਂ ਦੇ ਬੱਚਿਆਂ ਦੇ ਮਨਪਸੰਦ ਰੰਗਾਂ ਬਾਰੇ ਦੱਸਿਆ ਗਿਆ ਹੈ | ਪਾਈ ਚਾਰਟ ਨੂੰ ਧਿਆਨ ਨਾਲ ਦੇਖੋ ਅਤੇ ਉੱਤਰ ਦਿਓ ।

(a) ਜਮਾਤ ਦੇ ਕਿੰਨੇ ਬੱਚਿਆਂ (ਨਾਤਮਕ ਰੂਪ ਵਿੱਚ) ਨੂੰ ਹਰਾ ਰੰਗ ਪਸੰਦ ਹੈ ?
(b) ਜਮਾਤ ਦੇ ਬੱਚਿਆਂ ਵੱਲੋਂ ਕਿਹੜੇ ਰੰਗ ਨੂੰ ਸਭ ਤੋਂ ਵੱਧ ਪਸੰਦ ਕੀਤਾ ਗਿਆ ਹੈ ?
(c) ਜੇਕਰ ਜਮਾਤ ਵਿੱਚ ਕੁੱਲ 40 ਬੱਚੇ ਹਨ, ਤਾਂ ਜਮਾਤ ਦੇ ਕਿੰਨੇ ਬੱਚਿਆਂ ਨੂੰ ਹਰਾ ਰੰਗ ਪਸੰਦ ਹੈ ?
ਹੱਲ:
(a) ਜਮਾਤ ਦੇ ਜਿੰਨੇ ਬੱਚਿਆਂ ਨੂੰ ਹਰਾ ਰੰਗ ਪਸੰਦ ਹੈ = \(\frac{1}{4}\)
(b) ਜਮਾਤ ਦੇ ਬੱਚਿਆਂ ਵੱਲੋਂ ਜਿਸ ਰੰਗ ਨੂੰ ਸਭ ਤੋਂ ਵੱਧ ਪਸੰਦ ਕੀਤਾ ਗਿਆ = ਲਾਲ
(c) ਜਮਾਤ ਦੇ ਜਿੰਨੇ ਬੱਚਿਆਂ ਨੂੰ ਹਰਾ ਰੰਗ ਪਸੰਦ ਹੈ = 40 × \(\frac{1}{4}\) = 10

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 10 ਅੰਕੜਾ ਵਿਗਿਆਨ Ex 10.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 10 ਅੰਕੜਾ ਵਿਗਿਆਨ Ex 10.2

1. ਹੇਠਾਂ ਦਿੱਤੇ ਚਿੱਤਰਫ਼ ਵਿੱਚ, ਦੋ ਵੱਖੋ-ਵੱਖਰੇ ਸੈਸ਼ਨਾਂ 2014-15 ਅਤੇ 2015-16 ਦੌਰਾਨ ਜਮਾਤ ਪੰਜਵੀਂ ਦੇ ਸੈਕਸ਼ਨਾਂ A, B, C ਅਤੇ D ਵਿੱਚ ਮੁੰਡਿਆਂ ਦੀ ਗਿਣਤੀ ਦਰਸਾਈ ਗਈ ਹੈ ।

ਪ੍ਰਸ਼ਨ 1.
ਸੈਕਸ਼ਨ A ਵਿੱਚ ਕਿਸ ਸੈਸ਼ਨ ਦੌਰਾਨ ਮੁੰਡਿਆਂ ਦੀ ਗਿਣਤੀ ਜ਼ਿਆਦਾ ਹੈ ।
ਹੱਲ:
2015 – 16

ਪ੍ਰਸ਼ਨ 2.
ਸੈਕਸ਼ਨ D ਵਿੱਚ 2014-15 ਅਤੇ 2015-16 ਵਿੱਚ ਮੁੰਡਿਆਂ ਦੀ ਗਿਣਤੀ ……………….. ਹੈ । (ਬਰਾਬਰ – ਵੱਧ/ਘੱਟ)
ਹੱਲ:
ਬਰਾਬਰ

ਪ੍ਰਸ਼ਨ 3.
ਸੈਸ਼ਨ 2014-15 ਵਿੱਚ ਮੁੰਡਿਆਂ ਦੀ ਕੁੱਲ ਗਿਣਤੀ ਕਿੰਨੀ ਹੈ ?
ਹੱਲ:
(4 + 3 + 5 + 4) × 5 = 16 × 5 = 80

ਪ੍ਰਸ਼ਨ 4.
ਦੋਵੇਂ ਸੈਸ਼ਨਾਂ ਦੌਰਾਨ ਸੈਕਸ਼ਨ ਵਿੱਚ ਮੁੰਡਿਆਂ ਦੀ ਗਿਣਤੀ ਦਾ ਅੰਤਰ ਕਿੰਨਾ ਹੈ ?
ਹੱਲ:
30 – 25 = 5

ਪ੍ਰਸ਼ਨ 5.
ਸੈਸ਼ਨ 2015-16 ਵਿੱਚ ਮੁੰਡਿਆਂ ਦੀ ਗਿਣਤੀ 5 ਸੈਸ਼ਨ 2014-15 ਨਾਲੋਂ ਕਿੰਨੀ ਵੱਧ/ਘੱਟ ਹੈ ।
ਹੱਲ:
2015-16 ਵਿੱਚ ਮੁੰਡਿਆਂ ਦੀ ਗਿਣਤੀ 19 × 5 – 16 × 5 = 95 – 80 = 15 ਵੱਧ ਹੈ ।

2. ਹੇਠਾਂ ਦੋ ਛੜ ਗਾਫ਼ ਦਿੱਤੇ ਗਏ ਹਨ । ਇਹਨਾਂ ਵਿੱਚ ਦੋ ਵੱਖ-ਵੱਖ ਦਿਨਾਂ ਵਿੱਚੋਂ ਚਾਰ ਸ਼ਹਿਰਾਂ ਦਾ ਵੱਧ ਤੋਂ ਵੱਧ ਤਾਪਮਾਨ ਦਿਖਾਇਆ ਗਿਆ ਹੈ । ਇਹ ਸ਼ਹਿਰ ਹਨ-ਦਿੱਲੀ, ਸ਼ਿਮਲਾ, ਬੰਗਲੁਰੂ ਅਤੇ ਜੈਸਲਮੇਰ ।

ਦਸੰਬਰ ਉਪਰੋਕਤ ਚਾਰਟ ਤੋਂ ਪਤਾ ਕਰੋ :

ਪ੍ਰਸ਼ਨ 1.
ਜੂਨ ਨੂੰ ਕਿਹੜਾ ਸ਼ਹਿਰ ਸਭ ਤੋਂ ਵੱਧ ਗਰਮ ਹੈ ?
ਹੱਲ:
ਜੈਸਲਮੇਰ

ਪ੍ਰਸ਼ਨ 2.
1 ਦਸੰਬਰ ਨੂੰ ਕਿਹੜਾ ਸ਼ਹਿਰ ਸਭ ਤੋਂ ਵੱਧ ਠੰਡਾ ਹੈ ?
ਹੱਲ:
ਸ਼ਿਮਲਾ

ਪ੍ਰਸ਼ਨ 3.
1 ਜੂਨ ਅਤੇ 1 ਦਸੰਬਰ ਨੂੰ ਦਿੱਲੀ ਦੇ ਤਾਪਮਾਨ ਵਿੱਚ ਕਿੰਨਾ ਅੰਤਰ ਹੈ ?
ਹੱਲ:
33°C – 23°C = 10°C

ਪ੍ਰਸ਼ਨ 4.
1 ਜੂਨ ਅਤੇ 1 ਦਸੰਬਰ ਨੂੰ ਸ਼ਿਮਲਾ ਦੇ ਤਾਪਮਾਨ ਵਿੱਚ ਕਿੰਨਾ ਅੰਤਰ ਹੈ ?
ਹੱਲ:
22°C – 10°C = 12°C

ਪ੍ਰਸ਼ਨ 5.
ਕਿਹੜੇ ਸ਼ਹਿਰ ਵਿੱਚ 1 ਜੂਨ ਅਤੇ 1 ਦਸੰਬਰ ਦੇ ਵਿੱਚ ਤਾਪਮਾਨ ਵਿੱਚ ਸਭ ਤੋਂ ਘੱਟ ਬਦਲਾਅ ਆਇਆ ?
ਹੱਲ:
ਬੰਗਲੁਰੂ ।

3. ਹੇਠਾਂ ਦਿੱਤੇ ਛੜ ਗਰਾਫ਼ ਨੂੰ ਧਿਆਨ ਨਾਲ ਪੜ੍ਹੋ : ਪਤਾ ਕਰੋ

ਪ੍ਰਸ਼ਨ 1.
ਉਪਰੋਕਤ ਛੜ ਗਾਫ਼ ਸਾਨੂੰ ਕੀ ਜਾਣਕਾਰੀ ਦੇ ਰਹੇ ਹਨ ?
ਹੱਲ:
ਛੜ ਗ੍ਰਾਫ਼ ਤੋਂ ਸਾਨੂੰ ਜਮਾਤ ਤੀਜੀ ਅਤੇ ਚੌਥੀ ਦੇ ਬੱਚਿਆਂ ਦੁਆਰਾ ਖੇਡੀਆਂ ਜਾਣ ਵਾਲੀਆਂ ਖੇਡਾਂ ਦੇ ਬਾਰੇ ਪਤਾ ਲਗਦਾ ਹੈ.

ਪ੍ਰਸ਼ਨ 2.
ਕਿਹੜੀ ਖੇਡ ਜਮਾਤ ਤੀਜੀ ਅਤੇ ਚੌਥੀ ਦੇ ਬੱਚਿਆਂ ਦੁਆਰਾ ਬਰਾਬਰ ਖੇਡੀ ਜਾਂਦੀ ਹੈ ?
ਹੱਲ:
ਫੁੱਟਬਾਲ

ਪ੍ਰਸ਼ਨ 3.
ਜਮਾਤ ਤੀਜੀ ਅਤੇ ਜਮਾਤ ਚੌਥੀ ਦੇ ਖੋ-ਖੋ ਖੇਡਣ ਵਾਲੇ ਬੱਚਿਆਂ ਦੀ ਕੁੱਲ ਗਿਣਤੀ ਕਿੰਨੀ ਹੈ ?

ਹੱਲ:
15 + 35 = 50

ਪ੍ਰਸ਼ਨ 4.
ਜਮਾਤ ਤੀਜੀ ਅਤੇ ਚੌਥੀ ਦੇ ਬਾਸਕਟ ਬਾਲ ਖੇਡਣ ਵਾਲੇ ਬੱਚਿਆਂ ਦੀ ਕੁੱਲ ਗਿਣਤੀ ਕਿੰਨੀ ਹੈ ?
ਹੱਲ:
25 + 20 = 45

ਪ੍ਰਸ਼ਨ 5.
ਜਮਾਤ ਤੀਜੀ ਦੇ ਬੱਚਿਆਂ ਦੀ ਸਭ ਤੋਂ ਵੱਧ ਮਨਪਸੰਦ ਖੇਡ ਕਿਹੜੀ ਹੈ ?
ਹੱਲ:
ਫੁੱਟਬਾਲ

ਪ੍ਰਸ਼ਨ 6.
ਜਮਾਤ ਚੌਥੀ ਦੇ ਬੱਚਿਆਂ ਦੀ ਸਭ ਤੋਂ ਵੱਧ ਮਨਪਸੰਦ ਖੇਡ ਕਿਹੜੀ ਹੈ ?
ਹੱਲ:
ਖੋ-ਖੋ ।

Punjab State Board PSEB 5th Class Maths Book Solutions Chapter 10 ਅੰਕੜਾ ਵਿਗਿਆਨ Ex 10.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 5 Maths Chapter 10 ਅੰਕੜਾ ਵਿਗਿਆਨ Ex 10.1

ਪ੍ਰਸ਼ਨ 1.
ਇੱਕ ਸਕੂਲ ਦੇ ਬੱਚੇ ਪਿਕਨਿਕ ਲਈ ਚਿੜੀਆਘਰ ਗਏ । ਬੱਚਿਆਂ ਦੁਆਰਾ ਵੱਖ-ਵੱਖ ਜਾਨਵਰਾਂ ਦੀ ਗਿਣਤੀ ਦੇ ਅੰਕੜੇ ਇੱਕਤਰ ਕੀਤੇ ਗਏ, ਜਿਨ੍ਹਾਂ ਵਿੱਚੋਂ ਕੁਝ ਜਾਨਵਰਾਂ ਦੀ ਗਿਣਤੀ ਇਸ ਪ੍ਰਕਾਰ ਹੈ : ਬਾਂਦਰ-32, ਸ਼ੇਰ- 10, ਹਿਰਨ25, ਖਰਗੋਸ਼-27 ਅਤੇ ਲੂੰਬੜੀ-39 । ਇਹਨਾਂ ਅੰਕੜਿਆਂ ਨੂੰ ਸਾਰਣੀ ਦੇ ਰੂਪ ਵਿੱਚ ਪ੍ਰਗਟ ਕਰੋ ।


ਹੱਲ:
ਅਸੀਂ ਉਪਰੋਕਤ ਜਾਣਕਾਰੀ ਨੂੰ ਸਾਰਣੀ ਦੇ ਰੂਪ ਵਿਚ ਹੇਠਾਂ ਦਿੱਤੇ ਅਨੁਸਾਰ ਦਿਖਾ ਸਕਦੇ ਹਾਂ :

ਪ੍ਰਸ਼ਨ 2.
ਕਿਸੇ ਪਿੰਡ ਵਿੱਚ ਸਰਕਸ ਲੱਗੀ ਹੋਈ ਹੈ । ਸੋਮਵਾਰ ਤੋਂ ਸ਼ੁਕਰਵਾਰ ਤੱਕ ਸਰਕਸ ਦੇਖਣ ਆਏ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਚਿੱਤਰਫ਼ ਦੁਆਰਾ ਦਰਸਾਈ ਗਈ ਹੈ । ਹੇਠਾਂ ਦਿੱਤੇ ਚਿੱਤਰਫ਼ ਨੂੰ ਧਿਆਨ ਨਾਲ ਪੜ੍ਹ ਕੇ ਉੱਤਰ ਦਿਓ ।

1. ਮੰਗਲਵਾਰ ਨੂੰ ਕਿੰਨੇ ਬੱਚੇ ਸਰਕਸ ਦੇਖਣ ਆਏ ?
2. ਕਿਸ ਦਿਨ ਸਭ ਤੋਂ ਵੱਧ ਬੱਚੇ ਸਰਕਸ ਦੇਖਣ ਆਏ ਅਤੇ ਕਿੰਨੇ ?
3. ਕਿਸ ਦਿਨ ਸਭ ਤੋਂ ਘੱਟ ਬੱਚੇ ਸਰਕਸ ਦੇਖਣ ਆਏ ਅਤੇ ਕਿੰਨੇ ?
4. ਸੋਮਵਾਰ ਅਤੇ ਬੁੱਧਵਾਰ ਨੂੰ ਕੁੱਲ ਕਿੰਨੇ ਬੱਚਿਆਂ ਨੇ ਸਰਕਸ ਦੇਖੀ ?
5. ਵੀਰਵਾਰ ਅਤੇ ਸ਼ੁੱਕਰਵਾਰ ਸਰਕਸ ਦੇਖਣ ਵਾਲੇ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਵਿੱਚ ਕਿੰਨਾ ਅੰਤਰ ਹੈ ?

ਹੱਲ:

1. ਮੰਗਲਵਾਰ ਨੂੰ 3 × 25 = 75 ਬੱਚੇ ਸਰਕਸ ਦੇਖਣ ਆਏ ।
2. ਵੀਰਵਾਰ ਨੂੰ ਸਭ ਤੋਂ ਵੱਧ, 8 × 25 = 200 . ਬੱਚੇ ਕਸ ਦੇਖਣ ਆਏ ।
3.  ਸੋਮਵਾਰ ਨੂੰ ਸਭ ਤੋਂ ਘੱਟ, 2 × 25 = 50 ਬੱਚੇ ਸਰਕਸ ਦੇਖਣ ਆਏ ।
4.  ਸੋਮਵਾਰ ਅਤੇ ਬੁੱਧਵਾਰ ਨੂੰ ਕੁੱਲ (2 +5) × 25 = 7 × 25 = 175 ਬੱਚਿਆਂ ਨੇ ਸਰਕਸ ਦੇਖੀ ।
5. ਵੀਰਵਾਰ ਅਤੇ ਸ਼ੁੱਕਰਵਾਰ ਸਰਕਸ ਦੇਖਣ ਵਾਲੇ , ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਵਿੱਚ ਜਿੰਨਾ ਅੰਤਰ ਹੈ = 200 – 150 = 50.

ਪ੍ਰਸ਼ਨ 3.
ਪੰਜ ਵੱਖ-ਵੱਖ ਪਿੰਡਾਂ ਵਿੱਚ ਗਰੀਨ ਦਿਵਾਲੀ ਮਨਾਉਣ ਲਈ ਦਿਵਾਲੀ ਦੇ ਮੌਕੇ ਅੱਗੇ ਲਿਖੇ ਅਨੁਸਾਰ ਦਰੱਖ਼ਤ ਲਗਾਏ ਗਏ ।

(i) ਉਪਰੋਕਤ ਅੰਕੜਿਆਂ ਲਈ ਚਿੱਤਰਗ੍ਰਾਫ਼ ਤਿਆਰ ਕੀਤਾ ਜਾਵੇ ।

(ii) ਉਪਰੋਕਤ ਜਾਣਕਾਰੀ ਨੂੰ ਕੋਈ ਹੋਰ ਪੈਮਾਨਾ ਵਰਤ ਕੇ ਚਿੱਤਰਫ਼ ਤਿਆਰ ਕੀਤਾ ਜਾਵੇ ।
ਹੱਲ:
(i)

(ii)

ਪ੍ਰਸ਼ਨ 4.
ਤਿਉਹਾਰਾਂ ਮੌਕੇ ਕਿਸੇ ਮਿਠਾਈ ਦੀ ਦੁਕਾਨ ਵਿੱਚ ਇੱਕ ਹਫ਼ਤੇ ਵਿੱਚ ਵਰਤੇ ਗਏ ਦੁੱਧ ਦੀ ਮਾਤਰਾ ਹੇਠਾਂ ਦਿੱਤੇ ਛੜ ਗ੍ਰਾਫ਼ ਅਨੁਸਾਰ ਹੈ ।

1.  ਸਭ ਤੋਂ ਵੱਧ ਦੁੱਧ ਕਿਹੜੇ ਦਿਨ ਵਰਤਿਆ ਗਿਆ ?
2.  ਸਭ ਤੋਂ ਘੱਟ ਦੁੱਧ ਕਿਹੜੇ ਦਿਨ ਵਰਤਿਆ ਗਿਆ ?
3. ਕਿਹੜੇ ਦੋ ਦਿਨਾਂ ਦੌਰਾਨ ਇੱਕੋ ਜਿਹੀ ਮਾਤਰਾ ਵਿੱਚ ਦੁੱਧ ਵਰਤਿਆ ਗਿਆ ਅਤੇ ਕਿੰਨਾ ?
4. ਵੀਰਵਾਰ ਅਤੇ ਸ਼ੁੱਕਰਵਾਰ ਨੂੰ ਕੁੱਲ ਕਿੰਨਾ ਦੁੱਧ ਵਰਤਿਆ ਗਿਆ ?
5. ਐਤਵਾਰ ਨਾਲੋਂ ਮੰਗਲਵਾਰ ਨੂੰ ਕਿੰਨਾ ਘੱਟ ਦੁੱਧ ਵਰਤਿਆ ਗਿਆ ?
6. ਸਭ ਤੋਂ ਵੱਧ ਵਰਤੇ ਗਏ ਦੁੱਧ ਅਤੇ ਸਭ ਤੋਂ ਘੱਟ ਵਰਤੇ ਗਏ ਦੁੱਧ ਦਾ ਅੰਤਰ ਕਿੰਨਾ ਹੈ ?

ਹੱਲ:

1. ਐਤਵਾਰ,
2. ਬੁੱਧਵਾਰ,
3. ਸੋਮਵਾਰ ਅਤੇ ਸ਼ਨਿਚਰਵਾਰ,
4. 550
5. 350 l – 200 l = 150 l
6. 350 l – 100 l = 250 l.

ਪ੍ਰਸ਼ਨ 5.
ਇੱਕ ਦੁਕਾਨ ‘ਤੇ ਅਕਤੂਬਰ ਮਹੀਨੇ ਵਿੱਚ ਵੇਚੇ ਗਏ ਵੱਖ-ਵੱਖ ਕੰਪਨੀਆਂ ਦੇ ਮੋਬਾਇਲ ਸੈਂਟਾਂ ਦਾ ਵੇਰਵਾ ਹੇਠਾਂ ਦਿੱਤੇ ਅਨੁਸਾਰ ਹੈ :

ਉਪਰੋਕਤ ਜਾਣਕਾਰੀ ਨੂੰ ਦਰਸਾਉਂਦਾ ਛੜ ਫ਼ ਤਿਆਰ ਕੀਤਾ ਜਾਵੇ ।
ਸੰਕੇਤ – 8 ਸੈਟਾਂ ਦਾ ਪੈਮਾਨਾ ਲਿਆ ਜਾਵੇ
ਹੱਲ:

ਪ੍ਰਸ਼ਨ 6.
ਕਿਸੇ ਸਕੂਲ ਵਿੱਚ ਪਹਿਲੀ ਜਮਾਤ ਤੋਂ ਪੰਜਵੀਂ ਜਮਾਤ ਤੱਕ ਦੇ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ :

ਉਪਰੋਕਤ ਜਾਣਕਾਰੀ ਨੂੰ ਦਰਸਾਉਂਦਾ ਛੜ ਗ੍ਰਾਫ਼ ਤਿਆਰ ਕੀਤਾ ਜਾਵੇ ।
ਸੰਕੇਤ – 10 ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਦਾ ਪੈਮਾਨਾ ਲਿਆ ਜਾਵੇ ।
ਹੱਲ:

ਪ੍ਰਸ਼ਨ 7.

ਉਪਰੋਕਤ ਪਾਈ ਚਾਰਟ ਨੂੰ ਅੱਠ ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਹੈ । ਇਹ ਅਜੇ ਦੀ ਗੋਲਕ ਵਿੱਚ ਵੱਖ-ਵੱਖ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ ਨੂੰ ਦਰਸਾਉਂਦਾ ਹੈ ।
ਹੇਠਾਂ ਲਿਖੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ :

1. ਤੋਂ 5 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ (ਭਿੰਨਾਤਮਕ ਰੂਪ ਵਿੱਚ ਕਿੰਨੀ ਹੈ ? ਜੇਕਰ ਸਿੱਕਿਆਂ ਦੀ ਕੁੱਲ ਗਿਣਤੀ 80 ਹੋਵੇ ।
2. ਤੋਂ 2 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ ਕਿੰਨੀ ਹੈ ?
3. ਤੋਂ 5 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ ਦੱਸੋ ?
4. ਤੋਂ 10 ਦੇ ਸਿੱਕਿਆਂ ਦੀ ਰਾਸ਼ੀ ਕਿੰਨੀ ਬਣਦੀ ਹੈ ?
5. ਅਜੇ ਦੀ ਗੋਲਕ ਵਿੱਚ ਕੁੱਲ ਕਿੰਨੀ ਰਾਸ਼ੀ ਹੈ ?

ਹੱਲ :
1. \(\frac{3}{8}\)

2. \(\frac{2}{8}\) × 80 = 20

3. \(\frac{3}{8}\) × 80 = 30

4. ₹ 10 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ = \(\frac{1}{8}\) × 80 = 10
₹ 10 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦਾ ਕੁੱਲ ਮੁੱਲ
= ₹ 10 × 10 = ₹ 100

5. ₹ 1 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ = \(\frac{2}{8}\) × 80 = 20
₹ 2 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ = 20
₹ 5 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ = 30
₹ 10 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦੀ ਗਿਣਤੀ = 10
₹ 1 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦਾ ਮੁੱਲ = ₹ 1 × 20 = ₹ 20
₹ 2 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦਾ ਮੁੱਲ = ₹ 2 × 20 = ₹ 40
₹ 5 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦਾ ਮੁੱਲ = ₹ 5 × 30 = ₹ 150
₹ 10 ਵਾਲੇ ਸਿੱਕਿਆਂ ਦਾ ਮੁੱਲ = ₹ 10 ×x 10 = ₹ 100
ਅਜੇ ਦੀ ਗੋਲਕ ਵਿੱਚ ਜਿੰਨੀ ਰਾਸ਼ੀ ਹੈ : = ₹ 20 + ₹ 40 + ₹ 150 + 100
= ₹ 310.

ਪ੍ਰਸ਼ਨ 8.
ਦਿੱਤੇ ਗਏ ਪਾਈ ਚਾਰਟ ਨੂੰ 12 ਬਰਾਬਰ ਭਾਗਾਂ ਵਿੱਚ ਵੰਡਿਆ ਗਿਆ ਹੈ। ਦਿੱਤਾ ਗਿਆ ਪਾਈ ਚਾਰਟ ਕਿਸੇ ਸਕੂਲ ਦੇ 120 ਬੱਚਿਆਂ ਦੇ ਵੱਖੋਵੱਖਰੇ ਮਨਪਸੰਦ ਤਿਉਹਾਰਾਂ ਨੂੰ ਦਰਸਾ ਰਿਹਾ ਹੈ । ਇਸ ਨੂੰ ਧਿਆਨ ਨਾਲ ਪੜ੍ਹ ਕੇ ਹੇਠਾਂ ਦਿੱਤੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ ਦਿਓ ।

1. ਕਿੰਨੇ ਬੱਚਿਆਂ ਨੂੰ (ਭਿੰਨਾਤਮਕ ਰੂਪ ਵਿੱਚ ਦਿਵਾਲੀ ਦਾ ਤਿਉਹਾਰ ਪਸੰਦ ਹੈ ?
2. ਸਕੂਲ ਦੇ ਕੁੱਲ 120 ਬੱਚਿਆਂ ਵਿੱਚੋਂ ਹੋਲੀ ਦਾ ਤਿਉਹਾਰ ਪਸੰਦ ਕਰਨ ਵਾਲੇ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਕਿੰਨੀ ਹੈ ?
3. ਸਭ ਤੋਂ ਘੱਟ ਮਨਪਸੰਦ ਤਿਉਹਾਰ ਕਿਹੜਾ ਹੈ ?
4. ਦਿਵਾਲੀ ਅਤੇ ਬਸੰਤ ਪਸੰਦ ਕਰਨ ਵਾਲੇ ਬੱਚਿਆਂ ਦੀ ਗਿਣਤੀ ਦਾ ਅੰਤਰ ਕਿੰਨਾ ਹੈ ?

ਹੱਲ:

1. \(\frac{5}{12}\)
2.  \(\frac{4}{12}\) × 120 = 40
3.  ਦੁਸਹਿਰਾ
4.  (\(\frac{5}{12}\) – \(\frac{2}{12}\)) × 120
   = \(\frac{3}{12}\) × 120 = 30