Punjab State Board PSEB 9th Class Science Important Questions Chapter 8 Motion Important Questions and Answers.
PSEB 9th Class Science Important Questions Chapter 8 Motion
Long Answer Type Questions:
Question 1.
Derive mathematically the equations of motion.
Answer:
Equations of motion under uniform acceleration: The following are the equations of motion of an object moving in a straight line with uniform acceleration.
1. υ = u + at
2. S = ut + \(\frac{1}{2}\)at2
3. υ2 – u2 = 2aS
1. First Equation of Motion, υ = u + at
Let u be the initial velocity and ‘a’ be the uniform acceleration of a body in motion so that after every 1 sec its velocity increases by ‘a’.
Increase in velocity of the body after 1 sec = a
Secondary Increase in velocity of the body after 2 sec = a + a = 2 a
∴ Increase in velocity after t sec = a × t = at
Therefore, velocity of an object after t secs = Initial velocity + increase in velocity of the object after ‘t’ secs
or υ = u + at
2. Second equation of motion S = ut + \(\frac{1}{2}\)at2
Let ‘u’ be the initial velocity of the body in motion having uniform acceleration ‘a’ and after ‘t’ second the final velocity be ‘υ’.
∴ Increase in velocity of the body after 1sec = a
Velocity of the body after 1 sec from start of its motion = (u + a)
Velocity of the body 1 second before the end of its motion = (υ – a)


![]()
Question 2.
For uniform accelerated motion, draw by graphical method establish the following equations of motion:
1. υ = u + at
2. S = ut + \(\frac{1}{2}\)at2
3. υ2 = u2 + 2aS
Answer:
Consider an object moving with initial velocity ‘u’ along a straight line and uniform acceleration ‘a’. Suppose its final velocity becomes υ after time t and during this time it travels a distance S. If time is represented along X-axis and velocity along Y-axis, then velocity-time graph obtained will be BA, an ipchned straight line. With its help we can derive the various equators of motion.
Here OA = ED = u,
OC = EB = υ and OE = t = AD
(a)Equation for velocity-time relation. We know that
Acceleration = Slope of velocity-time graph AB or

This proves the first equation of motion.
(b) Equation for position-time relation
We know that area below velocity-time graph and time axis gives the distance covered by the body.
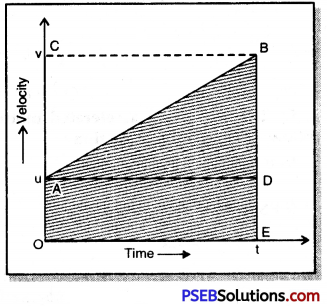
(S = ut + \(\frac{1}{2}\)at2)
Distance travelled by the object in time t is
S = Area of the trapezium OABE
= Area of rectangle OADE + Area of triangle ADB
= OA × OE + \(\frac{1}{2}\)DB × AD
a = \(\frac{\mathrm{DB}}{\mathrm{AD}}=\frac{\mathrm{DB}}{t}\)
or DB = at
= u × t + \(\frac{1}{2}\)at × t
or S = ut + \(\frac{1}{2}\)at2
This proves the second equation of motion.
(c) Equation for position-velocity relation (υ2 – u2 = 2aS).
The distance travelled by object in time t is:
S = Area of trapezium OABE
= \(\frac{1}{2}\)(EB + OA) × OE
= \(\frac{1}{2}\)(EB + ED) × OE …….. (1)

Question 3.
Draw velocity-time graph for a body moving with uniform velocity. Hence show that the area under the velocity-time graph gives the distance travelled by the body in a given time interval.
Answer:
Distance covered as area under the velocity-time graph. In Fig. straight line PQ is the velocity-time graph of a body moving with a uniform velocity, ‘υ’ represented by OP.
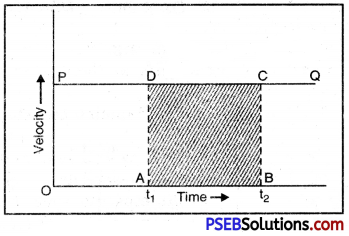
Area of rectangle ABCD
= AD × AB
= OP × AB
= υ × (t2 – t1)
= Velocity × time
= Distance travelled in time interval (t2 – t1)
Hence, the area under the velocity-time graph gives the distance travelled by the body in the given time interval.
![]()
Question 4.
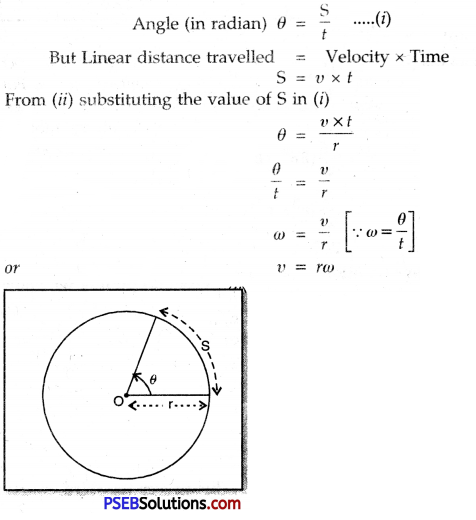
What is meant by Angular velocity? How is it related to linear velocity? Derive the relation.
Answer:
Angular velocity: The angle traced out by a body moving along a circular path in unit time is called Angular velocity. It is usually represented by a greek letter ω (omega). If θ is the angle covered by a body in time ‘t’, then
Angular velocity (ω) = \(\frac{Angle traced out by the moving body(θ)}{t}\)
∴ ω = \(\frac{θ}{t}\)
or θ = ωt
Relation between Linear velocity and Angular velocity:
Suppose a body in motion in a circular path of radius ‘r’ having linear velocity υ. Suppose ‘S’ is the linear distance covered by the body in time ‘t’ and relative to this, ‘θ’ is the angular displacement produced, then
Short Answer Type Questions:
Question 1.
Define rest and motion. Give one example for each.
Answer:
- Rest: A body is said to be at rest if it does not change its position with respect to its surroundings. A book lying on the table in a room is at rest with respect to the other objects in the room.
- Motion: A body is said to be in motion if it changes its position with time with respect to its surroundings. A car running on the road is in motion with respect to the electricpole, trees along the roadside.
![]()
Question 2.
Show that rest and motion are relative terms.
Or
Can an object be af rest as well as in motion at the same time?
Answer:
An object may be at rest relative to one surrounding object and at the same time it may be in motion with respect to some other object. For example, a passenger sitting in moving train is at rest relative to other co-passengers. But since he is sharing the motion of the train, so he is in motion relative to the outside trees, lamp posts etc. Thus, rest and motion are relative terms.
Question 3.
Give some points of differences between distance and displacement.
Or
Give two differences between distance and displacement.
Answer:
Differences between distance and displacement:
| Distance | Displacement |
| 1. Distance is the length of the actual path covered by a body, irrespective of its direction of motion. | Displacement is the shortest distance between the initial and final positions of a body in a given direction. |
| 2. Distance between two given points may be same or different for different paths chosen. | Displacement between two given points is always same. |
| 3. It is a scalar quantity. | It is a vector quantity. |
| 4. Distance covered is always positive or zero. | Displacement covered may be positive, negative or zero. |
Question 4.
What is meant by uniform motion?Give an example.
Answer:
Uniform motion. If an object covers equal distances in equal intervals of time, hoxvever small the time interval may be, then the motion of the object is said to be uniform motion. For example, suppose a bus moves 10 km in the first 15 minutes, 10 km in second 15 minutes, 10 km in third 15 minutes and so on. Then one can say that the bus is in uniform motion.
Question 5.
Define the term velocity. What is its SI unit?Is it a scalar or vector quantity?
Answer:
Velocity: Velocity of a body is defined as the displacement produced per unit time. It is also defined as the speed of a body in a given direction.
Velocity = Displacement/Time
If ‘S’ is the distance travelled by a body in a given direction and t is the time taken to travel that distance, then the velocity ‘υ’ is given by
υ = \(\frac{S}{t}\)
The SI unit of velocity is m s-1.
Velocity is a vector quantity because it requires both magnitude and direction for its complete description.
Symbols of Physical Quantities and Important Formulae:
(A) Symbols of Physical Quantities
- Time = t
- Speed = v
- Distance = S
- Initial Velocity = u
- Final Velocity = v
- Acceleration = a
- Average Velocity = Vav
(B) Important Formulae:
If initial velocity u at time t velocity υ and uniform acceleration a Then the under given relations are called Equations motion:
υ = u + at (Velocity at time t)
S = ut + \(\frac{1}{2}\)at2(Displacement in time ‘t’)
υ2 = u2 + 2aS (Velocity square relation)
Displacement in n th The Second of time (Sn) = u + (2n – 1)
![]()
Numerical Problems (Solved):
Question 1.
A police car running on a highway with a speed of 30 km/h fires on the vehicle of thiefs running in the same direction at a speed of 192 km/h. If the velocity of the bullet is 150 m/s then with what velocity the bullet will hit the thiefs?
Solution:
Velocity of the bullet fired = 150 m/s
= 150 × \(\frac{18}{5}\)km/h = 540 km/h
∴ Total speed = Speed of police vehicle + Speed of bullet
= 30 km/h + 540 km/h = 570 km/h
Speed of the bullet relative to the speed of thief’s vehicle in the same direction
= (570 – 192) km/h
= 378 km/h
= \(\frac{378 \times 1000}{60 \times 60}\) m/s
= 105 m/s
Question 2.
A train 50 m long travels on a plain and level track and reached a post in 5 secs. Find
1. speed of the train
2. the time train will take to cross 450 m long bridge.
Solution:
1. Since the train takes 5 secs to reach the post, it covers a distance equal to its own length, then
speed of train = \(\frac{Total distanve travelled}{Total time taken}\)
= \(\frac{50m}{5s}\)
= 10 m/s
2. Distance travelled by the train to cross the bridge
= Length of the bridge + Length of train
= 450 m + 50 m
= 500 m
∴ Time taken to cross the bridge = \(\frac{Total distance covered}{speed of the train}\)
= \(\frac{500m}{10m/s}\)
= 50 s
Question 3.
A cheetah is the fastest land animal and can achieve a peak velocity of 100 km/h upto distances less than 500 m. If a cheetah spots his prey at a distance of 100 m. What is the minimum time it will take to get its prey, if the average velocity attained by it is 90 km/h.
Solution:
Here, υ = 90 km/h
= \(\frac{90 \times 1000 \mathrm{~m}}{3600 \mathrm{~s}}\)
= 25 m/s
s = 100m
Minimum time, t = \(\frac{s}{υ}\)
= \(\frac{100}{25}\) = 4s.
![]()
Question 4.
A car travels a certain distance with a speed of 50 km/h and returns with a speed of 40 km/h. Calculate the average speed for the whole journey.
Solution:
Let the one-way distance = x km

Question 5.
On a 100 km track, a train travels the first 30 km at a uniform speed of 30 km h-1. How fast must the train travel the next 70 km so as to average 40 km h-1 for the entire trip?
solution:
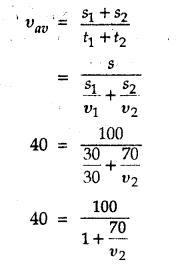

Question 6.
A railway train 50 m long passes over a bridge 250 m long with uniform velocity of 10 m s-1. How long will it take to completely, pass over the bridge?
Solution:
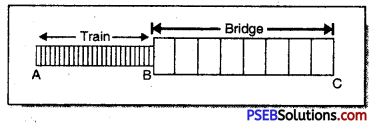
To completely pass over the bridge, the train will have to cover the length of the bridge, as well as its own length i.e., AB + BC
∴ Total distance to be covered, S = 50 + 250 = 300 m
Velocity of train, u = 10 m s-1
Here velocity is uniform, hence
a = 0 m s-2
Using S = ut + \(\frac{1}{2}\)at2
300 = 10t + 0
or t = 30 s
Hence train will pass completely over the bridge in 30 s.
![]()
Question 7.
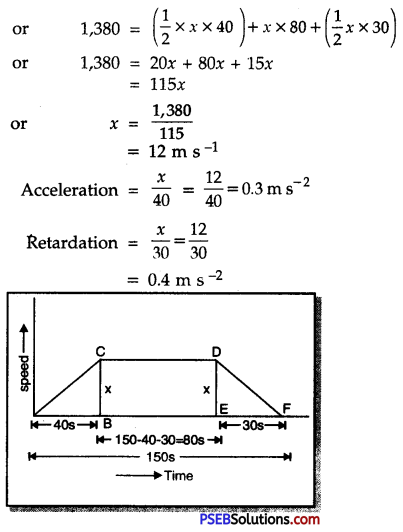
A car starts from rest and moves with uniform acceleration for 40 s. It then moves with uniform velocity attained by it and is finally brought to rest in 30 s under uniform retardation. The car covers a total distance of 1,380 m in 2.5 min. Calculate constant speed, acceleration and retardation.
Solution:
Let x be the constant speed. Now the total distance covered is equal to total area between velocity-time graph and time axis. Therefore
Distance covered = area of ∆ABC + area of rectangle BCDE + area of ADEF
Question 8.
The graph shown in Fig. indicates the position of body at different positions. Calculate the speed of the body as it moves from (i) A to B; (ii) B to C and (iii) C to D.
Solution:
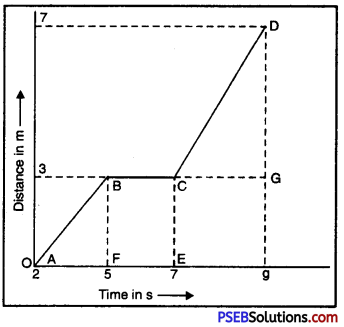
Speed from A to B = Slope of AB
= \(\frac{\mathrm{BF}}{\mathrm{AF}}=\frac{3-0}{5-2}\) = 1ms-1
(ii) Speed from B to C is zero since slope of BC is zero. From B to C, the body is at rest.
(iii) Speed between C and D = Slope of CD
= \(\frac{D G}{C G}=\frac{7-3}{9-7}\)
= \(\frac{4}{2}\) = 2ms-1
Very Short Answer Type Questions:
Question 1.
What is motion?
Answer:
Motion: When an object changes its position with time then it is said to be in motion.
![]()
Question 2.
What is displacement of object?
Answer:
Displacement. The change in position of an object in a given direction is known as displacement. It is measured by the shortest distance moved by an object from its initial position to final position.
Question 3.
Which device shows the speed of vehicles?
Answer:
Odometer.
Question 4.
What is uniform motion?
Answer:
Uniform motion. When a body covers equal distances in equal intervals of time then its motion is called uniform motion.
Question 5.
Give two examples of non-uniform motion.
Answer:
1. A car moving on the road.
2. A man doing exercise in park.
Question 6.
Define speed.
Answer:
Speed. The distance travelled by a body in a unit time is called its speed.
![]()
Question 7.
What is the SI unit of speed?
Answer:
S.I. unit of speed is ms-1.
Question 8.
How is average speed obtained?
Answer:
Average speed. It is the total distance travelled by an object divided by the time taken to travel that distance.
Average Speed = \(\frac{Total distance travelled}{Total time taken}\)
Question 9.
What is velocity?
Answer:
Velocity: The speed in a particular direction is called velocity.
Or
It is the distance travelled by an object in a particular direction.
Question 10.
What is acceleration?
Answer:
Acceleration. It is defined as the rate of change of velocity with time.
Acceleration = \(\frac{Change of velocity}{Total time taken}\)
Question 11.
What is the SI unit of acceleration?
Answer:
ms-2
Question 12.
A cricket player tosses the ball upward and again catches it. What is the total displacement?
Answer:
Total displacement is zero.
![]()
Question 13.
Is displacement a scalar or vector quantity?
Answer:
Displacement is a vector quantity because it needs both magnitude and direction for its complete representation.
Question 14.
What would be acceleration of a body if its velocity-time graph is line parallel to the time axis?
Answer:
Zero, as the body possesses uniform velocity.
Question 15.
A body is moving along the boundary of a square plot of land with constant speed. Does its velocity remain unchanged?
Answer:
No. because its velocity changes due to change in direction.
Question 16.
What will be the position-time graph of a city bus standing at rest at a depot?
Answer:
A straight line parallel to the time axis.
Question 17.
What is the nature of the distance-time graph for an object moving uniformly along a straight long road?
Answer:
A straight line inclined to the time axis.
![]()
Question 18.
Does the speedometer of a car measure its average speed?
Answer:
No. It measures only instantaneous speed.