Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.2
Question 1.
In the given figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
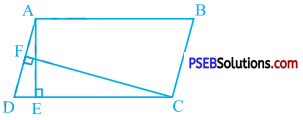
Answer:
The area of a parallelogram is the product of its base and the altitude corresponding to that base.
Here, in parallelogram ABCD, the altitude corresponding to base DC is AE and the altitude corresponding to base AD is CF.
∴ ar(ABCD) = DC × AE = AD × CF
∴ DC × AE = AD × CF
∴ AB × AE = AD × CF (∵ AB = DC In parallelogram ABCD)
∴ 16 × 8 = AD × 1O
∴ AD = \(\frac{16 \times 8}{10}\)
∴ AD = \(\frac{128}{10}\)
∴ AD = 12.8 cm
![]()
Question 2.
If E, F, G and H are respectively the midpoints of the sides of a parallelogram ABCD, show that ar(EFGH) = \(\frac{1}{2}\)ar (ABCD).
Answer:
In parallelogram ABCD. E, F, G and H are the midpoints of AB, BC. CD and DA respectively.
Draw GE.
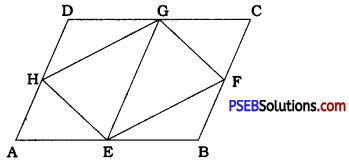
In parallelogram ABCD, AB || CD and AB = CD.
∴ BE || CG and BE (\(\frac{1}{2}\) AB) = CG (\(\frac{1}{2}\) CD)
∴ Quadrilateral EBCG is a parallelogram.
∴ GE || BC
Now, ∆ EFG and parallelogram EBCG are on the same base GE and between the same parallels GE and BC.
∴ ar(EFG)= \(\frac{1}{2}\)ar (EBCG) ………………. (1)
Similarly, ∆ EHG and parallelogram AEGD are on the same base GE and between the same parallels GE and DA.
∴ ar(EHG) = \(\frac{1}{2}\)ar (AEGD) ……………….. (2)
Adding (1) and (2),
ar (EFG) + ar (EHG) = \(\frac{1}{2}\) ar (EBCG) + \(\frac{1}{2}\) ar (AEGD)
∴ ar (EFGH) = \(\frac{1}{2}\) [ar (EBCG) + ar (AEGD)]
∴ ar (EFGH) = \(\frac{1}{2}\) ar (ABCD)
![]()
Question 3.
p and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar (APB) = ar (BQC).
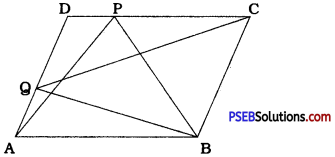
Answer:
Here, ∆ APB and parallelogram ABCD are on the same base AB and between the same parallels AB and CD.
∴ ar (APB) = \(\frac{1}{2}\)ar (ABCD) …………… (1)
Similarly, ∆ BQC and parallelogram ABCD are on the same base BC and between the same parallels BC and DA.
∴ ar (BQC) = \(\frac{1}{2}\)ar (ABCD) ……………… (2)
From (1) and (2),
ar(APB) = ar(BQC)
![]()
Question 4.
In the given figure, P is a point in the interior of a parallelogram ABCD. Show that,
(i) ar (APB) + ar (PCD) = \(\frac{1}{2}\)ar (ABCD)
(ii) ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
[Hint: Through P, draw a line parallel to AB.]
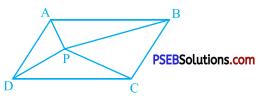
Answer:
Through P, draw a line parallel to AB which intersects BC at Q and AD at R.
Now, in quadrilateral ABQR,
AB || QR (By construction)
BQ || AR (In parallelogram ABCD, BC || AD)
∴ Quadrilateral ABQR is a parallelogram.
Similarly, DCQR is a parallelogram.
∆ APB and parallelogram ABQR are on the same base AB and between the same parallels AB and QR.
∴ ar(APB) = \(\frac{1}{2}\)ar (ABQR) ……………….. (1)
Similarly, ∆ PCD and parallelogram DCQR are on the same base DC and between the same parallels DC and QR.
∴ ar(PCD) = \(\frac{1}{2}\)ar (DCQR) ………………… (2)
Adding (1) and (2),
= ar(APB) + ar (PCD)
= \(\frac{1}{2}\)ar (ABQR) + \(\frac{1}{2}\)ar (DCQR)
∴ ar (APB) + ar (PCD)
= \(\frac{1}{2}\) [ar (ABQR) + ar (DCQR)]
∴ ar (APB) + ar (PCD) = \(\frac{1}{2}\)ar (ABCD) …………………. (3)
Now, through P, draw a line parallel to AD which intersects AB at S and CD at T.
Then, as above, it can be proved that
ar(APD) + ar(PBC) = \(\frac{1}{2}\)ar (ABCD) ……………………. (4)
From (3) and (4),
ar (APD) + ar (PBC) = ar (APB) + ar (PCD)
![]()
Question 5.
In the given figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that:
(i) ar (PQRS) = ar (ABRS)
(ii) ar(AXS) = \(\frac{1}{2}\)ar (PQRS)
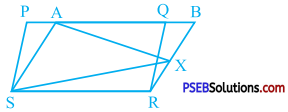
Answer:
Parallelograms PQRS and ABRS are on the same base RS and between the same parallels PB and SR.
∴ ar (PQRS) = ar (ABRS) …………….. (1)
∆ AXS and parallelogram ABRS are on the same base AS and between the same parallels AS and BR.
∴ ar (AXS) = \(\frac{1}{2}\)ar (ABRS) ………………… (2)
From (1) and (2),
ar (AXS) = \(\frac{1}{2}\)ar (PQRS)
![]()
Question 6.
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the field Is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
Answer:
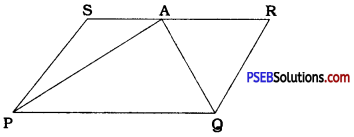
By taking any point A on RS and joining it to points P and Q, the field is divided into three triangular parts as ∆ PSA, ∆ APQ and ∆ QRA.
Here, ∆ APQ and parallelogram PQRS are on the same base PQ and between the same parallels PQ and SR.
∴ ar (APQ) = \(\frac{1}{2}\)ar (PQRS)
∴ ar (PSA) + ar(QRA) = \(\frac{1}{2}\)ar(PQRS)
Thus, ar (APQ) = ar (PSA) + ar (QRA)
Now, as the farmer wants to sow wheat and pulses in equal portions of the field separately.
she has two options as below to do so:
(1) She should sow wheat in ∆ APQ and pulses in ∆ PSA as well as ∆ QRA.
(2) She should sow pulses in ∆ APQ and wheat in ∆ PSA as well as ∆ QRA.