Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 6 Lines and Angles Ex 6.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 6 Lines and Angles Ex 6.1
Question 1.
In the given figure, lines AB and CD intersect at O. If ∠ AOC + ∠ BOE = 70° and ∠ BOD = 40°, find ∠ BOE and reflex ∠ COE.
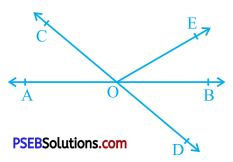
Answer:
Lines AB and CD intersect at O.
∴ ∠ AOC = ∠ BOD (Vertically opposite angles)
Now, ∠ BOD = 40° (Given)
∴ ∠ AOC = 40°
Moreover, ∠ AOC + ∠ BOE = 70° (Given)
∴ 40° + ∠ BOE = 70°
∴ ∠BOE = 70° – 40°
∴ ∠ BOE = 30°
∠ BOD and ∠ BOE are adjacent angles with common arm ray OB.
∴ ∠ DOE = ∠ BOD + ∠ BOE = 40° + 30° = 70°
Reflex ∠ COE = ∠ COD + ∠ DOE
= 180° + 70° (∠ COD is a straight angle as ray OA stands on line CD.)
= 250°
Thus, ∠ BOE = 30° and reflex ∠ COE = 250°.
![]()
Question 2.
In the given figure, lines XY and MN intersect at O. If ∠ POY = 90° and a : b = 2 : 3, find c.
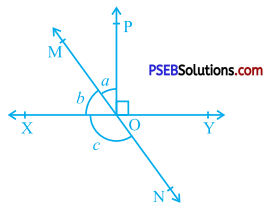
Answer:
Ray OP stands on line XY.
Hence, ∠XOP and ∠POY from a linear pair of angles.
∴ ∠ XOP + ∠ POY = 180°
∴ ∠ XOP + 90° = 180°
∴ ∠ XOP = 90°
∠XOM and ∠MOP are adjacent angles.
∴ ∠ XOM + ∠ MOP = ∠XOP
∴ b + a = 90° …………. (i)
Now, a : b = 2 : 3
If a = 2x, then b = 3x.
∴ 3x + 2x = 90° [From (1)]
∴ 5x = 90°
∴ x = 18°
Then, ∠ XOM = b = 3x = 3 × 18° = 54°
and ∠ MOP = a = 2x = 2 × 18° = 36°
Now, ∠ MOY = ∠ MOP + ∠ POY (Adjacent angles)
∴ ∠ MOY = 36° + 90° = 126°
Lines XY and MN intersect at O.
∴ ∠ XON and ∠ MOY are vertically opposite angles.
∴ ∠ XON = ∠ MOY
∴ c = 126°
![]()
Question 3.
In the given figure, ∠ PQR = ∠ PRQ, then prove that ∠ PQS = ∠ PRT.
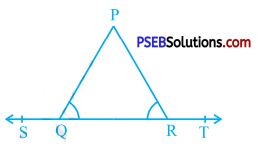
Answer:
Ray QP stands on line ST.
∴ ∠ PQR and ∠ PQS form a linear pair of angles.
∴ ∠ PQR + ∠ PQS = 180°
Ray RP stands on line ST.
∴ ∠ PRQ and ∠ PRT form a linear pair of angles.
∴ ∠ PRQ + ∠ PRT = 180°
∴ ∠ PQR + ∠ PRT = 180° (Given : ∠ PQR = ∠ PRQ)
Then, ∠ PQR + ∠ PQS = ∠ PQR + ∠ PRT = 180°
∴ ∠ PQS = ∠ PRT
![]()
Question 4.
In the given figure, if x + y = w + z, then prove that AOB is a line.
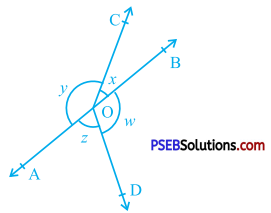
Answer:
We know that sum of all the angles round any given point is 360°.
∴ x + y + z + w = 360°
∴ x + y + x + y = 360° (Given : x + y = w + z)
∴2x + 2y = 360°
∴ 2 (x + y) = 360°
∴ x + y = 180°
∴ ∠ COB + ∠ COA = 180°
But, ∠ COB and ∠ COA are adjacent angles and their sum is 180°.
∴ ∠ COB and ∠ COA are angles of a linear pair.
Hence, AOB is a line.
![]()
Question 5.
In the given figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that.
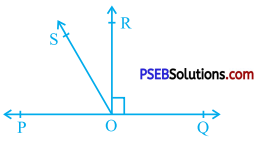
Answer:
∠ ROS = \(\frac{1}{2}\) (∠ QOS – ∠ POS).
Ray OR is perpendicular to line PQ.
∴ ∠ QOR = ∠ POR = 90°
Now, ∠ QOR and ∠ ROS are adjacent angles with common arm ray OR.
∴ ∠ QOS = ∠ QOR + ∠ ROS
∴ ∠ QOS = 90° + ∠ ROS ……………….. (1)
Similarly, ∠ POS and ∠ ROS are adjacent angles with common arm ray OS.
∴ ∠ POR = ∠ POS + ∠ ROS
∴ 90° = ∠ POS + ∠ ROS
∴ ∠ POS = 90° – ∠ ROS ………………… (2)
Subtracting (2) from (1), we get
∠ QOS – ∠ POS = (90° + ∠ ROS) – (90° – ∠ ROS)
∴ ∠ QOS – ∠ POS = 90° + ∠ ROS – 90° + ∠ ROS
∴ ∠ QOS – ∠ POS = 2∠ ROS
∴ ∠ ROS = \(\frac{1}{2}\) (∠ QOS – ∠ POS)
![]()
Question 6.
It is given that ∠ XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ ZYP, find ∠ XYQ and reflex ∠ QYP.
Answer:
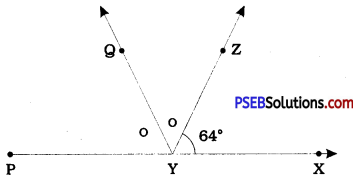
∠ XYZ + ∠ PYZ = 180° [Angles of a linear pair]
∴ 64° + ∠ PYZ= 180° [Given ∠ XYZ = 64°]
∴ ∠ PYZ = 180°-64°
∴ ∠ PYZ = 116°
Ray YQ bisects ∠ PYZ.
∴ ∠ PYQ = ∠ QYZ = \(\frac{1}{2}\) ∠ PYZ = \(\frac{1}{2}\) × 116° = 58°
∴ ∠ XYQ = ∠ XYZ + ∠ QYZ [Adjacent angles]
∴ ∠ XYQ = 64° + 58°
∴ ∠ XYQ = 122°
XY is produced to P.
∴ ∠ XYP is a straight angle.
∴ ∠ XYP = 180°
Reflex ∠ QYP = ∠ XYQ + ∠ XYP
= 122° + 180°
= 302°