Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 Statistics Ex 14.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.4
Question 1.
The following number of goals were scored by a team in a series of 10 matches:
2, 3. 4, 5, 0. 1, 3, 3, 4, 3
Find the mean, median and mode of these scores.
Answer:
Here, n = 10.
Mean X̄ = \(\frac{\Sigma x_{i}}{n}\)
= \(\frac{2+3+4+5+0+1+3+3+4+3}{10}\)
= \(\frac{28}{10}\)
= 2.8
Thus, the mean of the given scores is 2.8 goals.
Arranging the observations in the ascending order, we get:
0, 1, 2, 3, 3, 3, 3, 4, 4, 5
Since n = 10 is an even number, \(\frac{n}{2}\) = 5 and \(\frac{n}{2}\) + 1 = 6.
Median M
= \(\frac{\left(\frac{n}{2}\right) \text { th observation }+\left(\frac{n}{2}+1\right) \text { th observation }}{2}\)
= \(\frac{5 \text { th } \text { observation }+6 \text { th } \text { observation }}{2}\)
= \(\frac{3+3}{2}\) = 3
Thus, the median of the given scores is 3 goals.
In the given data, observation 3 occurs most frequently (4 times). Hence, the mode of the data is 3 goals.
![]()
Question 2.
In a mathematics test given to 15 students, the following marks (out of 100) are recorded :
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
Find the mean, median and mode of this data.
Answer:
Here, n = 15.
Mean X̄ = \(\frac{\Sigma x_{i}}{n}\)
= \(\begin{gathered}
41+39+48+52+46+62+54+40 \\
+96+52+98+40+42+52+60 \\
\hline 15
\end{gathered}\)
= \(\frac{822}{15}\) = 54.8
Thus, the mean of the data is 54.8 marks.
Arranging the observations in the ascending order, we get:
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
Here, n = 15 is an odd number.
Median M = \(\left(\frac{n+1}{2}\right)\)th observation
= \(\left(\frac{15+1}{2}\right)\)th observation
= 8 th observation
= 52
Thus, the median of the data is 52 marks.
In the given data, observation 52 occurs most frequently (3 times). Hence, the mode of the data is 52 marks.
![]()
Question 3.
The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
Answer:
Here, the median = 63 and n = 10.
∴ \(\frac{n}{2}\) = 5 and \(\frac{n}{2}\) + 1 = 6
Median M
= \(\frac{\left(\frac{n}{2}\right) \text { th observation }+\left(\frac{n}{2}+1\right) \text { th observation }}{2}\)
∴ 63 = \(\frac{5 \text { th } \text { observation }+6 \text { th } \text { observation }}{2}\)
∴ 63 = \(\frac{(x)+(x+2)}{2}\)
∴63 × 2 = x + x + 12
∴126 = 2x + 2
∴ 2x = 124
∴ x = 62
![]()
Question 4.
Find the mode of 14, 25, 14, 28, 18, 17, 18, 14, 23, 22, 14, 18.
Answer:
Here, just by simple observation, it is clearly seen that observation 14 occurs most frequently, i.e., 4 times.
Hence, the mode of the data is 14.
Question 5.
Find the mean salary of 60 workers of a factory from the following table:
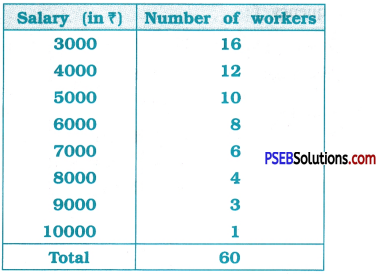
Answer:
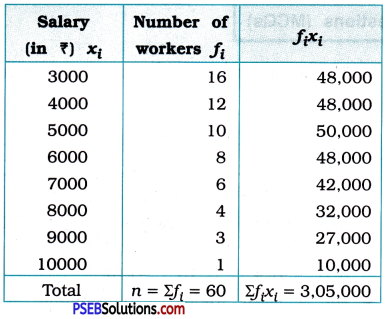
Mean X̄ = \(\frac{\Sigma f_{i} x_{i}}{n}\)
= \(\) = \(\frac{3,05,000}{60}\) = 5083.33
Thus, the mean salary is ₹ 5083.33.
![]()
Question 6.
Give one example of a situation in which
(i) the mean is an appropriate measure of central tendency.
Answer:
For the students studying in the same class, usually their level of knowledge and understanding would be more or less equal. There would be a few student having this level low and there would be a few students having this level high. Their level of knowledge and understanding would be reflected in the marks scored by them at an examination. Hence, the mean of marks scored by them at an examination is an appropriate measure of central tendency.
(ii) the mean is not an appropriate measure of central tendency but the median is an appropriate measure of central tendency.
Answer:
If we consider the monthly income of the people of certain region, the mean is not an appropriate measure of central tendency but the median is an appropriate measure of central tendency.