PSEB 9th Class Maths Solutions Chapter 14 Statistics Ex 14.3

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 14 Statistics Ex 14.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 14 Statistics Ex 14.3

Question 1.
A survey conducted by an organisation for the cause of illness and death among the women between the ages 15-44 (in years) worldwide, found the following figures (in %):

Causes	Female fatality rate (%)
1. Reproductive health conditions	31.8
2. Neuropsychiatric conditions	25.4
3. Injuries	12.4
4. Cardiovascular conditions	4.3
5. Respiratory conditions	4.1
6. Other causes	22.0

(i) Represent the information given above graphically.
Answer:

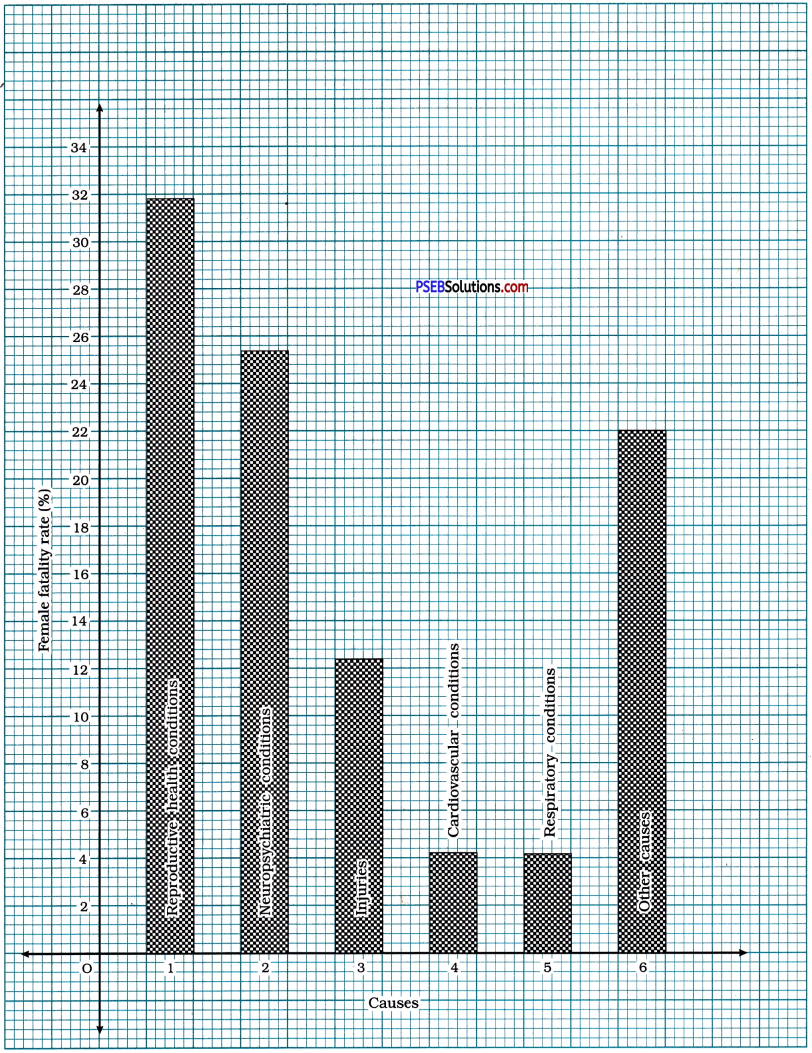
(ii) Which condition is the major cause of women’s ill health and death worldwide?
Answer:
‘Reproductive health conditions’ is the major cause of womens ill health and death worldwide.

(iii) Try to find out, with the help of your teacher, any two factors which play a major role in the cause in (ii) above being the major cause.
Answer:
‘Malnutrition’ and ‘Lack of necessary medical facilities’ can be considered as two other factors which play a major role in female fatality.

Question 2.
The following data on the number of girls (to the nearest ten) per thousand boys in different sections of Indian society is given below:

Section	Number of girls per thousand bays
Scheduled Caste (SC)	940
Scheduled Tribe (ST)	970
Non-SC/ST	920
Backward districts	950
Non-backward districts	920
Rural	930
Urban	910

(i) Represent the information above by a bar graph.
(ii) In the classroom discuss what conclusions can be arrived at from the graph.
Answer:

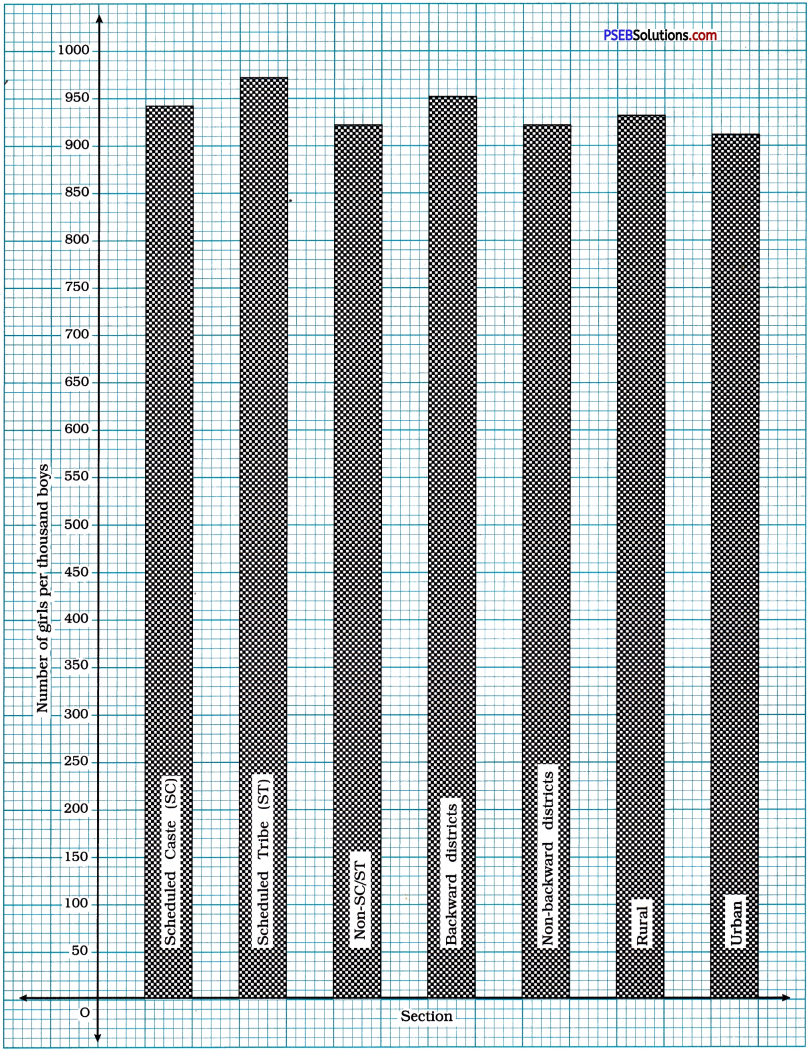
Question 3.
Given below are the seats won by different political parties in the polling outcome of a state assembly elections:

(i) Draw a bar graph to represent the polling results.
Answer:
Seats won by different political parties

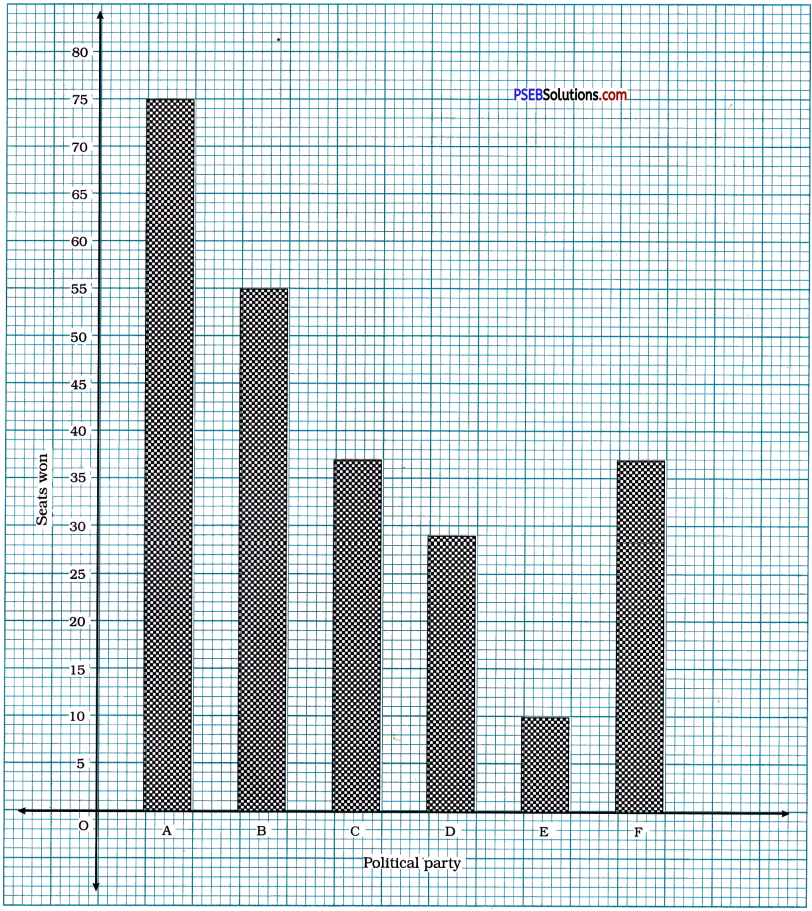
(ii) Which political party won the maximum number of seats?
Answer:
Political party: A won the maximum number of seats.

Question 4.
The length of 40 leaves of a plant are measured correct to one millimetre, and the obtained data is represented in the following table:

Length (in mm)	Number of leaves
118-126	3
127-135	5
136-144	9
145-153	12
154-162	.5
163-171	4
172-180	2

(i) Draw a histogram to represent the given data. [Hint: First make the class intervals continuous.]
(ii) Is there any other suitable graphical representation for the same data?
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?
Answer:
Making the class intervals continuous, we get the following table:

Length (in mm)	Number of leaves
117.5-126.5	3
126.5- 135.5	5
135.5-144.5	9
144.5-153.5	12
153.5- 162.5	5
162.5-171.5	4
171.5-180.5	2

(i) Length of leaves in millimetre

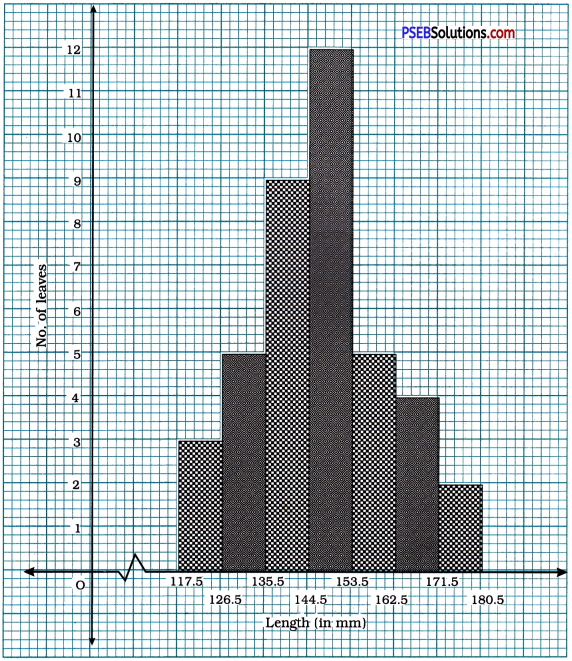
(ii) Yes. The given data can also be represented by ‘Frequency polygon’.

(iii) It is not correct to conclude that the maximum number of leaves are 153 mm long, because even if the frequency of class 145-153 is 12, we do not have the information about the length of each of those 12 leaves individually.

Question 5.
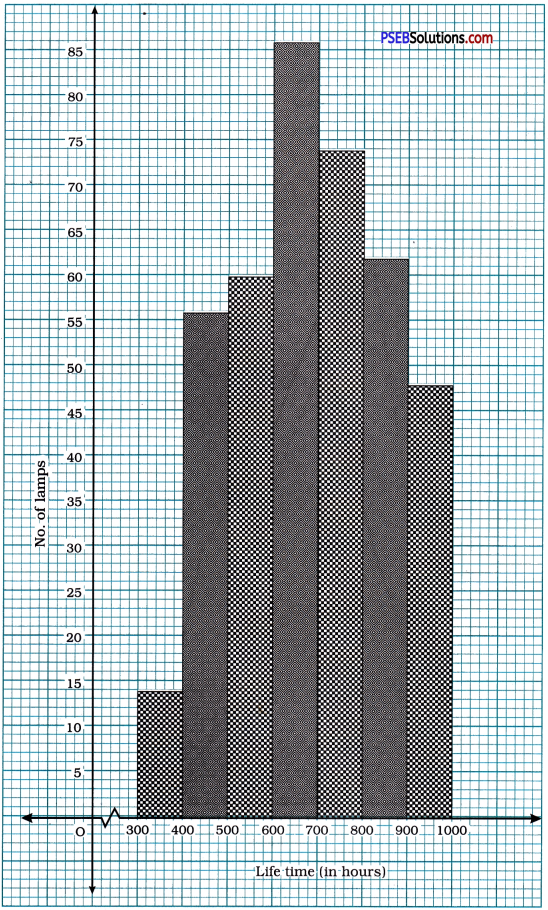
The following table gives the life times of 400 neon lamps:

Life time (in hours)	Number of lamps
300 – 400	14
400 – 500	56
500 – 600	60
600 – 700	86
700 – 800	74
800 – 900	62
900 – 1000	48

(i) Represent the given information with the help of a histogram.
Answer:

(ii) How many lamps have a life time of 700 hours or more than 700 hours ?
Answer:
The-frequencies of classes 700-800, 800-900 and 900-1000 are 74, 62 and 48 respectively.
Hence, the life time of 184 (74 + 62 + 48) lamps is 700 hours or more than 700 hours.

Question 6.
The following table gives the distribution of students of two sections according to the marks obtained by them:

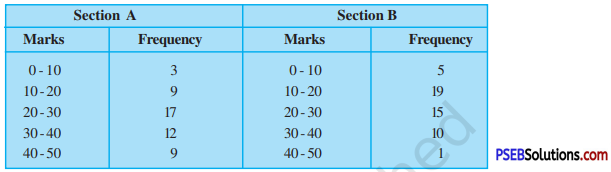
Represent the marks of the students of both the sections on the same graph by two frequency polygons. From the two polygons compare the performance of the two sections.
Answer:
To draw the frequency polygons of both the sections, we find the class marks of each class and prepare the following tables:

Section A

Marks	Class mark	Frequency
0-10	5	3
10-20	15	9
20-30	25	17
30-40	35	12
40-50	45	9

Section B

Marks	Class mark	Frequency
0-10	5	5
10-20	15	19
20-30	25	15
30-40	35	10
40-50	45	1

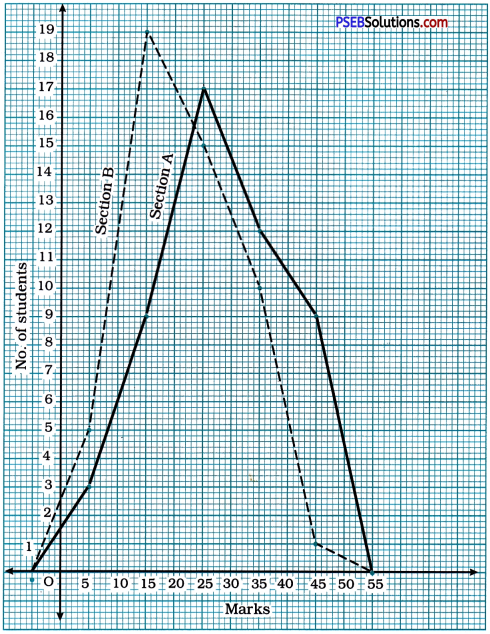
Comparing the performance of both the sections from the frequency polygons, we observe that the performance of students of section A is better than the performance of students of section B.

Question 7.
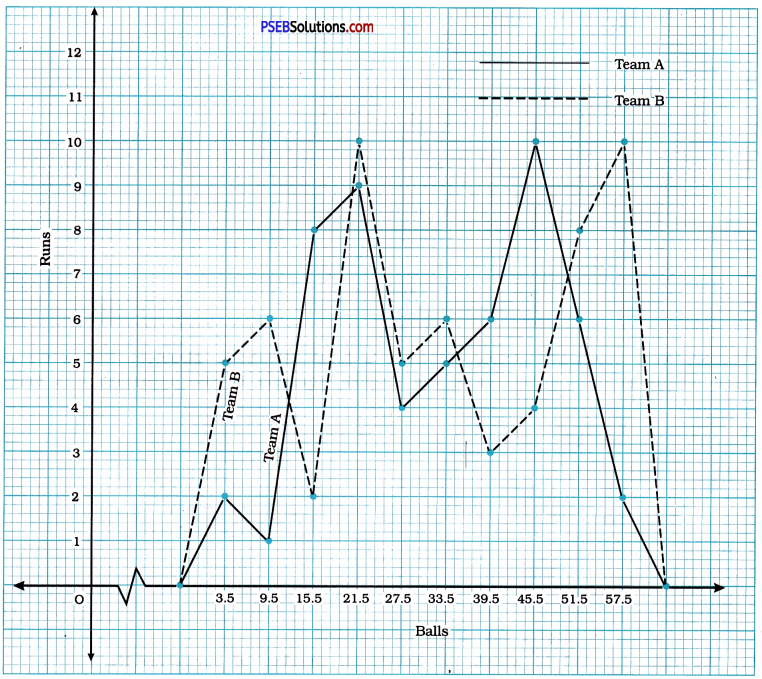
The runs scored by two teams A and B on the first 60 balls in a cricket match are given below:

Number of balls	Team A	Team B
1-6	2	5
7-12	1	6
13-18	8	2
19-24	9	10
25-30	4	5
31-36	5	6
37-42	6	3
43-48	10	4
49-54	6	8
55-60	2	10

Represent the data of both the teams on the same graph by frequency polygons.
[Hint: First make the class intervals continuous.]
Answer:

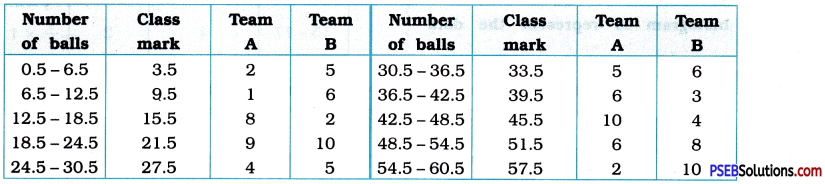
Number of runs made by Team A and Team B in first 60 balls.

Question 8.
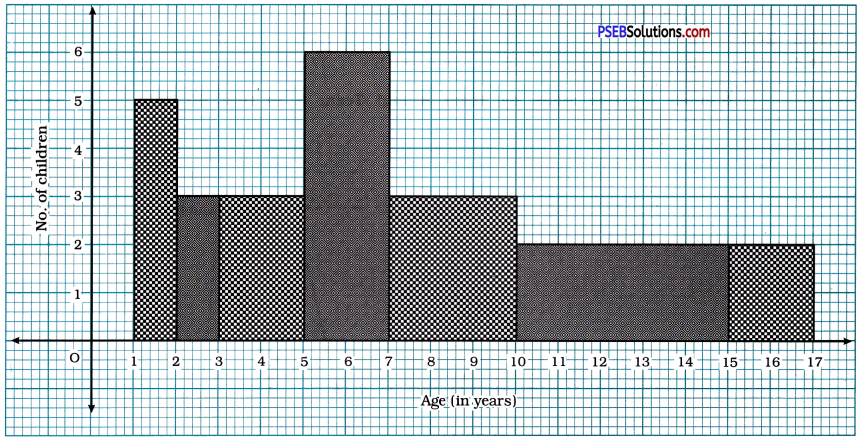
A random survey of the number of children of various age groups playing in a park was found as follows:

Age (in years)	Number of children
1-2	5
2-3	3
3-5	6
5-7	12
7-10	9
10-15	10
15-17	4

Draw a histogram to represent the data above.
Answer:

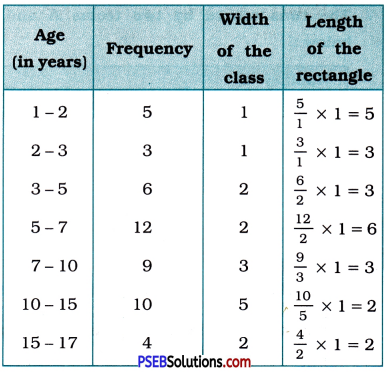
Children of various age groups playing in a park

Question 9.
100 surnames were randomly picked up from a local telephone directory and a frequency distribution of the number of letters in the English alphabet in the surnames was found as follows:

Number of letters	Number of surnames
1-4	6
4-6	30
6-8	44
8-12	16
12-20	4

(i) Draw a histogram to depict the given information.
(ii) Write the class interval in which the maximum number of surnames lie.
Answer:

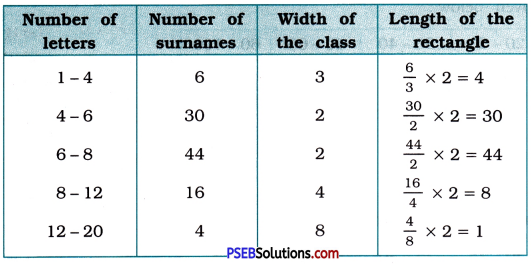
(i) Information regarding the number of surnames having given number of letters
Answer:

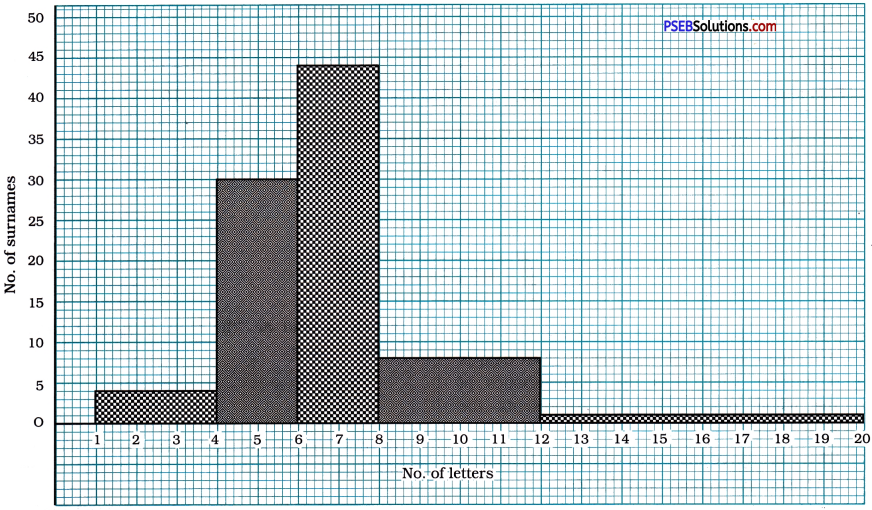
(ii) Write the class interval in which the maximum number of surnames lie.
Answer:
The maximum number of surnames lie in the class interval 6-8.