Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 8 Comparing Quantities Ex 8.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.3
1. Calculate the amount and compound interest on:
Question (a)
₹ 10,800 for 3 years at 12\(\frac {1}{2}\) per annum compounded annually.
Solution:
Here, P = ₹ 10,800;
R = 12\(\frac {1}{2}\) % = \(\frac {25}{2}\) %;
T = 3 years; ∴ n = 3
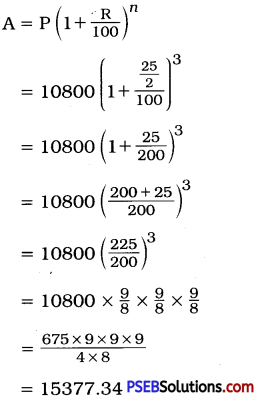
Amount = ₹ 15,377.34
Compound’interest = Amount – Principal
= ₹ (15377.34 – 10800)
= ₹ 4577.34
![]()
Question (b)
₹ 18,000 for 2\(\frac {1}{2}\) years at 10% per annum compounded annually.
Solution:
Here, P = ₹ 18,000; R = 10 %;
T = 2\(\frac {1}{2}\) years; ∴ n = 2 + \(\frac {1}{2}\)

Amount = ₹ 22,869
Compoimd interest = Amount – Principal
= ₹ (22869 – 18000)
= ₹ 4869
Question (c)
₹ 62,500 for 1\(\frac {1}{2}\) years at 8% per annum compounded half yearly.
Solution:
Here, the interest is compounded half-yearly.
Here, P = ₹ 62,500; R = \(\frac {8}{2}\) = 4 %
T = 1\(\frac {1}{2}\) years ∴ n = \(\frac {3}{2}\) × 2 = 3

Amount = ₹ 70,304
Compound interest = Amount – Principal
= ₹ (70304 – 62500)
= ₹ 7804
![]()
Question (d)
₹ 8000 for 1 year at 9 % per annum compounded half-yearly.
(You could use the year-by-year calculation using SI formula to verify.)
Solution:
Here, the interest is compounded half-yearly.
Here, P = ₹ 8000; R = \(\frac {9}{2}\) %;
T = 1 year ∴ n = 2

Amount = ₹ 8736.20
Compound interest = Amount – Principal
= ₹ (8736.20 – 8000)
= ₹ 736.20
[Note : By finding simple interest also we can calculate.)
SI = \(\frac {PRT}{100}\)
= \(\frac{8000 \times 9 \times 1}{2 \times 100}\)
= ₹ 376.20
Thus, total interest of 1 year
= ₹ (360 + 376.20)
= ₹ 736.20
![]()
Question (e)
₹ 10,000 for 1 year 8% per annum compounded half yearly.
Solution:
Here, the interest is compounded half-yearly.
Here, P = ₹ 10,000; R = \(\frac {8}{2}\) = 4 %;
T = 1 year ∴ n = 1 × 2 = 2
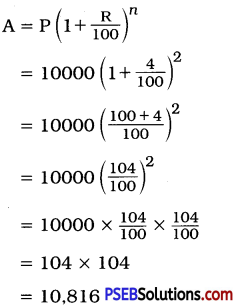
Amount = ₹ 10,816
Compound interest = Amount – Principal
= ₹ (10816 – 10000)
= ₹ 816
2. Kamala borrowed ₹ 26,400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?
(Hint: Find A for 2 years with interest is compounded yearly and then find SI on the 2nd year amount for \(\frac {4}{12}\) years)
Solution:
[Note: Here, find amount after 2 years by compound interest. This amount is principal for \(\frac {4}{12}\) year. For this \(\frac {4}{12}\) year, find simple interest.)
Here, P = ₹ 26,400; R = 15%;
T = 2 years ∴ n = 2

Now, ₹ 34,914 will be principal to find interest of 4 months.
SI = \(\frac {PRT}{100}\)
= \(\frac{34914 \times 15 \times 4}{100 \times 12}\)
= \(\frac{174570}{100}\)
= ₹ 174570
= ₹ 1745.70
Amount = ₹ (34914 + 1745.70)
= ₹ 36,659.70
Thus, Kamala Mil have to pay ₹ 36,659.70 to clear the loan.
![]()
3. Fabina borrows ₹ 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much?
Solution:
For Fabina:
Here, P = ₹ 12,500; R = 12%; T = 3 years
SI = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{12500 \times 12 \times 3}{100}\)
= 125 × 12 × 3
= ₹ 4500
Simple interest = ₹ 4500
For Radha:
Here, P = ₹ 12,500; R = 10%;
T = 3 years ∴ n = 3
![]()

Amount = ₹ 16,637.50
Compound interest = Amount – Principal
= ₹ (16637.50 – 12500)
= ₹ 4137.50
Fabina has to pay ₹ 4500 as interest and Radha has to pay ₹ 4137.50 as interest.
∴ Fabina has to pay more interest.
Difference in interest = ₹ (4500 – 4137.50)
= ₹ 362.50
Thus, Fabina has to pay ₹ 362.50 more than Radha as interest.
4. I borrowed ₹ 12,000 from Jamshed at 6 % per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what extra amount would I have to pay?
Solution:
For Simple Interest:
Here, P = ₹ 12,000; R = 6 %; T = 2 years
SI = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}\)
= \(\frac{12000 \times 6 \times 2}{100}\)
= 120 × 6 × 2
= ₹ 1440
SI = ₹ 1440
For Compound Interest:
Here, P = ₹ 12,000, R = 6 %
T = 2 years ∴ n = 2
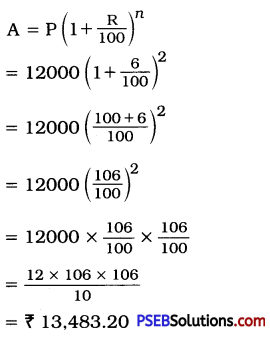
= ₹ 13,483.20
Amount = ₹ 13,483.20
CI = A – P
= ₹ (13483.20 – 12000)
= ₹ 1483.20
∴ Extra amount to be paid
= ₹ (1483.20 – 1440)
= ₹ 43.20
Thus, I have to pay ₹ 43.20 as extra amount.
![]()
5. Vasudevan invested ₹ 60,000 at an interest rate of 12% per annum compounded half-yearly. What amount would he get.
Question (i)
after 6 months?
Solution:
Interest after 6 months:
Here, P = ₹ 60,000; R = \(\frac {12}{2}\) = 6%;
T = 6 months ∴ n = 1

∴ Amount = ₹ 63,600
Question (ii)
after 1 year?
Solution:
After 1 year:
∴ Amount = ₹ 67,416
Here, P = ₹ 60,000; R = \(\frac {12}{2}\) = 6 %;
T = 1 year ∴ n = 2
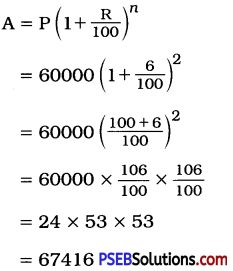
∴ Amount = ₹ 67, 146
Thus, Vasudevan will get ₹ 63,600 after 6 months and ₹ 67,416 after 1 year.
![]()
6. Arif took a loan of ₹ 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after 1\(\frac {1}{2}\) years if the interest is
Question (i)
compounded annually.
Solution:
Calculation of CI annually:
Here, P = ₹ 80,000; R = 10 %;
T = 1\(\frac {1}{2}\) year
For 1st year:
R = 10% and n = 1

∴ Amount of CI after 1 year = ₹ 88,000
Now, calculate simple interest of ₹ 88,000 for 6 months.
P = ₹ 88,000; R = 10 %;
T = 6 months = \(\frac {1}{2}\) year
∴ Interest = \(\frac{P \times R \times T}{100}\)
= \(\frac{88000 \times 10 \times 1}{100 \times 2}\)
= 4400
∴ Interest of 6 months = ₹ 4400
Thus, A = P + I
= ₹ (88000 + 4400)
= ₹ 92,400
Thus, according to CI, Arif has to pay ₹ 92,400
Question (ii)
compounded half yearly.
Solution:
If interest is compounded half yearly
Here, P = ₹ 88000, R = \(\frac {10}{2}\) = 5%
T = 1\(\frac {1}{2}\) years ∴ n = 3

∴ Amount = ₹ 92,610
Thus, according to half-yearly CI, Arif has to pay ₹ 92,610
∴ Difference = ₹ (92,610 – 92,400)
= ₹ 210
![]()
7. Maria invested ₹ 8,000 in a business. She would be paid interest at 5% per annum compounded annually. Find
Question (i)
The amount credited against her name at the end of the second year,
Solution:
(i) Here, P = ₹ 8000, R = 5 %,
T = 2 years ∴ n = 2
![]()

Thus, amount credited against Marlas name at the end of second year is ₹ 8820.
Question (ii)
The interest for the 3rd year.
Solution:
To find the interest for the 3rd year:
P = ₹ 8820, R = 5%, T = 1 years
SI = \(\frac{\mathrm{PRT}}{100}=\frac{8820 \times 5 \times 1}{100}\) = 441
The interest for 3rd year is ₹ 441
OR
The interest for the 3rd year:
Here, P = ₹ 8000, R = 5 %, T = 3 years ∴ n = 3

∴ At the end of 3rd year ₹ 9261 will be credited against Maria’s name.
∴ Interest of the 3rd year = Amount of 3 years – Amount of 2 years
= ₹ (9261 – 8820)
= ₹ 441
![]()
8. Find the amount and the compound interest on ₹ 10,000 for 1\(\frac {1}{2}\) years at 10% per annum, compounded half-yearly. Would this interest be more than the interest he would get if it was compounded annually?
Solution:
(i) Here, interest is compounded half-yearly.
Here, P = ₹ 10,000; R = \(\frac {10}{2}\) = 5 %;
T = 1\(\frac {1}{2}\) years ∴ n = 3
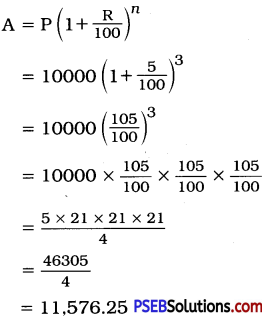
Amount = ₹ 11,576.25
CI = A – P
= ₹ (11576.25 – 10000)
= ₹ 1576.25
(ii) Here, interest is compounded yearly. CI for 1 year:
Here, P = ₹ 10,000; R = 10%;
T = 1 year ∴ n = 1
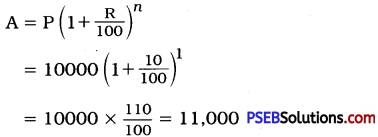
Amount at the end of 1 year = ₹ 11,000
∴ CI = A – P
= ₹ (11000 – 10000)
= ₹ 1000
Now, calculate SI for 6 months.
Here, P = ₹ 11,000; R = 10%; T = \(\frac {1}{2}\) year
SI = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}=\frac{11000 \times 10 \times 1}{100 \times 2}\)
= 550
∴ Total interest of 1\(\frac {1}{2}\) years = ₹ (1000 + 550)
= ₹ 1550
After comparing (i) and (ii), we can conclude ₹ 1576.25 > ₹ 1550
∴ Yes, the interest is more if compounded half-yearly.
![]()
9. Find the amount which Ram will get on ₹ 4096, if he gave it for 18 months at 12\(\frac {1}{2}\) % per annum, interest being compounded half-yearly.
Solution:
Here, interest is compounded half-yearly.
Here, P = ₹ 4096, R = 12\(\frac{1}{2} \times \frac{1}{2}=\frac{25}{4}\)
T = 18 months = 1\(\frac {1}{2}\) years ∴ n = 3

Amount = ₹ 4913
Thus, Ram will get ₹ 4913 at the end of period.
10. The population of a place increased to 54,000 in 2003 at a rate of 5% per annum
Question (i)
find the population in 2001.
Solution:
[Note: In 1st case, we have to find P as population of 2003 is given. From that we have to find population of 2001.]
Population in 2003 = 54,000
Here, A = 54,000; R = 5%; T = 2 years ∴ n = 2

∴ P = 48979.59 (approx)
P = 48980 (approx)
Thus, the population in 2001 is 48,980.
![]()
Question (ii)
What would be its population in 2005?
Solution:
Here, P = 54,000; R = 5 %;
T = 2 years ∴ n = 2

Thus, the population in 2005 is 59,535.
11. In a Laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours if the count was initially 5,06,000.
Solution:
Initial count of bacteria = 5,06,000
Rate of increasing = 2.5% per hour
Bacteria count after 2 hours
Here, P = 5,06,000, R = 2.5 % = \(\frac {5}{2}\)%;
T = 2 hours ∴ n = 2
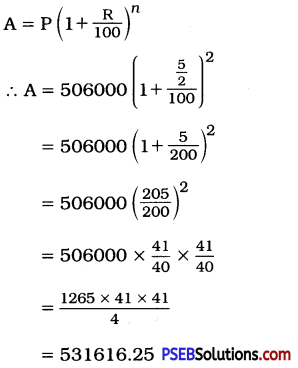
A = 531616 (approx)
Thus, the number of bacteria count after 2 hours will be 5,31,616 (approx).
![]()
12. A scooter was bought at ₹ 42,000. Its value depreciated at the rate of 8 % per annum. Find its value after one year.
Solution:
CP of a scooter = ₹ 42,000
Here, P = ₹ 42,000; R = 8 %; T = 1 ∴ n = 1
R = – 8 % (as depreciation)

Thus, the value of a scooter after 1 year will be ₹ 38,640.