PSEB 8th Class Maths Solutions Chapter 6 Squares and Square Roots InText Questions

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 6 Squares and Square Roots InText Questions and Answers.

PSEB 8th Class Maths Solutions Chapter 6 Squares and Square Roots InText Questions

Try These (Textbook Page No. 90)

1. Find the perfect square numbers between (i) 30 and 40 (ii) 50 and 60
Solution:
(i) Since,
1 × 1 = 1,
2 × 2 = 4,
3 × 3 = 9,
4 × 4 = 16,
5 × 5 = 25,
6 × 6 = 36,
7 × 7 = 49.
Thus, 36 is the only perfect square number between 30 and 40.

(ii) Since, 7 × 7 = 49 and 8 × 8 = 64.
∴ There is no perfect square number between 49 and 64.
Thus, there is no perfect square number between 50 and 60.

Try These (Textbook Page No. 90 – 91)

1. Can we say whether the following numbers are perfect squares? How do we know ?
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 1069
(vi) 2061
Write five numbers which you can decide by looking at their units digit that they are not square numbers.
Solution:
(i) 1057
The ending digit is 7. All square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.
∴ 1057 cannot be a perfect square.

(ii) 23453
The ending digit is 3. All square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.
∴ 23453 cannot be a perfect square.

(iii) 7928
The ending digit is 8. All square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.
∴ 7928 cannot be a perfect square.

(iv) 222222
The ending digit is 2. All square numbers end with 0, 1, 4, 5, 6 or s 9 at unit’s place.
∴ 222222 cannot be a perfect square.

(v) 1069
The ending digit is 9. All square jj numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.
∴ 1069 may or may not be a square number.
30 × 30 = 900, 31 × 31 = 961,
32 × 32 = 1024 and 33 × 33 = 1089.
e.g. No natural number between 1024 and 1089 is a perfect square.
∴ 1069 cannot be a perfect square.

(vi) 2061
The ending digit is 1. All square s numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.
∴ 2061 may or may not be a square number.
45 × 45 = 2025, 46 × 46 = 2116,
e.g. No natural number between 2025 and 2116 is a square number.
∴ 2061 is not a square number.

2. Write five numbers which you cannot decide just by looking at their unit’s digit (or units place) whether they are square numbers or not.
Solution:
Any natural number ending with 0, 1, 4, 5, 6 or 9 can be or cannot be a square number.
Five such numbers are :
719, 2431, 524, 215, 326
[Note: You can write many more numbers.]

Try These (Textbook Page No. 91)

1. Which of 1232, 772, 822, 1612, 1092 would end with digit 1 ?
Solution:
The square of those numbers end in 1 which end in either 1 or 9. Here, the square of 161 and 109 would end in 1.
OR
The number having 1 or 9 in units place has the digit 1 in units place of its square.

Try These (Textbook Page No. 91)

Which of the following numbers would have digit 6 at unit place ?
(i) 19²
(ii) 24²
(iii) 26²
(iv) 36²
(v) 34²
Solution:
The number having 4 or 6 in the units place has the digit 6 in units place of its square. Except 19² all other numbers have 6 in their units place.
OR
(i) 19²
Units place digit is 9.
∴ 19² would not have units digit as 6. (9 × 9 = 81)

(ii) 24²
Units place digit is 4.
∴ 24² would have units digit as 6. (4 × 4= 16)

(iii) 26²
Units place digit is 6.
∴ 26² would have 6 at units place. (6 × 6 = 36)

(iv) 36²
Units place digit is 6.
∴ 36² would have 6 at units place. (6 × 6 = 36)

(v) 34²
Units place digit is 4.
∴ 34² would have 6 at units place. (4 × 4 = 1²)

Try These (Textbook Page No. 92)

What will be the “one’s digit” in the square of the following numbers ?

Question (i).
1234
Solution:
1234
The ending digit is 4.
4 × 4 = 16
∴ (1234)² will have 6 as the one’s place.

Question (ii).
26387
Solution:
26387
The ending digit is 7.
7 × 7 = 49
∴ (26387)² will have 9 as the one’s place.

Question (iii).
52698
Solution:
52698
The ending digit is 8.
8 × 8 = 64
∴ (52698)² will have 4 as the one’s place.

Question (iv).
99880
Solution:
99880
The ending digit is 0.
0 × 0 = 0
∴ (99880)² will have 0 as the one’s place.

Question (v).
21222
Solution:
21222
The ending digit is 2.
2 × 2 = 4
∴ (21222)² will have 4 as the one’s place.

Question (vi).
9106
Solution:
9106
The ending digit is 6.
6 × 6 = 36
∴ (9106)² will have 6 as the one’s place.

Try These (Textbook Page No. 92)

1. The square of which of the following numbers would be an odd number/an even number? Why?

Question (i).
727
Solution:
727
Here, the ending digit is 7.
It is an odd number.
∴ Its square is also an odd number.

Question (ii).
158
Solution:
158
Here, the ending digit is 8.
It is an even number.
∴ Its square is also an even number.

Question (iii).
269
Solution:
269
Here, the ending digit is 9.
It is an odd number.
∴ Its square is also an odd number.

Question (iv).
1980
Solution:
1980
Here, the ending digit is 0.
It is an even number.
∴ Its square is also an even number.

2. What will be the number of zeros in the square of the following numbers?

Question (i).
60
Solution:
60
In 60, number of zero is 1.
∴ (60)² will have 2 zeros. (∵ 60² = 3600)

Question (ii).
400
Solution:
400
In 400, number of zeros are 2.
∴ (400)² will have 4 zeros.
(∵ 400² = 160000)

Try These (Textbook Page No. 94)

1. How many natural numbers lie between 9² and 10²? Between 11² and 12²?
Solution:
(a) We can find 2n natural numbers between two consecutive natural numbers, n² and (n + 1)².
Here, n = 9, n + 1 = 9 + 1 = 10.
∴ Natural numbers between 9² and 10² are 2n = 2 × 9 = 18.
Thus, 18 natural numbers lie between 9² and 10².

(b) We can find 2n natural numbers between two consecutive natural numbers, n² and (n + 1)².
Here, n = 11, n + 1 = 11 + 1 = 12.
∴ Natural numbers between 11² and 12² are 2n = 2 × 11 = 22.
Thus, 22 natural numbers lie between 112 and 122.

2. How many non square numbers lie between the following pairs of numbers:

Question (i).
100² and 101²
Solution:
100² and 101²
Here, n = 100 and n + 1 = 100 + 1
= 101
∴ non square numbers between 100² and 101² = 2 × n
= 2 × 100
= 200
Thus, 200 non square numbers lie between 100² and 101².

Question (ii).
90² and 91²
Solution:
90² and 91²
Here, n = 90 and n + 1 = 90 + 1 = 91.
∴ Natural numbers between 90² and 91²
= 2 × n
= 2 × 90
= 180.
Thus, 180 non square numbers lie between 90² and 91².

Question (iii).
1000² and 1001²
Solution:
1000² and 1001²
Here, n = 1000 and
n + 1 = 1000 + 1 = 1001.
∴ Natural numbers between 1000² and 1001²
= 2 × n
= 2 × 1000
= 2000.
Thus, 2000 non square numbers lie between 1000² and 1001².

Try These (Textbook Page No. 94)

Find whether each of the following numbers is a perfect square or not:

Question (i).
121
Solution:
121
121 – 1 = 120, 120 – 3 = 117
117-5 = 112, 112 – 7 = 105
105-9 = 96, 96 – 11 = 85
85 – 13 = 72, 72 – 15 = 57
57- 17 = 40, 40 – 19 = 21
21 – 21=0
e.g. 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21
Thus, 121 is a perfect square.

Question (ii).
55
Solution:
55
55 – 1 = 54, 54 – 3 = 51
51 – 5 = 46, 46 – 7 = 39
39 – 9 = 30, 30 – 11 = 19
19 – 13 = 6, 6 – 15 = – 9
Thus, 55 cannot be expressed as the sum of successive odd numbers starting from 1.
∴ 55 is not a perfect square.

Question (iii).
81
Solution:
81
81 – 1 = 80, 80 – 3 = 77
77 – 5 = 72, 72 – 7 = 65
65 – 9 = 56, 56 – 11 = 45
32 – 15 = 17, 32 – 15 = 17
17 – 17 = 0
∴ 81 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17
Thus, 81 is a perfect square.

Question (iv).
49
Solution:
49
49 – 1 = 48, 48 – 3 = 45
45 – 5 = 40, 40 – 7 = 33
33 – 9 = 24, 24 – 11 = 13
13 – 13 = 0
∴ 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13
Thus, 49 is a perfect square.

Question (v).
69
Solution:
69
69 – 1 = 68, 68 – 3 = 65
65 – 5 = 60, 60 – 7 = 53
53-9 = 44, 44 – 11 = 33
33- 13 = 20, 20 – 15 = 5
5 – 17 = – 12
Thus, 69 cannot be expressed as the sum of successive odd numbers starting from 1.
∴ 69 is not a perfect square.

Try These (Textbook Page No. 95)

1. Express the following as the sum of two consecutive integers:

Question (i).
21²
Solution:
Remember : n² = \(\frac{n^{2}-1}{2}+\frac{n^{2}+1}{2}\)
21²
n = 21

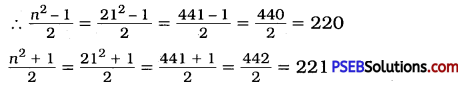
∴ 21² = 220 + 221 = 441

Question (ii).
13²
Solution:
13²
n = 13

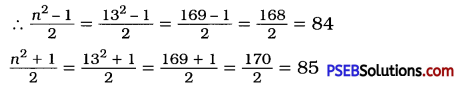
∴ 13² = 84 + 85 = 169

Question (iii).
11²
Solution:
11²
n = 11

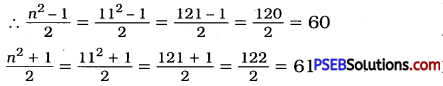
∴ 11² = 60 + 61 = 121

Question (iv).
19²
Solution:
19²
n = 19

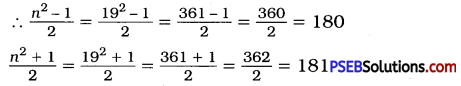
∴ 19² = 180 + 181 = 361

2. Do you think the reverse is also true, e.g. is the sum of any two consecutive positive integers is perfect square of a number? Give example to support your answer.
Solution:
No, the reverse is not always true.
(i) 3 + 4 = 7, 7 is not a perfect square.
(ii) 10 + 11 = 21, 21 is not a perfect square.
But,
(i) 4 + 5 = 9, 9 is a perfect square.
(ii) 12 + 13 = 25, 25 is a perfect square.

Try These (Textbook Page No. 95)

Write the square, making use of the above pattern:

Question (i).
111111²
Solution:
(111111)²
The given number is a six-digit number,
∴ middle number 6

Question (ii).
1111111²
Solution:
(1111111)²
The given number is a seven-digit number.
∴ middle number 7

Try These (Textbook Page No. 95)

Can you find the square of the following numbers using the above pattern ?
(i) 6666667²
(ii) 66666667²
Solution:
(i) Yes, 6666667² = 44444448888889
(ii) Yes, 66666667² = 4444444488888889

Try These (Textbook Page No. 97)

Find the squares of the following numbers containing 5 in unit’s place:

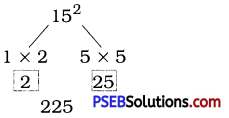
Question (i).
15
Solution:
[Note : A number with unit digit 5, e.g. a5
(a5)² = a(a + 1) × 100 + 25]
( i ) (15)² = 1 × (1 + 1) × 100 + 25
= 1 × 2 × 100 + 25
= 200 + 25
= 225
Hint:

Question (ii).
95
Solution:
(95)² = 9 (9 + 1) × 100 + 25
= 9 × 10 × 100 + 25
= 9000 + 25
= 9025

Question (iii).
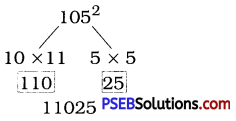
105
Solution:
(105)² = 10 × (10 + 1) × 100 + 25
= 10 × 11 × 100 + 25
= 11000 + 25
= 11025
Hint:

Question (iv).
205
Solution:
(205)² = 20 × (20 + 1) × 100 + 25
= 20 × 21 × 100 + 25
= 42000 + 25
= 42025

Try These (Textbook Page No. 99)

Question (i).
11² = 121. What is the square root of 121 ?
Solution:
Square root of 121 is 11.

Question (ii).
14² = 196. What is the square root of 196 ?
Solution:
Square root of 196 is 14.

Think, Discuss and Write (Textbook Page No. 99)

Question (i).
(-1)² = 1. Is – 1, a square root of 1 ?
Solution:
[Note: There are two (positive as well as negative) integral square roots of a perfect square number.]
(- 1) × (- 1) = 1, (- 1)² = 1
∴ Square root of 1 can also be (-1).

Question (ii).
(-2)² = 4. Is -2, a square root of 4 ?
Solution:
(- 2) × (- 2) = 4, (-2)² = 4
∴ Square root of 4 can also be (-2).

Question (iii).
(-9)² = 81. Is – 9, a square root of 81 ?
Solution:
(-9) × (-9) = 81, (- 9)² = 81
∴ Square root of 81 can also be (-9).

Try These (Textbook Page No. 100)

By repeated subtraction of odd numbers starting from 1, find whether the following numbers are perfect squares or not? If the number is a perfect square then find its square root:

Question (i).
121
Solution:
Subtracting the successive odd numbers from 121 :
121 – 1 = 120, 120 – 3 = 117
117 – 5 = 112, 112 – 7 = 105
105 – 9 = 96, 96 – 11 = 85
85 – 13 = 72, 72 – 15 = 57
57 – 17 = 40, 40 – 19 = 21
21 – 21 = 0
∴ \(\sqrt{121}\) = 11
∴ 121 is a perfect square.

Question (ii).
55
Solution:
∵ 55 – 1 = 54, 54 – 3 = 51
51 – 5 = 46, 46 – 7 = 39
39 – 9 = 30, 30 – 11 = 19
19 – 13 = 6, 6 – 15 = – 9
55 does not reduced to 0 after subtracting odd numbers starting from 1.
∴ 55 is not a perfect square.

Question (iii).
36
Solution:
∵ 36 – 1 = 35, 35 – 3 = 32
32 – 5 = 27, 27 – 7 = 20
20 – 9 = 11, 11 – 11 = 0
∴ \(\sqrt{36}\) = 6
∴ 36 is a perfect square.

Question (iv).
49
Solution:
49 – 1 = 48, 48 – 3 = 45
45 – 5 = 40, 40 – 7 = 33
33 – 9 = 24, 24 – 11 = 13
13- 13 = 0
∴ \(\sqrt{49}\) = 7
∴ 49 is a perfect square.

Question (v).
90
Solution:
90 – 1 = 89, 89 – 3 = 86
86 – 5 = 81, 81 – 7 = 74
74 – 9 = 65, 65 – 11 = 54
54 – 13 = 41, 41 – 15 = 26
26 – 17 = 9, 9 – 19 = – 10
90 does not reduced to 0 after subtracting odd numbers starting from 1.
∴ 90 is not a perfect square.

Think, Discuss and Write (Textbook Page No. 103)

Can we say that if a perfect square is of n-digits, then its square root will have \(\frac{n}{2}\) digits if n is even or \(\frac{(n+1)}{2}\) if n is odd ?
Solution:
Yes, we can say that if a perfect square is of n-digits, then its square root will have
(a) \(\frac{n}{2}\) digits, if n is even.
(b) \(\frac{(n+1)}{2}\) digits, if n is odd.

Try These (Textbook Page No. 105)

Without calculating square roots, find the number of digits in the square root of the following numbers:

Question (i).
25600
Solution:
Here, the number of digits, n = 5 (an odd number.)
∴ Number of digits in the square root of 25600 = \(\frac{(n+1)}{2}\)
= \(\frac{5+1}{2}\)
= \(\frac {6}{2}\)
= 3

Question (ii).
100000000
Solution:
Here, the number of digits, n =9 (an odd number.)
∴ Number of digits in the square root of 100000000 = \(\frac{(n+1)}{2}\)
= \(\frac{9+1}{2}\)
= \(\frac {10}{2}\)
= 5

Question (iii).
36864
Solution:
Here, the number of digits, n = 5 (an odd number.)
∴ Number of digits in the square root of 36864 = \(\frac{(n+1)}{2}\)
= \(\frac{5+1}{2}\)
= \(\frac {6}{2}\)
= 3

Try these (Textbook Page No. 107)

Estimate the value of the following to the nearest whole number:

Question (i).
\(\sqrt{80}\)
Solution:
\(\sqrt{80}\)
10² = 100, 9² = 81, 8² = 64
∴ 80 is between 64 and 81.
∴ 64 < 80 < 81
∴ 8² < 80 < 9²
∴ 8 < \(\sqrt{80}\) < 9
Thus, \(\sqrt{80}\) lies between 8 and 9.
\(\sqrt{80}\) is much closer to 81 than 64.
∴ \(\sqrt{80}\) is approximately 9.

Question (ii).
\(\sqrt{1000}\)
Solution:
\(\sqrt{1000}\)
30² = 900, 31² = 961, 32² = 1024
∴ 1000 is between 961 and 1024.
∴ 961 < 1000 < 1024
∴ 31² < 1000 < 32²
∴ 31 < \(\sqrt{1000}\) < 32
Thus, \(\sqrt{1000}\) lies between 31 and 32.
\(\sqrt{1000}\) is much closer to 32 than 31.
∴ \(\sqrt{1000}\) is approximately 32.

Question (iii).
\(\sqrt{350}\)
Solution:
\(\sqrt{350}\)
18² = 324 and 19² = 361
∴ 350 is between 324 and 361.
∴ 324 < 350 < 361
∴ 18² < 350 < 19²
∴ 18 < \(\sqrt{350}\) < 19
Thus, \(\sqrt{350}\) lies between 18 and 19.
\(\sqrt{350}\) is much closer to 19 than 18.
∴ \(\sqrt{350}\) is approximately 19.

Question (iv).
\(\sqrt{500}\)
Solution:
\(\sqrt{500}\)
22² = 484 and 23² = 529
∴ 500 is between 484 and 529.
∴ 484 < 500 < 529
∴ 22² < 500 < 23²
∴ 22 < \(\sqrt{500}\) < 23
Thus, \(\sqrt{500}\) lies between 22 and 23.
\(\sqrt{500}\) is much closer to 22 than 23.
∴ \(\sqrt{500}\) is approximately 22.