Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 9 Understanding Elementary Shapes Ex 9.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 6 Maths Chapter 9 Understanding Elementary Shapes Ex 9.4
1. Classify each of the following triangles as scalene, isosceles or equilateral:
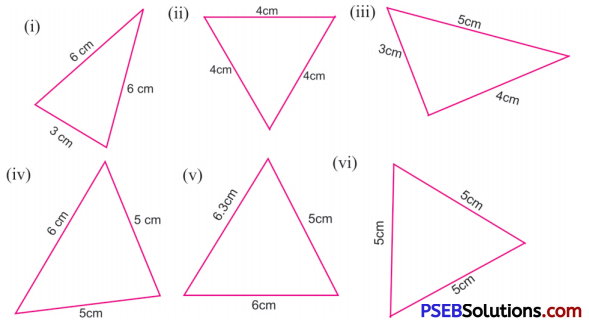
Solution:
(i) Here, two sides of triangle are equal in length.
∴ It is an isosceles triangle.
(ii) Here, all the three sides of the triangle are equal in length.
∴ It is an equilateral triangle.
(iii) Here, no two sides are equal in length.
∴ It is scalene triangle.
(iv) Here, two sides of triangle are equal in length.
∴ It is an isosceles triangle.
(v) Here, no two sides are equal in length.
∴ It is scalene triangle.
(vi) Here, all the three sides of the triangle are equal in length.
∴ It is equilateral triangle.
![]()
2. Classify each of the following triangles as acute, obtuse or right triangle:
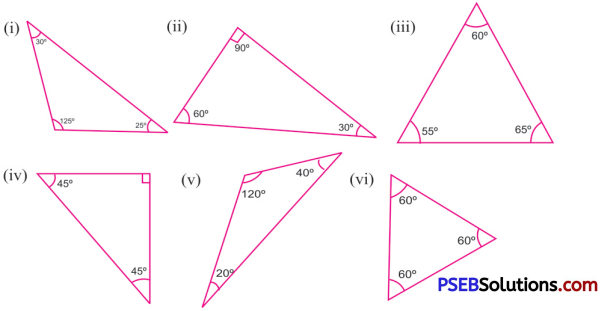
Solution:
(i) Here, one angle is 120°, which is obtuse angle.
∴ It is an obtuse-angled triangle.
(ii) Here, one angle is 90°, which is right angle.
∴ It is an right-angled triangle.
(iii) Here, each angle is acute angle.
∴ It is an acute-angled triangle.
(iv) Here, one angle is 90°, which is right angle.
∴ It is an right-angled triangle.
(v) Here, one angle is 120°, which is obtuse angle.
∴ It is an obtuse-angled triangle.
(vi) Here, each angle is 60°, which is actute angle.
∴ It is an actute angled triangle.
3. Which of the following triangles are possible with the given angles?
Question (i)
60°, 60°, 60°
Solution:
In a triangle sum of the three angles of a triangle is equal to 180°.
Here, sum of the three angles of triangle is:
60° + 60° + 60° = 180°
∴ This triangle is possible.
![]()
Question (ii)
110°, 50°, 30°
Solution:
Here, sum of the three angles of triangle is:
110° + 50° + 30°= 190° ≠ 180°
∴ This triangle is not possible.
Question (iii)
65°, 55°, 60°
Solution:
Here, sum of the three angles of triangle is:
65°+ 55°+ 60°= 180°
∴ This triangle is possible.
Question (iv)
90°, 40°, 50°
Solution:
Here, sum of the three angles of triangle is:
90°+ 40°+ 50°= 180°
∴ This triangle is possible.
Question (v)
48°, 62°, 50°
Solution:
Here, sum of the three angles of triangle is:
48°+ 62°+ 50°= 160° ≠ 180°
∴ This triangle is not possible.
![]()
Question (vi)
90°, 95°, 30°.
Solution:
Here, sum of the three angles of triangle is:
90°+ 95°+ 30° =215° ≠ 180°
∴ This triangle is not possible.
4. Classify each of the following triangles as scalene, isosceles or equilateral triangle:
Question (i)
4 cm, 5 cm, 6 cm
Solution:
The sides of triangle are 4 cm, 5 cm, 6 cm
No, two sides of this triangle are equal.
∴ This is a scalene triangle.
Question (ii)
5 cm, 7 cm, 5 cm
Solution:
The sides of triangle are 5 cm, 7 cm, 5 cm
Here, two sides are equal each of 5 cm in length.
∴ This is an isosceles triangle.
![]()
Question (iii)
4.2 m, S3 m, 6.1 m
Solution:
The sides of triangle are 4.2 m, 5.3 m, 6.1 m
Here, all sides are of different length.
∴ This is a scalene triangle.
Question (iv)
3.5 cm, 3.5 cm, 33 cm
Solution:
The sides of triangle are 3.5 cm, 3.5 cm, 3.5 cm
All the sides of triangle are of equal length.
∴ This is an equilateal triangle.
Question (v)
8 cm, 4.2 cm, 4.2 cm
Solution:
The sides of triangle are 8 cm, 4.2 cm, 4.2 cm
Here, two sides of the triangle are of equal length.
∴ This is an isosceles triangle.
Question (vi)
2 cm, 3 cm, 4 cm.
Solution:
The sides of triangle are 2 cm, 3 cm, 4 cm
All the sides of the triangle are of different lengths
∴ This is a scalene triangle.
![]()
5. Name the following triangles in both ways: (Based on sides and angles)
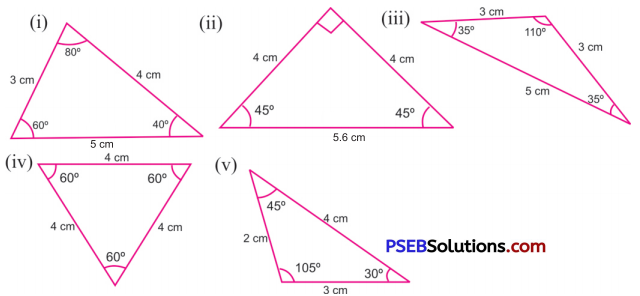
Solution:
(i) Based on sides: In this triangle, no two sides of the triangle are equal.
∴ This is a scalene triangle.
Based on angles: All the three angles of the triangle are acute.
∴ This is an acute-angled triangle.
(ii) Based on sides: In this triangle, two sides are of equal length each is 4 cm.
∴ This is an isosceles triangle.
Based on angles: In this triangle, one angle is of 90° which is a right angle.
∴ This is a right-angled triangle.
(iii) Based on sides: In this triangle, two sides are of equal length.
∴ This is an isosceles triangle.
Based on angles: In this triangle one angle is of 110°, which is obtuse angle.
∴ This is an obtuse-angled triangle.
(iv) Based on sides: In this triangle, all the sides are of equal length i.e. each = 4 cm.
∴ This is an equilateral triangle.
Based on angles: In this triangle, all the angles are acute angles.
∴ This is an acute-angled triangle.
(v) Based on sides: In this triangle, all the three sides are of different lengths.
∴ This is a scalene triangle.
Based on angles: In this triangle, one angle is 105°, which is obtuse angle.
∴ This is an obtuse-angled triangle.
![]()
6. Fill in the blanks:
Question (i)
A triangle has …………. sides.
Solution:
3
Question (ii)
A triangle has …………. vertices.
Solution:
3
Question (iii)
A triangle has …………. angles.
Solution:
3
Question (iv)
A triangle has …………. parts.
Solution:
6
Question (v)
A triangle whose all sides are different is known as ………………. .
Solution:
Scalene triangle
![]()
Question (vi)
A triangle whose all angles are acute is known as ……………….. .
Solution:
Acute angled triangle
Question (vii)
A triangle whose two sides are equal is known as ……………….. .
Solution:
Isosceles triangle
Question (viii)
A triangle whose one angle is obtuse is known as ……………….. .
Solution:
obtuse-angled triangle
Question (ix)
A triangle whose all sides are equal is known as ……………….. .
Solution:
Equilateral triangle
Question (x)
A triangle whose one angle is right angle is known as ……………….. .
Solution:
Right-angled triangle
7. State True or False:
Question (i)
Each equilateral triangle is an isosceles triangle.
Solution:
True
![]()
Question (ii)
Each acute-angled triangle is a scalene triangle.
Solution:
False
Question (iii)
Each isosceles triangle is an equilateral triangle.
Solution:
False
Question (iv)
There are two obtuse angles in an obtuse triangle.
Solution:
False
Question (v)
In right triangle, there is only one right angle.
Solution:
True
![]()
Question (vi)
Right triangle can never be isosceles.
Solution:
False.