Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 2 Whole Numbers Ex 2.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 6 Maths Chapter 2 Whole Numbers Ex 2.1
1. Answer the following questions:
Question (a)
Write the smallest whole number.
Solution:
The smallest Whole number = 0
![]()
Question (b)
Write the smallest natural number.
Solution:
The smallest natural number = 1
Question (c)
Write the successor of 0 in whole numbers.
Solution:
Successor of 0 = 0 + 1 = 1
Question (d)
Write the predecessor of 0 in whole numbers.
Solution:
Predecessor of 0 is whole number is not possible.
Question (e)
Write the Largest whole number.
Solution:
Largest whole number is not possible.
2. Which of the following statements are True (T) and which are False (F)?
Question (a)
Zero is the smallest natural number.
Solution:
False
![]()
Question (b)
Zero is the smallest whole number.
Solution:
True
Question (c)
Every whole number is a natural number.
Solution:
False
Question (d)
Every natural number is a whole number.
Solution:
True
Question (e)
1 is the smallest whole number.
Solution:
False
Question (f)
The natural number 1 has no predecessor in natural numbers.
Solution:
True
Question (g)
The whole number 1 has no predecessor in whole numbers.
Solution:
False
![]()
Question (h)
Successor of the largest two-digit number is smallest three-digit number.
Solution:
True
Question (i)
The successor of a two-digit number is always a two-digit number.
Solution:
False
Question (j)
300 is the predecessor of 299.
Solution:
False
Question (k)
500 is the successor of 499.
Solution:
True
Question (l)
The predecessor of a two-digit number is never a single-digit number.
Solution:
False
3. Write the successor of each of following:
Question (a)
100909
Solution:
Successor of 100909
= 100909 + 1
= 100910
![]()
Question (b)
4630999
Solution:
Successor of 4630999
= 4630999 + 1
= 4631000
Question (c)
830001
Solution:
Successor of 830001
= 830001 + 1
= 830002
Question (d)
99999.
Solution:
Successor of 99999
= 99999 + 1
= 100000
4. Write the predecessor of each of following:
Question (a)
1000
Solution:
Predecessor of 1000 = 1000 – 1
= 999
![]()
Question (b)
208090
Solution:
Predecessor of 208090 = 208090 – 1
= 208089
Question (c)
7654321
Solution:
Predecessor of 7654321 = 7654321 – 1
= 7654320
Question (d)
12576.
Solution:
Predecessor of 12576 = 12576 – 1
= 12575
5. Represent the following numbers on the number line: 2, 0, 3, 5, 7, 11, 15.
Solution:
Draw a line. Mark a point on it. Label it ‘O’. Mark a second point to the right of 0. Label it 1. The distance between these points labelled as 0 and 1 is called unit distance. On this line, mark a point to the right of 1 and at unit distance from 1 and label it 2. In this way go on labeling points at unit distance as 3, 4, 5, …………… on the line.
![]()
6. How many whole numbers are there between 22 and 43?
Solution:
Whole numbers between 22 and 43 are 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42
∴ There are 20 whole numbers between 22 and 43.
Or [(43 – 22) – 1 = 21 – 1 = 20].
![]()
7. Draw a number line to represent each of following on it.
Question (a)
3 + 2
Solution:
We draw a number line and move 3 steps from 0 to the right and mark this point as A.
Now, starting from A we move 2 steps towards right and move at B.
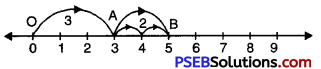
OA = 4, AB = 2, OB = 5
Hence, OB = 3 + 2 = 5.
Question (b)
4 + 5
Solution:
We draw a number line.
Starting from point 0 (i.e. zero), we move 4 steps to the right and mark this point as A.
Now, starting from A we move 5 steps towards right and arrive at B.
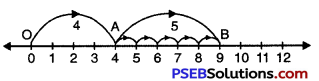
OA = 4, AB = 5, OB = 9
Hence, OB = 4 + 5 = 9.
![]()
Question (c)
6 + 2
Solution:
We draw a number line.
Starting from point 0 (i.e. zero), we move 6 steps to the right and mark this point as A.
Now, starting from A we move 2 steps towards right and arrive at B.

OA = 6, AB = 2, OB = 8
Hence, OB = 6 + 2 = 8.
Question (d)
8 – 3
Solution:
We draw a number line.
Starting from point 0 (i.e. zero), we move 8 steps to the right and arrive at A.
Now, starting from A we move 3 steps to the left of A and arrive at B.

OA = 8, AB = 3, OB = 5
Hence, OB = 8 – 3 = 5.
Question (e)
7 – 4
Solution:
We draw a number line.
Starting from point 0 (i.e. zero), we move 7 steps to the right and arrive at A.
Now, starting from A we move 4 steps to the left of A and arrive at B.

OA = 7, AB = 4, OB = 3
Hence, OB = 7 – 4 = 3.
![]()
Question (f)
7 – 2
Solution:
We draw a number line.
Starting from point 0 (i.e. zero), we move 7 steps to the right and arrive at A.
Now, starting from A, we move 2 steps to the left of A and arrive at B.

OA = 7, AB = 2, OB = 5
Hence, OB = 7 – 2 = 5.
Question (g)
3 × 3
Solution:
We draw a number line.
Starting from 0 we move 3 units to the right of 0 to arrive at A.
We make two more such same moves starting from A (total 3 moves of 3 units each) to reach finally at C which represents 9.
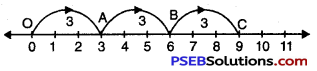
Hence, 3 × 3 = 9.
Question (h)
2 × 5
Solution:
We draw a number line.
We start from 0 move 5 units at a time to right.
We make 2 such moves. We shall reach at 10.
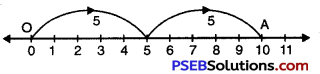
So, 2 × 5 = 10.
![]()
Question (i)
3 × 5
Solution:
We draw a number line.
We start from 0, move 5 units at a time to right.
We make 3 such moves. We shall reach at 15.
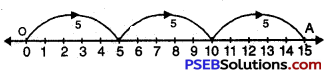
So, 3 × 5 = 15
Question (j)
9 ÷ 3
We draw a number line.
Starting from 0, we move 9 units to the right of 0 to arrive at A.
Now, from A take moves of 3 units to the left of A till we reach at ‘O’. We observe that there are 3 moves.
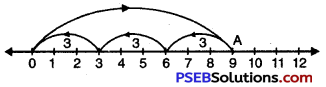
So, 9 ÷ 3 = 3.
Question (k)
12 ÷ 4
We draw a number line.
Starting from 0, we move 12 units to the right of 0 to arrive at A.
Now, from A take moves of 4 units to the left of A till we reach at ‘O’. We observe that there are 3 moves.
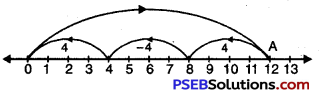
So, 12 ÷ 4 = 3.
![]()
Question (l)
10 ÷ 2
Solution:
We draw a number line.
Starting from 0, we move 10 units to the right of 0 to arrive at A.
Now, from A take moves of 2 units to the left c A till we reach at ‘O’. We observe that there are 5 moves.
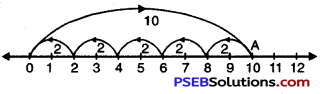
So, 10 ÷ 2 = 5.
8. Fill in the blanks with the appropriate symbol < or > :
Question (i)
(a) 25 ……………. 205
(b) 170 …………… 107
(c) 415 …………… 514
(d) 10001 ………….. 9999
(e) 2300014 ………….. 2300041
(f) 99999 …………… 888888.
Solution:
(a) 25 < 205 (b) 170 > 107
(c) 415 < 514 (d) 10001 > 9999
(c) 2300014 < 2300041
(f) 99999 < 888888.