Punjab State Board PSEB 6th Class Maths Book Solutions Chapter 10 Practical Geometry Ex 10.5 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 6 Maths Chapter 10 Practical Geometry Ex 10.5
1. Draw the following angles in both directions (Left and right) by protractor:
Question (i)
75°
Solution:
Steps of Construction:
1. Draw a ray OA.
![]()
2. Place the protractor on ray OA such that its centre lies on the initial point O and 0-180° base line along OA.

3. Mark a point B on the paper against the mark of 75° (inner scale) on the protractor.
4. Remove the protractor and join OB.
Thus, required angle \(\angle AOB\) = 75°.
If ray OA lies to the left of the centre (midpoint) of the baseline, start reading the angle on the outer scale from 0° and mark 75°. Join OB, then \(\angle AOB\) = 75°.
![]()
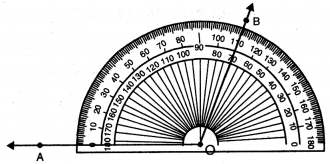
Question (ii)
110°
Solution:
Steps of Construction:
1. Draw a ray OA.
![]()
2. Place the protractor on OA such that its centre lies on the initial point O and 0-180° base line along OA.
3. Mark a point B on the paper against the mark of 110° (inner scale) on the protractor.
4. Remove the protractor and join OB.
Thus, required angle \(\angle AOB\) = 110°.
If the ray OA lies to the left of the centre (mid point) of the base line, start reading the angle on the outer scale from 0° and mark 110°. Join OB, then \(\angle AOB\) = 110°.
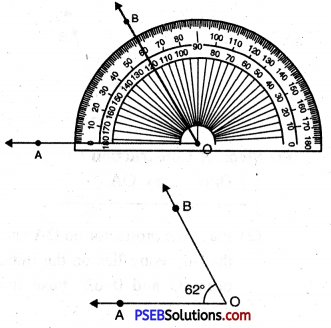
Question (iii)
62°
Solution:
Steps of Construction:
1. Draw a ray OA.
![]()
2. Place the protractor on OA such that its centre lies on the initial point O and 0-62° base line along OA.
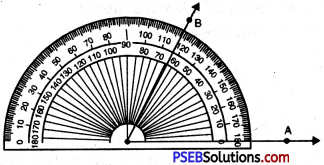
3. Mark a point B on the paper against the mark of 62° (inner scale) on the protractor.
4. Remove the protractor and join OB.
Thus, required angle \(\angle AOB\) = 62°.
If the ray OA lies to the left of the centre (midpoint) of the baseline, start reading the angle on the outer scale from 0° and mark 62°. Join OB, then \(\angle AOB\) = 62°.
![]()
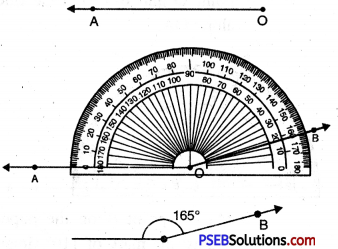
Question (iv)
165°
Solution:
Steps of Construction:
1. Draw a ray OA.
![]()
2. Place the protractor on OA such that its centre lies on the initial point O and 0-180° baseline along OA.
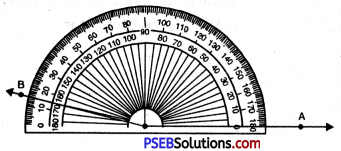
3. Mark a point B on the paper against the mark of 165° (inner scale) on the protractor.

4. Remove the protractor and join OB.
Thus, required angle
\(\angle AOB\) = 165°
If the ray OA lies to the left of the centre (mid point) of the base line, start reading the angle on the outer scale from 0° and mark 165°. Join OB, then \(\angle AOB\) = 165°.
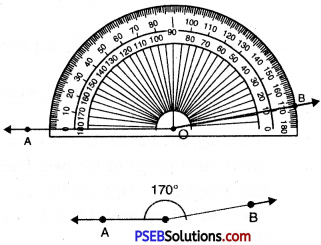
Question (v)
170°
Solution:
Steps of Construction:
1. Draw a ray OA.
![]()
2. Place the protractor on ray OA such that its centre lies on the initial point O and 0-480° base line along OA.
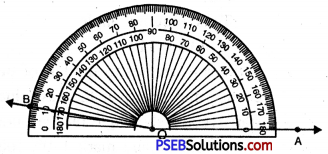
3. Mark a point B on the paper against the mark of 170° (inner scale) on the protractor.

4. Remove the protractor and join OB.
Thus, required angle \(\angle AOB\) = 170°.
If the ray OA lies to the left of the centre (mid point) of the base line, start reading the angle on the outer scale from 0° and mark 170°. Join OB, then \(\angle AOB\) = 170°.
![]()
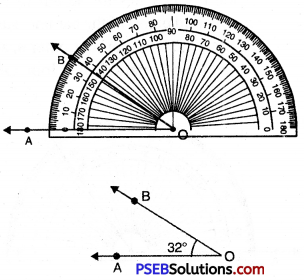
Question (vi)
32°
Solution:
Steps of Construction:
1. Draw a ray OA.
![]()
2. Place the protractor on OA such that its centre lies on the initial point O and 0-180° base line along OA.
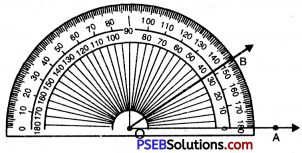
3. Mark a point B on the paper against the mark of 32° (inner scale) on the protractor.
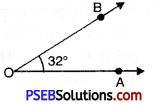
4. Remove the protractor and join OB.
Thus, required angle \(\angle AOB\) = 32°.
If the ray OA lies to the left of the centre (mid point) of the base line, start reading the angle on the outer scale from 0° and mark 32°. Join OB, then \(\angle AOB\) = 32°.
Question (vii)
128°
Solution:
Steps of Construction:
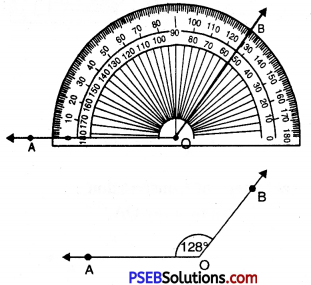
1. Draw a ray OA.
![]()
Place the protractor on OA such that its centre lies on the initial point O and 0-180° base line along OA.

3. Mark a point B on the paper against the mark of 128° (inner scale) on the protractor.

4. Remove the protractor and join OB.
Thus, required angle
\(\angle AOB\) = 128°.
If the ray OA lies to the left to the centre (mid point) of the bar line, start reading the angle on the outer scale from 0° and mark 128°. Join OB, then \(\angle AOB\) = 128°.
![]()
Question (viii)
25°
Solution:
Steps of Construction:
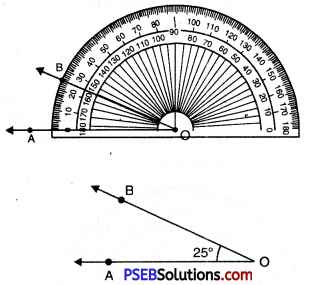
1. Draw a ray OA.
![]()
2. Place the protractor on OA such that its centre lies on the initial point O and 0-180° base line along OA.

3. Mark a point B on the paper against the mark of 25° (inner scale) on the protractor.
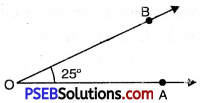
4. Remove the protractor and join OB.
Thus, required angle \(\angle AOB\) = 25°.
If the ray OA lies to the left of the centre (mid point) of the base line, start reading the angle on the outer scale from 0° and mark 25°. Join OB, then \(\angle AOB\) = 25°.
![]()
Question (ix)
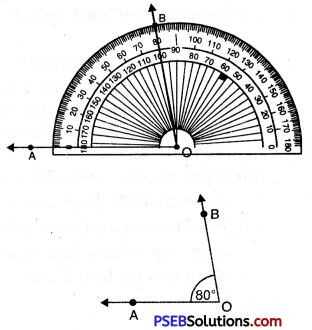
80°
Solution:
Steps of Construction:
1. Draw a ray OA.
![]()
2. Place the protractor on OA such that its centre lies on the initial point O and 0-180° base line along OA.
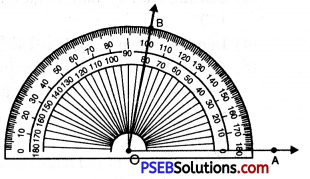
3. Mark a point B on the paper against the mark of 80° (inner scale) on the protractor.
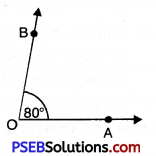
4. Remove the protractor and join OB.
Thus, required angle \(\angle AOB\) = 80°.
If the ray OA lies to the left to the centre (mid point) of the bar line, start reading the angle on the outer scale from 0° and mark 80°. Join OB, then \(\angle AOB\) = 80°.
Question (x)
135°.
Solution:
Steps of Construction:
1. Draw a ray OA.
![]()
2. Place the protractor on OA such that its centre lies on the initial point O and 0-180° base line along OA.
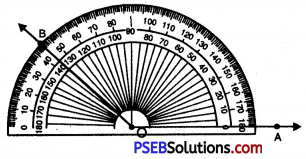
3. Mark a point B on the paper against the mark of 135° (inner scale) on the protractor.
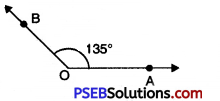
4. Remove the protractor and join OB.
Thus, required angle \(\angle AOB\) = 135°.

If the ray OA lies to the left to the centre (mid point) of the bar line, start reading the angle on the outer scale from 0° and mark 135°. Join OB, then \(\angle AOB\) = 135°.
![]()
2. Bisect the following angles by compasses:
Question (i)
48°
Solution:
Steps of Construction:
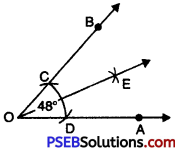
1. Draw a ray OA.
2. Place the centre of the protractor at O.
3. Starting with 0° mark point B at 48°.
4. Join OB. Then \(\angle AOB\) = 48°.
5. With O as centre and using compasses, draw an arc that cuts both rays of \(\angle AOB\) at C and D respectively.
6. With C as centre and radius more than half of CD. Draw an arc.
7. With D as centre and same radius as in step 6 draw another arc which cuts the first arc at point
E.
8. Join OE, then OE is the bisector of angle \(\angle AOB\) = 48°.
Measure \(\angle AOB\) and \(\angle AOB\)
\(\angle AOB\) = \(\angle AOB\) = 24°.
Question (ii)
140°
Solution:
Steps of Construction:
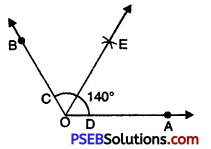
1. Draw a ray OA.
2. Place the centre of the protractor at O.
3. Starting with 0° mark point B at 140°.
4. Join OB. Then \(\angle AOB\) = 140°.
5. With O as centre and using compasses, draw an arc that cuts both rays of \(\angle AOB\) at C and D respectively.
6. With C as centre and radius more than half of CD. Draw an arc.
7. With D as centre and same radius as in step 6 draw another arc which cuts the first arc at point E.
8. Join OE, then OE is the bisector of angle \(\angle AOB\) = 140°.
On measurement \(\angle AOE\) = \(\angle BOE\) = 70°.
![]()
Question (iii)
75°
Solution:
Steps of Construction:
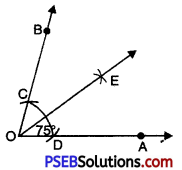
1. Draw a ray OA.
2. Place the centre of the protractor at O.
3. Starting with 0° mark point B at 75°.
4. Join OB. Then \(\angle AOB\) = 75°.
5. With O as centre and using compasses, draw an arc that cuts both rays of \(\angle AOB\) at C and D respectively.
6. With C as centre and radius more than half of CD. Draw an arc.
7. With D as centre and same radius as in step 6 draw another arc which cuts the first arc at point E.
8. Join OE, then OE is the bisector of angle \(\angle AOB\) = 75°.
On measurement
\(\angle AOE\) = \(\angle BOE\) = 37.5°.
Question (iv)
64°
Solution:
Steps of Construction:
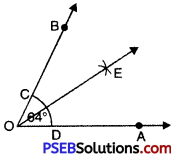
1. Draw a ray OA.
2. Place the centre of the protractor at O.
3. Starting with 0° mark point B at 64°.
4. Join OB. Then \(\angle AOB\) = 64°.
5. With O as centre and using compasses, draw an arc that cuts both rays of \(\angle AOB\) at C and D respectively.
6. With C as centre and radius more than half of CD. Draw an arc.
7. With D as centre and same radius as in step 6 draw another arc which cuts the first arc at point E.
8. Join OE, then OE is the bisector of angle \(\angle AOB\) = 64°.
On measurement
\(\angle AOE\) = \(\angle BOE\) = 32°.
![]()
Question (v)
124°.
Solution:
Steps of Construction:
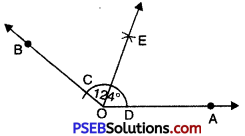
1. Draw a ray OA.
2. Place the centre of the protractor at O.
3. Starting with 0° mark point B at 124°.
4. Join OB. Then \(\angle AOB\) = 124°.
5. With O as centre and using compasses, draw an arc that cuts both rays of \(\angle AOB\) at C and D respectively.
6. With C as centre and radius more than half of CD. Draw an arc.
7. With D as centre and same radius as in step 6 draw another arc which cuts the first arc at point E.
8. Join OE, then OE is the bisector of angle \(\angle AOB\) = 124°.
On measurement \(\angle AOE\) = \(\angle BOE\) = 62°.
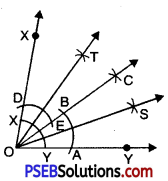
3. Draw an angle of 80° and bisect it in to four equal parts by compasses.
Solution:
1. Draw a line OY of any length.
2. Place the centre of the protractor at O.
3. Starting with 0 mark a point X at 80°.
4. Join OX. Then \(\angle XOY\) = 80°.
5. With O as centre and using compass, draw an arc that cuts both rays of \(\angle XOY\). Name the point of intersection as X’ and Y’.
6. With Y’ as centre, draw an arc whose radius is more than half the length X’Y’.
7. With the same radius and with X’ as a centre, draw another arc which cut the first arc at point C.
8. With O as centre and using compass, draw an arc that cuts both rays of \(\angle COY\). Name the points of intersection as B and A.
9. With A as centre, draw an arc whose radius is more than half the length AB.
10. With the same radius and with B as centre, draw another arc which cuts the first arc at point S.
11. With O as centre and using compass, draw an arc that cuts both rays of \(\angle XOC\) . Name the points of intersection as D and E.
12. With E as centre, draw an arc whose radius is more than half the length DE.
13. With the same radius and with E as centre, draw another arc which bisects the first arc at T. Then OT is the bisector of \(\angle XOC\).
Thus \(\overline{\mathrm{OS}}, \overline{\mathrm{OC}} \text { and } \overline{\mathrm{OT}}\) divide, \(\angle AOB\) = 80° into four equal parts.
![]()
4. Draw a right angle and bisect it.
Solution:
1. Draw a ray OB.
2. Place the centre of the protractor at O.
3. Starting with 0° mark point A at 90°.
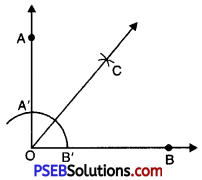
4. Join OA. Then \(\angle AOB\) = 90°
5. With O as centre and using compasses, draw an arc that cuts both rays of \(\angle AOB\). Name the points of intersection as A’ and B’.
6. With B’ as centre, draw an arc whose radius is more than half of the length B’A’.
7. With the same radius and with A’ as a centre, draw another arc which cuts the first arc at point C. Join OC bisects \(\angle AOB\).
5. Draw the following angles by ruler and compasses:
Question (i)
30°
Solution:
To Construct angle of 30°
Steps of Construction:
1. Draw a line segment OA.
2. With O as centre and any suitable radius draw an arc cutting OA at point C.
3. With C as centre and same radius as before draw another arc cutting the previous arc at E.
4. Join OE and produce it to B. \(\angle AOB\) = 60°.
5. Bisect \(\angle AOB\).
Thus \(\angle AOM\) = \(\angle MOB\) = 30°.
![]()
Question (ii)
45°
Solution:
To Construct Angle of 45°:
Steps of Construction:
1. Draw a line segment OA.
2. With O as centre and any suitable radius draw an arc cutting OA at point C.
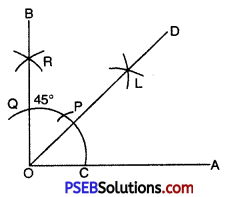
3. With C as centre and same radius cut off the arc at P and then with P as centre and the same radius cut off the arc again at Q.
4. With P and Q as centres and any suitable radius (more than half of PQ) or even the same radius draw arc cutting each other at R.
5. Join OR and produce it to B. Then \(\angle AOB\) = 90°.
6. Bisect \(\angle AOB\).
7. OD is the bisector of \(\angle AOB\).
\(\angle BOD\) = \(\angle DOA\) = 45°.
Question (iii)
135°
Solution:
To Construct Angle of 135°.
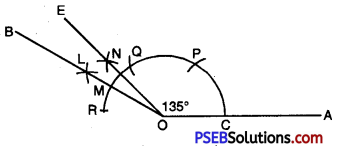
Steps of Construction:
1. Draw a line segment OA.
2. With O as centre and any suitable radius draw an arc cutting OA at point C.
3. With C as centre and the same radius cut off the arc at P and then with P as centre and the same radius cut off the arc again at Q and then with Q as centre the same radius cut off the arc again at R.
4. With Q and R as centres and radius more than half of RQ draw arcs cutting each other at L.
5. Join OL and produce it to B. Then \(\angle AOB\) = 150°.
6. Take a point M on the arc where OL intersects the arc.
7. With M and Q as centres and radius more than half of MQ draw arcs cutting each other at N.
8. Join ON and produce it to E. \(\angle AOE\) = 135°.
![]()
Question (iv)
180°
Solution:
To Construct Angle of 180°.
Steps of Construction:
1. Draw a line AB and mark a point C on it.
2. Taking C as centre and with any suitable radius, draw an are PQ cutting AB at P and Q.
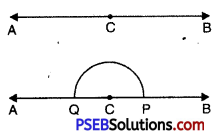
3. Here \(\angle ACB\) = 180° (It is a straight line).
Question (v)
120°
Solution:
To Construct Angle of 120°:
Steps of Construction:
1. Draw a line segment OA.
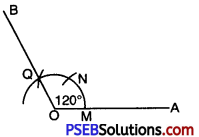
2. With O as centre and any suitable radius draw an arc cutting OA at point M.
3. With M as centre and same radius draw an arc which cuts the arc at N and then with N as centre and the same radius cut off the arc again at Q.
4. Join OQ and produce it to B.
Then \(\angle AOB\) = 120°.
![]()
Question (vi)
75°.
Solution:
To Construct Angle of 75°.
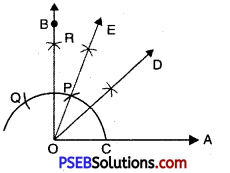
Steps of Construction:
1. Draw a line segment OA.
2. With O as centre and any suitable radius draw an arc cutting OA at C.
3. With C as centre and same radius cut off the arc at P and then with P as centre and the same radius cut off the arc again at Q.
4. With P and Q as centres and radius more than half of PQ draw arcs cutting each other at R.
5. Join OR and produce it to B. \(\angle AOB\) = 90°.
6. Bisect \(\angle AOB\).
7. OD is the bisector of \(\angle AOB\).
\(\angle BOD\) = \(\angle DOA\) = 45°.
8. Again draw OE bisector of \(\angle DOB\).
Thus angle \(\angle EOA\) = 75°.
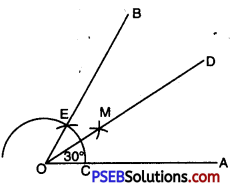
6. Draw an angle of 30° by protractor and bisect it by a ruler and compasses.
Solution:
Steps of Construction:
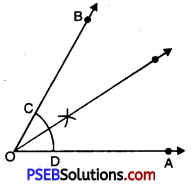
1. Draw a ray OA.
2. Place the centre of the protractor at O.
3. Starting with 0° mark point B at 30°.
4. Join OB. Then \(\angle AOB\) = 30°.
5. With O as centre and using compasses draw an arc that cuts both rays of \(\angle AOB\), with the point intersection as C and D.
6. With C as centre, draw an arc whose radius is more than half of the length of CD.
7. With D as centre and same radius as in step 6 draw another arc which cuts the first arc at point E.
8. Join OE, it bisect \(\angle AOE\).