Punjab State Board PSEB 12th Class Physics Book Solutions Chapter 8 Electromagnetic Waves Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Physics Chapter 8 Electromagnetic Waves
PSEB 12th Class Physics Guide Electromagnetic Waves Textbook Questions and Answers
Question 1.
Figure 8.6 shows a capacitor made of two circular plates each of radius 12 cm, and separated by 5.0 cm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15 A.
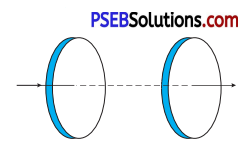
(a) Calculate the capacitance and the rate of charge of potential difference between the plates.
(b) Obtain the displacement current across the plates.
(c) Is Kirchhoffs first rule (junction rule) valid at each plate of the capacitor? Explain.
Answer:
(a) Capacitance of capacitor is given by the relation
C = \(\frac{\varepsilon_{0} A}{d}\) = \(\frac{8.854 \times 10^{-12} \times \pi \times(0.12)^{2}}{5 \times 10^{-2}}\)
= 8.01F
Also \(\frac{d Q}{d t}\) = \(\frac{d V}{d t}\)
∴ \(\frac{d V}{d t}\) = \(\frac{0.15}{8.01 \times 10^{-12}}\)
= 1.87 × 1010V /s
(b) Displacement current Id = ε0 × \(\frac{d}{d t}\) (ΦE)
Again ΦE – EA across Hence,(negative end constant).
Hence, Id = ε0 A\(\frac{d E}{d t}\)
Again, E = \(\frac{Q}{\varepsilon_{0} A}\)
So, \(\frac{d E}{d t}=\frac{i}{\varepsilon_{0} A}\)
which corresponds id = i = 1.5A
(c) Yes, Kirchhoffs law is valid provided by current, we mean the sum of condition and displacement current.
![]()
Question 2.
A parallel plate capacitor (Fig. 8.7) made of circular plates each of radius R = 6.0 cm has a capacitance C = 100 pF. The capacitor is connected to a 230 V ac supply with a (angular) frequency of 300 rad s-1.

(a) What is the rms value of the conduction current?
(b) Is the conduction current equal to the displacement current?
(c) Determine the amplitude of B at a point 3.0 cm from the axis between the plates.
Answer:
(a) Irms = Vrms × Cω
= 230 × 100 × 1012 × 300
= 6.9 × 10-6 A = 6.9 μ A
(b) Yes, we know that the deviation is correct even if I is steady DC or AC (oscillating in time) can be proved as
Id = ε0\(\frac{d}{d t}\) (σ) = ε0\(\frac{d}{d t}\) (EA) (> σ = EA)
ε0A \(\frac{d E}{d t}\) = ε0A \(\frac{d}{d t}\) (\(\frac{\sigma}{\varepsilon_{0}}\))
ε0A \(\frac{d}{d t}\) (\(\frac{\sigma}{\varepsilon_{0} A}\)) (> σ = \(\frac{q}{A}\))
ε0A × \(\frac{1}{\varepsilon_{0} A} \cdot \frac{d q}{d t}\) = I
which is the required proof.
(c) The region formula for magnetic field
B = \(\frac{\mu_{0} r}{2 \pi R^{2}}\)id
even if Id is oscillating (and so magnetic field B): The formula is valid. ID oscillates in phase as i0 = i (peak value of current). Now, we have
B0 = \(\frac{\mu_{0} r}{2 \pi R^{2}}\)i0
where B0 and i0 are the amplitude of magnetic field and current respectively.
So, i0 = √2Irms = 6.96 × 1.414 μA = 9.76μA
Given, r = 3 cm, R = 6cm
B0 = \(\frac{\mu_{0} r i_{0}}{2 \pi R^{2}}\)
= \(\frac{10^{-7} \times 2 \times 3 \times 10^{-2} \times 9.76 \times 10^{-6}}{(6)^{2} \times\left(10^{-2}\right)^{2}}\)
= 1.633 × 10-11 T
Question 3.
What physical quantity is the same for X-rays of wavelength 10-10 m, red light of wavelength 6800 Å and radiowaves of wavelength 500 m?
Answer:
X-rays, red light and radiowaves all are the electromagnetic waves. They have different wavelengths and frequencies. But the physical quantity which is same for all of these is the velocity of light in vacuum which is denoted by c and is equal to 3 × 108 ms-1 W
![]()
Question 4.
A plane electromagnetic wave travels in vacuum along z-direction. What can you say about the directions of its electric and magnetic field vectors? If the frequency of the wave is 30 MHz, what is its wavelength?
Answer:
In an electromagnetic wave’s propagation vector \(\vec{K}\), electric field vector \(\vec{E}\) and magnetic field vector \(\vec{K}\) form a right handed system. As the propagation vector is along Z-direction, electric field vector will be along X-direction and magnetic field vector will be along Y-direction.
Frequency v = 30 MHz = 30 × 106Hz
Speed of light c = 3 × 108 ms-1
Wavelength, λ = \(\frac{c}{v}\) = \(\frac{3 \times 10^{8}}{30 \times 10^{6}}\) = 10 m
Question 5.
A radio can tune in to any station in the 7.5 MHz to 12 MHz hand. What is the corresponding wavelength band?
Answer:
Speed of wave c = 3 × 108 ms-1
When frequency, V1 = 7.5MHz = 7.5 × 106 Hz
Wavelength, λ1 = \(\frac{c}{v_{1}}\) = \(\frac{3 \times 10^{8}}{7.5 \times 10^{6}}\) = 40m
When frequency, V2 12 MHZ = 12 × 106HZ
Wavelength, λ2 = \(\frac{c}{v_{2}}\) = \(\frac{3 \times 10^{8}}{12 \times 10^{6}}\) = 25m
Wavelength band is from 25 m to 40 m.
Question 6.
A charged particle oscillates about its mean equilibrium position with a frequency of 109 Hz. What is the frequency of the electromagnetic waves produced by the oscillator?
Answer:
According to Maxwell’s theory, an oscillating charged particle with a frequency v radiates electromagnetic waves of frequency v.
So, the frequency of electromagnetic waves produced by the oscillator is v = 109 Hz.
![]()
Question 7.
The amplitude of the magnetic field part of a harmonic electromagnetic wave in vacuum is B0 =510 nT. What is the amplitude of the electric field part of the wave?
The relation between magnitudes of magnetic and electric field vectors in vacuum is
\(\frac{E_{0}}{B_{0}}\) = c
⇒ E0 = B0C
Here, B0 = 510 × 10-9T, c = 3 × 108 ms-1
E0 = 510 × 10-9 × 3 × 108 = 153N/C
Question 8.
Suppose that the electric field amplitude of an electromagnetic wave is E0 = 120 N/C and that its frequency is v = 50.0 MHz. (a) Determine, B0, ω, k and λ. (b) Find expressions for E and B.
Answer:
Electric field amplitude, E0 = 120 N/C
Frequency of source, v = 50.0 MHz = 50 × 106 Hz
Speed of light, c = 3 × 108 m/s
(a) Magnitude of magnetic field strength is given as
B0 \(\frac{E_{0}}{\mathcal{C}}\) = \(\frac{120}{3 \times 10^{8}}\)
40 × 10-8T
= 400 × 10-9 T
= 400 nT
Angular frequency of source is given as
ω = 2πv = 2π × 50 × 106
= 3.14 × 108 rad/s
Propagation constant is given as
k = \(\frac{\omega}{c}\) = \(\frac{3.14 \times 10^{8}}{3 \times 10^{8}}\) = 1.05 rad /m
Wavelength of wave is given us
λ = \(\frac{c}{v}\) = \(\frac{3 \times 10^{8}}{50 \times 10^{6}}\) = 6.0m
(b) Suppose the wave is propagating in the positive x direction. Then, the electric field vector will be in the positive y direction and the magnetic field vector will be in the positive z direction. This is because all three vectors are mutually perpendicular.
Equation of electric field vector is given as
\(\vec{E}\) = E0sin (kx – ωt) ĵ
= 120 sin [1.05 x – 3.14 × 108t] ĵ
And, magnetic field vector is given as
\(\vec{B}\) = B0 sin (kx – ωt)k̂
\(\vec{B}\) = (4 × 10-7)sin[1.05 x – 3.14 × 108t]k̂
![]()
Question 9.
The terminology of different parts of the electromagnetic spectrum is given in the text. Use the formula E – hv (for energy of a quantum of radiation : photon) and obtain the photon energy in units of eV for different parts of the electromagnetic spectrum. In what way are the different scales of photon energies that you obtain related to the sources of electromagnetic radiation?
Answer:
Energy of a photon is given as
E = hv = \(\frac{h c}{\lambda}\)
where,
h = Planck’s constant = 6.6 × 10-34 Js
c = Speed of light = 3 × 108 m/s
λ = Wavelength of radiation
∴ E = \(\frac{6.6 \times 10^{-34} \times 3 \times 10^{8}}{\lambda}\) = \(\frac{19.8 \times 10^{-26}}{\lambda}\) = J
= \(\frac{19.8 \times 10^{-26}}{\lambda \times 1.6 \times 10^{-19}}\) = \(\frac{12.375 \times 10^{-7}}{\lambda}\) = eV
The given table lists the photon energies for different parts of an electromagnetic spectrum for different λ.

The photon energies for the different parts of the spectrum of a source indicate the spacing of the relevant energy levels of the source.
Question 10.
In a plane electromagnetic wave, the electric field oscillates sinusoidally at a frequency of 2.0 × 1010Hz and amplitude 48 Vm-1.
(a) What is the wavelength of the wave?
(b) What is the amplitude of the oscillating magnetic field?
(c) Show that the average energy density of the E field equals the average energy density of the B field, [c = 3 × 108 ms-1]
Answer:
Frequency of the electromagnetic wave, v = 2.0 × 1010 Hz
Electric field amplitude, E0 = 48 V m-1
Speed of light, c = 3 × 108 m/s
(a) Wavelength of the wave is given as
λ = \(\frac{\mathcal{C}}{\mathrm{v}}\) = \(\frac{3 \times 10^{8}}{2 \times 10^{10}}\) 0.015 m
(b) Magnetic field strength is given as
B0 = \(\frac{E_{0}}{c}\)
= \(\frac{48}{3 \times 10^{8}}\) = 1.6 × 10-7 T
(c) Let UE and UB be the energy density of \(\) field and \(\) field respectively. Energy density of the electric field is given as
UE = \(\frac{1}{2}\) ε0E2
And, energy density of the magnetic field is given as
UB = \(\frac{1}{2 \mu_{0}}\)2
We have the relation connecting E and B as
E = cB ………….. (1)
where,
c = \(\frac{1}{\sqrt{\varepsilon_{0} \mu_{0}}}\) ……………. (2)
Putting equation (2) in equation (1), we get
E = \(\frac{1}{\sqrt{\varepsilon_{0} \mu_{0}}}\)B
Squaring both sides, we get
E2 = \(\frac{1}{\varepsilon_{0} \mu_{0}}\) B2
ε0E2 = \(\frac{B^{2}}{\mu_{0}}\)
\(\frac{1}{2}\)ε0E2 = \(\frac{1}{2} \frac{B^{2}}{\mu_{0}}\)
⇒ UE = EB
![]()
Question 11.
Suppose that the electric field part of an electromagnetic wave in vacuum is
E = {(3.1 N/C) cos [(1.8 rad/m) y + (5.4 × 106 rad/s) t]}î
(a) What is the direction of propagation?
(b) What is the wavelength λ ?
(c) What is the frequency v?
(d) What is the amplitude of the magnetic field part of the wave?
(e) Write an expression for the magnetic field part of the wave.
Answer:
(a) Wave is propagating along negative y-axis.
(b) Standard equation of wave is \(\vec{E}\) = E0 cos(ky + cot)î
Comparing the given equation with standard equation, we have
E0 = 3.1 N/C, k = 1.8 rad/m, ω = 5.4 × 106 rad/s
Propagation constant k = \(\frac{2 \pi}{\lambda}\)
∴ λ = \(\frac{2 \pi}{k}\) = \(\frac{2 \times 3.14}{1.8}\) m = 3.49 m
(c) We have ω = 5.4 × 106 rad/s
Frequency, v = \(\frac{\omega}{2 \pi}\) = \(\frac{5.4 \times 10^{6}}{2 \times 3.14}\) Hz
= 8.6 × 105 Hz
(d) Amplitude of magnetic field,
B0 = \(\frac{E_{0}}{c}\) = \(\frac{3.1}{3 \times 10^{8}}\) = 1.03 × 10-8 T
(e) The magnetic field is vibrating along Z-axis because \(\vec{K}\),\(\vec{E}\),\(\vec{B}\) form a right handed system -ĵ × î = k̂
> Expression for magnetic field is
\(\vec{B}\) = B0 cos(ky+ ωt)k̂
= [1.03 × 10-8Tcos{(1.8rad / m) y +(5.4 × 6 rad/s)t}]k̂
Question 12.
About 5% of the power of a 100 W light bulb is converted to visible radiation. What is the average intensity of visible radiation
(a) at a distance of 1 m from the bulb?
(b) at a distance of 10 m?
Assume that the radiation is emitted isotropically and neglect reflection.
Answer:
Power in visible radiation, P = \(\frac{5}{100}\) × 100 = 5W
For a point source, intensity I = \(\frac{P}{4 \pi r^{2}}\), where r is distance from the source.
(a) When distance r = 1 m,
I = \(\frac{5}{4 \pi(1)^{2}}=\frac{5}{4 \times 3.14}\) = 0.4 W/m2
(b) When distance r = 10 m,
I = \(\frac{5}{4 \pi(10)^{2}}=\frac{5}{4 \times 3.14 \times 100}\)
= 0.004 W/m2
![]()
Question 13.
Use the formula λm T = 0.29 cm K to obtain the characteristic temperature ranges for different parts of the electromagnetic spectrum. What do the numbers that you obtain tell you?
Answer:
A body at a particular temperature produces a continuous spectrum of wavelengths. In case of a black body, the wavelength corresponding to maximum intensity of radiation is given according to Planck’s law. It can be given by the relation,
λm = \(\frac{0.29}{T}\) cm K
where, λm = maximum wavelength
T = temperature
Thus, the temperature for different wavelengths can be obtained as
For λm = 10-4 cm; T = \(\frac{0.29}{10^{-4}}\) = 2900°K
For λm = 5 × 10-5 cm; T = \(\frac{0.29}{5 \times 10^{-5}}\) = 5800°K
For λm = 10-6 cm; T = \(\frac{0.29}{10^{-6}}\) = 290000 °K and so on.
The numbers obtained tell us that temperature ranges are required for obtaining radiations in different parts of an electromagnetic spectrum. As the wavelength decreases, the corresponding temperature increases.
Question 14.
Given below are some famous numbers associated with electromagnetic radiations in different contexts in physics. State the part of the electromagnetic spectrum to which each belongs.
(a) 21 cm (wavelength emitted by atomic hydrogen in interstellar space).
(b) 1057 MHz (frequency of radiation arising from two close energy levels in hydrogen; known as Lamb shift).
(c) 2.7 K (temperature associated with the isotropic radiation filling all space-thought to be a relic of the ‘big-bang’ origin of the universe).
(d) 5890 Å – 5896 Å (double lines of sodium).
(e) 14.4 keV [energy of a particular transition in 57 Fe nucleus associated with a famous high resolution spectroscopic method (Mossbauer spectroscopy)].
Answer:
(a) 21 cm belongs to short wavelength end of radiowaves (or Hertizan waves).
(b) Wavelength, λ = \(\frac{c}{v}\) = \(\frac{3 \times 10^{8}}{1057 \times 10^{6}}\) = 0.28 m = 28 cm.
This also belongs to short wavelength end of radiowaves.
(c) From relation λmT = 0.29 × 10-2 K,
λm = \(\frac{0.29 \times 10^{-2} \mathrm{~K}}{T}=\frac{0.29 \times 10^{2}}{2.7}\)
= 0.107 × 10-2m= 0.107 cm.
This corresponds to microwaves.
(d) Wavelength doublet 5890Å – 5896Å belongs to the visible region. These are emitted by sodium vapour lamp.
(e) From relation, E = \(\frac{h c}{\lambda}\)
we have λ = \(\frac{h c}{E}\)
λ = \(\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{14.4 \times 10^{3} \times 1.6 \times 10^{-19}} \mathrm{~m}\)
= 0.86 × 10-10 m = 0.86 Å
It belongs to the X-ray region of electromagnetic spectrum.
![]()
Question 15.
Answer the following questions :
(a) Long distance radio broadcasts use short-wave bands. Why?
(b) It is necessary to use satellites for long distance TV transmission. Why?
(c) Optical and radiotelescopes are built on the ground but X-ray astronomy is possible only from satellites orbiting the earth Why?
(d) The small ozone layer on top of the stratosphere is crucial for human survival. Why?
(e) If the earth did not have an atmosphere, would its average surface temperature be higher or lower than what it is now?
(f) Some scientists have predicted that a global nuclear war on the earth would be followed by a severe ‘nuclear winter’ with a devastating effect on life on earth. What might be the basis of this prediction?
Answer:
(a) Long distance radio broadcasts use short-wave bands because only these bands can be refracted by the ionosphere.
(b) Yes, it is necessary to use satellites for long distance TV transmissions because television signals are of high frequencies and high energies. Thus, these signals are not reflected by the ionosphere. Hence, satellites are helpful in reflecting TV signals. Also, they help in long distance TV transmissions.
(c) With reference to X-ray astronomy, X-rays are absorbed by the atmosphere. However, visible and radiowaves can penetrate it. Hence, optical and radiotelescopes are built on the ground, while X-ray astronomy is possible only with the help of satellites orbiting the Earth.
(d) The small ozone layer on the top of the stratosphere is crucial for human survival because it absorbs harmful ultraviolet radiations present in sunlight and prevents it from reaching the Earth’s surface.
(e) In the absence of an atmosphere, there would be no greenhouse effect on the surface of the Earth. As a result, the temperature of the Earth would decrease rapidly, making it chilly and difficult for human survival.
(f) A global nuclear war on the surface of the Earth would have disastrous consequences. Post nuclear war, the Earth will experience severe winter as the war will produce clouds of smoke -that would cover maximum parts of the sky, thereby preventing solar light form reaching the atmosphere. Also, it will lead to the depletion of the ozone layer.