Punjab State Board PSEB 12th Class Physics Important Questions Chapter 3 Current Electricity Important Questions and Answers.
PSEB 12th Class Physics Important Questions Chapter 3 Current Electricity
Very short answer type questions
Question 1.
Two identical cells, each of emf E, having negligible internal resistance, are connected in parallel with each other across an external resistance R. What is the current through this resistance?
Answer:
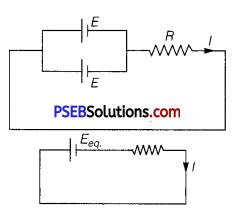
⇒ I = \(\frac{E_{\text {eq. }}}{R+r_{\text {eq. }}}\)
Given,internal resistance, r = 0
∴ I = \(\frac{E_{\mathrm{eq} .}}{R}\)
Question 2.
Define mobility of a charge carrier. What is its relation with relaxation time?
Answer:
It is defined as how fast electron moves from one place to another.
It is also defined as drift velocity per unit electric field. The SI unit of mobility is m2/V-sec and it is denoted as μ.
μ = \(\frac{\left|v_{d}\right|}{E}=\frac{e E \tau}{m E}=\frac{e \tau}{m}\)
⇒ μ ∝ τ
![]()
Question 3.
Define the term ‘relaxation time’ in a conductor.
Answer:
The average time between successive collisions of electrons conductor is known as relaxation time.
Question 4.
Write the expression for the drift velocity of charge carriers in a conductor of length ‘L’ across which a potential difference ‘V’ is applied.
Answer:
vd = \(\frac{e V}{m L}\)τ
Question 5.
For household electrical wiring, one uses Cu wires or Al wires. What considerations are kept in mind? (NCERT Exemplar)
Answer:
Two considerations are required: (i) cost of metal, and (ii) good conductivity of metal. Cost factor inhibits silver. Cu and Al are the next best conductors.
Question 6.
Define the current sensitivity of a galvanometer. Write its SI unit.
Answer:
Ratio of deflection produced in the galvanometer and the current flowing through it is called current sensitivity.
Current sensitivity Si = \(\frac{\theta}{I}\)
SI unit of current sensitivity Si is division/ampere or radian/ampere.
![]()
Question 7.
Nichrome and Copper wires of same length and same radius are connected in series. Current I is passed through them. Which wire gets heated up more? Justify your answer.
Answer:
Nichrome, since its resistance is high.
Question 8.
Why are alloys used for making standard resistance coils?
(NCERT Exemplar)
Answer:
Alloys have:
- low value of temperature coefficient and the resistance of the alloy does not vary much with rise in temperature.
- high resistivity, so even a smaller length of the material is sufficient to design high standard resistance.
Question 9.
What is the advantage of using thick metallic strips to join wires in a potentiometer? (NCERT Exemplar)
Answer:
The metal strips have low resistance and need not be counted in the potentiometer length l of the null point. One measures only their lengths along the straight segments (of length 1 metre each). This is easily done with the help of centimeter rulings or meter ruler and leads to accurate measurements.
Question 10.
Is the motion of a charge across junction momentum conserving? Why or why not? (NCERT Exemplar)
Answer:
When an electron approaches a junction, in addition to the uniform electric field E facing it normally, it keep the drift velocity fixed as drift velocity depend on E by the relation
Vd = \(\frac{e E \tau}{m}\)
This result into accumulation of charges on the surface of wires at the junction. These produce additional field. These fields change the direction of momentum.
Thus, the motion of a charge across junction is not momentum conserving.
![]()
Short answer type questions
Question 1.
Sketch a graph showing the variation of resistivity of carbon with temperature.
Or Plot a graph showing temperature dependence of resistivity for a typical semiconductor. How is this behaviour explained?
Answer:
The resistivity of a typical semiconductor (carbon) decreases with increase of temperature. The graph is shown in figure.
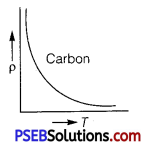
Explanation: In semiconductor the number density of free electrons (n) increases with increase in temperature (T) and consequently the relaxation period decreases. But the effect of increase in n has higher impact than decrease of τ. So, resistivity decreases with increase in temperature.
Question 2.
Two cells of emf ε1 and ε2 having internal resistances r1 and r2 respectively are connected in parallel as shown. Deduce the expressions for the equivalent emf and equivalent internal resistance of a cell which can replace the combination between the points B1 and B2.
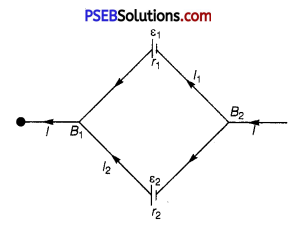
Answer:
Consider a parallel combination of the cells. I1 and I2 are the currents leaving the positive electrodes of the cells. At point B1, I1 and I2 flow in whereas current I flows out. Therefore, we have
I = I1 + I2 …………….. (1)
Let V(B1) and V(B2) be the potentials at B1 and B2 respectively.
Then, considering the first cell, the potential difference across its terminals is V(B1) – V(B2). Hence, from equation V = E – Ir we have
V = V(B1) – V(B2) = E1 – I1r1 …………… (2)
Points B1 and B2 are connected exactly Similarly to the second cell. Hence, considering the second cell, we also have
V = V(B1) – V(B2)
= E2 – I2r2 …………… (3)
Combining equations (1), (2) and (3), we have
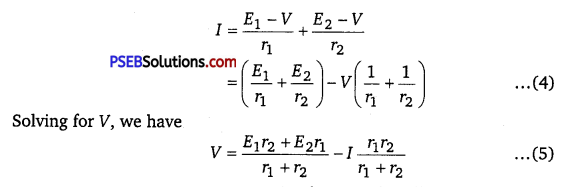
If we want to replace the combination by a single cell, between Bl and B2, of emf Eeq and internal resistance req, we would have
V = Eeq – Ireq
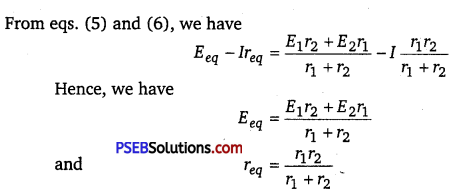
![]()
Question 3.
State Kirchhoff s rules of current distribution in an electrical network.
Or State KirchhofPs rules. Explain briefly how these rules are justified.
Answer:
Junction Rule: In an electric circuit, the algebraic sum of currents at any junction is zero.
At any junction, the sum of the currents entering the junction is equal to the sum of currents leaving the junction.
ΣI = 0
Justification: This rule is based on the law of conservation of charge.
Loop Rule: The algebraic sum of changes in potential around any closed loop involving resistors and cells in the loop must be zero.
ΣΔV = 0
or The algebraic sum of emf s in any loop of a circuit is equal to the
sum of products of currents and resistances in it.
ΣΔE = ΣIR
Justification: This rule is based on the law of conservation of energy,
Question 4.
Define the term current density of a metallic conductor. Deduce the relation connecting current density (J) and the conductivity σ of the conductor, when an electric field E, is applied to it.
Answer:
Current density at a point in a conductor is defined as the amount of current flowing per unit area of the conductor around that point provided the area is held in a direction normal to the current,
J = \(\frac{I}{A}\)
Current density is a vector quantity. Its direction is the direction of motion of positive charge. The unit of current density is ampere/metre2 or [Am-2].
Relation between J, σ and E

![]()
Question 5.
What is Wheatstone bridge? Deduce the condition for which Wheatstone bridge is balanced.
Or The given figure shows a network of resistances R1, R2, R3 and R4.
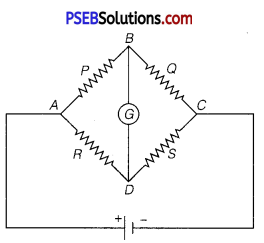
Using Kirchhoffs laws, establish the balance condition for the network.
Or Use Kirchhoffs law to obtain the balance Wheatstone’s bridge.
Answer:
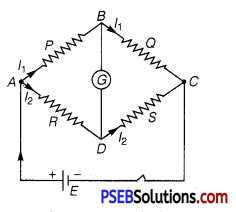
The Wheatstone bridge is an arrangement of four resistances. In this bridge, four resistances are connected on four arms of quadrilateral. In one diagonal, a battery and a key are connected. In second diagonal a galvanometer is connected as shown in fig. Consider P,Q,R and S four resistances are connected on the sidesAB,BC, AD and DC of the quadrilateral respectively.
Galvanometer G is connected between points B and D and a battery E is connected between A and C. Now in balance condition, when the deflection in a galvanometer is zero in closed mesh ABDA, then by applying Kirchhoffs law,
I1p – IR = 0
or I1P = I2R ………….. (1)
In closed mesh CBDC,
I1Q = I2S ……………… (2)
Dividing (1) by (2) \(\frac{P}{Q}=\frac{R}{S}[latex]
This is the balanced condition of the Wheatstone bridge.
Question 6.
First a set of n equal resistors of R each are connected in series to a battery of emf E and internal resistance R. A current I is observed to flow. Then the n resistors are connected in parallel to the same battery. It is observed that the current is increased 10 times. What is n ? (NCERT Exemplar)
Answer:
When n resistors are in series, I = [latex]\frac{E}{R+n R}\) ;
When n resistors are in parallel, \(\frac{E}{R+\frac{R}{n}}\) 10I
\(\frac{1+n}{1+\frac{1}{n}}\) = 10 ⇒ \(\frac{1+n}{n+1}\) n = 10
∴ n = 10
![]()
Question 7.
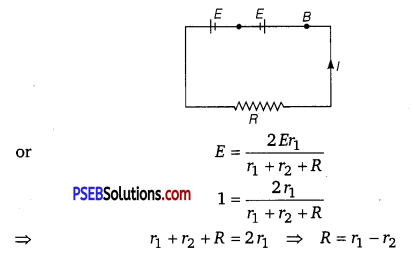
Two cells of same emf E but internal resistance r and r1 and r2 are connected in series to an external resistor R (Fig.). What should be the value of R so that the potential difference across the terminals of the first cell becomes zero. NCERT Exemplar)
Answer:
I = \(\frac{E+E}{R+r_{1}+r_{2}}\)
V1 = E – Ir1 = E – \(\frac{2 E}{r_{1}+r_{2}+R}\) r1 = 0
Long answer type questions
Question 1.
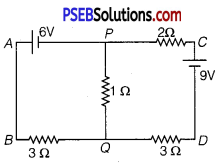
(i) Find the magnitude and direction of current in 1Ω resistor in given circuit.
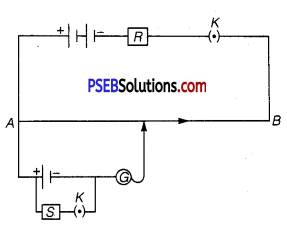
(ii)Two students X and Y perform an experiment on potentiometer separately using the circuit diagram shown below.
Keeping other things unchanged (a) X increases the value of resistance R, (b) Y decreases the value of resistance S in the set up. How will these changes affect the position of null point in each case and why?
Answer:
(i) For the mesh APQBA
-6 -1 (I2 – I1) + 3I1 = 0
or -I2 + 4I1 = 6 …………… (1)
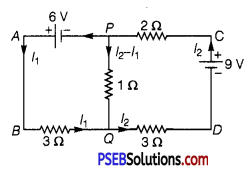
For the mesh PCDQP
2I2 – 9 + 3I2 + 1(I2 – I1) = 0
or 6I2 – I1 = 9 …………… (2)
Solving eqs. (1) and (2), we get
I = \(\frac{45}{23}\) A
I= \(\frac{42}{23}\) A
∴ Current through the 1Ω resistor = (I2 – I1) = \(\) A
(ii) (a) By increasing resistance R, the current in main circuit decreases, so potential gradient decreases. Hence, a greater length of wire would be needed for balancing the same potential difference. So, the null point would shift towards right (i.e., towards B).
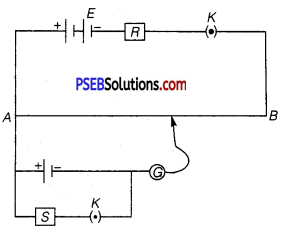
(b) By decreasing resistance S, the terminal potential difference V = \(\frac{E}{1+\frac{r}{S}}\) across cell decreases, so balance is obtained at small length i.e., point will be obtained at smaller length. So, the null point would shift towards left (i.e., towards A).
![]()
Question 2.
A room has AC run for 5 hours a day at a voltage of 220 V. The wiring of the room consists of Cu of 1 mm radius and a length of 10m. Power consumption per day is 10 commercial units. What fraction of it goes in the joule heating in wires? What would happen if the wiring is made of aluminium of the same dimensions? [ρCu = 1.7 × 10-8Ωm, ρAL = 2.7 × 10-8Ωm] (NCERT Exemplar)
Answer:
Power consumption in a day i.e., in 5 hours = 10 units
Or power consumption per hour = 2 units
Or power consumption = 2 units = 2 kW = 2000 W
Also, we know that power consumption in resistor,
P = V × I
⇒ 2000 W = 220 V × I
or I = 9 A
Now, the resistance of wire is given by R = ρ \(\frac{l}{A}\)
where, A is cross-sectional area of conductor. Power consumption in first current carrying wire is given by
P = I2 . R
ρ \(\frac{l}{A}\) I2 = 1.7 × 10-8 × \(\frac{10}{\pi \times 10^{-6}}\) × 81 = 4J/s A
The fractional loss due to the joule heating in first wire
= \(\frac{4}{2000}\) × 100 = 0.2%
Power loss in Al wire = 4\(\frac{\rho_{A l}}{\rho_{C u}}\) = 1.6 × 4 = 6.4 J/s
The fractional loss due to the joule heating in second wire
= \(\frac{6.4}{2000}\) × 100 =0.32%