Punjab State Board PSEB 12th Class Physics Important Questions Chapter 12 Atoms Important Questions and Answers.
PSEB 12th Class Physics Important Questions Chapter 12 Atoms
Very short answer type questions
Question 1.
Why is the classical (Rutherford) model for an atom of electron orbiting around the nucleus not able to explain the atomic structure?
Answer:
The classical method could not explain the atomic structure as the electron revolving around the nucleus are accelerated and emit energy as the result, the radius of the circular paths goes on decreasing. Ultimately electrons fall into the nucleus, which is not in practice.
Question 2.
Consider two different hydrogen atoms. The electron in each atom is in an excited state. Is it possible for the electrons to have different energies but the same orbital angular momentum according to the Bohr model? (NCERT Exemplar)
Answer:
According to Bohr model electrons having different energies belong to different levels having different values of n. So, their angular momenta will be different, as.
L = \(\frac{n h}{2 \pi} \text { or } L \propto n\)
Question 3.
State Bohr’s quantization condition for defining stationary orbits.
Answer:
According to Bohr’s quantization condition, electrons are permitted to revolve in only those orbits in which the angular momentum of electron is an integral multiple of \(\frac{h}{2 \pi}\) i.e.,
mvr = \(\frac{n h}{2 \pi}\) ,Where n = 1,2,3, ………………
m, y, rare mass, speed, and radius of electron respectively and h being Planck’s constant.
![]()
Question 4.
Define ionization energy. What Is Its value for a hydrogen atom?
Answer:
Ionisation Energy: The minimum amount of energy required to remove an electron from the ground state of the atom is known as ionization energy.
Ionisation energy for hydrogen atom =E∞ – E1 = – (-13.6 eV) = 13.6 eV
Question 5.
When an electron falls from a higher energy to a lower energy level, the difference in the energies appears in the form of electromagnetic radiation. Why cannot it be emitted as other forms of energy? (NCERT Exemplar)
Answer:
The transition of an electron from a higher energy to a lower energy level can appear in the form of electromagnetic radiation because electrons interact only electromagnetically.
Question 6.
Where is H a -line of the Balmer series in the emission spectrum of hydrogen atom obtained?
Answer:
Hα -line of the Balmer series in the emission spectrum of hydrogen atom is obtained in visible region.
Question 7.
Imagine removing one electron from He4 and He3. Their energy levels, as worked out on the basis of Bohr model will be very close. Explain why. (NCERT Exemplar)
Answer:
This is because both the nuclei are very heavy as compared to electron mass.
Question 8.
The mass of H-atom is less than the sum of the masses of a proton and electron. Why is this so? (NCERT Exemplar)
Answer:
Einstein’s mass-energy equivalence gives E – mc2.
Thus the mass of an H-atom is mp + me – \(\frac{B}{C^{2}}\)
where B ≈ 13.6 eV is the binding energy. It is less than the sum of masses of a proton and an electron.
Question 9.
Assume that there is no repulsive force between the electrons in an atom but the force between positive and negative charges is given by Coulomb’s law as usual. Under such circumstances, calculate the ground state energy of a He-atom. (NCERT Exemplar)
Answer:
For a He-nucleus with charge 2 e and electrons of charge -e, the energy level in ground state is -En = Z2\(\frac{-13.6 \mathrm{eV}}{n^{2}}=2^{2} \frac{-13.6 \mathrm{eV}}{1^{2}}\)= -54.4eV
Thus, the ground state will have two electrons each of energy E and the total ground state energy would be -(4 x 13.6) eV = -54.4 eV.
Question 10.
Would the Bohr formula for the H-atom remain unchanged if proton had a charge (+ 4/3)e and electron a charge (-3/4)e, where e = 1.6 x 10-19 C ? Give reasons for your answer. (NCERT Exemplar)
Answer:
Yes, since the Bohr formula involves only the product of the charges.
Short answer type questions
Question 1.
In an experiment of α-particle scattering by a thin foil of gold, draw a plot showing the number of particles scattered versus the scattering angle θ. Why is it that a very small fraction of the particles are scattered at θ > 90°?
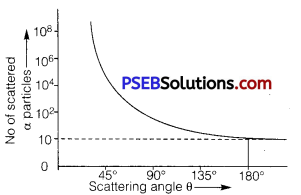
Answer:
A small fraction of the alpha particles scattered at angle θ > 90° is due to the reason. That if impact parameter ‘b’ reduces to zero, coulomb force increases, hence alpha particles are scattered at angle θ>9O°, and only one alpha particle is scattered at angle 180°.
Question 2.
(i) State Bohr postulate of hydrogen atom that gives the relationship for the frequency of emitted photon in a transition,
(ii) An electron jumps from fourth to first orbit in an atom. How many maximum number of spectral lines can be emitted by the atom? To which series these lines correspond?
Answer:
(i) Bohr’s Third Postulate: It states that an electron might make a transition from one of its specified non-radiating orbits to another of lower energy. When it does so, a photon is emitted having energy equal to the energy difference between the initial and final states. The frequency of the emitted photon is given by
hv = Ei – Ef
Where Ei and Ef are the energies of the initial and final states and Ei > Ef.
(ii) Electron jumps from fourth to first orbit in an atom
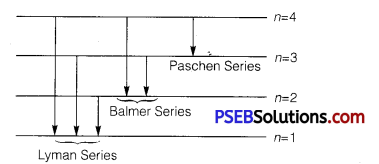
∴ Maximum number of spectral lines can be
4c2 = \(\frac{4 !}{2 ! 2 !}=\frac{4 \times 3}{2}\) = 6
The line responds to Lyman series (e– jumps to 1st orbit), Balmer series (e– jumps to 2nd orbit), Paschen series (e– jumps to 3rd orbit).
![]()
Question 3.
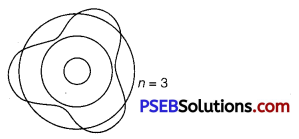
Using de Broglie’s hypothesis, explain with the help of a suitable diagram, Bohr’s second postulate of quantization of energy levels in a hydrogen atom.
Answer:
According to de Broglie’s hypothesis.
λ = \(\frac{h}{m v}\) ……………………….. (i)
According to de Broglie’s condition of stationary orbits, the stationary orbits are those which contain complete de Broglie wavelength.
2πr = nλ ………………………….. (2)
Substituting value of λ from eq. (2) in eq. (1), we get
2πr = n \(\frac{h}{m v}\)
⇒ mvr = n \(\frac{h}{2 \pi}\) ………………………… (3)
This is Bohr’s postulate of quantisation of energy levels.
Question 4.
In the study of Geiger-Marsden experiment on scattering of α-particles by a thin foil of gold, draw the trajectory of a-particles in the coulomb field of target nucleus. Explain briefly how one gets the information on the size of the nucleus from this study. From the relation R = R0 A1/3, where, R0 is constant and A is the mass number of the nucleus, show that nuclear matter density is independent of A.
Answer:
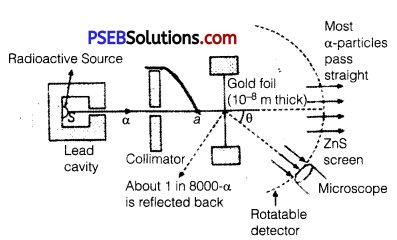
From this experiment, the following is observed :
1. Most of the α-particles pass straight through the gold foil. It means that they do not suffer any collision with gold atoms.
2. About one α-particle in every 8000 α-particles deflects by more than 90°. As most of the a-particles gounder flected and only a- few get deflected, this shows that most of the space in an atom is empty and at the center of the atom, there exists a nucleus.
By the number of a-particles get deflected, the information regarding size of the nucleus can be known.
If m is the average mass of the nucleus and R is the nuclear radius, then mass of nucleus = mA, where A is the mass number of the element. Volume of the nucleus,

This shows that the nuclear density is independent of A.
Question 5.
Show that the first few frequencies of light that is emitted when electrons fall to nth level from levels higher than n, are approximate harmonics (L e., in the ratio 1: 2: 3,…) when n>> 1. (NCERTExempiar)
Answer:
The frequency of any line in a series in the spectrum of hydrogen-like atoms corresponding to the transition of electrons from (n + p) level to nth level can be expressed as a difference of two terms:
Vmn = \(c R Z^{2}\left[\frac{1}{(n+p)^{2}}-\frac{1}{n^{2}}\right] \)
where, m=n+p,(p=1,2,3,…………………………..)
and R is Rydberg constant.
For p << n
Vmn = \(c R Z^{2}\left[\frac{1}{n^{2}}\left(1+\frac{p}{n}\right)^{-2}-\frac{1}{n^{2}}\right]\)

Thus, the first few frequencies of light that is emitted when electrons fall to the nth level from levels higher than n, are approximate harmonic (i. e., in the ratio 1:2:3,…) when n>>1.
![]()
Long answer type questions
Question 1.
Using the postulates of Bohr’s model of hydrogen atom, obtain an expression for the frequency of radiation emitted when atom make a transition from the higher energy state with quantum number n1 to the lower energy state with quantum number nf (nf < ni).
Or
Using Bohr’s postulates, obtain the expression for the total energy of the electron in the stationary states of the hydrogen atom. Hence draw the energy level diagram showing how the line spectra corresponding to Balmer series occur due to transition between energy levels.
Or
Using Rutherford model of the atom, derive the expression for the total energy of the electron in hydrogen atom. What is the significance of total negative energy possessed by the electron?
Answer:
Suppose m be the mass of an electron and v be its speed in nth orbit of radius r. The centripetal force for revolution is produced by electrostatic attraction between electron and nucleus.
\(\frac{m v^{2}}{r}=\frac{1}{4 \pi \varepsilon_{0}} \frac{(Z e)(e)}{r^{2}}\) …………………… (1) [Form rutherford Model]
or mv2 = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Z e^{2}}{r}\)
So, Kinetic energy Ek = \(\frac{1}{2} m v^{2}\)
Ek = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Z e^{2}}{2 r}\)
Potential energy (PE) = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{(Z e)(-e)}{r}=-\frac{1}{4 \pi \varepsilon_{0}} \frac{Z e^{2}}{r}\)
Total energy E = \(E_{K}+P E=\frac{1}{4 \pi \varepsilon_{0}} \frac{Z e^{2}}{2 r}+\left(-\frac{1}{4 \pi \varepsilon_{0}} \frac{Z e^{2}}{r}\right)\)
= \(-\frac{1}{4 \pi \varepsilon_{0}} \frac{Z e^{2}}{2 r}\)
For nth orbit, E can be written as En
so,En = \(-\frac{1}{4 \pi \varepsilon_{0}} \frac{Z e^{2}}{2 r_{n}}\) …………………. (2)
Negative sign indicates that the electron remains bound with the nucleus (or electron-nucleus form an attractive system) From Bohr’s postulate for quantisation of angular momentum.
mvr = \(\frac{n h}{2 \pi}\)
⇒ v = \(\frac{n h}{2 \pi m r} \)
Substituting this value of v in equation (1), we get
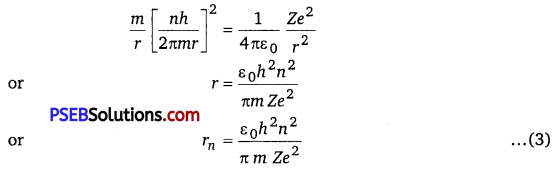
For Bohr’s radius, n = 1
Substituting value of rn in equation (2), we get
En = \(\frac{1}{4 \pi \varepsilon_{0}} \frac{Z e^{2}}{2\left(\frac{\varepsilon_{0} h^{2} n^{2}}{\pi m Z e^{2}}\right)}=-\frac{m Z^{2} e^{4}}{8 \varepsilon_{0} h^{2} n^{2}}\)
R is called Rydberg constant.
![]()
For hydrogen atom Z =1, En = \(\frac{-R c h}{n^{2}}\)
If ni and nf are the quantum numbers of initial and final states and Ei and
Ef are energies of electrons in H-atoms in initial and final state, we have

For Balmer series, nf=2, while ni =3, 4, 5, …… ∞.