Punjab State Board PSEB 12th Class Physics Important Questions Chapter 10 Wave Optics Important Questions and Answers.
PSEB 12th Class Physics Important Questions Chapter 10 Wave Optics
Very short answer type questions
Question 1.
Define the term ‘wavefront’.
Answer:
It is defined as the locus of all points in a medium vibrating in the same phase.
Question 2.
State Huygen’s principle of diffraction of light.
Answer:
When a wavefront strikes to the corner of an obstacle, lightwave bends around the corner because every point on the wavefront again behaves like a . light source and emit secondary wavelets in all directions (Huygen’s wave theory) including the region of geometrical shadow. This explains diffraction.
Question 3.
Define the term ‘coherent sources’ which are required to produce interference patterns in Young’s double-slit experiment.
Answer:
Two monochromatic sources, which produce light waves, having a constant phase difference are known as coherent sources.
![]()
Question 4.
Define Doppler’s effect in light.
Answer:
It states that whenever there is a relative motion between the observer and the source of light, the apparent frequency of light received by the observer is different from the actual frequency of the light emitted by the source of light.
Question 5.
Define Doppler shift.
Answer:
It is defined as the apparent change in the frequency or wavelength of light due to the relative motion between the source and the observer.
Question 6.
Define redshift.
Answer:
It is defined as the shifting of radiations from the source of light towards the red end of the spectrum when the source moves away from the stationary observer. The wavelength increases due to redshift.
Question 7.
Define limit of resolution of an optical instrument.
Answer:
It is defined as the minimum distance by which the timepoint objects are separated so that their images can be seen as just separated by the optical instrument.
Question 8.
Define resolving power of the optical instruments.
Answer:
It is defined as the reciprocal of the limit of resolution of the optical instrument.
Question 9.
How are resolving power of a telescope change by increasing or decreasing the aperture of the objective?
Answer:
We know that the resolving power of telescope is given by
R.P. = \(\frac{D}{1.22 \lambda}\)
As R.p. ∝ D, so by increasing or decreasing D (aperture) of the objective, the resolving power is increased or decreased.
![]()
Question 10.
Which of the following waves can be polarised (i) Heat waves (ii) Sound waves? Give reason to support your answer.
Answer:
Heatwaves are transverse or electromagnetic in nature whereas sound waves are not. Polarisation is possible only for transverse waves.
Question 11.
How is linearly polarised light obtain by the process of scattering of light? find the Brewster angle for air-glass interface, when the refractive index of glass = 1.5
Answer:
According to Brewster law
tan iB = μ
iB = tan-1 (μ)
iB = tan-1(l. 5)
iB = 56.30
Question 12.
A polaroid (I) is placed in front of a monochromatic source. Another polaroid (II) is placed in front of this polaroid (I) and rotated till no light passes. A third polaroid (III) is now placed in between (I) and (II). In this case, will light emerge from (II). Explain. (NCERT Exemplar)
Answer:
Only in the special cases when the pass axis of (III) is parallel to (I) or (II), there shall be no light emerging. In all other cases, there shall be light emerging because the pass axis of (I) is no longer perpendicular to the pass axis of (III).
Question 13.
What is the shape of the wavefront of earth for sunlight? (NCERT Exemplar)
Answer:
Spherical with huge radius as compared to the earth’s radius so that it is almost a plane.
Question 14.
Consider a point at the focal point of a convergent lens. Another convergent lens of short focal length is placed on the other side. What is the nature of the wavefronts emerging from the final image? (NCERT Exemplar)
Answer:
The focal point of a convergent lens is the position of real image formed by this lens when object is at infinity. When another convergent lens of short focal length is placed on the other side, the combination will form a real point image at the combined focus of the two lenses. The wavefronts emerging from the final image will be spherical.
![]()
Short answer type questions
Question 1.
State two conditions required for obtaining coherent sources. In Young’s arrangement to produce interference pattern, show that dark and bright fringes appearing on the screen are equally spaced.
Answer:
Conditions for obtaining coherent sources:
(i) Coherent sources of light should be obtained from a single source by same device.
(ii) The two sources should give monochromatic light.
The separation between the centres or two consecutive bright fringes is the width of a dark fringe.
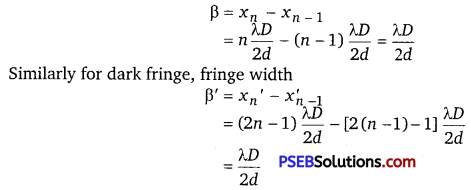
Hence, all bright and dark fringes are equally spaced on screen.
Question 2.
How will the interference pattern in Young’s double-slit experiment get affected, when
(i) distance between the slits S1 and S2 reduced and
(ii) the entire set-up is immersed in water? Justify your answer in each case.
Answer:
(i) The fringe width of interference pattern increases with the decrease in separation between S1S2 as
β ∝ \(\frac{1}{d}\)
(ii) The fringe width decrease as wavelength gets reduced when interference set up is taken from air to water.
Question 3.
What is the minimum angular separation between two stars, if a telescope is used to observe them with an objective of aperture 0.2 m? The wavelength of light used is 5900 A.
Answer:
Here, D = diameter of the objective of telescope = 0.2 m
λ = Wavelength of light used = 5900 Å = 5900 x 10-10 m
Let dθ = Minimum angular separation between two stars =?
Using the relation,
dθ = \(\frac{1.22 \lambda}{D}\) , we get
dθ = \(\frac{1.22 \times 5900 \times 10^{-10}}{0.2}= \) = 3.6 x 10-6 rad.
Question 4.
Distinguish between polarised and unpolarised light. Does the intensity of polarised light emitted by a polaroid depend on its orientation? Explain briefly. The vibrations in a beam of polarised light make an angle of 60° with the axis of the polaroid sheet. What percentage of light is transmitted through the sheet?
Answer:
A light which has vibrations in all directions in a plane perpendicular to the direction of propagation is said to be unpolarised light. The light from the sun, an incandescent bulb or a candle is unpolarised. If the electric field vector of a light wave vibrates just in one direction perpendicular to the direction of wave propagation, then it is said to be polarised or linearly polarised light.
Yes, the intensity of polarised light emitted by a polaroid depends on orientation of polaroid. When polarised light is incident on a polaroid, the resultant intensity of transmitted light varies directly as the square of the cosine of the angle between polarisation direction of light and the axis of the polaroid.
I ∝ cos2 θ or I = I0 cos2 θ
where I0 = maximum intensity of transmitted light;
θ = angle between vibrations in light and axis of polaroid sheet.
or I =I0 cos2 60° = \(\frac{I_{0}}{4}\)
Percentage of light transmitted = \(\frac{I}{I_{0}} \) x 100 = \(\frac{1}{4}\) x 100 = 25%
![]()
Question 5.
Find an expression for intensity of transmitted light, when a polaroid sheet is rotated between two crossed polaroids. In which position of the polaroid sheet will the transmitted intensity be maximum?
Answer:
Let us consider two crossed polarizers, P1 and P2 with a polaroid sheet P3 placed between them.
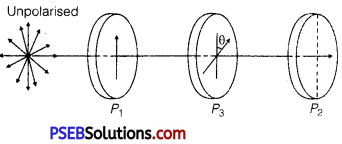
Let I0 be the intensity of polarised light after passing through the first polarizer P1.
If θ is the angle between the axes of P1 and P3, then the intensity of the polarised light after passing through P3 will be I =I0 cos2θ.
As P1 and P2 are crossed, the angle between the axes of P1 and P2 is 90°.
∴ The angle between the axes of P2 and P3 is (90° – 0).
The intensity of light emerging from P2 will be given by

The intensity of polarised light transmitted from P2 will be maximum, when ,
sin 2θ = maximum = 1
⇒ sin2θ = sin9O°
⇒ 2θ = 90°
⇒ θ = 45°
Also, the maximum transmitted intensity will be given by I = \(\frac{I_{0}}{4}\)
Question 6.
State Brewster’s law. The value of Brewster angle for a transparent medium is different for light of different colours. Give reason.
Answer:
Brewster’s Law: When unpolarized light is incident on the surface separating two media at polarising angle, the reflected light gets completely polarised only when the reflected light and the refracted light are perpendicular to each other. Now, refractive index of denser (second) medium with respect to rarer (first) medium is given by μ = tan iB, where iB = polarising angle.
Since refractive index is different for different colours (wavelengths), Brewster’s angle is different for different colours.
Question 7.
Can reflection result in plane polarised light if the light is incident on the interface from the side with higher refractive index? (NCERT Exemplar)
Answer:
When angle of incidence is equal to Brewster’s angle, the transmitted light is unpolarised and reflected light is plane polarised.
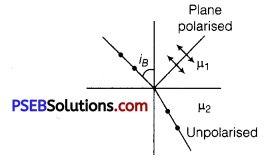
Consider the diagram in which unpolarised light is represented by dot and plane polarised light is represented by arrows.
Polarisation by reflection occurs when the angle of incidence is the Brewster’s angle
i.e., taniB = 1μ2 = \(\frac{\mu_{2}}{\mu_{1}}\) where μ2 < μ1
when the light rays travels in such a medium, the critical angle is
sin ic = \(\frac{\mu_{2}}{\mu_{1}}\)
where, μ2 < μ1
As | taniB| > | sin iC| for large angles iB <iC.
Thus, the polarisation by reflection occurs definitely.
Question 8.
Consider a two-slit interference arrangements (figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O. (NCERT Exemplar)
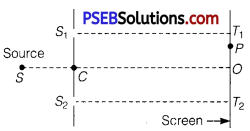
Answer:
From the given figure of two-slit interference arrangements, we can write

The minima will occur when S2P – S1P = (2 n -1)\(\frac{\lambda}{2}\)
i.e., [D2 +(D + X)2]1/2 -[D2 + (D -x)2]1/2
= \(\frac{\lambda}{2}\)
[for first minima n = 1]
If x = D
We can write [D2 +4D2]1/2 -[D2 +0]1/2 = \(\frac{\lambda}{2}\)
⇒ [5D2]1/2 – [D2]1/2 = \(\frac{\lambda}{2}\)
⇒ \(\sqrt{5}\)D – D = \(\frac{\lambda}{2}\)

![]()
Long answer type questions
Question 1.
In Young’s double-slit experiment, deduce the conditions for (i) constructive, and (ii) destructive interference at a point on the screen. Draw a graph showing variation of the resultant intensity in the interference pattern against position ‘X’ on the screen.
Answer:
Conditions for Constructive and Destructive Interference :
When two waves of same frequency and constant initial phase difference travel in the same direction along a straight line simultaneously, they superpose in such a way that the intensity of the resultant wave is maximum at certain points and minimum at certain other points. The phenomenon of redistribution of intensity due to superposition of two waves of same frequency and constant initial phase difference is called the interference.
The waves of same frequency and constant initial phase difference are called coherent waves. At points of medium where the waves arrive in the same phase, the resultant intensity is maximum and the interference at these points is said to be constructive. On the other hand, at points of medium where the waves arrive in opposite phase, the resultant intensity is minimum and the interference at these points is said to be destructive. The positions of maximum intensity are called maxima while those of minimum intensity are called minima. The interference takes place in sound and light both.
Mathematical Analysis: Suppose two coherent waves travel in the same direction along a straight line, the frequency of each wave is \(\frac{\omega}{2 \pi}\) and amplitudes of electric field are a1 and a2 respectively. If at any time t, the electric fields of waves at a point are y1 and y2 respectively and phase difference is, Φ then equation of waves may be expressed as
y1 = a1 sin ωt ………………………. (1)
y2 = a2 sin ωt +Φ) ……………………………………….. (2)
According to Young’s principle of superposition, the resultant displacement at that point will be
y = y1+y2 ……………………………….. (3)
Substituting values of y1 and y2 from (1) and (2) in (3), we get
y = a1 sin ωt + a2 sin(ωt + Φ)
Using trigonometric relation,
sin(ωt +Φ) = sinωtcosΦ +cosωtsinΦ
y = a1 sin ωt + a2(sinωtcosΦ) + cosωt sin Φ)
= (a1 +a2cos Φ) sinωt + (a2 sinΦ)cosωt …………………………….. (4)
Let a1 + a2 cosΦ = A cos θ ……………………………………… (5)
and a2 sinΦ = A sinθ ………………………………………… (6)
Where A and θ are new constants
Then equation (4) gives
y = A cosθ sinωt + A sinθ cosωt
= A sin (ωt +θ) ……………………………………………. (7)
This is the equation of the resultant disturbance. Clearly the amplitude of resultants disturbance is A and phase difference from first wave is 0. The values of A and 0 are determined by (5) and (6). Squaring (5) and (6) and then adding, we get
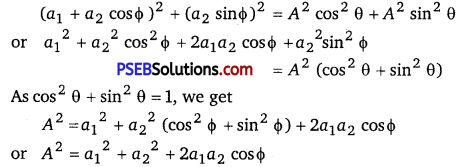
∴ Amplitude,
A = \(\sqrt{a_{1}^{2}+a_{2}^{2}+2 a_{1} a_{2} \cos \phi} \) …………………………… (8)
As the intensity of a wave is proportional to its amplitude in arbitrary units I = A2
∴ Intensity of resultant wave,
I = A2 = a12 + a22 + 2a1a2 cosΦ ……………………….. (9)
Clearly, the intensity of the resultant wave at any point depends on the amplitudes of individual waves and the phase difference between the waves at the point.
Constructive Interference: For maximum intensity at any point
cos Φ = +1
or phase difference Φ = 0,2π,4π,6π,……………………….
= 2nπ (n=0,1,2,3,……………………) …………………………………… (10)
The maximum intensity
Imax = a12+a22
= (a1+a2)2 …………………………..(11)
Path difference
Δ = \(\frac{\lambda}{2 \pi}\) x phase difference
= \(\frac{\lambda}{2 \pi} \) x 2nπ …………………………………………. (12)
Clearly, the maximum intensity is obtained in the region of superposition at those points where waves meet in the same phase or the phase difference between the waves is even multiple of π or path difference between them is the integral multiple of λ and maximum intensity is (a1 +a2)2
which is greater than the sum intensities of individual waves by an amount 2a1a2.
Destructive Interference : For minimum intensity at any point CosΦ = -1
or phase difference,
Φ = π,3π,5π,7π, …………………………..
– (2n-l)π, n = 1,2,3,… …………………………………. (13)
In this case the minimum intensity,
Imin =a12 +a22 – 2a1a2
= (a1-a2)2 ………………………… (14)
Path difference, Δ = \(\frac{\lambda}{2 \pi}\) x Phase difference
= \(\frac{\lambda}{2 \pi}\) x (2n – 1)π
= (2n-l) \(\frac{\lambda}{2}\)
Clearly, the minimum intensity is obtained in the region of superposition at those points where waves meet in opposite phase or the phase difference between the waves is odd multiple of π or path difference between the waves is odd multiple of \(\frac{\lambda}{2}\) and minimum intensity = (a1 -a2)2 which is less than the sum of intensities of the individual waves by an amount 2a1a2.
From equations (12) and (14) it is clear that the intensity 2a1a2 is transferred from positions of minima to maxima, this implies that the interference is based on conservation of energy i.e., there is no wastage of energy.
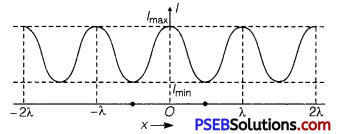
Variation of Intensity of light with position x is shown in fig.
![]()
Question 2.
Describe diffraction of light due to a single slit. Explain formation of a pattern of fringes obtained on the screen and plot showing variation of intensity with angle θ in single slit diffraction.
Answer:
Diffraction of Light at a Single Slit: When monochromatic light is made incident on a single slit, we get diffraction pattern on a screen placed behind the slit. The diffraction pattern contains bright and dark bands, the intensity of central band is maximum and goes on decreasing on both sides.
Explanation: Let AB be a slit of width ‘a’ and a parallel beam of monochromatic light is incident on it. According to Fresnel, the diffraction pattern is the result of superposition of a large number of waves, starting from different points of illuminated slit.
Let θ be the angle of diffraction for waves reaching at point P of screen and AN the perpendicular dropped from A on wave diffracted from B. The path difference between rays diffracted at points A and B,
Δ = BP – AP = BN
In ΔANB, ∠ANB = 90°
and ∠BAN = θ
∴ sinθ = \(\frac{B N}{A B}\) or BN = AB sinθ
As AB = width of slit = a
Path difference Δ = asinθ ……………………………… (1)
To find the effect of all coherent waves at P, we have to sum up their contribution, each with a different phase. This was done by Fresnel by rigorous calculations, but the main features may be explained by simple arguments given below :
At the central point C of the screen, the angle 0 is zero. Hence the waves starting from all points of slit arrive in the same phase. This gives maximum intensity at the central point C. If point P on screen is such that the path difference between rays starting from edges A and B is λ, then path difference,
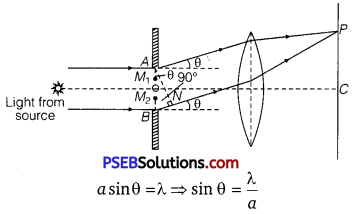
If angle θ is small,
sinθ = θ = \(\frac{\lambda}{a}\) ……………………………. (2)
Minima: Now we divide the slit into two equal halves AO and OB, each of width \(\frac{a}{2}\).
Now for every point, M1 in AO, there is a corresponding point M2 in OB, such that M1M2 = \(\frac{a}{2}\) .
Then path difference between waves arriving at P and starting from M1 and M2 will be \(\frac{a}{2}\) sin θ = \(\frac{\lambda}{2}\).
This means that the contributions from the two halves of slit AO and OB are opposite in phase and so cancel each other. Thus equation (2) gives the angle of diffraction at which intensity falls to zero. Similarly it may be shown that the intensity is zero for sin θ = \(\frac{n \lambda}{a}\) , with n as integer. Thus, the general condition of minima is asinθ = nλ ……………………………………… (3)
Secondary Maxima: Let us now consider angle θ such that
sin θ = θ = \(\frac{3 \lambda}{2 a}\)
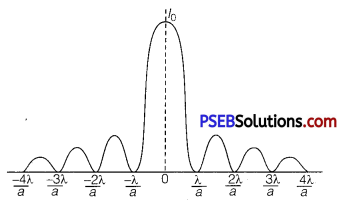
Which is midway between two dark bands given by
sin θ = θ = \(\frac{\lambda}{a} \) and sin θ = θ = \(\frac{2 \lambda}{a}\)
Let us now divide the slit into three parts. If we take the first two parts of slit, the path difference between rays diffracted from the extreme ends of the first two parts.
\(\frac{2}{3}\) a sin θ = \(\frac{2}{3} a \times \frac{3 \lambda}{2 a}\) = λ
Then the first two parts will have a path difference of \(\frac{\lambda}{2}\) and cancel the effect of each other. The remaining third part will contribute to the intensity at a point between two minima. Clearly, there will be maxima between first two minima, but this maximum will be of much weaker intensity than central maximum.
This is called first secondary maxima. In a similar manner, we can show that there are secondary maxima between any two consecutive minima; and the intensity of maxima will go on decreasing with increase of order of maxima.
In general, the position of nth maxima will be given by
a sin θ = \(\left(n+\frac{1}{2}\right)\) λ (n =1, 2, 3, 4,…) ………………………………… (4)
The intensity of secondary maxima decreases with increase of order n because with increasing n, the contribution of slit decreases.
For n = 2, it is one-fifth, for n = 3, it is one-seventh and so on.