PSEB 11th Class Practical Geography Chapter 2 पैमाना

Punjab State Board PSEB 11th Class Geography Book Solutions Practical Geography Chapter 2 पैमाना.

PSEB 11th Class Practical Geography Chapter 2 पैमाना

प्रश्न 1.
पैमाना किसे कहते हैं ?
उत्तर-
पैमाना (Scale)-पैमाना नक्शे और धरती के बीच एक अनुपात है। नक्शे पर किन्हीं दो स्थानों के बीच की दूरी और धरती पर स्थित उन्हीं दो स्थानों के बीच की वास्तविक दूरी के अनुपात को पैमाना कहते हैं।

(The scale of a map is the ratio of a distance on the map to the corrosponding distance on the ground.)
उदाहरण (Example)–यदि किसी नक्शे का पैमाना 1 सैं०मी० : 5 किलीमीटर है, तो इसका अर्थ है कि नक्शे पर 1 सैं०मी० की दूरी धरती के 5 किलोमीटर की दूरी को प्रकट करती है।।

प्रश्न 2.
पैमाने की क्या आवश्यकता है ?
उत्तर-
पैमाने की आवश्यकता-

• हर नक्शे के लिए पैमाना ज़रूरी होता है। पैमाने के बिना नक्शा एक स्कैच (Sketch) या रेखाचित्र (Diagram) ही रह जाता है। पैमाने के बिना अलग-अलग स्थानों की दूरी का अनुमान नहीं हो सकता।
• धरती का वास्तविक विस्तार बहुत बड़ा है। नक्शे पर इसका विस्तार वास्तविक विस्तार से कम होता है, इसलिए बड़े क्षेत्र को छोटे रूप में दिखाने के लिए पैमाने का प्रयोग जरूरी होता है।
• अलग-अलग स्थानों के नक्शे पर सापेक्ष स्थिति दिखाने के लिए पैमाना ज़रूरी होता है।

प्रश्न 3.
छोटे पैमाने और बड़े पैमाने में अंतर बताएँ।
उत्तर-
छोटे पैमाने (Small Scale)-

1. इस पैमाने में 1 सैं०मी० के द्वारा एक से अधिक किलोमीटर की दूरी प्रकट की जाती है।
2. उदाहरण के रूप में 1 सैं०मी० : 10 कि०मी० 1 इंच : 60 मील।
3. Small Scales are Scales of miles to the inch.
4. एटलस नक्शे, दीवारी नक्शे छोटे पैमाने पर बनाए जाते हैं।
5. इन नक्शों पर अधिक वर्णन नहीं दिखाए जा सकते।
6. नक्शे पर दिखाई दूरी कम होने के कारण इन्हें छोटे पैमाने के नक्शे कहा जाता है।

बड़ा पैमाना (Large Scale)-

1. इस पैमाने में 1 किलोमीटर की दूरी एक से अधिक सैंटीमीटरों के द्वारा प्रकट की जाती है।
2. उदाहरण के रूप में 10 सैं०मी० : 1 कि०मी० 6 इंच : 1 मील।
3. Large Scales are scales of inches to the mile.
4. जायदाद के नक्शे बड़े पैमाने पर बनाए जाते हैं।
5. इन नक्शों पर अधिक वर्णन दिखाया जा सकता है।
6. इन नक्शों पर दिखाई गई दूरी तुलना में अधिक होने के कारण इन्हें बड़े पैमाने के नक्शे कहा जाता है।

प्रश्न 4.
पैमाने के महत्त्व का उल्लेख करें।
उत्तर-
पैमाने का महत्त्व (Importance of Scale)-पैमाना मानचित्र कला (Cartography) का एक ज़रूरी अंग है-

1. पैमाना एक उपयोगी तकनीक है, जिसके द्वारा बड़े क्षेत्र को संक्षेप रूप में दिखाया जा सकता है।
2. पैमाने के बिना कोई भी नक्शा एक स्कैच (Sketch) या तस्वीर ही होता है।
3. पैमाने की मदद से दो स्थानों के बीच की वास्तविक दूरी का पता लगता है।
4. किसी नक्शे का क्षेत्रफल पैमाने की सहायता से पता लगाया जा सकता है।
5. पैमाने की सहायता से एक ही क्षेत्र के नक्शे छोटे (Reduce) या बड़े (Enlarge) किए जा सकते हैं।

प्रश्न 5.
पैमाने की विधियों का वर्णन करें।
उत्तर-
पैमाना (Scale)-साधारण शब्दों में दो स्थानों के बीच की नक्शे पर दूरी (Map Distance) और धरती पर वास्तविक दूरी (Actual Distanc) के अनुपात को पैमाना कहा जाता है। नक्शे पर पैमाना नीचे लिखे तीन रूपों में दिखाया जाता है-

1. कथनीय पैमाना या वर्णनात्मक पैमाना (Statement Scale)
2. प्रतिनिधि भिन्न (Representative Fraction)
3. रेखीय पैमाना या साधारण पैमाना (Linear Scale or Plain Scale)

1. कथनीय पैमाना (Statement Scale)-पैमाना प्रकट करने का यह सबसे आसान तरीका है। इससे पैमाने को शब्दों में प्रकट किया जाता है, इसलिए इसे शाब्दिक या वर्णनात्मक पैमाना भी कहते हैं।

जैसे-1 सैं०मी० : 5 कि०मी० ।
नोट-कथनीय पैमाना सदा अनुपात (:) के द्वारा ही लिखा जाता है, बराबर (=) का प्रयोग नहीं होता। 1 इंच : 6 मील।

गुण (Merits)—

1. यह सबसे आसान और सरल तरीका है, जिसे एक साधारण मनुष्य भी समझ सकता है।
2. इससे तुरंत ही स्पष्ट हो जाता है कि एक इंच कितने मील की दूरी नक्शे पर प्रकट करता है।
3. यह पैमाने का संक्षिप्त रूप है।
4. इसका अभ्यास जल्दी हो जाता है।

दोष (Demerits)-

1. इस तरीके से माप की एक ही इकाई का प्रयोग किया जा सकता है।
2. इस पैमाने को केवल उसी देश के लोग ही समझ सकते हैं, जिस देश की माप प्रणाली नक्शे पर प्रयोग की गई हो।
3. इस पैमाने के द्वारा नक्शे पर दूरी नापी जा सकती है।

2. प्रतिनिधि भिन्न (Representative Fraction) -पैमाने को नक्शे पर प्रकट करने के लिए एक भिन्न का प्रयोग किया जाता है, जिसे प्रतिनिधि भिन्न या अनुपाती भिन्न या प्रदर्शक भिन्न कहा जाता है। इसे संक्षिप्त रूप में R.F. लिखा जाता है। प्रतिनिधि भिन्न एक ऐसी भिन्न होती है, जिसका अंश (Numerator) सदा एक ही होता है और वह नक्शे पर दूरी (Map Distance) को प्रकट करता है, परंतु उसका हर Denominator धरती पर वास्तविक दूरी (Ground Distance) को प्रकट करता है। इसको नीचे लिखे नियम (Rule) द्वारा लिखा जाता है-

उदाहरण (Example) यदि किसी नक्शे की प्रतिनिधि भिन्न 1/50,000 है, तो इसका अर्थ है कि नक्शे पर दूरी की एक इकाई, धरती पर 50,000 इकाइयों की दूरी को प्रकट करती है। नक्शे पर 1 सैं०मी० की दूरी धरती पर 50,000 सैं०मी० की दूरी को दर्शाती है।

नियम (Rule) –

1. प्रतिनिधि भिन्न का अंश सदा एक होना चाहिए।
2. अंश और प्रत्येक दूरी की माप इकाई सदा एक होनी चाहिए और छोटी-से-छोटी हो।

गुण (Merits)-

• इस पैमाने में एक इकाई कई इकाइयों को प्रकट करती है, इसलिए इसे प्रतिनिधि भिन्न कहा जाता है।
• इस पैमाने को संख्यक पैमाना (Numerical Scale) भी कहा जाता है। यह एक प्राकृतिक पैमाना (Natural Scale)
• प्रतिनिधि भिन्न में दूरी की किसी भी इकाई (Unit) का प्रयोग किया जा सकता है। दूरी इंच या सैंटीमीटरों में भी लिखी जा सकती है। (R.F. is independent of units.)
• यह एक अंतर्राष्ट्रीय पैमाना (International Scale) है। इसका प्रयोग विश्व के सभी देशों में किया जा सकता है। यदि किसी नक्शे का कथनीय पैमाना 1″ = 1 मील हो, तो इसे केवल इंग्लैंड के लोग ही समझ सकते हैं। परंतु यदि इस पैमाने को प्रतिनिधि भिन्न के रूप में लिखा जाए, तो R.E. = 1/63,360 होगा। इसे मीट्रिक प्रणाली में भारत और फ्रांस के लोग आसानी से समझ सकते हैं कि नक्शे पर 1 सैं०मी० की दूरी धरती पर 63,360 सैं०मी० की दूरी प्रकट करती है।
• प्रतिनिधि भिन्न को कथनीय पैमाने में बदला जा सकता है।

दोष (Demerits)-

• इस पैमाने से नक्शे पर सीधी दूरियाँ नहीं मापी जा सकतीं।
• गणित के प्रयोग के कारण इसे साधारण मनुष्य नहीं समझ सकता।
• रेखीय पैमाना (Linear Scale)-इस पैमाने को रेखीय पैमाना या साधारण पैमाना (Plain Scale) या ग्राफिक पैमाना (Graphic Scale) भी कहा जाता है। इसमें एक सरल रेखा को मुख्य भागों और उपभागों में विभाजित करके पैमाने को प्रकट किया जाता है। इसकी लंबाई 15 सैं०मी० या 6 इंच होती है। इस रेखा को समान मुख्य भागों (Primary Division) और उपभागों (Secondary Divisions) में बाँटा जाता है। कुल संख्या एक पूर्ण अंक (Round Number) होती है, जिसके आसानी से उपभाग किए जा सकते हैं।

गुण (Merits)-

1. इस पैमाने से सीधे रूप में दूरी मापी जा सकती है।
2. दूरी मापने के लिए किसी हिसाब की ज़रूरत नहीं होती।
3. नक्शे को फोटोग्राफी की विधि से बड़ा या छोटा करने पर पैमाने की रेखा उसी अनुपात में छोटी या बड़ी हो जाती है।
4. इस पैमाने के प्रयोग के लिए अभ्यास की आवश्यकता होती है।

पैमाने का परिवर्तन
(CONVERSION OF SCALE)
कथनीय पैमाने से प्रतिनिधि भिन्न ज्ञात करना ।

प्रश्न 1.
यदि कथनीय पैमाना 1 सैंटीमीटर : 3 किलोमीटर हो, तो प्रतिनिधि भिन्न बताएँ। (If the statement of scale is 1 cm : 3 km, find out the R.F.)
उत्तर-

\(\frac{1}{3,00,000}\)(दोनों तरफ माप इकाई समान होनी चाहिए, इसलिए किलोमीटर के सैंटीमीटर बनाएँ)
अथवा 1 : 3,00,000
नोट-प्रतिनिधि भिन्न केवल भिन्न होती है। इसके अंश या हरेक के साथ सैंटीमीटर या इंच आदि माप नहीं लिखे जाते।

प्रश्न 2.
यदि कथनीय पैमाना 1 सैंटीमीटर : 50 मीटर हो, तो प्रतिनिधि भिन्न बताएँ। (If the statement of the scale is 1 cm = 50 m, find out the R.F.)
उत्तर-
कथनीय पैमाना = 1 cm = 50 m.

\(\frac{1}{5000}\) या 1 : 5000.

प्रश्न 3.
यदि कथनीय पैमाना 1 इंच : 2 मील हो, तो प्रतिनिधि भिन्न बताएँ। (If the statement of scale is 1 inch : 2 miles, find out the R.F.)
उत्तर-
कथनीय पैमाना = 1 inch = 2 railes.

(दोनों तरफ माप इकाई समान होनी चाहिए, इसलिए मीलों के इंच बनाएँ)
= \(\frac{1}{1,26,720}\) या 1 : 1,26,720.

प्रश्न 4.
यदि कथनीय पैमाना 6 इंच : 1 मील हो, तो प्रतिनिधि भिन्न बताएँ। (If the statement of scale is 6 inches : 1 mile, find out the R.F.)
उत्तर-
कथनीय पैमाना = 6 inch : 1 miles.

= \(\frac{1}{10,560}\) या 1 : 10,560.
नोट-प्रतिनिधि भिन्न का अंश सदा (1) होता है।

QUESTIONS TYPE-II

प्रतिनिधि भिन्न से कथनीय पैमाना ज्ञात करना

प्रश्न 5.
यदि प्रतिनिधि भिन्न 1/5,00,000 हो, तो कथनीय पैमाना किलोमीटरों में बताएँ। (If R.F. of a map is 1/5,00,000, find out the statement of the scale in kilometers.)
उत्तर-
प्रतिनिधि भिन्न (R.F.) = \(\frac{\text { Map Distance }}{\text { Ground Distance }}\)
R.F. = \(\frac{1}{5,00,000}\)
∴ 1 cm : 5,00,000 (क्योंकि किलोमीटर दूरी की मूल इकाई सैंटीमीटर होती है।)
1 cm : \(\frac{5,00,000}{1,00,000}\) km (क्योंकि 1 km = 1,00,000 cm)
कथनीय पैमाना = 1 cm = 5 km.

प्रश्न 6.
यदि प्रतिनिधि भिन्न 1/1,90,080 हो, तो कथनीय पैमाना मीलों में बताएँ। (If R.F. of a map is 1/1,90,080, find out the statement scale in miles.)
उत्तर-
प्रतिनिधि भिन्न (R.F.) = \(\frac{\text { Map Distance }}{\text { Ground Distance }}\)
R.F. = \(\frac{1}{1,90,080}\)
1 inch = 1,90,080 inches (क्योंकि मीलों की मूल इकाई इंच होती है।)
1 inch = \(\frac{1,90,080}{63,360}\) miles
= 3 miles (क्योंकि 1 मील = 63,360 इंच)
कथनीय पैमाना = 1 inch : 3 miles.

प्रश्न 7.
यदि प्रतिनिधि भिन्न 1/1,000,000 हो, तो कथनीय पैमाना मीलों में और किलोमीटरों में बताएं।
(If R.F. of a map is 1/1,000,000, find out the statement of the scale in both miles and kilometres.)
उत्तर-
(i) मीलों में (In miles)
R.F. = \(\frac{\text { Map Distance }}{\text { Ground Distance }}\)
R.F. = \(\frac{1}{1,000,000}\)
1 inch = 1,000,000 inches
1 inch = \(\frac{1,000,000}{63,360}\) miles (∵1 mile = 63,360 inches)
= 15.78 miles approximately
कथनीय पैमाना = 1 inch : 15.78 miles.

(ii) किलोमीटरों में (In kms)
R.F. = \(\frac{1}{1,000,000}\)
1 cm. = 1,000,000 cms.
1.cm. = \(\frac{1,000,000}{1,00,000}\)
= 10 kms.
कथनीय पैमाना = 1 cm : 10 km.

QUESTIONS TYPE III

प्रतिनिधि भिन्न और वास्तविक दूरी ज्ञात करना

प्रश्न 8.
दो स्थानों के बीच वास्तविक दूरी 40 kms है और नक्शे पर यह दूरी 5 cm रेखा से प्रकट की गई है। नक्शे की प्रतिनिधि भिन्न बताएँ।
उत्तर-
नक्शे पर 5 सैं.मी. दूरी प्रकट करती है = 40 कि०मी० भूमि पर दूरी
नक्शे पर 1 सें.मी. दरी प्रकट करती है = \(\frac{40 \times 1,00,000 \mathrm{~cm}}{5}\)
= 8,00,000 cm
= \(\frac{1}{8,00,000}\)
अथवा दूसरे ढंग से R.F. = \(\frac{\text { Map Distance }}{\text { Ground Distance }}\)
= \(\frac{5 \mathrm{cms}}{40,00,000 \mathrm{~cm}}\)
= \(\frac{1}{8,00,000}\)

प्रतिनिधि भिन्न के नियम-

• R.F. का अंश सदा एक (1) होना चाहिए।
• अंश और हरेक की दूरी एक ही इकाई में होनी चाहिए।

प्रश्न 9.
दो स्थानों की नक्शे पर आपसी दूरी 5 सें.मी. है। नक्शे की प्रतिनिधि भिन्न 1/200,000 है। उन दो स्थानों की भूमि पर वास्तविक दूरी बताएँ।
उत्तर-
प्रतिनिधि भिन्न (R.F.) = \(\frac{1}{2,00,000}\)
नक्शे पर 1 सैं०मी० की दूरी प्रकट करता है = 2,00,000 सैं.मी. भूमि पर
नक्शे पर 5 सैं०मी० की दूरी प्रकट करता है = \(\frac{2,00,000 \times 5}{1,00,000}\) kms
= 10 kms.

QUESTIONS TYPE IV

रेखीय पैमाने की रचना-विधि (Drawing of a Linear or Plain Scale)

इस विधि में नक्शे की दूरी को एक सरल रेखा के द्वारा प्रकट किया जाता है। इस रेखा को कुछ मुख्य समान भागों (Primary Divisions) में बाँटा जाता है। प्रत्येक मुख्य भाग को गौण भागों (Secondary Divisions) में बाँटा जाता है।

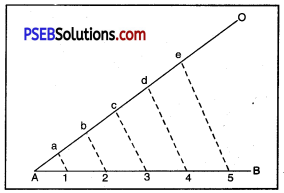
पहली विधि-मान लो कि किसी सरल रेखा AB को पाँच समान भागों में बाँटना है। A बिंदु पर एक न्यून कोण (Acute angle) ∠OAB बनाएँ। रेखा AO पर A से 0 की ओर बराबर दूरी पर पाँच बिंदु a, b, c, d, e लगाएँ। बिंदु e और b को एक सरल रेखा से मिलाएँ। सैट स्कवैर की सहायता से बिंदु d, c, b और a से समानांतर रेखाएँ खींचें। ये रेखाएँ AB को पाँच बराबर भागों में बांटती हैं।

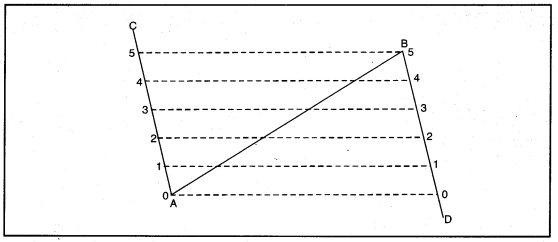
दूसरी विधि-मान लो कि किसी सरल रेखा AB को पाँच बराबर भागों में बाँटना है। AB रेखा के दोनों सिरों A और B पर विपरीत दिशा में दो लंब कोण बनाएँ। अब बिंदु A से बराबर दूरी पर A से C की ओर पाँच चिहन 1, 2, 3,4,5 लगाएँ। इसी प्रकार बिंदु B से पाँच बराबर चिह्न D की ओर लगाएँ। चित्र के अनुसार इन बिंदुओं को मिलाकर समानांतर रेखाएँ खींचे। ये रेखाएँ AB रेखा को पाँच बराबर भागों में बाँटेंगी।

सावधानियाँ-
1. सरल रेखा की लंबाई-सरल रेखा की आदर्श लंबाई लगभग 6 इंच या 15 सें.मी. हो, ताकि मुख्य भाग और उपभाग आसानी से पढ़े जा सकें।

2. पूर्ण अंक-रेखीय पैमाने के मुख्य भाग और उपभाग पर दिखाई गई दूरी पूर्ण अंक (Round Number) में होनी चाहिए, जैसे-5, 10, 15, 20.

3. मुख्य भाग और उपभाग-रेखीय भाग को मुख्य भाग और उपभाग में बाँटा जाए।

4. कथनीय और प्रतिनिधि भिन्न-रेखीय पैमाने के ऊपर कथनीय पैमाना और सरल रेखा के नीचे प्रतिनिधि भिन्न लिखना चाहिए।

5. पैमाने का शून्य (जीरो)-सरल रेखा पर दायीं ओर मुख्य भाग और बायीं ओर उपभाग शुरू होते हैं। बायीं ओर के पहले भाग से ज़ीरो शुरू होता है।

6. माप इकाई-रेखीय पैमाने पर दूरी अंकों में लिखी जाती है और माप इकाई शब्दों में जैसे-किलोमीटर या मील।

7. शेड करना-पैमाने के आधे भाग पर एक सरल रेखा खींच कर पैमाने के दो भाग हो जाते हैं। एक भाग को छोड़कर ऊपर नीचे शेड किया जाता है।

QUESTIONS TYPE-V

कथनीय पैमाने से रेखीय पैमाना बनाना

प्रश्न 10.
यदि कथनीय पैमाना 1 सैं.मी. : 10 कि.मी. हो, तो रेखीय पैमाना बनाएँ।
(Draw a plain scale for a map whose scale is 1 cm: 10 km.)
उत्तर-
नक्शे पर 1 cm दूरी भूमि पर प्रकट करती है = 10 km.
नक्शे पर 15 cm दूरी भूमि पर प्रकट करती है = 10 x 15
= 150 km.
∴ सरल रेखा की दूरी 15 cm. चाहिए।
(नोट – 150 km. एक पूर्ण अंक है।)

रचना (Construction)-15 सैं०मी० लंबी रेखा के 15 मुख्य भाग करें। हर मुख्य भाग 10 कि०मी० की दूरी प्रकट करता है। सबसे बायीं ओर की तरफ मुख्य भाग को दो उपभागों में बाँटें, तो हर एक उपभाग 5 कि०मी० दूरी को दर्शाएगा।

प्रश्न 11.
1 सैं०मी० : 7 कि०मी० के कथनीय पैमाने के लिए रेखीय पैमाना बनाएँ।
(Draw a plain scale for a map whose scale is 1 cm. : 7 km.)
उत्तर-
कथनीय पैमाने से स्पष्ट है
1 सैं०मी० प्रकट करता है = 7 कि०मी० दूरी
15 सैं०मी० प्रकट करता है = 7 x 15
= 105 कि०मी०
परंतु 105 पूर्ण अंक नहीं है। इसके निकट की पूर्ण संख्या 100 कि०मी० है। इसलिए 100 कि०मी० की दूरी पर नक्शे की दूरी खोजें।
7 कि०मी० की दूरी प्रकट की जाती है = 1 सैं०मी० से
1 कि०मी० की दूरी प्रकट की जाती है = 1/7 सैं०मी० से.
100 कि०मी० की दूरी प्रकट की जाती है = 100/7 सैं०मी० से = 14.3 सैं०मी० (लगभग)

रचना (Construction)-14.3 सैं०मी० लंबी रेखा लेकर इसे पाँच मुख्य भागों में बाँटें । हर मुख्य भाग 20 कि०मी० की दूरी प्रकट करता है सबसे बायीं ओर वाले मुख्य भाग को चार उपभागों में बाँटें, तो हर एक उपभाग 5 कि०मी० की दूरी को दर्शाएगा।

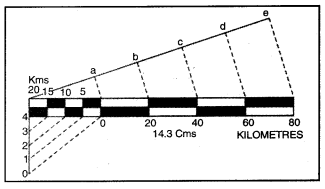
प्रश्न 12.
4 इंच : 1 मील के कथनीय पैमाने के लिए रेखीय पैमाना बनाएँ, जिस पर गज दिखाए जा सकें।
(Draw a plain scale to show yards for a map whose scale is 4 inches : 1 mile)
उत्तर-
4 इंच की दूरी प्रकट करती है = 1 मील
= 1760 गज
1 इंच की दूरी प्रकट करती है = \(\frac{1760}{4}\) गज
6 इंच की दूरी प्रकट करती है = \(\frac{1760}{4}\) x 6
= 2640 गज परंतु 2640 पूर्ण अंक नहीं हैं। इसके निकट की पूर्ण संख्या 3000 गज हैं।
1760 गज की दूरी प्रकट की जाती है = 4 इंच
1 गज की दरी प्रकट की जाती है = \(\frac{4}{1760}\)
3000 गज की दूरी प्रकट की जाती है = \(\frac{4}{1760}\) x 3000
= 6.8 इंच

रचना (Construction) : 6.8 इंच लंबी रेखा को 6 मुख्य भागों में बाँटें। हर एक मुख्य भाग 500 गज की दूरी प्रकट करेगा। बायीं ओर वाले मुख्य भाग को पाँच उपभागों में बाँटे। हर एक उपभाग 100 गज की दूरी को प्रकट करेगा।

QUESTIONS TYPE VI

प्रतिनिधि भिन्न से रेखीय पैमाना बनाना

प्रश्न 13.
यदि प्रतिनिधि भिन्न \(\frac{1}{100000}\) हो, तो रेखीय पैमाना बनाएँ।
(Draw a plain scale to show kilometers for a map whose R.F. is \(\frac{1}{100000}\)).
उत्तर-
1 सैं०मी० प्रकट करता है = 1,00,000 सैं०मी०
= 1 कि०मी०
15 सैं०मी० प्रकट करता है = 15 कि०मी०

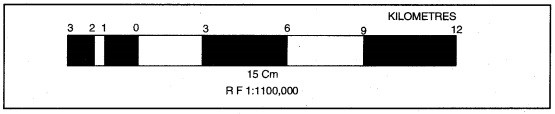
रचना (Construction)-15 सैं०मी० रेखा को पाँच मुख्य भागों में बाँटें। हर-एक मुख्य भाग 3 कि०मी० की दूरी को प्रकट करेगा। बायीं ओर वाले मुख्य भाग को तीन उपभागों में बाँटें। हर-एक उपभाग 1 कि०मी० की दूरी को प्रकट करेगा।

प्रश्न 14.
यदि प्रतिनिधि भिन्न \(\frac{1}{50000}\) हो, तो रेखीय पैमाना बनाएँ, जिसमें कि०मी० और मी० प्रकट किए जा सकें। इस पैमाने पर 4 कि०मी० और 600 मीटर की दूरी प्रकट करें।
(Draw a plain scale to show kilometers and meters for a map. Whose scale is \(\frac{1}{50000}\))
Show a distance of 4 km. and 60 meters on this scale.)
उत्तर-
1 सैं०मी० की दूरी प्रकट करता है = 50,000 सैं०मी०
= \(\frac{50000}{100000}\)
= \(\frac{1}{2}\)कि०मी०
16 सै०मी० की दूरी प्रकट करता है = \(\frac{1}{2}\) x 16
= 8 कि०मी०

रचना (Construction)-16 सैं०मी० लंबी रेखा लें। इसे 8 मुख्य भागों में बाँटें। हर एक भाग 1 कि०मी० को प्रकट करेगा। बायीं ओर वाले मुख्य भाग को पाँच उपभागों में बाँटें। हर एक भाग 200 मीटर को प्रकट करेगा ।
रेखीय पैमाने पर 4 कि०मी० और 600 मी० की दूरी = 4 कि०मी० + 600 मी०
= 4 मुख्य भाग + 3 उपभाग
चिह्न लगाकर यह दूरी चित्र के अनुसार दिखाएँ।

प्रश्न 15.
अमृतसर और जालंधर की वास्तविक दूरी 78 कि०मी० है, जिसे नक्शे पर 5.2 सैं०मी० द्वारा दर्शाया गया है। नक्शे का पैमाना बताएँ।
(The distance between Amritsar and Jalandhar is 78 km. It is shown by a distance of 5.2 cm. on the map. Find out the scale of the map.)
उत्तर-
\(\frac{52}{10}\)
1 सैं॰मी॰ दूरी प्रकट करती है =\(\frac{78 \times 10}{52}\)
= 15 कि०मी०
इसलिए पैमाना = 1 cm. : 15 कि०मी०

प्रश्न 16.
यदि प्रतिनिधि भिन्न \(\frac{1}{100000}\) हो, तो रेखीय पैमाना (मीलों में) बनाएँ।
(Draw a plain scale to show miles for a map whose R.F. is \(\frac{1}{100000}\))
उत्तर-
1 इंच दूरी प्रकट करती है = 1,000,000 इंच
\(\frac{100000}{63,360}\) मील
6 इंच दूरी प्रकट करती है =
\(\frac{100000}{63,360}\) x 6
= \(\frac{100,000}{1056}\)
= \(\frac{12500}{132}\)
= \(\frac{3125}{33}\) मील
= 94.69 मील

परंतु \(\frac{3125}{33}\) या 94.69 मील पूर्ण अंक नहीं है।
इसके निकट की पूर्ण संख्या 100 मील है। 100 मील के लिए नक्शे पर दूरी बताएँ। \(\frac{100000}{63360}\)
मील प्रकट किए जाते हैं = 1 इंच से
1 मील प्रकट किया जाता है = \(\frac{63,360 \times 1}{1,000,000}\) इंच
100 मील प्रकट किए जाते हैं = \(\frac{63,360 \times 100}{1,000,000}\)
= \(\frac{6336}{1000}\)
= 6.336 इंच
= 6.3 इंच (लगभग)

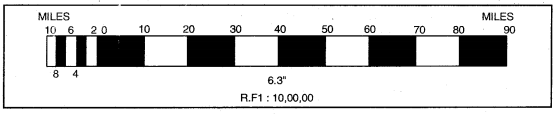
रचना (Construction)–6.3 इंच सरल रेखा लें। इसको 10 भागों में बाँटें। हर एक मुख्य भाग 10 मील की दूरी को प्रकट करता है। बायीं ओर वाले मुख्य भाग को 5 उपभागों में बाँटें। हर एक उपभाग 2 मील की दूरी को प्रकट करता है।