PSEB 11th Class Physics Important Questions Chapter 14 Oscillations

Punjab State Board PSEB 11th Class Physics Important Questions Chapter 14 Oscillations Important Questions and Answers.

PSEB 11th Class Physics Important Questions Chapter 14 Oscillations

Very Short Answer Type Questions

Question 1.
What are the basic properties required by a system to oscillate?
Answer:
Inertia and elasticity are the properties which are required by a system to oscillate.

Question 2.
All oscillatory motions are periodic and vice-versa. Is it true?
Answer:
No, there are other types of periodic motions also. Circular motion and rotatory motion are periodic but non-oscillatory.

Question 3.
Give three important characteristics of a SHM.
Answer:
Three important characteristics of an SHM are amplitude, time period (or frequency) and phase.

Question 4.
What is the force equation of a SHM?
Answer:
According to force equation of SHM, F = -kx,
where k is a constant known as force constant.

Question 5.
Under what condition is the motion of a simple pendulum be simple harmonic? (NCERT Exemplar)
Answer:
When the displacement amplitude of the pendulum is extremely small as compared to its length.

Question 6.
A simple pendulum is transferred from earth to the surface of Moon. How will its time period be affected?
Answer:
As value of g on Moon is less than that on earth, in accordance with the relation T = \(2 \pi \sqrt{l / g}\) , the time period of oscillations of a simple pendulum on Moon will be greater.

Short Answer Type Questions

Question 1.
A girl is swinging in the sitting position. How will the period of the swing be changed if she stands up?
Solution:
This can be explained using the concept of a simple pendulum. We know that the time period of a simple pendulum is given by
T = \(2 \pi \sqrt{\frac{l}{g}} \text { i.e., } T \propto \sqrt{l}\)
When the girl stands up, the distance between the point of suspension and the center of mass of the swinging body decreases i.e., I decreases, so T will also decrease.

Question 2.
A particle is subjected to two simple harmonic motions
x₁ = A₁ sinωt
And
x₂ = A₂ sin \(\left(\omega t+\frac{\pi}{\mathbf{3}}\right)\)
Find (i) the displacement at t = 0
(ii) the maximum speed of the particle and
(iii) the maximum acceleration of the particle
Solution:
(i) At t = 0, x₁ = A₁ sin ωt = 0
And
x₂ = A₂ sin \(\left(\omega t+\frac{\pi}{3}\right)=\frac{A_{2} \sqrt{3}}{2}\)
Thus the resultant displacement at t = 0 is

Question 3.
The maximum acceleration of a simple harmonic oscillator Is a₀ and the maximum velocity is v₀. What is the displacement amplitude?
Solution:
Let A be the displacement amplitude and o be the angular frequency of the simple harmonic oscillator.
Then, a₀ = ω²A ……………………………. (i)
and v₀ = ωA …………………………………………………. (ii)
Squaring eq. (ü) and dividing from eq. (j), we get
\(\frac{v_{0}^{2}}{a_{0}}=\frac{\omega^{2} A^{2}}{\omega^{2} A}\) = A or A = \(\frac{v_{0}^{2}}{a_{0}}\)

Question 4.
A particle performs SHM on a rectilinear path. Starting from rest, it travels x₁ distance in first second, and in the next second, it travels x₂ distance. Find out the amplitude of this SHM.
Solution :
Because the particle starts from rest, so its starting point will be extreme position.
Thus, the displacement of the particle from the mean position after one second
A-x₁ = A cos ωt = A cos ω ……………………………… (i) [puttingt =1 s]
where A is the amplitude of the SHM and for next second
A – (x₁ + x₂) = Acosωt
= Acos2ω = A[2cos²ω-1]
[putting t = 2s]
[ ∵ cos 2 ω =
2 [cos² ω -1] ……………………………………………. (ii)
From eqs. (i) and (ii), we have

Question 5.
Apartide is executing SHM. If ν₁ and ν₂ are the speeds of the particle at distance x₁ and x² from the equilibrium position, show that the frequency of oscillations is
f = \(\frac{1}{2 \pi}\left(\frac{v_{1}^{2}-v_{2}^{2}}{x_{2}^{2}-x_{1}^{2}}\right)^{1 / 2} \)
Solution:
The displacement of a particle executing SHM is given by
x = Acosωt
\(\frac{d x}{d t}\) = – ωAsin ωt
∴ velocity,ν = \(\frac{d x}{d t}\)
or ν²=A²ω²sin2ωt

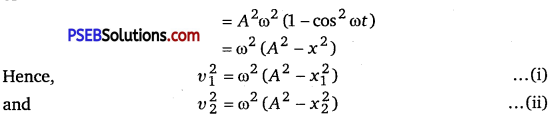
Subtracting eq. (ii) from eq. (i), we get

Question 6.
Define the restoring force and it characteristics in case of an oscillating body.
Answer:
A force which takes the body back towards the mean position in oscillation is called restoring force. Characteristic of Restoring force: The restoring force is always directed towards the mean position and its magnitude of any instant is directly proportional to the displacement of the particle from its mean position of that instance.

Long Answer Type Questions

Question 1.
A person normally weighing 50 kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0 s^-1 and an amplitude 5.0 cm. A weighing machine on the platform gives the persons weight against time.
(i) Wifi there be any change in weight of the body, during the oscillation?
(ii) If answer to part (i) is yes, what will be the maximum and minimum reading In the machine and at which position? (NCERT Exemplar)
Solution:
This is a case of variable acceleration. In accelerated motion, weight of body depends on the magnitude and direction of acceleration for upward or downward motion.
(i) Hence, the weight of body changes.
(ii) Considering the situation in two extreme positions, as their acceleration is maximum in magnitude.

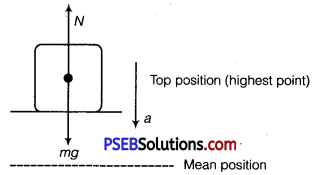
Wehave mg-N=ma
Note at the highest point, the platform is accelerating downward.
⇒ N=mg – ma

But a = ω²A (in magnitude)
∴ N = mg – mω²A
where, A = amplitude of motion
Given, m = 50 kg, frequency v = 2 s^-1
∴ ω = 2πv = 4πrad/s
A = 5cm = 5 x 10^-2 m
∴ N = 50 x 9.8 – 50 x (4π²) X 5 x 10^-2
= 50 [9.8-16π² x 5 x 10^-2]
= 50 [9.8 – 7.89] = 50 x 1.91 = 95.5N

When the platform is at the lowest position of its oscillation,

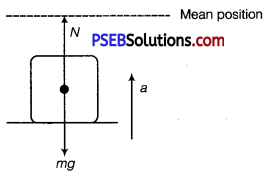
It is accelerating towards mean position that is vertically upwards. Writing the equation of motion
N – mg = ma = mω²A
or N = mg + mat2A = m [g + ω²A]
Putting the data

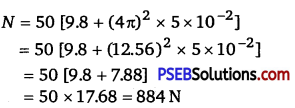
Now, the machine reads the normal reaction.
It is clear that maximum weight = 884 N (at lowest point)
minimum weight = 95.5 N (at top point)