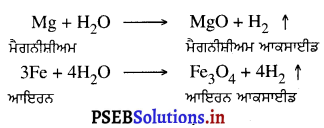
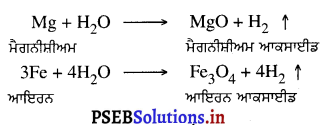
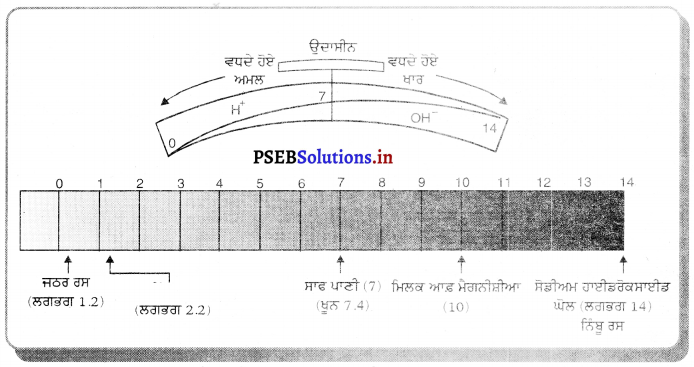
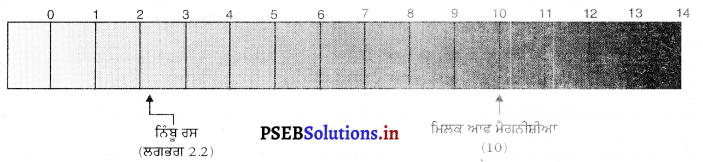
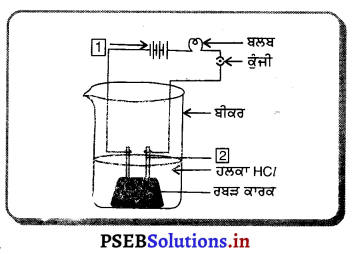
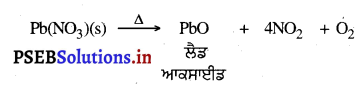
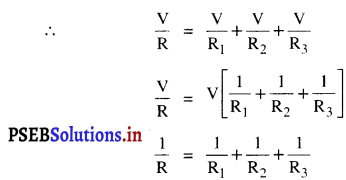
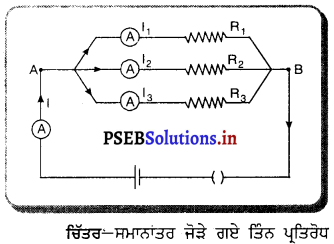
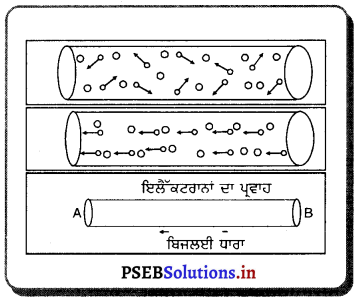
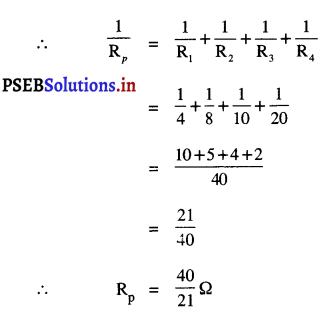
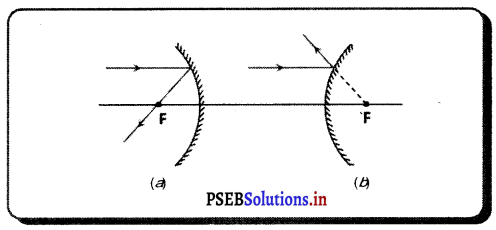
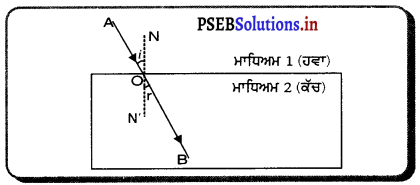
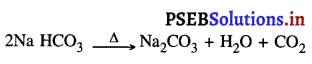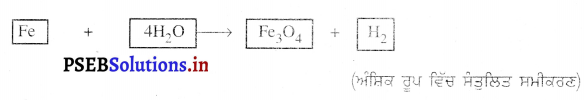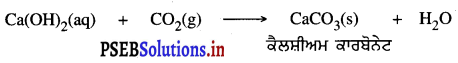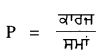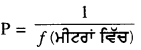Punjab State Board PSEB 9th Class Science Important Questions Chapter 1 हमारे आस-पास के पदार्थ Important Questions and Answers.
PSEB 9th Class Science Important Questions Chapter 1 हमारे आस-पास के पदार्थ
दीर्घ उत्तरात्मक प्रश्न (Long Answer Type Questions)
प्रश्न 1.
पदार्थ की विशेषताएं क्या हैं? पदार्थ की तीन अवस्थाओं के गुण संक्षेप में लिखिए।
उत्तर-
- पदार्थ स्थान घेरते हैं – वस्तु द्वारा घेरा हुआ स्थान आयतन कहलाता है। सभी वस्तुएं स्थान तो घेरती हैं, लेकिन समान रूप में नहीं घेरती हैं। कुछ वस्तुएं कम और कुछ वस्तुएं अधिक स्थान घेरती हैं; जैसे-एक पुस्तक, पैंसिल की अपेक्षा अधिक स्थान घेरती है।
- पदार्थ भार रखते हैं – सभी वस्तुओं में भार होता है, पर सभी में समान रूप से भार नहीं होता है। यह इस पर निर्भर करता है जो कि वस्तु में अणु कितनी दृढ़ता से व्यवस्थित हैं।
सभी पदार्थों को तीन अवस्थाओं में वर्गीकृत किया गया है-
ठोस (Solid) – ऐसे पदार्थ जिनकी आकृति और आयतन दोनों ही निश्चित होते हैं, ठोस कहलाते हैं; जैसे-पत्थर, लोहा आदि।
ठोस के गुण-
- ठोस का आयतन निश्चित होता है।
- ठोस की आकृति निश्चित होती है।
- से कटोर और दृढ़ होते हैं।
- ठोस बहते नहीं हैं। इनका ढेर लगाया जा सकता है।
- ठोसों को संपोड़ित नहीं किया जा सका है।
- ठोसों के अणुओं के मध्य अधिक आकर्षण बल पाया जाता है।
- ठोस में बहुत-से मुक्त पृष्ठ हो सकते हैं।
द्रव (Liquids ) – वह पदार्थ जिनका आयतन तो निश्चित होता है, परंतु आकृति निश्चित नहीं होती है तथा एक मुक्त पृष्ठ होता है, द्रव कहलाता है। उदाहरण-जल, दूध आदि।
- द्रव का आयतन निश्चित होता है।
- द्रव की आकृति निश्चित नहीं होती है। यह उसी बर्तन की आकृति ग्रहण कर लेता है जिसमें रखा जाता है।
- द्रव के रखने के लिए बर्तन की आवश्यकता होती है।
- द्रव इसका ऊपरी पृष्ठ खुला होता है।
- द्रव के अणुओं के मध्य लगने वाला आकर्षण बल, ठोसों की अपेक्षा कम होता है।
गैस (Gas) – वह पदार्थ जिसमें न तो आकृति और न ही आयतन निश्चित होता है, गैस कहलाता है। यह सरलता से संपीड़ित हो जाता है और इसका कोई मुक्त पृष्ठ नहीं होता है। उदाहरण-ऑक्सीजन, नाइट्रोजन, भाप आदि।
गैसों के गुण-
- गैसों की आकृति निश्चित नहीं होती है। ये जिस बर्तन में रखी जाती हैं, उसी का आकार ग्रहण कर लेती हैं।
- गैसों का आयतन निश्चित नहीं होता है। ये उसी बर्तन का आयतन ग्रहण कर लेती हैं, जिसमें इनको रखा जाता
- गैस को संपीड़ित किया जा सकता है।
- गैस का मुक्त पृष्ठ नहीं होता है।
- गैस के अणुओं के बीच आकर्षण बल कम होता है।
- गैस सभी दिशाओं में बह सकती है।
![]()
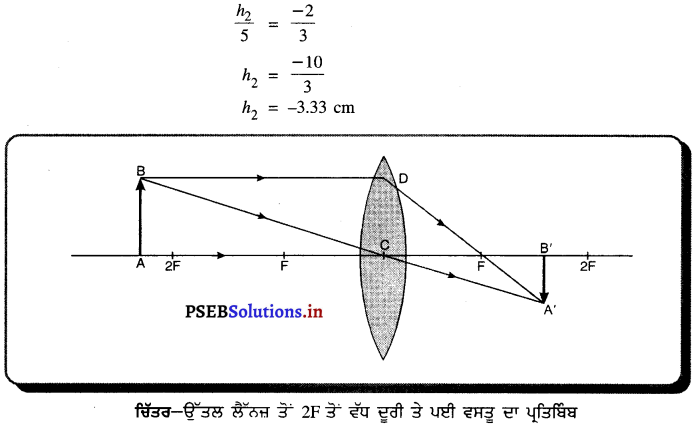
प्रश्न 2.
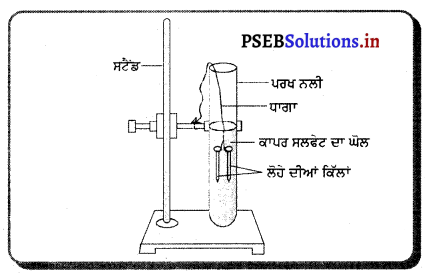
(क) प्रयोग द्वारा सिद्ध करें कि वाष्पन से ठंडक पैदा होती है।
(ख) वे उदाहरण दें जहाँ वाष्पन लाभदायक होता है।
उत्तर-
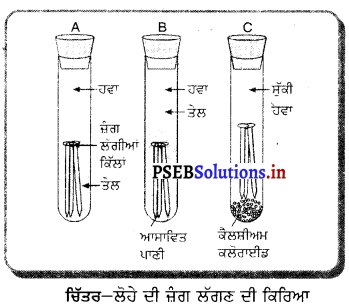
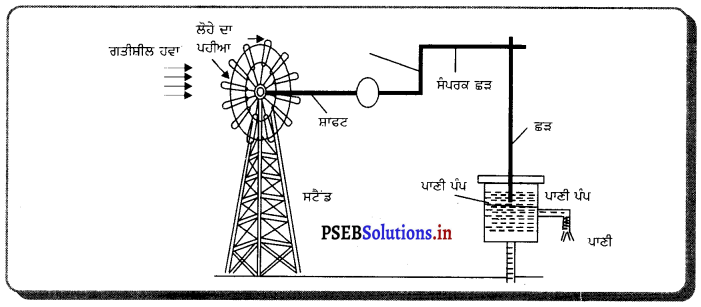
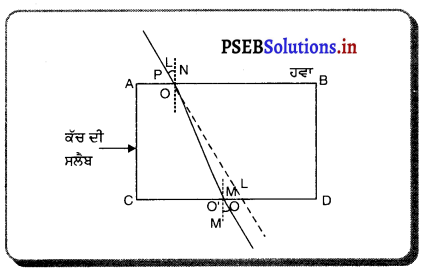
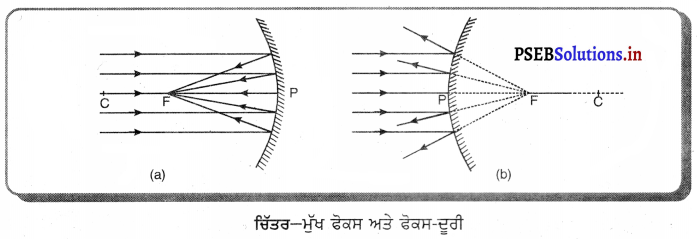
(क) प्रयोग – लकड़ी के टुकड़े पर थोड़ा-सा पानी छिड़क कर ईथर से भरे बीकर को ऊपर रख देते हैं। ईथर की वाष्पन दर बढ़ाने के लिए ईथर को फूंक मारते हैं जैसा कि चित्र में दिखाया गया है । पानी से वाष्पन की गुप्त ऊष्मा अवशोषित कर ली जाती है। यह ठंडा हो जाता है और अंत में जम जाता है तथा बर्फ बन जाता है।

(ख) वाष्पन द्वारा ठंडक पैदा करने के उदाहरण-
- गर्मियों में हम ज़मीन पर पानी छिड़कते हैं। सतह से पानी वाष्पित होता है और वाष्पन के लिए गुप्त ऊष्मा यह करने से अवशोषित करता है जिससे ज़मीन ठंडी हो जाती है।
- गर्मियों के मौसम में प्रयुक्त होने वाले वाटर कूलर (डैज़र्ट कूलर) इसी नियम पर आधारित हैं कि वाष्पन से ठंडक पैदा होती है। चटाइयों ( पंड) पर छिड़का जा रहा पानी वाष्पित होता है और ठंडक पैदा होती है।
- जब बाहर का ताप बहुत आंधक ने तो हमारे शरीर पर पसीना आता है। जैसे ही हमें पसीना आता है, वाष्पन क्रिया होती हैं और ठंडक महेंसूस होता है।
- नहाने के बाद हमारे शरीर पर स्थित पानी का वाष्पन होता है जिससे ठंडक महसूस होती है। यह ठंडक और अधिक महसूस होगी यदि हम पंखे के नीचे आ खड़े हों। पंखे की हवा वाष्पन की दर बढ़ाती है, अत: ठंडक बढ़ती है।
- चुसकी लेने से पहले चाय के गर्म कप में फूंक मारी जाती है जिससे वाष्पन में वृद्धि हो जाती है तथा ताप में कमी हो जाती है।
- गर्मियों में वृक्षों में नए पत्ते आ जाते हैं। इन पत्तों से पानी का वाष्पन काफ़ी तीव्रता से होता है। फलस्वरूप ये
- मिट्टी के बर्तनों या सुराहियों में पानी ठंडा रहता है। मिट्टी के बर्तनों की सतह पर बहुत बारीक लिद्र होते हैं। पानी इन छिद्रों में से बाहर रिसता रहता है और वाष्पित होता रहता है तथा सुराही के पानी से वाष्पन की गुप्त ऊष्णा अवशोषित कर लेता है।
- परिणामस्वरूप सुराही में पड़ा पानी ठंडा हो जाता है। (8) कई बार घड़े के गिर्द एक गोला कपड़ा रखा जाता है ताकि पानी की वाष्पन क्रिया तेज हो और यह शीघ्रता से ठंडा हो सके।
- गर्मियों में कुत्ते प्रायः अपनी जीभ बाहर निकाले रखते हैं ताकि उन्हें ठंडक महसूस हो। वे ऐसा इसलिए करते हैं क्योंकि उनकी चमड़ी से पसीना नहीं आता।
- जब नाखूनों की पॉलिश हटाने के लिए एसीटोन नामक द्रव को प्रयोग में लाते हैं तो नाखूनों के आस-पास त्वचा पर लगने से वह वहाँ से ऊष्मा को प्राप्त कर वाष्पीकृत हो जाती है जिससे ठंडक महसूस होती है।
प्रश्न 3.
क्वथन (Boiling) की परिभाषा दीजिए। यह वाष्यन से कैसे भिन्न है ?
उत्तर-
कवथन या उबाल क्रिया – जब द्रव का सतही दबाव वायुमंडलीय दबाव के बराबर हो जाता है तब द्रव अवस्था से वाष्प अवस्था में बदलने की क्रिया को उबाल क्रिया या क्वथन क्रिया कहते हैं।
पानी का क्वथनांक (Boiling point) – 100°C है। अशुद्धियाँ प्राय. क्वथनांक को कम कर देती हैं। द्रव की सतह पर दबाव में वृद्धि से उबाल दर्जे में वृद्धि होती है। यह दाब के कारण पानी (द्रव) के क्वथनांक में वृद्धि का सिद्धांत प्रेशर कुकर के निर्माण में प्रयुक्त होता है।
वाष्पन तथा क्वथन में अंतर-
| क्वथन | वाष्पन |
| (1) इस क्रिया के दौरान ताप बदलता है। | (1) इस क्रिया के दौरान ताप पूर्णतया स्थिर रहता है। |
| (2) यह सभी तापों पर होता रहता है। | (2) यह केवल क्वथनांक पर होता है। |
| (3) यह सतह पर होने वाली क्रिया है। | (3) यह द्रव के सभी कणों पर होता है। |
| (4) यह एक शांत और धीमी क्रिया है। | (4) यह तेज़ और एक ध्वनि उत्पन्न करने वाली क्रिया है। |
| (5) यह सतह के क्षेत्रफल, वायु, वेग आदि की वृद्धि से बढ़ जाती है। | (5) यह इनके परिवर्तनों के होने पर स्थिर रहता है। |
| (6) इस क्रिया में बुलबुले नहीं बनते। | (6) इस क्रिया में बुलबुले बनते हैं। |
| (7) इसमें ठंड उत्पन्न होती है। | (7) इसमें ठंड उत्पन्न नहीं होती। |
प्रश्न 4.
वाष्पीकरण को प्रभावित करने वाले कारकों का वर्णन कीजिए।
उत्तर-
पदार्थ के कण सदा गतिशील रहते हैं। निश्चित तापमान पर उसके कणों में गतिज ऊर्जा होती है। जिस कारण वाष्पीकरण होता रहता है पर निम्नलिखित कारकों से इसकी दर प्रभावित होती है-
- सतह क्षेत्र बढ़ने से – वाष्पीकरण एक सतही प्रक्रिया है। जब सतह का क्षेत्र बढ़ा दिया जाता है तो वाष्पीकरण की दर बढ़ जाती है। इसलिए किसी गिलास में डाले गए गर्म दूध की अपेक्षा प्लेट में डाला गया गर्म दूध जल्दी ठंडा हो जाता है। गीले कपड़ों को सुखाने के लिए उन्हें धूप में फैलाया जाता है।
- तापमान में वृद्धि – द्रव का तापमान जितना अधिक होगा उसका वाष्पीकरण भी उतना ही जल्दी होगा। इस से पदार्थ के कणों को पर्याप्त गतिज ऊर्जा प्राप्त होती है।
- आर्द्रता में कमी – यदि वायु में नमी की मात्रा कम हो तो वाष्पीकरण शीघ्र होता है पर वायु में नमी होने के कारण वाष्पीकरण देर से होता है। वर्षा के दिनों में गीले कपड़ों को इसी कारण सूखने में देर लगती है।
- हवा की गति में तीव्रता – तेज़ हवा में वाष्पीकरण शीघ्र होता है। हवा तेज़ होने के कारण जलवाष्प हवा के साथ उड़ जाते हैं जिस कारण आसपास के जल वाष्पों की मात्रा घट जाती है।
- पदार्थ की प्रकृति – पेट्रोल, स्पिरिट आदि ऐसे द्रव हैं जिनकी प्रकृति अधिक तेजी से वाध्वीकृत होने की है।
- दबाव में कमी – द्रवों पर दबाव कम होने से वाष्पीकरण की क्रिया अधिक तेजी से होती है।
प्रश्न 5.
ऊष्मा और तापमान में अंतर लिखिए।
उत्तर-
ऊष्मा और तापमान में अंतर-
| ऊष्या | नापमान |
| 1. यह ऊर्जा का एक रूप है। | 1. यह एक अवाया है। इससे ऊष्मा के बहने की दिशा का पता लता है। |
| 2. इसमें गर्मी या सर्दी की संवेदना का अनुभव होता है। | 2. वस्तु का गुणधर्म होने के कारण यह उभा के प्रवाह को निश्चित करता है। |
| 3. इसे कैलोरी या किलो-कैलोरी में मापते हैं। इसका यांत्रिक मात्रक जूल (J) है। | 3. इसे अंशो में मा५ है। |
| 4. यह वस्तु में ऊर्जा की मात्रा है। | 4. यह वस्तु का भौतिक है। |
| 5. इसे कैलोरीमीटर से मापते हैं। | 5. इसे तापमापी से मापत हैं। |
| 6. यह वस्तु की संहति, प्रकृति और तापक्रम पर निर्भर करती है। | 6. यह वस्तु की संहति, प्रकृति और तापक्रम पर निर्भर नहीं करता। |
| 7. यह एक कारण है। | 7. यह ऊष्मा का प्रभाव है। |
लघु उत्तरात्मक प्रश्न (Short Answer Type Questions)
प्रश्न 1.
पदार्थ किसे कहते हैं ? स्पष्ट कीजिए।
उत्तर-
पदार्थ – हमारे दैनिक जीवन में प्रयोग में लायी जाने वाली अनेक प्रकार की नस्तुएं हैं। इसका रूप, सा, गुण, आकार, उपयोग आदि अलग-अलग होते हैं पर फिर भी हमारे लिए उपयोगा हैं। नमक का पानी में घोल और चीनी का पानी में घोल देखने में एक से प्रतीत होते हैं पर दोनों एक-दूपरे से भिन्न हैं : मेला, कुम भ पानी, हवा, पेसिल, पत्थर, दूध, माँस, दालें, अनाज आदि सभी पदार्थ हैं। पदार्थ वे वस्तुएँ हैं जो स्थान घरती हैं और रखती हैं इसलिए हमारे आस-पास की सभी वस्तुएँ पदार्थ की श्रेणी में रखी जाती हैं।
![]()
प्रश्न 2.
पदार्थ का वर्गीकरण कीजिए।
उत्तर-
पदार्थ को अनेक प्रकार से वर्गीकृत किया जा सकता है। आधुनिक काल में इसका वो करण प्रायः दो आधारों पर किया जाता है-
(I) भौतिक अवस्था के आधार पर : ठोस द्रव और गैस
(II) रासायनिक संरचना के आधार पर : तत्त्व, यौगिक और मिश्रण।
प्रश्न 3.
प्रयोग द्वारा सिद्ध कीजिए कि पदार्थ कणों से बने होते हैं और कणों के बीच खाली स्थान होता
उत्तर-
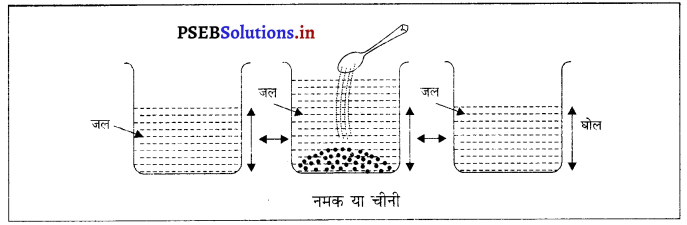
प्रयोग – एक 100 ml का बीकर लो। इसे जल से लगभग आधा भर दो और जल के स्तर पर निशान लगा दो। अब इसमें कुछ नमक या चीनी डालो और जल के स्तर को देखो। यह कुल बह गया है। नमक या चीनी को छड़ की सहायता से अच्छी तरह हिलाओ। इसके घुल जाने के पश्चात् जल का तल फिर से कम हो जाएगा।
निष्कर्ष – इससे प्रमाणित होता है कि जल के अणुओं के बाच खाली स्थान होता है। हिलाने पर नमक या चीनी के अणु उन खाली स्थानों में चले गए और जल का स्तर कम हो गया। पदार्थ कणों से बनने के कारण ही नमक या चीनी पूरी तरह जल में घुल गई।
प्रश्न 4.
प्रयोग द्वारा सिद्ध कीजिए कि पदार्थ के कण अति सूक्ष्म होते हैं ।
उत्तर-
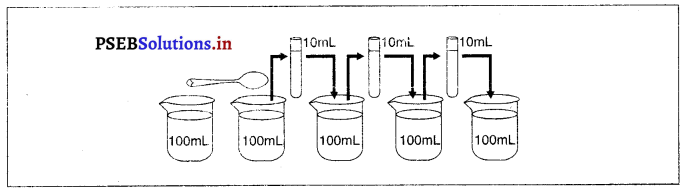
प्रयोग – पोटाशियम परमैंगनेट के दो या तीन क्रिस्टलों को 100 मि.ली० जल में घोल दें। इस घोल से परखनली में लगभग 10 मि०ली. घोल निकाल कर 90 मि०ली० साफ जल में मिला दें। फिर इस घोल से 10 मि०ली० निकाल कर उसे भी 90 मि०ली० साफ जल में मिला दें। इसी प्रकार इस घोल को 5 से 8 बार दोहराओ और घोल को तनु करते रहो । आप देखेंगे कि जल अब भी रंगीन रहेगा।
निष्कर्ष- इससे सिद्ध होता है कि पोटाशियम परमैंगनेट के केवल एक क्रिस्टल में अनेक सूक्ष्म कण होते हैं ।
प्रश्न 5.
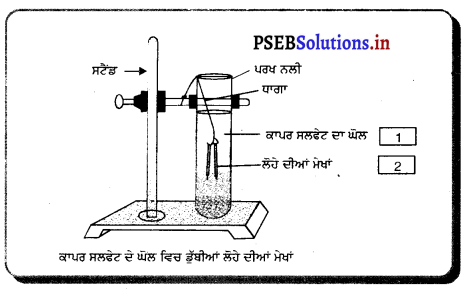
प्रयोग द्वारा ठोस, द्रव और गैसों पर दबाव का प्रभाव प्रदर्शित करना ।
उत्तर-

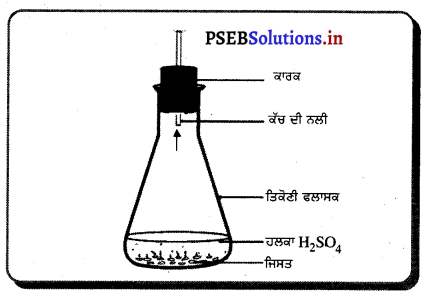
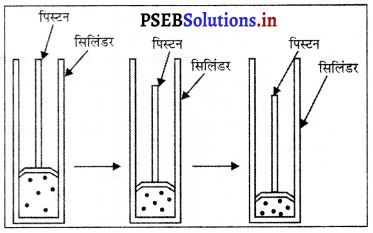
प्रयोग – 100 ml की तीन सिरिंज लेकर उनके सिरों को चित्र के अनुसार बंद कर दो। सभी सिरिंजों के पिस्टन को हटा लें। पहली सिरिंज में हवा, दूसरी में जल और तीसरी में चॉक के टुकड़े भर दें। सिरिंज के पिस्टन की गतिशीलता आसान बनाने के लिए उस पर थोड़ी वैसलीन लगा दें और उसे वापस सिरिंज में लगाएं। अब पिस्टन को संपीडित करने का प्रयत्न करें।
पिस्टन वायु से भरी सिरिंज में आसानी से गति करता है पर पानी से भरी सिरिंज में पिस्टन बहुत थोड़ी गति करता है। चॉक के टुकड़ों पर संपीडन बिल्कुल नहीं होता।
निष्कर्ष – गैसें सबसे अधिक संपीड्य होती हैं। द्रवों को अधिक नहीं दबाया जा सकता पर ठोस पर दबाव का प्रभाव नहीं पड़ता। गैसें सबसे अधिक संपीड्य होती हैं।
प्रश्न 6.
पदार्थ का भौतिक अवस्था के आधार पर वर्गीकरण कीजिए।
उत्तर-
विश्व की विभिन्न वस्तुओं को भौतिक आधार पर ठोस, तरल और गैस नामक तीन अवस्थाओं में वर्गीकृत किया जा सकता है।
ठोस – ठोस का निश्चित रूप और आकार होता है तथा इसका निश्चित घनफल होता है। प्रायः ये कठोर होते हैं और इन पर दबाव नहीं डाला जा सकता। उदाहरण-लकड़ी, पत्थर, चीनी, नमक।
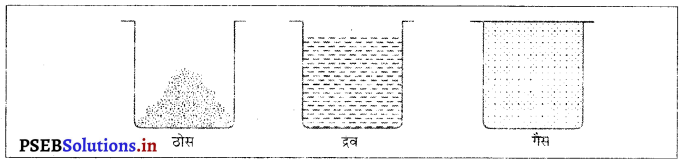
द्रव – तरल का निश्चित आकार नहीं होता पर निश्चित घनफल अवश्य होता है। ये उसी बर्तन का आकार ले लेते हैं जिसमें इन्हें डाला जाता है। इनमें बहने की प्रवृत्ति होती है। इसलिए इन्हें द्रव भी कहते हैं । उदाहरण पानी, दूध, तेल, एल्कोहल।
गैस – गैस का न तो निश्चित आकार होता है और न ही निश्चित घनफल। इस पर दबाव डाला जा सकता है। यह उस बर्तन में पूर्ण रूप से फैल कर उसी का रूप ले लेती है जिसमें इसे डाला जाता है। उदाहरण-ऑक्सीजन, हाइड्रोजन, वायु, कार्बन डाइऑक्साइड।
![]()
प्रश्न 7.
ठोस, द्रव और गैस की स्थिति अंतरा आण्विक बल के आधार पर स्पष्ट कीजिए।
उत्तर-
प्रत्येक पदार्थ अति छोटे कणों से बनता है। ये कण स्थिर न हो कर लगातार गतिशील रहते हैं। ऊष्मा ऊर्जा से इनकी गतिज ऊर्जा बढ़ जाती है। ये एक-दूसरे पर आकर्षण बल लगाते हैं जिसे अंतरा आण्विक बल कहते हैं । इनके आधार पर ठोस, द्रव, गैस की स्थिति की व्याख्या की जा सकती है।
ठोस – इनमें कण एक-दूसरे के बहुत निकट होते हैं और कणों के बीच बहुत कम रिक्त स्थान होता है । इनके बीच आकर्षण बल बहुत अधिक होता है और वे केवल घूर्णन गति कर सकते हैं । इसलिए उनका निश्चित आकार और घनफल होता है।
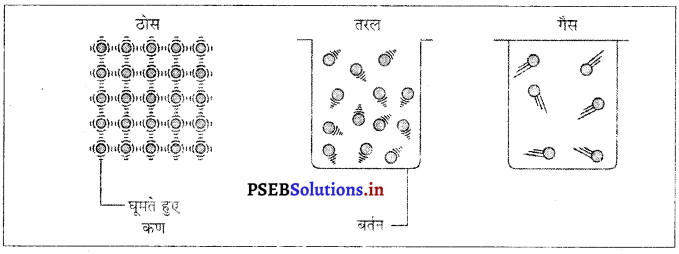
द्रव – इनमें कण एक-दूसरे से दूर-दूर होते हैं और कणों के बीच पर्याप्त रिक्त स्थान होता है जिसके परिणामस्वरूप इनमें आकर्षण बल अपेक्षाकृत कमजोर होता है पर यह इतना कमजोर नहीं होता कि कण एक-दूसरे से अलग हो जाएं। इसीलिए द्रव पदार्थों का निश्चित आकार नहीं होता पर उनका निश्चित घनफल होता है। वे उस बर्तन का आकार ग्रहण कर लेते हैं जिसमें डाले जाते हैं।
गैस – गैसों में कणों की स्थिति बहुत ढीली होती है और उन के बीच रिक्त स्थान बहुत अधिक होते हैं। उन के बीच आकर्षण बल न के बराबर ही होता है और तीव्र वेग से सभी दिशाओं में इधर-उधर गति कर सकते हैं। इसीलिए गैस का न तो निश्चित आकार होता है और न ही निश्चित घनफल। इनके कणों में बड़े रिक्त स्थानों के कारण उन्हें दबाया जा सकता है और वे बर्तन की दीवारों पर दबाव डाल सकती हैं।
प्रश्न 8.
अवस्था परिवर्तन से आप क्या समझते हैं ? स्पष्ट कीजिए।
उत्तर-
तापमान और दबाव पर निर्भर कर कोई पदार्थ ठोस, तरल और गैस अवस्थाओं को प्राप्त कर सकता है जिसे अवस्था परिवर्तन कहते हैं। यदि किसी वस्तु का द्रवणांक सामान्य तापमान से अधिक हो तो वह ठोस कहलाती है और यदि उसका क्वथनांक सामान्य तापमान से अधिक हो तो वह द्रव कहलाती है। सामान्य दबाव पर यदि क्वथनांक कम हो तो उसे गैस कहते हैं। तापमान और दबाव में परिवर्तन से किसी पदार्थ को ठोस, तरल और गैस अवस्थाएं दी जा सकती

हैं। बर्फ को गर्म करने से वह द्रव में और द्रव को गर्म करने से वाष्प में बदला जा सकता है। वाष्प को ठंडा करने से द्रव और द्रव को ठंडा करने से उसे ठोस में बदला जा सकता है।

प्रश्न 9.
एक प्रयोग द्वारा सिद्ध कीजिए कि तापमान के परिवर्तन से पदार्थ की अवस्था में परिवर्तन होता
उत्तर-
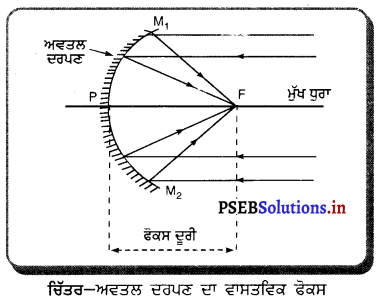
प्रयोग – एक बीकर में लगभग 150 ग्राम बर्फ का टुकड़ा लें और उसे स्टैंड पर इस प्रकार रखें कि थर्मामीटर का बल्ब उसको स्पर्श करे। चित्रानुसार उपकरण को लगाएं। बीकर को धीमी आंच पर गर्म करें।
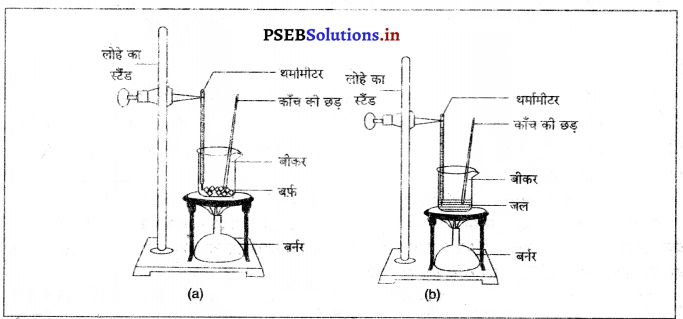
जब बर्फ पिघलने लगे तो तापमान नोट करो। जब पूरी बर्फ जल में परिवर्तित हो जाए तो फिर तापमान नोट करो। जब जल उबलने लगे और भाप बनने लगे तब तापमान को नोट करो।
निष्कर्ष – बर्फ 0°C पर पिघलती है। जब सारी बर्फ पिघल कर पानी में बदल जाती है तब भी उसका तापमान 0°C होता है। जल की द्रव अवस्था से गैसीय अवस्था में परिवर्तन 100°C पर होता है।
प्रश्न 10.
पदार्थ की अवस्था पर ताप और दाब का क्या प्रभाव पड़ता है ? स्पष्ट करो।
उत्तर-
ताप और दाब का पदार्थ की अवस्था पर प्रभाव पड़ता है। जब किसी ठोस को गर्म किया जाता है तो उस के कणों की गतिज ऊर्जा बढ़ जाती है। वे तेजी से कंपन करते हैं और अधिक स्थान ग्रहण करते हैं और वे फैलने लगते हैं। एक निश्चित तापमान पर वे आकर्षण के बंधन से मुक्त हो स्वतंत्रतापूर्वक घूमने लगते हैं। तब उसके अणुओं की गति नहीं बढ़ती और उनका व्यवस्था और क्रम में परिवर्तन होने लगता है तब वे तरल अवस्था में बदल जाते हैं । तल को गर्म करने से अणुओं का वेग बढ़ जाता है। उनकी गतिज ऊर्जा बढ़ जाती है। तेज़ गति वाले अणुओं का सवेग जब उन पर भीतर की तरफ लग रहे बल से अधिक बढ़ जाता है तो वे वाष्प अवस्था में बदल जाते हैं और तरल की सतह से बाहर निकल आते हैं।
![]()
प्रश्न 11.
जल और एल्कोहल के निश्चित आयतन को परस्पर मिलाने पर मिश्रण का आयतन प्रारंभ में लिए गए जल और एल्कोहल के योग से कम हो जाता है। क्यों ? स्पष्ट कीजिए।
उत्तर-
काँच की एक नली के आधे भाग में जल भरो। इस के शेष आधे भाग को एथिल एल्कोहल से भर दो। इसे अच्छी तरह से हिलाओ। नली में कुछ रिक्त स्थान दिखाई देगा। कुछ समय बाद इसे फिर देखो। मिश्रण का आयतन प्रारंभ में लिए गए जल और एल्कोहल के आयतन के योग से कुछ कम दिखाई देगा क्योंकि एल्कोहल के कण जल के अंतरा-अणुक अवकाश के मध्य समायोजित हो जाते हैं।
प्रश्न 12.
ठोस, द्रव तथा गैस में अंतर स्पष्ट कीजिए।
उत्तर-
ठोस, द्रव तथा गैस में अंतर-
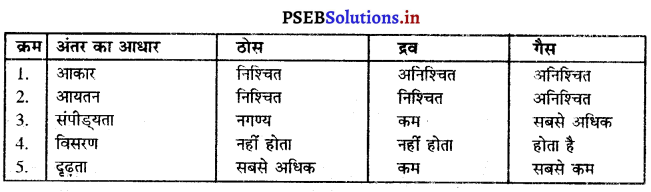
प्रश्न 13.
शीतलन के लिए 0°C के पानी की अपेक्षा 0°C की बर्फ़ अधिक प्रभावी क्यों होती है ?
उत्तर-
0°C ताप की बर्फ °C के पानी की अपेक्षा ठंडा करने में अधिक प्रभावपूर्ण होती है क्योंकि वह 0°C के पानी में बदलने के लिए अपनी गलन की गुप्त ऊष्मा के बराबर ऊष्मा लेती है और फिर ताप वृद्धि के लिए ऊष्मा प्राप्त करती है जबकि 0°C तापमान का पानी केवल ताप में वृद्धि के लिए ही ऊष्मा को प्राप्त करता है।
प्रश्न 14.
दाँतों को आइसक्रीम बर्फ के जल की अपेक्षा अधिक ठंडी क्यों प्रतीत होती है ?
उत्तर-
आइसक्रीम को पिघलने के लिए गलन की गुप्त ऊष्मा की आवश्यकता होती है जो दाँतों से अवशोषित की जाती है। इस गुप्त ऊष्मा का मान अधिक होता है जिसके परिणामस्वरूप दाँतों को आइसक्रीम बर्फ के जल की अपेक्षा अधिक ठंडी प्रतीत होती है।
प्रश्न 15.
बर्फ गलन की गुप्त ऊष्मा क्या है ? इसका क्या अर्थ है ?
उत्तर-
बर्फ गलन की गुप्त ऊष्मा 3.34 × 105 J/kg (या 80 cal/g) है। इसका अर्थ यह है कि 0°C पर 1 kg बर्फ 3.34 × 105 जूल ऊष्मा अवशोषित करके 0°C पर 1 kg पानी में बदलती है या 1 kg पानी 0°C पर 3.34 × 105 जूल ऊष्मा विसर्जित करके 0°C पर बर्फ में बदल जाता है।
![]()
प्रश्न 16.
भाप के वाष्पन की गुप्त ऊष्मा क्या है ? इसका क्या अर्थ है ?
उत्तर-
भाप के वाष्पन की गुप्त ऊष्मा 22.5 × 105 J/kg (या 540 cal/g) है। इसका अर्थ यह है कि 100° पर 1kg पानी 22.5 × 105 जूल ऊष्मा अवशोषित करके 100°C ताप वाली भाप में बदल जाता है या 100°C पर 1 kg भाप 22.5 × 105 जूल ऊष्मा विसर्जित करके 100°C ताप वाले पानी में बदल जाती है।
प्रश्न 17.
उबलते पानी और उसी ताप की भाप में से, किससे जलन अधिक कष्टकर होती है ? कारण स्पष्ट कीजिए।
उत्तर-
भाप सदा ही उबलते पानी से अधिक गंभीर जलन उत्पन्न करती है। जब पानी 100°C तापमान पर उबलता है तो 100°C वाष्प में परिवर्तित होता है। उसे 536 कैलोरी / ग्राम या 2260 जूल / ग्राम ऊष्मा की आवश्यकता होती है जिसे गुप्त ऊष्मा कहते हैं । इसीलिए उबलते पानी से भाप में ऊष्मा अधिक होती है क्योंकि उसमें गुप्त ऊष्मा भी सम्मिलित होती है। इसी कारण वह अधिक गंभीर जलन उत्पन्न करती है।
प्रश्न 18.
जब मोटे कांच से बने गिलास में उबलता हुआ पानी ( या बर्फ ) डाल दिया जाता है तो यह तिड़क क्यों जाता है ?
उत्तर-
जब मोटे कांच से बने गिलास में उबलता हुआ पानी डाला जाता है तो ताप वृद्धि के कारण गिलास का आंतरिक भाग फैल जाता है। क्योंकि कांच ऊष्मा का कम चालक है इसलिए बाहर बहुत कम ऊष्मा आती है। बाहरी सतह से कांच बहुत कम फैलता है। इसी कारण गिलास तिड़क जाता है।
प्रश्न 19.
ठोस प्रसार की कुछ हानियां बताओ।
उत्तर-
ठोस प्रसार की कुछ हानियां-
- जब कांच के गिलास में गर्म पानी डाला जाता है तो यह तिड़क जाता है ।
- इस प्रसार के कारण रेल की पटरियां टेढ़ी हो सकती हैं तथा गाड़ियां उलट सकती हैं।
- कंकरीट या अन्य सामान्य फ़र्श तिड़क सकते हैं।
- भाप या गर्म पानी से पानी की पाइपें मुड़ सकती हैं।
- गर्मियों में लंबी तारें बिछाई जाती हैं ताकि सर्दियों में सिकुड़ने की क्रिया को पूरा किया जा सके।
- इस्पात से बने पुल फैल कर सहारे की दीवारें तोड़ सकते हैं।
- घड़ियां गर्मियों में पीछे और सर्दियों में आगे जा सकती हैं।
प्रश्न 20.
जब बहुत गर्म चाय कांच के गिलास में डाली जाती है तो यह तिड़क क्यों जाता है ?
उत्तर-
गर्म पानी या चाय डालने पर मोटा कांच का गिलास तिड़क जाता है । गर्म द्रव गिलास के आंतरिक भाग को बाहरी तल से पहले प्रसारित कर देता है। इस तरह उत्पन्न तनाव कांच के लिए इतना अधिक होता है जो इसके लिए असहनीय हो जाता है और गिलास तिड़क जाता है।
प्रश्न 21.
रेल की दो पटरियों के बीच प्रसार के लिए खाली स्थान रखा जाता है, क्यों ? व्याख्या करो।
उत्तर-
गर्मियों में रेल पटरियां गर्म होकर फैलती हैं। यदि प्रसार के लिए खाली स्थान न रखा जाए तो यह मुड़ सकती हैं तथा रेल पटरी से उतर सकती है। इसलिए दो पटरियों के बीच खाली स्थान छोड़ा जाता है. ताकि इन्हें प्रसार के लिए स्थान मिल सके।
![]()
प्रश्न 22.
जब तालाब जम जाते हैं, तो भी मछलियां कैसे जीवित रहती हैं ? ।
उत्तर-
पानी के असंगत प्रसार के कारण बहुत कड़ाके की सर्द में भी झीलों और तालाबों के पानी की ऊपरी सतह ही जमती है। ऊपर जमी बर्फ के नीचे का पानी नहीं जमता । परिणामस्वरूप मछलियां तथा अन्य जल जीव जीवित रहते हैं। यदि पानी का प्रसार एक जैसा होता है तो झीलों और तालाबों का सारे का सारा पानी जम जाता है तो जल जीवों तथा जल-वनस्पति का बचना असंभव होता।
प्रश्न 23.
किसी धात्वीय बर्तन की अपेक्षा सुराही में रखा पानी अधिक ठंडा क्यों होता है ?
उत्तर-
सुराही के छिद्रों में से पानी बाहर आ जाता है जो निरंतर इसकी सतह से वाष्पित होता रहता है। वाष्पन के लिए अभीष्ट ऊष्मा सुराही के अंदर पड़े पानी से ली जाती है। इस ऊष्मा हानि के कारण पानी ठंडा हो जाता है।
प्रश्न 24.
‘पदार्थ की गुप्त ऊष्मा’ की परिभाषा लिखो।
उत्तर-
गुप्त ऊष्मा की वह मात्रा है जो किसी पदार्थ द्वारा ठोस से द्रव या द्रव से गैस (वाष्प) अवस्था परिवर्तित करते समय बिना किसी ताप वृद्धि के अवशोषित की जाती है।
प्रश्न 25.
गलन की गुप्त ऊष्मा तथा वाष्यन की गुप्त ऊष्मा की परिभाषा दें।
उत्तर-
गलन की ऊष्मा – बिना ताप परिवर्तित किए किसी पदार्थ के इकाई पुंज द्वारा ठोस अवस्था से द्रव अवस्था में बदलते समय अवशोषित ऊष्मा की मात्रा को उस पदार्थ की गलन ऊष्मा कहते हैं।
वाष्पन की गुप्त ऊष्मा-बिना ताप परिवर्तित किए किसी पदार्थ के इकाई पुंज द्वारा द्रव अवस्था से गैस अवस्था में बदलते समय अवशोषित ऊष्मा की मात्रा को उस पदार्थ की वाष्पन की गुप्त ऊष्मा कहते हैं।
प्रश्न 26.
गर्मियों में कभी-कभी सोडा वाटर की बोतलें फट जाती हैं क्यों?
उत्तर-
गर्मियों में वायुमंडल का ताप बढ़ने से सोडा-वाटर में भरी गैस का दाब गर्म होने से बढ़ जाता है जिसके कारण कभी-कभी सोडा वाटर की बोतलें फट जाती हैं।
![]()
प्रश्न 27.
नहाने के तुरंत बाद हमें ठंड क्यों महसूस होती है ?
उत्तर-
नहाने के तुरंत बाद शरीर पर पानी की कुछ बूंदें रह जाती हैं। इन बूंदों का वाष्पीकरण होता है। वाष्पीकरण के लिए आवश्यक ऊष्मा हमारे शरीर से ले ली जाती है जिसके कारण हमें ठंड महसूस होती है।
प्रश्न 28.
गर्मियों में सड़कों पर छिड़काव क्यों किया जाता है?
उत्तर-
वाष्पन से ठंडक उत्पन्न होती है। सड़कों पर किए गए छिड़काव के कारण वाष्पन क्रिया तीव्र होती है। वाष्पण के लिए जो ऊष्मा की आवश्यकता होती है वह सड़क से ली जाती है जिस कारण सड़कें ठंडी हो जाती हैं।
प्रश्न 29.
किस प्रकार सिद्ध करोगे कि पदार्थ के कण निरंतर गतिशील होते हैं ?
उत्तर-
जलती हुई अगरबत्ती की सुगंध पदार्थ के कणों के गतिशील होने के कारण दूर से अनुभव की जा सकती है। गर्म खाने की महक दूर से अनुभव की जा सकती है। रबड़ को लगी आग को बहुत दूर से जाना जा सकता है। इत्र की गंध पदार्थ के कणों के गतिशील होने के कारण ही दूर तक फैल जाती है।
प्रश्न 30.
ठोस का ठोस में विसरण क्या है ? स्पष्ट कीजिए।
उत्तर-
दो धातु के टुकड़ों को कसकर बाँधकर कुछ वर्षों तक रख देने से कभी-कभी एक धातु के कण दूसरे में विसरित हो जाते हैं। इसे ठोस में ठोस का विसरण कहते हैं। ठोस के कण अपने स्थान से ज़्यादा गति नहीं करते। वे अपने माध्य स्थान पर ही दोलन करते हैं। इसलिए ठोस पदार्थों में दूसरे ठोस पदार्थ में विसरित होने के गुण प्रायः नहीं होते।
प्रश्न 31.
गैसों में संपीड्यता के अधिक होने के तीन उपयोग लिखिए।
उत्तर-
- द्रवीकृत पेट्रोलियम गैस (LPG) को सिलिंडरों में भरा जाता है ताकि ईंधन के रूप में प्रयुक्त की जा सके।
- अस्पतालों में रोगियों को दी जाने वाली ऑक्सीजन गैस सिलिंडरों में संपीडित की जाती है।
- प्राकृतिक गैस (CNG) का वाहनों में प्रयोग इसी गुण के आधार पर किया जाता है।
प्रश्न 32.
गर्म करने पर ठोसों की अवस्था में परिवर्तन लिखिए।
उत्तर-
ठोस को गर्म करने पर उसके अणुओं की कंपन गति बढ़ती है। गतिज ऊर्जा बढ़ने के साथ अंतर आण्विक बल कम होने लगता है। एक निश्चित ताप पर अणुओं के कंपन का आयाम इतना बढ़ जाता है कि वे आकर्षण के बंधन से मुक्त होकर स्वतंत्रतापूर्वक घूमने लगते हैं। एक निश्चित ताप के पहुँचने पर ठोस के अणुओं की गतिज ऊर्जा नहीं बढ़ती है, बल्कि उनकी व्यवस्था तथा क्रम में परिवर्तन होने लगता है। अत: ठोस द्रव में परिवर्तित होने लगता है।
![]()
प्रश्न 33.
गर्म करने पर द्रव की अवस्था में परिवर्तन लिखिए।
उत्तर-
द्रव को गर्म करने पर उसके अणुओं की गतिज ऊर्जा काफ़ी बढ़ जाती है, और अणु एक-दूसरे से काफ़ी दूर होते जाते हैं। ऐसे अणु जिनकी गतिज ऊर्जा बहुत अधिक होती है, द्रव की सतह पर आने पर सतह को छोड़कर वायुमंडल में चले जाते हैं। इस प्रकार अणुओं के बीच अंतरा अणुक आकर्षण बल नहीं के बराबर हो जाता है और द्रव वाष्प में निरंतर परिवर्तित होने लगता है।
प्रश्न 34.
द्रव के ठंडा होने की अवस्था में परिवर्तन लिखिए।
उत्तर-
जब किसी द्रव को ठंडा किया जाता है तो इसके अणु ऊष्मीय ऊर्जा खो देते हैं। इससे उनकी गति धीमी हो जाती है। गति धीमी होने से अंतराअणुक बल बढ़ जाते हैं। यह तब तक चलता रहता है, जब तक कि अंतराअणुक बल, कंपन करते हुए अणुओं की ऊर्जा से अधिक नहीं हो जाते। इस प्रकार अणु एक स्थिति में रहते हैं। इस समय द्रव, ठोस अवस्था में परिवर्तित होता है।

प्रश्न 35.
गैस के ठंडा होने पर अवस्था परिवर्तन लिखिए।
उत्तर-
जब गैस को ठंडा किया जाता है, इसके अणु ऊष्मा ऊर्जा को खो देते हैं। इससे अणुओं की गति धीमी हो जाती है। यह तब तक चलता रहता है, जब तक कि गैस के अणुओं की ऊर्जा, अंतराअणुक बलों से कम नहीं हो जाती है। इस प्रकार, अणु एक-दूसरे से जुड़ जाते हैं और निर्बल अंतराअणुक बलों द्वारा बँधे रहते हैं। इसीलिए गैस, द्रव अवस्था में परिवर्तित हो जाती है।
प्रश्न 36.
पदार्थ की तीन अवस्थाओं में परिवर्तन को रेखाचित्र की सहायता से प्रदर्शित कीजिए।
उत्तर-
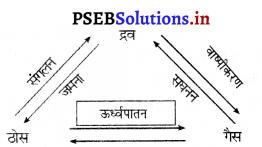
प्रश्न 37.
ऊर्ध्वपातन विधि का वर्णन कीजिए।
उत्तर-
ऊर्ध्वपातन विधि में ठोस को गर्म कर सीधा वाष्प में या वाष्प को सीधा ठोस में बदला जाता है। इस प्रक्रिया में द्रव नहीं बनता।
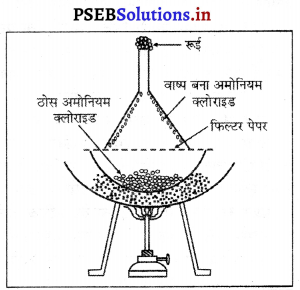

इस विधि से अमोनियम क्लोर इड, नैप्थालीन, आयोडीन, कपूर आदि को सरलता से प्राप्त कर लिया जाता है।
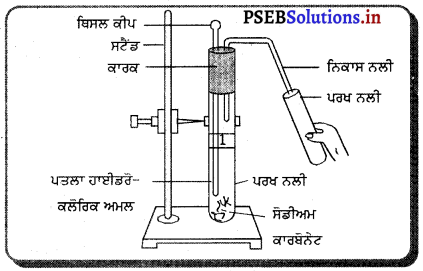
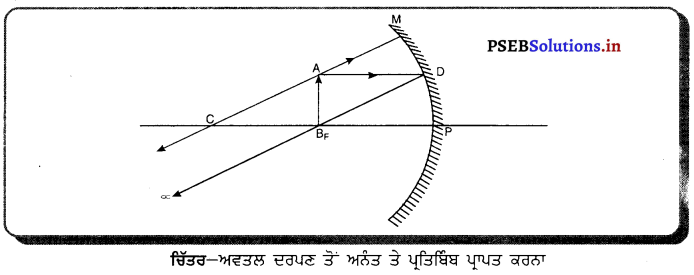
चीनी की प्याली में थोड़ा कपूर या अमोनियम क्लोराइड लें। इस पर फिल्टर पेपर रख कर उस पर उल्टा कीप रखें। कीप के सिरे पर रूई का एक टुकड़ा रख दें। गर्म करने पर वाष्प बना कपूर या अमोनियम क्लोराइड प्राप्त हो जाएगा।
![]()
प्रश्न 38.
बर्फीले पानी से भरे गिलास की बाहरी सतह पर पानी की बूंदें क्यों दिखाई देती हैं?
उत्तर-
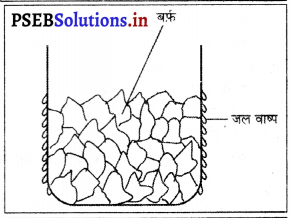
किसी बर्तन में हम बर्फीला पानी रखते हैं। जल्दी ही बर्तन की बाहरी सतह पर हमें पानी की बूंदें नज़र आने लगेंगी। वायु में उपस्थित जल वाष्प की ऊर्जा ठंडे पानी के संपर्क में आकर कम हो जाती है और यह द्रव अवस्था में बदल जाता है, जो हमें पानी की बूंदों के रूप में नज़र आता है।
प्रश्न 39.
दाब बढ़ाने से किसी द्रव पर क्या प्रभाव पड़ता है ?
उत्तर-
पदार्थ की विभिन्न अवस्थाएं घटक कणों के बीच की दूरी में अंतर के कारण होती हैं। दाब बढ़ाने से पदार्थों के कणों को समीप लाया जा सकता है। ताप में कमी करके इससे गैस को द्रव अवस्था में बदला जा सकता है।
प्रश्न 40.
प्लाज्मा क्या है ? ये कहाँ-कहाँ देखा जा सकता है ?
उत्तर-
प्लाज्मा पदार्थ की एक अवस्था है जिसमें कण आयनीकृत गैस के रूप में होते हैं। ये अत्यधिक ऊर्जावान और उत्तेजित होते हैं । इसे अग्रलिखित में देखा जा सकता है-
- लोटसेंट ट्यूब और नियॉन बल्ब में।
- सूर्य और तारों की चमक में।
प्रश्न 41.
प्लाज्मा भिन्न रंगों को प्रकट क्यों करता है ?
उत्तर-
विशेष प्रकार की गैसों में विद्युत् ऊर्जा प्रवाहित करने पर गैसें आयनीकृत हो जाती हैं। गैस के स्वभाव के अनुसार विशेष रंग की चमक उत्पन्न होती है।
प्रश्न 42.
बोस आइंस्टाइन कंडनसेट से क्या तात्पर्य है ?
उत्तर-
एक भारतीय वैज्ञानिक सत्येंद्रनाथ बोस ने सन् 1920 में पदार्थ की पाँचवीं अवस्था के लिए कुछ गणनाएँ की थीं। उनके आधार पर अल्बर्ट आइंस्टीन ने पदार्थ की एक नई अवस्था की भविष्यवाणी की थी। इसी को बोस आइंस्टाइन कंडनसेट (BEC) कहा जाता है। बाद में अमेरिका के तीन वैज्ञानिकों एरिक ए कॉर्नेल, उल्फगैंग केटरले और कार्ल ई वेमैन ने BEC की अवस्था प्राप्त करने पर नोबेल पुरस्कार प्राप्त किया था।
प्रश्न 43.
BEC किस प्रकार तैयार किया जाता है ?
उत्तर-
सामान्य वायु के घनत्व के एक लाखवें हिस्से से कम घनत्व वाली गैस को अत्यधिक कम तापमान पर ठंडा करने से BEC तैयार किया जाता है।
अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
हमारे चारों ओर की वस्तुएं किस कारण भिन्न दिखाई देती हैं ?
उत्तर-
आकार, आकृति और बनावट में भिन्नता के कारण वे भिन्न दिखाई देती हैं।
![]()
प्रश्न 2.
पदार्थ किसे कहते हैं ?
उत्तर-
विश्व की हर वस्तु जिस भी सामग्री से बनती है, जो स्थान घेरती है और जिसका द्रव्यमान होता है, उसे पदार्थ कहते हैं।
प्रश्न 3.
पदार्थ के पाँच उदाहरण दीजिए।
उत्तर-
हवा, भोजन, पत्थर, जल, पौधे।
प्रश्न 4.
पंचतत्व किसे कहते हैं ?
उत्तर-
हमारे देश के प्राचीन दार्शनिकों ने सभी वस्तुओं को बनाने वाले पदार्थ को पाँच मूल तत्वों में वगीकृत किया था जिन्हें पंचतत्व कहते हैं।
प्रश्न 5.
पंचतत्व कौन-कौन से हैं ?
उत्तर-
वायु, पृथ्वी, अग्नि, जल और आकाश।
प्रश्न 6.
यूनानी दार्शनिक कितने तत्वों का मूल मानते थे ?
उत्तर-
चार।
![]()
प्रश्न 7.
यूनानी दार्शनिकों के द्वारा स्वीकार किए जाने वाले चार मूल तत्वों के नाम लिखिए।
उत्तर-
पृथ्वी, अग्नि, वायु और जल।
प्रश्न 8.
आधुनिक वैज्ञानिक पदार्थ को किस आधार पर वर्गीकृत करते हैं ?
उत्तर-
भौतिक गुणधर्म और रासायनिक प्रकृति।
प्रश्न 9.
पदार्थ किससे बनते हैं ?
उत्तर-
पदार्थ कणों से मिलकर बनते हैं।
प्रश्न 10.
पोटेशियम परमैंगनेट के बहुत थोड़े क्रिस्टलों से भी जल रंगीन क्यों हो जाता है ?
उत्तर-
पोटेशियम परमैंगनेट के केवल एक क्रिस्टल में अनेक सूक्ष्म कण होते हैं।
प्रश्न 11.
पदार्थ के कण कितने छोटे हो सकते हैं ?
उत्तर-
पदार्थ के कण इतने छोटे हो सकते हैं कि उनकी कल्पना भी हम नहीं कर सकते।
प्रश्न 12.
पदार्थ के कणों के बीच में क्या होता है ?
उत्तर-
पदार्थ के कणों के बीच रिक्त स्थान होता है।
![]()
प्रश्न 13.
नमक, चीनी, डेटॉल आदि पानी में क्यों घुल जाते हैं ?
उत्तर-
पदार्थों के कणों के बीच पर्याप्त रिक्त स्थान होने के कारण।
प्रश्न 14.
अगरबत्ती की सुगंध दूर तक किस कारण से फैल जाती है ?
उत्तर-
पदार्थ के कणों के निरंतर गतिशील होने के कारण।
प्रश्न 15.
नमक पानी में क्यों घुल जाता है ?
उत्तर-
जब नमक को पानी में घोलते हैं तो नमक के कण पानी के कणों के बीच रिक्त स्थानों में समावेशित हो जाते हैं।
प्रश्न 16.
पानी में शहद की शुद्धता किस प्रकार परखी जा सकती है ?
उत्तर-
यदि पानी में शहद एक वर्ण रेखा के रूप में गिरता है तो वह शुद्ध माना जाता है।
प्रश्न 17.
तापमान बढ़ाने से कणों पर क्या प्रभाव पड़ता है ?
उत्तर-
उनकी गतिज ऊर्जा बढ़ जाती है।
![]()
प्रश्न 18.
पदार्थ के कण निरंतर गतिशील किस कारण रहते हैं ?
उत्तर-
गतिज ऊर्जा के कारण।
प्रश्न 19.
विसरण किसे कहते हैं ?
उत्तर-
दो विभिन्न पदार्थों के कणों का स्वत: मिलना विसरण कहलाता है।
प्रश्न 20.
गर्म करने पर विसरण पर क्या प्रभाव पड़ता है ?
उत्तर-
गर्म करने पर विसरण तेज़ हो जाता है।
प्रश्न 21.
पदार्थ के कणों पर बल क्या प्रभाव डालता है ?
उत्तर-
यह बल कणों को एक साथ रखता है।
प्रश्न 22.
भौतिक अवस्था के आधार पर पदार्थ की अवस्थाएं कौन-कौन-सी हैं ?
उत्तर-
ठोस, द्रव और गैस।
प्रश्न 23.
ठोस पदार्थों के तीन गुण लिखिए।
उत्तर-
ठोस पदार्थों का निश्चित आकार, स्पष्ट सीमाएँ और स्थिर आयतन होता है।
प्रश्न 24.
बल लगाने से ठोस पदार्थों पर क्या प्रभाव पड़ता है ?
उत्तर-
बल लगाने से भी ठोस पदार्थ अपना आकार बनाए रखते हैं। अधिक बल लगाने से वे टूट सकते हैं पर अपना आकार नहीं बदलते।
प्रश्न 25.
रबड़ को खींच कर इसका आकार बदला जा सकता है तो फिर यह ठोस क्यों है ?
उत्तर-
रबड़ पर बल लगाने से यह अपना आकार बदलता है पर बल हटा लेने से यह पुनः अपने मूल आकार को प्राप्त कर लेता है। अत्यधिक बल लगाने पर यह टूट जाता है। इसलिए यह ठोस है।
![]()
प्रश्न 26.
चीनी, नमक, शक्कर आदि को जिन बर्तनों में रखते हैं, ये उन्हीं बर्तनों का आकार ले लेते हैं पर फिर भी ये ठोस क्यों कहलाते हैं ?
उत्तर-
चीनी, नमक, शक्कर आदि को जिन बर्तनों में रखते हैं, ये उन्हीं का आकार ले लेते हैं। पर फिर भी ये ठोस हैं क्योंकि इनके क्रिस्टलों के आकार नहीं बदलते।
प्रश्न 27.
स्पंज का संपीडन संभव क्यों होता है ?
उत्तर-
स्पंज का संपीडन इसमें विद्यमान छिद्रों से हवा बाहर निकलने के कारण संभव होता है।
प्रश्न 28.
द्रव किसे कहते हैं ?
उत्तर-
द्रव निश्चित आयतन वाले तरल हैं जिनमें बहाव का गुण होता है और ये आकार बदलते हैं।
प्रश्न 29.
जल के किस गुण के कारण जलीय जंतु जीवित रह पाते हैं ?
उत्तर-
वातावरण में विद्यमान ऑक्सीजन गैस विसरित होकर जल में मिल जाती है जो जलीय जंतुओं के जीवन के लिए अनिवार्य होती है।
प्रश्न 30.
जल में कौन-सी गैस विसरित होकर पौधों के लिए आवश्यकताओं की पूर्ति करती है ?
उत्तर-
कार्बन डाइऑक्साइड गैस।
प्रश्न 31.
द्रव में किन-किन का विसरण संभव है ?
उत्तर-
द्रव में ठोस, द्रव और गैस तीनों का विसरण संभव है।
प्रश्न 32.
ठोस की अपेक्षा द्रव में विसरण की दर अधिक क्यों होती है ?
उत्तर-
ठोस की अपेक्षा द्रव में पदार्थ के कण स्वतंत्र रूप से गति करते हैं और उन कणों में रिक्त स्थान भी अधिक होते हैं।
![]()
प्रश्न 33.
ठोस, द्रवों और गैसों में अपेक्षाकृत संपीड्यता किसमें सबसे अधिक होती है ?
उत्तर-
गैसों में।
प्रश्न 34.
वाहनों में कौन-सी संपीडित गैस प्रयुक्त की जाती है ?
उत्तर-
संपीडित प्राकृतिक गैस (CNG)।
प्रश्न 35.
घरों में ईंधन के रूप में कौन-सी गैस प्रयुक्त की जाती है ?
उत्तर-
द्रवीकृत पेट्रोलियम गैस (LPG)।
प्रश्न 36.
इत्र और अगरबत्ती की सुगंध तेज़ी से क्यों फैल जाती है ?
उत्तर-
कणों की तेज़ गति और अत्यधिक रिक्त स्थानों के कारण गैसों का विसरण बहुत तीव्रता से हो जाता है।
प्रश्न 37.
पानी द्रव्य की किन-किन अवस्थाओं में पाया जाता है ?
उत्तर-
पानी ठोस (बर्फ), द्रव, गैस (वाष्प) अवस्थाओं में पाया जाता है।
प्रश्न 38.
ठोस की विशेषताएं लिखिए।
उत्तर-
ठोस प्रायः कठोर होते हैं जिन पर दबाव नहीं डाला जा सकता। इनका निश्चित आकार और घनफल होता है।
![]()
प्रश्न 39.
द्रव की विशेषताएं लिखिए।
उत्तर-
द्रव का निश्चित घनफल होता है पर कोई निश्चित आकार नहीं होता। इस पर भी अधिक दबाव नहीं डाला जा सकता। यह प्रायः बहते हैं।
प्रश्न 40.
गैस की विशेषताएं लिखिए।
उत्तर-
गैस दबाव को सहन करने वाला द्रव्य है जिसे किसी भी आकार के बर्तन में भरा जा सकता है। इसका निश्चित आकार और घनफल नहीं होता।
प्रश्न 41.
ठोस, तरल और गैस के चार-चार उदाहरण दो।
उत्तर-
ठोस = लकड़ी, पत्थर, चीनी, नमक।
तरल = पानी, दूध, तेल, एल्कोहल।
गैस = वायु, ऑक्सीजन, हाइड्रोजन, कार्बन डाइऑक्साइड।
प्रश्न 42.
CNG का पूरा नाम लिखिए।
उत्तर-
Compressed Natural Gas (दबाव सहित प्राकृतिक गैस)।
प्रश्न 43.
ठोस प्रायः निश्चित आकार के क्यों होते हैं ?
उत्तर-
ठोस वस्तुओं को बनाने वाले कण एक-दूसरे के बहुत निकट होते हैं और उनके बीच आकर्षण बल बहुत अधिक होता है इसलिए ठोस प्रायः निश्चित आकार के होते हैं।
प्रश्न 44.
किसी टायर में हवा अधिक क्यों भरी जा सकती है ?
उत्तर-
गैसों के द्वारा अधिक दबाव सहने के गुण के कारण किसी टायर में अधिक हवा भरी जा सकती है। गैसों के कण गति करने में स्वतंत्र होते हैं और वे टायर में शीघ्र फैल सकते हैं।
प्रश्न 45.
गैसों की आकृति और आयतन निश्चित क्यों नहीं होता ?
उत्तर-
गैसों के अणु एक-दूसरे से काफ़ी दूरी पर होते हैं। इन्हें गति करने और अपने स्थान से चारों ओर घूमने में पर्याप्त स्वतंत्रता होती है इसलिए इनकी आकृति और आयतन निश्चित नहीं होता।
प्रश्न 46.
जल पदार्थ की कितनी अवस्थाओं में रहता है ?
उत्तर-
तीन अवस्थाओं में।
![]()
प्रश्न 47.
जल की तीनों अवस्थाओं के नाम लिखिए।
उत्तर-
ठोस = बर्फ, द्रव = जल, गैस = जलवाष्प।
प्रश्न 48.
तापमान में वृद्धि के कारण जब ठोस पिघल कर द्रव बन जाता है तो उसे क्या कहते हैं ?
उत्तर-
गलनांक।
प्रश्न 49.
तापमान की SI इकाई क्या है ?
उत्तर-
केल्विन।
प्रश्न 50.
0°C कितने केल्विन के बराबर होता है ?
उत्तर-
0°C सेल्सियस = 273.16K .
प्रश्न 51.
केल्विन से सेल्सियस में बदलने के लिए तापमान में कितना घटाना चाहिए ?
उत्तर-
273 घटाना चाहिए।
प्रश्न 52.
सेल्सियस से केल्विन में बदलने के लिए तापमान में कितना जोड़ना चाहिए ?
उत्तर-
273 जोड़ना चाहिए।
![]()
प्रश्न 53.
संगलन क्या है ?
उत्तर-
गलने की प्रक्रिया यानि ठोस से द्रव अवस्था में परिवर्तन को संगलन कहते हैं।
प्रश्न 54.
जल का क्वथनांक क्या है ?
उत्तर-
जल का क्वथनांक 373 K (100°C) है।
प्रश्न 55.
ऊर्ध्वपातन क्या है ?
उत्तर-
द्रव अवस्था में परिवर्तित हुए बिना ठोस अवस्था से सीधे गैस और वापस ठोस में बदलने की प्रक्रिया को ऊर्ध्वपातन कहते हैं।
प्रश्न 56.
शुष्क बर्फ किसे कहते हैं ?
उत्तर-
ठोस कार्बन डाइऑक्साइड को शुष्क बर्फ कहते हैं।
प्रश्न 57.
दाब के मापन की इकाई क्या है ?
उत्तर-
ऐटमॉस्फीयर (atm)।
प्रश्न 58.
दाब की SI इकाई क्या है ?
उत्तर-
पास्कल (Pa)।
प्रश्न 59.
सामान्य दाब किसे कहते हैं ?
उत्तर-
समुद्र की सतह पर वायुमंडलीय दाब एक ऐटमॉसफीयर होता है और इसे सामान्य दाब कहते हैं।
प्रश्न 60.
कोई द्रव बिना क्वथनांक पर पहुँचे वाष्प अवस्था में किस प्रकार पहुँचता है ?
उत्तर-
वाष्पन क्रिया से।
प्रश्न 61.
वाष्पन क्रिया का एक उदाहरण दीजिए।
उत्तर-
धूप में गीले कपड़ों का सूखना।
![]()
प्रश्न 62.
क्वथनांक से कम तापमान पर द्रव के वाष्पन में परिवर्तन की प्रक्रिया को क्या कहते हैं ?
उत्तर-
वाष्पीकरण।
प्रश्न 63.
वाष्पीकरण की दर किन-किन कारणों से बढ़ती है ?
उत्तर-
सतह क्षेत्र बढ़ने से, तापमान में वृद्धि, आर्द्रता में कमी, हवा की गति में वृद्धि।
प्रश्न 64.
तापमान बढ़ने से वाष्पीकरण की क्रिया तेज़ क्यों हो जाती है ?
उत्तर-
कणों को पर्याप्त गतिज ऊर्जा मिलने के कारण।
प्रश्न 65.
हवा की गति बढ़ने से कपड़े जल्दी क्यों सूखते हैं ?
उत्तर-
जल वाष्पों के कण हवा के साथ उड़ जाते हैं जिस कारण आस-पास के जल वाष्प की मात्रा घट जाती है।
प्रश्न 66.
आर्द्रता किसे कहते हैं ?
उत्तर-
वायु में विद्यमान जल वाष्प की मात्रा को आर्द्रता कहते हैं।
प्रश्न 67.
आर्द्रता का वाष्पन से क्या संबंध है ?
उत्तर-
वायु में जल कणों की मात्रा बढ़ने से वाष्पीकरण की दर घट जाती है।
![]()
प्रश्न 68.
कपड़ों को सुखाने के लिए उन्हें फैलाया क्यों जाता है ?
उत्तर-
उनके सतही क्षेत्र को बढ़ाने के लिए ताकि वाष्पीकरण की दर बढ़ाई जा सके।
प्रश्न 69.
वाष्पीकरण का शीतलता से क्या संबंध है ?
उत्तर-
वाष्पीकरण से शीतलता बढ़ती है।
प्रश्न 70.
गर्मियों में सूती कपड़ों का प्रयोग क्यों किया जाता है ?
उत्तर-
सूती कपड़ों में जल का अवशोषण अधिक होता है जिसका वायुमंडल में सरलता से वाष्पीकरण हो जाता है जिस कारण तापमान कम हो जाता है।
प्रश्न 71.
प्लाज्मा अवस्था में कण किस रूप में होते हैं ?
उत्तर-
इस अवस्था में कणं अत्यधिक ऊर्जा वाले और अधिक उत्तेजित होते हैं। ये कण आयनीकृत गैस के रूप में होते हैं।
प्रश्न 72.
लोरसेंट ट्यूब और नियॉन बल्ब में क्या होता है ?
उत्तर-
प्लाज्मा होता है।
प्रश्न 73.
सूर्य और तारों में चमक किस कारण होती है ?
उत्तर-
प्लाज्मा के कारण।
![]()
प्रश्न 74.
तारों में प्लाज्मा किस कारण बनता है ?
उत्तर-
उच्च तापमान के कारण।
प्रश्न 75.
BEC किस प्रकार तैयार किया जाता है ?
उत्तर-
सामान्य वायु के घनत्व के एक लाखवें भाग जितने कम घनत्व वाली गैस को बहुत ही कम तापमान पर ठंडा करने से BEC तैयार होता है।
प्रश्न 76.
‘बोस-आइंस्टीन कंडनसेशन’ की अवस्था प्राप्त करने के लिए भौतिकी में किसे नोबेल पुरस्कार दिया गया था ?
उत्तर-
सन् 2001 में अमेरिका के एरिक ए० कॉर्नेल, उलगैंग केटरले तथा कार्ल ई० वेमैन को।
प्रश्न 77.
किसे लॉग ऑन करके पदार्थ की चौथी और पाँचवीं अवस्था के बारे में जानकारी प्राप्त की जा सकती है ?
उत्तर-
WWW.Chem4kids.com