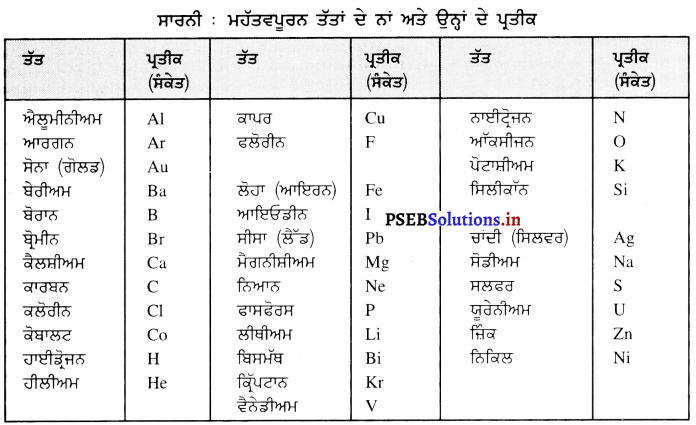
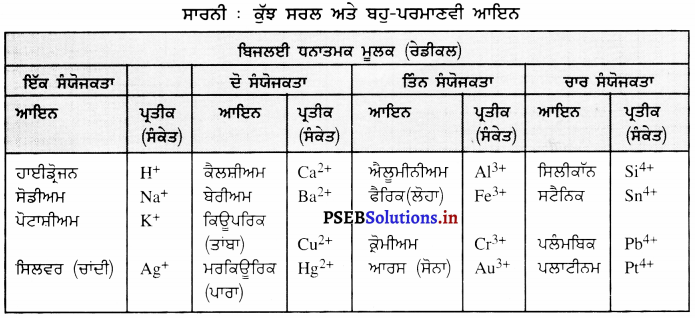
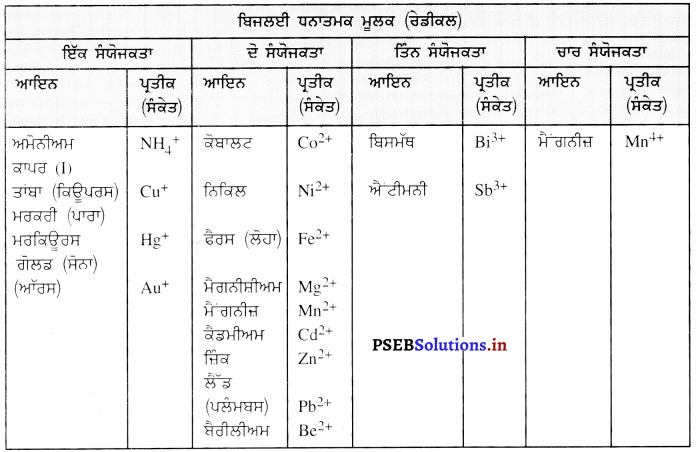
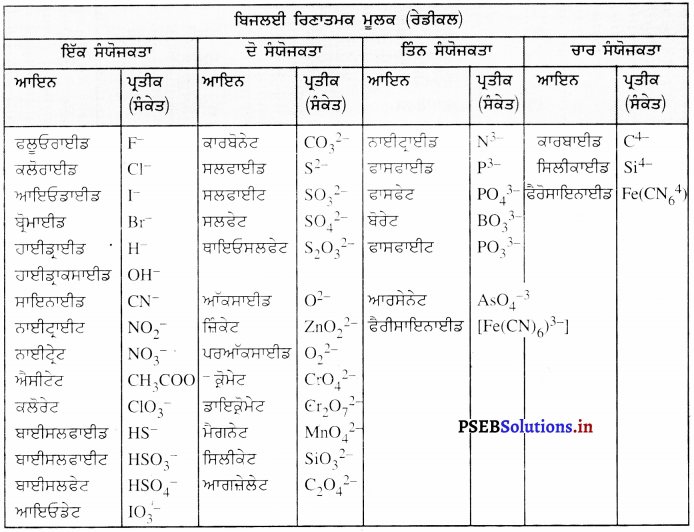
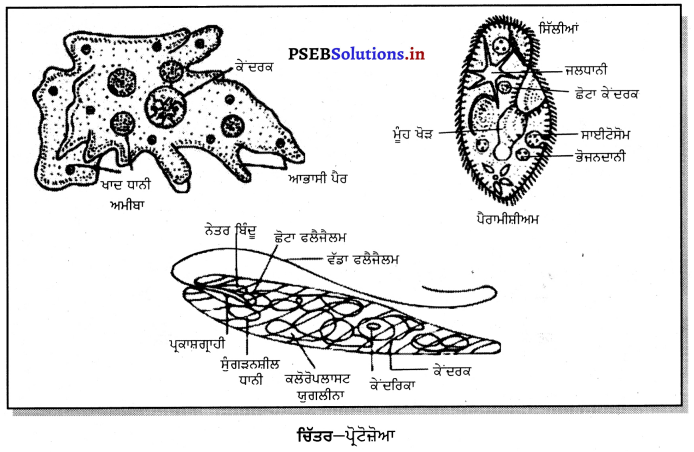
Punjab State Board PSEB 9th Class Science Book Solutions Chapter 12 ਧੁਨੀ Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Science Chapter 12 ਧੁਨੀ
PSEB 9th Class Science Guide ਧੁਨੀ Textbook Questions and Answers
ਅਭਿਆਸ ਦੇ ਪ੍ਰਸ਼ਨ
ਪ੍ਰਸ਼ਨ 1.
ਧੁਨੀ ਕੀ ਹੈ ਅਤੇ ਕਿਵੇਂ ਉਤਪੰਨ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
ਧੁਨੀ (Sound) – ਧੁਨੀ ਊਰਜਾ ਦਾ ਇੱਕ ਰੂਪ ਹੈ ਜੋ ਸਾਡੇ ਕੰਨਾਂ ਵਿੱਚ ਸੁਣਨ ਦਾ ਅਨੁਭਵ ਪੈਦਾ ਕਰਦੀ ਹੈ ।
ਧੁਨੀ ਉਤਪੰਨ ਕਰਨਾ – ਅਸੀਂ ਭਿੰਨ-ਭਿੰਨ ਵਸਤੁਆਂ ਵਿੱਚ ਤੁਣਕਾ ਮਾਰ ਕੇ, ਰਗੜ ਕੇ, ਫੁਕ-ਮਾਰ ਕੇ ਜਾਂ ਉਹਨਾਂ ਨੂੰ ਹਿਲਾ ਕੇ ਧੁਨੀ ਉਤਪੰਨ ਕਰ ਸਕਦੇ ਹਾਂ ਅਰਥਾਤ ਵਸਤੁਆਂ ਵਿੱਚ ਕੰਪਨ ਪੈਦਾ ਕਰਕੇ ਧੁਨੀ ਪੈਦਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । ਕੰਪਨ ਦਾ ਅਰਥ ਹੈ ਕਿਸੇ ਵਸਤੂ ਦਾ ਤੇਜ਼ੀ ਨਾਲ ਬਾਰ-ਬਾਰ ਇੱਧਰ-ਉੱਧਰ ਗਤੀ ਕਰਨਾ ।
ਪ੍ਰਸ਼ਨ 2.
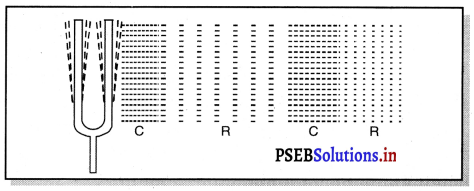
ਇੱਕ ਚਿੱਤਰ ਦੀ ਸਹਾਇਤਾ ਨਾਲ ਵਰਣਨ ਕਰੋ ਕਿ ਧੁਨੀ ਦੇ ਸ੍ਰੋਤ ਨੇੜੇ ਵਾਯੂ ਵਿੱਚ ਨਪੀੜਨ (Compressions) ਅਤੇ ਵਿਰਲਾਂ (Rarefactions) ਕਿਵੇਂ ਉਤਪੰਨ ਹੁੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਧੁਨੀ ਸ੍ਰੋਤ ਦੇ ਨੇੜੇ ਵਾਯੂ ਵਿੱਚ ਨਪੀੜਨ ਅਤੇ ਵਿਰਲਾਂ (ਨਿਖੇੜਨ) ਦਾ ਉਤਪੰਨ ਹੋਣਾ – ਧੁਨੀ ਦੇ ਸੰਚਾਰ ਲਈ ਹਵਾ ਸਭ ਤੋਂ ਸਾਧਾਰਨ ਮਾਧਿਅਮ ਹੈ । ਜਦੋਂ ਕੋਈ ਵਸਤ ਕੰਪਨ ਕਰਦੀ ਹੋਈ ਅੱਗੇ ਵੱਲ ਵੱਧਦੀ ਹੈ ਤਾਂ ਇਹ ਆਪਣੇ ਸਾਹਮਣੇ ਦੀ ਹਵਾ ਨੂੰ ਧੱਕਦੀ ਹੋਈ ਨਪੀੜਦੀ ਹੈ ਅਤੇ ਇਸ ਤਰ੍ਹਾਂ ਇੱਕ ਉੱਚ ਦਬਾਅ ਵਾਲਾ ਖੇਤਰ ਪੈਦਾ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਖੇਤਰ ਨੂੰ ਨਪੀੜਨ (C) ਕਹਿੰਦੇ ਹਨ । ਇਹ ਨਪੀੜਨ ਕੰਪਨ ਕਰ ਰਹੀ ਵਸਤੁ ਤੋਂ ਦੁਰ ਅੱਗੇ ਵੱਲ ਗਤੀ ਕਰਦਾ ਹੈ । ਜਦੋਂ ਕੰਪਨ ਕਰਦੀ ਵਸਤੁ ਪਿੱਛੇ ਵੱਲ ਕੰਪਨ ਕਰਦੀ ਹੈ ਤਾਂ ਇੱਕ ਘੱਟ ਦਬਾਅ ਵਾਲਾ ਖੇਤਰ ਉਤਪੰਨ ਹੋ ਜਾਂਦਾ ਹੈ, ਜਿਸਨੂੰ ਨਿਖੇੜਨ ਜਾਂ ਵਿਰਲਨ (R) ਕਹਿੰਦੇ ਹਨ । ਜਦੋਂ ਵਸਤੁ ਕੰਪਨ ਕਰਦੀ ਹੈ (ਅਰਥਾਤ ਅੱਗੇ ਅਤੇ ਪਿੱਛੇ ਤੇਜ਼ੀ ਨਾਲ ਗਤੀ ਕਰਦੀ ਹੈ। ਤਾਂ ਹਵਾ ਵਿੱਚ ਨਪੀੜਨ ਅਤੇ ਨਿਖੇੜਨ ਦੀ ਇੱਕ ਲੜੀ ਬਣ ਜਾਂਦੀ ਹੈ । ਇਹੋ ਨਪੀੜਨ (C) ਅਤੇ ਨਿਖੇੜਨ (R) ਧੁਨੀ ਤਰੰਗ ਬਣਾਉਂਦੇ ਹਨ ਜਿਹੜੀ ਮਾਧਿਅਮ ਵਿੱਚ ਦੀ ਹੋ ਕੇ ਅਗਾਂਹ ਸੰਚਾਰ ਕਰਦੀ ਹੈ । ਨਪੀੜਨ (C) ਉੱਚ ਦਬਾਅ ਦਾ ਖੇਤਰ ਅਤੇ ਨਿਖੇੜਨ (R) ਘੱਟ ਦਬਾਅ ਦਾ ਖੇਤਰ ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 3.
ਕਿਹੜੇ ਪ੍ਰਯੋਗ ਨਾਲ ਇਹ ਦਰਸਾਇਆ ਜਾ ਸਕਦਾ ਹੈ ਕਿ ਧੁਨੀ ਸੰਚਾਰਣ ਦੇ ਲਈ ਪਦਾਰਥਮਈ ਮਾਧਿਅਮ (material medium) ਦੀ ਜ਼ਰੂਰਤ ਹੁੰਦੀ ਹੈ ?
ਉੱਤਰ-
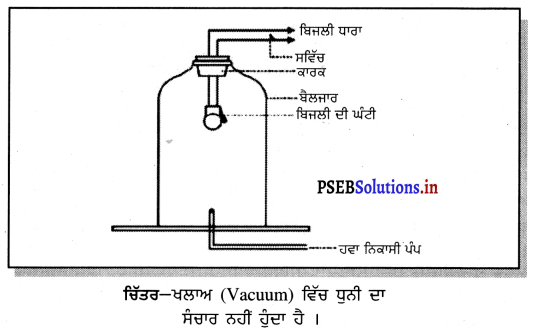
ਧੁਨੀ ਸੰਚਾਰਣ ਲਈ ਪਦਾਰਥਮਈ ਮਾਧਿਅਮ ਦੀ ਜ਼ਰੂਰਤ – ਧੁਨੀ ਇੱਕ ਯੰਤ੍ਰਿਕ ਤਰੰਗ ਹੈ ਅਤੇ ਇਸਦੇ ਸੰਚਾਰ ਲਈ ਕਿਸੇ ਪਦਾਰਥ ਜਿਵੇਂ ਹਵਾ, ਪਾਣੀ, ਸਟੀਲ ਆਦਿ ਦਾ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ । ਧੁਨੀ ਨਿਰਵਾਤ (ਨਿਰਵਾਯੂ ਵਿੱਚ ਨਹੀਂ ਚਲ ਸਕਦੀ ਹੈ । ਇਸਨੂੰ ਹੇਠਾਂ ਦਿੱਤੇ ਪ੍ਰਯੋਗ ਦੁਆਰਾ ਸਿੱਧ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ-
ਪ੍ਰਯੋਗ – ਇੱਕ ਬਿਜਲਈ ਘੰਟੀ ਅਤੇ ਇੱਕ ਕੱਚ ਦਾ ਹਵਾ ਰੋਧੀ ਬੈਲਜਾਰ ਲਓ । ਬਿਜਲਈ ਘੰਟੀ ਨੂੰ ਬੈਲਜਾਰ ਵਿੱਚ ਲਟਕਾਓ । ਬੈਲਜਾਰ ਨੂੰ ਚਿੱਤਰ ਵਾਂਗ ਹਵਾ-ਨਿਕਾਸੀ ਪੰਪ ਨਾਲ ਜੋੜੋ । ਘੰਟੀ ਦਾ ਸਵਿੱਚ ਦਬਾਉਣ ਤੇ ਤੁਹਾਨੂੰ ਉਸਦੀ ਧੁਨੀ ਸੁਣਾਈ ਦੇਵੇਗੀ । ਹੁਣ ਹਵਾ-ਨਿਕਾਸੀ ਪੰਪ ਨੂੰ ਚਲਾਓ । ਜਦੋਂ ਬੈਲਜਾਰ ਦੀ ਹਵਾ ਹੌਲੀ-ਹੌਲੀ ਬਾਹਰ ਨਿਕਲਦੀ ਹੈ, ਘੰਟੀ ਦੀ ਧੁਨੀ ਹੌਲੀ ਹੁੰਦੀ ਜਾਂਦੀ ਹੈ, ਜਦੋਂ ਕਿ ਉਸ ਵਿਚੋਂ ਉਹੀ ਬਿਜਲੀ ਧਾਰਾ ਗੁਜ਼ਰ ਰਹੀ ਹੈ । ਕੁਝ ਸਮੇਂ ਬਾਅਦ ਜਦੋਂ ਬੈਲਜਾਰ ਵਿੱਚ ਬਹੁਤ ਘੱਟ ਹਵਾ ਬਾਕੀ ਰਹਿ ਜਾਂਦੀ ਹੈ ਤਾਂ ਤੁਹਾਨੂੰ ਬਹੁਤ ਮੱਧਮ ਧੁਨੀ ਸੁਣਾਈ ਦਿੰਦੀ ਹੈ । ਜੇਕਰ ਬੈਲਜਾਰ ਦੀ ਸਾਰੀ ਹਵਾ ਬਾਹਰ ਕੱਢ ਦਿੱਤੀ ਜਾਵੇ ਤਾਂ ਤੁਸੀਂ ਘੰਟੀ ਦੀ ਧੁਨੀ ਨੂੰ ਸੁਣ ਨਹੀਂ ਪਾਉਗੇ । ਇਸ ਤੋਂ ਸਿੱਧ ਹੁੰਦਾ ਹੈ ਕਿ ਧੁਨੀ ਲਈ ਪਦਾਰਥਮਈ ਮਾਧਿਅਮ ਦਾ ਹੋਣਾ ਜ਼ਰੂਰੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਧੁਨੀ ਨੂੰ ਲੰਮੇ-ਦਾਅ ਜਾਂ ਲਾਂਗੀਚਿਊਡੀਨਲ ਤਰੰਗ ਕਿਉਂ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਧੁਨੀ ਤਰੰਗਾਂ ਲੰਮੇ-ਦਾਅ ਜਾਂ ਲਾਂਗੀਚਿਊਡੀਨਲ ਤਰੰਗਾਂ ਕਹਾਉਂਦੀਆਂ ਹਨ ਕਿਉਂਕਿ ਇਹਨਾਂ ਤਰੰਗਾਂ ਵਿੱਚ ਮਾਧਿਅਮ (ਹਵਾ) ਦੇ ਕਣਾਂ ਦਾ ਵਿਸਥਾਪਨ ਹਲਚਲ ਦੇ ਸੰਚਰਣ ਦੀ ਦਿਸ਼ਾ ਦੇ ਸਮਾਨੰਤਰ ਹੁੰਦਾ ਹੈ । ਕਣ ਇੱਕ ਸਥਾਨ ਤੋਂ ਦੂਜੇ ਸਥਾਨ ਤੱਕ ਗਤੀ ਨਹੀਂ ਕਰਦੇ ਪਰੰਤੁ ਆਪਣੀ ਮੱਧ ਸਥਿਤੀ ਵਿਰਾਮ ਅਵਸਥਾ ਵਾਲੀ ਸਥਿਤੀ ਦੇ ਅੱਗੇ-ਪਿੱਛੇ ਡੋਲਨ ਕਰਦੇ ਹਨ । ਕਿਸੇ ਮਾਧਿਅਮ ਵਿੱਚ ਧੁਨੀ ਨਿਖੇੜਨਾਂ (C) ਅਤੇ ਵਿਰਲਨਾਂ (R) ਦੇ ਰੂਪ ਵਿੱਚ ਅਗਾਂਹ ਵੱਲ ਤੁਰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 5.
ਧੁਨੀ ਦਾ ਕਿਹੜਾ ਗੁਣ ਕਿਸੇ ਹਨੇਰੇ ਕਮਰੇ ਵਿੱਚ ਹੋਰ ਸਾਥੀਆਂ ਨਾਲ ਬੈਠੇ ਤੁਹਾਡੇ ਮਿੱਤਰ ਦੀ ਅਵਾਜ਼ ਪਹਿਚਾਣਨ ਵਿੱਚ ਤੁਹਾਡੀ ਸਹਾਇਤਾ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਧੁਨੀ ਦੀ ਗੁਣਵੱਤਾ ਵਾਲੇ ਲੱਛਣ ਦੇ ਅਧਾਰ ‘ਤੇ ਅਸੀਂ ਹਨੇਰੇ ਵਿੱਚ ਬੈਠੇ ਮਿੱਤਰਾਂ ਦੀ ਅਵਾਜ਼ ਦੀ ਪਹਿਚਾਣ ਕਰ ਸਕਦੇ ਹਾਂ ।
ਪ੍ਰਸ਼ਨ 6.
ਬੱਦਲ ਦੀ ਗਰਜ ਅਤੇ ਚਮਕ ਨਾਲ-ਨਾਲ ਇੱਕੋ ਸਮੇਂ ਉਤਪੰਨ ਹੁੰਦੇ ਹਨ ਪਰੰਤੂ ਚਮਕ ਦਿਖਾਈ ਦੇਣ ਦੇ ਕੁਝ ਸੈਕਿੰਡ ਬਾਅਦ ਗਰਜ ਸੁਣਾਈ ਦੇਂਦੀ ਹੈ | ਅਜਿਹਾ ਕਿਉਂ ਹੁੰਦਾ ਹੈ ? |
ਉੱਤਰ-
ਅਕਾਸ਼ੀ ਬਿਜਲੀ ਦੀ ਚਮਕ ਅਤੇ ਬੱਦਲ ਦੀ ਗਰਜ ਨਾਲ-ਨਾਲ ਉਤਪੰਨ ਹੁੰਦੇ ਹਨ । ਪ੍ਰਕਾਸ਼ ਦੀ ਚਾਲ (3 × 108 m/s) ਧੁਨੀ ਦੀ ਚਾਲ (340 m/s) ਨਾਲੋਂ ਬਹੁਤ ਜ਼ਿਆਦਾ ਹੈ । ਇਸ ਲਈ ਧੁਨੀ ਦੀ ਅਵਾਜ਼ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਪ੍ਰਕਾਸ਼ ਬਹੁਤ ਪਹਿਲਾਂ ਪਹੁੰਚ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 7.
ਕਿਸੇ ਵਿਅਕਤੀ ਦੀ ਔਸਤ ਸੁਣਨਯੋਗ ਸੀਮਾ (Hearing Range) 20 Hz ਤੋਂ 20 kHz ਹੈ । ਇਹਨਾਂ ਦੋ ਆਤੀਆਂ ਦੇ ਲਈ ਧੁਨੀ ਤਰੰਗਾਂ ਦੀ ਤਰੰਗ ਲੰਬਾਈ ਪਤਾ ਕਰੋ । ਹਵਾ ਵਿੱਚ ਧੁਨੀ ਦਾ ਵੇਗ 344 ms-1 ਹੈ ।
ਹੱਲ:
(i) ਪਹਿਲੀ ਸਥਿਤੀ ਜਦੋਂ ਸਣਨਯੋਗ ਰੰਜ ਦੀ ਹੇਠਲੀ ਸੀਮਾ ਹੈ
ਇੱਥੇ ਧੁਨੀ ਦੀ ਆਕ੍ਰਿਤੀ (v1 ) = 20 Hz
ਹਵਾ ਵਿੱਚ ਧੁਨੀ ਦਾ ਵੇਗ (υ1 ) = 344 ms-1
ਤਰੰਗ ਲੰਬਾਈ (λ1) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, υ1 = v1 × λ1
ਜਾਂ λ1 = \(\frac{v_{1}}{v_{1}}\)
= \(\frac{344}{20}\)
∴ ਤਰੰਗ ਲੰਬਾਈ (λ1) = 17.2 m ……………… (1)
(ii) ਦੂਸਰੀ ਸਥਿਤੀ ਜਦੋਂ ਸੁਣਨਯੋਗ ਰੇਂਜ ਦੀ ਉਪਰਲੀ ਸੀਮਾ ਹੈ
ਹੁਣ, ਧੁਨੀ ਦੀ ਆਕ੍ਰਿਤੀ (v2) = 20 kHz
= 20 × 1000 Hz
= 2 × 104 Hz
ਹਵਾ ਵਿੱਚ ਧੁਨੀ ਦਾ ਵੇਗ (V2 = V1) = 344 ms-1
ਤਰੰਗ ਲੰਬਾਈ (λ2) = ?
∴ 2 = \(\frac{344}{2 \times 10^{4}}\)
= \(\frac{172}{10000}\)
= 0.0172 m …………………. (2)
![]()
ਪ੍ਰਸ਼ਨ 8.
ਦੋ ਬੱਚੇ ਕਿਸੇ ਐਲੂਮੀਨੀਅਮ ਪਾਈਪ ਦੇ ਦੋਵੇਂ ਸਿਰਿਆਂ ‘ਤੇ ਹਨ । ਇੱਕ ਬੱਚਾ ਪਾਈਪ ਦੇ ਸਿਰੇ ‘ਤੇ ਪੱਥਰ ਨਾਲ ਸੱਟ ਮਾਰਦਾ ਹੈ । ਦੂਜੇ ਸਿਰੇ ‘ਤੇ ਬੈਠੇ ਬੱਚੇ ਤੱਕ ਹਵਾ ਅਤੇ ਐਲੂਮੀਨੀਅਮ ਵਿੱਚ ਵੀ ਜਾਣ ਵਾਲੀ ਧੁਨੀ ਤਰੰਗਾਂ ਦੁਆਰਾ ਲਏ ਗਏ ਸਮੇਂ ਦਾ ਅਨੁਪਾਤ (Ratio) ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਮੰਨ ਲਓ ਪਾਈਪ ਦੀ ਲੰਬਾਈ = l
ਹਵਾ ਵਿੱਚ ਧੁਨੀ ਦਾ ਵੇਗ (Va) = 346 ms-1
ਐਲੂਮੀਨੀਅਮ ਵਿੱਚ ਧੁਨੀ ਦਾ ਵੇਗ (VAl) = 6420 ms-1
∴ ਹਵਾ ਵਿੱਚੋਂ ਹੋ ਕੇ ਜਾਣ ਲਈ ਧੁਨੀ ਨੂੰ ਲੱਗਿਆ ਸਮਾਂ (ta) = 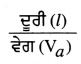
= \(\frac{l}{346}\)s
ਐਲੂਮੀਨੀਅਮ ਵਿੱਚੋਂ ਹੋ ਕੇ ਜਾਣ ਲਈ ਧੁਨੀ ਨੂੰ ਲੱਗਿਆ ਸਮਾਂ (tAl) = \(\frac{l}{V_{\mathrm{Al}}}\)
= \(\frac{l}{6420}\)s

= \(\frac{6420}{346}\)
= \(\frac{18.55}{1}\)
∴ ta : tAl = 18.55 : 1
ਪ੍ਰਸ਼ਨ 9.
ਕਿਸੇ ਧੁਨੀ ਸ੍ਰੋਤ ਦੀ ਆਕ੍ਰਿਤੀ 100 Hz ਹੈ । ਇੱਕ ਮਿੰਟ ਵਿੱਚ ਇਹ ਕਿੰਨੀ ਵਾਰ ਕੰਪਨ ਕਰੇਗਾ ?
ਹੱਲ:
ਸੋਤ ਦੀ ਆਕ੍ਰਿਤੀ = 100 Hz
ਅਰਥਾਤ ਸ੍ਰੋਤ ਦੁਆਰਾ 1 ਸੈਕੰਡ ਵਿੱਚ ਕੀਤੇ ਗਏ ਕੰਪਨਾਂ ਦੀ ਸੰਖਿਆ = 100
∴ 1 ਮਿੰਟ = 60 ਸੈਕੰਡ ਵਿੱਚ ਕੀਤੇ ਗਏ ਕੰਪਨਾਂ ਦੀ ਸੰਖਿਆ = 100 × 60
= 6000
ਪ੍ਰਸ਼ਨ 10.
ਕੀ ਧੁਨੀ ਪਰਾਵਰਤਨ ਦੇ ਉਹਨਾਂ ਨਿਯਮਾਂ ਦਾ ਪਾਲਣ ਕਰਦੀ ਹੈ ਜਿਨ੍ਹਾਂ ਦਾ ਪਾਲਣ ਪ੍ਰਕਾਸ਼ ਦੀਆਂ ਤਰੰਗਾਂ ਕਰਦੀਆਂ ਹਨ ? ਇਹਨਾਂ ਨਿਯਮਾਂ ਨੂੰ ਸਮਝਾਓ ।
ਉੱਤਰ-
ਧੁਨੀ ਦੇ ਪਰਾਵਰਤਨ ਦੇ ਨਿਯਮ ਪੂਰਣ ਰੂਪ ਨਾਲ ਉਹੀ ਹਨ ਜਿਹੜੇ ਪ੍ਰਕਾਸ਼ ਦੀਆਂ ਤਰੰਗਾਂ ਪ੍ਰਦਰਸ਼ਿਤ ਕਰਦੀਆਂ ਹਨ | ਪ੍ਰਕਾਸ਼ ਵਾਂਗ ਧੁਨੀ ਵੀ ਠੋਸ ਜਾਂ ਦ੍ਰਵ ਦੀ ਸਤ੍ਹਾ ਤੋਂ ਪਰਾਵਰਤਿਤ ਹੁੰਦੀ ਹੈ । ਇਹ ਨਿਯਮ ਹਨ-
ਨਿਯਮ 1 – ਪਰਾਵਰਤਕ ਤਲ ਦੇ ਕਿਸੇ ਬਿੰਦੂ ‘ਤੇ ਆਪਤਿਤ ਧੁਨੀ ਤਰੰਗ ਅਤੇ ਅਭਿਲੰਬ ਦੇ ਵਿਚਾਲੇ ਦਾ ਕੋਣ ਅਤੇ ਪਰਾਵਰਤਿਤ ਧੁਨੀ ਤਰੰਗ ਅਤੇ ਅਭਿਲੰਬ ਵਿਚਾਲੇ ਬਣਿਆ ਕੋਣ ਹਮੇਸ਼ਾ ਬਰਾਬਰ ਹੁੰਦਾ ਹੈ ।
ਨਿਯਮ 2 – ਅਪਾਤੀ ਧੁਨੀ ਤਰੰਗ, ਅਭਿਲੰਬ ਅਤੇ ਪਰਾਵਰਤਿਤ ਧੁਨੀ ਤਰੰਗ ਤਿੰਨੋਂ ਇੱਕ ਹੀ ਧਰਾਤਲ ਵਿੱਚ ਹੁੰਦੇ ਹਨ ।
ਪ੍ਰਸ਼ਨ 11.
ਕਿਸੇ ਦੂਰ ਪਈ ਵਸਤੂ ਤੋਂ ਧੁਨੀ ਪਰਾਵਰਤਿਤ ਹੋਣ ਕਰਕੇ ਗੂੰਜ ਪੈਦਾ ਹੁੰਦੀ ਹੈ । ਮੰਨ ਲਉ ਧੁਨੀ ਸ੍ਰੋਤ ਅਤੇ ਪਰਾਵਰਤਿਤ ਸਤ੍ਹਾ (ਦੂਰ ਪਈ ਵਸਤੂ) ਵਿੱਚਕਾਰ ਦੂਰੀ ਸਥਿਰ ਰਹੇ ਤਾਂ ਕਿਸ ਦਿਨ ਗੂੰਜ (echo) ਜਲਦੀ ਸੁਣਾਈ ਦੇਵੇਗੀ
(i) ਜਿਸ ਦਿਨ ਤਾਪਮਾਨ ਵੱਧ ਹੈ ?
(i) ਜਿਸ ਦਿਨ ਤਾਪਮਾਨ ਘੱਟ ਹੈ ?
ਉੱਤਰ-
ਜਿਸ ਦਿਨ ਤਾਪਮਾਨ ਵੱਧ ਹੈ ਉਸ ਦਿਨ ਧੁਨੀ ਦੀ ਚਾਲ ਵੱਧ ਹੋਵੇਗੀ । ਇਸ ਲਈ ਉਸ ਦਿਨ ਗੂੰਜ (ਪ੍ਰਤੀ ਧੁਨੀ) ਜਲਦੀ ਸੁਣਾਈ ਦੇਵੇਗੀ ।
ਪ੍ਰਸ਼ਨ 12.
ਧੁਨੀ ਤਰੰਗਾਂ ਦੇ ਪਰਾਵਰਤਨ ਦੇ ਦੋ ਵਿਹਾਰਕ ਉਪਯੋਗ ਲਿਖੋ ।
ਉੱਤਰ-
ਧੁਨੀ ਤਰੰਗਾਂ ਦੇ ਪਰਾਵਰਤਨ ਦੇ ਵਿਵਹਾਰਕ ਉਪਯੋਗ-
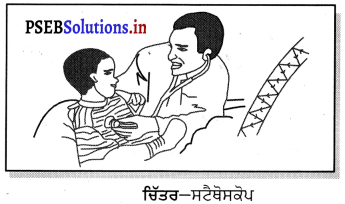
(i) ਸਟੈਥੋਸਕੋਪ ਇੱਕ ਡਾਕਟਰੀ ਯੰਤਰ ਹੈ ਜਿਹੜਾ ਸਰੀਰ ਦੇ ਅੰਦਰ ਮੁੱਖ ਤੌਰ ‘ਤੇ ਦਿਲ ਅਤੇ ਫੇਫੜਿਆਂ ਵਿੱਚ ਉਤਪੰਨ ਹੋਣ ਵਾਲੀ ਧੁਨੀ ਨੂੰ ਸੁਣਨ ਦੇ ਕੰਮ ਆਉਂਦਾ ਹੈ । ਸਟੈਥੋਸਕੋਪ ਵਿੱਚ ਮਰੀਜ਼ ਦੇ ਦਿਲ ਦੀ ਧੜਕਣ ਦੀ ਧੁਨੀ, ਵਾਰ-ਵਾਰ ਪਰਾਵਰਤਨ ਦੇ ਕਾਰਣ ਡਾਕਟਰ ਦੇ ਕੰਨਾਂ ਤੱਕ ਪਹੁੰਚਦੀ ਹੈ ।
(ii) ਮੈਗਾਫੋਨ ਜਾਂ ਲਾਊਡ-ਸਪੀਕਰ, ਹਾਰਨ, ਤੂਤੀ, ਸ਼ਹਿਨਾਈ ਵਰਗੇ ਸੰਗੀਤਕ ਯੰਤਰਾਂ ਦਾ ਅੱਗੇ ਵਾਲਾ ਖੁੱਲਾ ਭਾਗ ਸ਼ੰਕੂ ਆਕਾਰ ਦਾ ਬਣਾਇਆ ਜਾਂਦਾ ਹੈ ਤਾਂ ਜੋ ਸ੍ਰੋਤ ਤੋਂ ਉਤਪੰਨ ਹੋਣ ਵਾਲੀਆਂ ਧੁਨੀ ਤਰੰਗਾਂ ਨੂੰ ਬਾਰ-ਬਾਰ ਪਰਾਵਰਤਿਤ ਕਰਕੇ ਸ੍ਰੋਤਿਆਂ ਵੱਲ ਅੱਗੇ ਵਾਲੀ ਦਿਸ਼ਾ ਵਿੱਚ ਭੇਜਿਆ ਜਾ ਸਕੇ ।

![]()
ਪ੍ਰਸ਼ਨ 13.
500 ਮੀਟਰ ਉੱਚੀ ਕਿਸੇ ਮੀਨਾਰ ਦੀ ਚੋਟੀ ਤੋਂ ਇੱਕ ਪੱਥਰ ਮੀਨਾਰ ਦੇ ਅਧਾਰ ਉੱਪਰ ਸਥਿਤ ਇੱਕ ਪਾਣੀ ਦੇ ਤਲਾਬ ਵਿੱਚ ਸੁੱਟਿਆ ਜਾਂਦਾ ਹੈ । ਪਾਣੀ ਵਿੱਚ ਇਸਦੇ ਡਿੱਗਣ ਦੀ ਧੁਨੀ ਚੋਟੀ ਉੱਤੇ ਕਦੋਂ ਸੁਣਾਈ ਦੇਵੇਗੀ ? g = 10 m/s2 ਅਤੇ ਧੁਨੀ ਦੀ ਚਾਲ = 340 ms) .
ਹੱਲ:
ਇੱਥੇ ਆਰੰਭਿਕ ਵੇਗ (u) = 0
ਮੀਨਾਰ ਦੀ ਉੱਚਾਈ (ਅਰਥਾਤ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ) (S) = 500 ਮੀਟਰ
| ਗੁਰੂਤਵੀ ਪ੍ਰਵੇਗ (g) = 10 m/s2
ਸਮੀਕਰਣ
S = ut +\(\frac { 1 }{ 2 }\)gt2 ਤੋਂ
500 = 0 × t + \(\frac { 1 }{ 2 }\) × 10 × t2
500 = 0 + 5 × t2
t2 = \(\frac{500}{5}\)
= 100
t = \(\sqrt{100}\)
∴ t = 10 ਸੈਕਿੰਡ
ਹੁਣ ਧੁਨੀ ਨੇ ਉੱਪਰ ਚੋਟੀ ਵੱਲ ਜਾਣਾ ਹੈ ਅਤੇ ਧੁਨੀ ਦਾ ਵੇਗ ‘g’ ਤੋਂ ਸੁਤੰਤਰ ਹੈ
∴ t’ = 
= \(\frac{500}{340}\)
= 1.47 ਸੈਕਿੰਡ
ਧੁਨੀ ਨੂੰ ਉੱਪਰ ਆਉਣ ਲਈ ਲੱਗਿਆਂ ਕੁੱਲ ਸਮਾਂ = t + t’
= (10 +1.47) ਸੈਕਿੰਡ
= 11.47 ਸੈਕਿੰਡ
ਪ੍ਰਸ਼ਨ 14.
ਇੱਕ ਧੁਨੀ ਤਰੰਗ 339 m/s ਦੀ ਚਾਲ ਨਾਲ ਚੱਲ ਸਕਦੀ ਹੈ । ਜੇਕਰ ਇਸਦੀ ਤਰੰਗ ਲੰਬਾਈ 1.5 m ਹੋਵੇ, ਤਾਂ ਤਰੰਗ ਦੀ ਆਕ੍ਰਿਤੀ ਕਿੰਨੀ ਹੋਵੇਗੀ ? ਕੀ ਇਹ ਸੁਣਨਯੋਗ ਹੋਵੇਗੀ ?
ਹੱਲ:
ਧੁਨੀ ਤਰੰਗ ਦੀ ਚਾਲ (V) = 339 m/s
ਤਰੰਗ ਲੰਬਾਈ (λ) = 1.5 m
ਤਰੰਗ ਦੀ ਆਕ੍ਰਿਤੀ (v) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, ਆਤੀ (v) = \(\frac{\mathrm{V}}{\lambda}=\frac{339}{1.5}\)
= 226 Hz
ਹਾਂ, ਇਹ ਸੁਣਨਯੋਗ ਹਨ ਕਿਉਂਕਿ ਇਹਨਾਂ ਦੀ ਆਤੀ ਸੁਣਨ ਸੀਮਾ (20 Hz ਤੋਂ 20,000 Hz) ਦੇ ਵਿੱਚ ਹੈ ।
ਪ੍ਰਸ਼ਨ 15.
ਬਹੁਗੂੰਜ (reverberation) ਕੀ ਹੈ ? ਇਸਨੂੰ ਕਿਵੇਂ ਘੱਟ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ?
ਉੱਤਰ-
ਬਹੁਗੂੰਜ (reverberation) – ਧੁਨੀ ਦਾ ਪਰਾਵਰਤਨ ਬਹੁਗੂੰਜ ਅਖਵਾਉਂਦਾ ਹੈ । ਜੇਕਰ ਕਿਸੇ ਵੱਡੇ ਹਾਲ ਵਿੱਚ ਧੁਨੀ ਦੇ ਉਤਪੰਨ ਹੋਣ ਤੋਂ ਬਾਅਦ ਧੁਨੀ ਦਾ ਦੀਵਾਰਾਂ ਅਤੇ ਛੱਤ ਤੋਂ ਬਾਰ-ਬਾਰ ਪਰਾਵਰਤਨ, ਜਿਸਦੇ ਕਾਰਣ ਧੁਨੀ ਲਗਾਤਾਰ ਬਣੀ ਰਹਿੰਦੀ ਹੈ, ਨੂੰ ਬਹੁਗੂੰਜ ਕਹਿੰਦੇ ਹਨ | ਬਹੁਗੰਜ ਬੇਲੋੜੀ ਧੁਨੀ ਹੁੰਦੀ ਹੈ ਕਿਉਂਕਿ ਇਸ ਕਾਰਣ ਸਪੱਸ਼ਟ ਸੁਣਾਈ ਨਹੀਂ ਦਿੰਦਾ ਹੈ । ਇਸਨੂੰ ਘੱਟ ਕਰਨ ਲਈ ਹਾਲ ਦੀਆਂ ਦੀਵਾਰਾਂ ਅਤੇ ਛੱਤ ਉੱਪਰ ਧੁਨੀ ਸੋਖਕ ਪਦਾਰਥ ਜਿਵੇਂ ਨਪੀੜੇ ਹੋਏ ਫਾਈਬਰ ਬੋਰਡ, ਖੁਰਦਰਾ ਪਲਸਤਰ ਜਾਂ ਭਾਰੀ ਪਰਦੇ ਲਗਾ ਕੇ ਢੱਕਿਆ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 16.
ਧੁਨੀ ਦੇ ਉੱਚੇਪਨ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ? ਇਹ ਕਿਹੜੇ ਕਾਰਕਾਂ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ?
ਉੱਤਰ-
ਧੁਨੀ ਦਾ ਉੱਚਾਪਨ ਕੰਨਾਂ ਦੀ ਸੰਵੇਦਨਸ਼ੀਲਤਾ ਦਾ ਮਾਪ ਹੈ । ਇਹ ਤੀਬਰਤਾ ਦੇ ਸਮਾਨ ਕਿਸੇ ਇਕਾਈ ਖੇਤਰਫਲ ਵਿੱਚੋਂ 1 ਸੈਕਿੰਡ ਵਿੱਚ ਗੁਜ਼ਰਨ ਵਾਲੀ ਧੁਨੀ ਉਰਜਾ ਨਹੀਂ ਹੈ । ਦੋ ਧੁਨੀਆਂ ਸਮਾਨ ਤੀਬਰਤਾ ਦੀਆਂ ਹੋ ਸਕਦੀਆਂ ਹਨ ਪਰ ਫਿਰ ਵੀ ਇਹਨਾਂ ਵਿੱਚੋਂ ਇੱਕ ਧੁਨੀ ਨੂੰ ਦੂਸਰੀ ਧੁਨੀ ਦੀ ਤੁਲਨਾ ਵਿੱਚ ਵੱਧ ਉੱਚੀ ਧੁਨੀ ਦੇ ਰੂਪ ਵਿੱਚ ਸੁਣਿਆ ਜਾ ਸਕਦਾ ਹੈ ਕਿਉਂਕਿ ਕੰਨ ਇਸ ਧੁਨੀ ਲਈ ਸੰਵੇਦਨਸ਼ੀਲ ਹਨ ।
ਪ੍ਰਸ਼ਨ 17.
ਚਮਗਾਦੜ ਆਪਣਾ ਸ਼ਿਕਾਰ ਫੜਨ ਲਈ ਪਰਾਧੁਨੀ ਦਾ ਉਪਯੋਗ ਕਿਵੇਂ ਕਰਦਾ ਹੈ ? ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
ਚਮਗਾਦੜ ਹਨੇਰੀ ਰਾਤੀ ਵਿੱਚ ਆਪਣੇ ਭੋਜਨ ਨੂੰ ਖੋਜਣ ਦੇ ਲਈ ਉੱਡਦੇ ਵਕਤ ਪਧੁਨੀ ਤਰੰਗਾਂ ਉਤਸਰਜਿਤ ਕਰਦੀ ਹੈ ਅਤੇ ਪਰਿਵਰਤਨ ਦੇ ਬਾਅਦ ਇਹਨਾਂ ਦੀ ਟੋਹ (detect) ਲਗਾ ਲੈਂਦੀ ਹੈ । ਚਮਗਾਦੜ ਦੁਆਰਾ ਉਤਪੰਨ ਉੱਚ ਤਿੱਖਾਪਣ ਵਾਲੀ ਪਰਾਧੁਨੀ ਚਿੱਚੋਂ ਦੀਆਂ ਅਵਾਜ਼ਾਂ, ਰੁਕਾਵਟਾਂ ਜਾਂ ਪਤੰਗਿਆਂ ਤੋਂ ਪਰਾਵਰਤਿਤ ਹੋ ਕੇ ਚਮਗਾਦੜ ਦੇ ਕੰਨਾਂ ਤੱਕ ਪਹੁੰਚਦੀਆਂ ਹਨ । ਇਹਨਾਂ ਪਰਾਵਰਤਿਤ ਅਵਾਜ਼ਾਂ ਦੀ ਪ੍ਰਕਿਰਤੀ ਤੋਂ ਚਮਗਾਦੜ ਨੂੰ ਪਤਾ ਚਲਦਾ ਹੈ ਕਿ ਰੁਕਾਵਟ ਜਾਂ ਪਤੰਗਾ (ਸ਼ਿਕਾਰ) ਕਿੱਥੇ ਹੈ ਅਤੇ ਕਿਸ ਪ੍ਰਕਾਰ ਦਾ ਹੈ । ਉਹ ਸਹਿਜੇ ਹੀ ਉਸ ਦਾ ਸ਼ਿਕਾਰ ਕਰ ਲੈਂਦਾ ਹੈ ।

![]()
ਪ੍ਰਸ਼ਨ 18.
ਵਸਤੂਆਂ ਨੂੰ ਸਾਫ ਕਰਨ ਲਈ ਪਰਾਸਰਵਣ ਧੁਨੀ ਦਾ ਉਪਯੋਗ ਕਿਵੇਂ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ?
ਉੱਤਰ-
ਪਰਾਧੁਨੀ ਨੂੰ ਆਮ ਤੌਰ ‘ਤੇ ਉਨ੍ਹਾਂ ਭਾਗਾਂ ਨੂੰ ਸਾਫ ਕਰਨ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਤੱਕ ਪਹੁੰਚਣਾ ਕਠਿਨ ਹੁੰਦਾ ਹੈ, ਜਿਵੇਂ ਸਪਿਰਲਾਕਾਰ ਨਲੀ, ਟੇਢੇ-ਮੇਢੇ ਅਕਾਰ ਵਾਲੇ ਪੁਰਜ਼ੇ, ਇਲੈੱਕਟ੍ਰਾਨਿਕ ਉਪਕਰਣ ਆਦਿ । ਜਿਹੜੀਆਂ ਵਸਤੂਆਂ ਨੂੰ ਸਾਫ ਕਰਨਾ ਹੁੰਦਾ ਹੈ ਉਹਨਾਂ ਨੂੰ ਸਾਫ ਕਰਨ ਵਾਲੇ ਘੋਲ ਵਿੱਚ ਰੱਖਿਆ ਜਾਂਦਾ ਹੈ ਅਤੇ ਇਸ ਘੋਲ ਵਿੱਚ ਪਰਾਧੁਨੀ ਤਰੰਗਾਂ ਭੇਜੀਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਉੱਚ ਆਵਤੀ ਦੇ ਕਾਰਣ, ਧੂੜ, ਚਿਕਨਾਈ ਅਤੇ ਗੰਦਗੀ ਦੇ ਕਣ ਅਲੱਗ ਹੋ ਕੇ ਹੇਠਾਂ ਡਿੱਗ ਜਾਂਦੇ ਹਨ । ਇਸ ਪ੍ਰਕਾਰ ਵਸਤੂ ਚੰਗੀ ਤਰ੍ਹਾਂ ਸਾਫ ਹੋ ਜਾਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 19.
ਸੋਨਾਰ ਦੀ ਕਾਰਜ-ਵਿਧੀ (working) ਅਤੇ ਉਪਯੋਗਾਂ ਦਾ ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
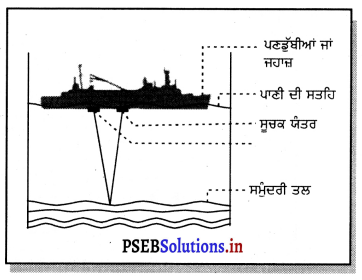
ਸੋਨਾਰ (SONAR) – ਸੋਨਾਰ ਇੱਕ ਅਜਿਹੀ ਜਗਤ ਹੈ ਜਿਸ ਵਿੱਚ, ਪਾਣੀ ਅੰਦਰ ਪਈਆਂ ਵਸਤੂਆਂ ਦੀ ਦੁਰੀ, ਦਿਸ਼ਾ ਅਤੇ ਚਾਲ ਮਾਪਣ ਦੇ ਲਈ ਪਧੁਨੀ ਤਰੰਗਾਂ ਦਾ ਉਪਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਕਾਰਜਵਿਧੀ – ਸੋਨਾਰ ਵਿੱਚ ਇੱਕ ਟਰਾਂਸਮੀਟਰ ਅਤੇ ਇੱਕ ਸੂਚਕ ਯੰਤਰ ਹੈ ਜਿਸ ਨੂੰ ਕਿਸੇ ਕਿਸ਼ਤੀ ਜਾਂ ਜਹਾਜ਼ ਵਿੱਚ ਲਗਾਇਆ ਜਾਂਦਾ ਹੈ ।
ਟਰਾਂਸਮੀਟਰ ਪਧੁਨੀ ਤਰੰਗਾਂ ਉਤਪੰਨ ਕਰਦਾ ਅਤੇ ਛੱਡਦਾ ਹੈ । ਇਹ ਤਰੰਗਾਂ ਪਾਣੀ ਵਿੱਚ ਚਲਦੀਆਂ ਹਨ ਅਤੇ ਸਮੁੰਦਰੀ ਤਲ ਵਿੱਚ ਪਈ ਵਸਤੂ ਦੇ ਨਾਲ ਟਕਰਾਉਣ ਤੋਂ ਬਾਅਦ ਪਰਾਵਰਤਿਤ ਹੋ ਕੇ ਸੂਚਕ ਯੰਤਰ ਦੁਆਰਾ ਹਿਣ ਕਰ ਲਈਆਂ ਜਾਂਦੀਆਂ ਹਨ । ਸੂਚਕ ਯੰਤਰ ਪਰਾਧੁਨੀ ਤਰੰਗਾਂ ਨੂੰ ਬਿਜਲਈ ਸੰਕੇਤਾਂ ਵਿੱਚ ਬਦਲ ਦਿੰਦਾ ਹੈ । ਪਾਣੀ ਵਿੱਚ ਧੁਨੀ ਦੀ ਚਾਲ ਅਤੇ ਧੁਨੀ ਦੇ ਧੁਨੀ-ਸੋਤ (Transmitter) ਤੋਂ ਜਾਣ ਅਤੇ ਆਉਣ ਦਾ ਸਮਾਂ-ਅੰਤਰਾਲ ਪਤਾ ਕਰਕੇ ਉਸ ਵਸਤੂ ਦੀ ਦੁਰੀ ਪਤਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ । ਮੰਨ ਲਓ ਪਰਾਧੁਨੀ ਸੰਕੇਤ ਦੇ ਭੇਜਣ ਅਤੇ ਵਾਪਸ ਪ੍ਰਾਪਤ ਕਰਨ ਦਾ ਸਮਾਂ ਅੰਤਰਾਲ ‘t’ ਹੈ ਅਤੇ ਸਮੁੰਦਰ ਵਿੱਚ ਧੁਨੀ ਦੀ ਚਾਲ V ਹੈ ਤਾਂ ਸਤ੍ਹਾ ਤੋਂ ਵਸਤੂ ਦੀ ਦੂਰੀ 2 d ਹੋਵੇਗੀ
∴ 2 d = V × t
ਇਸ ਵਿਧੀ ਨੂੰ ਪਰਾਧੁਨੀ ਗਸ਼ਤ (Echo-Ranging) ਕਹਿੰਦੇ ਹਨ ।
ਉਪਯੋਗ – ਸੋਨਾਰ ਦਾ ਉਪਯੋਗ ਸਮੁੰਦਰ ਦੀ ਡੂੰਘਾਈ ਪਤਾ ਕਰਨ ਅਤੇ ਸਮੁੰਦਰ ਅੰਦਰ ਸਥਿਤ ਚੱਟਾਨਾਂ, ਪਣਡੁੱਬੀਆਂ, ਬਰਫ ਦੇ ਤੋਦੇ (lceberg), ਡੁੱਬੇ ਹੋਏ ਜਹਾਜ਼ ਆਦਿ ਦੀ ਜਾਣਕਾਰੀ ਪ੍ਰਾਪਤ ਕਰਨ ਦੇ ਲਈ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 20.
ਇੱਕ ਪਣਡੁੱਬੀ ਉੱਪਰ ਲੱਗੀ ਸੋਨਾਰ ਯੁਕਤੀ ਸੰਕੇਤ ਭੇਜਦਾ ਹੈ ਅਤੇ ਗੂੰਜ (echo) 5 s ਬਾਅਦ ਗ੍ਰਹਿਣ ਕਰਦਾ ਹੈ । ਜੇਕਰ ਪਣਡੁੱਬੀ ਤੋਂ ਵਸਤੁ ਦੀ ਦੂਰੀ 3625 m ਹੋਵੇ ਤਾਂ ਧੁਨੀ ਦੀ ਚਾਲ ਦਾ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਧੁਨੀ ਤਰੰਗ ਅਤੇ ਟੋਹੇ ਜਾਣ ਦੇ ਵਿਚਕਾਰ ਲੱਗਿਆ ਸਮਾਂ t = 5 s.
ਸਮੁੰਦਰ ਦੀ ਡੂੰਘਾਈ (d) = 3625 m
ਪਰਾਸਰਵਣ ਧੁਨੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ (24) = 2 × 3625 m
= 7250 m
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, 2d = ਧੁਨੀ ਦੀ ਚਾਲ × ਸਮਾਂ
7250 = ਧੁਨੀ ਦੀ ਚਾਲ × 5
∴ ਧੁਨੀ ਦੀ ਚਾਲ (υ) = \(\frac{7250}{5}\)
= 1450 m/s
ਪ੍ਰਸ਼ਨ 21.
ਕਿਸੇ ਧਾਤ ਦੇ ਬਲਾਕ ਵਿੱਚ ਦੋਸ਼ਾਂ (defects) ਦਾ ਪਤਾ ਲਗਾਉਣ ਦੇ ਲਈ ਪਰਾਸਰਵਣ ਧੁਨੀ ਦਾ ਉਪਯੋਗ ਕਿਵੇਂ ਕੀਤਾ ਜਾਂਦਾ ਹੈ ? ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
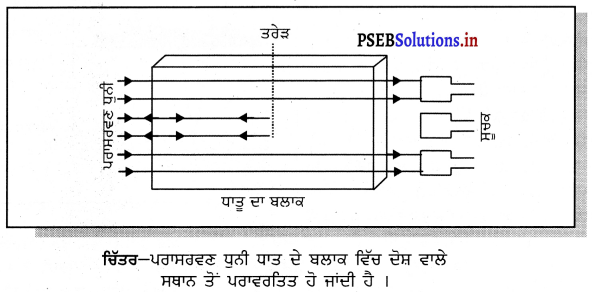
ਪਰਾਧੁਨੀ ਦਾ ਉਪਯੋਗ ਧਾਤ ਦੇ ਬਲਾਕਾਂ ਵਿੱਚ ਦਰਾਰਾਂ ਅਤੇ ਹੋਰ ਦੋਸ਼ਾਂ ਦਾ ਪਤਾ ਲਗਾਉਣ ਲਈ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ । ਧਾਤਵੀ ਵਸਤੂਆਂ ਨੂੰ ਅਕਸਰ ਵੱਡੇ-ਵੱਡੇ ਭਵਨਾਂ, ਪੁਲਾਂ, ਮਸ਼ੀਨਾਂ ਅਤੇ ਵਿਗਿਆਨਕ ਉਪਕਰਨਾਂ ਬਣਾਉਣ ਵਾਸਤੇ ਵਰਤੋਂ ਵਿੱਚ ਲਿਆਇਆ ਜਾਂਦਾ ਹੈ । ਧਾਤਾਂ ਦੇ ਬਲਾਕਾਂ ਵਿੱਚ ਦਰਾਰਾਂ ਜਾਂ ਛੇਕ ਜੋ ਬਾਹਰ ਤੋਂ ਦਿਖਾਈ ਨਹੀਂ ਦਿੰਦੇ ਢਾਂਚੇ ਦੀ ਬਣਤਰ ਦੀ ਮਜ਼ਬੂਤੀ ਘੱਟ ਕਰ ਦਿੰਦੇ ਹਨ । ਪਰਾਧੁਨੀ ਤਰੰਗਾਂ ਧਾਤ ਦੇ ਬਲਾਕ ਵਿੱਚੋਂ ਦੀ ਲੰਘਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ਅਤੇ ਆਰ-ਪਾਰ ਹੋਣ ਵਾਲੀਆਂ ਤਰੰਗਾਂ ਦਾ ਪਤਾ ਲਗਾਉਣ ਲਈ ਸੂਚਕ ਯੰਤਰ ਦਾ ਉਪਯੋਗ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਜੇਕਰ ਥੋੜ੍ਹਾ ਜਿਹਾ ਹੀ ਨੁਕਸ ਹੈ ਤਾਂ ਪਰਾਧੁਨੀ ਤਰੰਗਾਂ ਪਰਾਵਰਤਿਤ ਹੋ ਜਾਂਦੀਆਂ ਹਨ ਜੋ ਦੋਸ਼ ਹੋਣ ਦੀ ਪਰਿਸਥਿਤੀ ਨੂੰ ਦਰਸਾਉਂਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 22.
ਮਨੁੱਖੀ ਕੰਨ ਕਿਸ ਤਰ੍ਹਾਂ ਕੰਮ ਕਰਦਾ ਹੈ ? ਵਰਣਨ ਕਰੋ ।
ਉੱਤਰ-
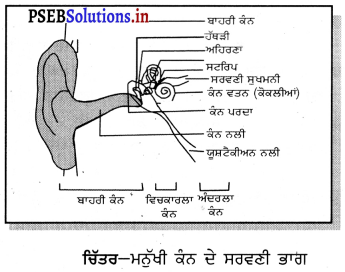
ਮਨੁੱਖੀ ਕੰਨ ਦੀ ਕਾਰਜ ਵਿਧੀ- ਮਨੁੱਖ ਦੇ ਬਾਹਰੀ ਕੰਨ ਨੂੰ “ਪਿੰਨਾਂ’ ਜਾਂ” ‘‘ਕੰਨ ਪਲੱਵ’’ ਕਹਿੰਦੇ ਹਨ ਜੋ ਆਲੇ-ਦੁਆਲੇ ਦੇ ਵਾਤਾਵਰਣ ਤੋਂ ਧੁਨੀ ਨੂੰ ਇਕੱਠਾ ਕਰਦਾ ਹੈ । ਇਹ ਇਕੱਠੀ ਕੀਤੀ ਧੁਨੀ ਕੰਨ ਨਲੀ ਵਿੱਚੋਂ ਗੁਜ਼ਰਦੀ ਹੋਈ ਕੰਨ ਨਲੀ ਦੇ ਸਿਰੇ ਉੱਪਰ ਲੱਗੀ ਪਤਲੀ ਝਿੱਲੀ ’ਤੇ ਡਿੱਗਦੀ ਹੈ । ਇੱਥੇ ਮਾਧਿਅਮ ਦੀ ਨਪੀੜਨ ਕਾਰਣ ਤਿੱਲੀ ਦੇ ਬਾਹਰ ਵੱਲ ਦਬਾਅ ਵੱਧ ਜਾਂਦਾ ਹੈ ਜੋ ਕੰਨ ਨੂੰ ਅੰਦਰ ਵੱਲ ਧੱਕਦਾ ਹੈ । ਨਿਖੇੜਨਾਂ ਦੇ ਪਹੁੰਚਣ ‘ਤੇ ਕੰਨ ਦਾ ਪਰਦਾ ਬਾਹਰ ਵੱਲ ਗਤੀ ਕਰਦਾ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਪਰਦਾ ਕੰਪਨ ਕਰਨ ਲੱਗਦਾ ਹੈ । ਕੰਨ ਦੇ ਮੱਧ ਭਾਗ ਵਿੱਚ ਲੱਗੀਆਂ ਤਿੰਨ ਹੱਡੀਆਂ (ਹਥੌੜੀ, ਐਨਵਿਲ ਅਤੇ ਸਟਰਿੱਪ) ਇਹਨਾਂ ਕੰਪਨਾਂ ਨੂੰ ਕਈ ਗੁਣਾਂ ਵੱਡਾ ਕਰ ਦਿੰਦੀਆਂ ਹਨ ਅਤੇ ਇਹਨਾਂ ਦਬਾਅ ਪਰਿਵਰਤਨਾਂ ਨੂੰ ਕੰਨ ਦੇ ਅੰਦਰਲੇ ਭਾਗ ਤੱਕ ਪਹੁੰਚਾ ਦਿੰਦੀਆਂ ਹਨ । ਇੱਥੇ ਇਹਨਾਂ ਦਬਾਅ ਪਰਿਵਰਤਨਾਂ ਨੂੰ ਬਿਜਲੀ ਸੰਕੇਤਾਂ ਵਿੱਚ ਬਦਲ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ ਅਤੇ ਸੁਣਨ ਤੰਤੂਆਂ ਰਾਹੀਂ ਦਿਮਾਗ ਤੱਕ ਭੇਜ ਦਿੱਤਾ ਜਾਂਦਾ ਹੈ । ਦਿਮਾਗ ਇਹਨਾਂ ਦੀ ਧੁਨੀ ਰੂਪ ਵਿੱਚ ਵਿਆਖਿਆ ਕਰਦਾ ਹੈ ।
![]()
Science Guide for Class 9 PSEB ਧੁਨੀ InText Questions and Answers
ਪਾਠ-ਪੁਸਤਕ ਦੇ ਪ੍ਰਸ਼ਨਾਂ ਦੇ ਉੱਤਰ
ਪ੍ਰਸ਼ਨ 1.
ਕਿਸੇ ਮਾਧਿਅਮ ਵਿੱਚ ਕੰਪਨ ਕਰਦੀ ਵਸਤੂ ਦੁਆਰਾ ਉਤਪੰਨ ਹੋਈ ਧੁਨੀ ਤੁਹਾਡੇ ਕੰਨਾਂ ਤੱਕ ਕਿਵੇਂ ਪਹੁੰਚਦੀ ਹੈ ?
ਉੱਤਰ-
ਮਾਧਿਅਮ ਵਿੱਚ ਧੁਨੀ ਦਾ ਕੰਨਾਂ ਤੱਕ ਸੰਚਾਰ-ਜਦੋਂ ਵਸਤੁ ਕੰਪਨ ਕਰਦੀ ਹੋਈ ਅੱਗੇ ਵੱਲ ਵੱਧਦੀ ਹੈ ਤਾਂ ਇਹ ਆਪਣੇ ਸਾਹਮਣੇ ਦੇ ਹਵਾ ਕਣਾਂ ਨੂੰ ਨਪੀੜਦੀ ਹੈ ਜਿਸ ਤੋਂ ਉੱਚ ਦਬਾਅ ਵਾਲਾ ਖੇਤਰ ਪੈਦਾ ਹੋ ਜਾਂਦਾ ਹੈ । ਇਸ ਖੇਤਰ ਨੂੰ ਨਪੀੜਨ ਕਹਿੰਦੇ ਹਨ । ਇਹ ਦਾਬ ਕੰਪਨ ਕਰ ਰਹੀ ਵਸਤੁ ਤੋਂ ਅੱਗੇ ਵੱਲ ਗਤੀ ਕਰਦਾ ਹੈ । ਜਦੋਂ ਇਹ ਕੰਪਨ ਕਰ ਰਹੀ ਵਸਤੁ ਪਿੱਛੇ ਵੱਲ ਕੰਪਨ ਕਰਦੀ ਹੈ ਤਾਂ ਇਕ ਘੱਟ ਦਬਾਅ ਵਾਲਾ ਖੇਤਰ ਉਤਪੰਨ ਹੋ ਜਾਂਦਾ ਹੈ ਜਿਸਨੂੰ ਨਿਖੇੜਨ (ਵਿਰਲਨ) ਕਹਿੰਦੇ ਹਨ ।
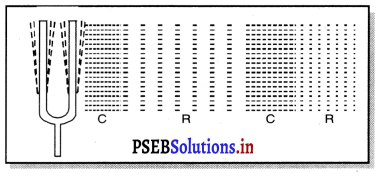
ਜਦੋਂ ਕੰਪਨ ਕਰ ਰਹੀ ਵਸਤੂ ਅੱਗੇ ਅਤੇ ਪਿੱਛੇ ਤੇਜ਼ੀ ਨਾਲ ਗਤੀ ਕਰਦੀ ਹੈ ਤਾਂ ਹਵਾ ਵਿੱਚ ਨਪੀੜਨ ਅਤੇ ਨਿਖੇੜਨ ਦੀ ਇੱਕ ਲੜੀ ਬਣ ਜਾਂਦੀ ਹੈ ਅਰਥਾਤ ਧੁਨੀ ਤਰੰਗ ਬਣ ਜਾਂਦੀ ਹੈ । ਇਸ ਤਰ੍ਹਾਂ ਇੱਕ ਮਾਧਿਅਮ ਵਿੱਚ ਧੁਨੀ ਸੰਚਾਰ ਘਣਤਾ ਦੇ ਪਰਿਵਰਤਨ ਦੇ ਸੰਚਾਰ ਦੇ ਰੂਪ ਵਿੱਚ ਹੁੰਦਾ ਹੈ ਜੋ ਸਾਡੇ ਕੰਨ ਤੱਕ ਪਹੁੰਚ ਕੇ ਪੇਸਕ ਝਿੱਲੀ ਨੂੰ ਧੱਕਦੀ ਹੈ ਅਤੇ ਉਸ ਵਿੱਚ ਕੰਪਨ ਪੈਦਾ ਕਰਦੀ ਹੈ ਜਿਸ ਤੋਂ ਸਾਨੂੰ ਧੁਨੀ ਦਾ ਅਨੁਭਵ ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 2.
ਤੁਹਾਡੇ ਸਕੂਲ ਦੀ ਘੰਟੀ ਧੁਨੀ ਕਿਵੇਂ ਉਤਪੰਨ ਕਰਦੀ ਹੈ, ਵਿਆਖਿਆ ਕਰੋ ।
ਉੱਤਰ-
ਜਦੋਂ ਸਕੂਲ ਦੀ ਘੰਟੀ ਨੂੰ ਹਥੌੜੇ ਨਾਲ ਸੱਟ ਮਾਰੀ ਜਾਂਦੀ ਹੈ ਤਾਂ ਇਹ ਕੰਪਨ ਕਰਨ ਲੱਗਦੀ ਹੈ ਜਿਸ ਤੋਂ ਧੁਨੀ ਤਰੰਗਾਂ ਉਤਪੰਨ ਹੁੰਦੀਆਂ ਹਨ । ਹੁਣ ਜੇਕਰ ਘੰਟੀ ਨੂੰ ਹੌਲੀ ਜਿਹਾ ਛੂਹ ਦਿੱਤਾ ਜਾਏ ਤਾਂ ਸਾਨੂੰ ਇਹਨਾਂ ਕੰਪਨਾਂ ਦਾ ਅਨੁਭਵ ਹੋਵੇਗਾ ।
ਪ੍ਰਸ਼ਨ 3.
ਧੁਨੀ ਤਰੰਗਾਂ ਨੂੰ ਯੰਤਰਿਕ ਤਰੰਗਾਂ ਕਿਉਂ ਕਹਿੰਦੇ ਹਨ ?
ਉੱਤਰ-
ਧੁਨੀ ਇੱਕ ਪ੍ਰਕਾਰ ਦੀ ਉਰਜਾ ਹੈ ਜਿਹੜੀ ਆਪਣੇ ਆਪ ਨਹੀਂ ਪੈਦਾ ਹੋ ਸਕਦੀ । ਇਸ ਨੂੰ ਪੈਦਾ ਕਰਨ ਲਈ ਯੰਤਰਿਕ ਉਰਜਾ ਦੀ ਲੋੜ ਪੈਂਦੀ ਹੈ ਭਾਵੇਂ ਉਹ ਤਾਲੀ ਵਜਾ ਕੇ ਜਾਂ ਫਿਰ ਹਥੌੜੇ ਨਾਲ ਘੰਟੀ ਤੇ ਸੱਟ ਮਾਰ ਕੇ ਹੈ । ਇਹ ਧੁਨੀ ਉਰਜਾ ਤਰੰਗਾਂ ਦੇ ਰੂਪ ਵਿੱਚ ਮਾਧਿਅਮ ਦੇ ਕਣਾਂ ਵਿੱਚ ਹਿਲ-ਜੁਲ ਪੈਦਾ ਕਰਕੇ ਸੰਚਾਰਿਤ ਹੁੰਦੀ ਹੈ । ਇਸ ਲਈ ਇਸਨੂੰ ਯੰਤਰਿਕ ਤਰੰਗਾਂ ਦਾ ਨਾਂ ਦਿੱਤਾ ਗਿਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ 4.
ਮੰਨ ਲਉ ਕਿ ਤੁਸੀਂ ਆਪਣੇ ਮਿੱਤਰ ਨਾਲ ਚੰਦਰਮਾ ਉੱਤੇ ਗਏ ਹੋਏ ਹੋ । ਕੀ ਤੁਸੀਂ ਆਪਣੇ ਮਿੱਤਰ ਦੁਆਰਾ ਉਤਪੰਨ ਧੁਨੀ ਸੁਣ , ਸਕਦੇ ਹੋ ?
ਉੱਤਰ-
ਧੁਨੀ ਦੇ ਸੰਚਰਣ ਲਈ ਹਵਾ ਜਾਂ ਕਿਸੇ ਹੋਰ ਪਦਾਰਥਕ ਮਾਧਿਅਮ ਦੀ ਲੋੜ ਹੁੰਦੀ ਹੈ । ਚੰਦਰਮਾ ਤੇ ਅਜਿਹਾ ਕੋਈ ਮਾਧਿਅਮ ਨਹੀਂ ਹੈ ਜਿਸ ਕਰਕੇ ਨਿਰਵਾਤ ਵਿੱਚ ਧੁਨੀ ਇੱਕ ਥਾਂ ਤੋਂ ਦੂਜੀ ਥਾਂ ਤੱਕ ਨਹੀਂ ਜਾ ਸਕਦੀ । ਇਸ ਲਈ ਤੁਸੀਂ ਆਪਣੇ ਮਿੱਤਰ ਨਾਲ ਗੱਲਬਾਤ ਨਹੀਂ ਕਰ ਸਕਦੇ ਹੋ ।
ਪ੍ਰਸ਼ਨ 5.
ਤਰੰਗ ਦਾ ਕਿਹੜਾ ਗੁਣ ਹੇਠਾਂ ਦਿੱਤੀਆਂ ਨੂੰ ਨਿਰਧਾਰਿਤ ਕਰਦਾ ਹੈ ?
(a) ਉੱਚਾਪਨ (Loudness)
(b) ਤਿੱਖਾਪਣ ((Pitch)
ਉੱਤਰ-
(a) ਉੱਚਾਪਨ (Loudness) – ਕਿਸੇ ਧੁਨੀ ਤਰੰਗ ਦੀ ਪ੍ਰਬਲਤਾ (ਉੱਚਾਪਨ) ਦਾ ਅਨੁਮਾਨ ਉਸਦੇ ਆਯਾਮ ਤੋਂ ਲਗਾਇਆ ਜਾਂਦਾ ਹੈ । ਧੁਨੀ ਤਰੰਗ ਦਾ ਆਯਾਮ ਵਸਤੂ ਨੂੰ ਕੰਪਨ ਕਰਾਉਣ ਲਈ ਬਲ ਦੇ ਪਰਿਮਾਣ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ । ਜ਼ਿਆਦਾ ਬਲ ਦੀ ਮਾਤਰਾ ਲਗਾਉਣ ਨਾਲ ਪ੍ਰਬਲ ਧੁਨੀ ਉਤਪੰਨ ਹੁੰਦੀ ਹੈ । ਪ੍ਰਬਲ ਧੁਨੀ ਵੱਧ ਦੂਰੀ ਚੱਲ ਸਕਦੀ ਹੈ ਕਿਉਂਕਿ ਇਸ ਵਿੱਚ ਵੱਧ ਊਰਜਾ ਹੁੰਦੀ ਹੈ । ਜਿਉਂ-ਜਿਉਂ ਧੁਨੀ ਸੋਤ ਤੋਂ ਦੂਰ ਫੈਲਦੀ ਹੈ ਇਸਦਾ ਉੱਚਾਪਨ ਘੱਟ ਜਾਂਦਾ ਹੈ ।
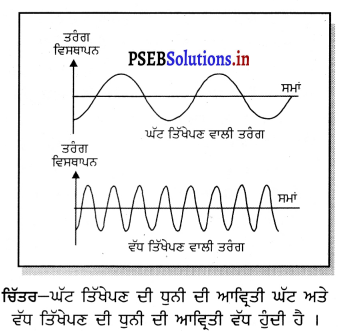
(b) ਤਿੱਖਾਪਣ (Pitch) – ਕਿਸੇ ਉਤਸਰਜਿਤ ਧੁਨੀ ਦੀ ਆਵਿਤੀ ਨੂੰ ਤਿੱਖਾਪਣ ਕਹਿੰਦੇ ਹਨ । ਧੁਨੀ ਦਾ ਤਿੱਖਾਪਣ ਉਸਦੀ ਆਵਤੀ ਨਿਰਧਾਰਿਤ ਕਰਦਾ ਹੈ । ਕਿਸੇ ਸੋਤ ਦਾ ਕੰਪਨ ਜਿੰਨਾ ਜ਼ਿਆਦਾ ਜਲਦੀ ਹੋਵੇਗਾ ਉਸ ਦੀ ਆਤੀ ਓਨੀ ਜ਼ਿਆਦਾ ਹੋਵੇਗੀ ਅਤੇ ਉਸ ਦਾ ਤਿੱਖਾਪਣ ਵੀ ਜ਼ਿਆਦਾ ਹੋਵੇਗਾ । ਇਸੇ
ਘੱਟ ਤਿੱਖੇਪਣ ਵਾਲੀ ਤਰੰਗ ਤਰ੍ਹਾਂ ਧੁਨੀ ਦਾ ਤਿੱਖਾਪਣ ਘੱਟ ਹੋਵੇਗਾ ਜੇਕਰ ਉਸਦੀ ਆਵਿਤੀ ਘੱਟ ਹੋਵੇਗੀ । ਜ਼ਿਆਦਾ ਤਿੱਖੇਪਣ ਵਾਲੀ ਧੁਨੀ ਵਿੱਚ ਕਿਸੇ ਨਿਸ਼ਚਿਤ ਬਿੰਦੂ ਤੋਂ ਇਕਾਈ ਸਮੇਂ ਵਿੱਚ ਲੰਘ ਰਹੇ ਨਪੀੜਨਾਂ ਦੀ ਸਮਾਂ ਸੰਖਿਆ ਜ਼ਿਆਦਾ ਹੋਵੇਗੀ ।
![]()
ਪ੍ਰਸ਼ਨ 6.
ਅਨੁਮਾਨ ਲਗਾਓ ਕਿ ਹੇਠ ਦਿੱਤੀਆਂ ਵਿੱਚੋਂ ਕਿਹੜੀ ਧੁਨੀ ਦਾ ਤਿੱਖਾਪਣ (Pitch) ਜ਼ਿਆਦਾ ਹੈ ?
(a) ਗਿਟਾਰ (Guitar)
(b) ਕਾਰ ਦਾ ਹਾਰਨ ।
ਉੱਤਰ-
(a) ਗਿਟਾਰ ।
ਪ੍ਰਸ਼ਨ 7.
ਕਿਸੇ ਧੁਨੀ ਦੀ ਤਰੰਗ ਲੰਬਾਈ, ਆਕ੍ਰਿਤੀ, ਆਵਰਤਕਾਲ (Time Period) ਅਤੇ ਆਯਾਮ ਤੋਂ ਕੀ ਭਾਵ ਹੈ ?
ਉੱਤਰ-
(i) ਤਰੰਗ ਲੰਬਾਈ (Wave Length) – ਮਾਧਿਅਮ ਦੇ ਕਿਸੇ ਕਣ ਨੂੰ ਇੱਕ ਕੰਪਨ ਕਰਨ ਵਿੱਚ ਲੱਗੇ ਸਮੇਂ ਦੌਰਾਨ ਤਰੰਗ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ ਹੁੰਦੀ ਹੈ ।
ਜਾਂ
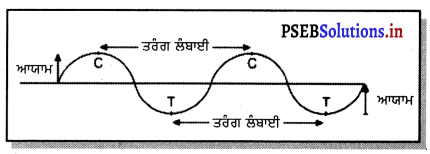
ਇਹ ਲਾਂਗੀਚਿਊਡੀਨਲ ਤਰੰਗ ਦੀਆਂ ਦੋ ਲਾਗਲੀਆਂ ਨਪੀੜਨਾਂ ਜਾਂ ਦੋ ਲਾਗਲੀਆਂ ਨਿਖੇੜਨਾਂ ਦੇ ਵਿਚਾਲੇ ਦੀ ਦੂਰੀ ਹੁੰਦੀ ਹੈ । ਤਰੰਗ ਲੰਬਾਈ ਨੂੰ ‘λ’ (ਗੀਕ ਅੱਖਰ ਲੈਮਡਾ) ਨਾਲ ਦਰਸਾਇਆ ਜਾਂਦਾ ਹੈ । ਇਸ ਦਾ S.I. ਮਾਤ੍ਰਿਕ ਮੀਟਰ (m) ਹੈ ।
(ii) ਆਕ੍ਰਿਤੀ (Frequency) – ਕਿਸੇ ਮਾਧਿਅਮ ਵਿੱਚ ਤਰੰਗ ਸੰਚਰਣ ਦੌਰਾਨ ਮਾਧਿਅਮ ਦੇ ਕਿਸੇ ਕਣ ਦੁਆਰਾ ਇੱਕ ਸੈਕੰਡ ਵਿੱਚ ਪੂਰੀਆਂ ਕੀਤੀਆਂ ਗਈਆਂ ਕੰਪਨਾਂ ਦੀ ਸੰਖਿਆ ਹੁੰਦੀ ਹੈ । ਇਸਨੂੰ ਤਾਂ ਨਾਲ ਪ੍ਰਦਰਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਆੜੀ ਦਾ S.I. ਮਾਤ੍ਰਿਕ ਹਰਟਜ਼ (Hz) ਹੈ । ਆਤੀ ਨੂੰ ਕਿਸੇ ਬਿੰਦੂ ਤੋਂ ਗੁਜ਼ਰਨ ਵਾਲੀਆਂ ਨਪੀੜਨਾਂ ਜਾਂ ਨਿਖੇੜਨਾਂ ਦੀ ਗਿਣਤੀ ਦੁਆਰਾ ਮਾਪਿਆ ਜਾਂਦਾ ਹੈ ।
(iii) ਆਵਰਤ ਕਾਲ (Time Period) – ਤਰੰਗ ਸੰਚਰਣਾ ਦੌਰਾਨ ਮਾਧਿਅਮ ਦੇ ਕਿਸੇ ਕਣ ਦੁਆਰਾ ਇੱਕ ਕੰਪਨ ਨੂੰ ਪੂਰਾ ਕਰਨ ਲਈ ਲੱਗਿਆ ਸਮਾਂ ਹੁੰਦਾ ਹੈ । ਇਸਨੂੰ ‘T’ ਨਾਲ ਪ੍ਰਦਰਸ਼ਿਤ ਕਰਦੇ ਹਨ । ਇਸ ਦਾ S.I. ਮਾਤ੍ਰਿਕ ਸੈਕੰਡ ਹੈ ।
ਜਾਂ
ਧੁਨੀ ਤਰੰਗ ਦੀਆਂ ਦੋ ਲਾਗਲੀਆਂ ਨਪੀੜਨਾਂ ਜਾਂ ਨਿਖੇੜਨਾਂ ਨੂੰ ਇੱਕ ਬਿੰਦੂ ਤੋਂ ਲੰਘਣ ਲਈ ਲੱਗਿਆ ਸਮਾਂ ਹੁੰਦਾ ਹੈ ।
(iv) ਆਯਾਮ (Amplitude) – ਮਾਧਿਅਮ ਦੇ ਕਿਸੇ ਕਣ ਦਾ ਮੱਧ ਸਥਿਤੀ ਦੇ ਦੋਨਾਂ ਪਾਸੇ ਵੱਧ ਤੋਂ ਵੱਧ ਵਿਸਥਾਪਨ ਨੂੰ ਆਯਾਮ ਕਹਿੰਦੇ ਹਨ । ਇਸਨੂੰ ਆਮ ਤੌਰ ਤੇ ‘A’ ਅੱਖਰ ਨਾਲ ਪ੍ਰਦਰਸ਼ਿਤ ਕੀਤਾ ਜਾਂਦਾ ਹੈ । ਧੁਨੀ ਤਰੰਗ ਲਈ ਇਸ ਦਾ ਮਾ ਦਬਾਅ ਜਾਂ ਘਣਤਾ ਦਾ ਮਾਕ ਹੀ ਹੁੰਦਾ ਹੈ । ਧੁਨੀ ਦੀ ਪ੍ਰਬਲਤਾ ਜਾਂ ਤਿੱਖਾਪਣ ਇਸਦੇ ਆਯਾਮ ‘ਤੇ ਨਿਰਭਰ ਕਰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 8.
ਕਿਸੇ ਧੁਨੀ ਤਰੰਗ ਦੀ ਤਰੰਗ ਲੰਬਾਈ λ ਅਤੇ ਆਕ੍ਰਿਤੀ (υ) ਉਸਦੇ ਵੇਗ ( v) ਨਾਲ ਕਿਵੇਂ ਸੰਬੰਧਿਤ ਹਨ ?
ਉੱਤਰ-
ਧੁਨੀ ਤਰੰਗ ਦਾ ਵੇਗ = ਤਰੰਗ ਲੰਬਾਈ × ਆਕ੍ਰਿਤੀ
ਜਾਂ v = λ × υ (frequency)
ਪ੍ਰਸ਼ਨ 9.
ਕਿਸੇ ਦਿੱਤੇ ਗਏ ਮਾਧਿਅਮ ਵਿੱਚ ਇੱਕ ਧੁਨੀ ਤਰੰਗ ਦੀ ਆਕ੍ਰਿਤੀ 220 Hz ਅਤੇ ਵੇਗ (velocity) 440 m/s ਹੈ । ਤਰੰਗ ਦੀ ਤਰੰਗ ਲੰਬਾਈ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਧੁਨੀ ਦਾ ਵੇਗ υ = 440 ms
ਧੁਨੀ ਦੀ ਆਵਿਤੀ (v) = 220 Hz
ਧੁਨੀ ਦੀ ਤਰੰਗ ਲੰਬਾਈ (λ) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ
υ = v × λ
440 = 220 × λ
∴ λ = \(\frac{440}{220}\)
ਅਰਥਾਤ ਤਰੰਗ ਲੰਬਾਈ (λ) = 2 m
ਪ੍ਰਸ਼ਨ 10.
ਕਿਸੇ ਧੁਨੀ ਸ੍ਰੋਤ ਤੋਂ 450 m ਦੀ ਦੂਰੀ ‘ਤੇ ਬੈਠਾ ਹੋਇਆ ਕੋਈ ਮਨੁੱਖ 50 Hz ਦੀ ਧੁਨੀ ਸੁਣਦਾ ਹੈ । ਸੋਤ ਤੋਂ ਮਨੁੱਖ ਤੱਕ ਪਹੁੰਚਣ ਵਾਲੇ ਦੋ ਕੁਮਵਾਰ ਨਪੀੜਨਾਂ (two successive compressions) ਵਿੱਚ ਕਿੰਨਾ ਸਮਾਂ-ਅੰਤਰਾਲ ਹੋਵੇਗਾ ?
ਹੱਲ:
ਦਿੱਤਾ ਹੈ, ਧੁਨੀ ਦੀ ਆਤੀ (v) = 500 ਹਰਟਜ਼ (Hz)
ਕੁਮਵਾਰ ਦੋ ਨਪੀੜਨਾਂ ਦੇ ਵਿਚਾਲੇ ਦੀ ਦੂਰੀ ਨੂੰ ਲੱਗਿਆ ਸਮਾਂ ਅੰਤਰਾਲ (ਆਵਰਤ ਕਾਲ (T) = ?
ਅਸੀਂ ਜਾਣਦੇ ਹਾਂ, ਆਵਰਤਕਾਲ (T) = 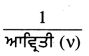
= \(\frac{1}{500}\)
= 0.002 ਸੈਕਿੰਡ
![]()
ਪ੍ਰਸ਼ਨ 11.
ਧੁਨੀ ਦਾ ਉੱਚਾਪਨ ਅਤੇ ਤੀਬਰਤਾ ਵਿੱਚ ਅੰਤਰ ਦੱਸੋ ।
ਉੱਤਰ-
ਧੁਨੀ ਦੇ ਉੱਚਾਪਨ ਅਤੇ ਤੀਬਰਤਾ ਵਿੱਚ ਅੰਤਰ-
| ਉੱਚਾਪਨ | ਤੀਬਰਤਾ |
| 1. ਧੁਨੀ ਲਈ ਉੱਚਾਪਨ ਕੰਨਾਂ ਦੀ ਸੰਵੇਦਨਸ਼ੀਲਤਾ ਦਾ ਮਾਪ ਹੈ । | 1. ਇਹ ਇਕਾਈ ਖੇਤਰਫਲ ਵਿੱਚੋਂ ਇੱਕ ਸੈਕਿੰਡ ਵਿੱਚ ਲੰਘਣ ਵਾਲੀ ਉਰਜਾ ਹੈ । |
| 2. ਧੁਨੀ ਦੇ ਉੱਚੇਪਨ ਨੂੰ ਮਾਪਿਆ ਨਹੀਂ ਜਾ ਸਕਦਾ ਹੈ । | 2. ਧੁਨੀ ਦੀ ਤੀਬਰਤਾ ਨੂੰ ਮਾਪਿਆ ਜਾ ਸਕਦਾ ਹੈ । |
| 3. ਵੱਖ-ਵੱਖ ਸੁਣਨ ਵਾਲਿਆਂ ਲਈ ਉੱਚਾਪਨ ਵੱਖ-ਵੱਖ ਹੋ ਸਕਦਾ ਹੈ । | 3. ਸਾਰਿਆਂ ਲਈ ਧੁਨੀ ਦੀ ਤੀਬਰਤਾ ਇੱਕੋ ਜਿਹੀ ਹੁੰਦੀ ਹੈ । |
| 4. ਪਰਾਧੁਨੀ ਤਰੰਗਾਂ ਦਾ ਸੁਣਾਈ ਨਾ ਦੇਣ ਕਾਰਨ ਉੱਚਾਪਨ ਸਿਫਰ ਹੁੰਦਾ ਹੈ । | 4. ਪਰਾਧੁਨੀ ਤਰੰਗਾਂ ਲਈ ਤੀਬਰ ਹੁੰਦੀ ਹੈ । |
ਪ੍ਰਸ਼ਨ 12.
ਹਵਾ, ਪਾਣੀ ਜਾਂ ਲੋਹੇ ਵਿੱਚੋਂ ਕਿਸ ਮਾਧਿਅਮ ਵਿੱਚ ਧੁਨੀ ਸਭ ਤੋਂ ਤੇਜ਼ ਚਲਦੀ ਹੈ ?
ਉੱਤਰ-
ਲੋਹੇ ਵਿੱਚੋਂ ਧੁਨੀ ਹਵਾ ਅਤੇ ਪਾਣੀ ਦੇ ਮੁਕਾਬਲੇ ਸਭ ਤੋਂ ਤੇਜ਼ ਚਲਦੀ ਹੈ । ਲੋਹੇ ਵਿੱਚ ਧੁਨੀ ਦਾ ਵੇਗ 5950ms-1 ਹੁੰਦਾ ਹੈ ।
ਪ੍ਰਸ਼ਨ 13.
ਕੋਈ ਗੂੰਜ 3s ਬਾਅਦ ਸੁਣਾਈ ਦਿੰਦੀ ਹੈ । ਜੇਕਰ ਧੁਨੀ ਦੀ ਚਾਲ 342 ms-1 ਹੋਵੇ ਤਾਂ ਸੋਤ ਅਤੇ ਪਰਾਵਰਤਿਤ ਸੜਾ ਦੇ ਵਿਚਕਾਰ ਕਿੰਨੀ ਦੂਰੀ ਹੋਵੇਗੀ ?
ਹੱਲ:
ਧੁਨੀ ਦਾ ਵੇਗ (v) = 342 ms-1
ਗੂੰਜ ਸੁਣਾਈ ਦੇਣ ਲਈ ਲੱਗਾ ਸਮਾਂ (t) = 3 s
ਧੁਨੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ (S) = v × t
= 342 × 3
= 1026 m
3 s ਵਿੱਚ ਧੁਨੀ ਨੇ ਸੋਤ ਤੋਂ ਪਰਾਵਰਤਕ ਸੜਾ ਅਤੇ ਫਿਰ ਪਰਾਵਰਤਕ ਸੜਾ ਤੋਂ ਸ੍ਰੋਤ ਤੱਕ ਵਾਪਸ ਆਉਣਾ ਹੈ ।
∴ ਸ੍ਰੋਤ ਅਤੇ ਪਰਾਵਰਤਕ ਸੜਾ ਵਿਚਕਾਰ ਦੂਰੀ = \(\frac{1026}{2}\)
= 513 m
ਪ੍ਰਸ਼ਨ 14.
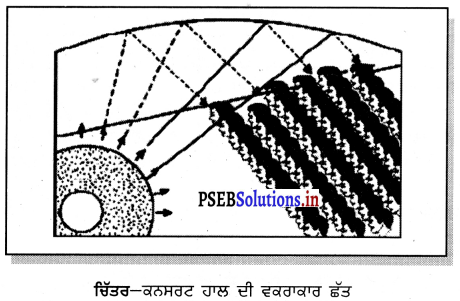
ਕਨਸਰਟ ਹਾਲ ਦੀਆਂ ਛੱਤਾਂ ਵਕਰਾਕਾਰ ਕਿਉਂ ਹੁੰਦੀਆਂ ਹਨ ?
ਉੱਤਰ-
ਕਨਸਰਟ ਹਾਲ ਦੀਆਂ ਛੱਤਾਂ ਵਕਰਾਕਾਰ ਬਣਾਈਆਂ ਜਾਂਦੀਆਂ ਹਨ ਤਾਂ ਜੋ ਧੁਨੀ ਪਰਾਵਰਤਨ ਤੋਂ ਬਾਅਦ ਪਰਾਵਰਤਿਤ ਧੁਨੀ ਹਾਲ ਦੇ ਸਾਰੇ ਭਾਗਾਂ ਵਿੱਚ ਇੱਕ ਸਮਾਨ ਪਹੁੰਚ ਕੇ ਸਪੱਸ਼ਟ ਸੁਣਾਈ ਦੇਵੇ ਜਿਵੇਂ ਕਿ ਚਿੱਤਰ ਵਿੱਚ ਦਰਸਾਇਆ ਗਿਆ ਹੈ ।
ਪ੍ਰਸ਼ਨ 15.
ਆਮ ਮਨੁੱਖ ਲਈ ਸੁਣਨ ਸੀਮਾ ਕੀ ਹੈ ?
ਉੱਤਰ-
ਆਮ ਮਨੁੱਖ ਲਈ ਧੁਨੀ ਦੀ ਸੁਣਨ ਸੀਮਾ ਲਗਭਗ 20 Hz ਤੋਂ 20,000 Hz ਤੱਕ ਹੁੰਦੀ ਹੈ ।
ਪ੍ਰਸ਼ਨ 16.
ਹੇਠ ਦਿੱਤਿਆਂ ਨਾਲ ਸੰਬੰਧਿਤ ਆਕ੍ਰਿਤੀਆਂ ਦੀ ਸੀਮਾ ਕੀ ਹੈ ?
(a) ਨੀਮ ਧੁਨੀ
(b) ਪਰਾਧੁਨੀ
ਉੱਤਰ-
(a) ਨੀਮ ਧੁਨੀ (infrasonic sound) ਲਈ ਧੁਨੀ ਦੀ ਆਵਿਤੀ ਸੀਮਾ 20 Hz ਹੈ ।
(b) ਪਰਾਧੁਨੀ (ultrasonic sound) ਲਈ ਧੁਨੀ ਦੀ ਆਤੀ ਸੀਮਾ 20 kHz (ਅਰਥਾਤ 20,000 Hz) ਹੈ ।
![]()
ਪ੍ਰਸ਼ਨ 17.
ਇੱਕ ਪਣਡੁੱਬੀ ਸੋਨਾਰ ਪਰਾ-ਸਰਵਣ ਧੁਨੀ ਛੱਡਦਾ ਹੈ ਜਿਹੜੀ ਪਾਣੀ ਦੇ ਅੰਦਰ ਇੱਕ ਖੜੀ ਚੱਟਾਨ ਨਾਲ ਟਕਰਾ ਕੇ 1.02 s ਮਗਰੋਂ ਵਾਪਸ ਆਉਂਦੀ ਹੈ । ਜੇਕਰ ਖਾਰੇ ਪਾਣੀ (sea water) ਵਿੱਚ ਧੁਨੀ ਦੀ ਚਾਲ 1531 ms ਹੋਵੇ, ਤਾਂ ਚੱਟਾਨ ਦੀ ਦੂਰੀ ਪਤਾ ਕਰੋ ।
ਹੱਲ:
ਧੁਨੀ ਨੂੰ ਪਣਡੁੱਬੀ ਤੋਂ ਚੱਟਾਨ ਤੱਕ ਅਤੇ ਵਾਪਸ ਪਹੁੰਚਣ ਲਈ ਲੱਗਾ ਸਮਾਂ = 1.02 s
ਖਾਰੇ ਪਾਣੀ ਵਿੱਚ ਪਰਾਧੁਨੀ ਦੀ ਚਾਲ = 1531 m/s
ਧੁਨੀ ਦੁਆਰਾ ਤੈਅ ਕੀਤੀ ਗਈ ਦੂਰੀ 2 d = ਧੁਨੀ ਚਾਲ × ਸਮਾਂ
= 1531 × 1.02
= 1561.62 m
∴ ਪਣਡੁੱਬੀ ਅਤੇ ਚੱਟਾਨ ਵਿੱਚ ਦੂਰੀ, d = \(\frac{1561.62}{2}\)
= 780.81 m
ਅਰਥਾਤ ਪਣਡੁੱਬੀ ਤੋਂ ਚੱਟਾਨ ਦੀ ਦੂਰੀ = 780.81 m














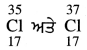 ਹੀ ਹਨ ਜਿਨ੍ਹਾਂ ਦਾ ਪਰਮਾਣੂ ਸੰਖਿਆ ਇੱਕ ਸਮਾਨ ਅਰਥਾਤ 17 ਹੈ, ਪਰੰਤੂ ਇੱਕ ਦਾ ਪਰਮਾਣੂ ਪੁੰਜ ਸੰਖਿਆ 35 ਅਤੇ ਦੂਜੇ ਦਾ ਪਰਮਾਣੂ ਪੁੰਜ ਸੰਖਿਆ 37 ਹੈ ।
ਹੀ ਹਨ ਜਿਨ੍ਹਾਂ ਦਾ ਪਰਮਾਣੂ ਸੰਖਿਆ ਇੱਕ ਸਮਾਨ ਅਰਥਾਤ 17 ਹੈ, ਪਰੰਤੂ ਇੱਕ ਦਾ ਪਰਮਾਣੂ ਪੁੰਜ ਸੰਖਿਆ 35 ਅਤੇ ਦੂਜੇ ਦਾ ਪਰਮਾਣੂ ਪੁੰਜ ਸੰਖਿਆ 37 ਹੈ ।