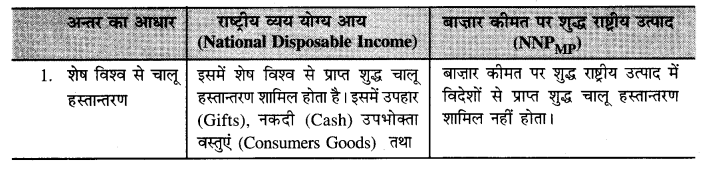
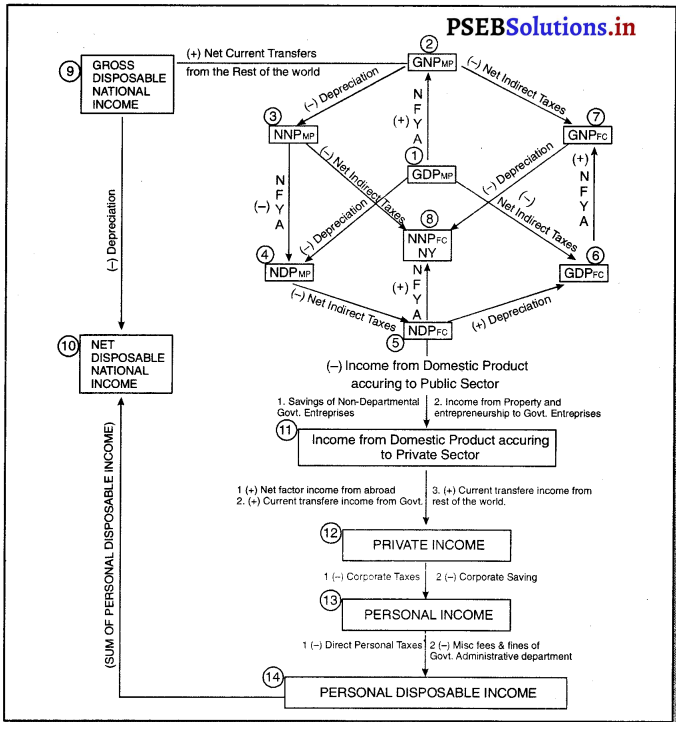
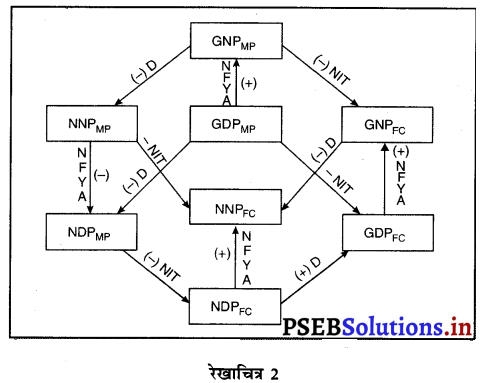
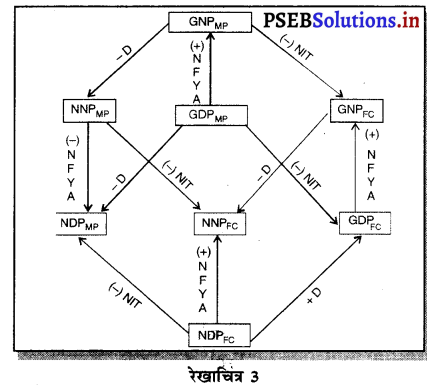
Punjab State Board PSEB 12th Class Economics Book Solutions Chapter 5 राष्ट्रीय आय का माप Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Economics Chapter 5 राष्ट्रीय आय का माप
PSEB 12th Class Economics राष्ट्रीय आय का माप Textbook Questions and Answers
I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)
प्रश्न 1.
राष्ट्रीय आय को मापने की मुख्य विधियाँ कौन सी हैं ?
उत्तर-
- आय विधि
- उत्पादन विधि
- व्यय विधि।
प्रश्न 2.
प्राथमिक क्षेत्र से क्या अभिप्राय है ?
उत्तर-
प्राथमिक क्षेत्र का सम्बन्ध कृषि क्षेत्र से होता है जिसमें प्राकृतिक साधनों को प्रयोग करके उत्पादन किया जाता है।
प्रश्न 3.
गौण क्षेत्र से क्या अभिप्राय है ?
उत्तर-
गौण क्षेत्र का अर्थ निर्माण क्षेत्र से होता है जैसा कि उद्योग, निर्माण कार्य, गैस इत्यादि।
प्रश्न 4.
अर्थव्यवस्था के तृतीय क्षेत्र अथवा सेवा क्षेत्र में क्या अभिप्राय है ?
उत्तर-
इस क्षेत्र में सेवाएँ शामिल की जाती हैं जैसा कि यातायात, बीमा, आवास इत्यादि।

प्रश्न 5.
मूल्य वृद्धि विधि से क्या अभिप्राय है ?
उत्तर-
मूल्य वृद्धि का अर्थ वस्तुओं के मूल्य में वृद्धि करने से होता है। मूल्य वृद्धि = उत्पाद के मूल्य – मध्यवर्ती उपभोग।
प्रश्न 6.
गैर साधन आगतों से क्या अभिप्राय है ?
उत्तर-
गैर साधन आगतें वह नाशवान वस्तुएं तथा सेवाएं होती हैं जिनका प्रयोग वस्तुओं तथा सेवाओं के उत्पादन के लिए किया जाता है।
प्रश्न 7.
मूल्य वृद्धि विधि का वैकल्पिक नाम क्या है ?
उत्तर-
मूल्य वृद्धि विधि को उत्पाद विधि भी कहा जाता है।
प्रश्न 8.
दोहरी गणना की समस्या से क्या अभिप्राय है ?
उत्तर-
एक ही वस्तु के मूल्य को एक से अधिक बार गणना को दोहरी गणना कहा जाता है।
प्रश्न 9.
उत्पाद वृद्धि से क्या अभिप्राय है ?
अथवा
राष्ट्रीय आय के माप की उत्पाद विधि से क्या अभिप्राय है ?
उत्तर-
एक वर्ष में देश की घरेलू सीमा के भीतर उत्पादित की गई अन्तिम वस्तुओं तथा सेवाओं के योग को अन्तिम उत्पाद कहा जाता है। इसके बाज़ारी मूल्य को राष्ट्रीय आय कहते हैं।
प्रश्न 10.
आय वृद्धि में साधन आय को कितने भागों में विभाजित किया जाता है ?
अथवा
साधन आय के मुख्य अंश बताएँ।
उत्तर-
- कर्मचारियों का मेहनताना
- परिचालन अधिशेष
- मिश्रित आय
- विदेशों से शुद्ध साधन आय।
प्रश्न 11.
व्यय वृद्धि से क्या अभिप्राय है ?
उत्तर-
एक वर्ष में एक देश में सकल घरेलू उत्पाद पर किये गए अन्तिम खर्च को बाज़ारी कीमतों पर मूल्य ज्ञात करके योग किया जाए तो इसको व्यय वृद्धि द्वारा सकल घरेलू उत्पाद कहा जाता है।

प्रश्न 12.
निजी अन्तिम उपभोग खर्च से क्या अभिप्राय है ?
उत्तर-
निजी अन्तिम उपभोग खर्च एक देश में वर्तमान उपभोग पर वस्तुओं तथा सेवाओं के खर्च का योग होता
प्रश्न 13.
अन्तिम निवेश खर्च से क्या अभिप्राय है?
उत्तर-
अन्तिम निवेश में-
- कुल घरेलू स्थाई पूँजी निर्माण
- स्टॉक में परिवर्तन
- शुद्ध निर्यात को शामिल किया जाता है।
प्रश्न 14.
पूंजी हस्तान्तरण से क्या अभिप्राय है ?
उत्तर-
पूंजी हस्तान्तरण वह हस्तान्तरण होता है जिसका भुगतान बचत या सम्पत्ति में से अदा किया जाता है।
प्रश्न 15.
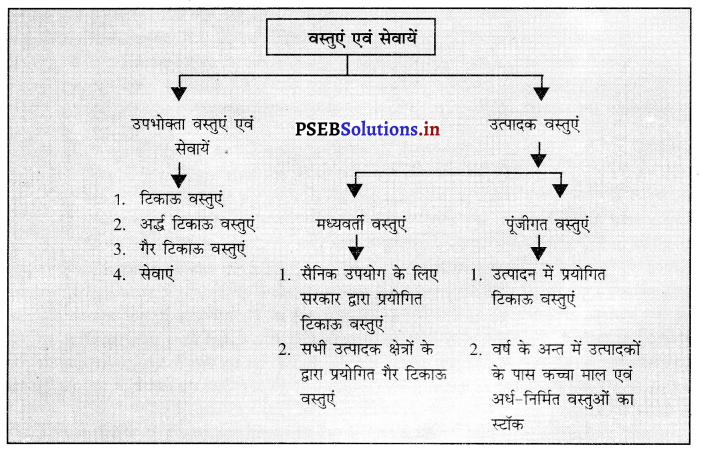
मध्यवर्ती वस्तुओं से क्या अभिप्राय है ?
उत्तर-
मध्यवर्ती वस्तुएँ वे वस्तुएँ होती हैं जिन का प्रयोग वस्तुओं तथा सेवाओं के उत्पादन में किया जाता है।
प्रश्न 16.
अन्तिम वस्तुओं से क्या अभिप्राय है ?
उत्तर-
वह वस्तुएँ जिनका प्रयोग उपभोग के लिए अथवा पूंजी निर्माण के लिए किया जाता है।
प्रश्न 17.
घिसावट से क्या अभिप्राय है अथवा स्थिर पूँजी का उपभोग क्या होता है ?
उत्तर-
वस्तुओं का उत्पादन करते समय मशीनों, औज़ारों इत्यादि के मूल्य में जो कमी हो जाती है उस को स्थिर पूँजी का उपभोग या घिसावट कहा जाता है।
प्रश्न 18.
बन्द अर्थव्यवस्था से क्या अभिप्राय है ?
उत्तर-
बन्द अर्थव्यवस्था वह अर्थव्यवस्था है जिसका शेष विश्व के देशों से आर्थिक सम्बन्ध नहीं होता।
प्रश्न 19.
खली अर्थव्यवस्था से क्या अभिप्राय है ?
उत्तर-
खुली अर्थव्यवस्था वह अर्थव्यवस्था है जिसका आर्थिक सम्बन्ध शेष विश्व के देशों से होता है।
प्रश्न 20.
स्टॉक में परिवर्तन अथवा माल सूची में परिवर्तन से क्या अभिप्राय है ?
उत्तर-
माल सूची अथवा स्टॉक में परिवर्तन = अन्तिम स्टॉक – प्रारम्भिक स्टॉक।

प्रश्न 21.
चालू कीमत पर राष्ट्रीय आय से क्या अभिप्राय है ?
उत्तर-
चालू कीमत पर राष्ट्रीय आय का अभिप्राय है एक वर्ष में उत्पादित वस्तुओं तथा सेवाओं का प्रचलित कीमतों पर मूल्य का माप।
प्रश्न 22.
स्थिर कीमत पर राष्ट्रीय आय से क्या अभिप्राय है ?
उत्तर-
वस्तुओं तथा सेवाओं का मूल्य आधार वर्ष की कीमतों द्वारा मापते हैं तो इसको स्थिर कीमत पर राष्ट्रीय आय कहते हैं।
प्रश्न 23.
मौद्रिक राष्ट्रीय आय को वास्तविक राष्ट्रीय आय में परिवर्तित कैसे किया जाता है ?
उत्तर-
वास्तविक राष्ट्रीय आय = img
प्रश्न 24.
मौद्रिक आय को अपस्फायक (deflate) करने का सूत्र बताएँ।
उत्तर-
GNP deflator = \(\frac{\text { Money value of GNP }}{\text { Real Value of GNP }} \times 100\)
प्रश्न 25.
राष्ट्रीय आय के माप के लिए खर्च विधि का वर्णन करें।
उत्तर-
एक लेखा वर्ष में बाज़ार कीमतों पर कुल घरेलू उत्पादन पर किये गए अन्तिम उपभोग खर्च के माप को खर्च विधि कहा जाता है।
प्रश्न 26.
अन्तिम उपभोग खर्च से क्या अभिप्राय है ?
उत्तर-
वह खर्च जो कि अन्तिम वस्तुओं तथा सेवाओं पर खर्च किया जाता है उसको अन्तिम उपभोग खर्च कहते हैं।
प्रश्न 27.
अन्तिम उपभोग खर्च में कौन-कौन सी मदें शामिल की जाती हैं ?
उत्तर-
- निजी अन्तिम उपभोग खर्च
- सरकारी अन्तिम उपभोग खर्च
- अन्तिम निवेश खर्च
- शुद्ध विदेशी निवेश।
प्रश्न 28.
निजी अन्तिम उपभोग खर्च से क्या अभिप्राय है ?
उत्तर-
निजी परिवारों तथा निजी गैर लाभकारी संस्थाओं द्वारा वर्तमान उपभोग पर वस्तुओं तथा सेवाओं के खर्च के योग को निजी अन्तिम उपभोग खर्च कहते हैं।

प्रश्न 29.
मूल्य वृद्धि = उत्पाद का मूल्य (-) …..
उत्तर-
मध्यवर्ती उपभोग।
प्रश्न 30.
वस्तुओं का उत्पादन करते समय मशीनों और औज़ारों के मूल्य में जो कमी हो जाती है को ………………. कहते हैं।
उत्तर-
स्थिर पूँजी का उपभोग अथवा घिसावट।
प्रश्न 31.
अर्थव्यवस्था में जिस क्षेत्र का सम्बन्ध उद्योग, घरों के निर्माण, गैस आदि से होता है को ……. कहते हैं।
(क) प्राथमिक क्षेत्र
(ख) गौत्र क्षेत्र
(ग) टरशरी क्षेत्र
(घ) कोई भी नहीं।
उत्तर-
(ख) गौत्र क्षेत्र।
प्रश्न 32.
राष्ट्रीय आय का माप करते समय जिन वस्तुओं का मूल्य एक से अधिक बार जुड़ जाता है को ……………. गणना कहते हैं।
(क) बार-बार
(ख) दोहरी
(ग) सौ बार
(घ) कोई भी नहीं।
उत्तर-
(ख) दोहरी।
प्रश्न 33.
वह अर्थव्यवस्था जिसका सम्बन्ध बाकी विश्व के देशों से नहीं होता को ………………. कहा जाता
(क) बन्द अर्थव्यवस्था
(ख) खुली अर्थव्यवस्था
(ग) विश्व अर्थव्यवस्था
(घ) कोई भी नहीं।
उत्तर-
(क) बन्द अर्थव्यवस्था।
प्रश्न 34.
वह अर्थव्यवस्था जिसका सम्बन्ध बाकी विश्व के देशों के साथ होता है को … कहते हैं।
उत्तर-
खुली अर्थव्यवस्था।
प्रश्न 35.
माल सूची अथवा स्टॉक में परिवर्तन = अन्तिम स्टॉक (-) ………….
उत्तर-
प्रारंभिक स्टॉक।

प्रश्न 36.
अन्तिम उपभोग व्यय = निजी अन्तिम उपभोग व्यय + सरकारी अन्तिम उपभोग व्यय + अन्तिम निवेश व्यय + ………
उत्तर-
शुद्ध विदेशी निवेश।
प्रश्न 37.
राष्ट्रीय आय में प्राथमिक क्षेत्र का सम्बन्ध कृषि क्षेत्र से होता है।
उत्तर-
सही।
प्रश्न 38.
एक वस्तु के मूल्य को बार-बार राष्ट्रीय आय में जोड़ने से बचने के लिए मध्यवर्ती वस्तुओं को राष्ट्रीय आय में जोड़ना चाहिए।
उत्तर-
ग़लत।
प्रश्न 39.
उत्पाद का मूल्य – मध्यवर्ती उपभोग = मूल्य वृद्धि ।
उत्तर-
सही।
प्रश्न 40.
जो वस्तुएँ अन्तिम उपभोग वस्तुओं के उत्पादन के लिए प्रयोग की जाती है उनको मध्यवर्ती वस्तुएँ कहा जाता है।.
उत्तर-
सही।
प्रश्न 41.
घिसावट को स्थिर पूँजी का उपभोग भी कहते हैं।
उत्तर-
सही।
II. अति लय उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
राष्ट्रीय आय को मापने की मुख्य विधियां कौन-सी हैं ?
उत्तर-
राष्ट्रीय आय को मापने की मुख्य विधियां तीन हैं-
- आय विधि-इस विधि में एक वर्ष में उत्पादन के साधनों को सेवाओं के बदले में जो आय प्राप्त होती है, उसके जोड़ द्वारा राष्ट्रीय आय का माप किया जाता है।
- उत्पादन विधि-उत्पादन विधि में एक लेखा वर्ष में देश के प्रत्येक उत्पादक द्वारा किए गए योगदान के जोड़ से राष्ट्रीय आय का माप किया जाता है।
- खर्च विधि-इस विधि में एक लेखा वर्ष में बाजार कीमत पर किए कुल अन्तिम खर्च का जोड़ किया जाता |
प्रश्न 2.
प्राथमिक क्षेत्र से क्या अभिप्राय है ?
उत्तर-
प्राथमिक क्षेत्र का सम्बन्ध कृषि क्षेत्र से होता है जिसमें प्राकृतिक साधनों का प्रयोग करके उत्पादन किया जाता है। इसके उप-क्षेत्र इस प्रकार हैं-
- कृषि तथा पशु पालन
- जंगल उद्योग तथा शहतीर बनाना
- मछली उद्योग
- खनन।
प्रश्न 3.
गौण क्षेत्र से क्या अभिप्राय है ?
उत्तर-
गौण क्षेत्र का अर्थ निर्माण क्षेत्र से होता है। इसके मुख्य उप-क्षेत्र इस प्रकार हैं-
- उद्योग
- निर्माण कार्य
- विद्युत्, गैस तथा जल आपूर्ति।
प्रश्न 4.
अर्थव्यवस्था के तृतीय क्षेत्र अथवा सेवा क्षेत्र से क्या अभिप्राय है ?
उत्तर-
इस क्षेत्र में सेवाएं शामिल की जाती हैं जैसे कि-
- यातायात, संचार तथा संग्रहण
- बीमा तथा बैंक सेवाएं
- व्यापार तथा होटल
- आवास निर्माण
- सरकारी प्रशासन तथा सुरक्षा
- अन्य सेवाएं।
प्रश्न 5.
मूल्य वृद्धि विधि से क्या अभिप्राय है ?
उत्तर-
राष्ट्रीय आय को उत्पाद विधि द्वारा मापने के लिए मूल्य वृद्धि विधि अधिक उपयुक्त विधि है। इस विधि में देश में प्रत्येक उत्पादक द्वारा उत्पादित वस्तुओं के मूल्य में से मध्यवर्ती वस्तुओं का मूल्य घटाकर अन्तिम वस्तुओं तथा सेवाओं के बाज़ार मूल्य को ज्ञात किया जाता है जिससे दोहरी गणना की समस्या स्वयं हल हो जाती है।
मूल्य वृद्धि = उत्पाद का मूल्य – मध्यवर्ती उपभोग (Value Added = Value of Output – Intermediate Consumption)

प्रश्न 6.
दोहरी गणना की समस्या से क्या अभिप्राय है ?
उत्तर-
एक वस्तु के मूल्य की गणना जब एक से अधिक बार की जाती है तो इसको दोहरी गणना कहा जाता है। जब एक वर्ष में एक देश में उत्पाद के मूल्य में से मध्यवर्ती वस्तुओं के मूल्य को घटा दिया जाए तो अन्तिम वस्तुओं का मूल्य प्राप्त हो जाता है। इससे दोहरी गणना की समस्या का हल हो जाता है।
प्रश्न 7.
निजी अन्तिम उपभोग खर्च से क्या अभिप्राय है ?
उत्तर-
निजी अन्तिम उपभोग खर्च का अर्थ एक देश में वर्तमान उपभोग पर वस्तुओं तथा सेवाओं के खर्च का योग होता है जो कि निजी परिवारों तथा निजी गैर-लाभकारी संस्थाओं द्वारा किया जाता है।
प्रश्न 8.
अन्तिम निवेश खर्च से क्या अभिप्राय है ?
उत्तर-
एक वर्ष में एक देश में जो उत्पादन किया जाता है उसका सारा भाग उपभोग नहीं किया जाता बल्कि इसमें से कुछ भाग आने वाले समय में वस्तुओं के उत्पादन के लिए रख लिया जाता है जिसमें-
- कुल घरेलू स्थाई पूंजी निर्माण
- स्टॉक में परिवर्तन
- शुद्ध निर्यात को शामिल किया जाता है।
प्रश्न 9.
पूँजी हस्तान्तरण से क्या अभिप्राय है ?
उत्तर-
पूँजी हस्तान्तरण वह हस्तान्तरण होते हैं जिनका भुगतान बचत या सम्पत्ति में से अदा किया जाता है। इस हस्तान्तरण को प्राप्त करने वाला अपनी बचत तथा सम्पत्ति में इसको शामिल कर लेता है।
प्रश्न 10.
साधन आगतों तथा गैर-साधन आगतों में अन्तर बताएँ।
उत्तर-
साधन आगतों में उत्पादन के साधनों भूमि, श्रम, पूँजी तथा उद्यम को शामिल किया जाता है। इनको प्राथमिक आगतें कहते हैं। गैर-साधन आगतों में गैर-टिकाऊ उत्पादक वस्तुओं तथा सेवाओं को शामिल किया जाता है, जो कच्चे माल के रूप में प्रयोग की जाती हैं। यह मध्यवर्ती वस्तुएँ होती हैं जिनको अन्तिम वस्तुओं के उत्पादन में प्रयोग किया जाता है।
प्रश्न 11.
मध्यवर्ती तथा अन्तिम वस्तुओं में अन्तर बताएँ।
उत्तर-
मध्यवर्ती वस्तुएँ-वह वस्तुएँ होती हैं, जिनका प्रयोग वस्तुओं तथा सेवाओं के उत्पादन में किया जाता है अथवा उनको दोबारा बिक्री के लिए प्रयोग किया जाता है। अन्तिम वस्तुएँ-वह वस्तुएँ हैं जिनका उत्पादन उनके उपभोग के लिए किया जाता है, अथवा इनका प्रयोग पूँजी निर्माण के लिए होता है।
प्रश्न 12.
घिसावट से क्या अभिप्राय है ? या स्थिर पूँजी का उपभोग क्या होता है ?
उत्तर-
स्थिर भण्डार का प्रयोग करते समय इसके मूल्य में जो कमी हो जाती है उसको घिसावट कहा जाता है और वस्तुओं का उत्पादन करते समय मशीनों, औज़ारों इत्यादि के मूल्य में जो कमी हो जाती है, उसको स्थिर पूंजी का उपभोग या घिसावट कहा जाता है।
प्रश्न 13.
खुली तथा बन्द अर्थव्यवस्था से क्या अभिप्राय है ?
उत्तर-
बन्द अर्थव्यवस्था वह अर्थव्यवस्था है, जिसका शेष विश्व के देशों से आर्थिक सम्बन्ध नहीं होता। खुली अर्थव्यवस्था वह अर्थव्यवस्था है जिसका आर्थिक सम्बन्ध अन्य देशों से होता है। यह एक व्यावहारिक धारणा है। इस अर्थव्यवस्था में आयात तथा निर्यात किया जाता है।

प्रश्न 14.
स्टॉक में परिवर्तन या माल सची में परिवर्तन से क्या अभिप्राय है ?
उत्तर-
स्टॉक में परिवर्तन को माल सूची परिवर्तन भी कहा जाता है। एक फ़र्म द्वारा जिन वस्तुओं का उत्पादन किया जाता है, वह सारा माल बिकता नहीं। उसका कुछ भाग बच जाता है। दूसरे वर्ष जब फ़र्म उत्पादन करती है तो पिछले वर्ष जो माल बच गया था उसको प्रारम्भिक स्टॉक कहा जाता है और साल के अन्त में जो माल बच जाता है उसको अन्तिम स्टॉक कहा जाता है।
स्टॉक में परिवर्तन = अन्तिम स्टॉक – प्रारम्भिक स्टॉक |
III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)
प्रश्न 1.
राष्ट्रीय आय का माप करने के लिए किस प्रकार के आँकड़ों की आवश्यकता होती है ?
उत्तर-
राष्ट्रीय आय का माप करने की तीन विधियां हैं। इन विधियों में निम्नलिखित प्रकार के आंकड़ों की आवश्यकता होती है।
1. उत्पादन विधि या मूल्य वृद्धि-उत्पादन विधि अथवा मूल्य वृद्धि विधि में साधन लागत पर शुद्ध मूल्य वृद्धि के आंकड़ों की आवश्यकता होती है। इनमें-
- प्राथमिक क्षेत्र
- गौण क्षेत्र
- टरशरी क्षेत्र
- विदेशों से शुद्ध साधन आय के आँकड़ों की सहायता से राष्ट्रीय आय का माप किया जाता है।
2. आय विधि-आय विधि में उत्पादन के साधनों की वित्त वर्ष में प्राप्त शुद्ध आय का जोड़ किया जाता है। इसमें
- शुद्ध लगान
- शुद्ध ब्याज
- शुद्ध मज़दूरी
- शुद्ध लाभ तथा
- विदेशों से प्राप्त शुद्ध साधन आय के आंकड़ों का जोड़ किया जाता है।
3. व्यय विधि-खर्च विधि में
- निजी उपभोग खर्च
- सरकारी उपभोग खर्च
- सकल घरेलू पूँजी निर्माण
- शुद्ध निर्यात
- मूल्य ह्रास या घिसावट
- शुद्ध अप्रत्यक्ष कर
- विदेशों से प्राप्त शुद्ध साधन आय के आँकड़ों की आवश्यकता होती है।
प्रश्न 2.
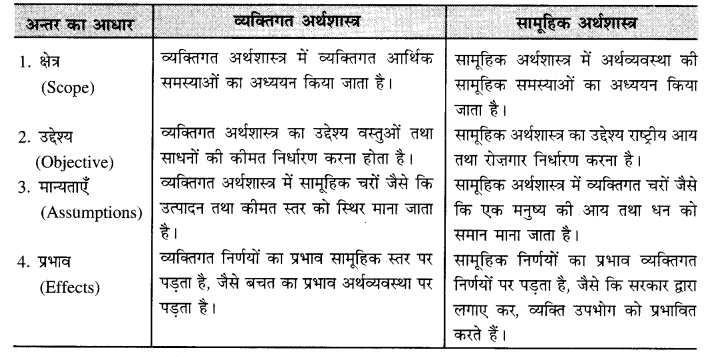
प्राथमिक क्षेत्र तथा गौण क्षेत्र में अन्तर स्पष्ट करें।
उत्तर-
प्राथमिक क्षेत्र तथा गौण क्षेत्र में मुख्य अन्तर इस प्रकार हैं –
| प्राथमिक क्षेत्रमा |
गौण क्षेत्र |
| 1. प्राथमिक क्षेत्र में प्रकृति अधिक प्रभावशाली तत्त्व होता है। |
1. गौण क्षेत्र में मनुष्य अधिक प्रभावशाली तत्त्व होता है। |
| 2. प्राथमिक क्षेत्र में प्राकृतिक साधनों से सम्बन्धित क्रियाएँ शामिल की जाती हैं। |
2. गौण क्षेत्र में प्राथमिक क्षेत्र में उत्पादन वस्तुओं से सम्बन्धित क्रियाएँ शामिल की जाती है। |
| 3. प्राथमिक क्षेत्र में कृषि उत्पादन महत्त्वपूर्ण होता है। |
3. गौण क्षेत्र में औद्योगिक उत्पादन महत्त्वपूर्ण होता है। |
| 4. प्राथमिक क्षेत्र में भूमि उत्पादन का मुख्य साधन होता है। |
4. गौण क्षेत्र में पूँजी तथा उद्यमी उत्पादन का मुख्य साधन होता है। |
प्रश्न 3.
(i) प्राथमिक क्षेत्र (ii) गौण क्षेत्र (iii) तीसरे क्षेत्र के उद्यमों में अन्तर स्पष्ट करें।
उत्तर-
- प्राथमिक क्षेत्र के उद्यम-इस क्षेत्र में प्राकृतिक संसाधनों का प्रयोग किया जाता है। इसमें भूमि उत्पादन का मुख्य साधन होता है। उद्यमी गेहूँ, चावल, कपास, मक्की आदि वस्तुओं का उत्पादन करते हैं।
- गौण क्षेत्र के उद्यम-गौण क्षेत्र में उद्योगों द्वारा प्राथमिक क्षेत्र के उत्पादन का प्रयोग करके और वस्तुओं का उत्पादन किया जाता है। जैसे-लकड़ी से मेज़ बनाना, सूत से कपड़ा बुनना आदि। यह वस्तुएं जीने के लिए आवश्यक होती हैं।
- तीसरे क्षेत्र के उद्यम-तीसरा क्षेत्र सेवाओं का क्षेत्र है। इस क्षेत्र में बैंकिंग, बीमा, सेहत, शिक्षा आदि से सम्बन्धित सेवाएँ शामिल की जाती हैं। इन सेवाओं से मनुष्य का विकास होता है।
प्रश्न 4.
एक अर्थव्यवस्था में उत्पादन इकाइयों का वर्गीकरण किस आधार पर किया जाता है ? उदाहरण देकर स्पष्ट करें।
अथवा
संक्षेप में उत्पादन इकाइयों के प्राथमिक, गौण तथा तीसरे क्षेत्र के वर्गीकरण को स्पष्ट करें।
उत्तर-
एक अर्थव्यवस्था में उत्पादन इकाइयों को तीन भागों प्राथमिक, गौण तथा टरश्यरी क्षेत्र में विभाजित किया जाता है।
- प्राथमिक क्षेत्र की उत्पादन इकाइयाँ-इस क्षेत्र में प्राकृतिक साधनों का प्रयोग करके उत्पादन किया जाता है। उदाहरण के लिए कृषि उत्पादन, मछली उत्पादन, लट्ठा बनाना आदि।
- गौण क्षेत्र की उत्पादन इकाइयाँ-इस क्षेत्र में प्राथमिक क्षेत्र के उत्पादन का प्रयोग करके और वस्तुओं तथा सेवाओं का उत्पादन किया जाता है। जैसा कि कपास से कपड़ा बनाना, लोहे से साइकिल, स्कूटर तथा कार का निर्माण करना।
- सेवाओं या तीसरे क्षेत्र की उत्पादन इकाइयाँ-इस क्षेत्र से प्राथमिक तथा गौण क्षेत्र के उद्योगों को तीसरे क्षेत्र द्वारा सेवाएँ प्रदान की जाती हैं। जैसा कि जहाज़रानी, बीमा, बैंकिंग आदि के उद्यम इस क्षेत्र में शामिल किए जाते

प्रश्न 5.
उत्पाद के मूल्य से क्या अभिप्राय है ?
उत्तर-
एक देश में एक वित्तीय वर्ष में उत्पादित वस्तुओं तथा सेवाओं के बाजार कीमत पर मूल्य को उत्पादन का मूल्य कहते हैं । यदि उत्पादन की गई वस्तु की समस्त मात्रा बिक जाती है, तो उत्पाद का मूल्य बिक्री के मूल्य के समान होता है। यदि उत्पादन वस्तु की अधिक मात्रा बिक जाती है और कुछ भाग बिना बिक्री के कारण बच जाता है तो इसको माल सूची के रूप में रख लिया जाता है। माल सूची में परिवर्तन को स्टॉक में परिवर्तन कहा जाता है।
उत्पाद का मूल्य = बिक्री + स्टॉक में परिवर्तन स्टॉक में परिवर्तन का अर्थ है अन्तिम स्टॉक तथा प्रारम्भिक स्टॉक में अन्तर। इसलिए स्टॉक में परिवर्तन का माप करने के लिए हम अन्तिम स्टॉक में से प्रारम्भिक स्टॉक को घटा देते हैं। इस प्रकार उत्पाद के मूल्य का माप किया जाता है।
प्रश्न 6.
मूल्य वृद्धि को उदाहरण द्वारा स्पष्ट करें।
उत्तर-
मूल्य वृद्धि का अर्थ है, उत्पाद का मूल्य (-) मध्यवर्ती उपभोग। उदाहरण के लिए एक किसान 1000 रुपए की गेहूँ का उत्पादन करता है। उसने गेहूँ का उत्पादन करने के लिए 400 रुपए खर्च किए। यह गेहूँ आटा मिल वाला खरीद लेता है तथा इससे आटा बनाकर दुकानदारों को 1500 रुपए में बेच देता है। दुकानदार यह आटा उपभोगियों को 2000 रुपए में बेच देते हैं। मूल्य वृद्धि का माप इस प्रकार किया जाएगा।
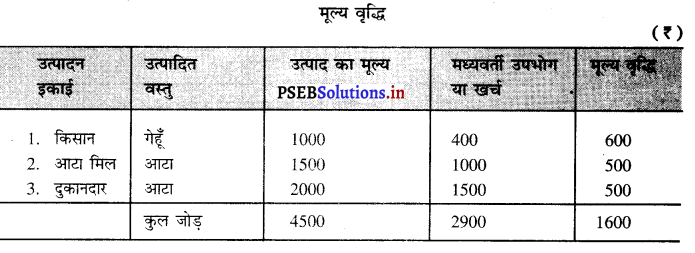
मूल्य वृद्धि = उत्पाद का मूल्य – मध्यवर्ती उपभोग
=4500 – 29000
= ₹ 1600 उत्तर
प्रश्न 7.
राष्ट्रीय आय को मापने की आय विधि का वर्णन करें।
उत्तर –
राष्ट्रीय आय का माप करने के लिए आय विधि एक महत्त्वपूर्ण विधि है। इस विधि द्वारा भिन्न-भिन्न उत्पादन के साधनों को प्राप्त होने वाली आय का योग किया जाता है। आय विधि की मुख्य अवस्थाएं इस प्रकार हैं-
प्रथम अवस्था-सबसे पहले उत्पादन की इकाइयों की पहचान की जाती है जिनको प्राथमिक क्षेत्र (Primary Sector), गौण क्षेत्र (Secondary Sector) तथा सेवाएं क्षेत्र (Teritiary Sector) में विभाजित किया जाता है।
दूसरी अवस्था- इस अवस्था में उत्पादन के साधनों की आय का वर्गीकरण किया जाता है जिसमें निम्नलिखित मुख्य भाग होते हैं
- कर्मचारियों का मेहनताना
- परिचालन अधिशेष
- मिश्रित आय
- विदेशों से शुद्ध साधन आय।
3. तृतीय अवस्था-
- उत्पादन के साधनों को किए गए भुगतान को घरेलू साधन आय कहा जाता है।
- शुद्ध राष्ट्रीय आय = शुद्ध घरेलू आय + विदेशों से प्राप्त शुद्ध साधन आय
- सकल राष्ट्रीय आय = शुद्ध राष्ट्रीय आय + मूल्य घिसावट
- बाजार कीमतों पर सकल राष्ट्रीय उत्पाद = सकल राष्ट्रीय आय + शुद्ध अप्रत्यक्ष कर इस प्रकार आय विधि द्वारा राष्ट्रीय आय का माप किया जाता है।
प्रश्न 8.
आय विधि से राष्ट्रीय आय की गणना करते समय किन बातों का ध्यान रखना चाहिए ?
उत्तर-
आय विधि द्वारा राष्ट्रीय आय का माप करते समय निम्नलिखित सावधानियों का ध्यान रखने की आवश्यकता है-
- गैर-कानूनी काम जैसे कि जुआ, तस्करी इत्यादि से प्राप्त आय को राष्ट्रीय आय में शामिल नहीं किया जाता।
- आकस्मिक आय जैसे कि लॉटरी से प्राप्त आय तथा पूंजीगत लाभ को राष्ट्रीय आय में शामिल नहीं किया जाता।
- हस्तान्तरण आय जैसे कि बुढ़ापा पेन्शन, बेरोज़गारी भत्ता इत्यादि को राष्ट्रीय आय में शामिल नहीं किया जाता।
- स्व-उपभोग के लिए रखी गई वस्तुओं को राष्ट्रीय आय में शामिल किया जाता है, परन्तु स्व-उपभोग की सेवाओं को इसमें शामिल नहीं किया जाता।
- पुरानी वस्तुओं को राष्ट्रीय आय में शामिल नहीं किया जाता परन्तु पुरानी वस्तुओं की बिक्री के कारण प्राप्त हुई दलाली अथवा कमीशन को शामिल किया जाता है।
- नए तथा पुराने शेयर, बाँड़ों को बेच कर प्राप्त होने वाली आय को राष्ट्रीय आय में शामिल नहीं किया जाता।
- मकान मालिकों के मकान का आरोपित किराया राष्ट्रीय आय में शामिल किया जाता है।
- लाभ अथवा निगम कर लाभांश तथा अविभाजित लाभ तीनों ही लाभ के अंश होते हैं । इसलिए यदि लाभ दिया गया हो तो अन्य अंशों को शामिल नहीं करना चाहिए।
- व्यक्तिगत आय कर कर्मचारियों की मेहनत का ही भाग होते हैं इसलिए आय कर देने से पूर्व ही कर्मचारियों के मेहनताने को शामिल किया जाता है।
- अप्रत्यक्ष कर (Indirect Taxes) जैसे कि बिक्री कर, उत्पादन कर, वस्तु की कीमत में शामिल होते हैं। बाज़ार कीमत और राष्ट्रीय आय का अनुपात लगाते समय इनको अलग से शामिल नहीं किया जाता है।

प्रश्न 9.
मूल्य वृद्धि विधि की मुख्य अवस्थाओं को स्पष्ट करें।
अथवा
बाजार कीमत पर सकल मूल्य वृद्धि का माप करते समय भिन्न-भिन्न अवस्थाओं की व्याख्या करें।
अथवा
एक उदाहरण की सहायता से मूल्य वृद्धि समझाइए।
उत्तर-
मूल्य वृद्धि विधि द्वारा राष्ट्रीय आय का माप करते समय निम्नलिखित अवस्थाएं होती हैं
1. प्रथम अवस्था (First Step)- इस विधि में एक देश की घरेलू सीमा में उद्यमों की पहचान की जाती है, जिनको तीन क्षेत्रों में विभाजित किया जाता है।
- प्राथमिक क्षेत्र
- गौण क्षेत्र
- तीसरा क्षेत्र।
2. द्वितीय अवस्था (Second Step)-शुद्ध मूल्य वृद्धि का अनुमान लगाने के लिए उत्पाद के मूल्य में से मध्यवर्ती वस्तुओं की लागत को घटाया जाता है। इस प्रकार मूल्य वृद्धि = उत्पादन का मूल्य — मध्यवर्ती वस्तुओं की लागत शुद्ध मूल्य वृद्धि = मूल्य वृद्धि – मूल्य घिसावट
3. तृतीय अवस्था (Third Step)-इसमें घरेलू सीमा के भीतर शुद्ध मूल्य वृद्धि का पता लगाकर अन्य धारणाओं का अनुमान लगाया जाता है। इस विधि के अनुसार राष्ट्रीय आय का माप इस प्रकार किया जाता हैराष्ट्रीय आय = प्राथमिक क्षेत्र में शुद्ध मूल्य वृद्धि + गौण क्षेत्र में शुद्ध मूल्य वृद्धि + सेवा क्षेत्र में शुद्ध मूल्य वृद्धि + विदेशों से प्राप्त शुद्ध साधन आय बाज़ार कीमत पर सकल मूल्य वृद्धि = सकल घरेलू मूल्य वृद्धि, बाज़ार कीमत पर सकल घरेलू उत्पाद के बराबर होती है।
प्रश्न 10.
उत्पाद विधि में बाज़ार कीमत पर कुल राष्ट्रीय उत्पाद के घटकों की व्याख्या करें।
उत्तर-
बाज़ार कीमत पर राष्ट्रीय उत्पाद का माप करते समय अन्तिम वस्तुओं तथा सेवाओं का योग किया जाता है, जिसके मुख्य घटक इस प्रकार हैं
बाज़ार कीमत पर कुल राष्ट्रीय उत्पाद = उपभोगी वस्तुएं तथा सेवाएं (C) + कुल घरेलू निजी निवेश (I) + सरकार द्वारा उत्पादित वस्तुएं तथा सेवाएं (G) + शुद्ध निर्यात (X – M) Gross National Product at Market Prices = C + I + G (X – M)
- उपभोगी वस्तुएं तथा सेवाएं-इसमें टिकाऊ उपभोगी वस्तुएं, एक प्रयोग वाली उपभोगी वस्तुओं तथा उपभोगी सेवाएं शामिल की जाती हैं।
- कुल घरेलू निजी निवेश-इसमें स्टॉक में निवेश, आवास निर्माण, सकल घरेलू निजी स्थिर पूंजी निर्माण को शामिल किया जाता है।
- सरकार द्वारा उत्पादित वस्तुएं तथा सेवाएं-इसमें सरकारी निवेश तथा वस्तुओं तथा सेवाओं के उत्पादन को शामिल किया जाता है।
- शुद्ध निर्यात-इसमें निर्यात में से आयात का मूल्य घटा कर राष्ट्रीय आय का पता किया जाता है। यदि हम इन वस्तुओं तथा सेवाओं का मूल्य बाज़ारी कीमतों पर ज्ञात करके जोड़ लेते हैं तो इसको बाज़ार कीमतों पर कुल राष्ट्रीय उत्पादन कहा जाता है।
प्रश्न 11.
मूल्य वृद्धि विधि में घरेलू साधन आय के मुख्य घटकों की व्याख्या करें।
उत्तर-
मूल्य वृद्धि विधि में राष्ट्रीय आय का माप करते समय उत्पाद के मूल्य में से मध्यवर्ती वस्तुओं के उपभोग को घटाया जाता है। इससे वस्तु की दो बार गणना की समस्या का हल हो जाता है। मूल्य वृद्धि विधि वह विधि है जो घरेलू सीमा के भीतर प्रत्येक उत्पादक के उद्यम का माप करती है। इस विधि में घरेलू साधन आय के मुख्य घटक इस प्रकार होते हैं-
घरेलू साधन आय = प्राथमिक क्षेत्र में मूल्य वृद्धि + गौण क्षेत्र में मूल्य वृद्धि + तीसरे क्षेत्र में मूल्य वृद्धि – मूल्य घिसावट – शुद्ध अप्रत्यक्ष कर
जब हम भिन्न-भिन्न क्षेत्रों में बाज़ार कीमत पर कुल मूल्य वृद्धि का माप कर लेते हैं तो हमारे पास बाज़ार कीमत पर सकल मूल्य वृद्धि अथवा सकल घरेलू उत्पाद प्राप्त होता है।
इसमें से मूल्य घिसावट घटाने से बाज़ार कीमत पर शुद्ध मूल्य वृद्धि अथवा शुद्ध घरेलू उत्पाद प्राप्त हो जाता है। यदि इसमें से शुद्ध अप्रत्यक्ष कर (अप्रत्यक्ष कर – आर्थिक सहायता) घटा दिया जाए तो साधन लागत पर शुद्ध मूल्य वृद्धि अथवा घरेलू साधन आय प्राप्त हो जाती है। यदि हम राष्ट्रीय आय ज्ञात करना चाहते हैं तो हम घरेलू साधन आय में विदेशों से शुद्ध साधन आय का योग कर लेते हैं।
प्रश्न 12.
उत्पाद विधि की मुख्य सावधानियां बताएं।
अथवा
मूल्य वृद्धि विधि की मुख्य सावधानियों को स्पष्ट करें।
उत्तर-
- इस विधि में पुरानी वस्तुओं की खरीद अथवा बेच से प्राप्त आय को राष्ट्रीय आय में शामिल नहीं किया जाता, परन्तु पुरानी वस्तुओं की बेच से कमीशन अथवा दलाली को शामिल किया जाता है।
- स्व-उपभोग के लिए उत्पादित वस्तुओं के आरोपित मूल्य (Imputed Value) को राष्ट्रीय आय में शामिल किया जाता है, परन्तु स्व-उपभोग की सेवाओं को मूल्य वृद्धि में शामिल नहीं किया जाता।
- मध्यवर्ती वस्तुओं के मूल्य को मूल्य वृद्धि में शामिल नहीं किया जाता, परन्तु अन्तिम वस्तुओं तथा सेवाओं के मूल्य को मूल्य वृद्धि में शामिल किया जाता है।
- जिन मकानों में मालिक स्वयं निवास करते हैं उनके आरोपित किराए (Imputed Rent) को मूल्य वृद्धि में शामिल किया जाता है।
- सरकारी क्षेत्र में कर्मचारियों के मेहनताने को ही शामिल किया जाता है, जबकि इस क्षेत्र में लाभ, ब्याज, घिसावट के उचित आंकड़े प्राप्त न होने के कारण इनको शामिल नहीं किया जाता।
- मूल्य वृद्धि द्वारा घरेलू उत्पाद की गणना की जाती है। यदि हम राष्ट्रीय उत्पाद ज्ञात करना चाहते हैं तो इसमें विदेशों से प्राप्त शुद्ध साधन आय को शामिल किया जाता है।
प्रश्न 13.
उत्पाद विधि की मुख्य कठिनाइयों का वर्णन करें।
उत्तर-
उत्पाद विधि की मुख्य कठिनाइयां इस प्रकार हैं-
- राष्ट्रीय आय का माप करते समय केवल अन्तिम वस्तुओं तथा सेवाओं के मूल्य को ही शामिल किया जाता है, परन्तु साधारणतया दोहरी गणना की समस्या उत्पन्न होती है।
- कम विकसित देशों में वस्तु विनिमय प्रणाली (Barter system) प्रचलित होती है। इसलिए राष्ट्रीय आय का अनुमान लगाना कठिन हो जाता है।
- वस्तुओं तथा सेवाओं के मूल्य का माप बाज़ार में प्रचलित कीमतों द्वारा किया जाता है, परन्तु बाज़ार कीमतों में परिवर्तन होता रहता है, इसलिए राष्ट्रीय आय का उचित अनुमान नहीं लगाया जा सकता।
- स्व-उपभोग की वस्तुओं का आरोपित मूल्य (Imputed Value) राष्ट्रीय आय के माप में शामिल किया जाता है, परन्तु आरोपित मूल्य का उचित अनुमान लगाना कठिन होता है।
- राष्ट्रीय आय से सम्बन्धित उचित आंकड़े प्राप्त नहीं होते क्योंकि लोग अशिक्षित तथा अज्ञानी होते हैं। इसलिए राष्ट्रीय आय की गणना करते समय कठिनाइयों का सामना करना पड़ता है।
प्रश्न 14.
दोहरी गणना की समस्या पर नोट लिखें।
उत्तर-
उत्पाद विधि द्वारा राष्ट्रीय आय का माप करते समय केवल अन्तिम वस्तुओं तथा सेवाओं का मूल्य जोड़ा जाता है। मध्यवर्ती मूल्य को शामिल नहीं किया जाता क्योंकि इससे एक वस्तु का मूल्य एक से अधिक बार राष्ट्रीय आय में शामिल हो जाता है। इस प्रकार राष्ट्रीय आय का उचित अनुमान नहीं लगाया जा सकता, बल्कि इससे राष्ट्रीय आय अधिक नज़र आती है। इसको दोहरी गणना की समस्या कहते हैं। उदाहरणतया एक किसान 1,000 रुपए की कपास पैदा करता है तथा धागा बनाने वाली फैक्टरी को बेच देता है।
धागा फैक्टरी इससे धागा बनाकर 1,800 रुपए में कपड़ा बनाने वाली फैक्टरी को बेच देती है। कपड़ा फैक्टरी इसका कपड़ा बनाकर 5,000 रुपए में उपभोक्ताओं को बेच देती है। यदि हम तीनों उत्पादकों के मूल्य को जोड़ते हैं तो हमारे पास उत्पादन मूल्य 1,000 + 1,500 + 5,000 = 7,500 रुपए प्राप्त होता है।
परन्तु इसको शुद्ध उत्पाद नहीं कहा जाता। हम देखते हैं कि वास्तविक उत्पादन कपड़े का हुआ है जिसका मूल्य 5,000 रुपए है। इसलिए इसको ही राष्ट्रीय आय में जोड़ना चाहिए। यदि मध्यवर्ती वस्तुओं कपास तथा धागे के मूल्य को शामिल किया जाए तो इससे दोहरी गणना की समस्या उत्पन्न होती है। इसका हल मूल्य वृद्धि विधि द्वारा किया जाता है।
प्रश्न 15.
राष्ट्रीय आय के माप के लिए खर्च विधि का वर्णन करें।
उत्तर-
राष्ट्रीय आय के माप की तृतीय विधि खर्च विधि है। इस विधि को उपभोग तथा निवेश विधि अथवा आय खर्च विधि भी कहा जाता है। इस विधि के अनुसार एक लेखा वर्ष में बाजार कीमतों पर कुल घरेलू उत्पाद पर किए गए अन्तिम खर्च का माप किया जाता है। अन्तिम खर्च दो प्रकार का होता है
(i) उपभोग खर्च (Consumption Expenditure)
(ii) निवेश खर्च (Investment Expenditure)
(i) उपभोग खर्च को दो भागों में विभाजित किया जाता है-
(a) निजी अन्तिम उपभोग खर्च
(b) सरकारी अन्तिम उपभोग खर्च
(ii) निवेश खर्च को तीन भागों में विभाजित किया जाता है
(a) सकल स्थाई पूंजी निर्माण
(b) स्टॉक में परिवर्तन
(c) शुद्ध निर्यात।
इस प्रकार यदि हम अन्तिम उपभोग खर्च का योग कर लेते हैं तो बाज़ार कीमत पर कुल उत्पाद खर्च का मूल्य प्राप्त हो जाता है अर्थात्
+ सरकारी अन्तिम उपभोग खर्च (G) + घरेलू निवेश खर्च (I)
+ शुद्ध विदेशी निवेश (X – M)

प्रश्न 16.
राष्ट्रीय आय का माप खर्च विधि द्वारा करते समय क्या सावधानियां प्रयोग करनी चाहिएं ?
उत्तर-
राष्ट्रीय आय का माप करते समय खर्च विधि में निम्नलिखित सावधानियों का प्रयोग करना चाहिए
- सरकार द्वारा किए गए हस्तान्तरण भुगतान तथा खर्च को राष्ट्रीय आय में शामिल नहीं किया जाता।
- पुराने अथवा नए शेयर व बांड पर किया गया खर्च कुल खर्च में शामिल नहीं किया जाता।
- कुल खर्च का माप करते समय मध्यवर्ती खर्च को राष्ट्रीय आय में शामिल नहीं किया जाता केवल अन्तिम खर्च को ही शामिल किया जाता है।
- पुरानी वस्तुओं पर किए गए खर्च को कुल खर्च में शामिल नहीं किया जाता।
- कुल खर्च में कुल निवेश को शामिल किया जाता है। इसमें घिसावट का खर्च भी शामिल होता है।
- निर्यात में देश-वासियों को विदेशों से प्राप्त ब्याज, लगान, लाभ तथा मज़दूरी शामिल किए जाते हैं। इसी प्रकार आयात में विदेशियों द्वारा हमारे देश में से प्राप्त लाभ, ब्याज, इत्यादि को शामिल किया जाता है। इस प्रकार शुद्ध निर्यात का माप निर्यात में से आयात घटा कर किया जाता है।
प्रश्न 17.
राष्ट्रीय आय मापने की विधियों की समानता पर संक्षेप नोट लिखें।
उत्तर-
राष्ट्रीय आय के माप के लिए आय विधि, उत्पाद विधि तथा खर्च विधि का प्रयोग किया जाता है। इन तीनों विधियों द्वारा राष्ट्रीय आय का माप किया जाता है तो प्राप्त नतीजे में समानता पाई जाती है क्योंकि तीनों विधियां राष्ट्रीय आय का माप भिन्न-भिन्न स्तरों पर करती हैं जैसे कि आय विधि में राष्ट्रीय आय का माप आय सृजन (Income Generation) के स्तर पर किया जाता है। उत्पाद विधि में राष्ट्रीय आय का माप अन्तिम वस्तुओं तथा सेवाओं के उत्पादन स्तर (Production of final goods and services) द्वारा किया जाता है।
खर्च विधि में राष्ट्रीय आय का माप उपभोग खर्च तथा निवेश खर्च (Consumption and Expenditure) के स्तर पर किया जाता है। इन विधियों में से किसी भी विधि का प्रयोग किया जाए, परिणाम समान निकलते हैं। इस कारण तीनों विधियों में समानता पाई जाती है अर्थात् सकल राष्ट्रीय आय = सकल राष्ट्रीय उत्पाद = सकल राष्ट्रीय खर्च।
प्रश्न 18.
विदेशों से प्राप्त शुद्ध साधन आय से क्या अभिप्राय है ?
उत्तर-
किसी देश के निवासियों द्वारा विदेशों में उत्पादन के साधन तथा सेवाएं प्रदान की जाती हैं जिसके बदले में उनको आय प्राप्त होती है। इस देश में गैर-निवासी भी साधन सेवाएं प्रदान करते हैं। इससे वह जो आय अर्जित करते हैं वह विदेशों को चली जाती है। इस देश के साधनों द्वारा प्राप्त की गई आय तथा विदेशियों द्वारा इस देश में से प्राप्त की गई आय के अन्तर को विदेशों से प्राप्त शुद्ध साधन आय कहा जाता है। विदेशों से शद्ध साधन आय धनात्मक अथवा ऋणात्मक हो सकती है। जब किसी देश की घरेलू आय ज्ञात हो तथा हम राष्ट्रीय आय ज्ञात करना चाहते हैं तो घरेलू आय में विदेशों से शुद्ध साधन आय को जोड़ा जाता है। घरेलू आय राष्ट्रीय आय से कम भी हो सकती है अथवा अधिक भी हो सकती है।
प्रश्न 19.
आय विधि, उत्पाद विधि तथा खर्च विधि के मुख्य घटक बताएं।
उत्तर-
- आय विधि (Income Method) के मुख्य घटक बाजार कीमत पर राष्ट्रीय आय = कर्मचारियों का मेहनताना + परिचालन अधिशेष + मिश्रित आय + विदेशों से शुद्ध साधन आय + मूल्य घिसावट + शुद्ध अप्रत्यक्ष कर।
- उत्पाद विधि (Value Added Method) बाज़ार कीमत पर सकल राष्ट्रीय आय = बाज़ार कीमत पर प्राथमिक क्षेत्र में सकल मूल्य वृद्धि + बाज़ार कीमत पर गौण क्षेत्र में सकल मूल्य वृद्धि + बाज़ार कीमत पर तृतीय क्षेत्र में सकल मूल्य वृद्धि + विदेशों में शुद्ध साधन आय।
- खर्च विधि (Expenditure Method) बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद = निजी अन्तिम उपभोग खर्च + सरकारी अन्तिम उपभोग खर्च + सकल घरेलू स्थाई पूंजी निर्माण + स्टॉक में परिवर्तन + शुद्ध निर्यात + विदेशों से शुद्ध साधन आय।
प्रश्न 20.
आय विधि में घरेलू साधन आय के घटकों की व्याख्या करें।
उत्तर-
आय विधि में घरेलू साधन आय के मुख्य घटक निम्नलिखित हैं
1. कर्मचारियों की मेहनत (Compensation of Employees)-कर्मचारियों की मेहनत से अभिप्राय उत्पादकों द्वारा अपने कर्मचारियों को काम के बदले में किए गए भुगतान से होता है। कर्मचारियों के वेतन तथा मजदूरी के मुख्य अंश इस प्रकार होते हैं
- नकद मज़दूरी तथा वेतन
- किस्म के रूप में आय
- सामाजिक सुरक्षा में मालिकों का योगदान।
2. परिचालन अधिशेष (Operating Surplus)-इसमें सम्पत्ति से प्राप्त आय तथा उद्यमवृत्ति से प्राप्त आय को शामिल किया जाता है। परिचालन अधिशेष की मुख्य मदें इस प्रकार हैं
- किराया तथा रायल्टी
- ब्याज
- लाभ (लाभांश + निगम कर + अविभाजित लाभ)।
3. मिश्रित आय (Mixed Income)-मिश्रित आय से अभिप्राय स्व-रोज़गार पर लगे लोगों की काम तथा सम्पत्ति दोनों से प्राप्त मिश्रित आय से होता है। उदाहरणतया किसान, दुकानदार, प्राइवेट डॉक्टर को प्राप्त होने वाली आय में उनकी मेहनत की मज़दूरी, पूंजी का ब्याज, भूमि अथवा मकान का किराया तथा उद्यमवृत्ति से प्राप्त लाभ इत्यादि शामिल होते हैं। इस कारण इस आय को मिश्रित आय कहा जाता है।
(A) मूल्य वृद्धि या उत्पाद विधि (Value Added Or Product Method)
IV. दीर्घ उत्तरीय प्रश्न । (Long Answer Type Questions)
प्रश्न 1.
मूल्य वृद्धि विधि या उत्पाद विधि से क्या अभिप्राय है ? इस विधि द्वारा राष्ट्रीय आय को मापने में जुड़ने वाले चरणों की रूप-रेखा स्पष्ट करें। मूल्य वृद्धि विधि की सावधानियां बताएं।
(Give an outline of the steps involved in the estimation of National Product by Value Added Method or Product Method. Explain the precautions in Value Added Method.)
उत्तर-
राष्ट्रीय उत्पाद या राष्ट्रीय आय की गणना के लिए उत्पाद विधि अथवा मूल्य वृद्धि विधि का प्रयोग किया जाता है। इस विधि को शुद्ध उत्पाद विधि (Net Output Method) या औद्योगिक मूल्य विधि (Industrial Origin Method) भी कहा जाता है। मूल्य वृद्धि विधि वह विधि है जिसमें राष्ट्रीय आय का माप करने के लिए एक देश में एक लेखा वर्ष में उत्पादित वस्तुओं तथा सेवाओं का दोहरी गणना के बिना माप होता है।
(Value Added Method or Product Method is the method of measurement of national income by adding the goods and services produced in the domestic territory of a country in a year without double counting.)
मूल्य वृद्धि विधि से राष्ट्रीय आय के माप की अवस्थाएं (Steps in measurement of National Income in Value Added Method)
1. प्रथम अवस्था (First Step)—इसमें सर्वप्रथम देश की उत्पादक इकाइयों का वर्गीकरण तीन क्षेत्रों में किया जाता है-
(i) प्राथमिक क्षेत्र (Primary Sector)-इस क्षेत्र में प्राकृतिक साधनों के प्रयोग द्वारा उत्पादन किया जाता है। इसके उप-क्षेत्र हैं
(a) कृषि तथा पशुपालन
(b) जंगल उद्योग तथा शहतीर बनाना
(c) मछली उद्योग
(d) खानों का उत्पादन।
(ii) गौण क्षेत्र (Secondary Sector)-इसके उप-क्षेत्र हैं
(a) उद्योग
(b) निर्माण
(c) जल आपूर्ति, विद्युत् गैस इत्यादि।
(iii) तीसरा क्षेत्र (Tertiary Sector)-इसके उप-क्षेत्र हैं—
(a) यातायात, संचार तथा संग्रहण
(b) व्यापार, होटल तथा जलपान गृह
(c) बैंक तथा बीमा
(d) स्थिर सम्पत्ति, मकानों की मालकी तथा व्यापारिक सेवाएं
(e) सार्वजनिक प्रशासन तथा सुरक्षा
(f) अन्य सेवाएं।
2. दूसरी अवस्था (Second Step)-दूसरी अवस्था में हर एक उत्पादन इकाई के मूल्य का माप किया जाता है। इस उद्देश्य के लिए उत्पाद के मूल्य में से मध्यवर्ती उपभोग का मूल्य निकाल दिया जाए तो हमारे पास कुल मूल्य वृद्धि प्राप्त हो जाती है।
मूल्य वृद्धि = उत्पाद का मूल्य – मध्यवर्ती उपभोग Value Added = Value of Output – Intermediate Consumption
(A) उत्पाद का मूल्य-वह मूल्य है जोकि एक फ़र्म द्वारा एक साल में वस्तुओं तथा सेवाओं को बाज़ार में प्रचलित कीमत पर गुणा करने से प्राप्त होता है। फ़र्म द्वारा एक वर्ष में जो उत्पादन किया जाता है इसका कुछ भाग बिक जाता है तथा कुछ भाग स्टॉक के रूप में बच जाता है। इसलिए उत्पाद का मूल्य = बिक्री + स्टॉक में परिवर्तन
Value of Output = Sales + Change in Stock
स्टॉक में परिवर्तन प्रारम्भिक स्टॉक में से अन्तिम स्टॉक को घटाने से प्राप्त होता है।
स्टॉक में परिवर्तन = अन्तिम स्टॉक – प्रारम्भिक स्टॉक
Change in Stock = Closing Stock – Opening Stock
(B) मध्यवर्ती उपभोग-उत्पादन प्रक्रिया के दौरान कच्चे माल पर जो खर्च किया जाता है उसको मध्यवर्ती उपभोग कहा जाता है। इसमें उत्पादन के साधनों भूमि, श्रम, पूंजी तथा उद्यमकर्ता की लागत को शामिल नहीं किया जाता। इस प्रकार मूल्य वृद्धि विधि द्वारा राष्ट्रीय आय का माप करने के लिए उत्पादन मूल्य में से मध्यवर्ती वस्तुओं का मूल्य घटाया जाता है। इस विधि में राष्ट्रीय आय की दोहरी गणना की समस्या उत्पन्न नहीं होती।
उदाहरण के लिए एक किसान ₹ 1000 के मूल्य की कपास पैदा करता है। उसने कच्चे माल के रूप में ₹ 300 खर्च किए हैं। किसान को हम फ़र्म A कहते हैं। फर्म A ने यह कपास फ़र्म B को बेच दी जोकि धागे का उत्पादन करती है तथा फ़र्म B ने ₹ 1500 मूल्य का धागा बनाकर फर्म C को बेच दिया। फ़र्म C ने इस धागे से कपड़ा बनाकर उपभोगियों को ₹ 2500 में बेच दिया। मूल्य वृद्धि का माप इस प्रकार किया जाएगा –
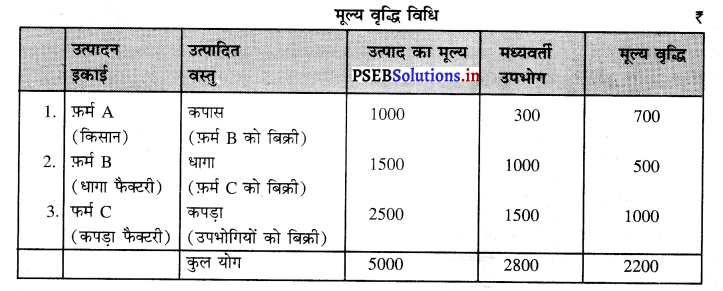
मूल्य वृद्धि = उत्पाद का मूल्य – मध्यवर्ती उपभोग
= 5000 – 2800 = ₹ 2200
फ़र्म A द्वारा मूल्य वृद्धि = 1000 – 300 = ₹ 700
फ़र्म B द्वारा मूल्य वृद्धि = 1500 – 1000 = ₹ 500
फ़र्म C द्वारा मूल्य वृद्धि = 2500 – 1500 = ₹ 1000
कुल मूल्य वृद्धि Gross Value Added = ₹ 2200
इसको बाज़ार कीमत पर सकल घरेलू उत्पाद (GDPMP) कहा जाता है।

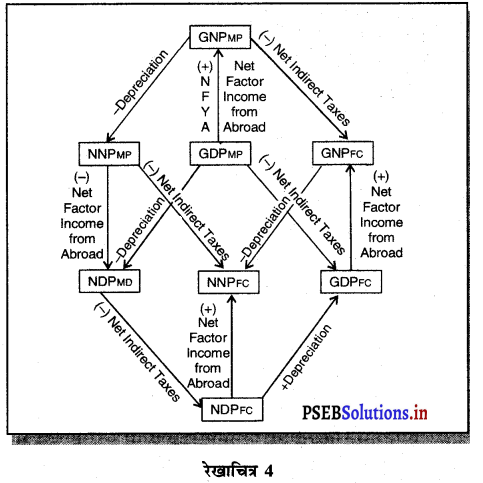
3. तीसरी अवस्था (Third Step)-अब राष्ट्रीय आय की धारणाओं का अध्ययन करते हैं। इस सम्बन्ध में निम्नलिखित मदों को ध्यान में रखना चाहिए
- मूल्य ह्रास या घिसावट (Depreciation)
- शुद्ध अप्रत्यक्ष कर (Net Indirect Taxes = Indirect Taxes – Subsidies)
- विदेशों से शुद्ध साधन आय (Net Factor Income from Abroad) राष्ट्रीय आय का माप करते समय मूल्य वृद्धि से सम्बन्धित निम्नलिखित धारणाएं होती हैं
1. कुल मूल्य वृद्धि = बाज़ार कीमत पर सकल घरेलू उत्पाद Gross Value Added = Gross Domestic Product at Market Prices
बाजार कीमत पर सकल मूल्य वृद्धि एक देश की घरेलू सीमा में एक वर्ष में उत्पादित वस्तुओं तथा सेवाओं का मूल्य होता है।
2. बाजार कीमत पर शुद्ध घरेलू उत्पाद = बाज़ार कीमत पर सकल घरेलू उत्पाद – घिसावट
Gross Domestic Product at Market Prices = GDPMP – Depreciation
3. साधन लागत पर शुद्ध घरेलू उत्पाद = बाज़ार कीमत पर शुद्ध घरेलू उत्पाद – शुद्ध अप्रत्यक्ष कर
Net Domestic Product at Factor Cost = NDPMP – Net Indirect Taxes
4.साधन लागत पर शुद्ध राष्ट्रीय उत्पाद = साधन लागत पर शुद्ध घरेलू उत्पाद + विदेशों से शुद्ध साधन आय
Net National Product at Factors Cost = NDPFC + Net Factor Income from Abroad
अथवा
5. साधन लागत पर शुद्ध राष्ट्रीय उत्पाद = राष्ट्रीय आय = कर्मचारियों का मुआवज़ा लाभ + लगान + ब्याज + मिश्रित आय
NNPFC = N.I. = Compensation of Employees + Rent + Interest + Profit + Mixed Income.
प्रश्न 2.
मूल्य वृद्धि विधि या उत्पादन विधि की सावधानियां बताएं। (Explain the Precautions of Value Added Method or Product Method.)
उत्तर-
मूल्य वृद्धि विधि या उत्पादन विधि द्वारा राष्ट्रीय आय का माप करते समय कुछ मदों को शामिल किया जाता है तथा कुछ मदों को शामिल नहीं किया जाता।
कौन-सी मदों को शामिल नहीं करना चाहिए (Which Items should be Excluded)-
- पुरानी वस्तुओं के क्रय-विक्रय-पुरानी वस्तुओं के क्रय-विक्रय को राष्ट्रीय आय में शामिल नहीं किया जाता है क्योंकि यह चालू वर्ष में उत्पादन नहीं की गईं।
- गैर-कानूनी कामों से आय-गैर-कानूनी काम जैसा कि जुआ, समगलिंग, चोरी इत्यादि से आय को राष्ट्रीय आय में शामिल नहीं किया जाता।
- मध्यवर्ती वस्तुओं का मूल्य-मध्यवर्ती वस्तुओं को भी राष्ट्रीय आय में शामिल नहीं किया जाता क्योंकि इससे दोहरी गणना की समस्या उत्पन्न हो जाती है।
- स्व-उपभोग की सेवाएं-स्व-उपभोग की सेवाओं को मूल्य वृद्धि में शामिल नहीं किया जाता जैसा कि पिता द्वारा पुत्र को पढ़ाना, इत्यादि क्योंकि इनके सेवा फल का अनुमान लगाना कठिन होता है।
- कम्पनी द्वारा ब्रान्ड की बिक्री-किसी कम्पनी द्वारा ब्रान्डस की बिक्री से प्राप्त आय को राष्ट्रीय आय में _शामिल नहीं किया जाता क्योंकि यह वित्तीय लेन-देन है।
कौन-सी मदों को मूल्य वृद्धि में शामिल करना चाहिए
(Which Items should be Included in Value Added)
- पुरानी वस्तुओं की बिक्री से दलाली-पुरानी वस्तुओं की बिक्री से दलाली को राष्ट्रीय आय में शामिल करना चाहिए क्योंकि यह वर्तमान सेवा का फल है।
- उत्पादकों द्वारा स्व-उपभोग-इसको राष्ट्रीय आय में शामिल किया जाता है क्योंकि यह उत्पादन बाज़ार में बिक्री के लिए नहीं आता इसलिए इस उत्पादन का आरोपित मूल्य शामिल किया जाता है।
- मकान मालिकों का आरोपित किराया-जिन मकानों में मालिक स्वयं रहते हैं उनका आरोपित किराया, राष्ट्रीय आय में शामिल किया जाता है।
- सरकारी क्षेत्र में कर्मचारियों का मेहनताना-सरकारी क्षेत्र में राष्ट्रीय आय का माप करते समय सरकारी क्षेत्र के कर्मचारियों का मेहनताना शामिल किया जाता है। लगान, ब्याज तथा लाभ को शामिल नहीं किया जाता क्योंकि इनके आंकड़े प्राप्त नहीं होते।
- पूंजी का स्व-लेखा उत्पादन-सरकारी, निगमित तथा पारिवारिक क्षेत्र में उत्पन्न की गई अचल पूंजी को भी राष्ट्रीय आय में शामिल किया जाता है।
- अन्तिम वस्तुओं का मूल्य-उत्पाद विधि में राष्ट्रीय आय का अनुमान लगाते समय केवल अन्तिम वस्तुओं के मूल्य को ही शामिल किया जाता है।
प्रश्न 3.
दोहरी माप की समस्या से क्या अभिप्राय है ? राष्ट्रीय आय का माप करते समय दोहरे माप की समस्या को कैसे दूर किया जा सकता है ?
उत्तर-
दोहरी माप की समस्या का अर्थ (Meaning of Problem of Double Counting) उत्पादन विधि द्वारा जब राष्ट्रीय आय का माप किया जाता है तो इसमें केवल अन्तिम वस्तुओं तथा सेवाओं को ही शामिल किया जाता है। कई बार मध्यवर्ती वस्तुओं की गणना भी हो जाती है जिससे दोहरी गणना की समस्या भी उत्पन्न हो जाती है। दोहरी गणना का अर्थ किसी वस्तु के मूल्य को एक बार से अधिक बार राष्ट्रीय आय में शामिल करने से होता है परन्तु सब वस्तुएं अन्तिम वस्तुएं नज़र आती हैं जबकि उनका प्रयोग मध्यवर्ती वस्तुओं के रूप में होता है। इसको हम एक उदाहरण द्वारा स्पष्ट करते हैं मान लीजिए एक किसान गेहूं उत्पन्न करता है तथा एक आटा मिल वाले को 1000 रुपए की बेच देता है।
आटा मिल वाले के लिए गेहूं अन्तिम मध्यवर्ती वस्तु है जिसको वह आटे में बदलकर बेकरी वाले को 1500 रुपए में बेच देता है। आटा मिल के लिए आटा अन्तिम वस्तु है पर बेकरी वाले के लिए यह मध्यवर्ती वस्तु है क्योंकि बेकरी वाला इससे बिस्कुट बनाकर अन्तिम उपभोक्ताओं को 2000 रुपए में बेच देता है। यदि हम प्रत्येक आदान-प्रदान को राष्ट्रीय आय में शामिल कर लेते हैं तो उससे वस्तु का उत्पादन मूल्य बहुत अधिक हो जाता है जबकि मूल्य वृद्धि इस बात को प्रकट करती है कि वस्तु के मूल्य में कितनी वृद्धि हुई है, उसको राष्ट्रीय आय में शामिल करना चाहिए।
यदि हम कुल उत्पाद का मूल्य राष्ट्रीय आय में शामिल करते हैं तो इसमें एक वस्तु का मूल्य कई बार जुड़ जाता है। इसलिए दोहरी गणना से बचने के लिए अन्तिम वस्तुओं तथा सेवाओं के मूल्य को राष्ट्रीय में जोड़ना चाहिए जैसे कि बेकरी वाले ने अन्तिम उपभोक्ताओं को 2000 रुपए के बिस्कुट बेचे हैं जिसको राष्ट्रीय आय में शामिल करना चाहिए। लेकिन इस विधि में ग़लती होने की सम्भावना होती है तथा किसी मध्यवर्ती वस्तु का मूल्य इसमें जुड़ जाए तो दोहरी गणना की समस्या उत्पन्न हो जाती है।
दोहरी गणना की समस्या का हल (Solution of the Problem of Double Counting) – राष्ट्रीय आय का माप करते समय यदि हम मूल्य वृद्धि (Value Added) की विधि को अपनाते हैं, तो दोहरी गणना की समस्या उत्पन्न नहीं होती। इसको निम्नलिखित सूची पत्र द्वारा स्पष्ट किया जा सकता है|
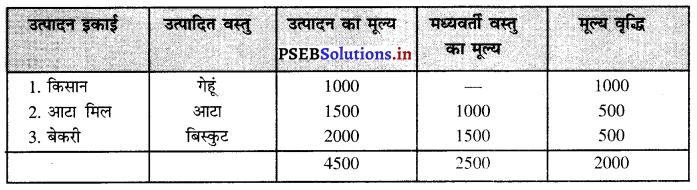
उत्पादन का मूल्य = ₹4500
मध्यवर्ती वस्तु का मूल्य = ₹ 2500
मूल्य वृद्धि = ₹ 2000
इस प्रकार यदि हम उत्पादन का मूल्य शामिल करते हैं तो ₹ 4500 का उत्पादन किया गया है। परन्तु इसमें से मध्यवर्ती वस्तुओं का मूल्य 2500 भी शामिल है। यदि हम उत्पाद मूल्य में से मध्यवर्ती वस्तुओं का मूल्य घटा देते हैं तो इससे अन्तिम वस्तु का मूल्य प्राप्त हो जाता है जिसको मूल्य वृद्धि कहा जाता है। मूल्य वृद्धि विधि द्वारा राष्ट्रीय आय का माप करते समय दोहरी गणना की समस्या का हल हो जाता है।
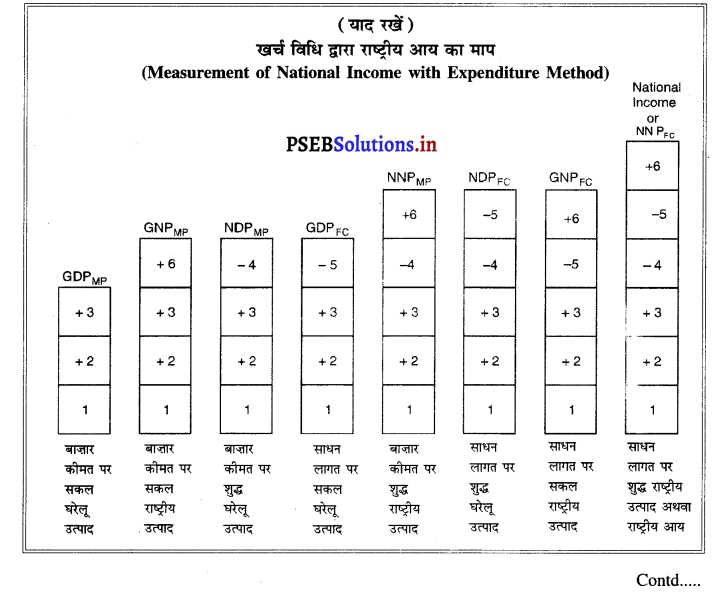
याद रखें मूल्य वृद्धि विधि द्वारा राष्ट्रीय आय की गणना (Measurement of National Income with Value Added Method)
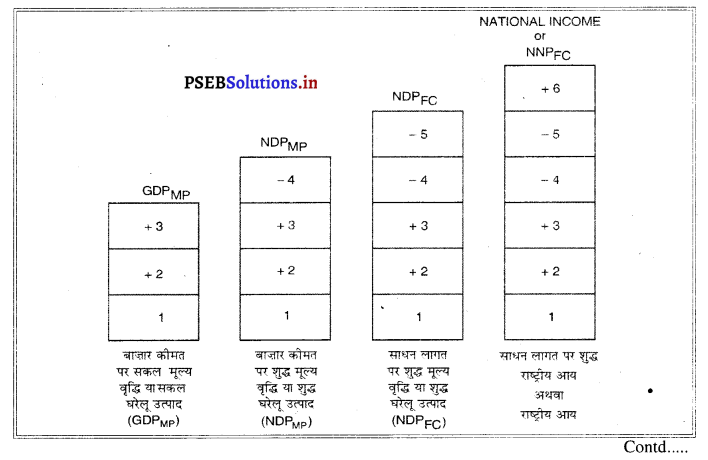
- प्राथमिक क्षेत्र में बाज़ार कीमत पर सकल मूल्य वृद्धि
- गौण क्षेत्र में बाजार कीमत पर सकल मूल्य वृद्धि
- तीसरे क्षेत्र में बाज़ार कीमत पर सकल मूल्य वृद्धि
- मूल्य ह्रास या मूल्य घिसावट
- शुद्ध अप्रत्यक्ष कर (अप्रत्यक्ष कर – सहायता)
- विदेशों से प्राप्त शुद्ध साधन आय।
V. संख्यात्मक प्रश्न (Numericals)
प्रश्न 1.
निम्नलिखित आंकड़ों के आधार पर फ़र्म A तथा फ़र्म B द्वारा की गई मूल्य वृद्धियों का आंकलन करें।

हल (Solution):
फ़र्म A तथा फ़र्म B द्वारा मूल्य वृद्धि
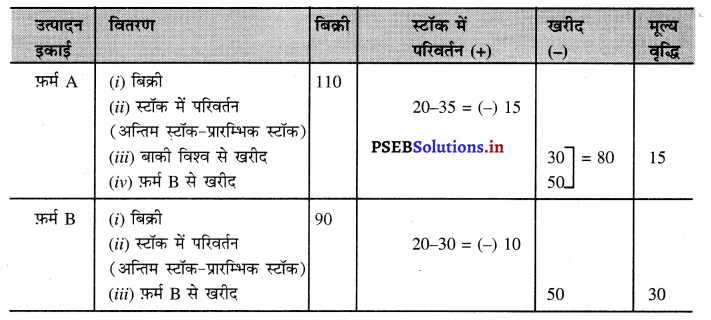
फ़र्म A द्वारा मूल्य वृद्धि = बिक्री + स्टॉक में परिवर्तन – खरीद
= 110 + (-15) – 80
= ₹ 15 लाख उत्तर
फ़र्म B द्वारा मूल्य वृद्धि = बिक्री + स्टॉक में परिवर्तन – खरीद
= 90 + (-10) – 50
= ₹ 30 लाख उत्तर

प्रश्न 2.
निम्नलिखित आंकड़ों के आधार पर फ़र्म x तथा फ़र्म Y द्वारा की गई मूल्य वृद्धियों को ज्ञात करें।

हल (Solution) :
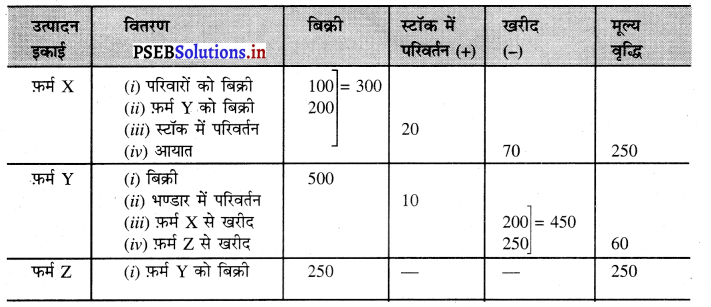
फ़र्म X द्वारा मूल्य वृद्धि = बिक्री + भण्डार में परिवर्तन – खरीद
= 300 + 20 – 70
= ₹ 250 लाख उत्तर
फ़र्म Y द्वारा मूल्य वृद्धि = 500 + 10 – 450 = ₹ 60 लाख उत्तर
प्रश्न 3.
निम्न आंकड़ों द्वारा फ़र्म A तथा फ़र्म B की मूल्य वृद्धि ज्ञात करें


हल (Solution) :
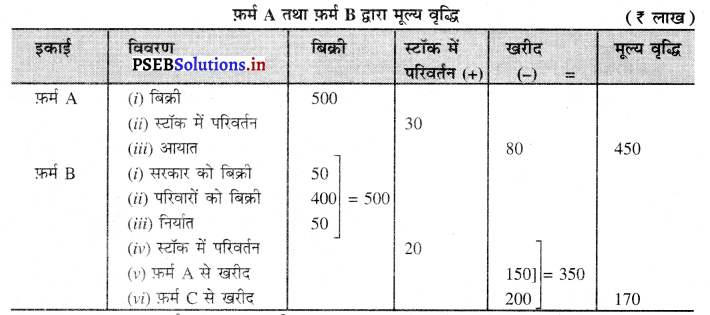
फ़र्म A द्वारा मूल्य वृद्धि = ₹ 450 लाख
फ़र्म B द्वारा मूल्य वृद्धि = ₹ 170 लाख उत्तर
प्रश्न 4.
निम्न आंकड़ों के आधार पर C उद्योग की मूल्य वृद्धि ज्ञात करें-

हल (Solution) :
उद्योग A, B, C तथा D द्वारा कुल बिक्री = ₹ 130 लाख
- उद्योग, A द्वारा मूल्य वृद्धि = बिक्री – खरीद = ₹ 20 – 0 = 20 लाख
- उद्योग B द्वारा मूल्य वृद्धि = ₹ 40 लाख
- उद्योग D द्वारा मूल्य वृद्धि = ₹ 30 लाख
- उद्योग A, B तथा D द्वारा मूल्य वृद्धि = 20 + 40 + 30 = ₹ 90 लाख
- उद्योग C द्वारा मूल्य वृद्धि = 130 – 90 = ₹ 40 लाख उत्तर
(A, B, C, D द्वारा मूल्य वृद्धि – ABD द्वारा मूल्य-वृद्धि)
प्रश्न 5.
निम्नलिखित आंकड़ों द्वारा साधन लागत पर शुद्ध मूल्य वृद्धि ज्ञात करें


हल (Solution) :
साधनं लागत पर शुद्ध मूल्य वृद्धि = बिक्री + अन्तिम स्टॉक – प्रारम्भिक स्टॉक – मध्यवर्ती उपभोग — बिक्री कर + सहायता – स्थिर पूंजी का उपभोग
= 1000 + 80 – 40 – 640 – 30 + 10 – 100 = ₹ 280 लाख उत्तर
प्रश्न 6.
निम्नलिखित आंकड़ों द्वारा फर्म A की बाज़ार कीमत पर शुद्ध मूल्य वृद्धि ज्ञात करें।

हल (Solution) :
बाजार कीमत पर शुद्ध मूल्य वृद्धि = बिक्री + स्टॉक में परिवर्तन – घिसावट – मध्यवर्ती वस्तुओं की खरीद
= 700 + 40 – 80 – 400 = ₹ 260 हज़ार उत्तर
प्रश्न 7.
फ़र्म A ने ₹500 गैर-साधन आगतों (Inputs) पर खर्च किए और ₹ 900 के मूल्य की वस्तुओं का उत्पादन किया। इसने ₹ 600 के मूल्य की वस्तुएं फ़र्म B तथा ₹ 300 के मूल्य की वस्तुएं उपभोक्ताओं को बेचीं। फ़र्म A की सकल मूल्य वृद्धि ज्ञात करें।
हल (Solution):
फ़र्म A द्वारा सकल मूल्य वृद्धि = उत्पादन वस्तुओं का मूल्य – ग़ैर-साधन आगतों पर खर्च = 900 (600 + 300) – 500 = ₹400 उत्तर
प्रश्न 8.
निम्नलिखित आंकड़ों द्वारा साधन लागत पर शुद्ध मूल्य वृद्धि ज्ञात करें।

हल (Solution):
साधन लागत पर शुद्ध मूल्य वृद्धि = बिक्री + स्टॉक में परिवर्तन (अन्तिम स्टॉक – प्रारम्भिक स्टॉक) – मूल्य घिसावट – उत्पादन कर – मध्यवर्ती उपभोग ।
= 200 + 10 – 15 – 12 – 20 – 48 = ₹ 115 लाख उत्तर

प्रश्न 9.
निम्नलिखित आंकड़ों की सहायता से
(क) उत्पादन का मूल्य
(ख) साधन लागत पर शुद्ध मूल्य वृद्धि ज्ञात करें।

हल-
(क) उत्पादन का मूल्य – बिक्री + स्टॉक में वृद्धि
= 27,560 + 1,690
= ₹ 29,250 करोड़ उत्तर
(ख) साधन लागत पर शुद्ध मूल्य वृद्धि = बिक्री + स्टॉक में वृद्धि – मध्यवर्ती उपभोग – अप्रत्यक्ष कर – स्थाई पूंजी का उपभोग + आर्थिक सहायता = 27,560 + 1,690 – 3,575 – 2,000 – 1,345 + 1,550
= ₹ 23,880 करोड़ उत्तर
प्रश्न 10.
निम्नलिखित आंकड़ों की सहायता से ज्ञात कीजिए।
(क) बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद
(ख) बाजार कीमत पर शुद्ध राष्ट्रीय उत्पाद
(ग) राष्ट्रीय आय

हल (Solution) :
(क) बाजार कीमत पर सकल राष्ट्रीय उत्पाद = बिक्री + साल के अन्त में स्टॉक – साल के आरम्भ में स्टॉक – मध्यवर्ती उपभोग
= 70,000 + 25,000 – 5,000 – 10,000 = ₹ 80,000 लाख उत्तर
(ख) बाज़ार कीमत पर शुद्ध राष्ट्रीय उत्पाद = बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद – घिसावट लागत = 80,000 – 1,000 = ₹ 79,000 लाख उत्तर
(ग) राष्ट्रीय आय = बाज़ार कीमत पर शुद्ध राष्ट्रीय उत्पाद – अप्रत्यक्ष कर + आर्थिक सहायता = 79,000 – 300 + 100 = ₹ 78,800 लाख उत्तर
(B) आय विधि (Income Method)
IV. दीर्घ उरीय प्रश्न (Long Answer Type Questions)
प्रश्न 1.
राष्ट्रीय आय के माप की आय विधि की व्याख्या करें।
(Explain the Income Method for measurement of National Income.)
उत्तर-
राष्ट्रीय आय का अर्थ एक वर्ष में एक देश के साधारण निवासियों द्वारा उत्पादित आय के साधनों के रूप में कार्य करने से जो आय मज़दूरी, लगान, ब्याज तथा लाभ के रूप में प्राप्त होती है, उसके योग को राष्ट्रीय आय कहा (The sum of incomes accuring to the factors of Production supplied by the norma! Residents of a country during a year is called National Income.) एक वर्ष में उत्पादन के साधनों श्रम, पूंजी, भूमि तथा उद्यम को कार्य करने के बदले में मजदूरी, लगान, ब्याज तथा लाभ के रूप में जो आप प्राप्त हाती है, उसके योग को राष्ट्रीय आय कहा जाता है। आय विधि को साधन भुगतान विधि (Factor Paynient Method) अथवा वर्गीकृत कार्यों के अनुसार विधि (Distributed Share Method) भी कहा जाता।
उत्पादन प्रक्रिया के परिणामस्वरूप आय का सृजन होता है। उत्पादन के समय जो आय उत्पादन के साधनों को प्राप्त होती है उसको उद्यमियों की साधन लागत तथा उत्पादन के साधनों की आय कहा जाता है। आय विधि द्वारा राष्ट्रीय आय का माप करते समय निम्नलिखित अवस्थाओं में से निकलना पड़ता है-
1. प्रथम अवस्था (First Stage)-इस विधि में सबसे पहले देश की घरेलू सीमा के भीतर आने वाली इकाइयों का पता किया जाता है जिनको प्राथमिक क्षेत्र (Primary Sector), गौण क्षेत्र (Secondary Sector) तथा तृतीय क्षेत्र (Teritiary Sector) में विभाजित किया जाता है।
2. द्वितीय अवस्था (Second Stage)-इसके पश्चात् उत्पादन इकाइयों को दिए जाने वाले भुगतान का अनुमान लगाया जाता है जैसे कि-
(a) कर्मचारियों की मेहनत-मज़दूरी तथा वेतन + किस्म के रूप में आय + सामाजिक सुरक्षा योजनाओं में मालिकों का योगदान + रिटायर हुए कर्मचारियों की पेन्शन।
(b) परिचालन अधिशेष-इसमें सम्पत्ति तथा उद्यमवृत्ति से प्राप्त आय को शामिल किया जाता है जिसमें निम्नलिखित आय शामिल होती है
- किराया अथवा लगान तथा रायल्टी
- ब्याज
- लाभ (लाभांश + निगम कर + उद्यमियों की बचत या अविभाजित लाभ)
(c) मिश्रित आय-इसमें स्व-रोज़गार पर लगे लोगों के कार्य तथा सम्पत्ति से प्राप्त आय शामिल होती है। यदि हम ऊपर दी गई आय का योग कर लेते हैं तो इसको शुद्ध घरेलू आय कहा जाता है।
(d) विदेशों से प्राप्त शुद्ध साधन आय-एक देश के लोगों द्वारा विदेशों में प्रदान की गई साधन सेवाओं के बदले में प्राप्त होने वाली आय तथा एक देश की घरेलू सीमा के भीतर गैर-निवासियों द्वारा सेवाओं के बदले में दी जाने वाली आय के अन्तर को शुद्ध विदेशी साधन आय कहा जाता है। यदि हम शुद्ध घरेलू आय में विदेशों से प्राप्त शुद्ध साधन आय को जोड़ लेते हैं तो इसको राष्ट्रीय आय (National Income) कहते हैं।
3. तृतीय अवस्था (Third Stage)-इस अवस्था में साधन आय का अनुमान लगाया जाता है। विभिन्न धारणाओं को इस प्रकार स्पष्ट किया जा सकता है-
- शुद्ध घरेलू आय (NDPFC) कर्मचारियों का मेहनताना + परिचालन अधिशेष + मिश्रित आय
- शुद्ध राष्ट्रीय आय अथवा साधन लागत पर शुद्ध राष्ट्रीय उत्पाद = कर्मचारियों का मेहनताना + परिचालन अधिशेष + मिश्रित आय + विदेशों से शुद्ध साधन आय + मूल्य घिसावट अथवा शुद्ध घरेलू आय + विदेशों से शुद्ध साधन आय = शुद्ध साधन आय + मूल्य घिसावट
- सकल राष्ट्रीय आय या साधन लागतों पर सकल राष्ट्रीय उत्पाद = कर्मचारियों का मेहनताना + परिचालन अधिशेष + मिश्रित आय + विदेशों से शुद्ध साधन आय + मूल्य घिसावट
- बाज़ार कीमत पर सकल राष्ट्रीय आय-कर्मचारियों का मेहनताना + परिचालन अधिशेष + मिश्रित आय + विदेशों से शुद्ध साधन आय + मूल्य घिसावट + शुद्ध अप्रत्यक्ष कर अथवा = सकल राष्ट्रीय आय + शुद्ध अप्रत्यक्ष कर
प्रश्न 2.
आय विधि में ध्यान रखने योग्य सावधानियों का वर्णन करें। (Explain the Precautions regarding Income Method.)
अथवा
राष्ट्रीय आय का माप करते समय आय विधि में कौन-सी मदों को शामिल किया जाता है तथा कौन-सी मदों को शामिल नहीं किया जाता ?
(Which items should be included in National Income and which items should not be included in National Income while calculating National Income in Income Method ?)
उत्तर-
आय विधि द्वारा राष्ट्रीय आय का माप करते समय कुछ मदों को राष्ट्रीय आय में शामिल किया जाता है जबकि कुछ अन्य मदों को शामिल नहीं किया जाता। निम्नलिखित मदों से प्राप्त आय को राष्ट्रीय आय में शामिल किया जाएगा (Items to be included in National Income)
राष्ट्रीय आय का माप करते समय आय विधि में उन स्रोतों से प्राप्त आय को राष्ट्रीय आय में शामिल किया जाता है जोकि उत्पादक होती हैं तथा जिन क्रियाओं को करने की सरकार आज्ञा देती है अर्थात् कानूनी (Legal) तथा उत्पादक (Productive) क्रियाओं को राष्ट्रीय आय में शामिल किया जाता है क्योंकि यह आय का सृजन करती है।
- गायक, डान्सर तथा अभिनेताओं की आय राष्ट्रीय आय में शामिल की जाती है।
- सरकार द्वारा निःशुल्क इलाज पर खर्च, सड़कों, नहरों तथा रोशनी पर खर्च राष्ट्रीय आय में शामिल किया जाता
- सरकारी कर्मचारियों को दिया जाने वाला मेडिकल भत्ता राष्ट्रीय आय में शामिल किया जाता है।
- भविष्य निधि में श्रमिकों का योगदान राष्ट्रीय आय में शामिल किया जाता है।
- मूल्य घिसावट को कुल उत्पादन में शामिल किया जाता है परन्तु शुद्ध उत्पादन में शामिल नहीं किया जाता।
- निगम कर, लाभांश तथा अविभाजित लाभ, यह लाभ के भाग होते हैं इसलिए इनको राष्ट्रीय आय में शामिल किया जाता है, परन्तु यदि लाभ दिया गया हो तो यह तीनों भाग उसमें शामिल होते हैं। इसलिए इनको अलग से शामिल नहीं किया जाता।
- मज़दूरी, किस्म के रूप में मजदूरी तथा सामाजिक सुरक्षा, भविष्य निधि इत्यादि कर्मचारियों के मेहनताने के भाग होते हैं। यदि कर्मचारियों का मेहनताना शामिल किया जाता है तो इनको अलग से शामिल नहीं किया जाता।
- जिन मकानों में मकान मालिक स्वयं रहते हैं उनका आरोपित किराया राष्ट्रीय आय में शामिल किया जाता है।
- पुरानी वस्तुओं की बिक्री पर दी जाने वाली दलाली को राष्ट्रीय आय में शामिल किया जाता है।
अग्रलिखित मदों को राष्ट्रीय आय में शामिल नहीं किया जाता (Items not to be Included in National Income)-
- हस्तान्तरण भुगतान जैसे कि बुढ़ापा पेन्शन, बेरोज़गारी भत्ता इत्यादि को राष्ट्रीय आय में शामिल नहीं किया जाता।
- गैर-कानूनी कामों जैसे कि जुआ, समगलिंग, चोरी इत्यादि से प्राप्त आय को इसमें शामिल नहीं किया जाता।
- स्व-उपभोग सेवाओं को राष्ट्रीय आय में शामिल नहीं किया जाता जबकि स्व-उपभोग वस्तुओं को इसमें शामिल किया जाता है।
- पुरानी वस्तुओं जैसे कि पुराना मकान, पुरानी पुस्तकों इत्यादि की बिक्री से प्राप्त आय को शामिल नहीं किया जाता।
- शेयर, बांड इत्यादि को बेचने से प्राप्त होने वाली आय को राष्ट्रीय आय में शामिल नहीं किया जाता।
- आकस्मिक लाभ अथवा पूंजीगत लाभ को राष्ट्रीय आय में शामिल नहीं किया जाता।
- अप्रत्यक्ष कर साधन लागत पर, राष्ट्रीय उत्पाद में शामिल नहीं होते परन्तु बाज़ार कीमत पर यह शामिल किए जाते हैं।
- मृत्यु कर, सम्पत्ति कर, उपहार कर इत्यादि को राष्ट्रीय आय में शामिल नहीं किया जाता।
- राष्ट्रीय ऋण पर ब्याज को राष्ट्रीय आय में शामिल नहीं किया जाता।
आय विधि द्वारा राष्ट्रीय आय का माप करते समय शामिल होने वाली मदों तथा न शामिल होने वाली मदों को ध्यान में रखना चाहिए।
याद रखें आय विधि द्वारा राष्ट्रीय आय की गणना (Measurement of National Income with Income Method)
- कर्मचारियों का मेहनताना (नकद मज़दूरी + किस्म के रूप में आय + सामाजिक सुरक्षा योजनाओं में मालिकों का योगदान + रिटायर हुए कर्मचारियों की पेन्शन)
- परिचालन अधिशेष (किराया अथवा लगान तथा रायल्टी + ब्याज + लाभ (लाभांश + निगम कर + उद्यमियों की बचत या अविभाजित लाभ)
- मिश्रित आय
- विदेशों से प्राप्त शुद्ध साधन आय
- मूल्य घिसावट अथवा स्थिर पूंजी का उपयोग
- शुद्ध अप्रत्यक्ष कर (अप्रत्यक्ष कर – आर्थिक सहायता)

V. संख्यात्मक प्रश्न (Numericals)
प्रश्न 1.
निम्नलिखित आंकड़ों की सहायता से
(i) घरेलू आय
(ii) राष्ट्रीय आय की गणना करेंमदें

हल (Solution) :
(i) घरेलू आय = मज़दूरी + किराया + ब्याज + लाभांश + मिश्रित आय + अविभाजित आय + निगम कर + सामाजिक सुरक्षा में योगदान = 50,000 + 10,000 + 1000 + 5000 + 1500 + 500 + 400 + 600 = ₹ 69,000 करोड़ उत्तर
(ii) राष्ट्रीय आय = घरेलू आय + विदेशों से प्राप्त शुद्ध साधन आय = 69,000 + 3000 = ₹72,000 करोड़ उत्तर
प्रश्न 2.
निम्नलिखित आंकड़ों की सहायता से

हल (Solution):
(i) घरेलू आय = लगान + ब्याज + लाभांश + स्व-नियोजकों की मिश्रित आय + कर्मचारियों का मेहनताना = 80 + 100 + 210 + 250 + 500 = ₹ 1140 करोड़ उत्तर
(ii) राष्ट्रीय आय = घरेलू आय + विदेशों से शुद्ध साधन आय = 1140 + (-20) = ₹ 1120 करोड़ उत्तर
प्रश्न 3.
निम्नलिखित आंकड़ों से राष्ट्रीय आय ज्ञात करेंमदें

हल (Solution):
(i) घरेलू आय = स्व-नियोजितों की मिश्रित आय + परिचालन अधिशेष + मज़दूरी तथा वेतन + मालिकों का सामाजिक सुरक्षा में अंशदान
= 200 + 900 + 500 + 50 = ₹ 1650 करोड़
(ii) राष्ट्रीय आय = घरेलू आय + विदेशों से शुद्ध साधन आय = 1650 + (-10) = ₹ 1640 करोड़ उत्तर।
प्रश्न 4.
संमत 1982-83 में भारत देश के लिए निम्नलिखित आंकड़े दिए गए हैं :मदें

हल (Solution):
(i) घरेलू साधन आय = कर्मचारियों का मुआवज़ा + किराया + ब्याज + लाभ + मिश्रित आय = 49651 + 10209 + 4794 + 6926 + 50416 = ₹ 1,21,996 करोड़ उत्तर
(ii) राष्ट्रीय आय = घरेलू साधन आय + निवल विदेशी साधन आय = 1,21,996 + (-7) = ₹ 1,21,989 करोड़ उत्तर
प्रश्न 5.
निम्नलिखित आंकड़ों द्वारा किसी फ़र्म की
(i) उत्पाद विधि
(ii) आय विधि से राष्ट्रीय आय में योगदान ज्ञात करें।
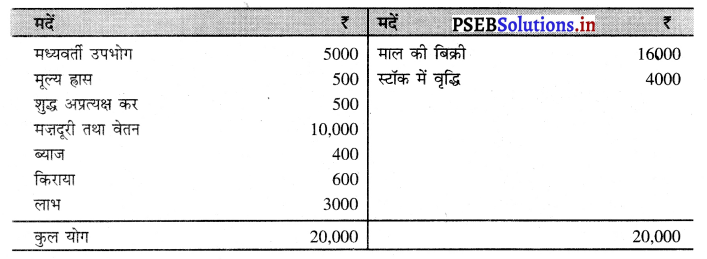
हल (Solution) :
(i) उत्पाद विधि राष्ट्रीय आय = बिक्री + स्टॉक में वृद्धि – मध्यवर्ती उपभोग – मूल्य ह्रास – शुद्ध अप्रत्यक्ष कर = 16000 + 4000 -5000 – 500 – 500 = ₹ 14000 करोड़ उत्तर
(ii) आय विधि राष्ट्रीय आय = मजदूरी तथा वेतन + ब्याज + किराया + लाभ = 10,000 + 400 + 600 + 3000 = ₹ 14000 करोड़ उत्तर

प्रश्न 6.
निम्नलिखित आंकड़ों द्वारा
(a) उत्पाद विधि
(a) आय विधि से बाज़ार कीमत पर सकल घरेलू उत्पाद ज्ञात करें।

हल (Solution) :
उत्पादन विधि बाजार कीमत पर सकल घरेलू आय = (प्राथमिक क्षेत्र का उत्पादन + द्वितीयक क्षेत्र का उत्पादन + तृतीय क्षेत्र का उत्पादन) – (प्राथमिक क्षेत्र का मध्यवर्ती उपभोग + द्वितीयक क्षेत्र का मध्यवर्ती उपभोग + तृतीयक क्षेत्र का मध्यवर्ती उपभोग)
= (1000 + 900 + 700) – (500 + 400 + 300) = ₹ 1400 करोड़
आय विधि बाज़ार कीमत पर सकल घरेलू उत्पाद = कर्मचारियों का वेतन + परिचालन अधिशेष + मिश्रित आय + स्थाई पूंजी का उपभोग + शुद्ध अप्रत्यक्ष कर
= 400 + 650 + 300 + 40 + 10 = ₹ 1400 करोड़ उत्तर
प्रश्न 7.
निम्नलिखित आंकड़ों से परिचालन अधिशेष ज्ञात करें।

हल (Solution) :
परिचालन अधिशेष = (i) – (ii) – (iii) – (iv) – (v) + (vi) – (vii) = 1000 – 200 – 200 – 30 – 20 + 50 -100 = ₹ 500 करोड़ उत्तर
प्रश्न 8.
निम्नलिखित आंकड़ों से परिचालन अधिशेष ज्ञात करें। मदें

हल (Solution):
परिचालन अधिशेष = (i) – (ii) – (iii)– (iv) – (v)
= 1200 – 60 – 40 – 450 – 50 = ₹ 600 Crores उत्तर
་
प्रश्न 9.
निम्नलिखित आंकड़ों से ज्ञात करें
(क) घरेलू साधन आय
(ख) राष्ट्रीय आय

उत्तर-
(क) घरेलू साधन आय = (i) + (ii) + (iii) + (iv) + (v)
= 50,000 + 12,000 + 15,000 + 18,000 + 40,000
= ₹ 1,35,000 करोड़ उत्तर
(ख) राष्ट्रीय आय = घरेलू साधन आय + (vi) = 1,35,000 + 15,000 = ₹ 1,50,000 करोड़ उत्तर

प्रश्न 10.
निम्नलिखित आंकड़ों से ज्ञात करें।

उत्तर-
घरेलू साधन आय = (i) + (ii) + (iii) + (iv) + (1)
= 75,000 + 18.000 + 22.500 + 27,000 + 60,000
= ₹ 2,02,500
करोड़ उत्तर राष्ट्रीय आय = घरेलू साधन आय + (vi)
= 2,02,500 + 22,500 = ₹ 2,25,000 करोड़ उत्तर
प्रश्न 11.
निम्नलिखित आंकड़ों से ज्ञात करें :
 उत्तर-
उत्तर-
(क) घरेलू साधन आय-कर्मचारियों का मेहनताना + ब्याज + लाभ तथा लाभांश + किराया + मिश्रित आय
(i) ब्याज
= 50,000 + 12,000 + 15,000 + 18,000 + 40,000
= ₹ 1,35,000 करोड़ उत्तर
(ख) राष्ट्रीय आय-घरेलू साधन आय + विदेशों से प्राप्त शुद्ध साधन आय
= 1,35,000 + 15,000
= ₹ 1,50,000 करोड़ उत्तर
प्रश्न 12.
निम्न आंकड़ों से कुल घरेलू उत्पाद बाज़ार कीमत पर (GDPMP) और शुद्ध राष्ट्रीय उत्पाद साधन लागतों पर (NNPFC) ज्ञात करो।

उत्तर-
बाज़ार कीमत पर कुल घरेलू उत्पाद (GDPMP) = शुद्ध अप्रत्यक्ष कर + स्थाई पूँजी का उपभोग + लगान + लाभ + ब्याज + रायल्टी + मज़दूरी और वेतन + सामाजिक सुरक्षा में मालिकों का अंशदान।= 38 + 35 + 10 + 27 + 23 + 20 + 150 + 25
= ₹ 328 करोड़ उत्तर
साधन लागतों पर शुद्ध राष्ट्रीय उत्पाद (NNPFC) = बाज़ार कीमतों पर कुल राष्ट्रीय उत्पाद – शुद्ध अप्रत्यक्ष कर — स्थाई पूँजी का उपभोग + विदेशों से प्राप्त साधन आय
= 328 – 38 – 35 + (-5)
= ₹ 250 करोड़ उत्तर
(C) खर्च विधि (Expenditure Method)
IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)
प्रश्न 1.
राष्ट्रीय आय के माप की खर्च विधि की व्याख्या करें। (Explain the Expenditure Method for the measurement of National Income.)
उत्तर-
राष्ट्रीय आय को मापने की तीसरी विधि खर्च विधि है जिसको उपभोग तथा निवेश विधि (Consumption and Investment Method) भी कहा जाता है। इस विधि को स्पष्ट करते हुए कुजनेटस ने कहा है, “राष्ट्रीय आय, एक वर्ष में एक देश की उत्पादक प्रणाली में जो वस्तुएं तथा सेवाएं अन्तिम उपभोक्ताओं द्वारा उपभोग की जाती हैं अथवा देश के पूंजीगत पदार्थों में शुद्ध वृद्धि करती हैं, उनका योग है।”
खर्च विधि की मुख्य अवस्थाएं-खर्च विधि में मुख्य अवस्थाएं इस प्रकार होती हैं –
1. प्रथम अवस्था-सबसे पहले उन इकाइयों की पहचान की जाती है जो अन्तिम उपभोग खर्च करते हैं तथा जिनको खर्च विधि में शामिल किया जाता है।
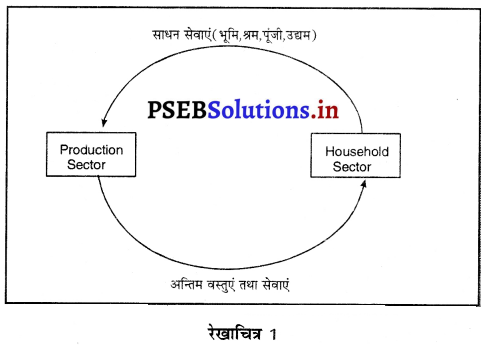
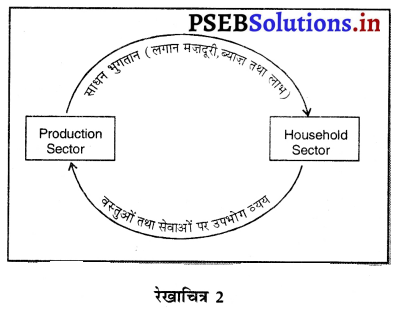
A. पारिवारिक क्षेत्र (Household Sector)
B. उत्पादक क्षेत्र (Production Sector)
C. सरकारी क्षेत्र (Government Sector)
D. शेष विश्व क्षेत्र (Rest of the World Sector)
2. दूसरी अवस्था-इस अवस्था में अन्तिम खर्च का वर्गीकरण किया जाता है। अन्तिम खर्च के वर्गीकरण को इस प्रकार स्पष्ट किया जा सकता है-
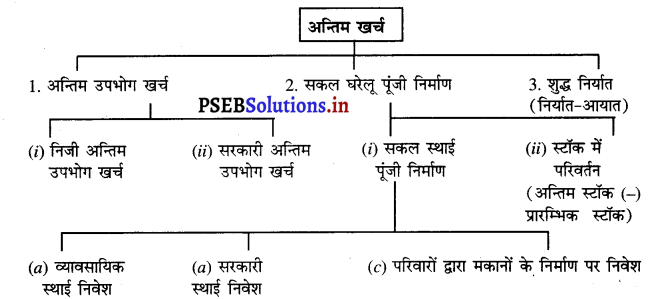
अन्तिम खर्च के मुख्य अंश इस प्रकार हैं –
1. अन्तिम उपभोग खर्च
- निजी अन्तिम उपभोग खर्च
- सरकारी अन्तिम उपभोग खर्च
2. सकल घरेलू पूंजी निर्माण
(i) सकल स्थाई पूंजी निर्माण
(a) व्यावसायिक स्थाई निवेश
(b) सरकारी स्थाई निवेश
(c) परिवारों द्वारा मकानों के निर्माण पर निवेश
(ii) स्टॉक में परिवर्तन (अन्तिम स्टॉक – प्रारम्भिक स्टॉक)
3. शुद्ध निर्यात (निर्यात – आयात)
तीसरी अवस्था
- निजी अन्तिम उपभोग खर्च- इसमें व्यक्तियों, परिवारों तथा गैर-लाभकारी निजी संस्थाओं द्वारा वस्तुओं और सेवाओं पर किए गए व्यय को शामिल किया जाता है।
- सरकारी अन्तिम उपभोग खर्च-इसमें सरकार के खर्च को शामिल करते हैं।
- सकल घरेलू पूंजी निर्माण-इसमें निवेश व्यय शामिल करते हैं जोकि स्थाई निवेश तथा माल सूची निवेश पर किया जाने वाला व्यय शामिल करते हैं।
- शुद्ध निर्यात-इसमें निर्यात वस्तुओं तथा सेवाओं में से आयात वस्तुओं तथा सेवाओं का मूल्य घटाने से शुद्ध निर्यात ज्ञात होता है।
- विदेशों से शुद्ध साधन आय-कुछ अर्थ-शास्त्री शुद्ध निर्यात के स्थान पर शुद्ध विदेशी निवेश की धारणा का प्रयोग करते हैं। इसमें आयात तथा निर्यात के अन्तर के अतिरिक्त विदेशों से शुद्ध साधन आय को शामिल किया जाता है।
यदि हम खर्च विधि द्वारा विभिन्न धारणाओं का माप करना चाहते हैं तो इसके लिए निम्न विधि प्रयोग की जाती है-
- बाजार कीमत पर सकल घरेलू उत्पाद = निजी अन्तिम उपाभोग खर्च + सरकारी अन्तिम उपभोग खर्च + सकल स्थिर पूंजी निर्माण + शुद्ध निर्यात।
- बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद = बाज़ार कीमत पर सकल घरेलू उत्पाद + विदेशों से शुद्ध साधन आय
- बाज़ार कीमतों पर शुद्ध राष्ट्रीय उत्पाद = बाजार कीमत पर सकल राष्ट्रीय उत्पाद-मूल्य घिसावट
- शुद्ध राष्ट्रीय आय = बाज़ार कीमत पर शुद्ध राष्ट्रीय उत्पाद-शुद्ध अप्रत्यक्ष कर |

प्रश्न 2.
खर्च विधि द्वारा राष्ट्रीय आय का माप करते समय सावधानियां बताएं। (Mention the Precautions while measuring National Income with Expenditure Method.)
उत्तर-
खर्च विधि द्वारा राष्ट्रीय आय का माप करते समय निम्नलिखित सावधानियों का प्रयोग करने की आवश्यकता होती है
- पुरानी वस्तुओं पर किए जाने वाले खर्च को अन्तिम खर्च में शामिल नहीं किया जाता क्योंकि यह खर्च वर्तमान वर्ष में उत्पादित वस्तुओं पर नहीं किया जाता बल्कि पहले से ही उत्पादित वस्तुओं पर किया जाता है।
- कुल खर्च का माप करते समय केवल अन्तिम खर्च को ही शामिल किया जाता है।
- अन्तिम खर्च में मध्यवर्ती खर्च को शामिल नहीं किया जाता।
- पुराने तथा नए शेयर तथा बांड पर किया गया खर्च कुल खर्च में शामिल नहीं किया जाता क्योंकि यह खर्च वस्तुओं तथा सेवाओं पर खर्च नहीं होता।
- सरकार द्वारा दिए गए हस्तान्तरण भुगतान पर खर्च को अन्तिम खर्च में शामिल नहीं किया जाता क्योंकि जिन व्यक्तियों द्वारा हस्तान्तरण भुगतान प्राप्त किया जाता है उनके द्वारा इसके बदले में कोई उत्पादक सेवा प्रदान नहीं की जाती।
- स्व-उपभोग पर किए गए खर्च को अन्तिम उपभोग में शामिल किया जाता है क्योंकि यह खर्च वर्तमान उत्पादन में से होता है।
- इस विधि द्वारा बाजार कीमतों पर कुल राष्ट्रीय उत्पादन मूल्य का पता चलता है। यदि हम साधन लागतों पर शुद्ध राष्ट्रीय उत्पाद अथवा राष्ट्रीय आय का पता करना चाहते हैं तो इसमें से शुद्ध अप्रत्यक्ष कर तथा स्थाई पूंजी का उपभोग घटा देना चाहिए।
- कुल खर्च विधि में सकल घरेलू पूंजी निर्माण की धारणा में सकल घरेलू स्थाई पूंजी निर्माण तथा स्टॉक में परिवर्तन का योग होता है।
प्रश्न 3.
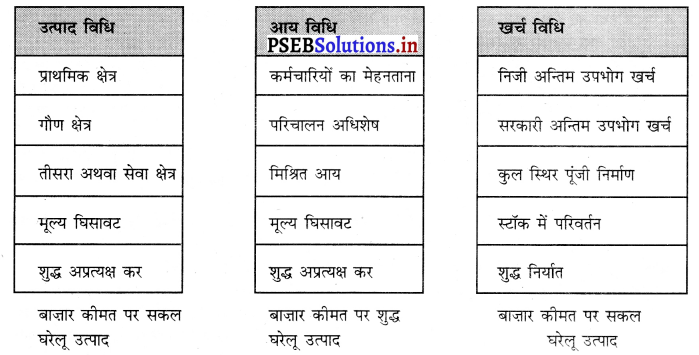
राष्ट्रीय आय, राष्ट्रीय उत्पाद तथा राष्ट्रीय खर्च में समानता को स्पष्ट करें। (Establish the Equality of National Income, National Product and National Expenditure.)
उत्तर-
राष्ट्रीय आय को मापने की तीन विधियां हैं-आय विधि, उत्पाद विधि तथा खर्च विधि। इन तीनों विधियों द्वारा राष्ट्रीय आय का योग एक-दूसरे के समान होता है क्योंकि जब उत्पादन प्रक्रिया में उत्पादन के साधनों को कार्य पर लगाया जाता है तो श्रम, भूमि, पूंजी तथा उद्यमी मिलकर उत्पादन करते हैं। इन उत्पादन के साधनों को कार्य करने के बदले में मेहनताना दिया जाता है अर्थात् कर्मचारियों को कार्य करने के लिए मज़दूरी तथा वेतन, भूमि का लगान, पूंजी का ब्याज तथा उद्यमी को लाभ प्राप्त होता है। यदि हम उत्पादन के साधनों को प्राप्त होने वाली आय का योग कर लेते हैं तो इसको राष्ट्रीय आय कहा जाता है। इसमें स्व-रोज़गार पर लगे मनुष्यों की मिश्रित आय भी शामिल होती है। इसलिए आय विधि के अनुसार सकल घरेलू उत्पाद का माप इस प्रकार किया जाता है |
बाजार कीमत पर सकल घरेलू उत्पाद (GDPMP) = कर्मचारियों का मेहनताना + परिचालन अधिशेष + मिश्रित आय + मूल्य घिसावट + शुद्ध अप्रत्यक्ष कर उत्पादन के साधन देश में जो उत्पादन करते हैं, उसके योग को बाज़ार कीमत पर सकल घरेलू उत्पाद कहा जाता है। उत्पादन के साधन अर्थ व्यवस्था के तीन क्षेत्रों में कार्य करते हैं—प्राथमिक क्षेत्र जिसमें कृषि, जंगल, खानों इत्यादि से प्राप्त उत्पादन को शामिल किया जाता है। गौण क्षेत्र में उद्योग, निर्माण, विद्युत्, गैस, जल आपूर्ति इत्यादि के उत्पादन को शामिल करते हैं। तीसरे क्षेत्र में सेवाओं को शामिल किया जाता है जैसे कि यातायात, संचार, व्यापार, होटल, बैंक, बीमा इत्यादि। यदि हम इन तीन क्षेत्रों में अन्तिम वस्तुओं तथा सेवाओं के उत्पादन का योग कर लेते हैं जिसको मूल्य वृद्धि विधि (Value Added Method) द्वारा मापा जाता है। इससे हम सकल घरेलू उत्पाद ज्ञात कर सकते हैं।
उत्पादन विधि (Production Method) के अनुसार सकल घरेलू उत्पाद का माप इस प्रकार किया जाता है-
बाजार कीमत पर सकल घरेलू उत्पाद (GDPMP) = प्राथमिक क्षेत्र का उत्पादन + गौण क्षेत्र का उत्पादन + तीसरे अथवा सेवा क्षेत्र का उत्पादन + मूल्य घिसावट + शुद्ध अप्रत्यक्ष कर उत्पादन के साधन कार्य करने के पश्चात् जो आय प्राप्त करते हैं उनको निजी उपभोग अथवा निवेश पर खर्च किया जाता है। देश की घरेलू सीमा के भीतर निजी अन्तिम उपभोग खर्च, सरकारी अन्तिम उपभोग खर्च, कुल स्थिर पूंजी निर्माण, स्टॉक में परिवर्तन तथा शुद्ध निर्यात को शामिल किया जाता है जिससे हमारे पास सकल घरेलू उत्पाद प्राप्त होता है। खर्च विधि (Expenditure Method) द्वारा सकल घरेलू उत्पाद का माप इस प्रकार किया जाता है
बाज़ार कीमत पर सकल घरेलू उत्पाद (GDPMP) = निजी अन्तिम उपभोग खर्च + सरकारी अन्तिम उपभोग खर्च + कुल स्थिर पूंजी निर्माण + स्टॉक में परिवर्तन + शुद्ध निर्यात । इस प्रकार यदि हम राष्ट्रीय आय को मापने के लिए भिन्न-भिन्न विधियों को देखते हैं तो स्पष्ट होता है कि परिभाषा के आधार पर इनमें समानता पाई जाती है।
अर्थात् राष्ट्रीय आय = राष्ट्रीय उत्पाद = राष्ट्रीय खर्च
इसमें चिह्न = समानता को प्रकट करता है।
इससे स्पष्ट होता है कि यह तीनों धारणाएं एक-दूसरे के समान होती हैं। इनमें समानता को एक रेखाचित्र द्वारा स्पष्ट किया जा सकता है –
प्रश्न 4.
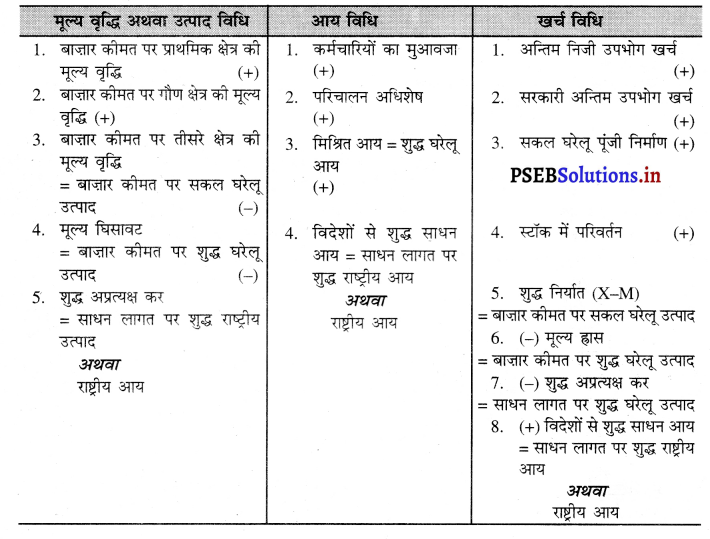
राष्ट्रीय आय की तीन विधियों का संक्षेप में वर्णन करें। (Describe briefly the three methods for the measurement of National Income.)
उत्तर-
राष्ट्रीय आय के माप की तीन विधियां हैं
1. मूल्य वृद्धि विधि अथवा उत्पाद विधि (Value Added Method or Production Method)
2. आय विधि (Income Method)
3. खर्च विधि (Expenditure Method)
1. मूल्य वृद्धि विधि अथवा उत्पाद विधि- इसमें प्राथमिक क्षेत्र, गौण क्षेत्र तथा तीसरे क्षेत्र में निम्नलिखित मदों का योग किया जाता है
- उपभोगी वस्तुएं
- निवेश वस्तुएं
- सरकार द्वारा उत्पादित वस्तुएं
शुद्ध निर्यात। इस क्षेत्र में अन्तिम उत्पादित वस्तुओं तथा सेवाओं का योग किया जाता है परन्तु दोहरी गणना की समस्या के हल के लिए मूल्य वृद्धि विधि (Value Added Method) का प्रयोग किया जाता है अर्थात् उत्पादित मूल्य में से मध्यवर्ती उपभोग का मूल्य तथा मूल्य घिसावट को घटाकर शुद्ध मूल्य वृद्धि प्राप्त हो जाती है। इस प्रकार शुद्ध मूल्य वृद्धि के अनुसार राष्ट्रीय आय की गणना इस प्रकार की जाती है राष्ट्रीय आय = प्राथमिक क्षेत्र में शुद्ध मूल्य वृद्धि + गौण क्षेत्र में शुद्ध मूल्य वृद्धि + तीसरे क्षेत्र में शुद्ध मूल्य वृद्धि + विदेशों से शुद्ध साधन आय।
1. आय विधि (Income Method)-आय विधि में प्राथमिक क्षेत्र, गौण क्षेत्र तथा सेवा क्षेत्र में साधन आय का योग होता है जिसके मुख्य अंग इस प्रकार हैं-
- कर्मचारियों का मेहनताना
- ग़ैर-मज़दूरी आय
- परिचालन अधिशेष
- विदेशों से शुद्ध साधन आय।
2. खर्च विधि (Expenditure Method) खर्च विधि में पारिवारिक क्षेत्र, सरकारी क्षेत्र तथा शेष विश्व क्षेत्र के अन्तिम खर्च का योग किया जाता है। अन्तिम खर्च का वर्गीकरण इस प्रकार होता है(i) अन्तिम उपभोग खर्च
(a) निजी अन्तिम उपभोग खर्च
(b) सरकारी अन्तिम उपभोग खर्च ।
(ii) अन्तिम निवेश खर्च
(a) सकल स्थाई पूंजी निर्माण
(b) स्टॉक में परिवर्तन
(c) शुद्ध निर्यात।
इस प्रकार खर्च विधि में राष्ट्रीय आय का माप निम्नलिखित विधि के अनुसार किया जाता है –
राष्ट्रीय आय = निजी अन्तिम उपभोग खर्च (C) + सरकारी अन्तिम उपभोग खर्च (G) + अन्तिम निवेश खर्च (I) + शुद्ध निर्यात (X – M)
इस प्रकार राष्ट्रीय आय के माप की तीन विधियों द्वारा इसका माप किया जा सकता है।
प्रश्न 5.
राष्ट्रीय आय के माप में कौन-सी मदों को शामिल किया जाना चाहिए और कौन-सी मदों को शामिल नहीं करना चाहिए ?
(Which Items should be included in National Income and which items should not be included ?)
उत्तर-
राष्ट्रीय आय का माप करते समय बहुत-सी समस्याएं उत्पन्न होती हैं। इसलिए यह जानकारी जरूरी है कि किन मदों को राष्ट्रीय आय में शामिल किया जाना चाहिए अथवा किन मदों को शामिल नहीं करना चाहिए।
निम्नलिखित मदों को राष्ट्रीय आय में शामिल किया जाता है (The following items are included in National Income) –
- स्वयं उपभोग की वस्तुओं को राष्ट्रीय आय में शामिल किया जाता है क्योंकि उन्हें बाज़ार में बेचा नहीं जाता।
- सेवानिवृत्ति पेन्शन को राष्ट्रीय आय में शामिल किया जाता है क्योंकि यह पहले की गई सेवा का फल है।
- स्वयं के व्यवसाय में लगे व्यक्तियों की आय को राष्ट्रीय आय में शामिल किया जाता है क्योंकि यह मिश्रित आय होती है।
- मालिकों द्वारा भविष्य निधि कोष में अंशदान को राष्ट्रीय आय में शामिल किया जाता है।
- सरकार द्वारा निःशुल्क प्रदान की गई सेवाओं पर व्यय को राष्ट्रीय आय में शामिल किया जाता है क्योंकि यह सरकार द्वारा किये गए खर्च का अंश होता है।
- सरकार द्वारा सुरक्षा पर किया गया खर्च राष्ट्रीय आय में शामिल किया जाता है। क्योंकि यह अन्तिम प्रदान की सेवाओं का अंश होता है।
- दलाली का कमीशन जोकि पुरानी वस्तुओं की बिक्री पर प्राप्त होता है उसको राष्ट्रीय आय में शामिल किया जाता है क्योंकि यह वर्तमान आय होती है।
- कलाकार जैसे कि गायक, अभिनेता आदि की आय को राष्ट्रीय आय में शामिल किया जाता है क्योंकि यह आर्थिक सेवाएं होती हैं।
- लाभांश को राष्ट्रीय आय में शामिल करते हैं क्योंकि यह निवेश से प्राप्त आय होती है।
- विदेशों से लाभ-विदेशों से इस देश के बैंकों द्वारा प्राप्त किया लाभ राष्ट्रीय आय का भाग होता है क्योंकि यह विदेशों से प्राप्त साधन आय है।
- विदेशों से किराया जो एक देश के नागरिक प्राप्त करते हैं। यह राष्ट्रीय आय का भाग होता है।
- विदेशी दूतावासों से भारतीय कर्मचारियों को प्राप्त मज़दूरी राष्ट्रीय आय में शामिल की जाती है।
- स्टॉक में परिवर्तन को राष्ट्रीय आय में शामिल किया जाता है।
- मालिकों का खुद मालकी के मकानों पर किराया राष्ट्रीय आय का अंश होता है।
- भारतीय विशेषज्ञों द्वारा विदेशों से कमाई आमदन को राष्ट्रीय आय में शामिल किया जाता है।
निम्नलिखित मदों को राष्ट्रीय आय में शामिल नहीं किया जाता (The Following Items are not included in National Income)
- पुरानी वस्तुओं की बिक्री से प्राप्त आय को राष्ट्रीय आय में शामिल नहीं किया जाता क्योंकि इनका मूल्य पहले ही राष्ट्रीय आय में शामिल होता है।
- गैर-कानूनी क्रियाएं जैसे कि जुआ, समगलिंग आदि को राष्ट्रीय आय में शामिल नहीं किया जाता।
- काला धन वह धन होता है जिस पर कर (Tax) नहीं दिया जाता। इसको भी राष्ट्रीय आय में शामिल नहीं किया जाता।
- वित्तीय सौदे जैसा कि शेयर, बान्ड्स, डिबैनचर आदि की क्रय-विक्रय को भी राष्ट्रीय आय में शामिल नहीं किया जाता।
- अनार्थिक क्रियाएं-जैसा कि बच्चे को दिया गया जेब खर्च घरेलू कार्य आदि को राष्ट्रीय आय में शामिल नहीं किया जाता।
- गृहणियों द्वारा किये गए घरेलू कार्य को भी राष्ट्रीय आय में शामिल नहीं किया जाता।
- अप्रत्यक्ष कर से प्राप्त आय को भी राष्ट्रीय आय में शामिल नहीं किया जाता।
- छात्रवृत्ति द्वारा प्राप्त आय को राष्ट्रीय आय में शामिल नहीं किया जाता क्योंकि इसके बदले में कोई सेवा प्रदान नहीं की जाती।
- पूंजीगत लाभ तथा अचानक लाभ को भी राष्ट्रीय आय में शामिल नहीं किया जाता। जैसा कि शेयर की कीमत में वृद्धि से आय अथवा लाटरी से प्राप्त आय।
- वृद्धावस्था पेन्शन जोकि हस्तान्तरण भुगतान होता है इसको भी राष्ट्रीय आय में शामिल नहीं करते।
- विदेशों से प्राप्त उपहार तथा सहायता भी हस्तान्तरण भुगतान है इसलिए इनको राष्ट्रीय आय में शामिल नहीं किया जाता।
- बेरोज़गारी भत्ता भी हस्तान्तरण भुगतान है इसलिए इसको राष्ट्रीय आय में शामिल नहीं किया जाता।
- मध्यवर्ती उपभोग जोकि अन्तिम वस्तुओं के उत्पाद के लिए प्रयोग किया जाता है इसको भी राष्ट्रीय आय में शामिल नहीं किया जाता।
- अन्वेषण के काम पर प्रयोग होने वाली वस्तुओं को भी राष्ट्रीय आय में शामिल नहीं किया जाता क्योंकि यह मध्यवर्ती वस्तुएं होती हैं।
- प्राकृतिक आपदाएं जैसा कि बाढ़, भूकम्प, सुनामी आदि समय किया गया खर्च राष्ट्रीय आय में शामिल नहीं किया जाता।
1. अन्तिम उपभोग खर्च
- निजी अन्तिम उपभोग खर्च
- सरकारी अन्तिम उपभोग खर्च
2. सकल घरेलू पूंजी निर्माण =
- सकल घरेलू स्थाई पूंजी निर्माण
- स्टॉक में परिवर्तन (अन्तिम स्टॉक – प्रारम्भिक स्टॉक)
3. शुद्ध निर्यात = (निर्यात – आयात)
4. मूल्य घिसावट अथवा मूल्य ह्रास
5. शुद्ध अप्रत्यक्ष कर = (अप्रत्यक्ष कर – सहायता)
6. विदेशों से शुद्ध साधन आय

V. संख्यात्मक प्रश्न (Numericals)
प्रश्न 1.
निम्नलिखित आंकड़ों द्वारा GNP, GDP, NNP, NDP, बाज़ार कीमत (Market Price) तथा साधन लागत (Factor Cost) पर ज्ञात करें।

उत्तर-
(i) बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद (GNPMP) = निजी उपभोग खर्च + सकल निवेश + सरकार द्वारा वस्तुओं तथा सेवाओं की खरीद + शुद्ध निर्यात + विदेशों से शुद्ध साधन आय ।
= 700 + 180 + 200 + 20 + (-10) = ₹ 1090 करोड़ उत्तर
(ii) बाज़ार कीमत पर शुद्ध राष्ट्रीय उत्पाद (NNPMP) = बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद – घिसावट = 1090 – 30 = ₹ 1060 करोड़ उत्तर
(iii) बाज़ार कीमत पर सकल घरेलू उत्पाद (GDPMP) = बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद – विदेशों से शुद्ध साधन आय = 1090 – (-10) = ₹ 1100 करोड़ उत्तर
(iv) बाज़ार कीमत पर शुद्ध घरेलू उत्पाद (NDPMP) = बाज़ार कीमत पर सकल घरेलू उत्पाद – घिसावट = 1100 – 30 = ₹ 1070 करोड़ उत्तर
(v) साधन लागत पर सकल राष्ट्रीय उत्पाद (GNPFC) = बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद – शुद्ध अप्रत्यक्ष कर = 1090 – 10 = ₹ 1080 करोड़ उत्तर
(vi) साधन लागत पर शुद्ध राष्ट्रीय उत्पाद (NNPFC) = साधन लागत पर सकल राष्ट्रीय उत्पाद – घिसावट = 1080 – 30 = ₹ 1050 करोड़ उत्तर
(vii) साधन लागत पर सकल घरेलू उत्पाद (GDPFC) = साधन लागत पर सकल राष्ट्रीय उत्पाद – शुद्ध अप्रत्यक्ष कर = 1100 – 10 = ₹ 1090 करोड़ उत्तर
(viii) साधन लागत पर शुद्ध घरेलू उत्पाद (NDPFC) = साधन लागत पर सकल घरेलू उत्पाद – घिसावट = 1090 – 30 = ₹ 1060 करोड़ उत्तर
प्रश्न 2.
निम्नलिखित आंकड़ों की सहायता से व्यय विधि द्वारा
(i) बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद (GNPMP)
(ii) बाज़ार कीमत पर सकल घरेलू उत्पाद (GDPMP) ज्ञात करें।

उत्तर-
(i) बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद (GNPMP) = निजी उपभोग खर्च + निजी निवेश खर्च + सरकार द्वारा वस्तुओं तथा सेवाओं की खरीद + शुद्ध निर्यात + विदेशों से शुद्ध साधन आय।
= 700 + (20 + 60 + 40 + 60) + 200 + (40 – 20) + (-10)
= ₹ 1090 करोड़ उत्तर
(ii) बाज़ार कीमत पर सकल घरेलू उत्पाद (GDPMP) = बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद – विदेशों से शुद्ध साधन आय
= 1090 – (-10) = ₹ 1100 करोड़ उत्तर
प्रश्न 3.
निम्नलिखित द्वारा सकल घरेलू उत्पाद ज्ञात करें

उत्तर:
सकल घरेलू उत्पाद = निजी उपभोग खर्च + सरकारी उपभोग खर्च + सकल घरेलू स्थिर निवेश + माल सूची में वृद्धि + वस्तुओं तथा सेवाओं का निर्यात – वस्तुओं तथा सेवाओं का आयात
= 45000 + 5000 + 5000 + 1000 + 6000 – 7000
= ₹ 55000 उत्तर
प्रश्न 4.
निम्नलिखित आंकड़ों से ज्ञात करें
(i) बाजार कीमत पर सकल राष्ट्रीय उत्पाद (GNPMP)
(ii) साधन लागत पर शुद्ध राष्ट्रीय उत्पाद (NNPFC)


उत्तर-
(i) बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद (GNPMP) = सरकारी अन्तिम उपभोग खर्च + सकल घरेलू पंजी निर्माण + शुद्ध निर्यात + निजी अन्तिम उपभोग खर्च + विदेशों से शुद्ध साधन आय
24 + 24 + (-4) + 161 + (-1) = ₹ 204 करोड़।
(ii) साधन लागत पर शुद्ध राष्ट्रीय उत्पाद (NNPFC) = बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद – शुद्ध अप्रत्यक्ष कर – स्थिर पूंजी का उपभोग
= 204 – 23 – 22 = ₹ 159 करोड़

प्रश्न 5.
निम्नलिखित आंकड़ों की सहायता से
(a) उत्पाद विधि
(a) आय विधि द्वारा बाजार कीमत पर सकल घरेलू उत्पाद ज्ञात करें

उत्तर-
(a) उत्पाद विधि (Production Method)
बाजार कीमत पर सकल घरेलू उत्पाद (GDPMP) = (प्राथमिक + गौण + तीसरे क्षेत्र में उत्पाद का मूल्य) – (प्राथमिक + गौण + तीसरे क्षेत्र में मध्यवर्ती उपभोग)
= (300 + 200 + 100) – (100 + 50 + 50) = ₹400 करोड़ उत्तर
(b) आय विधि (Income Method)
बाजार कीमत पर सकल घरेलू उत्पाद = कर्मचारियों की मज़दूरी + मिश्रित आय + परिचालन अधिशेष + स्थिर पूंजी का उपभोग + शुद्ध अप्रत्यक्ष कर ।
= 150 + 50 + 100 + 40 + 60 = ₹400 करोड़ उत्तर
प्रश्न 6.
निम्नलिखित आंकड़ों की सहायता से ज्ञात करें
(a) मूल्य वृद्धि विधि द्वारा साधन लागत पर शुद्ध राष्ट्रीय उत्पाद
(b) खर्च विधि द्वारा साधन लागत पर शुद्ध घरेलू उत्पाद

उत्तर-
(a) मूल्य वृद्धि विधि (Value Added Method)
साधन लागत पर शुद्ध राष्ट्रीय उत्पाद (NNPFC) = प्राथमिक क्षेत्र में मूल्य वृद्धि + गौण क्षेत्र में मूल्य वृद्धि + तीसरा क्षेत्र में मूल्य वृद्धि – अप्रत्यक्ष कर + आर्थिक सहायता + विदेशों से शुद्ध साधन आय – स्थिर पूंजी का उपभोग
= (1000 – 500) + (900 – 400) + (500 – 200) -110 + 20 – 30 – 90
= 500 + 500 + 300 – 110 + 20 – 30 – 90 = ₹ 1090 करोड़।
(b) खर्च विधि (Expenditure Method) साधन लागत पर शुद्ध घरेलू उत्पाद (GDPFC)= निजी अन्तिम उपभोग खर्च + सकल घरेलू पूंजी निर्माण + शुद्ध निर्यात – स्थिर पूंजी का उपभोग – अप्रत्यक्ष कर + आर्थिक सहायता
= 1000 + 200 + 350 + (- 60) – 90 – 110 + 20 = ₹ 1310 करोड़।
प्रश्न 7.
निम्नलिखित आंकड़ों से ज्ञात करें
(a) आय विधि द्वारा बाज़ार कीमत पर सकल घरेलू उत्पाद (GDPMP)
(b) खर्च विधि द्वारा साधन लागत पर शुद्ध राष्ट्रीय उत्पाद (NNPFC)

उत्तर-
(a) आय विधि बाज़ार कीमत पर सकल घरेलू उत्पाद (GDPMP) = ब्याज, लगान तथा लाभ + रायल्टी + स्वयं नियोजितों की मिश्रित आय + कर्मचारियों का मुआवज़ा + अप्रत्यक्ष कर — सहायता + स्थिर पूंजी का उपभोग
= 900 + 20 + 60 + 370 + 120 – 20 + 60 = ₹ 1510 करोड़ उत्तर
(b) खर्च विधि साधन लागत पर शुद्ध राष्ट्रीय उत्पाद (NNPFC) = सरकारी अन्तिम उपभोग खर्च + निजी अन्तिम उपभोग खर्च + सकल पूंजी निर्माण + शुद्ध निर्यात – अप्रत्यक्ष कर + सहायता – स्थिर पूंजी का उपभोग + विदेशों से शुद्ध साधन आय
= 100 + 800 + 620 + (-10) – 120 + 20 – 60 + (-10) = ₹ 1340 करोड़ उत्तर
प्रश्न 8.
निम्नलिखित आंकड़ों की सहायता से
(a) आय विधि
(b) व्यय विधि द्वारा सकल राष्ट्रीय आय ज्ञात करें

उत्तर-
(a) आय विधि (Income Method)
सकल राष्ट्रीय आय = विदेशों से साधन आय + कर्मचारियों का मेहनताना – विदेशों को साधन आय + स्थिर पूंजी का उपभोग + ब्याज + लगान + लाभ
= 10 + 150 – 15 + 15 + 40 + 40 + 100 = ₹ 340 करोड़ उत्तर
(b) व्यय विधि (Expenditure Method)
सकल राष्ट्रीय आय = विदेशों से प्राप्त साधन आय + शुद्ध घरेलू पूंजी निर्माण + अन्तिम निजी उपभोग खर्च – विदेशों को साधन आय + स्थिर पूंजी का उपभोग + निर्यात – आयात – अप्रत्यक्ष कर + सहायता + सरकारी अन्तिम उपभोग
‘खर्च = 10 + 50 + 220 – 15 + 15 + 20 – 25 – 30 + 10 + 85 = ₹ 340 करोड़ उत्तर

प्रश्न 9.
निम्नलिखित आंकड़ों द्वारा बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद
(a) आय विधि
(b) खर्च विधि से ज्ञात करें।
उत्तर-
आय विधि (Income Method) –
बाजार कीमत पर सकल राष्ट्रीय उत्पाद (GNPMP) = स्वयं नियोजितों की मिश्रित आय + कर्मचारियों का मेहनताना + विदेशों से शुद्ध साधन आय + शुद्ध अप्रत्यक्ष कर + स्थिर पूंजी का उपभोग + लाभ + लगान + ब्याज
SET-I = 400 + 500 + (-20) + 100 + 120 + 350 + 100 + 150 = ₹ 1700 करोड़
SET-II = 300 + 400 + (-10) + 60 + 100 + 250 + 80 + 70 = ₹ 1250 करोड़
SET-III = 500 + 600 + (-15) + 150 + 115 + 450 + 200 + 250 = ₹ 2250 करोड़
खर्च विधि (Expenditure Method)-
बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद (GNPMP) = निजी उपभोग खर्च + विदेशों से शुद्ध साधन आय + स्थिर पूंजी का उपभोग + शुद्ध घरेलू पूंजी निर्माण + शुद्ध निर्यात + सरकारी अन्तिम उपभोग खर्च
SET-I = 900 – 20 + 120 + 280 – 30 + 450 = ₹ 1700 करोड़
SET-II = 700 + 10 + 100 + 120 – 10 + 350 = ₹ 1270 करोड़
SET-III = 1100 – 15 + 115 + 375 – 25 + 700 = ₹ 2250 करोड़
प्रश्न 10.
निम्नलिखित आंकड़ों की सहायता से
(i) आय विधि
(ii) व्यय विधि द्वारा साधन लागत पर शुद्ध राष्ट्रीय उत्पाद अथवा राष्ट्रीय आय ज्ञात करें

उत्तर-
(a) आय विधि (Income Method)-
साधन लागत पर शुद्ध राष्ट्रीय उत्पाद अथवा राष्ट्रीय आय= कर्मचारियों का मेहनताना + विदेशों से शुद्ध साधन आय + लाभ + लगान + ब्याज + स्वयं नियोजितों की मिश्रित आय
SET-I = 1200 + (-20) + 800 + 400 + 620 + 700 = ₹ 3700 करोड़
SET-II = 600 + (-10) + 400 + 200 + 310 + 350 = ₹ 1850 करोड़
SET-III = 500 + (-10) + 220 + 90 + 100 + 400 = ₹ 1300 करोड
(b) व्यय विधि (Expenditure Method)-
साधन लागत पर शुद्ध राष्ट्रीय उत्पाद अथवा राष्ट्रीय आय= निजी अन्तिम उपभोग खर्च + सरकारी अन्तिम उपभोग खर्च + शुद्ध घरेलू पूंजी निर्माण + शुद्ध निर्यात – शुद्ध अप्रत्यक्ष कर + विदेशों से शुद्ध साधन आय
SET-I = 2000 + 1100 + 770 + (-30) – 120 + (-20) = ₹ 3700 करोड़
SET-II = 1000 + 550 + 385 + (-15) – 60 + (-10) = ₹ 1850 करोड़
SET-III = 900 + 400 + 200 + (-25) -165 + (-10) = ₹ 1300 करोड़
प्रश्न 11.
निम्नलिखित आंकड़ों के आधार पर सकल राष्ट्रीय आय की गणना
(a) आय विधि
(b) व्यय विधि द्वारा करें

उत्तर-
आय विधि (Income Method)-
सकल राष्ट्रीय उत्पाद अथवा आय = विदेशों से साधन आय + कर्मचारियों का मुआवज़ा + विदेशों को साधन आय + स्थिर पूंजी का उपभोग + ब्याज + लगान + लाभ
= 10 + 150 – 15 + 15 + 40 + 40 + 100 = ₹ 340 करोड़ उत्तर
खर्च विधि (Expenditure Method)
सकल राष्ट्रीय उत्पाद अथवा आय = विदेशों से साधन आय + शुद्ध घरेलू पूंजी निर्माण + निजी अन्तिम उपभोग खर्च – विदेशों को साधन आय + स्थिर पूंजी का उपभोग + निर्यात – आयात – अप्रत्यक्ष कर + आर्थिक सहायता + सरकारी अन्तिम उपभोग खर्च
= 10 + 50 + 220 – 15 + 15 + 20 – 25 – 30 + 10 + 85 = ₹ 340 करोड़ उत्तर
प्रश्न 12.
निम्नलिखित आंकड़े x फ़र्म के सम्बन्ध में दिये गए हैं। इस फ़र्म द्वारा साधन लागत पर सकल मूल्य वृद्धि ज्ञात करें।

उत्तर –
साधन लागत पर सकल मूल्य वृद्धि = बिक्री + स्टॉक में परिवर्तन (अन्तिम स्टॉक – प्रारम्भिक स्टॉक) + सहायता – मध्यवर्ती वस्तुओं की खरीद
= 500 + (20 – 30) + 40 – 300 = ₹ 230 हजार उत्तर

प्रश्न 13.
निम्नलिखित आंकड़ों की सहायता से बाजार कीमत पर शुद्ध मूल्य वृद्धि ज्ञात करें

उत्तर –
बाज़ार कीमत पर शुद्ध मूल्य वृद्धि = बिक्री + स्टॉक में परिवर्तन – मध्यवर्ती वस्तुओं की खरीद – घिसावट
SET-I = 700 + 40 – 400 – 80 = ₹ 260 हज़ार
SET-II = 300 + (-10) – 150 -20 = ₹ 120 हज़ार उत्तर
प्रश्न 14.
साधन लागत पर शुद्ध मूल्य वृद्धि ज्ञात करें

उत्तर
साधन लागत पर शुद्ध मूल्य वृद्धि = बिक्री + स्टॉक में वृद्धि (अन्तिम स्टॉक – प्रारम्भिक स्टॉक) – मध्यवर्ती उपभोग – बिक्री कर + सहायता – स्थिर पूंजी का उपभोग
= 500 + (40-20)- 320 – 15 +5 -50 = ₹ 140 लाख उत्तर
प्रश्न 15.
निम्नलिखित आंकड़ों से बाजार कीमत पर सकल घरेलू उत्पाद ज्ञात करें

उत्तर
बाज़ार कीमत पर सकल घरेलू उत्पाद = प्राथमिक क्षेत्र में उत्पाद का मूल्य – प्राथमिक क्षेत्र में मध्यवर्ती उपभोग + गौण क्षेत्र में उत्पाद का मूल्य – गौण क्षेत्र में मध्यवर्ती उपभोग + तीसरे क्षेत्र में उत्पाद का मूल्य – तीसरे क्षेत्र में मध्यवर्ती उपभोग
= 2000 – 1000 + 1800 – 800 + 1400 – 600 = ₹ 2800 करोड़ उत्तर
प्रश्न 16.
निम्नलिखित आंकड़ों से साधन लागत पर सकल मूल्य वृद्धि ज्ञात करें

उत्तर-
साधन लागत पर सकल मूल्य वृद्धि = बिक्री + स्टॉक में परिवर्तन – कच्चे माल की खरीद + आर्थिक सहायता
= 180 + 15 – 100 + 10 = ₹ 105 लाख उत्तर
प्रश्न 17.
निम्नलिखित आंकड़ों से आय विधि द्वारा राष्ट्रीय आय ज्ञात करें

उत्तर
राष्ट्रीय आय = कर्मचारियों का मेहनताना + परिचालन अधिशेष + विदेशों से शुद्ध साधन आय
= 1900 + 720 + (-20) = ₹ 2600 करोड़ उत्तर
प्रश्न 18.
निम्नलिखित आंकड़ों की सहायता से ज्ञात कीजिए :
(क) बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद
(ख) बाज़ार कीमत पर शुद्ध राष्ट्रीय उत्पाद


उत्तर-
(क) बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद = निजी उपभोग व्यय + सरकारी उपभोग व्यय + कुल पूंजी निर्माण + निर्यात – आयात + विदेशों से प्राप्त शुद्ध साधन आय
= 75,000 + 15,550 + 4,500 + 6,000 – 9,000 – 650
= ₹ 91,400 करोड़ उत्तर
(ख) बाज़ार कीमत पर शुद्ध राष्ट्रीय आय
= बाज़ार कीमत पर सकल राष्ट्रीय आय – घिसावट
= 91,400 – 600 = ₹ 90,800 करोड़ उत्तर
प्रश्न 19.
निम्नलिखित आंकड़ों की सहायता से ज्ञात कीजिए
(क) बाजार कीमत पर सकल राष्ट्रीय उत्पाद
(ख) बाज़ार कीमत पर शुद्ध राष्ट्रीय उत्पाद

उत्तर-
(क) बाज़ार. कीमत पर सकल राष्ट्रीय उत्पाद = निजी उपभोग व्यय + सरकारी उपभोग व्यय + कुल पूंजी निर्माण + निर्यात – आयात + विदेशों से प्राप्त शुद्ध राष्ट्रीय आय
= 85000 + 10550 + 2500 + 4000 – 8000 – 750 = ₹ 93,300 करोड़ उत्तर
(ख) बाजार कीमत पर शुद्ध राष्ट्रीय उत्पाद = बाजार कीमत पर सकल राष्ट्रीय उत्पाद – घिसावट = 93300 – 500 = ₹ 92,800 करोड़ उत्तर

प्रश्न 20.
निम्नलिखित आंकड़ों की सहायता से ज्ञात कीजिए :
(क) बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद
(ख) बाज़ार कीमत पर शुद्ध राष्ट्रीय उत्पाद

उत्तर
(क) बाज़ार कीमत पर सकल राष्ट्रीय आय = निजी उपभोग व्यय + सरकारी उपभोग व्यय + कुल पूंजी निर्माण + निर्यात – आयात + विदेशों से प्राप्त शुद्ध साधन
= 65000 + 20550 + 6500 + 2000 – 7000 – 550 = 86500 ₹ करोड़ उत्तर
(ख) बाजार कीमत पर शुद्ध राष्ट्रीय आय = बाज़ार कीमत पर सकल राष्ट्रीय आय – घिसावट
= 86500 – 400 = ₹ 86100 करोड़ उत्तर
प्रश्न 21.
निम्नलिखित आंकड़ों से ज्ञात करें
(क) राष्ट्रीय आय
(ख) बाजार कीमतों पर कुल घरेलू उत्पाद।

उत्तर-
(क) राष्ट्रीय आय = परिचालन अधिशेष + कर्मचारियों का पारिश्रमिक + मिश्रित आय + विदेशों से प्राप्त शुद्ध साधन आय
= 10,000 + 15350 + 7366 + (-) 110 = ₹ 32606 करोड़ उत्तर
(ख) बाजार कीमत पर कुल घरेलू उत्पाद
= परिचालन अधिशेष + कर्मचारियों का पारिश्रमिक + मिश्रित + मिश्रित आय + अप्रत्यक्ष कर – आर्थिक अनुदान + स्थायी पूंजी का उपभोग
= 10,000 + 15350 + 7366 + 5598-2655 + 4135
= ₹39794 करोड़ उत्तर
प्रश्न 22.
निम्नलिखित आंकड़ों की सहायता से ज्ञात कीजिए :
(क) राष्ट्रीय आय
(ख) बाज़ार कीमतों पर सकल घरेलू उत्पाद मदें

उत्तर-
राष्ट्रीय आय व्यय = 1 + 2 + 4 + 5 + 7 + 8-3-6 = 18557 + 20510 + 9860 + 13720 + 2560 – 2000 -110 – 15000 = ₹ 48097 करोड़ उत्तर
(ख) बाज़ार कीमतों पर सकल घरेलू उत्पाद = 1 + 2 + 4 + 8 + 5 -6 = 18557 + 20510 + 4860 + 2560 + 13720 – 15000
= ₹ 50207 करोड़ उत्तर
प्रश्न 23.
निम्नलिखित आंकड़ों से ज्ञात करें
(क) बाजार कीमत पर सकल राष्ट्रीय आय
(ख) बाजार कीमत पर शुद्ध राष्ट्रीय आय .

उत्तर-
(क) बाज़ार कीमत पर सकल राष्ट्रीय आय = (i) + (ii) + (iii) + (iv) – (v) + (vi)
= 1,00,000 + 12,500 + 2,500 + 6,000 – 9,000 + 750 = ₹ 1,12,750 उत्तर
(ख) बाज़ार कीमत पर शुद्ध राष्ट्रीय आय = बाजार कीमत पर सकल राष्ट्रीय उत्पादन
= 1,12,750 – 400 = ₹ 1,12,350 उत्तर

प्रश्न 24.
निम्नलिखित आंकड़ों से ज्ञात करें
(क)बाजार कीमत पर सकल राष्ट्रीय उत्पाद।
(ख) बाज़ार कीमत पर शुद्ध राष्ट्रीय उत्पाद।

उत्तर-
(क) बाजार कीमत पर सकल राष्ट्रीय उत्पाद = (i) + (ii) + (iii) + (iv) -(v) + (vi)
1,50,000 + 18,750 + 3,750 + 9,000 – 12,000 + 1,125 = ₹ 1,70,625
(ख) बाजार कीमत पर शुद्ध राष्ट्रीय उत्पाद = बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद – (vii)
= 1,70,625 – 600 = ₹ 1,70,025 उत्तर
प्रश्न 25.
निम्नलिखित आंकड़ों से ज्ञात करें
(क) बाजार कीमत पर सकल राष्ट्रीय उत्पाद।
(ख) बाजार कीमत पर शुद्ध राष्ट्रीय उत्पाद।

उत्तर-
(क) बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद = (i) + (ii) + (iii) + (iv) – (v) + (vi)
= 2,00,000 + 25,000 + 5,000 + 12,000 – 18,000 + 1,500
= ₹ 2,25,500 उत्तर
(ख) बाज़ार कीमत पर शुद्ध रीष्ट्रीय उत्पाद = बाज़ार कीमत पर सकल राष्ट्रीय उत्पाद – मूल्य ह्रास
= 2,25,500 – 800 = ₹ 2,24,700 उत्तर
प्रश्न 26.
निम्नलिखित की गणना करें।
(क) घरेलू साधन आय
(ख) राष्ट्रीय आय

उत्तर-
(क) घरेलू साधन आय = कर्मचारियों का मेहनताना + ब्याज + लाभ तथा लाभांश + किराया + मिश्रित आय
= 5000 + 500 + 600 + 800 + 3000 = ₹ 9900 करोड़ उत्तर
(ख) राष्ट्रीय आय = घरेलू साधन आय + विदेशों से शुद्ध साधन आय
= 9900 + 1000 = ₹ 10,900 करोड़ उत्तर
प्रश्न 27.
निम्नलिखित की गणना करें।
(क) घरेलू साधन आय
(ख) राष्ट्रीय आय

उत्तर-
SET-B
(क) घरेलू साधन आय = i + ii + iii + iv + v
= 10,000 + 1000 + 1200 + 1600 + 6000
= ₹ 19,800 करोड़ उत्तर
(ख) राष्ट्रीय आय = घरेलू साधन आय + vi
= 19,800 + 2000
= ₹ 21,800 करोड़ उत्तर
SET-C
(क) घरेलू साधन आय =i+ii + iii + iv + v
= 15000 + 1500 + 1800 + 2400 + 9000
= ₹ 29,700 करोड़ उत्तर
(ख) राष्ट्रीय आय = घरेलू साधन आय + vi
= 29,700 + 3000 = ₹ 32,700 करोड़ उत्तर
प्रश्न 28.
निम्नलिखित की गणना करें ।
(क) बाज़ार कीमत पर कुल राष्ट्रीय उत्पाद
(ख) राष्ट्रीय आय

उत्तर-
SET-B
(i) बाज़ार कीमत पर कुल राष्ट्रीय उत्पाद = बिक्री + (साल के अन्त में स्टॉक-साल के शुरू में स्टॉक) – मध्यवर्ती
उपभोग = 140000 + 40000 (50,000 – 10,000) – 20,000
= ₹ 1,60,000 करोड़ उत्तर
(ii) राष्ट्रीय आय = बाज़ार कीमत पर कुल राष्ट्रीय उत्पाद (-) घिसावट – शुद्ध अप्रत्यक्ष कर (प्रत्यक्ष कर – आर्थिक सहायता)
= 1,60,000 – 2000 – 400 (600 – 200)
= ₹ 1,57,600 करोड़ उत्तर
प्रश्न 29.
निम्नलिखित की गणना करें।
(क) बाज़ार कीमत पर कुल राष्ट्रीय उत्पाद
(ख) राष्ट्रीय आय

उत्तर-
(क) बाजार कीमत पर कुल राष्ट्रीय आय = बिक्री + (साल के अन्त में स्टॉक – साल के शुरू में स्टॉक) – मध्यवर्ती उपभोग
= 70,000 + 20000 (25,000 – 5000) – 10,000
= ₹ 80,000 करोड़ उत्तर
(ख) राष्ट्रीय आय = बाज़ार कीमत पर कुल राष्ट्रीय आय – घिसावट – शुद्ध अप्रत्यक्ष कर (अप्रत्यक्ष कर – आर्थिक सहायता) = 80,000 – 1000 – 200 (300 -100) = ₹ 78,800 करोड़ उत्तर

प्रश्न 30.
नीचे दिये गए आंकड़ों के आधार पर बाजार कीमत पर शुद्ध राष्ट्रीय उत्पाद (NNPMP) तथा साधन लागत पर शुद्ध राष्ट्रीय उत्पाद (NNPFC) ज्ञात करें :

उत्तर-
बाज़ार कीमत पर शुद्ध राष्ट्रीय उत्पाद = निजी अन्तिम उपभोग खर्च + सरकारी अन्तिम उपभोग खर्च + कुल स्थाई पूँजी निर्माण + स्टॉक में शुद्ध वृद्धि + वस्तुओं तथा सेवाओं का निर्यात – वस्तुओं तथा सेवाओं का आयात + विदेशों से शुद्ध साधन आय – स्थाई पूँजी का उपभोग।
= 510 + 70 + 130 + 30 + 48 – 56 + (-3) – 40 = ₹ 689 करोड़ उत्तर
साधन लागतों पर शुद्ध राष्ट्रीय उत्पाद (NNPFC) = बाज़ार कीमत पर कुल राष्ट्रीय उत्पाद – अप्रत्यक्ष कर + आर्थिक सहायता
= 689 – 90 + 18
= ₹ 617 करोड़ उत्तर
प्रश्न 31.
निम्नलिखित आंकड़ों से मुख्य वृद्धि ज्ञात करें।

उत्तर-
मुल्य वृद्धि = उत्पादन का मुल्य – मध्यवर्ती उपभोग
= 10000 – 2555 = ₹ 7445 करोड़ उत्तर
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()





























 उत्तर-
उत्तर-