Class 11

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 13 Hydrocarbons Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 13 Hydrocarbons

PSEB 11th Class Chemistry Guide Hydrocarbons InText Questions and Answers

Question 1.
How do you account for the formation of ethane during the chlorination of methane?
Answer:
Chlorination of methane proceeds via a free radical chain mechanism. The whole reaction takes place in the given three steps :
Step 1: Initiation : The reaction begins with the homolytic cleavage of Cl—Cl bond as:

Step 2: Propagation : In the second step, chlorine free radicals attack methane molecules and break down the C—H bond to generate methyl radicals as:

These methyl radicals react with other chlorine free radicals to form methyl chloride along with the liberation of a chlorine free radical.

Hence, methyl free radicals and chlorine free radicals set up a chain reaction. While HC1 and CH3C1 are the major products formed, other higher
halogenated compounds are also formed as:

Step 3: Termination : Formation of ethane is a result of the termination
of chain reactions taking place as a result of the consumption of reactants as:

Hence, by this process, ethane is obtained as a by-product of chlorination of methane.

Question 2.
Write IUPAC names of the following compounds : ,
(a) CH₃CH = C(CH₃)₂
(b) CH₂ = CH — C = C — CH₃

Answer:

Question 3.
For the following compounds, write structural formulas and IUPAC names for all possible isomers having the number of double or triple bond as indicated:
(a) C₄H₈ (one double bond)
(b) C₅H₈ (one triple bond)
Answer:
(a) The following structural isomers are possible for C₄H₈ with one double bond:

(b) The following structural isomers are possible for C5H8 with one triple bond:

Question 4.
Write IUPAC names of the products obtained by the ozonolysis of the following compounds:
(i) Pent-2-ene
(ii) 3,4-Dimethylhept-3-ene
(iii) 2-Ethylbut-l-ene
(iv) 1-Phenylbut-l-ene
Answer:
(i) Pent-2-ene undergoes ozonolysis as:

The IUPAC name of product (I) is ethanal and product (II) is propanal.
(ii) 3, 4-Dimethylhept-3-ene undergoes ozonolysis as:

The IUPAC name of product (I) is butan-2-one and product (II) is pentan-2-one.
(iii) 2-Ethylbut-l-ene undergoes ozonolysis as:

The IUPAC name of product (I) is pentan-3-one and product (II) is methanal.
(iv) 1-Phenylbut-l-ene undergoes ozonolysis as:

The IUPAC name of product (I) is benzaldehyde and product (II) is propanal.

Question 5.
An alkene ‘A’ on ozonolysis gives a mixture of ethanal and pentan-3-one. Write structure and IUPAC name of ‘A’.
Answer:

Question 6.
An alkene ‘A’ contains three C — C, eight C — Hσ bonds and one C — C π bond. ‘A’ on ozonolysis gives two moles of an aldehyde of molar mass 44 u. Write IUPAC name of ‘A’
Answer:
As per the given information, ‘A’ on ozonolysis gives two moles of an aldehyde of molar mass 44 u. The formation of two moles of an
aldehyde indicates the esence of identical structural units on both sides of the double bond containing carbon atoms.
Hence, the structure of ‘A’ can be represented as :
XC = CX
There are eight C—Ha bonds. Hence, there are 8 hydrogen atoms in ‘A’. Also, there are three C—C bonds. Hence, there are four carbon atoms present in the structure of‘A’.

Combining the inferences, the structure of A’ can be represented as:

‘A’ has 3 C — C bonds, 8 C — H bonds, and one C— C it bond. Hence, the IUPAC name of ‘A’ is But-‘ 2-ene.
Ozonolysis of ‘A’ takes place as:

The final product is ethanal with molecular mass
= [(2 x 12) + (4 x 1) + (1 x 16)]= 44 u

Question 7.
Propanal and pentan-3-one are the ozonolysis products of an alkene? What is the structural formula of the alkene?
Answer:

Question 8.
Write chemical equations for combustion reaction of the following hydrocarbons:
(i) Butane
(ii) Pentene
(iii) Hexyne
(iv) Toluene
Answer:
Combustion can be defined as a reaction of a compound with oxygen.

Question 9.
Draw the cis and trans structures of hex-2-ene. Which isomer will have higher b.p. and why?
Answer:
Hex-2-ene is represented as:

The cis-isomer will have higher boiling point due to more polar nature leading to stronger intermolecular dipole-dipole interactions thus requiring more heat energy to separate them, whereas trans form being non-polar have weak induced dipole interactions and so have lower boiling point.

Question 10.
Why is benzene extra ordinarily stable though it contains three double bonds?
Answer:
Resonance and delocalization of electrons generally leads to the stability of benzene molecule.

The dotted circle in the hybrid structure represents the six electrons which are delocalised between the six carbon atoms of the benzene ring. Therefore, presence of delocalised Jt electrons in benzene makes it more stable than the hypothetical cyclohexatriene.

Question 11.
What are the necessary conditions for any system to be aromatic?
Answer:
A compound is said to be aromatic if it satisfies the following three conditions:
(i) It should have a planar structure.
(ii) The π-electrons of the compound are completely delocalized in the ring.
(iii) The total number of π-electrons present in the ring should be equal to (4n + 2), where n = 0,1, 2….etc. This is known as Huckel’s rule.

Question 12.
Explain why the following systems are not aromatic?

Answer:

For the given compound, the number of π-electrons is six. But only four Tt-electrons are present within the ring. Also there is no conjugation of π-electrons within the ring and the compound is not planar in shape. Hence, the given compound is not aromatic in nature.

For the given compound, the number of π-electrons is four.
By Huckel’s rule,
4n + 2 = 4,
4n = 2, n = 1/2
For a compound to be aromatic, the value of n must be an integer (n = 0,1,2 …), which is not true for the given compound. Hence, it is not aromatic in nature.

For the given compound, the number of it-electrons is eight.
By Huckel’s rule.
4n + 2 = 8
4n = 6, n = 3/2
For a compound to be aromatic, the value of n must be an integer (n = 0,1, 2…). Since, the value of n is not an integer, the given compound is not aromatic in nature.

Question 13.
How will you convert benzene into
(i) p-nitrobromobenzene
(ii) m-nitrochlorobenzene
(iii) acetophenone
(iv) p-nitrotoluene
Answer:
(i) Benzene can be converted into p-nitrobromobenzene as:

(ii) Benzene can be converted into m-nitrochlorobenzene as:

(iii) Benzene can be converted into acetophenone as:

(iv) Benzene can be converted into p-nitrotoluene as:

Question 14.
In the alkane H₃C — CH₂ — C(CH₃)₂ — CH₂ — CH(CH₃)₂ identify 1°, 2°, 3° carbon atoms and give the number of H atoms bonded to each one of these.
Answer:

1° carbon atoms are those which are bonded to only one carbon atom, i.e., they have only one carbon atom as their neighbour. The given structure has five 1° carbon atoms and fifteen hydrogen atoms are attached to it.
2° carbon atoms are those which are bonded to two carbon atoms, i.e., they have two carbon atoms as their neighbours. The given structure has two 2° carbon atoms and four hydrogen atoms are attached to it.
3° carbon atoms are those which are bonded to three carbon atoms, i.e., they have three carbon atoms as their neighbours. The given structure has one 3° carbon atom and only one hydrogen atom is attached to it.

Question 15.
What effect does branching of an alkane chain has on its boiling point?
Answer:
Alkanes experience inter-molecular Van der Waals forces. The stronger the force, the greater will be the boiling point of the alkane.
As branching increases, the surface area of the molecule decreases which results in a small area of contact. As a result, the Van der Waals force also decreases which can be overcome at a relatively lower temperature. Hence, the boiling point of an alkane chain decreases with an increase in branching.

Question 16.
Addition of HBr to propene yields 2-bromopropane, while in the presence of benzoyl peroxide, the same .reaction yields
1- bromopropane. Explain and give mechanism.
Answer:
Addition of HBr to propene is an example of an electrophilic substitution reaction.
Hydrogen bromide provides an electrophile, H⁺. This electrophile attacks the double bond to form 1° and 2° carbocations as shown:

Secondary carbocations are more stable than primary carbocations. Hence, the former predominates since it will form at a faster rate. Thus, in the next step, Br^– attacks the carbocation to form 2 – bromopropane as the major product.

This reaction follows Markovnikov’s rule where the negative part of the addendum is attached to the carbon atom having a lesser number of hydrogen atoms.

In the presence of benzoyl peroxide an addition reaction takes place against Markovnikov’s rule. The reaction follows a free radical chain mechanism as:

Secondary free radicals are more stable than primary radicals. Hence, the former predominates since it forms at a faster rate. Thus, 1-bromopropane is obtained as the major product.

In the presence of peroxide, Br free radical acts as an electrophile. Hence, two different products are obtained on addition of HBr to propene in the absence and presence of peroxide.

Question 17.
Why does benzene undergo electrophilic substitution reactions easily and nucleophilic substitutions with difficulty?
Answer:
Benzene is a planar molecule having delocalized electrons above and below the plane of ring. Hence, it is electron-rich. As a result, it is highly attractive to electron deficient species i.e., electrophiles. Therefore, it undergoes electrophilic substitution reactions very easily. Nucleophiles are electron-rich. Hence, they are repelled by benzene. Hence, benzene undergoes nucleophilic substitutions with difficulty.

Question 18.
Write down the products of ozonolysis of 1, 2-dimethylbenzene (o-xylene). How does the result support Kekule structure for benzene?
Answer:
o-xylene has two resonance structures:

All three products, i.e., methyl glyoxal, 1, 2-dimethyl glyoxal, and glyoxal are obtained from two Kekule structures. Since all three products cannot be obtained from any one of the two structures, this proves that o-xylene is a resonance hybrid of two Kekule structures (I and II).

Question 18.
Arrange benzene, n-hexane and ethyne in decreasing order of acidic behaviour. Also give reason for this behaviour.
Answer:
Acidic character of a species is defined on the basis of ease with which it can lose its H-atoms.
The hybridization state of carbon in the given compound is:

As the s-character increases, the electronegativity of carbon increases and the electrons of C—H bond pair lie closer to the carbon atom. As a result, partial positive charge of H-atom increases and H+ ions are set free.
The s-character increases in the order:
sp³ < sp² < sp Hence, the decreasing order of acidic behaviour is Ethyne > Benzene > Hexane.

Question 20.
How would you convert the following compounds into benzene?
(i) Ethyne (ii) Ethene (iii) Hexane
Answer:
(i) Benzene from Ethyne:

Question 21.
Write structures of all the alkenes which on hydrogenation give 2-methyl butane.
Answer:
The basic skeleton of 2-methyl butane is

Putting double bonds at various different positions and satisfying the tetracovalency of each carbon, the structures of various alkenes which give 2-methyl butane on hydrogenation are:

Question 22.
Arrange the following set of compounds in order of their decreasing relative reactivity with an electrophile, E+
(a) Chlorobenzene, 2, 4-dinitrochlorobenzene, p-nitrochlorobenzene
(b) Toluene, p-H₃C—C₆H₄—NO₂, p-O₂N — C₆H₄ — NO₂
Answer:
Electrophiles are reagents that participate in a reaction by accepting an electron pair in order to bond to nucleophiles.
The higher the electron density on a benzene ring, the more reactive is the compound towards an electrophile, E+ (Electrophilic reaction).
(a) The presence of an electron withdrawing group (i.e., —NO₂ and Cl) deactivates the aromatic ring by decreasing the electron density. Since, —NO₂ group is more electron withdrawing (due to resonance effect) than the —Cl group (due to inductive effect) the decreasing order of reactivity is as follows :
Chlorobenzene > p-nitrochlorobenzene > 2, 4-dinitrochlorobenzene
(b) While —CH₃ is an electron donating group, —NO₃ group is electron withdrawing. Hence, toluene will have the maximum electron density and is most easily attacked by E⁺.
—NO₂ is an electron withdrawing group. Hence, when the number of —NO₂ substituents is greater, the order is as follows:
Toluene > p-CH₃—C₆H₄—NO₂ > p-ON₂—C₆H₄—NO₂

Question 23.
Out of benzene, m-dinitrobenzene and toluene which will undergo nitration most easily and why?
Answer:
The ease of nitration depends on the presence of electron density on the compound to form nitrates. Nitration reactions are examples of electrophilic substitution reactions where an electron-rich species is attacked by a nitronium ion (\(\mathrm{NO}_{2}^{-}\)).
Now, —CH₃ group is electron donating and —NO₂ is electron withdrawing. Therefore, toluene will have the maximum electron density among the three compounds followed by benzene. On the other hand, m-Dinitrobenzene will have the least electron density. Hence, it will undergo nitration with difficulty. Hence, the increasing order of nitration is as follows:

Question 24.
Suggest the name of a Lewis acid other than anhydrous aluminium chloride which can be used during ethylation of benzene.
Answer:
The ethylation reaction of benzene involves the addition of an ethyl group on the benzene ring. Such a reaction is called a Friedel-Crafts alkylation reaction. This reaction takes place in the presence of a Lewis acid.
Any Lewis acid like anhydrous FeCl₃, SnCl₄, BF₃ etc. can be used during the ethylation of benzene.

Question 25.
Why is Wurtz reaction not preferred for the preparation of alkanes containing odd number of carbon atoms? Illustrate your answer by taking one example.
Answer:
Wurtz reaction is limited for the synthesis of symmetrical alkanes (alkanes with an even number of carbon atoms) in the reaction, two
similar alkyl halides are taken as reactants and an alkane, containing double the number of carbon atoms, are formed. Example:

Wurtz reaction cannot be used for the preparation of unsymmetrical alkanes because if two dissimilar alkyl halides are taken as the reactants, then a mixture of alkanes is obtained as the products. Since the reaction involves free radical species, a side reaction also occurs to produce an alkene. For example, the reaction of bromomethane and iodoethane gives a mixture of alkanes.

The boiling point of alkanes (obtained in the mixture) are very close. Hence, it becomes difficult to separate them.

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 12 Organic Chemistry: Some Basic Principles and Techniques Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 12 Organic Chemistry: Some Basic Principles and Techniques

PSEB 11th Class Chemistry Guide Organic Chemistry: Some Basic Principles and Techniques InText Questions and Answers

Question 1.
What are hybridisation states of each carbon atom in the following compounds?
CH₂ = C = O, CH₃CH = CH₂, (CH₃)₂CO, CH₂ = CHCN, C₆H₆
Answer:

C — 1 is sp² hybridised.
C — 2 is sp hybridised.

C — 1 is sp³ hybridised
C — 2 is sp² hybridised
C — 3 is sp² hybridised

C — 1 and C — 3 are sp³ hybridised.
C — 2 is sp² hybridised.

C — 1 is sp² hybridised.
C — 2 is sp² hybridised.
C — 3 is sp hybridised.

(v) C₆H₆
All the 6 carbon atoms in benzene are sp² hybridised.

Question 2.
Indicate the o and n bonds in the following molecules:
C₆H₆, C₆H₁₂, CH₂Cl₂, CH₂ = C = CH₂, CH₃NO₂, HCONHCH₃
Answer:

Question 3.
Write bond line formulas for : isopropyl alcohol, 2,3-Dimethyl butanal, Heptan-4-one.
Answer:

Question 4.
Give the IUPAC names of the following compounds:

Answer:

Question 5.
Which of the following represents the correct IUPAC name for the compounds concerned?
(a) 2, 2 -Dimethylpentane or
2-Dimethylpentane (b) 2,4,7-Trimethyloctane or
2,5,7-Trimethyloctane (c) 2-Chloro-4-methylpentane or
4-Chloro-2-methylpentane (d) But-3-yn-1-ol or But-4-ol-1-yne.
Answer:
(a) The prefix di in the JUPAC name indicates that two identical substituent groups are present in the parent chain. Since two methyl groups are present in the C-2 of the parent chain of the given compound, the correct IUPAC name of the given compound is 2-2-dimethylpentane.
(b) Locant number 2, 4, 7 is lower than 2, 5, 7. Hence, the IUPAC name of the given compound is 2, 4, 7-trimethyloctane.
(c) If the substituents are present in the equivalent position of the parent chain, then the lower number is given to the one that comes first in the name according to the alphabetical order. Hence, the correct IUPAC name of the given compound is 2-chloro-4-methylpentane.
(d) Two functional groups—alcoholic and alkyne—are present in the given compound. The principal functional group is the alcoholic group. Hence, the parent chain will be suffixed with ol. The alkyne group is present in the C—3 of the parent chain. Hence, the correct IUPAC name of the given compound is But – 3-yn -1 – ol.

Question 6.
Draw formulas for the first five members of each homologous series beginning with the following compounds :
(a) H—COOH
(b) CH₃COCH₃
(c) H—CH = CH₂
Answer:
The first five members of each homologous series beginning with the given compounds are shown as follows:

Question 7.
Give condensed and bond line structural formulas and identify the functional group (s) present, if any, for :
(a) 2,2, 4-Trimethylpentane
(b) 2-Hydroxy-1, 2, 3 -propanetricarboxylic acid
(c) Hexanedial
Answer:

Question 8.
Identify the functional groups in the following compounds:

Answer:
The functional groups present in the given compounds are:
(a) Aldehyde (—CHO) Hydroxyl (—OH)
Methoxy (—OMe)
(b) Amino (—NH₂); primary amine (1° amine).
Ester (— O—CO—)
Triethylamine [N(C₂H₅)₂]; tertiary amine (3° amine).
(C) Nitro (—NO₂)
C = C double bond (—C = C—) .

Question 9.
Which of the two: 02NCH2CH20_ or CH3CH20 is expected to be more stable and why?
Answer:
NO₂ group is an electron-withdrawing group. Hence, it shows-I effect. By withdrawing the electrons toward it, the NO₂ group decreases the negative charge on the compound, thereby stabilising it. On the other hand, ethyl group is an electron-releasing group. Hence, the ethyl group shows +1 effect. This increases the negative charge on the compound, thereby destabilising it. Hence, O₂NCH₂CH₂O^– is expected to be more stable than CH₃CH₂O^–.

Question 10.
Explain why alkyl groups act as electron donors when attached to a π system,
Answer:
Due to hyperconjugation, alkyl groups act as electron donors when attached to a π-system as shown below :

Question 11.
Draw the resonance structures for the following compounds. Show the electron shift using curved-arrow notation.
(a) C₆H₂OH
(b) C₆H₅NO₂
(c) CH₃CH = CH CHO
(d) C₆H₅ -CHO

Answer:

Question 12.
What are electrophiles and nucleophiles? Explain with examples?
Answer:
Electrophiles: An electrophile is a reagent that takes away an electron pair. In other words, an electron-seeking reagent is called an electrophile (E⁺). Electrophiles are electron-deficient and can receive an electron pair.
Neutral electrophiles :

Charged electrophiles :

Nucleophiles : A nulceophile is a reagent that brings an electron pair. In other words, a nucleus-seeking reagent is called a nucleophile.

Question 13.
Identify the reagents shown in bold italic in the following equations as nucleophiles or electrophiles:

Answer:
Electrophiles are electron-deficient species and can receive an electron pair. On the other hand, nucleophiles are electron-rich species and can donate their electrons.

Here, HO^– acts as a nucleophile as it is an electron-rich species, i.e., it is a nucleus-seeking species.

Here, CN^– acts as a nucleophile as it is an electron-rich species i.e., it is a nucleus-seeking species.

Here, acts as an electrophile as it is an electron-deficient species.

Question 14.
Classify the following reactions in one of the reaction type studied in this unit.
(a) CH₃CH₂Br + HS^– → CH₃CH₂SH + Br^–
(b) (CH₃)₂ C = CH₂ +HCl → (CH₃)₂ ClC – CH₃
(c) CH₃CH₂Br + HO^– → CH₂ = CH₂ +H₂O + Br^–
(d) (CH₃)₃C— CH₂OH +HBr →(CH₃)₂CBrCH₂CH₂CH₃ + H₂O
Ans. (a) Nucleophilic substitution reaction
(b) Electrophilic addition reaction
(c) β-elimination reaction
(d) Nucleophilic substitution reaction with rearrangement.

Question 15.
What is the relationship between the members of following pairs of structures? Are they structural or geometrical isomers or resonance contributors?

Answer:
(a) Compounds having the same molecular formula but with different structures are called structural isomers. The given compounds have the same molecular formula but they differ in the position of the functional group (ketone group.)

In structure I, ketone group is at the C—3 of the parent chain (hexane chain) and in structure II, ketone group is at the C—2 of the parent chain (hexane chain). Hence, the given pair represents structural isomers.
(b) Compounds having the same molecular formula, the same constitution, and the sequence of covalent bonds, but with different relative positions of their atoms in space are called geometrical isomers.

In structures I and II, the relative position of deuterium (D) and hydrogen (H) in space are different. Hence, the given pairs represent geometrical isomers.
(c) The given structures are canonical structures or contributing structures. They are hypothetical and individually do not represent any real molecule. Hence, the given pair represents resonance structures, called resonance isomers.

Question 16.
For the following bond cleavages, curved-arrows are used to show the electron flow and classify each as homolysis or heterolysis. Identify reactive intermediate produced as free radical, carbocation and carboanion.


Answer:
(a) The bond cleavage using curved-arrows to show the electron flow of the given reaction can be represented as
It is an example of homolytic cleavage as one of the shared pair in a covalent bond goes with the bonded atom. The reaction intermediate formed is a free radical.

(b) The bond cleavage using curved-arrows to show the electron flow of the given reaction can be represented as

It is an example of heterolytic cleavage as the bond breaks in such a manner that the shared pair of electrons remains with the carbon of propanone. The intermediate formed is carbanion.
(c) The bond cleavage using curved-arrows to show the electron flow of the given reaction can be represented as

it is an example of heterolytic cleavage as the bond breaks in such a manner that the shared pair of electrons remains with the bromine ion. The reaction intermediate formed is a carbocation.
(d) The bond cleavage using curved-arrows to show the electron flow of the given reaction can be represented as

It is a heterolytic cleavage as the bond breaks in such a manner that the shared pair of electrons remains with one of the fragments. The intermediate formed is a carbocation.

Question 17.
Explain the terms inductive and electromeric effects. Which electron displacement effect explains the following correct orders of acidity of the carboxylic acids?
(a) Cl₃CCOOH > Cl₂CHCOOH > ClCH₂COOH
(b) CH₃CH₂OOH > (CH₃)₂ CHCOOH > (CH₃)₃C. COOH
Answer:
Inductive effect : The permanent displacement of sigma electrons along a saturated chain, whenever an electron withdrawing or electron donating group is present, is called inductive effect.
Inductive effect could be +I effect or -I effect. When an atom or group attracts electrons towards itself more strongly than hydrogen, it is said to possess -I effect. For example,

When an atom or group attracts electrons towards itself less strongly than hydrogen, it is said to possess +I effect. For example,

Electromeric effect : It involves the complete transfer of the shared pair of n electrons to either of the two atoms linked by multiple bonds in the presence of an attacking agent. For example,

Electromeric effect could be + E effect or – E effect.
+E effect : When the electrons are transferred towards the attacking reagent.

-E effect : When the electrons are transferred away from the attacking reagent.

(a) Cl₃CCOOH > Cl₂CHCOOH > ClCH₂COOH
The order of acidity can be explained on the basis of inductive effect (-I effect). As the number of chlorine atoms increases, the -I effect increases. With the increase in -7 effect, the acid strength also increases accordingly.

(b) CH₃CH₂COOH > (CH₃)₂CHCOOH > (CH₃)₃C.COOH
The order of acidity can be explained on the basis of inductive effect (+I effect.) As the number of alkyl groups increases, the +I effect also increases. With the increase in +I effect, the acid strength also increases accordingly.

Question 18.
Give a brief description of the principles of the following techniques taking an example in each case.
(a) Crystallisation (b) Distillation (c) Chromatography
Answer:
(a) Crystallisation : Crystallisation is one of the most commonly used techniques for the purification of solid organic compounds. Principle : It is based on the difference in the solubilities of the compound and the impurities in a given solvent. The impure compound gets dissolved in the solvent in which it is sparingly soluble at room temperature, but appreciably soluble at higher temperature. The solution is concentrated to obtain a nearly saturated solution. On cooling the solution, the pure compound crystallises out and is removed by filtration.
For example, iodoform is crystallised with alcohol, benzoic acid mixed with naphthalene can be purified by hot water.
(b) Distillation : This method is used to separate volatile liquids from non-volatile impurities or a mixture of those liquids that have a sufficient difference in their boiling points.
Principle : It is based on the fact that liquids having different boiling points vapourise at different temperatures. The vapours are then cooled and the liquids so formed are collected separately.
For example, chloroform (b.pt. 334 K) and aniline (b.pt. 457 K) are easily separated by the distillation. On boiling the vapours of lower boiling component are formed first so it is collected first in the receiver.
(c) Chromatography : It is one of the most useful methods for the separation and purification of organic compounds.
Principle : It is based on the difference in movement of individual components of a mixture through the stationary phase under the influence of mobile phase.
For example, a mixture of red and blue ink can be separated by chromatography. A drop of the mixture is placed on the chromatogram. The component of the ink, which is less adsorbed on the chromatogram, moves with the mobile phase while the less adsorbed component remains almost stationary.

Question 19.
Describe the method, which can be used to separate two compounds with different solubilities in a solvent S.
Answer:
Fractional crystallisation is the method used for separating two compounds with different solubilities in a solvent S.
The process of fractional crystallisation is carried out in four steps.
(a) Preparation of the solution: The powdered mixture is taken in a flask and the solvent is added to it slowly and stirred simultaneously. The solvent is added till the solute is just dissolved in the solvent. This saturated solution is then heated.
(b) Filtration of the solution: The hot saturated solution is then filtered through a filter paper in a China dish.
(c) Fractional crystallisation: The solution in the China dish is now allowed to cool. The less soluble compound crystallises first while the more soluble compound remains in the solution. After separating these crystals from the mother liquor, the latter is concentrated once again. The hot solution is allowed to cool and consequently, the crystals of the more soluble compound are obtained.
(d) Isolation and drying: These crystals are separated from the mother liquor by filtration. Finally, dried the crystals.

Question 20.
What is the difference between distillation, distillation under reduced pressure and steam distillation?
Answer:
The difference among distillation, distillation under reduced pressure, and steam distillation are given in the following table :

Question 21.
Discuss the chemistry of Lassaigne’s test.
Answer:
Lassaigne’s test : This test is employed to detect the presence of nitrogen, sulphur and halogens in an organic compound. These elements are present in the covalent form in an organic compound. These are converted into the ionic form by fusing the compound with sodium metal.

The cyanide, sulphide, and halide of sodium formed are extracted from the fused mass by boiling it in distilled water. The extract so obtained is called Lassaigne’s extract. This Lassaigne’s extract is then tested for the presence of nitrogen, sulphur and halogens.

(a) Test for nitrogen

Chemistry of the test: In the Lassaignes’s test for nitrogen in an organic compound, the sodium fusion extract is boiled with iron (II) sulphate and then acidified with sulphuric acid. In the process, sodium cyanide first reacts with iron (II) sulphate and forms sodium hexacyanoferrate(II). Then, on heating with sulphuric acid, some iron (II) gets oxidised to form iron (III) hexacyanoferrate(II) which is Prussian blue in colour. The chemical equations involved in the reaction can be represented as

(b) Test for sulphur

Chemistry of the test: In the Lassaigne’s test for sulphur in an organic compound, the sodium fusion extract is acidified with acetic acid and then lead acetate is added to it. The precipitation of lead sulphide, which is black in colour, indicates the presence of sulphur in the compound.

(ii) Lassaigne’s extract + Sodium nitroprusside → Violet colour
Chemistry of the test: The sodium fusion extract is treated with sodium nitroprusside. Appearance of violet colour also indicates the presence of sulphur in the compound.

If in an organic compound, both nitrogen and sulphur are present, then instead of NaCN, formation of NaSCN takes place.

This NaSCN (sodium thiocyanate) gives a blood red colour. Prussian colour is not formed due to the absence of free cyanide ions.

(c) Test for halogens

Chemistry of the test: In the Lassaigne’s test for halogens in an organic compound, the sodium fusion extract is acidified with nitric acid and then treated with silver nitrate.
x^– + Ag⁺ → AgX (X = Cl, Br, I)
If nitrogen and sulphur both are present in the organic compound, then the Lassaigne’s extract is boiled to expel nitrogen and sulphur, which would otherwise interfere in the test for halogens.

Question 22.
Differentiate between the principle of estimation of nitrogen in an organic compound by (i) Dumas method and (ii) Kjeldahl’s method.
Answer:
(i) In Dumas method, when a known mass of the nitrogen containing organic compound is heated with excess of CuO in an atmosphere of CO₂, nitrogen of the organic compound is converted into N₂ gas. The volume of N₂ thus obtained is converted into STP and the percentage of nitrogen is determined.
%N = \(\frac{28}{22400} \times \frac{\text { Vol. of } \mathrm{N}_{2} \text { at STP }}{\text { Mass of the substance taken }}\) x 100

(ii) In Kjeldahl’s method, a known mass of the nitrogen containing
organic substance is digested (heated) with conc. H₂SO₄ and CuSO₄ (in little amount) in Kjeldahl’s flask. Nitrogen present in the organic compound is quantitatively converted into (NH₄ )₂SO₄. (NH₄ )₂SO₄ thus obtained is boiled with excess of NaOH solution to liberate NH3 gas which is absorbed in a known excess of a standard solution of H₂SO₄ or HCl.
The volume of acid left after absorption of NH₃ is estimated by titration against a standard alkali solution. From the volume of the acid used, the percentage of nitrogen is determined by applying the equation,

Question 23.
Discuss the principle of estimation of halogens, sulphur and phosphorus present in an organic compound.
Answer:
Estimation of halogens : Halogens are estimated by the Carius method. In this method, a known quantity of organic compound is heated with fuming nitric acid in the presence of silver nitrate, contained in a hard glass tube called the Carius tube, taken in a furnace. Carbon and hydrogen that are present in the compound are oxidized to form CO₂ and H₂O respectively and the halogen present in the compound is converted into AgX. This AgX is then filtered, washed, dried, and weighed.
Let the mass of organic compound taken = m g

Estimation of sulphur : In this method, a known quantity of organic compound is heated with either fuming nitric acid or sodium peroxide in a hard glass tube called the Carius tube. Sulphur present in the compound, is oxidized to form sulphuric acid. On addition of excess of barium chloride to it, the precipitation of barium sulphate takes place. This precipitate is then filtered, washed, dried, and weighed.
Let the mass of organic compound taken -mg
Mass of BaSO₄ formed = m₁ g
% of sulphur = \(\frac{32 \times m_{1} \times 100}{233 \times m}\)

Estimation of phosphorus : In this method, a known quantity of organic compound is heated with fuming nitric acid. Phosphorus, present in the compound, is oxidized to form phosphoric acid. By adding ammonia and ammonium molybdate to the solution, phosphorus can be precipitated as ammonium phosphomolybdate.

Phosphorus can also be estimated by precipitated it as MgNH4P04 by adding magnesia mixture, which on ignition yields Mg2P207.
Let the mass of organic compound = m g
Mass of ammonium phosphomolybdate = m₁ g
Molar mass of ammonium phosphomolybdate = 1877 g

Question 24.
Explain the principle of paper chromatography.
Answer:
In paper chromatography, chromatography paper is used. This paper contains water trapped in it, which acts as the stationary phase. On the base of this chromatography paper, the solution of the mixture is spotted. The paper strip is then suspended in a suitable solvent, which acts the mobile phase. This solvent rises up the chromatography paper by capillary action and in this procedure it flows over the spot. The components are selectively retained on the paper (according to their differing partition in these two phases). The spots of different components travel with the mobile phase to different heights. The paper so obtained (shown in the given figure) is known as a chromatogram.

Question 25.
Why is nitric acid added to sodium extract before adding silver nitrate for testing halogens?
Answer:
While testing the Lassaigne’s extract for the presence of halogens, it is first boiled with dilute nitric acid. This is done to decompose NaCN to HCN and NA₂S to H₂S and to expel these gases. That is, if any nitrogen and sulphur are present in the form of NaCN and Na₂S they are removed. The chemical equations involved in the reaction are represented as
NaCN + HNO₃ > NaNO₃ + HCN
Na₂S + 2HNO₃ > 2NaNO₃ + H₂S

Question 26.
Explain the reason for the fusion of an organic compound with metallic sodium for testing nitrogen, sulphur and halogens.
Answer:
Nitrogen, sulphur, and halogens are covalently bonded in organic compounds. For their detection, they have to be first converted to ionic form. This is done by fusing the organic compound with sodium metal. This is called Lassaigne’s test. The chemical equations involved in the test are
Na + C + N → NaCN
Na + S + C + N → NaSCN
2Na + S → Na₂S
Na + X → NaX (X = Cl, Br, I)
Carbon, nitrogen, sulphur, and halogen come from organic compounds.

Question 27.
Name a suitable technique of separation of the components from a mixture of calcium sulphate and camphor.
Answer:
Calcium sulphate (CaSO₄) which is an inorganic compound and does not sublime can be separated from camphor which is an organic compound and sublimes by the simple technique of sublimation. This technique involves the direct conversion of a solid into the gaseous state on heating without passing through the intervening liquid state and vice-versa on cooling. Camphor sublimes and gets-deposited on the walls of the cooler portion of the funnel and CaSO₄ remains as such. The two components can thus be separated.

Question 28.
Explain, why an organic liquid vaporises at a temperature below its boiling point in its steam distillation?
Answer:
In steam distillation, the organic liquid starts to boil when the sum of vapour pressure due to the organic liquid (p₁) and the vapour pressure due to water (p₂) becomes equal to atmospheric pressure (p), that is P = P₁ + P₂– Since P₁ < p₂, organic liquid will vapourise at a lower temperature than its boiling point.

Question 29.
Will CCl₄ give white precipitate of AgCl on heating it with silver nitrate? Give reason for your answer.
Answer:
CCl₄ will not give the white precipitate of AgCl on heating it with silver nitrate. This is because the chlorine atoms are covalently bonded to carbon in CCl₄. To obtain the precipitate, it should be present in ionic form and for this, it is necessary to prepare the Lassaigne’s extract of CCl₄.

Question 30.
Why does solution of potassium hydroxide is used to absorb carbon dioxide evolved during the estimation of carbon present in an organic compound?
Answer:
Carbon dioxide is acidic in nature and potassium hydroxide is a strong base. Hence, carbon dioxide reacts with potassium hydroxide to form potassium carbonate and water as
2KOH + CO₂ → K₂CO₃ + H₂O
Thus, the mass of the U-tube containing KOH increases. This increase in the mass of U-tube gives the mass of CO₂ produced. From its mass, the percentage of carbon in the organic compound is calculated as
%C = \(\frac{12}{44} \times \frac{\text { Weight of } \mathrm{CO}_{2} \text { formed }}{\text { Weight of substance taken }}\) x 100

Question 31.
Why is it necessary to use acetic acid and not sulphuric acid for acidification of sodium extract for testing sulphur by lead acetate test?
Answer:
For testing of sulphur present in the organic compound the Lassaigne’s extract is acidified with acetic acid (CH₃COOH) and not sulphuric acid because lead acetate is soluble and does not interfere with the test. If sulphuric acid (H₂SO₄) is used, lead acetate will react with H₂SO₄ itself to form white ppt. of PbSO₄ as follows :

White ppt. of PbSO₄ so formed will interfere with this test of sulphur.

Question 32.
An organic compound contains 69% carbon and 48% hydrogen, the remainder being oxygen. Calculate the masses of carbon dioxide and water produced when 0.20 g of this substance is subjected to complete combustion.
Answer:

Question 33.
A sample of 0.50 g of an organic compound was treated according to Kjeldahl’s method. The ammonia evolved was absorbed in 50 ml of 0.5 M H₂SO₄. The residual acid required 60 mL of 0.5 M solution of NaOH for neutralisation. Find the percentage composition of nitrogen in the compound.
Ans. Volume of the acid taken = 50 mL of 0.5 M H₂SO₄
= 25 mL of 1.0 M H₂SO₄
Volume of alkali used for neutralization of excess acid = 60 mL of 0.5 M NaOH = 30 mL of 1.0 M NaOH
H₂SO₄ + 2NaOH → Na₂SO₄ + 2H₂O
1 mole of H₂SO₄ = 2 moles of NaOH
Hence, 30 mL of 1.0 M NaOH = 15 mL of 1.0 M H₂SO₄
∴ Volume of acid used by ammonia = 25 – 15 = 10 mL
%of nitrogen = \(\frac{1.4 \times \mathrm{N}_{1} \times \text { Volume of acid used }}{\mathrm{W}}\)
= \(\frac{1.4 \times 2 \times 10}{0.5}\) (N₁ = normality of acid and W = mass of organic compound)
= 56

Question 34.
0.3780 g of an organic chloro compound gave 0.5740 g of silver chloride in Carius estimation. Calculate the percentage of chlorine present in the compound.
Answer:
Given that,
Mass of organic compound = 0.3780 g
Mass of AgCl formed = 0.5740 g
1 mol of AgCl contains 1 mol of Cl
Thus, mass of chlorine in 0.5740 g of AgCl = \(\frac{35.5 \times 0.5740}{143.5}\) = 0.142g
∴ Percentage of chlorine = \(\frac{0.142}{0.3780}\) x 100 = 37.57%
Hence, the percentage of chlorine present in the given organic chloro compound is 37.57%.

Question 35.
In the estimation of sulphur by Carius method, 0.468 g of an organic sulphur compound afforded 0.668 g of barium sulphate. Find out the percentage of sulphur in the given compound.
Answer:
The mass of organic compound = 0.468 g
Mass of barium sulphate formed = 0.668 g
Percentage of sulphur = \(\frac{32}{233} \times \frac{\text { Mass of } \mathrm{BaSO}_{4} \text { formed }}{\text { Mass of substance taken }}\) x 100
= \(\frac{32}{233} \times \frac{0.668}{0.468}\) x 100 = 19.59%
Hence, the percentage of sulphur in the given compound is 19.59%.

Question 36.
In the organic compound,
CH₂ = CH – CH₂ – CH₂ – C = CH, the pair of hybridised orbitals involved in the formation of C₂ – C₃ bond is (a) sp – sp² (b) sp – sp³ (c) sp² – sp³ (d) sp³ – sp³
Answer:

In the given organic compound, the carbon atoms numbered as 1, 2, 3, 4, 5, and 6 are sp², sp², sp³, sp³, sp, and sp hybridised respectively. Thus, the pair of hybridised orbitals involved in the formation of C₂ – C₃ bond is sp² – sp².

Question 37.
In the Lassaigne’s test for nitrogen in an organic compound, the Prussian blue colour is obtained due to the formation of:
(a) Na₄[Fe(CN)₆]
(b)Fe₄[Fe(CN)₆]₃
(c) Fe₂[FeCN₆]
(d) Fe₃[Fe(CN)₆]₄
Answer:
(b) The Prussian blue colour is due to the formation of ferric ferro cyanide, Fe₄[Fe(CN)₆]₃.

Question 38.
Which of the following carbocations is most stable?

Answer:
(b) The order of stability of carbocation is 3° > 2° > 1°. 3° carbocation,

Question 39.
The best and latest technique for isolation, purification and separation of organic compounds is:
(a) Crystallisation
(b) Distillation
(c) Sublimation
(d) Chromatography
Answer:
(d) Chromatography is the best and latest technique for isolation, purification and separation of organic compounds.

Question 40.
The reaction:
CH₃CH₂I+KOH(aq) > CH₃CH₂OH +KI is classified as :
(a) electrophilic substitution
(b) nucleophilic substitution
(c) elimination
(d) addition
Answer:
(b) This is an example of nucleophilic substitution reaction. The hydroxyl group of KOH (OH^–) with a lone pair of itself acts as a nucleophile and substitutes iodide ion in CH₃CH₂I to form ethanol.

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 11 The p-Block Elements Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 11 The p-Block Elements

PSEB 11th Class Chemistry Guide The p-Block Elements InText Questions and Answers

Question 1.
Discuss the pattern of variation in the oxidation states of (i) B to T1 (ii) C to Pb.
Answer:

Boron and aluminium show an oxidation state of+3 only because they do not exhibit inert pair effect due to the absence of d- or f-electrons. Elements from Ga to T1 show two oxidation states, i.e., +1 and +3. The tendency to show +1 oxidation state increases down the group due to the inability of ns² electrons of valence shell to participate in bonding which is called inert pair effect. Therefore, Tl⁺ is more stable than Tl³⁺.

Carbon and silicon show an oxidation state of +4 only. In heavier members the tendency to show +2 oxidation state increases in the sequence Ge < Sn < Pb. It is due to the inability of ns² electrons of valence shell to participate in bonding (inert pair effect). Ge forms stable compounds in +4 state and only few compounds in +2 state. Sn forms compounds in both the oxidation states and lead compounds in +2 state is more stable than +4 oxidation state.

Question 2.
How can you explain higher stability of BC13 as compared to T1C13?
Answer:
Boron and thallium belong to group 13 of the periodic table. In this group, the +1 oxidation state becomes more stable on moving down the , group. BCl₃ is more stable than TlCl₃ because the +3 oxidation state of B is more stable than the +3 oxidation state of Tl. In Tl, the +3 state is highly oxidising and it reverts back to the more stable +1 state.

Question 3.
Why does boron trifluoride behave as a Lewis acid?
Answer:
BF₃ being electron deficient is a strong Lewis acid. It reacts with Lewis bases easily to complete the octet around boron.

Question 4.
Consider the compounds, BCl₃ and CCl₄. How will they behave with water? Justify.
Answer:
Being a Lewis acid, BCI3 readily undergoes hydrolysis. As a result, Boric ‘ acid is formed.
BCl₃ + 3H₂O → 3HCl + B(OH)₃
CCl₄ completely resists hydrolysis. Carbon does not have any vacant orbital. Hence, it cannot accept electrons from water to form an intermediate. When CCl₄ and water are mixed, they form separate layers.
CCl₄ + H₂O → No reaction.

Question 5.
Is boric acid a protic acid? Explain.
Answer:
Boric acid is not a protic acid. It is a weak monobasic acid, behaving as a Lewis acid.
B(OH)₃ + 2H₂O → [B (OH)₄]^– + H₃O₊
It behaves as an acid by accepting a pair of electrons from OH- ion.

Question 6.
Explain what happens when boric acid is heated.
Answer:
On heating boric acid (H₃BO₃) at 370 K or above, it changes to metaboric acid (HBO₂). On further heating, this yields boric oxide B₂O₃

Question 7.
Describe the shapes of BF₃ and \(\mathbf{B H}_{\mathbf{4}}^{-}\). Assign the hybridisation of boron in these species.
Answer:
(i) BF₃ : As a result of its small size and high electronegativity, boron tends to form monomeric covalent halides. These halides have a planar triangular geometry. This triangular shape is formed by the overlap of three sp² hybridised orbitals of boron with the sp-orbitals of three halogen atoms. Boron is sp² hybridised in BF₃.

(ii) \(\mathbf{B H}_{\mathbf{4}}^{-}\) : Boron-hydride ion (\(\mathbf{B H}_{\mathbf{4}}^{-}\)) is formed by the sp3 hybridisation of boron orbitals. Therefore, it is tetrahedral in structure.

Question 8.
Write reactions to justify amphoteric nature of aluminium.
Answer:
A substance is called amphoteric if it displays characteristics of both acids and bases. Aluminium dissolves in both acids and bases, showing amphoteric behaviour. ..
(i) 2Al(s) + 6HCl(aq) → 2Al³⁺(aq) + 6Cl^–(aq) + 3H₂(g)
(ii) 2Al(s) + 2NaOH(aq) + 6H₂O(Z) → 2Na⁺[Al(OH)₄]^–(aq) + 3H₂(g)

Question 9.
What are electron deficient compounds? Are BCI3 and SiCl4 electron deficient species? Explain.
Answer:
Electron deficient compounds are those in which the octet of all the atoms is not complete i.e., all the element present in the compound do not have 8e^– in their outer shell.
In trivalent state, the number of electrons around the central atom B in BCl₃ is six.

Such molecules have a tendency to accept a pair of electrons to achieve stability and hence, behave as Lewis acids.
In SiCl₄, the number of electrons around the central atom Si is eight so, it is electron precise molecule.

Question 10.
Write the resonance structures of \(\mathrm{CO}_{3}^{2-}\) and \(\mathrm{HCO}_{3}^{-}\).
Answer:

There are only two resonating structures for the bicarbonate ion.

Question 11.
What is the state of hybridisation of carbon in
(a) \(\mathrm{CO}_{3}^{2-}\)
(b) diamond
(c) graphite?
Answer:
(a) \(\mathrm{CO}_{3}^{2-}\) : C in \(\mathrm{CO}_{3}^{2-}\) is sp² hybridised and is bonded to three oxygen atoms.
(b) Diamond : Each carbon in diamond is sp³ hybridised and is bound to four other carbon atoms.
(c) Graphite : Each carbon atom in graphite is sp² hybridised and is bound to three other carbon atoms.

Question 12.
Explain the difference in properties of diamond and graphite on the basis of their structures.
Answer:

In diamond C is sp³ hybridised. Each C is tetrahedrally linked to four neighbouring carbon atoms through strong C – G sp³ – sp³ σ- bonds. The structure is highly rigid and this network extends to three dimensions. Whereas in graphite C is sp² hybridised. Each C is linked to three other C atoms forming hexagonal rings. Thus unlike diamond, graphite has a two-dimensional sheet like (layered) structure consisting of a number of benzene rings fused together. The various sheets or layers are held together by weak van der Waals forces. Based on the above structural differences between diamond and graphite, they can be summed up as follows:

Diamond:

1. It has a crystalline lattice.
2. In diamond, each carbon atom is sp³ hybridised and is bonded to four other carbon atoms through a o- bond.
3. It is made up of tetrahedral units.
4. The C—C bond length in diamond is 154 pm.
5. It has a rigid covalent bond network which is difficult to break.
6. It acts as an electrical insulator.

Graphite:

1. It has a layered structure.
2. In graphite, each carbon atom is sp² hybridised and is bonded to three other carbon atoms through a o- bond. The fourth electron forms a n bond.
3. It has a planar geometry.
4. The C—C bond length in graphite is 141.5 pm.
5. It is quite soft and its layers can be separated easily.
6. It is a good conductor of electricity.

Question 13.
Rationalise the given statements and give chemical reactions:
(a) Lead (II) chloride reacts with Cl₂ to give PbCl₄.
(b) Lead (IV) chloride is highly unstable towards heat.
(c) Lead is known not to form an iodide, Pbl₄.
Answer:
(a) Lead belongs to group 14 of the periodic table. The two oxidation states displayed by this group is +2 and +4. On moving down the group the +2 oxidation state’ becomes more stable and the +4 oxidation state becomes less stable.
This is because of the inert pair effect. Hence, PbCl4 is much less stable than PbCl₂. However, the formation of PbCl₄ takes place when chlorine gas is bubbled through a saturated solution of PbCl₂.
PbCl₂(s) + Cl₂(g) → PbCl₄(l)

(b) On moving down group IV, the higher oxidation state becomes unstable because of the inert pair effect. Pb(IV) is highly unstable and when heated it reduces to Pb(II)

(c) Lead is known not to form Pbl4. Pb (+4) is oxidising in nature and I^– is reducing in nature. A combination of Pb (IV) and iodide ion is not stable. Iodide ion is strongly reducing in nature. Pb(IV) oxidises I^– to I₂ and itself gets reduced to Pb (II)
PbI₄ → PbI₂ + I₂

Question 14.
Suggest reasons why the B-F bond lengths in \(\mathbf{B F}_{3}^{-}\) (130 pm) and \(\mathbf{B F}_{4}^{-}\) (143 pm) differ.
Answer:
The B—F bond length in \(\mathbf{B F}_{3}^{-}\) is shorter than the B—F bond length in \(\mathbf{B F}_{4}^{-}\). \(\mathbf{B F}_{3}^{-}\) is an electron-deficient species. With a vacant p-orbital on boron, the fluorine and boron atoms undergo pπ—pπ back bonding to remove this deficiency. This imparts a double-bond character to the B-F bond.

The double bond character causes the bond length to shorten in \(\mathbf{B F}_{3}^{-}\) (130 pm). However, when \(\mathbf{B F}_{3}^{-}\) coordinates with the fluoride ion, a change in hybridisation from sp² in (\(\mathbf{B F}_{3}^{-}\)) tp sp³ (in \(\mathbf{B F}_{4}^{-}\)) occurs.
Boron now forms 4σ-bonds and the double bond character is lost. This accounts for a B—F bond length of 143 pm in \(\mathbf{B F}_{4}^{-}\) ion.

Question 15.
If B—Cl bond has a dipole moment, explain why BC13 molecule has zero dipole moment.
Answer:
As a result of the difference in the electronegativities of B and Cl, the B—Cl bond is polar in nature. However the BC13 molecule is non-polar. This is because BCl₃ is trigonal planar in shape. It is a symmetrical molecule. Hence, the respective dipole-moments of the B-Cl bond cancel each other, thereby causing a zero-dipole moment.

Question 16.
Aluminium trifluoride is insoluble in anhydrous HF but dissolves on addition of NaF. Aluminium trifluoride precipitates out of the resulting solution when gaseous BF3 is bubbled through. Give reasons.
Answer:
Hydrogen fluoride (HF) is a covalent compound and has a very strong intermolecular hydrogen-bonding. Thus, it does not provide ions and aluminium fluoride (AlF) does not dissolve in it. Sodium fluoride (NaF) is an ionic compound and when it is added to the mixture, AlF dissolves. This is because of the availability of free F^–. The reaction involved in the process is:

When boron trifluoride (BF₃) is added to the solution, aluminium fluoride precipitates out of the solution. This happens because the tendency of boron to form complexes is much more than that of aluminium. Therefore, when BF₃ is added to the solution, B replaces Al from the complexes according to the following reaction :

Question 17.
Suggest a reason why CO is poisonous?
Answer:
Carbon monoxide is highly-poisonous because of its ability to form a complex with haemoglobin. The CO—Hb complex is more stable than the O₂—Hb complex. The former prevents Hb from binding with oxygen. Thus, a person dies because of suffocation on not receiving oxygen. It is found that the CO-Hb complex is about 300 times more stable than the O₂ – Hb complex.

Question 18.
How is excessive content of CO₂ responsible for global warming?
Answer:
Carbon dioxide is a very essential gas for our survival. However, an increased content of CO₂ in the atmosphere posses a serious threat. An increment in the combustion of fossil fuels, decomposition of limestone, and a decrease in the number of trees had led to greater levels of carbon dioxide. Carbon dioxide has the property of trapping the heat provided by sunrays. Higher the level of carbon dioxide, higher is the amount of heat trapped. This results in an increase in the atmospheric temperature, thereby causing global warming.

Question 19.
Explain structures of diborane and boric acid.
Answer:
(a) Diborane : B₂H₆ is an electron-deficient compound. B2H6 has only
12 electrons-6e~ from 6 H atoms and 3e^– each from 2 B atoms. Thus, after combining with 3 H atoms, none of the boron atoms has any electrons left. X-ray diffraction studies have shown the structure of diborane as:

H_t = terminal hydrogen
H_b = bridging hydrogen

2 boron and 4 terminal hydrogen atoms (H_t) lie in one plane, while the other two bridging hydrogen atoms (H_b) lie in a plane perpendicular to the plane of boron atoms. Again of the two bridging hydrogen atoms, one H atom lies above the plane and the other lies below the plane. The terminal bonds are regular two-centre two-electron (2c – 2e^–) bonds while the two bridging (B—H—B) bonds are three centre two electron (3c – 2e^–) bonds,

(b) Boric acid : Boric acid has a layered structure. Each planar BO₃ unit is linked to one another through H atoms. The H atoms form a covalent bond with a BO₃ unit, while a hydrogen bond is formed with another BO₃ unit. In the given figure, the dotted lines represent hydrogen bonds.

Question 20.
What happens when
(a) Borax is heated strongly,
(b) Boric acid is added to water,
(c) Aluminium is treated with dilute NaOH,
(d) BF3 is reacted with ammonia?
Answer:
(a) When heated, borax undergoes various transitions. It first loses water molecules and swells. Then, it turns into a transparent liquid, solidifying to form a glass-like material called borax bead.

(b) When boric acid is added to water, it accepts electrons from OH- ions.
B(OH)₃ +2HOH → [B(OH)₄]^– + H₃O⁺

(c) A1 reacts with dilute NaOH to form sodium tetrahydroxoaluminate (III). Hydrogen gas is liberated in the process.
Al(s) + 2NaOH(aq) + 6H₂O(I) → 2Na⁺Al(OH)₄(aq) + 3H₂(g)

(d) BF₃ (a Lewis acid) reacts with NH₃ (a Lewis base) to form an adduct. This results in a complete octet around B in BF₃.
F₃B + :NH₃ → F₃B ← NH₃

Question 21.
Explain the following reactions
(a) Silicon is heated with methyl chloride at high temperature in the presence of copper.
(h) Silicon dioxide is treated with hydrogen fluoride.
(c) CO is heated with ZnO.
(d) Hydrated alumina is treated with aqueous NaOH solution.
Answer:
(a) When silicon reacts with methyl chloride in the presence of copper (catalyst) and at a temperature of about 537 K, a class of organosilicon polymers called methyl-substituted chlorosilanes (MeSiCl3, Me₂SiCl₂, Me₃SiCl, andMe₄Si) are formed.

(b) When silicon dioxide (SiO₂) is heated with hydrogen fluoride (HF), it forms silicon tetrafluoride (SiF₄). Usually, the Si-0 bond is a strong bond and it resists any attack by halogens and most acids, even at a high temperature. However, it is attacked by HF.
SiO₂ + 4HF → SiF₄ + 2H₂O
The SiF₄ formed in this reaction can further react with HF to form hydrofluorosilicic acid.
SiF₄ + 2HF → H₂SiF₆

(c) When CO reacts with ZnO, it reduces ZnO to Zn. CO acts as a reducing agent.

(d) When hydrated alumina is added to sodium hydroxide, the former dissolves in the latter because of the formation of sodium meta-aluminate.
Al₂O₃ . 2H₂O + 2NaOH → 2NaAlO₂ + 3H₂O

Question 22.
Give reasons:
(i) Cone. HNO₃ can be transported in aluminium container,
(ii) A mixture of dilute NaOH and aluminium pieces is used to open drain.
(iii) Graphite is used as lubricant.
(iv) Diamond is used as an abrasive.
(v) Aluminium alloys are used to make aircraft body.
(vi) Aluminium utensils should not be kept in water overnight.
(vii) Aluminium wire is used to make transmission cables.
Answer:
(i) Concentrated HNO₃ can be stored and transported in aluminium containers as it reacts with aluminium to form a thin protective oxide layer on the aluminium surface. This oxide layer renders aluminium passive.
(ii) Sodium hydroxide and aluminium react to form sodium tetrahydroxoaluminate(III) and hydrogen gas. The pressure of the produced hydrogen gas is used to open blocked drains.
2A1 + 2NaOH + 6H₂O → 2Na⁺ [Al(OH)₄]^– + 3H₂
(iii) Graphite has a layered structure and different layers of graphite are bonded to each other by weak van der Waals’ forces. These layers can slide over each other. Graphite is soft and slippery. Therefore, graphite can be used as a lubricant.
(iv) In diamond, carbon is sp³ hybridised. Each carbon atom is bonded to four other carbon atoms with the help of strong covalent bonds. These covalent bonds are present throughout the surface, giving it a very rigid 3-D structure. It is very difficult to break this extended covalent bonding and for this reason, diamond is the hardest substance known. Thus, it is used as an abrasive and for cutting tools.
(v) Aluminium has a high tensile strength and is very light in weight. It can also be alloyed with various metals such as Cu, Mn, Mg, Si and Zn. It is very malleable and ductile. Therefore, it is used in making aircaft bodies.
(vi) The oxygen present in water reacts with aluminium to form a thin layer of aluminium oxide. This layer prevents aluminium from further reaction. However, when water is kept in an aluminium vessel for long period of time, some amount of aluminium oxide may dissolve in water. As aluminium ions are harmful, water should not be stored in aluminium vessels overnight.
(vii) Silver, copper, and aluminium are among the best conductors of – electricity. Silver is an expensive metal and silver wires are very expensive. Copper is quite expensive and is also very heavy. Aluminium is a very ductile metal. Thus, aluminium is used in making wires for electrical conduction.

Question 23.
Explain why is there a phenomenal decrease in ionisation enthalpy from carbon to silicon?
Answer: Electronic configuration of C is = 1s², 2s², 2p²
Electronic configuration of Si = 1s², 2s²2p⁶, 3s²3p²

As we proceed from C to Si in group 14, there is a sharp increase in covalent radius from 77 pm for C to 118 pm for silicon. Due to the increase in the size of the atom, there is a sharp fall in the value of ionisation enthalpy from carbon to silicon.

Question 24.
How would you explain the lower atomic radius of Ga as compared to Al?
Answer: Electronic configuration of Al and Ga are as ₁₃Al = 1s² 2s² 2p⁶ 3s² 3p¹ ;
₃₁Ga = 1s²2s²2p⁶3s²3p⁶3d¹⁰4s²4p¹

The screening tendency of d-electrons is poor. Thus, On moving from Al to Ga, shielding effect of 10 d-electrons is unable to compensate increased nuclear charge. Therefore, atomic radius of Ga is smaller than that of aluminium due to effective nuclear charge.

Question 25.
What are allotropes? Sketch the structure of two allotropes of carbon namely diamond and graphite. What is the impact of structure on physical properties of two allotropes?
Answer:
The phenomenon of existence of an element in two or more forms which differ in physical properties but have almost same chemical nature is known as allotropy and the different forms of the element are known as allotropes.

Crystalline carbon occurs mainly in two allotropic forms (i) graphite and (ii) diamond. A third allotropic form of carbon called fullerene was discovered in 1985 by H.W. Kroto, E. Smalley and R.F. Curl.

In diamond, each carbon is sp³ hybridised and is linked to other four atoms tetrahedrally. There is three dimensional network of carbon atoms in diamond. In graphite, each carbon is sp² hybridised and makes three sigma bonds with three neighbouring carbon atoms. It has layered structure and the layers are held by weak van der Waals’ forces.

Impact of the structures of diamond and graphite on physical properties of the two allotropes are as follows :

1. Diamond because of its h. iness, is used as an abrasive and in making dyes while graphite is soft that it marks paper and it is used as a dry lubricant in machines.
2. Diamond does not conduct electricity whereas graphite is a good conductor of electricity because of the presence of one free electron in each carbon atom.
3. Diamond is transparent while graphite is opaque.

Question 26.
(a) Classify following oxides as neutral, acidic, basic or amphoteric:
CO, B₂O₃, SiO₂, CO₂, Al₂O₃, PbO₂, Tl₂O₃
(b) Write suitable chemical equations to show their nature. Answer: (a) CO is neutral oxide.
B₂O₃, SiO₂, CO₂ are acidic oxides.
PbO₂ Al₂O₃ are amphoteric oxides.
Tl₂O₃ is basic oxide.

(b) (i) Being acidic B₂O₃, SiO₂ and CO₂ react with alkalis to form salts.
B₂O₃ + CuO → CU(BO₂)₂
SiO₂ + 2NaOH → Na₂SiO₃ + H₂O
CO₂ + H₂O → H₂CO₃

(ii) Being amphoteric PbO₂ and Al₂O₃ react with both acids and basses.
PbO₂ + 4HCl → PbCl₄ + 2H₂O
PbO₂ + 2NaOH → Na₂PbO₃ + H₂O
Al₂O₃ + 6HCl → 2AlCl₃ + 3H₂O
Al₂O₃ + 2NaOH → 2NaAlO₂ + H₂O

(iii) Being basic Tl₂O₃ react with acid
Tl₂O₃ + 3H₂SO₄ → Tl₂(SO₄)₃ + 3H₂O

Question 27.
In some of the reactions thallium resembles aluminium, whereas in others it resembles with group I metals. Support this statement by giving some evidences.
Answer:
Thallium belongs to group 13 of the periodic table. The most common oxidation state for this group is +3. However, heavier members of this group also display the +1 oxidation state. This happens because of the inert pair effect. Aluminium displays the +3 oxidation state and alkali metals display the +1 oxidation state. Thallium displays both the oxidation states. Therefore, it resembles both aluminium and alkali metals.
Thallium, like aluminium, forms compounds such as TlCl₃ and Tl₂O₃. It resembles alkali metals in compounds Tl₂0 and TlCl.

Question 28.
When metal X is treated with sodium hydroxide, a white precipitate (A) is obtained, which is soluble in excess of NaOH to give soluble complex (B). Compound (A) is soluble in dilute HC1 to form compound (C). The compound (A) when heated strongly gives (D), which is used to extract metal. Identify (X), (A), (B), (C) and (D). Write suitable equations to support their identities.
Answer:
The given metal X gives a white precipitate with sodium hydroxide and the precipitate dissolves in excess of sodium hydroxide. Hence, X must be aluminium.

The white precipitate (compound A) obtained is aluminium hydroxide. When an excess of the base is added the compound B formed is sodium tetrahydroxoaluminate (III).

Now, when dilute hydrochloric acid is added to aluminium hydroxide, aluminium chloride (compound C) is obtained.

Also, when compound A is heated strongly, it gives compound D. This compound is used to extract metal X. Aluminium metal is extracted from alumina. Hence, compound D must be alumina.

Question 29.
What do you understand by (a) inert pair effect (b) allotropy (c) catenation?
Answer:
(a) Inert pair effect : As one moves down the group, the tendency of s-block electrons to participate in chemical bonding decreases. This effect is known as inert pair effect. In case of group 13 elements, the electronic configuration is ns² np¹ and their group valency is +3. However, on moving down the group, the +1 oxidation state becomes more stable. This happens because of the poor shielding of the ns² electrons by the d-and f-electrons. As a result of the poor shielding, the ns² electrons are held tightly by the nucleus and so, they cannot participate in chemical bonding.

(b) Allotropy : Allotropy is the existence of an element in more than one form, having the same chemical properties but different physical properties. The various forms of an element are called allotropes. For example, carbon exists in three allotropic forms: diamond, graphite, and fullerenes.

(c) Catenation : The atoms of some elements (such as carbon) can link with one another through strong covalent bonds to form long chains or branches. This property is known as catenation. It is most common in carbon and quite significant in Si and S. *

Question 30.
A certain salt X, gives the following results :
(i) Its aqueous solution is alkaline to litmus.
(ii) It swells up to a glassy material Y on strong heating.
(iii) When cone. H₂SO₄ is added to a hot solution of X, white crystal of an acid Z separates out.
Write equations for all the above reactions and identify X, Y and z.
Answer:
(i) Aqueous solution of salt X is alkaline. It indicates that ‘X’ is the salt of a strong base and a weak acid.
(ii) On strong heating, the salt ‘X’ swells up to a glassy material Y. It indicates that the salt ‘X’ is borax.
(iii) Hot aqueous solution of borax on reaction with cone. H₂SO₄ gives crystals of orthoboric acid.
The equations for the reactions involved in the question are as follows :

Question 31.
Write balanced equations for:
(i) BF₃ + LiH
(ii) B₂H₆ + H₂O
(iii) NaH + B₂H₆
(iv) im
(v) Al + NaOH
(vi) B₂H₆ + NH₃
Answer:

Question 32.
Give one method for industrial preparation and one for laboratory preparation of CO and CO₂ each.
Answer:
Carbon monoxide : In the laboratory, CO is prepared by the dehydration of formic acid with cone. H2S04 at 373 K. The reaction involved is as follows :

CO is commercially prepared by passing steam over hot coke. The reaction involved is as follows:

Carbon dioxide : In the laboratory, CO₂ can be prepared by the action of dilute hydrochloric acid on calcium carbonate. The reaction involved is as follows:
CaCO₃ + 2HCl(aq) → CaCl₂(aq) + CO₂(g) + H₂O(l)

CO₂ is commercially prepared by heating limestone. The reaction involved is as follows:

Question 33.
An aqueous solution of borax is
(a) neutral
(b) amphoteric
(c) basic
(d) acidic
Answer:
(c) Borax is a salt of a strong base (NaOH) and weak acid (H₃BO₃). It is, therefore, basic in nature.

Question 34.
Boric acid is polymeric due to
(a) its acidic nature
(b) the presence of hydrogen bonds
(c) its monobasic nature
(d) its geometry
Answer:
(b) Boric acid is polymeric because of the presence of hydrogen bonds, (as it has polar O—H bonds)

Question 35.
The type of hybridisation of boron in diborane is (a) sp (b) sp² (c) sp³ (d) dsp²
Answer:
(c) Boron in diborane is sp3 hybridised.

Question 36.
Thermodynamically the most stable form of carbon is
(a) diamond
(b) graphite
(c) fullerenes
(d) coal
Answer:
(b) Graphite is thermodynamically the most stable form of carbon.

Question 37.
Elements of group 14
(a) exhibit oxidation state of +4 only
(b) exhibit oxidation state of +2 and +4
(c) formM^2- and M⁴⁺ ions
(d) formM²⁺ and M⁴⁺ ions
Answer:
(b) The elements of group 14 have 4 valence electrons. Therefore, the oxidation state of the group is +4. However, as a result of the inert pair effect, the lower oxidation state becomes more and more stable and the higher oxidation state becomes less stable. Therefore, this group exhibits +4 and +2 oxidation states.

Question 38.
If the starting material for the manufacture of silicones is RSiCl3, write the structure of the product formed.
Answer:
Hydrolysis of alkyltrichlorosilanes followed by condensation polymerisation gives cross-linked silicones.

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 10 The s-Block Elements Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 10 The s-Block Elements

PSEB 11th Class Chemistry Guide The s-Block Elements InText Questions and Answers

Question 1.
What are the common physical and chemical features of alkali metals?
Answer:
Physical properties of alkali metals are as follows :

1. They are quite soft and can be cut easily. Sodium metal can be easily cut using a knife.
2. They are light coloured and are mostly silvery white in appearance.
3. They have low density because of the large atomic sizes. The density increases down the group from Li to Cs. The only exception to this is K, which has lower density than Na.
4. The metallic bonding present in alkali metals is quite weak. Therefore they have low melting and boiling points.
5. Alkali metals and their salts impart a characteristic colour to flames. This is because the heat from the flame excites the electron present in the outermost orbital to a high energy level. When this excited electron reverts back to the ground state, it emits excess energy as radiation that falls in the visible region.
6. They also display photoelectric effect. When metals such as Cs and K are irradiated with light, they lose electrons.

Chemical properties of alkali metals are as follows :

Alkali metals are highly reactive due to their low ionization enthalpy. As we move down the group, the reactivity increases.
(1) They react with water to form respective oxides or hydroxides. As we move down the group, the reaction becomes more and more spontaneous.

(2) They react with water to form their respective hydroxides and dihydrogens. The general reaction for the same is given as :
2M + 2H²O → 2M⁺ + 2OH^– + H₂

(3) They react with dihydrogen to form metal hydrides. These hydrides are ionic solids and have high melting points.
2M + H₂ → 2M⁺ H^–

(4) Almost all alkali metals, except Li, react directly with halogens to form ionic halides.
2M + Cl₂ → 2MCl (M = Li, K, Rb, Cs)

Since Li⁺ ion is very small in size, it can easily distort the electron cloud around the negative halide ion. Therefore lithium halides are covalent in nature.

(5) They are strong reducing agents. The reducing power of alkali metals increases on moving down the group.
However, lithium is an exception. It is the strongest reducing agent among the alkali metals. It is because of its high hydration energy.

(6) They dissolve in liquid ammonia to form deep blue coloured solutions. Therefore, these solutions are conducting in nature.
M + (x + y) NH₃ → [M(NH₃)_x]⁺[M(NH₃)_y]^–

The ammoniated electrons cause the blue colour of the solution. These solutions are paramagnetic and if allowed to stand for some time, then they liberate hydrogen. This results in the formation of amides.
M⁺ + e^– + NH₃(l) → MNH + \(\frac{1}{2}\)H₂(g)

In a highly concentrated solution, the blue colour changes to bronze and the solution becomes diamagnetic.

Question 2.
Discuss the general characteristics and gradation in properties of alkaline earth metals.
Answer:
Physical and atomic properties of alkaline earth metals are as follows:

• The general electronic configuration of alkaline earth metals is (noble gas) ns².
• These metals lose two electrons to acquire the nearest noble gas configuration. Therefore, their oxidation state is +2.
• These metals have atomic and ionic radii smaller than that of alkali metals. Also when moved down the group, the effective nuclear charge decreases and this causes an increase in their atomic radii and ionic radii.
• Since the alkaline earth metals have large size, their ionization enthalpies are found to be fairly low. However, their first ionization enthalpies are higher than the corresponding group 1 metals.
• These metals are lustrous and silvery white in appearance. They are relatively less soft as compared to alkali metals.
• Atoms of alkaline earth metals are smaller than that of alkali metals. Also they have two valence electrons forming stronger metallic bonds. These two factors cause alkaline earth metals to have high melting and boiling points as compared to alkali metals.
• They are highly electropositive in nature. This is due to their low ionization enthalpies. Also the electropositive character increases on moving down the group from Be to Ba.
• Ca, Sr, and Ba impart characteristic colours to flames.
  Ca – Brick red Sr – Crimson red Ba – Apple green
  In Be and Mg, the electrons are too strongly bound to be excited. Hence, these do not impart any colour to the flame.

Chemical properties of alkaline earth metals are as follows :
The alkaline earth metals are less reactive than alkali metals and their reactivity increases on moving down the group.

(i) Reaction with air and water : Be and Mg are almost inert to air and water because of the formation of oxide layer on their surface.
(a) Powdered Be burns in air to form BeO and Be₃N₂.
(b) Mg, being more electropositive, burns in air with a dazzling sparkle to form MgO and Mg₃N₂.
(c) Ca, Sr, and Ba react readily with air to form respective oxides and nitrides.
(d) Ca, Ba, and Sr react vigorously even with cold water.

(ii) Alkaline earth metals react with halogens at high temperatures to form halides.
M + X₂ → MX₂ (X = F, Cl, Br, I)
(iii) All the alkaline earth metals, except Be, react with hydrogen to form hydrides.
(iv) They react readily with acids to form salts and liberate hydrogen gas.
M + 2HCl → MCl₂ + H₂(g) ↑
(v) They are strong reducing agents. However, their reducing power is less than that of alkali metals. As we move down the group, the reducing power increases.
(vi) Similar to alkali metals, the alkaline earth metals also dissolve in liquid ammonia to give deep blue coloured solutions.
M + (x – y) NH₃ → [M (NH₃)_x]²⁺ + 2 [e (NH₃)_y]^–

Question 3.
Why are alkali metals not found in nature?
Answer:
Alkali metals include lithium, sodium, potassium, rubidium, cesium, and francium. These metals have only one electron in their valence shell, which they lose easily, owing to their low ionization energies. Therefore, alkali metals are highly reactive and are not found in nature in their elemental state.

Question 4.
Find out the oxidation state of sodium in Na₂O₂.
Answer:
Let the oxidation state of Na be x. The oxidation state of oxygen, in case of peroxides, is -1.
Therefore, 2(x) + 2(-1) = 0 ⇒ 2x – 2 = 0 ⇒ 2x = 2 ⇒ x = ±1
Therefore, the oxidation state of sodium in Na₂O₂ is +1.

Question 5.
Explain why is sodium less reactive than potassium?
Answer:
In alkali metals, on moving down the group, the atomic size increases and the effective nuclear charge decreases.
Because of these factors, the outermost electron in potassium can be lost easily as compared to sodium. Hence, potassium is more reactive than sodium.

Question 6.
Compare the alkali metals and alkaline earth metals with respect to (i) ionization enthalpy (ii) basicity of oxides and (iii) solubility of hydroxides.
Answer:

• Ionization enthalpies : The first ionization enthalpies of the alkaline earth metals are higher than those of the corresponding alkali metals. This is due to their small size as compared to the corresponding alkali metals. But second ionization enthalpies of the alkaline earth metals are smaller than those of the corresponding alkali metals.
• Basicity of oxides : The oxides of the alkali and alkaline earth metals dissolves in water to form basic hydroxides. The alkaline earth metal hydroxides are however less basic and less stable than alkali metal hydroxides.
• Solubility of hydroxides : The solubility of hydroxides of alkaline earth metals is relatively less than their corresponding alkali metal hydroxides.

Question 7.
In what ways lithium shows similarities to magnesium in its chemical behaviour?
Answer:
Similarities between lithium and magnesium are as follows :
(i) Both Li and Mg react slowly with cold water.
(ii) The oxides of both Li and Mg are much less soluble in water and their hydroxides decompose at high temperature.
im 1

(iii) Both Li and Mg react withN2 to form nitrides.
im 2

(iv) Neither Li nor Mg form peroxides or superoxides.
(v) The carbonates of both are covalent in nature. Also, these decompose on heating.
im 3

(vi) Li and Mg do not form solid bicarbonates.
(vii) Both LiCl and MgCl₂ are soluble in ethanol owing to their covalent nature.
(viii) Both LiCl and MgCl₂ are deliquescent in nature. They crystallize from aqueous solutions as hydrates, for example, LiCl.₂H₂O and MgCl₂ . 8H₂O.

Question 8.
Explain why can alkali and alkaline earth metals not be obtained by chemical reduction methods?
Answer:
In the process of chemical reduction, oxides of metals are reduced using a stronger reducing agent. Alkali metals and alkaline earth metals are among the strongest reducing agents and the reducing agents that are stronger than them are not available. Therefore, they cannot be obtained by chemical reduction of their oxides.

Question 9.
Why are potassium and caesium, rather than lithium used in photoelectric cells?
Answer:
Potassium and caesium have much lower ionization enthalpy than that of lithium. Therefore, these metals on exposure to light emit electrons easily but lithium does not. That’s why K and Cs rather than Li are used in photoelectric cells.

Question 10.
When an alkali metal dissolves in liquid ammonia the solution can acquire different colours. Explain the reasons for this type of colour change.
Answer:
When an alkali metal is dissolved in liquid ammonia, it results in the formation of a deep blue coloured solution.
M + (x + y) NH₃ → [M (NH₃)_x]⁺ + [e^-1 (NH₃)_y] [Ammoniated electron]
The ammoniated electrons absorb energy corresponding to red region of visible light. Therefore, the transmitted light is blue in colour.
At a higher concentration (3 M), clusters of metal ions are formed. This causes the solution to attain a copper-bronze colour and a characteristic metallic lustre.

Question 11.
Beryllium and magnesium do not give colour to flame whereas other alkaline earth metals do so. Why?
Answer:
When an alkaline earth metal is heated, the valence electrons get excited to a higher energy level. When this excited electron comes back to its lower energy level, it radiates energy, which belongs to the visible region. Hence, the colour is observed. In Be and Mg, the electrons are strongly bound. The energy required to excite these electrons is very high. Therefore, when the electron reverts back to its original position the energy released does not fall in the visible region. Hence, no colour in the flame is seen.

Question 12.
Discuss the various reactions that occur in the Solvay process.
Answer:
In Solvay ammonia process, CO₂ is passed through brine, (a concentrated solution of NaCl) saturated with ammonia. The process involves the formation of a sparingly soluble sodium bicarbonate.
NaCl + NH₃ + CO₂ + H₂O → NaHCO₃↓ + NH₄Cl .
Sodium bicarbonate thus formed is filtered, dried and heated to obtain sodium carbonate.
im 4
CO₂ used in carbonating tower is prepared by heating calcium carbonate and the quicklime, CaO thus formed is dissolved in water to form slaked lime, Ca(OH)₂.
im 5
In ammonia recovery tower, NH3 is prepared by heating NH₄Cl with Ca(OH)₂.
im 6

Question 13.
Potassium carbonate cannot be prepared by Solvay process. Why?
Answer:
Solvay process cannot be used to prepare potassium carbonate. This is because unlike sodium bicarbonate, potassium bicarbonate is fairly soluble in water and does not precipitate out.

Question 14.
Why is Li₂CO₃ decomposed at a lower temperature whereas Na₂CO₃ at higher temperature?
Answer:
As we move down the alkali metal group, the electropositive character increases. This causes an increase in the stability of alkali carbonates.
However, lithium carbonate is not so stable to heat. This is because lithium carbonate is covalent. Lithium ion, being very small in size, polarizes a large carbonate ion, leading to the formation of more stable lithium oxide.
im 7
Therefore, lithium carbonate decomposes at a low temperature while a stable sodium carbonate decomposes at a high temperature.

Question 15.
Compare the solubility and thermal stability of the following compounds of the alkali metals with those of the alkaline earth metals (a) Nitrates (b) Carbonates (c) Sulphates.
Answer:
(a) Nitrates of alkali metals and alkaline earth metals :
(i) Nitrates of alkali metals are thermally not stable and decompose on heating to give MNO₂ and O₂ (except LiN03) whereas nitrates of alkaline earth metals decompose on heating give their oxides, nitrogen dioxide and oxygen gas.

im 8

(ii) Nitrates of alkali metals are highly soluble in water whereas alkaline earth metal nitrates are sparingly soluble and crystallise with six molecules of water.
(b) Carbonates of alkali metals and alkaline earth metals:
(i) Carbonates of alkali metals except Li are quite stable upto 1273 K and do not decompose, whereas carbonates of alkaline earth metals decompose at different temperatures, to give their oxides and carbon dioxide.

im 9

The thermal stability of carbonates of alkaline earth metals increase down the group.
BeCO₃ is least stable and BaCO₃ is most stable.

(ii) All the carbonates of alkali metals are generally soluble in water and their solubility increases rapidly on descending the group. This is due to the reason that their lattice energies decrease more rapidly than their hydration energies down the group. In the case of carbonates of alkaline earth metals they are sparingly soluble in water and their solubility decreases down the group from Be to Ba. For example, MgCO₃ is slightly soluble in water, but BaC03 is almost insoluble.

(c) Sulphates of alkali metals and alkaline earth metals :
(i) The sulphates of alkali metals are thermally quite stable whereas the sulphates of alkaline earth metals decompose on heating to give oxides and SO₃. The temperature of decomposition increases
down the group.
im 10

(ii) The sulphates of alkali metals Na and K are soluble in water. As far as the solubility of sulphates of alkaline earth metals in water is concerned, BeSO₄ and MgSO₄ are highly soluble, CaSO₄ is sparingly soluble, but the sulphates of Sr, Ba and Ra are virtually insoluble. Thus, the solubility of their sulphates in water decreases down the group.
BeSO₄ > MgSO₄ > CaSO₄ > SiSO₄ > BaSO₄

Question 16.
Starting with sodium chloride how would you proceed to prepare (i) sodium metal (ii) sodium hydroxide (iii) sodium peroxide (iv) sodium carbonate?
Answer:
(i) Sodium metal from sodium chloride: Sodium is prepared from fused (molten) sodium chloride. Sodium chloride is mixed with CaCl₂ and KF [to lower the M.Pt. of NaCl to 850-875 K] and subjected to electrolysis (in DOWN’S CELL) when the following reactions occur :

im 11

Sodium, liberated at the cathode, is collected in kerosene oil and chlorine gas is liberated at the anode.
(ii) Sodium hydroxide from sodium chloride: Sodium hydroxide (caustic soda) is generally prepared by the electrolysis of brine solution (NaCl solution in water) in Castner Kellner cell. A mercury cathode and carbon anode are used. Sodium metal discharged at the cathode combines with mercury to form sodium amalgam. Cl₂ gas is evolved at the anode.

im 12

The amalgam is treated with water to give sodium hydroxide and hydrogen gas.
2Na – amalgam + 2H₂O → 2NaOH + 2Hg + H₂↑

(iii) Sodium peroxide from sodium chloride: Sodium metal obtained, by the electrolysis of molten sodium chloride is heated with O₂ at about 575 K when sodium forms mainly sodium peroxide.

im 13

(iv) Sodium carbonate from sodium chloride: Sodium carbonate is prepared from an aqueous solution of NaCl by SOLVAY PROCESS. In this process, CO₂ is passed through NaCl solution saturated with ammonia, when following reactions occur :

2NH₃ + H₂O + CO₂ → (NH₄)₂ CO₃
(NH₄)₂ CO₃ + H₂O + CO₂ → 2NH₄HCO₃
NH₄HCO₃ + NaCl → NH₄Cl + NaHCO₃
im 14

Question 17.
What happens when (i) magnesium is burnt in air (ii) quick lime is heated with silica (iii) chlorine reacts with slaked lime (iv) calcium nitrate is heated?
Answer:
(i) Magnesium bums in air with a dazzling light to form MgO and Mg3N₂.
im 15

(ii) Quick lime (CaO) combines with silica (SiO₂) to form slag.
im 16

(iii) When chlorine is added to slaked lime, it gives bleaching powder.
im 17

(iv) Calcium nitrate, on heating decomposes to give calcium oxide.
im 18

Question 18.
Describe two important uses of each of the following (i) caustic soda (ii) sodium carbonate (iii) quicklime.
Answer:
(i) Uses of caustic soda
(a) It is used in soap industry.
(b) It is used as a reagent in laboratory.
(ii) Uses of sodium carbonate
(a) It is generally used in glass and soap industry.
(b) It is used as a water softener.
(iii) Uses of quick lime
(a) It is used as a starting material for obtaining slaked lime.
(b) It is used in the manufacture of glass and cement.

Question 19.
Draw the structure of (i) BeCl₂ (vapour) (ii) BeCl₂ (solid).
Answer:
(i) In the vapour state, BeCl₂ exists as a monomer with a linear structure.
im 19

(ii) In the solid state, BeCl₂ exists as a polymer in condensed phase.
im 20

Question 20.
The hydroxides and carbonates of sodium and potassium are easily soluble in water while the corresponding salts of magnesium and calcium are sparingly soluble in water. Explain.
Answer:
The atomic size of sodium and potassium is larger than that of magnesium and calcium. Thus, the lattice energies of carbonates and hydroxides formed by calcium and magnesium are much more than those of sodium and potassium.
Hence, carbonates and hydroxides of sodium and potassium dissolve readily in water whereas those of calcium and magnesium are only sparingly soluble.

Question 21.
Describe the importance of the following (i) limestone (ii) cement (iii) plaster of paris.
Answer:
(i) Importance of limestone
(a) It is used in the preparation of lime and cement.
(b) It is used as a flux during the smelting of iron ores.

(ii) Importance of cement
(a) It is used in plastering and in construction of bridges.
(b) It is used in concrete.

(iii) Importance of plaster of Paris
(a) It is used in surgical bandages.
(b) It is also used for making casts and moulds.

Question 22.
Why are lithium salts commonly hydrated and those of the other alkali ions usually anhydrous?
Answer:
Because of its smallest size among alkali metals, Li+ has the maximum degree of hydration. That’s why lithium salts are commonly hydrated and those of other alkali metal ions usually anhydrous.
im 21

Question 23.
Why is LiF almost insoluble in water whereas LiCl soluble not only in water but also in acetone?
Answer:
LiF is insoluble in water. On the contrary, LiCl is soluble not only in water, but also in acetone. This is mainly because of the greater ionic character of LiF as compared to LiCl. The solubility of a compound in water depends on the balance between lattice energy and hydration energy. Since fluoride ion is much smaller in size than chloride ion, the lattice energy of LiF is greater than that of LiCl. Also there is not much difference between the hydration energies of fluoride ion and chloride ion. Thus, the net energy change during the dissolution of LiCl in water is more exothermic than that during the dissolution of LiF in water. Hence, low lattice energy and greater covalent character are the factors making LiCl soluble not only in water, but also in acetone.

Question 24.
Explain the significance of sodium, potassium, magnesium and calcium in biological fluids.
Answer:
(i) Sodium (Na):
Sodium ions are found primarily in the blood plasma. They are also found in the interstitial fluids surrounding the cells.
(a) Sodium ions help in the transmission of nerve signals.
(b) They help in regulating the flow of water across the cell membranes.
(c) They also help in transporting sugars and amino acids into the cells.

(ii) Potassium (K):
Potassium ions are found in the highest quantity within the cell fluids.
(a) K⁺ ions help in activating many enzymes.
(b) They also participate in oxidising glucose to produce ATP.
(c) They also participate in transmitting nerve signals.

(iii) Magnesium (Mg) and calcium (Ca) :
Magnesium and calcium are referred to as macro-minerals. This term indicates their higher abundance in the human body system.
(a) Mg helps in relaxing nerves and muscles.
(b) Mg helps in building and strengthening bones.
(c) Mg maintains normal blood circulation in the human body system.
(d) Ca helps in the coagulation of blood.
(e) Ca also helps in maintaining homeostasis.

Question 25.
What happens when
(i) sodium metal is dropped in water?
(ii) sodium metal is heated in free supply of air?
(iii) sodium peroxide dissolves in water?
Answer:
(i) When sodium metal is dropped in water, it reacts violently to form sodium hydroxide and hydrogen gas. The chemical equation involved in the reaction is:
2Na(s) + 2H₂O(l) → 2NaOH(aq) + H₂(g)
(ii) On being heated in air, sodium reacts vigorously with oxygen to form sodium peroxide. The chemical equation involved in the reaction is:
2Na(s) + O₂(g) → Na₂O₂(s)
(iii) When sodium peroxide is dissolved in water, it is readily hydrolysed to form sodium hydroxide and water. The chemical equation involved in the reaction is:
Na₂O₂(s) + 2H₂O(7) → 2NaOH(aq) + H₂O₂(aq)

Question 26.
Comment on each of the following observations:
(a) The mobilities of the alkali metal ions in aqueous solution are Li⁺ < Na⁺ < K⁺ < Rb⁺ < Cs⁺
(b) Lithium is the only alkali metal to form a nitride directly.
(c) \(\mathbf{H}^{\ominus}\) for M²⁺ (aq) + 2e^– → M(s) (where M = Ca, Sr or Ba) is nearly constant.
Answer:
(a) On moving down the alkali group, the ionic and atomic sizes of the metals increase. The given alkali metal ions can be arranged in the increasing order of their ionic sizes as:
Li⁺ < Na⁺ < K⁺ < Rb⁺ < Cs⁺

Smaller the size of an ion, the more highly is it hydrated. Since, Li⁺ is the smallest, it gets heavily hydrated in an aqueous solution. On the other hand, Cs+ is the largest and so it is the least hydrated. The given alkali metal ions can be arranged in the decreasing order of their hydrations as:
Li⁺ > Na⁺ > K⁺ > Rb⁺ > Cs⁺
Greater the mass of a hydrated ion, the lower is its ionic mobility. Therefore, hydrated Li⁺ is the least mobile and hydrated Cs⁺ is the most mobile. Thus, the given alkali metal ions can be arranged in the increasing order of their mobilities as:
Li⁺ < Na⁺ < K⁺ < Rb⁺ < Cs⁺

(b) Unlike the other elements of group 1, Li reacts directly with nitrogen to form lithium nitride. This is because Li⁺ is very small in size and so its size is the most compatible with the N^3- ion. Hence, the lattice energy released is very high. This energy also overcomes the high amount of energy required for the formation of the N^3- ion.

(c) Electrode potential (\(\mathbf{E}^{\ominus}\)) of any M²⁺/M electrode depends upon three factors :
(i) Ionisation enthalpy
(ii) Enthalpy of hydration
(iii) Enthalpy of vaporisation
The combined effect of these factors is approximately the same for Ca, Sr, and Ba. Hence, their electrode potentials are nearly constant.

Question 27.
State as to why
(a) a solution of Na₂CO₃ is alkaline?
(b) alkali metals are prepared by electrolysis of their fused chlorides?
(c) sodium is found to be more useful than potassium?
Answer:
(a) When sodium carbonate is added to water, it hydrolyses to give sodium bicarbonate and sodium hydroxide (a strong base). As a result, the solution becomes alkaline.
Na₂CO₃ + H₂O → NaHCO₃ + NaOH

(b) It is not possible to prepare alkali metals by the chemical reduction of their oxides as they themselves are very strong reducing agents. They cannot be prepared by displacement reactions either (wherein one element is displaced by another). This is because these elements are highly electropositive. Electrolysis of aqueous solutions can neither be used to extract these elements. This is because the liberated metals react with water. Hence, to overcome these difficulties, alkali metals are usually prepared by the electrolysis of their fused chlorides.

(c) Blood plasma and the interstitial fluids surrounding the cells are the regions where sodium ions are primarily found. Potassium ions are located withimthe cell fluids. Sodium ions are involved in the transmission of nerve signals, in regulating the flow of water across the cell membranes, and in transporting sugars and amino acids into the cells. Hence, sodium is found to be more useful than potassium.

Question 28.
Write balanced equations for reactions between
(a) Na₂O₂ and water
(b) KO₂ and water
(c) Na₂O and CO₂
Answer:
(a) The balanced chemical equation for the reaction between Na202 and water is:
Na₂O₂(s) + 2H₂O(l) → 2NaOH(aq) + H₂O₂(aq)

(b) The balanced chemical equation for the reaction between K02 and water is:
2KO₂(s) + 2H₂O(l) → 2KOH(aq) + H₂O₂(aq) + O₂(g)
or 4KO₂(s) + 2H₂O(l) → 4KOH(aq) + 3O₂(g)

(c) The balanced chemical equation for the reaction between Na₂O and CO₂ is:
Na₂O(s) + CO₂(g) + Na₂CO₃

Question 29.
How would you explain the following observations?
(i) BeO is almost insoluble but BeSO₄ is soluble in water, ‘
(ii) BaO is soluble but BaSO₄ is insoluble in water,
(iii) Lil is more soluble than KI in ethanol.
Answer:
(i) BeO is almost insoluble in water and BeSO₄ is soluble in water. Be²⁺ is a small cation with a high polarising power and O^2- is a small anion. The size compatibility of Be²⁺ and O^2- is high. Therefore, the lattice energy released during their formation is also very high. When BeO is dissolved in water, the hydration energy of its ions is not sufficient to overcome the high lattice energy. Therefore, BeO is insoluble in water. On the other hand, \(\mathrm{SO}_{4}^{2-}\) ion is a large anion. Hence, Be²⁺ can easily polarise \(\mathrm{SO}_{4}^{2-}\) ions, making BeSO₄ unstable. Thus, the lattice energy of BeSO₄ is not very high and so it is soluble in water.

(ii) BaOis soluble in water, but BaSO₄ is not. Ba²⁺ is a large cation and O^2- is a small anion. The size compatibility of Ba²⁺ and O^2- is not high. As a result, BaO is unstable. The lattice energy released during its formation is also not very large. It can easily be overcome by the hydration energy of the ions. Therefore, BaO is, soluble in water. In BaSO₄, Ba+ and \(\mathrm{SO}_{4}^{2-}\) are both large-sized. The lattice energy released is high. Hence, it is not soluble in water.

(iii) Lil is more soluble than KI in ethanol. As a result, due to its small size, the lithium ion has a higher polarising power than the potassium ion. It polarises the electron cloud of the iodide ion to a much greater extent than the potassium ion. This causes a greater covalent character in Li than in KI. Hence, Lil is more soluble in ethanol.

Question 30.
Which of the alkali metal is having least melting point?
(a) Na (b) K (c) Rb (d) Cs
Answer:
(d) Atomic size increases as we move down the alkali group. As a result, the binding energies of their atoms in the crystal lattice decrease. Also, the strength of metallic bonds decreases on moving down a group in the periodic table.
This causes a decrease in the melting point. Among the given metals, Cs is the largest and has the least melting point.

Question 31.
Which one of the following alkali metals gives hydrated salts?
(a) Li (b) Na (c) K (d) Cs
Answer:
(a) Smaller the size of an ion, the more highly is it hydrated. Among the given alkali metals, Li is the smallest in size. Also, it has the highest charge density and highest polarising power. Hence, it attracts water molecules more strongly than the other alkali metals. As a result, it forms hydrated salts such as LiCl . 2 H2O. The other alkali metals are larger than Li and have weaker charge densities. Hence, they usually do not form hydrated salts.

Question 32.
Which one of the alkaline earth metal carbonates is thermally the most stable?
(a) MgCO₃
(b) CaCO₃
(c) SrCO₃
(d) BaCO₃
Answer:
(d) Thermal stability increases with the increase in the size of the cation present in the carbonate. The increasing order of the cationic size of the given alkaline earth metals is
Mg < Ca < Sr < Ba
Hence, the increasing order of the thermal stability of the given alkaline earth metal carbonates is
MgCO₃ < CaCO₃ < SrCO₃ < BaCO₃

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 9 Hydrogen Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 9 Hydrogen

PSEB 11th Class Chemistry Guide Hydrogen InText Questions and Answers

Question 1.
Justify the position of hydrogen in the periodic table on the basis of its electronic configuration.
Answer:
Hydrogen is the first element in the periodic table. It has the electronic configuration 1s¹. It is similar to alkali metal (ns¹) of group I. It shows resemblance with alkali metals of group I of the periodic table. So it can be placed above the alkali metals in group I of the periodic table.
On the other hand, the electronic configuration of hydrogen shows that it is short of one electron to the nearest noble gas configuration (He) having the electronic configuration 1s². Like halogens it forms covalent bonds (H₂, Cl₂, Br₂, etc.) as well as ionic bonds (e.g. Na⁺ H^–). It forms H⁺ ion by giving one electron and hydride ion (H^–) by gaining one electron. On the basis of its electronic configuration (1s²) hydrogen is placed with other ns¹ elements namely alkali metals in the group I as well as in group 17 of the periodic table. Thus, the position of hydrogen in the periodic table is anomalous.
Hydrogen with so many unique characteristics is, therefore best placed separately in the periodic table of elements.

Question 2.
Write the names of isotopes of hydrogen. What is the mass ratio of these isotopes?
Answer:
Hydrogen has following three isotopes :
1. Protium,\({ }_{1}^{1} \mathrm{H}\),
2. Deuterium, \({ }_{1}^{2} \mathrm{H}\) or D, and
3. Tritium, \({ }_{1}^{3} \mathrm{H}\) or T
The mass ratio of protium, deuterium and tritium is 1.008 : 2.014 : 3.016 or 1:2:3.

Question 3.
Why does hydrogen occur in a diatomic form rather than in a monoatomic form under normal conditions?
Answer:
The ionization enthalpy of hydrogen atom is very high (1312 kJ mol^-1). Hence, it is very hard to remove its electron. As a result, its tendency to exist in the monoatomic form is rather low. Instead, hydrogen forms a covalent bond with another hydrogen atom and exists as a diatomic (H₂) molecule.

Question 4.
How can the production of dihydrogen, obtained from ‘coal gasification’, be increased?
Answer:
Dihydrogen, produced by coal gasification method as :

The yield of dihydrogen (obtained from coal gasification) can be increased by reacting carbon monoxide (formed during the reaction) with steam in the presence of iron chromate as a catalyst.

This reaction is called the water-gas shift reaction. Carbon dioxide is removed by scrubbing it with a solution of sodium arsenite.

Question 5.
Describe the bulk preparation of dihydrogen by electrolytic method. What is the role of an electrolyte in this process?
Answer:
Electrolysis of acidified water using platinum electrodes gives dihydrogen.

The role of an electrolyte is to make water conducting.

Question 6.
Complete the following reactions :

Answer:

Question 7.
Discuss the consequences of high enthalpy of H-H bond in terms of chemical reactivity of dihydrogen.
Answer:
The ionization enthalpy of H-H bond is very high (1312 kJ mol^-1). This indicates that dihydrogen has a low tendency to form H+ ions. Its ionization enthalpy value is comparable to that of halogens. Hence, it forms diatomic molecules (H₂), hydrides with elements, and a large number of covalent bonds.
Since ionization enthalpy is very high, dihydrogen does not possess metallic characteristics (lustre, ductility, etc.) like metals.

Question 8.
What do you understand by (i) electron-deficient,
(ii) electron-precise, and (iii) electron-rich compounds of hydrogen? Provide justification with suitable examples.
Answer:
(i) An electron-deficient hydride : It has very few electrons, less than that required for representing its conventional Lewis structure e.g., diborane (B₂H₆). In B₂H₆, there are six bonds in all, out of which only four bonds are regular i.e., two electrons are shared by two atoms.
The remaining two bonds are three centered-two electron bonds i.e., two electrons are shared by three atoms. Hence, its conventional Lewis structure cannot be drawn.

(ii) An electron-precise hydride : It has sufficient number of electrons to be represented by its conventional Lewis structure e.g., CH₄. The Lewis structure can be written as :

Four regular bonds are formed where two electrons are shared by two atoms.

(iii) An electron-rich hybride : It contains excess electrons as lone pair e.g., NH₃

There are three regular bonds in all with a lone pair of electrons on the nitrogen atom.

Question 9.
What characteristics do you expect from an electron-deficient hydride with respect to its structure and chemical reactions?
Answer:
These hydrides do not have sufficient number of electrons to form normal covalent bonds, e.g., B in BF₃ has 6 electrons in its valence shell. These hydrides are trigonal planar in shape.

These hydrides act as Lewis acids, i.e., electron pair acceptor e.g.,

To make up the deficiency of electrons, these hydrides exist in polymeric forms e.g., B₂H₆, B₄H₁₀, etc. Electron deficient hydrides are very reactive. These reacts readily with metals and non-metals and their compounds, e.g.,

B₂H₆ + 3O₂(g) → B₂O₃(s) + 3H₂O(g)

Question 10.
Do you expect the carbon hydrides of the type (CraH2jt + 2) to act as ‘Lewis’ acid or base? Justify your answer.
Answer:
Carbon hydrides of the type C_nH_2n+2 are CH₄, C₂H₆ etc. in which number of electrons present are just sufficient to write down their conventional Lewis structures.

C has neither extra electrons nor less electrons. Such compounds of the formula C_nH_2n+2 are called ELECTRON-PRECISE compounds. They will act neither as Lewis acids nor as Lewis bases.

Question 11.
What do you understand by the term “non-stoichiometric hydrides”? Do you expect this type of the hydrides to be formed by alkali metals? Justify your answer.
Answer:
Non-stoichiometric hydrides are hydrogen-deficient compounds formed by the reaction of dihydrogen with d-block and f-block elements. These hydrides do not follow the law of constant composition.

For example :
LaH₂₈₇, YbH_2.55, TiH_{1.5 – 1.8} etc.
Alkali metals form stoichiometric hydrides. These hydrides are ionic in nature. Hydride ions have comparable sizes (208 pm) with alkali metal ions. Hence, strong binding forces exist between the constituting metal and hydride ion. As a result, stoichiometric hydrides are formed. Alkali metals will not form non-stoichiometric hydrides.

Question 12.
How do you expect the metallic hydrides to be useful for hydrogen storage? Explain.
Answer:
Metallic hydrides are hydrogen deficient, i.e., they do not hold the law of constant composition. It has been established that in the hydrides of Ni, Pd, Ce and Ac hydrogen occupies the interstitial position in lattices allowing further absorption of hydrogen on these metals. Metals like Pd, Pt, etc. have the capacity to accommodate a large volume of hydrogen. Therefore, they are used for the storage of hydrogen and serve as a source of energy.

Question 13.
How does the atomic hydrogen or oxy-hydrogen torch function for cutting and welding purposes? Explain.
Answer:
Atomic hydrogen atoms are produced by the dissociation of dihydrogen with the help of an electric arc. This releases a huge amount of energy (435.88 kJ mol^-1). This energy can be used to generate a temperature of 4000 K, which is ideal for welding and cutting metals. Hence, atomic k hydrogen or oxy-hydrogen torches are used for these purposes. For this reason, atomic hydrogen is allowed to recombine on the surface to be welded to generate the desired temperature.

Question 14.
Among NH₃, H₂O and HF, which would you expect to have highest magnitude of hydrogen bonding and why?
Answer:
The extent of hydrogen bonding depends upon electronegativity and the number of hydrogen atoms available for bonding. Among nitrogen, fluorine, and oxygen, the increasing order of their electronegativities are N < O < F. Hence, the order of the extent of hydrogen bonding is HF > H₂O > NH₃.

Question 15.
Saline hydrides are known to react with water violently producing fire. Can CO₂, a well known fire extinguisher, be used in this case? Explain.
Answer:
Saline hydrides (i.e., NaH, LiH, etc.) react with water to form a base and hydrogen gas. The chemical equation used to represent the reaction can be written as:
NaH(s) + H₂O(7) → NaOH(aq) + H₂(g)
This reaction is violent and produces fire.
This type of fire cannot be extinguished by CO₂ because it gets reduced by the hot metal hydride to form sodium format.
NaH + CO₂ → HCOONa

Question 16.
Arrange the following
(i) CaH₂, BeH₂ and TiH₂ in order of increasing electrical conductance.
(ii) LiH, NaH and CsH in order of increasing ionic character.
(iii) H-H, D-D and F-F in order of increasing bond dissociation enthalpy.
(iv) NaH, MgH₂ and H₂O in order of increasing reducing property.
Answer:
(i) BeH₂ < CaH₂ < TiH₂
(ii) LiH < NaH < CsH
(iii) F—F < H—H < D—D
(iv) H₂O < MgH₂ < NaH

Question 17.
Compare the structures of H₂O and H₂O₂.
Answer:
In gaseous phase, water molecule has a bent form with a bond angle of 104.5°. The O—H bond length is 95.7 pm. The structure can be shown as:

Hydrogen peroxide has a non-planar structure both in gas and solid phase. The dihedral angle in gas and solid phase is 111.5° and 90.2° respectively.

Question 18.
What do you understand by the term ‘auto-protolysis’ of water? What is its significance?
Answer:
Auto-protolysis (self-ionization) of water is a chemical reaction in which two water molecules react to produce a hydroxide ion (OH^–) and a hydronium ion (H₃O⁺).

The reaction involved can be represented as :

Auto-protolysis of water indicates its amphoteric nature i.e., its ability to act as an acid as well as a base. The acid-base reaction can be written as :

Question 19.
Consider the reaction of water with F₂ and suggest, in terms of oxidation and reduction, which species are oxidized/reduced.
Answer:

In these reactions, water acts as a reducing agent and hence itself gets oxidised to either oxygen or ozone. Fluorine acts as an oxidising agent and hence itself reduced to F^– ion.

Question 20.
Complete the following chemical reactions.
(i) PbS(s) + H₂O₂(ciq) →
(ii) MnO^–₄(aq) + H₂O₂(aq) →
(iii) CaO(s) + H₂O(g) →
(iv) AlCl₃(g) + H₂O(Z) →
(v) Ca₃N₂(s) + H₂O(l) →
Classify the above into (a) hydrolysis, (b) redox and (c) hydration reactions.
Answer:
(i) PbS(s) + 4H₂O₂(aq) → PbSO₄(s) + 4H₂O(l)
H₂O₂ is acting as an oxidizing agent in the reaction. Hence, it is a redox reaction.

(ii) 2MnO₄^– (aq) + 5H₂O₂(Z) + 6H⁺(aq) → 2Mn²⁺(aq) + 8H₂O(Z) + 5O₂(g)
H₂O₂ is acting as a reducing agent in the acidic medium, thereby oxidizing MnO^–₄(aq). Hence, the given reaction is a redox reaction.

(iii) CaO(s) + H₂O(g) → Ca(OH)₂(aq)
The reactions in which a compound reacts with water to produce other compounds are called hydrolysis reactions. The given reaction is hydrolysis reaction.

(iv) AlCl₃(g) + 6H₂O(Z) → [Al(OH₂)₆]³⁺ (aq) + 3Cl^–(aq)
It is a hydration reaction, because A1C13 is hydrated to [Al(OH₂)₆]³⁺.

(v) Ca₃N₂(s) + 6H₂O(Z) → 3Ca(OH)₂(aq) + 2NH₃(aq)
The reactions in which a compounds reacts with water to produce other compounds are called hydrolysis reactions. The given reaction represents hydrolysis of Ca₃N₂.

Question 21.
Describe the structure of the common form of ice.
Answer:
Ice is the crystalline form of water. It takes a hexagonal form if crystallized at atmospheric pressure, but condenses to cubic form if the temperature is very low.
The three-dimensional structure of ice is represented as :

The structure is highly ordered and has hydrogen bonding. Each oxygen atom is surrounded tetrahedrally by four other oxygen atoms at a distance of 276 pm. The structure also contains wide holes that can hold molecules of appropriate sizes interstitially.

Question 22.
What causes the temporary and permanent hardness of water?
Answer:
Temporary hardness of water is due to the presence of soluble salts of magnesium and calcium in the form of hydrogen carbonates (MHCO₃, where M = Mg, Ca) in water.
Permanent hardness of water is due to the presence of soluble salts of calcium and magnesium in the form of chlorides in water.

Question 23.
Discuss the principle and method of softening of hard water by synthetic ion-exchange resins.
Answer:
The process of treating permanent hardness of water using synthetic resins is based on the exchange of cations (e.g., Na⁺, Ca²⁺, Mg²⁺ etc.) and anions (e.g.,Cl^– , \(\mathrm{SO}_{4}^{2-}\), \(\mathrm{HCO}_{3}^{-}\) etc.) present in water by H⁺ and OH^– ions respectively.

Synthetic resins are of two types :
1. Cation exchange resins
2. Anion exchange resins

Cation exchange resins are large organic molecules that contain the -SO₃H group. The resin is firstly changed to RNa (from ROS₃H) by treating it with NaCl. This resin then exchanges Na⁺ ions with Ca²⁺ and Mg²⁺ ions, thereby making the water soft.

2RNa + M²⁺ (aq) → R₂M(s) + 2Na⁺ (aq)

There are cation exchange resins in H+ form. The resins exchange H⁺ ions for Na⁺, Ca²⁺ and Mg²⁺ ions.

2RH + M²⁺ (aq) ⇌ MR₂(s) + 2H⁺(aq)

Anion exchange resins exchange OH- ions for anions like Cl^–, \(\) and \(\) present in water.

During the complete process, water first passes through the cation exchange process. The water obtained after this process is free from mineral cations and is acidic in nature.
This acidic water is then passed through the anion exchange process where OH^– ions neutralize the H⁺ ions and de-ionize the water obtained.

Question 24.
Write chemical reactions to show the amphoteric nature of water.
Answer:
Water is amphoteric in character. It behaves both as an acid as well as a base. With acids stronger than itself, it behaves as a base and with bases stronger than itself, it acts as an acid.

Question 25.
Write chemical reactions to justify that hydrogen peroxide can function as an oxidizing as well as reducing agent.
Answer:
Hydrogen peroxide, H₂O₂ acts as an oxidizing as well as a reducing agent in both acidic and alkaline media. Reactions involving oxidizing actions are :

Question 26.
What is meant by ‘demineralised’ water and how can it be obtained?
Answer:
Water which does not contain cations and anions is called ‘demineralised’ water. It is soft water. Demineralised water is obtained the same way as soft water is obtained from hard water. Demineralised or deionised water is obtained by passing hard water first through a cation exchange resin (RCOOH or RSO₃H) which removes Ca²⁺ and Mg²⁺ ions from hard water by exchanging them with H⁺ ions and then passing through an anion exchange resin which removes Cl^– and \(\mathrm{SO}_{4}^{2-}\) ions present in hard water by exchanging them with OH^– ions.

Question 27.
Is demineralised or distilled water useful for drinking purposes? If not, how can it be made useful?
Answer:
Water is an important part of life. It contains several dissolved nutrients that are required by human beings, plants and animals for survival.
Demineralised water is free from all soluble minerals. Hence, it is not fit for drinking.
It can be made useful only after the addition of desired minerals in specific amounts, which are important for growth.

Question 28.
Describe the usefulness of water in biosphere and biological systems.
Answer:
Water is essential for all forms of life. It constitutes around 65% of the human body and 95% of plants. Water plays an important role in the biosphere owing to its high specific heat, thermal conductivity, surface tension, dipole moment and dielectric constant.
The high heat of vaporization and heat of capacity of water helps in moderating the climate and body temperature of all living beings.
It acts as a carrier of various nutrients required by plants and animals for various metabolic reactions.
Water is also required for photosynthesis in plants which releases O₂ into the atmosphere.

Question 29.
What properties of water make it useful as a solvent? What types of compound can it (i) dissolve, and (ii) hydrolyse?
Answer:
Water because of its high dielectric constant (78.39) has the ability to dissolve most of the inorganic (ionic) compounds and is, therefore, regarded as a universal solvent. Whereas the solubility of ionic compounds takes place due to ion-dipole interactions (i.e., solvation of ions) the solubility of covalent compounds such as alcohols, amines, urea, glucose, sugar etc. takes place due to tendency of these molecules to form hydrogen bonds with water.

(i) It can dissolve both ionic compounds as well as covalent compounds which can form hydrogen bonds with water.
Ionic compounds whose lattice energy is lower than hydration energy get dissolved in water.
(ii) Water can hydrolyse many oxides (metallic and non-metallic), hydrides, carbides, nitrides, phosphides and many other salts e.g.,

CaO(s) + H₂O(l) → Ca(OH)₂
SO₂(g) + H₂O(l) → H₂SO₃(aq)
CaH₂(s) + 2H₂O(l) → Ca(OH)₂(uq) + 2H₂(g)
SiCl₄(l) + 4H₂O(l) → SiO₂ -2H₂O(s) + 4HCl(aq)
Al₄C₃ + 12H₂O(l) → 4Al(OH)₃ + 3CH₄
Ca₃P₂(s) + 6H₂O → 3Ca(OH)₂ + 2PH₃

Question 30.
Knowing the properties of H20 and DaO, do you think that D20 can be used for drinking purposes?
Answer:
Heavy water (D₂O) acts as a moderator, i.e., it slows the rate of a reaction. Due to this property of D₂O, it cannot be used for drinking purposes because it will slow down anabolic and catabolic reactions takes place in the body and lead to a casualty.

Question 31.
What is the difference between the terms ‘hydrolysis’ and ‘hydration’?
Answer:
Hydrolysis is defined as a chemical reaction in which hydrogen and hydroxide ions (H+ and OH- ions) of water molecule react with a compound to form products. For example :
NaH + H₂O → NaOH + H₂
Hydration is defined as the addition of one or more water molecules to ions or molecules to form hydrated compounds. For example :
CUSO₄ + 5H₂O → CUSO₄ . 5H₂O

Question 32.
How can saline hydrides remove traces of water from organic compounds? ’
Answer:
Saline hydrides are ionic in nature. They react with water to form a metal hydroxide along with the liberation of hydrogen gas. The reaction of saline hydrides with water can be represented as :
AH(s) + H20(Z) → AOH(aq) + H2(g)
(where, A= Na, Ca, )

When added to an organic solvent, they react with water present in it. Hydrogen escapes into the atmosphere leaving behind the metallic hydroxide.Then, the dry organic solvent distills over.

Question 33.
What do you expect the nature of hydrides is, if formed by elements of atomic number 15, 19, 23 and 44 with dihydrogen? Compare their behaviour towards water,
Answer:
The elements of atomic number 15, 19, 23 and 44 are nitrogen, potassium, vanadium and ruthenium respectively.
1. Hydride of nitrogen
Hydride of nitrogen (NH₃) is a covalent molecule. It is an electron-rich hydride owing to the presence of excess electrons as a lone pair on nitrogen.

2. Hydride of potassium
Dihydrogen forms an ionic hydride with potassium owing to the high electropositive nature of potassium. It is crystalline and non-volatile in nature.

3. Hydrides of Vanadium and Ruthenium
Both vanadium and ruthenium belong to the d-block of the periodic table. The metals of d-block form metallic or non-stoichiometric hydrides. Hydrides of vanadium and ruthenium are therefore, metallic in nature having a deficiency of hydrogen.

4. Behaviour of hydrides towards water
Potassium hydride reacts violently with water as :
KH(s) + H₂O(aq) → KOH(aq) + H₂(g)
Ammonia (NH₃) behaves as a Lewis base and reacts with water as :
H₂O(Z) + NH₃(aq) ⇌ OH^–(aq) + \(\mathrm{NH}_{4}^{+}\)(aq)
Hydrides of vanadium and ruthenium do not react with water. Hence, the increasing order of reactivity of the hydrides is as: H < NH₃ < KH.

Question 34.
Do you expect different products in solution when aluminium (III) chloride and potassium chloride treated separately with
(i) normal water (ii) acidified water, and (iii) alkaline water? Write equations wherever necessary.
Answer:
Potassium chloride (KCl) is the salt of a strong acid (HCl) and strong base (KOH). Hence, it is neutral in nature and does not undergo hydrolysis in normal water. It dissociates into ions as follows :

In acidified and alkaline water, the ions do not react and remain as such. Aluminium (III) chloride is the salt of a strong acid (HCl) and weak base [Al(OH)₃]. Hence, it undergoes hydrolysis in normal water.

In acidified water, H⁺ ions react with Al(OH)₃ forming water and giving Al³⁺ ions. Hence, in acidified water, AlCl₃ will exist as Al³⁺(aq) and Cl^–(aq) ions.

In alkaline water the following reaction takes place :

Question 35.
How does H₂O₂ behave as a bleaching agent?
Answer:
H₂O₂ acts as a bleaching agent due to the nascent oxygen.
H₂O₂ → H₂O + O
Coloured matter + [O] → Colourless matter
It bleaches materials like silk, hair, ivory, cotton, wool, etc.

Question 36.
What do you understand by the terms :
(i) hydrogen economy (ii) hydrogenation (iii) ‘syngas’ (iv) water-gas shift reaction (v) fuel-cell?
Answer:
(i) Hydrogen economy : Hydrogen economy is a technique of using dihydrogen in an efficient way. It involves transportation and storage of dihydrogen in the form of liquid or gas.
Dihydrogen releases more energy than petrol and is more eco-friendly. Hence, it can be used in fuel cells to generate electric power. Hydrogen economy is about the transmission of this energy in the form of dihydrogen.

(ii) Hydrogenation : It refers to the addition of dihydrogen to another reactant. This process is used to reduce a compound in the presence of a suitable catalyst. For example, hydrogenation of vegetable oil using nickel as a catalyst gives edible fats such as vanaspati ghee etc.

(iii) Syngas : Syngas is a mixture of carbon monoxide and dihydrogen. Since the mixture of the two gases is used for the synthesis of methanol, it is called syngas, synthesis gas, or water gas.

Syngas is produced on the action of steam with hydrocarbons or coke at a high temperature in the presence of a catalyst.

(iv) Water gas shift reaction : The production of hydrogen by reacting carbon monoxide (CO) of syngas mixtures with steam in the presence of iron chromate as catalyst is called water-gas shift reaction.

CO₂ is removed by scrubbing with sodium arsenite solution.
(v) Fuel cell: It is a device which converts the energy produced during the combustion of a fuel directly into electrical energy. One such fuel cell is hydrogen-oxygen fuel cell. It does not cause any pollution. Fuel cells generated electricity with conversion efficiency of 70-85%.

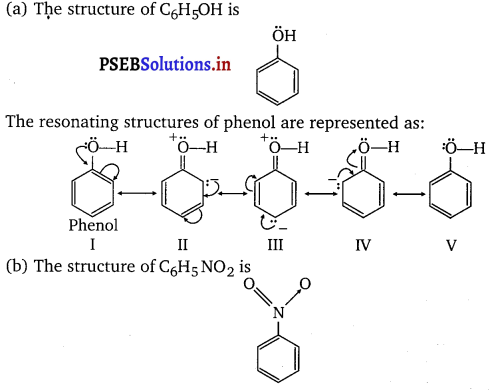
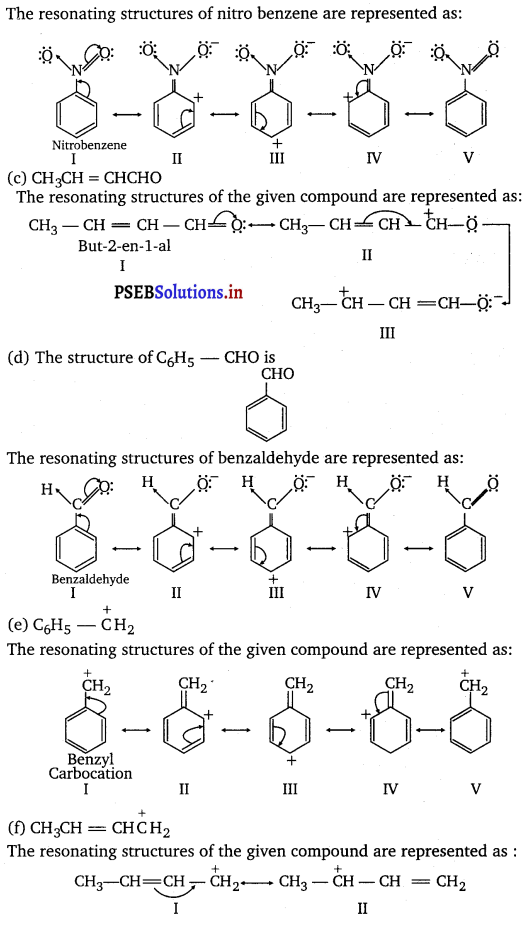
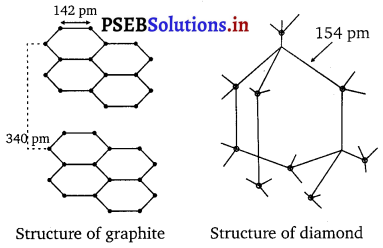
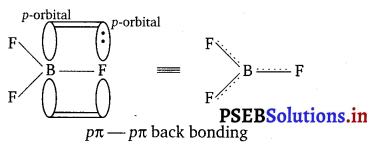
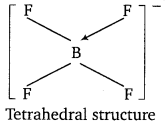
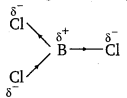
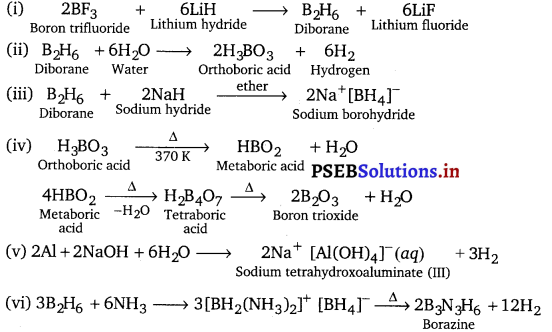
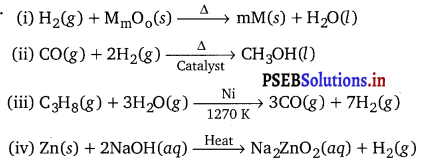
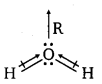
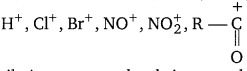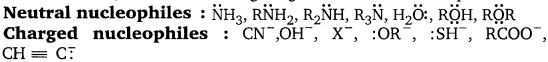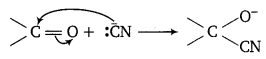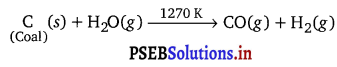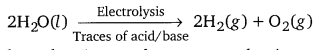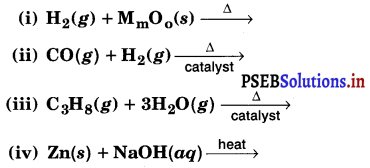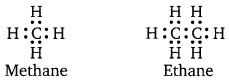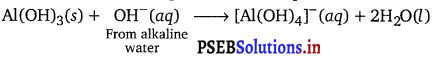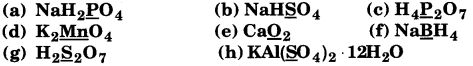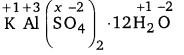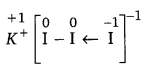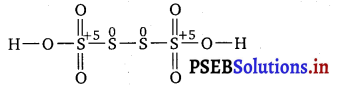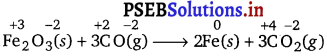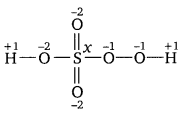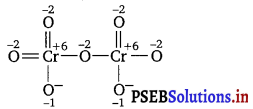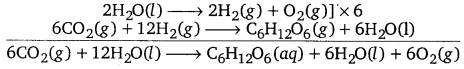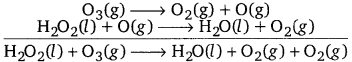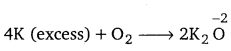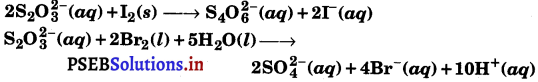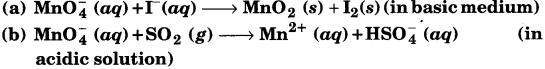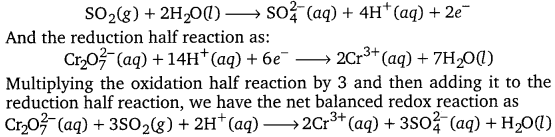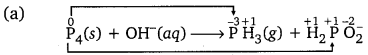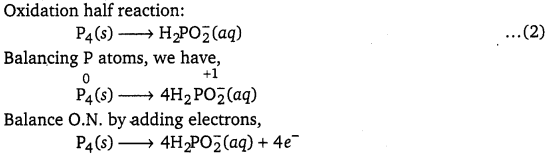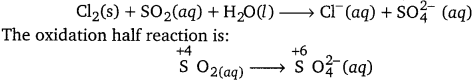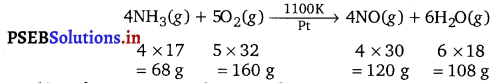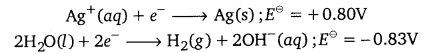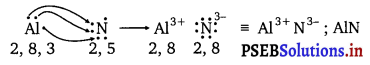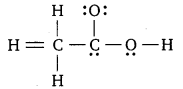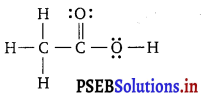Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 8 Redox Reactions Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 8 Redox Reactions

PSEB 11th Class Chemistry Guide Redox Reactions InText Questions and Answers

Question 1.
Assign oxidation numbers to the underlined elements in each of the following species:

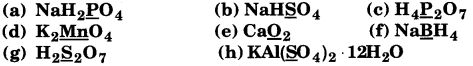
Answer:
(a) Let the oxidation number of P be x.
Oxidation number of Na = +1
Oxidation number of H = +1
Oxidation number of O = – 2
In neutral compounds, the sum of the oxidation numbers of all the atoms is zero.
1 (+1) + 2 (+1) +1 00 + 4 (-2) = 0
1 + 2 + x – 8 = 0
3 + x + (-8) – 0
x = 8 – 3
⇒ x = + 5
Hence, the oxidation number of P is +5.

(b) Let the oxidation number of S be x.

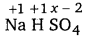
1 (+1) +1 (+1) +1 (x) + 4 (-2) = 0
⇒ 1 + 1 + x – 8 = 0
⇒ x = + 6
Hence, the oxidation number of S is +6.

(c) Let the oxidation number of P be x.

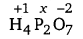
4 (+1) + 2 (x) + 7 (-2) = 0
⇒ 4 + 2x – 14 = 0
⇒ 2x = +10
⇒ x = + 5
Hence, the oxidation number of P is + 5.

(d) Let the oxidation number of Mn is x.

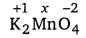
2 (+1) + x + 4 (-2) = 0
⇒ 2 + x — 8 = 0
⇒ x = + 6
Hence, the oxidation number of Mn is + 6.

(e) Let the oxidation number of O be x.

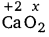
1 (+ 2) + 2 (x) = 0
⇒ 2 + 2x = 0
⇒ x = – 1
Hence, the oxidation number of O is -1.

(f) Let the oxidation number of B be x.

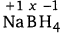
1 (+1)+1 (x) + 4 (-1) = 0
⇒ 1 + x – 4 = 0
⇒ x = + 3
Hence, the oxidation number of B is + 3.

(g) Let the oxidation number of S is x.

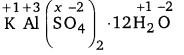
2 (+1) + 2 (x) + 7 (-2) = 0
⇒ 2 + 2x -14 = 0
⇒ 2x = +12
x = +6
Hence, the oxidation number of S is + 6.

(h) Let the oxidation number of S be x.

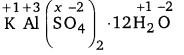
1 (+1) +1 (+ 3) + 2 (x) + 8 (-2) +12 (2 x 1 + (-2)) = 0
⇒ 1 + 3 + 2x -16 + 24 – 24 = 0
⇒ 2x = 12
x = + 6
Hence, the oxidation number of S is + 6.

Question 2.
What are the oxidation number of the underlined elements in each of the following and how do you rationalise your results?


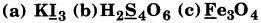
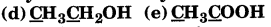
Answer:
(a) In

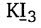
the oxidation number (O. N.) of K is +1. Hence, the average oxidation number of I is \(\frac{-1}{3}\). However, O.N. cannot be fractional.
Therefore, we will have to consider the structure of KI₃ to find the oxidation states.
In a KI₃ molecule, an atom of iodine forms a coordinate covalent bond with an iodine molecule.

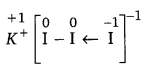
Hence, in a KI₃ molecule, the O.N. of the two I atoms forming the I₂ molecule is 0, whereas the O.N. of the I atom forming the coordinate bond is -1.

(b) Let the oxidation number of S be x.

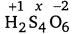
2 (+1) + 4 (x) + 6 (-2) = 0
=» 2 + 4x – 12 = 0
⇒ 4x = +10
⇒ x = + 2 \(\frac{1}{2}\)
However, O.N. cannot be fractional. Hence S must be present in different oxidation states in the molecule.

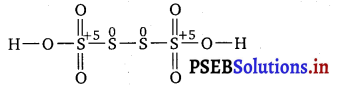
The O.N. of two of the four S atoms is +5 and the O.N. of the other two S atoms is 0.

(c) Let the oxidation number of Fe be x.

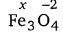
3(x) + 4(-2) = 0
3x – 8 = 0
x = \(+\frac{8}{3}\)
However O.N. cannot’be fractional. Here, one of the three Fe atoms exhibits the O.N. of +2 and the other two Fe atoms exhibit the O.N. of+3

(d) Let oxidation number of C be x.

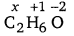
2 (x) + 6 (+1) + 1 (-2) = 0
2x + 4 = 0
x = -2
Hence, the O.N. of C is – 2

(e) Let the oxidation number of C be x.

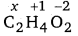
2 (x) + 4 (+1) + 2 (-2) = 0
2x = 0
x = 0
Therefore, the average oxidation number of C is zero.
Let us consider the structure of CH₃COOH

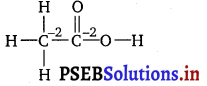
Oxidation number of atom = 1(+1) + x+1(-2) +1(-1) = 0
x = +2
Similarly, oxidation number of C₂ atom
3(+1) + x+ 1(-1) = 0
x = -2.

Question 3.
Justify that the following reactions are redox reactions:
(a) CuO (s) + H₂(g) → Cu(s) + H₂O(g)
(b) Fe₂O₃ (s) + 3CO(g) → 2Fe(s) + 3CO₂(g)
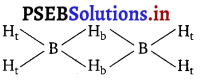
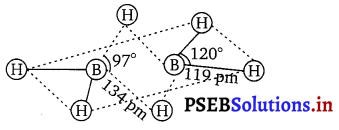
(c) 4BCl₃ (g) + 3LiAlH₄ (s) → 2B₂H₆(g) + 3LiCl (s) + 3 AlCl₃(S)
(d) 2K (s) + F₂ (g) → 2K⁺F^–(s)
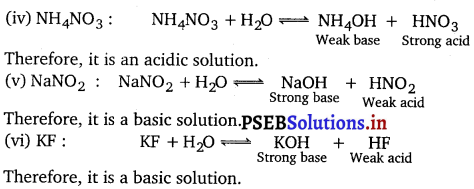
(e) 4NH₃(g) + 5O₂(g) → 4NO(g) + 6H₂O (g)
Answer:
(a) CuO (s) + H₂(g) → Cu(s) + H₂O(g)
Let us write the oxidation number of each element involved in the given reaction as :

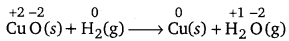
Here, the oxidation number of Cu decreases from +2 in CuO to 0 in Cu i.e., CuO is reduced to Cu. Also, the oxidation number of H increases from 0 in H₂ to +1 in H₂O i.e., H₂ is oxidized to H₂O. Hence, this reaction is a redox reaction.

(b) Fe₂O₃ (s) + 3CO(g) → 2Fe(s) + 3CO₂(g)
Let us write the oxidation number of each element in the given reaction as:

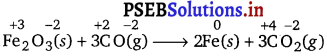
Here, the oxidation number of Fe decreases from +3 in Fe₂O₃ to 0 in Fe i.e., Fe₂O₃ is reduced to Fe. On the other hand, the oxidation number of C increases from +2 in CO to +4 in CO₂ i.e., CO is oxidized to CO₂.
Hence, the given reaction is a redox reaction.

(c) 4BCl₃ (g) + 3LiAlH₄ (s) → 2B₂H₆(g) + 3LiCl (s) + 3 AlCl₃(S)
The oxidation number of each elements in the given reaction can be represented as:

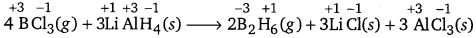
In this reaction, the oxidation number of B decreases from +3 in BCl₃ to -3 in B₂H_6- i.e., BCl₃ is reduced to B₂H₆. Also, the oxidation number of H increases from -1 in LiAlH₄ to +1 in B₂H₆ i.e., LiAlH₄ is oxidized to B₂H₆. Hence, the given reaction is a redox reaction.

(d) 2K (s) + F₂ (g) → 2K⁺F^–(s)
The oxidation number of each element in the given reaction can be represented as:

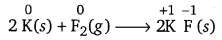
In this reaction, the oxidation number of K increases from 0 in K to +1 in KF i.e., K is oxidized to KF. On the other hand, the oxidation number of F decreases from 0 in F₂ to -1 in KF i.e., F₂ is reduced to KF.
Hence, the above reaction is a redox reaction.

(e) 4NH₃(g) + 5O₂(g) → 4NO(g) + 6H₂O (g)
The oxidation number of each elements in the given reaction can be represented as:

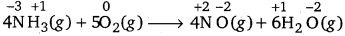
Here, the oxidation number of N increases from -3 in NH₃ to +2 in NO. On the other hand, the oxidation number of O₂ decreases from 0 in O₂ to -2 in NO and H₂O i.e.,O₂ is reduced. Hence, the given reaction is a redox reaction.

Question 4.
Fluorine reacts with ice and results in the change:
H₂O(S) + F₂(g) → HF(g) + HOF(g)
Justify that this reaction is a redox reaction.
Ans. Let us write the oxidation number of each atom involved in the given reaction above its symbol as:

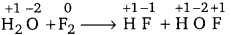
Here, we have observed that the oxidation number of F increases from 0 in F₂ to +1 in HOF. Also, the oxidation number decreases from 0 in F₂ to -1 in HF. Thus, in the above reaction, F is both oxidized and reduced. Hence, the given reaction is a redox reaction.

Question 5.
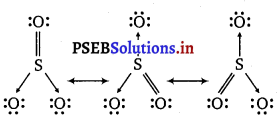
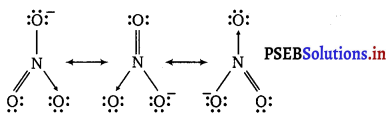
Calculate the oxidation number of sulphur, chromium and nitrogen in H₂SO₅, \(\mathrm{Cr}_{2} \mathrm{O}_{7}^{2-}\) and \(\mathrm{NO}_{3}^{-}\). Suggest structure of these compounds. Count for the fallacy.
Answer:

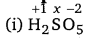
2 (+1) +1 (x) + 5 (-2) = 0
⇒ 2 + x -10 = 0
⇒ x = + 8
However, the O.N. of S cannot be +8. S has six valence electrons. Therefore, the O.N. of S cannot be more than +6. The structure of H2S05 is shown as follows :

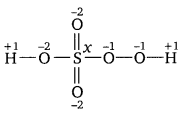
Now, 2 (+1) +1 (x) + 3 (-2) + 2 (-1) – 0
⇒ 2 + x – 6 – 2 = 0
⇒ x = + 6
Therefore, the O.N. of S is +6.

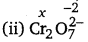
2 (x) + 7 (-2) = – 2 ⇒ 2x -14 = – 2
⇒ x = + 6
The structure of Cr2Oy is shown as follows:

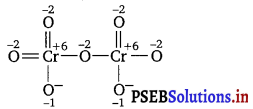
Let the oxidation number of each Cr atom be
4(-2) + (-2) +1(-2) + 2x = 0
– 8 – 2 – 2 + 2x = 0
2x = +12
x = +6

Oxidation number of Cr in \(\mathrm{Cr}_{2} \mathrm{O}_{7}^{2-}\) is same.
Hence, there is no fallacy.

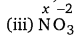
1 (x) + 3(-2) = -1
= x – 6 = -1
x = +5
The structure of \(\mathrm{NO}_{3}^{-}\) is shown as follows:

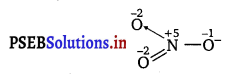
Let the oxidation number of N be x.
1(-1) + x + 1(-2) + 1(-2) = 0
x = + 5
Oxidation number of N in \(\mathrm{NO}_{3}^{-}\) ion is same.
Hence, there is no fallacy.

Question 6.
Write formulas for the following compounds:
(a) Mercury (II) chloride
(b) Nickel (II) sulphate
(c) Tin (IV) oxide
(d) Thallium (I) sulphate
(e) Iron (III) sulphate
(f) Chromium (III) oxide
Answer:
(a) Mercury (II) chloride: Hg (II) Cl₂
(b) Nickel (II) sulphate: Ni (II) SO₄
(c) Tin (IV) oxide : Sn (IV) O₂
(d) Thallium (I) sulphate: Tl₂ (I) SO₄
(e) Iron (III) sulphate: Fe₂(III) (SO₄)₃
(f) Chromium (III) oxide: Cr₂(III)O₃

Question 7.
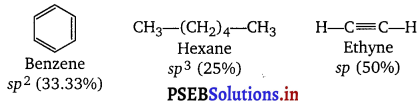
Suggest a list of the substances where carbon can exhibit oxidation states from -4 to +4 and nitrogen from -3 to +5.
Answer:
The substances where carbon can exhibit oxidation states from -4 to +4 are listed in the following table :

Substance	Formula	Oxidation State of Carbon
Methane	CH4	-4
Ethane	C2H6	-3
Ethene	C2H4	-2
Ethyne	C2H2	-1
Dichloromethane	CH2Cl2	0
Hexachlorobenzone	C6Cl6	+1
Carbon monoxide	CO	+2
Oxalic acid	(COOH)2	+3
Carbon dioxide	CO2	+4

The substances where nitrogen can exhibit oxidation sates from -3 to +5 are listed in in the following table.

Substance	Formula	Oxidation State of Nitrogen
Ammonia	NH3	-3
Hydrazine	N2H4	-2
Hydride	N2H2	-1
Dinitrogen gas	N2	0
Nitrous oxide	N2O	+1
Nitric oxide	NO	+2
Dinitrogen trioxide	N2O3	+3
Nitrogen dioxide	NO2	+4
Nitrogen pentoxide	N2O5	+5

Question 8.
While sulphur dioxide and hydrogen peroxide can act as oxidising as well as reducing agents in their reactions, ozone and nitric acid act only as oxidants. Why?
Answer:
(i) In sulphur dioxide (SO₂), the oxidation number (O.N.) of S is +4 and the range of the O.N. that S can have is from +6 to -2.
Therefore, SO₂ can act as an oxidising as well as reducing agent.
(ii) In hydrogen peroxide (H₂O₂), the O.N. of O is -1 and the range of the O.N. that O can have is from 0 to -2. O can sometimes also attain the oxidation numbers +1 and +2. Hence, H₂O₂ can act as an oxidising as well as reducing agent.
(iii) In ozone (O₃) the O.N. of O is zero and the range of the O.N. that O can have is from 0 to -2. Therefore, the O.N. of O can only decrease in this case. Hence,O₃ acts only as an oxidant.
(iv) In nitric acid (HNO₃) the O.N. of N is +5 and the range of the O.N. that N can have is from +5 to -3. Therefore, the O.N. of N can only decrease in this case. Hence, HNO₃ acts only as an oxidizing agent.

Question 9.
Consider the reactions:
(a) 6CO₂(g) + 6H₂O(l) → C₆H₁₂O₆ (aq) + 6O₂(g)
(b) O₃(g) + H₂O₂(Z) → H₂O(1) + 2O₂(g)
Why it is more appropriate to write these reactions as:
(a) 6CO₂ (g) + 12H₂O(1) → C₆H₁₂O₆ (aq) + 6H₂O(l) + 6O₂ (g)
(b) O₃(g) + H₂O₂(Z) → + H₂O(Z) + O₂(g) + O₂(g)
Also suggest a technique to investigate the path of the above (a) and (b) redox reactions.
Answer:
(a) The process of photosynthesis involves two steps :
Step 1: H₂O decomposes to give H₂ and O₂.
2H₂O(l) → 2H₂(g) + O₂(g)
Step 2: The H₂ produced in step 1 reduces CO₂ thereby producing glucose (C₆H₁₂O₆) and H₂O.
6CO₂(g) + 12H₂(g) → C₆H₁₂O₆(S) + 6H₂O(l)
Now, the net reaction of the process is given as:

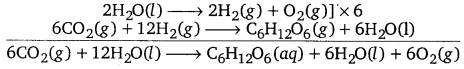
It is more appropriate to write the reaction as given above because water molecules are also produced in the process of photosynthesis.
The path of this reaction can be investigated by using radioactive H₂O¹⁸ in place of H₂O

(b) O₂ is produced from each of the two reactants O₃ and H₂O₂. For this reason O₂ is written twice.
The given reaction involves two steps. First O₃ decomposes to form O₂ and O. In the second step H₂O₂ reacts with the O produced in the first step thereby producing H₂O and O₂.

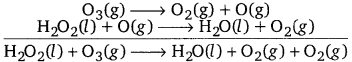
The path of this reaction can be investigating by using \(\mathrm{H}_{2} \mathrm{O}_{2}^{18}\) or \(\mathrm{O}_{3}^{18}\).

Question 10.
The compound AgF₂ is unstable compound. However, if formed, the compound acts as a very strong oxidizing agent. Why?
Answer:
AgF₂ → Ag + F₂
The oxidation state of Ag in Ag F₂ is +2. But +2 is an unstable oxidation state of Ag. Therefore, whenever Ag F₂ is formed, silver readily accepts an electron to form Ag⁺. This helps to bring the oxidation state of Ag down from +2 to a more stable state of +1. As a result, Ag F₂ acts as a very strong oxidizing agent.

Question 11.
Whenever a reaction between an oxidising agent and a reducing agent is carried out, a compound of lower oxidation state is formed if the reducing agent is in excess and a compound of higher oxidation state is formed if the oxidising agent is in excess. Justify this statement giving two illustrations.
Answer:
Whenever a reaction between an oxidising agent and a reducing agent is carried out, a compound of lower oxidation state is formed if the reducing agent is in excess and a compound of higher oxidation state is formed if the oxidising agent is in excess. This can be illustrated as follows:
(i) P₄ and F₂ are reducing and oxidising agents respectively.
If an excess of P₄ is treated with F₂ then PF₃ will be produced, where in the oxidation number (O.N.) of P is +3.

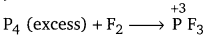
However, if P₄ is treated with an excess of F₂, then PF₅ will be produced, wherein the O.N. of P is +5.

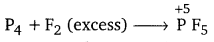
(ii) K acts as a reducing agent, whereas O₂ is an oxidising agent.
If an excess of K reacts with O₂, then K₂O will be formed, wherein the O.N. of O is -2.

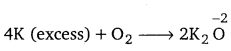
However, if K reacts with an excess of O₂, then K₂O₂ will be formed, wherein the O.N. of O is -1.

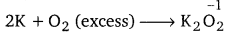
Question 12.
How do you account for the following observations?
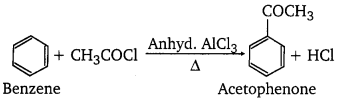
(a) Though alkaline potassium permanganate and acidic potassium permanganate both are used as oxidants, yet in the manufacture of benzoic acid from toluene we use alcoholic potassium permanganate as an oxidant. Why? Write a balanced redox equation for the reaction.
(b) When concentrated sulphuric acid is added to an inorganic mixture containing chloride, we get colourless pungent smelling gas HCl, but if the mixture contains bromide then we get red vapour of bromine. Why?
Answer:
(a) Oxidation of toluene to benzoic acid in acidic medium.

Oxidation of toluene to benzoic acid in basic and neutral medium.

On industrial scale, alcoholic potassium permanganate is preferred to acidic or alkaline potassium permanganate because in the presence of alcohol, both the reactants KMnO₄ and C₆H₅CH₃ are mixed very well and form homogeneous solution and in homogeneous medium reaction takes place faster than in heterogeneous medium. Further more in neutral medium, OH^– ions are produced in the reaction itself.

(b)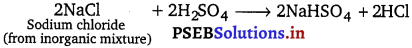

HCl is a weak reducing agent. k cannot reduce H₂SO₄ to SO₂ that’s why pungent smelling gas HCl is obtained.

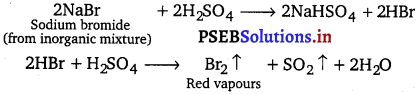
HBr is a strong reducing agent, it reduces H₂S0₄ to SO₂ and is itselfoxidised to Br₂. That’s why we get red vapours of bromine when conc.
H₂SO₄ reacts with inorganic mixture containing bromide salt.

Question 13.
Identify the substance oxidised, reduced, oxidising agent andreducing agent for each of the following reactions:
(a) 2AgBr(s) + C₆H₆O₂(aq) → 2Ag(s) + 2HBr(aq) + C₆H₄O₂(aq)
(b) HCHO(l) +2 [Ag (NH₃)₂]⁺ (aq) + 3OH^–(aq) → 2Ag(s) + HCOO^–(aq) + 4NH₃(aq) + 2H₂O (l)
(c) HCHO(l) + 2Cu²⁺ (aq) + 5 OH^– → Cu₂O (s) +HCOO^–(aq) + 3H₂O(l)
(d) N₂H₄ (Z) + 2H₂O₂ (1) → N₂ (g) + 4H₂O (l)
(e) Pb (s) +PbO₂ (s) + 2H₂SO₄ (ag) → 2PbSO₄(s) + 2H₂O(l)
Answer:
(a) Oxidised substance -C₆H₆O₂
Reduced substance – AgBr
Oxidising agent – AgBr
Reducing agent -C₆H₆O₂

(b) Oxidised substance – HCHO
Reduced substance – [Ag (NH₃)₂]⁺
Oxidising agent – [Ag (NH₃)₂]⁺
Reducing agent – HCHO

(c) Oxidised substance – HCHO
Reduced substance -Cu²⁺
Oxidising agent – Cu²⁺
Reducing agent – HCHO

(d) Oxidised substance – N₂H₄
Reduced substance -H₂O₂
Oxidising agent-H₂O₂
Reducing agent -N₂H₄

(e) Oxidised substance – Pb
Reduced substance – PbO₂
Oxidising agent – Pb O₂
Reducing agent – Pb

Question 14.
Consider the reactions:

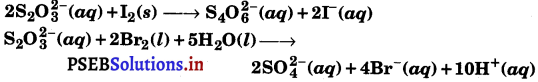
Why does the same reductant, thiosulphate react differently with iodine and bromine?
Answer:
The average oxidation number (O.N.) of S in \(\mathrm{S}_{2} \mathrm{O}_{3}^{2-}\) is +2. Being a stronger oxidising agent than I₂, Br₂ oxidises \(\mathrm{S}_{2} \mathrm{O}_{3}^{2-}\) to \(\mathrm{S}_{2} \mathrm{O}_{4}^{2-}\) in which the O.N. of S is +6. However I₂ is a weak oxidising agent. Therefore, it oxidises \(\mathrm{S}_{2} \mathrm{O}_{3}^{2-}\) to \(\mathrm{S}_{4} \mathrm{O}_{6}^{2-}\) in which the average O.N. of S is only +2.5. As a result, \(\mathrm{S}_{2} \mathrm{O}_{3}^{2-}\) reacts differently with iodine and bromine. ,

Question 15.
Justify giving reactions that among halogens, fluorine is the best oxidant and among hydrohalic compounds, hydroiodic acid is the best reductant.
Answer:
(i) F₂ can oxidize Cl^– to Cl₂, Br^– to Br₂ and I^– to I₂ as:
F₂(aq) + 2Cl^–(s) → 2F^–(aq) + Cl₂(g)
F₂(aq) + 2Br^–(aq) → 2F^–(aq) + Br₂(7)
F₂(aq) + 2I^–(aq) → 2F^–(aq) + I₂(s)

On the other hand, Cl₂, Br₂ and I₂ cannot oxidize F^– to F₂. The oxidizing power of halogens increases in the order of I₂ < Br₂ < Cl₂ < F₂. Hence fluorine is the best oxidant among halogens.

(ii) HI and HBr can reduce H₂SO₄ to SO₂, but HCl and HF cannot. Therefore HI and HBr are stronger reductants than HCl and HF.

2HI + H₂SO₄ → I₂ + SO₂ + 2H₂O
2HBr + H₂SO₄ → Br₂ + SO₂ + 2H₂O

Again, I- can reduce Cu²⁺ to Cu⁺ but Br^– cannot.

4I^–(aq) + 2Cu²⁺(aq) → Cu₂I₂(s) + I₂(aq)

Hence, hydroiodic acid is the best reductant among hydrohalic compounds.
Thus, the reducing power of hydrohalic acids increases in the order of
HF < HCl < HBr < HI.

Question 16.
Why does the following reaction occur?
\(\mathrm{XeO}_{6}^{4-}\)(aq) + 2F^– (aq) + 6H⁺(aq) → XeO₃(g) +F₂(g) + 3H₂O(i)
What conclusion about the compound Na₄XeO₆ (of which \(\mathrm{XeO}_{6}^{4-}\) is a part) can be drawn from the reaction.
Answer:
The given reaction occurs because \(\mathrm{XeO}_{6}^{4-}\) oxidizes being an oxidizing agent and F^– reduces \(\mathrm{XeO}_{6}^{4-}\)

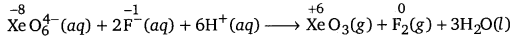
In this reaction, the oxidation number (O.N.) of Xe decreases from +8 in \(\mathrm{XeO}_{6}^{4-}\) to +6 in XeO₃ and the O.N. of F increases from -1 in F^– to 0 in F₂.
Hence, we can conclude that Na₄XeO₆ is a strong oxidizing agent thanF^–.

Question17.
Consider the reactions:
(a) H₃PO₂ (aq) + 4 AgNO₃ (aq) + 2H₂O(l) → H₃PO₄ (aq) + 4Ag(s) + 4HNO₃ (aq)
(b) H₃PO₂ (oqr) + 2CuSO₄ (aq) + 2 H₂O(0 → H₃PO₄ (aq) + 2Cu(s) +H₂SO₄ (aq)
(c) C₆H₅CHO(l) + 2[Ag (NH₃)₂]+ (aq) + 3OH^– (aq) → C₆H₅COO^–(aq) + 2Ag(s) + 4NH₃ (aq) + 2H₂O(l)
(d) C₆H₅CHO(l) + 2Cu²⁺(aq) + 5OH^–(aqf) → No change observed.
What inference do you draw about the behaviour of Ag⁺ and Cu²⁺ from these reactions?
Answer:
Ag⁺ and Cu²⁺ act as an oxidizing agents in reactions (a) and (b) respectively.
In reaction (c), Ag⁺ oxidizes C₆H₅CHO to C₆H₅COO^–, but in reaction (d) Cu²⁺ cannot oxidize C₆H₅CHO. Hence, we can say that Ag⁺ is a stronger oxidising agent than Cu²⁺.

Question 18.
Balance the following redox reactions by ion-electron method:


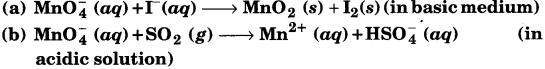
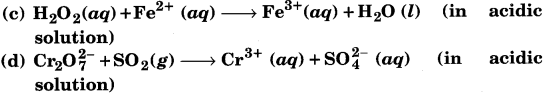
Answer:
(a) Step 1 : The two half reactions involved in the given reaction are:
Oxidation half reaction :

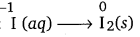
Reduction half reaction:

Step 2 : Balancing I in the oxidation half reaction, we have
2I^– (aq) → I₂(s)
Now, to balance the charge, we add 2 e“ to the RHS of the reaction.
2I^–(aq) → I₂(s) + 2e^–

Step 3 : In the reduction half reaction, the oxidation state of Mn has reduced from +7 to +4. Thus, 3 electrons are added to the LHS of the reaction.
\(\mathrm{MnO}_{4}^{-}\) + 3e^– → MnO₂(aq)
Now, to balance the charge, we add 4 OH“ ions to the RHS of the reaction as the reaction is taking place in a basic medium.
\(\mathrm{MnO}_{4}^{-}(a q)^{-}\) + 3e^– → MnO₂(aq) + 4OH^–

Step 4 : In this equation, there are 6 O atoms on the RHS and 4 O atoms on the LHS. Therefore, two water molecules are added to the LHS.
\(\mathrm{MnO}_{4}^{-}\) (aq) + 2H₂O + 3e^– → MnO₂(aq) + 4OH^–

Step 5 : Equalising the number of electrons by multiplying the oxidation half reaction by 3 and the reduction half reaction by 2, we have:
6I^–(aq) → 3I₂(s) + 6e^–
2 \(\mathrm{MnO}_{4}^{-}\)(aq) + 4H₂O + 6e^– → 2MnO₂(s) + 8OH^–(aq)

Step 6 : Adding the two half reactions, we have the net balanced redox reaction as:
6I^–(aq) + 2\(\mathrm{MnO}_{4}^{-}\)(aq) + 4H₂O(l) → 3I₂(s) + 2MnO₂(s) + 8OH^–(aq)

(b) Following the steps as in part (a) we have the oxidation half reaction as:
SO₂(g) + 2H₂O(Z) → \(\mathrm{HSO}_{4}^{-}\)(aq) + 3H⁺ (aq) + 2e^– (aq)
And the reduction half reaction as:
\(\mathrm{MnO}_{4}^{-}\)(aq) + 8H⁺(aq) + 5e^– → Mn²⁺(aq) + 4H₂O(l)

Multiplying the oxidation half reaction by 5 and the reduction half reaction by 2, and then by adding them, we have the net balanced redox reaction as :

2Mno₄^–(aq) + 5SO₂(g) + 2H₂O(Z) + H⁺(aq) → 2Mn(aq) + 5HSO₄^–((aq)

(c) Following the steps as in part (a), we have the oxidation half reaction as:
Fe²⁺(aq) → Fe³⁺(aq) + e^–

And the reduction half reaction as:
H₂O₂(aq) + 2H⁺ (aq) + 2e^– → 2H₂O(l)

Multiplying the oxidation half reaction by 2 and then adding it to the reduction half reaction, we have the net balanced redox reaction as:
H₂O₂(aq) + 2Fe²⁺(aq) + 2H⁺(aq) → 2Fe³⁺ (aq) + 2H₂O(Z)

(d) Following the steps as in part (a), we have the oxidation half reaction as:

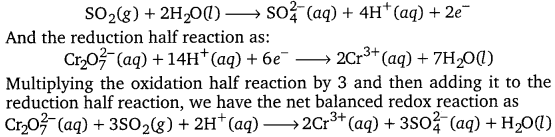
Question 19.
Balance the following equations in basic medium by ion-electron method and oxidation number methods and identify the oxidising agent and the reducing agent.
(a) P₄(s) + OH^–(aq) → PH₃(g) + H₂PO₂^–(aq)
(b) N₂H₄(l) + CIO₃^–(aqr) → NO(g) + Cl^–(g)
(c) Cl₂O₇(g) + H₂O₂(aqr) → ClO^–₂(aq) + O₂(g) + H⁺
Answer:

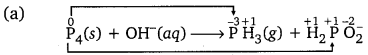
O.N. increases by 1 per P atom.
P₄ acts both as an oxidising as well as a reducing agent.

Oxidation number method:
Total decrease in O.N. of P₄ in PH₃ = 3 x 4 = 12
Total increase in O.N. of P₄ in H₂PO₂ = 1 x 4 = 4
Therefore, to balance increase/decrease in O.N. multiply PH₃ by 1 and H₂PO₂^– by 3, we have,

P₄(s) + OH^–(aq) → PH₃(g) + 3H₂PO₂^–(aq)

To balance O atoms, multiply OH- by 6, we have,

P₄(s) + 6OH^–(aq) → PH₃(g) + 3H₂PO₂^–(aq)

To balance H atoms, add 3H₂O to L.H.S. and 3OH^– to the R.H.S. we have,

P₄ (s) + 6OH^–(aq) + 3H₂O(l) → PH₃(g) + 3H₂PO₂^–(aq) + 3OH^–(aq)
or P₄(s) + 3OH^–(aq) + 3H₂O(l) → PH₃(g) + 3H₂PO₂^–(aq) …(1)

Thus, Eq. (1) represents the correct balanced equation.

Ion-electron method : The two half reactions are:

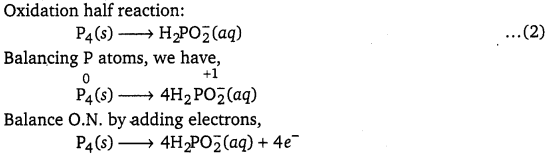
Oxidation number method :
Total increase in O.N. of N = 2 x 4 = 8
Total decrease in O.N. of Cl = 1 x 6 = 6
Therefore, to balance increase/decrease in O.N. multiply N₂H₂ by 3 and \(\mathrm{ClO}_{3}^{-}\) by 4, we have,

3N₂H₄(l) + 4ClO₃^– (aq) → NO(g) + Cl^–(aq)

To balance N and Cl atoms, multiply NO by 6 and Cl^– by 4, we have,

3N₂H₄(l) + 4ClO₃^–(aq) → 6NO(g) + 4Cl^–(aq)

Balance O atoms by adding 6H₂O, in R.H.S.

3N₂H₄(l) + 4ClO₃^–(aq) → 6NO(g) + 4Cl^–(aq) + 6H₂O (l) …(1)

H atoms get automatically balanced and thus Eq. (1) represents the correct balanced equation.

Ion electron method :

Oxidation number method :
Total decrease in O.N. of Cl₂O₇ = 4 x 2 = 8
Total increase in O.N. of H₂O₂ = 2 x 1 = 2
∴ To balance increase/decrease in O.N. multiply H₂O₂ and O₂ by 4, we have,

Question 20.
What type of information can you draw from the following reaction?
(CN)₂(g) + 2OH^–(aq) → CN^–(aq) + CNO^–(aq) + H₂O(l)
Answer:
The oxidation number of carbon in (CN)₂ CN^– and CNO^– is +3, +2 and +4 respectively. These are obtained as shown below:
Let the oxidation number of C be x.
(i) (CN)₂
2 (x – 3) = 0
∴ x = +3

(ii) CN^–
x -3 = -1
∴ x = +2

(iii) CNO^–
x – 3 – 2 = -1
∴ x = + 4

The oxidation number of carbon in the various species is:

The following information we can drawn from the above reaction :
(i) Decomposition of cyanogen in the cyanide ion (CN^–) and cyanate ion (CNO^–) occurs in basic medium.
(ii) Cyanogen (CN)₂ acts as both reducing agent as well as oxidising agent.
(iii) The reaction is an example of disproportionation reaction.
(iv) Cyanogen (CN)₂ is called pseudohalogen while CN^–, CNO^– ions are called pseudohalide ions.

Question 21.
The Mn³⁺ ion is unstable in solution and undergoes disproportionation to give Mn²⁺, MnO₂ and H⁺ ion. Write a balanced ionic equation for the reaction.
Answer:
The given reaction can be represented as:

Mn³⁺ (aq) → Mn²⁺(aq) + MnO₂(s) + H⁺(aq)

The oxidation half equation is:

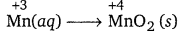
The oxidation number is balanced by adding one electron as:
Mn³⁺(aq) → MnO₂(s) + e^–

The charge is balanced by adding 4H+ ion as :
Mn³⁺(aq) → MnO₂(s) + 4H⁺ (aq) + e^–

The O atoms and H+ ions are balanced by adding 2H20 molecules as:
Mn³⁺(aq) + 2H₂O(l) → MnO₂(s) + 4H⁺ (aq) + e^– …(1)

The reduction half equation is:
Mn³⁺(aq) → Mn²⁺(aq)

The oxidation number is balanced by adding one electron as :
Mn³⁺ (aq) + e^– → Mn²⁺ (aq) … (2)

The balanced chemical equation can be obtained by adding equation (1) and (2) as :
2Mn³⁺(aq) + 2H₂O(l) → MnO₂(s) + Mn²⁺(aq) + 4H⁺(aq)

Question 22.
Consider the elements: Cs, Ne, I and F
(a) Identify the element that exhibits only negative oxidation state.
(b) Identify the element that exhibits only positive oxidation state.
(c) Identify the element that exhibits both positive and negative oxidation states.
(d) Identify the element which exhibits neither the negative nor the positive oxidation state.
Answer:
(a) F exhibits only negative oxidation state of-1.
(b) Cs exhibits only positive oxidation state of +1
(c) I exhibits both positive and negative oxidation states. It exhibits oxidation states of-1, 0, +1, + 3, + 5, and + 7.
(d) The oxidation state of Ne is zero. It exhibits neither negative nor positive oxidation states.

Question 23.
Chlorine is used to purify drinking water. Excess of chlorine is harmful. The excess of chlorine is removed by treating with sulphur dioxide. Present a balanced equation for this redox change taking place in water.
Answer:
The given redox reaction can be represented as:

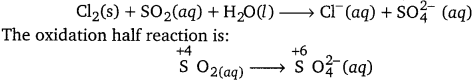
Question 24.
Refer to the periodic table given in your book and now answer the following questions:
(a) Select the possible non-metals that can show disproportionation reaction.
(b) Select three metals that can show disproportionation reaction.
Answer:
In disproportionation reaction, one of the reacting substances always contains an element that can exist in at least three oxidation states.

Question 25.
In Ostwald’s process for the manufacture of nitric acid, the first step involves the oxidation of ammonia gas by oxygen gas to give nitric oxide gas and steam. What is the maximum weight of nitric oxide that can be obtained starting only with lO.OOg of ammonia and 20.00 g of oxygen?
Answer:
The balanced chemical equation for the given reaction is given as:

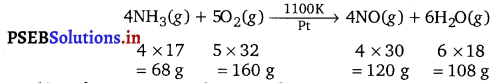
68 g of NH₃ reacts with 160 g of O₂
Therefore 10 g of NH₃ reacts with \(\frac{160 \times 10}{68}\). g of O₂ or 23.53 g of O₂
But the available amount of O₂ is 20 g which is less than the amount required to react with 10 g NH₃. So, O₂ is the limiting reagent and it limits the amount of NO produced. From the above balanced equation.
160 g of O₂; produces 120 g NO.
Therefore, 20 g of O₂; produces = \(\frac{120 \times 20}{160}\) = 15 g NO

Question 26.
Using the standard electrode potentials given in the table 8.1,
predict if the reaction between the following is feasible: *
(a) Fe³⁺ (aq) and I^– (aq)
(b) Ag⁺ (aq) and Cu (s)
(c) Fe³⁺ (aq) and Cu(s)
(d) Ag (s) and Fe³⁺ (aq)
(e) Br₂ (aq) and Fe²⁺(aqr)
Answer:

Question 27.
Predict the products of electrolysis in each of the following:
(i) An aqueous solution of AgNO₃ with silver electrodes.
(ii) An aqueous solution of AgNO₃ with platinum electrodes
(iii) A dilute solution of H₂SO₄ with platinum electrodes.
(iv) An aqueous solution of CuCl₂ with platinum electrodes,
Answer:
(i) AgNO₃ ionizes in aqueous solutions to form Ag⁺ and \(\mathrm{NO}_{3}^{-}\) ions.
On electrolysis, either Ag⁺ ions or H₂O molecules can be reduced at the cathode. But the reduction potential of Ag⁺ ions is higher than that of H₂O.

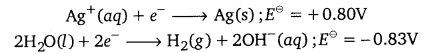
Hence, Ag+ ions are reduced at the cathode. Similarly, Ag metal or H20 molecules can be oxidized at the anode. But the oxidation potential of Ag is higher than that of H20 molecules.

Ag(s) → Ag⁺(aq) + e^– ;\(E^{\ominus}\) = -0.80V

2H₂O₂(g) → O₂(g) + 4H⁺(aq) + 4e^– ;\(E^{\ominus}\) = -1.23V
Therefore, Ag metal gets oxidized at the anode.

(ii) Pt cannot be oxidized easily. Hence, at the anode, oxidation of water occurs to liberate O₂. At the cathode, Ag⁺ ions are reduced and get deposited.

(iii) H₂SO₄ ionizes in aqueous solutions to give H⁺ and \(\mathrm{SO}_{4}^{2-}\) ions.

H₂SO₄ (aq) → 2H⁺(aq) + \(\mathrm{SO}_{4}^{2-}\) (aq)

On electrolysis, either of H⁺ ions or H₂O molecules can get reduced at the cathode. But the reduction potential of H⁺ ions is higher than that of H₂O molecules.

2H⁺(aq) + 2e^– → H₂(g); \(E^{\ominus}\) = 0.0 V
2H₂O(aq) + 2e^– → H₂(g) + 2OH^–(aq): \(E^{\ominus}\) = – 0.83V

Hence, at the cathode, H⁺ ions are reduced to liberate H₂ gas.
On the other hand, at the anode, either of \(\mathrm{SO}_{4}^{2-}\) ions or H₂O molecules can get oxidized. But the oxidation of \(\mathrm{SO}_{4}^{2-}\) involves breaking of more bonds than that of H₂O molecules. Hence, \(\mathrm{SO}_{4}^{2-}\) ions have a lower oxidation potential than H₂O. Thus, H₂O is oxidized at the anode to liberate O₂ molecules.

(iv) In aqueous solutions, CuCl₂ ionizes to give Cu²⁺ and Cl^– ions as
CuCl₂ (aq) → Cu²⁺ (aq) + 2Cl^– (aq)

On electrolysis either of Cu²⁺ ions or H₂O molecules can get reduced at the cathode. But the reduction potential of Cu²⁺ is more than that of H₂O molecules.

Cu²⁺(aq) + 2e^– → Cu(aq) ;\(E^{\ominus}\) = + 0.34V ;
H₂O(l) + 2e^– → H₂(g) + 2OH^– ;\(E^{\ominus}\) = – 0.83V

Hence, Cu²⁺ ions are reduced at the cathode and get deposited.
Similarly, at the anode, either of Cl^– or H₂O is oxidized. The oxidation , potential of H₂O is higher than that of Cl^–

2Cl^–(aq) → Cl₂(g) + 2e^– ;\(E^{\ominus}\) = -1.36V :K
2H₂O(l) → O₂(g) + 4H⁺(aq) + 4e^– ;\(E^{\ominus}\) = -1.23V

But oxidation of H₂O molecules occurs at a lower electrode potential . than that of Cl^– ions because of over-voltage (extra voltage required to liberate gas). As a result, Cl^– ions are oxidized at the anode to liberate Cl₂ gas. :

Question 28.
Arrange the following metals in the order in which they displace each other from the solution of their salts.
Al, Cu, Fe, Mg and Zn. ‘
Answer:
A metal of stronger reducing power displaces another metal of weaker reducing power from its solution of salt.
The order of the increasing reducing power of the given metals is
Cu < Fe < Zn < Al < Mg. Hence, we can say that Mg can displace Al from its salt solution, but Al cannot displace Mg. Thus, the order in which the given metals displace each other from the solution of their salts is given below:
Mg > Al > Zn > Fe > Cu

Question 29.
Given the standard electrode potentials:
K⁺ / K = – 2.93V, Ag⁺ / Ag = 0.80 V, Hg²⁺ /Hg = 0.79 V
Mg²⁺/ Mg = -2.37 V, Cr³⁺/Cr = -0.74 V Arrange these metals in their increasing order of reducing power.
Answer:
The lower the electrode potential, the stronger is the reducing agent. Therefore, the increasing order of the reducing power of the given metal is
Ag < Hg < Cr < Mg < K.

Question 30.
Depict the galvanic cell in which the reaction Zn(s) + 2Ag⁺(aqr) → Zn²⁺(aqr) + 2Ag(s) takes place, further show:
(i) which of the electrode is negatively charged,
(ii) the carriers of the current in the cell, and
(iii) individual reaction at each electrode.
Answer:
The galvanic cell corresponding to the given redox reaction can be represented as:
Zn / Zn²⁺ (aq) | | Ag⁺(aq) / Ag
(i) Zn electrode is negatively charged because at this electrode, Zn oxidizes to Zn²⁺ and the leaving electrons accumulate on this electrode.
(ii) Ions are the carriers of current in the cell.
(iii) The reaction taking place at Zn electrode can be represented as:
Zn(s) → Zn²⁺ (aq) + 2e^–
and the reaction taking place at Ag electrode can be represented as:
Ag⁺(aq) + e^– → Ag(s)

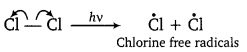
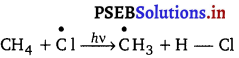
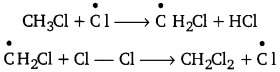
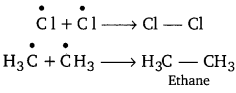
Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 7 Equilibrium Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 7 Equilibrium

PSEB 11th Class Chemistry Guide Equilibrium InText Questions and Answers

Question 1.
A liquid is in equilibrium with its vapour in a sealed container at a fixed temperature. The volume of the container is suddenly increased.
(a) What is the initial effect of the change on vapour pressure?
(b) How do rates of evaporation and condensation change initially?
(c) What happens when equilibrium is restored finally and what will be the final vapour pressure?
Answer:
(a) If the volume of the container is suddenly increa50sed, then the vapour pressure would decrease initially. This is because the amount of vapour remains the same, but the volume increases suddenly. As a result, the same amount of vapour is distributed in a larger volume.
(b) Since the temperature is constant, the rate of evaporation also remains constant. When the volume of the container is increased, the density of the vapour phase decreases. As a result, the rate of collisions of the vapour particles also decreases. Hence, the rate of condensation decreases initially.
(c) When equilibrium is restored finally, the rate of evaporation becomes equal to the rate of condensation. In this case, only the volume changes while the temperature remains constant. The vapour pressure depends on temperature and not on volume. Hence, the final vapour pressure will be equal to the original vapour pressure of the system.

Question 2.
What is K_c for the following equilibrium when the equilibrium concentration of each substance is: [SO₂] = 0.60M,[O₂] = 0.82M and [SO₃] = 1.90 M?
2SO₂(g) + O₂(g) ↔ 2SO₃(g)
Answer:
The given reaction is
2SO₂(g) + O₂(g) ↔ 2SO₃(g)
Equilibrium constant
K_c = \(\frac{\left[\mathrm{SO}_{3}\right]^{2}}{\left[\mathrm{SO}_{2}\right]^{2}\left[\mathrm{O}_{2}\right]}=\frac{(1.90 \mathrm{M})^{2}}{(0.60 \mathrm{M})^{2}(0.82 \mathrm{M})}\)
= 12.238 M^-1

Question 3.
At a certain temperature and total pressure of 10⁵ Pa, iodine vapour contains 40% by volume of I atoms I₂(g) ⇌ 2I(g)
Calculate K_p for the equilibrium.
Answer:
Given, I₂(g) ⇌ 2I(g)
I atoms in iodine vapours = 40% by volume
So, iodine vapours of I₂ molecules = 60% by volume

Question 4.
Write the expression for the equilibrium constant, Kc for each of the following reactions:
(i) 2NOCl(g) ⇌ 2NO (g) + Cl₂(g)
(ii) 2CU(NO₃)₂(S) ⇌ 2CuO(s) + 4NO₂(g) + O₂(g)
(iii) CH₃COOC₂H₅(oq) + H₂O(l) ⇌ CH₃COOH(aq) + C₂H₅OH(ag)
(iv) Fe³⁺(aq) + 3OH^–(aq) ⇌ Fe(OH)₃(s)
(v) I₂(s) + 5F₂ ⇌ 2IF₅
Answer:

Question 5.
Find out the value of K_c for each of the following equilibria from the value of Kp.
(i) 2NOCl(g) ⇌ 2NO(g) + Cl₂(g); K_p = 1.8 x 10^-2 at 500 K
(ii) CaCO₃(s) ⇌ CaO(s) + CO₂(g); K_p = 167 at 1073 K
Answer:
The relation between K_p and K_c is given as
K_p = K_c(RT)^Δn
(i) 2NOCl(g) ⇌ 2NO(g) + Cl₂(g); K_p = 1.8 x 10^-2 at 500 K.
Δn = 3 – 2 = 1
R = 0.0831 bar L mol^-1K^-1
T = 500 K
K_p =1.8 x 10^-2
K_p = K_c( RT)^Δn
1.8 x 10^-2 = K_c(0.0831 x 500)¹
K_c = \(\frac{1.8 \times 10^{-2}}{0.0831 \times 500}\) = 4.33 x 10^-4

(ii) CaCO₃(s) ⇌ CaO(s) + CO₂(g); K_p = 167 at 1073 K
Δn = 2 -1 = 1
R = 0.0831 bar L mol^-1K^-1
T = 1073 K
K_p =167
Now, K_p = K_c(RT)^Δn
⇒ 167 = K_c(0.0831 x 1073)¹
⇒ K_c = \(\frac{167}{0.0831 \times 1073}\) = 1.87

Question 6.
For the following equilibriuih, K_c = 6.3 x 10¹⁴ at 1000 K
NO(g) + O₃(g) ⇌ NO₂(g) + O₂(g)
Both the forward and reverse reactions in the equilibrium are elementary bimolecular reactions. What is K_c, for the reverse reaction?
Answer:
It is given that K_c for the forward reaction is 6.3 x 10¹⁴ at 1000 K.
Then, K_c for the reverse reaction will be,
NO₂(g) + O₃(g) ⇌ NO(g) + O₃(g)
K_c = \(\frac{1}{K_{c}}=\frac{1}{6.3 \times 10^{14}}\) = 1.59 x 10^-15

Question 7.
Explain why pure liquids and solids can be ignored while writing the equilibrium constant expression?
Answer:
For a pure substance (both solids and liquids),

Now, the molecular mass and density (at a particular temperature) of a pure substance is always fixed and is accounted for in the equilibrium constant. Therefore, the values of pure substances are not mentioned in the equilibrium constant expression.

Question 8.
Reaction between N₂ and O₂ takes place as follows:
2N₂(g) + O₂(g) ⇌ 2N₂O(g)
If a mixture of 0.482 mol of N₂ and 0.933 mol of O₂ is placed in a 10 L reaction vessel and allowed to form N₂O at a temperature for which K_c = 2.0 x 10^-37 , determine the composition of equilibrium mixture.
Answer:
Let the concentration of N₂O at equilibrium be x.
The given reaction is :

The value of equilibrium constant i.e., K_c = 2.0 x 10^-37 is very small which means negligible amounts of N₂ and O₂ react.

Question 9.
Nitric oxide reacts with Br₂ and gives nitrosyl bromide as per reaction given below:
2NO(g) + Br₂(g) ⇌ 2NOBr(g)
When 0.087 mol of NO and 0.0437 mol of Br₂ are mixed in a closed container at constant temperature, 0.0518 mol of NOBr is obtained at equilibrium. Calculate equilibrium amount of NO andBr₂.
Answer:
The balanced chemical equation is

Given, 2x = 0.0518
x = 0.0259 mol
Moles of NO at equilibrium = 0.087 – 2x
= 0.087-0.0518
= 0.0352 mol
Moles of Br2 at equilibrium = 0.0437 – x
= 0.0437 – 0.0259
= 0.0178 mol

Question 10.
At 450 K, K_p = 2.0 x 10¹⁰/bar for the given reaction at equilibrium.
2SO₂(g) + O₂(g) ⇌ 2SO₃(g)
What is K_c at this temperature?
Answer:
The given reaction is
2SO₂(g) + O₂(g) ⇌ 2SO₃Cg)
Δn = 2 – 3 = -1
T = 450 K
R = 0.0831 bar L K^-1 mol^-1
K_p = 2.0 x 10¹⁰ bar^-1
We know that,
K_p = K_c(RT)^Δn
=> 2.0 x 10¹⁰ bar^-1 = k_c(0.0831 L bar K^-1 mol^-1 x 450 K)^-1
\(K_{c}=\frac{2.0 \times 10^{10} \mathrm{bar}^{-1}}{\left(0.0831 \mathrm{~L} \mathrm{barK} \mathrm{K}^{-1} \mathrm{~mol}^{-1} \times 450 \mathrm{~K}\right)^{-1}}\)
K_c = (2.0 x 10¹⁰ bar^-1) (0.0831 L bar K^-1mol^-1450 K)
= 74.79 x 10¹⁰ L mol^-1 = 7.48 x 10¹¹ L mol^-1

Question 11.
A sample of HI(g) is placed in flask at a pressure of 0.2 atm. At equilibrium the partial pressure of HI(g) is 0.04 atm. What is K_p for the given equilibrium?
2HI(g) ⇌ H₂(g) + I₂(g)
Answer:
The given reaction is

∵ Decrease is pressure of HI = 0.2 – 0.04 = 0.16 atm;
So equilibrium pressure of H₂ is \(\frac{0.16}{2}\) = 0.08 atm and for I₂ is \(\frac{0.16}{2}\) = 0.08 atm
as two moles of HI on dissociation gives 1 mol of H₂ and 1 mol of I₂.
Therefore,
K_p = \(\frac{p_{\mathrm{H}_{2}} \times p_{\mathrm{I}_{2}}}{\left(p_{\mathrm{HI}}\right)^{2}}=\frac{0.08 \times 0.08}{(0.04)^{2}}=\frac{0.0064}{0.0016}\) = 4.0
Hence, the value of K_p is 4.0.

Question 12.
A mixture of 1.57 mol of N₂,1.92 mol of H₂ and 8.13 mol of NH₃ is introduced into a 20 L reaction vessel at 500 K. At this temperature, the equilibrium constant, K_c for the reaction
N₂(g) + 3H₂(g) ⇌ 2NH₃(g) is 1. 7 x 10².
Is the reaction mixture at equilibrium? If not, what is the direction of the net reaction?
Answer:
The given reaction is :
N₂(g) + 3H₂(g) 2NH₃(g)
Given, [N₂] = \(\frac{1.57}{20}\) = 0.0785 M
[H₂] = \(\frac{1.92}{20}\) = 0.096 M
[NH₃] = \(\frac{8.13}{20}\) = 0.4065 M
Now, reaction quotient Q_c. is :
Q_c = \(\frac{\left[\mathrm{NH}_{3}\right]^{2}}{\left[\mathrm{~N}_{2}\right]\left[\mathrm{H}_{2}\right]^{3}}=\frac{(0.4065)^{2}}{(0.0785)(0.096)^{3}}\) = 2.4 x 10³M^-2
Since Q_c ≠ K_c the reaction mixture is not in equilibrium.
Again Q_c > K_c. Hence, the reaction will proceed in the reverse direction.

Question 13.
The equilibrium constant expression for a gas reaction is, K_c = \(\frac{\left[\mathrm{NH}_{3}\right]^{4}\left[\mathrm{O}_{2}\right]^{5}}{\left[\mathrm{NO}^{4}\left[\mathrm{H}_{2} \mathrm{O}\right]^{6}\right.}\)
Write the balanced chemical equation corresponding to this expression.
Answer:
The balanced chemical equation corresponding to the given expression can be written as :
4NO(g) + 6H₂O(l) ⇌ 4NH₃(g) + 5O₂(g)

Question 14.
One mole of H₂O and one mole of CO are taken in 10 L vessel and heated to 725 K. At equilibrium 40% of water (by mass) reacts with CO according to the equation,
H₂O(g) + CO(g) ⇌ H₂(g) + CO₂(g)
Calculate the equilibrium constant for the reaction.
Answer:
The given reaction is

H₂O reacted = 40% of 1 mol of H₂O = 0.4 mol
x = 0.4 mol 1 – x = 1 – 0.4 = 0.6 mol
Therefore, the equilibrium constant for the reaction,
K_c = \(\) = 0.444

Question 15.
At 700 K, equilibrium constant for the reaction
H₂(g) + I₂(g) ⇌ 2HI(g)
is 54.8. If 0.5 mol L^-1 of Hl(g) is present at equilibrium at 700 K, what are the concentration of H₂(g) and I₂(g) assuming that we initially started with HI(g) and allowed it to reach equilibrium at 700 K?
Answer:
The given reaction is
H₂(g) + I₂(g) ⇌ 2HI(g); K_c = 54.8
Or the reaction
2HI(g) ⇌ H₂(g) + I₂(g); K_c‘ = \(\)
Given, [HI] = 0.5 mol L^-1
According to equation
[H₂] = [I₂] = x mol L^-1
Therefore,
\(\frac{\left[\mathrm{H}_{2}\right]\left[\mathrm{I}_{2}\right]}{[\mathrm{HI}]^{2}}=K_{c}^{\prime}\)
⇒ \(\frac{x \times x}{(0.5)^{2}}=\frac{1}{54.8}\)
⇒ x² = \(\frac{0.25}{54.8}\)
⇒ x = 0.06754
x = 0.068 mol L^-1
Hence, at equilibrium, [H₂] = [I₂] = x = 0.068 mol L^-1

Question 16.
What is the equilibrium concentration of each of the substances in the equilibrium when the initial concentration of IC1 was 0.78 M?
2ICl(g) ⇌ I₂(g) + Cl₂(g); K_c = 0.14
Answer:

Question 17.
K_p = 0.04 atm at9 K for the equilibrium shown below. What is the equilibrium concentration of C₂H₆ when it is placed in a flask at 4.0 atm pressure and allowed to come to equilibrium?
Answer:

Question 18.
Ethyl acetate is formed by the reaction between ethanol acid and acetic acid and the equilibrium is represented as :
CH₃COOH(l) + C₂H₅OH (l) ⇌ CH₃COOC₂H₅(Z) + H₂O(l)
(i) Write the concentration ratio (reaction quotient), Q_c, for this reaction (note: water is not in excess and is not a solvent in this reaction)
(ii) At 293 K, if one starts with 1.00 mol of acetic acid and 0.18 mol of ethanol, there is 0.171 mol of ethyl acetate in the final equilibrium mixture. Calculate the equilibrium constant.
(iii) Starting with 0.5 mol of ethanol and 1.0 mol of acetic acid and maintaining it at 293 K, 0.214 mol of ethyl acetate is found after sometime. Has equilibrium been reached?
Answer:

Question 19.
A sample of pure PCl₅ was introduced into an evacuated vessel at 473K. After equilibrium was attained, concentration of PCl₅ was found to be 0.5 x 10^-1 mol L^-1. If value of K is 8.3 x 10^-3, what are the concentrations of PCl₃ and Cl₂ at equilibrium?
PCl₅ (g) ⇌ PCl₃(g) + Cl₂(g)
Answer:
The given reaction is

It is given that the value of equilibrium constant, K = 8.3 x 10^-3.
K_c = \(\frac{\left[\mathrm{PCl}_{3}\right]\left[\mathrm{Cl}_{2}\right]}{\left[\mathrm{PCl}_{5}\right]}\)
[Given, [PCl₅]_equili = 0.5 x 10^-1 mol L^-1]
\(\frac{x \times x}{0.5 \times 10^{-1}}\) = 8.3 x 10^-3
⇒ x² = 4.15 x10^-4
⇒ x = 2.04 x 10^-2 = 0.0204 mol L^-1 = 0.02 mol L^-1
Therefore, at equilibrium,
[Pcl₃] = [Cl₂] = 0.02 mol L^-1

Question 20.
One of the reaction that takes place in producing steel from iron ore is the reduction of iron (H) oxide by carbon monoxide to give iron metal and CO₂.
FeO(s) + CO(g) ⇌ Fe(s) + CO₂ (g); K_p = 0.265 atm at 1050 K. What are the equilibrium partial pressures of CO and ₂ at 1050 K if the initial partial pressures are P_Co = 1.4 atm and pCO₂ = 0.80 atm?
Answer:
(i) The given reaction is

Since Q_p > K_p, the reaction will proceed in the backward direction.
Therefore, we can say that the pressure of CO will increase while the pressure of CO₂ will decrease.
Now,let the increase in pressure of CO = decrease in pressure of CO₂ be p.
Hence pCO₂ = 0.80 – p and P_CO = 1.4 + p
and K_p = \(\frac{p_{\mathrm{CO}_{2}}}{p_{\mathrm{CO}}}\)
0.265 = \(\frac{0.80-p}{1.4+p}\)
0.371 + 0.265p = 0.80 — p= 1.265p= 0.429
p = 0.339atm
Hence, at equilibrium
P_CO2 = 0.80 – 0.339 = 0.461 atm
And, equilibrium partial pressure of
P_CO = 1.4 + 0.339 = 1.739 atm.

Question 21.
Equilibrium constant, K_c for the reaction
N₂(g) + 3H₂(g) ⇌ 2NH₃(g) at 500 K is 0.06 1.
At a particular time, the analysis shows that composition of the
reaction mixture is 3.0 mol L^-1 N₂,2.0 mol L^-1 H₂ and 0.5 mol L^-1 NH₃ Is the reaction at equilibrium? if not in which direction
does the reaction tend to proceed to reach equilibrium?
Answer:
The given reaction is
N₂(g) + 3H₂(g) ⇌ 2NH₃(g);K_c = 0.061 at 500K
Given, [N₂] = 3.0mol L^-1, [H₂] = 2.0 mol L^-1, [NH₃] = 0.5 mol L^-1
So, Q = \(\frac{\left[\mathrm{NH}_{3}\right]^{2}}{\left[\mathrm{~N}_{2}\right]\left[\mathrm{H}_{2}\right]^{3}}=\frac{(0.5)^{2}}{(3.0)(2.0)^{3}}\) = 0.0104
It is given that K_c = 0.06 1
Since Q_c ≠ K_c, the reaction is not at equilibrium.
Since Q_c < K_c, the reaction will proceed in the forward direction to reach equilibrium.

Question 22.
Bromine monochloride, BrCl decomposes into bromine and chlorine and reaches the equilibrium:
2BrCl(g) ⇌ Br₂(g) + Cl₂(g)
for which K_c = 32 at 500 K. If initially pure BrCl is present at a concentration of 3.3 x 10^-3 mol L^-1, what is its molar concentration in the mixture at equilibrium?
Answer:

x = 11.312(3.30 x 10^-3 – x)
x = 0.03732 – 11.312x
x + 11.312x = 0.03732
x = \(\frac{0.03732}{12.312}\)= 3.0321 x 10^-3 mol L^-1
[BrCl]_equili = (3.30 x 10^-3 – 3.032 x 10^-3) mol L^-1
= 2.68 x 10^-4 mol L^-1

Question 23.
At 1127 K and 1 atm pressure, a gaseous mixture of CO and CO₂ in equilibrium with solid carbon has 90.55% CO by mass
C(s) + CO₂(g) ⇌ 2CO(g)
Calculate K_c for this reaction at the above temperature.
Answer:
Let the total mass of the gaseous mixture be 100g.
Mass of CO = 90.55 g
and, mass of CO₂ = (100 – 90.55) = 9.45 g
Now, number of moles of CO,
n_CO = \(\frac{90.55}{28}\) = 3.234 mol
(Molar mass of CO = 28 g mol^-1 )
Now, number of moles of CO₂,
n_CO = \(\)
(Molar mass of CO₂ = 44 g mol^-1 )

For the given reaction, Δn = 2 -1 = 1
We know that,
K_p = K_c(RT)^Δn
⇒ 14.19 = K_c(0.0831 x 1127)¹
⇒ K_c = 0.154 (approximately)

Question 24.
Calculate (a) \(\Delta \boldsymbol{G}^{\ominus}\) and (b) the equilibrium constant for the formation of N02 from NO and Oa at 298K
NO(g) + \(\frac{1}{2}\)O₂(g) ⇌ NO₂(g)
where \(\Delta_{f} \boldsymbol{G}^{\ominus}\) (N02)= 52.0 kJ/mol; \(\Delta_{f} \boldsymbol{G}^{\ominus}\) (NO) = 87.0kJ/mol;
\(\Delta_{f} \boldsymbol{G}^{\ominus}\) (O2) = 0 kJ/mol
Answer:
(a) The given reaction is
N0(g) + \(\frac{1}{2}\)O₂(g) ⇌ NO₂(g)

= (52.0 – 87.0 + \(\frac{1}{2}\) x 0 )kJ mol^-1 = -35.0 kJ mol^-1

(b) \(\Delta_{r} G^{\ominus}\) = – 2.303 RT logK_c
-35.0 = – 2.303 x 0.0831 x 298 log K_c
∴ log K_c= \(\frac{35}{5.7058}\)= 6.134
∴ K_c = antilog 6.134 = 1.361 x 10⁶.

Question 25.
Does the number of moles of reaction products increase, decrease or remain same when each of the following equilibria is subjected to a decrease in pressure by increasing the volume?
(a) PCl₅(g) ⇌ PCl₃(g) +Cl₂(g)
(b) CaO (s) + CO₂ (g) ⇌ CaCO₃ (s)
(c) 3Fe(s) + 4H₂O (g) ⇌ Fe₃O₄ (s) + 4H₅(g)
Answer:
(a)The number of moles of reaction products will increase. According to Le-Chatelier’s principle, if pressure is decreased, then the equilibrium shifts in the direction in which the number of moles of gases is more. In the given reaction, the number of moles of gaseous products is more than that of gaseous reactants. Thus, the reaction will proceed in the forward direction. As a result, the number of moles of reaction products will increase.
(b) The number of moles of reaction products will decrease.
(c) The number of moles of reaction products remains the same

Question 26.
Which of the following reactions will get affected hy increasing the pressure?
Also, mention whether change will cause the reaction to go into forward or backward direction.
(i) COCl₂(g) ⇌ CO(g) +Cl₂(g)
(ii) CH₄(g) + 2S₂(g) ⇌ CS₂(g) + 2H₂S(g)
(iii) CO₂(g) + C(S) ⇌ 2CO(g)
(iv) 2H₂(g) +CO(g) ⇌ CH₃OH(g)
(v) CaCO₃(s) ⇌ CaO(s) + CO₂(g)
(vi) 4NH₃(g) + 5O₂(g) ⇌ 4NO(g) + 6H₂O(g)
Answer:
In all the above reactions, the reaction no. (ii) proceeds with the same no. of moles on both sides
i.e., n_p = n_r = 3 .
∴ This reaction will not be affected by the increase in pressure i. e., the direction of equilibrium will not be affected by the increase in pressure. All other reactions will be affected by the increase in pressure.
(i) COCl₂(g) ⇌ CO(g) +Cl₂(g)
n_p > n_r , n_p = 2; nr = 1
∴ Equilibrium will shift to the left increasing pressure.
(iii) CO₂(g) + C(S) ⇌ 2CO(g)
Here, n_r – 1; n_p = 2, therefore n_p > n_r
∴ Equilibrium will go to left on increase of pressure.
(iv) 2H₂(g) +CO(g) ⇌ CH₃OH(g)
Here, n_r = 3; n_p = 1 therefore n_p < n_r
∴ Equilibrium will shift to the right on increasing pressure.
(v) CaCO₃(s) ⇌ CaO(s) + CO₂(g)
Here n_r = 0; n_p = 1, therefore n_p > n_r
∴ Equilibrium will shift backwards (left) on increasing the pressure.
(vi) 4NH₃(g) + 5O₂(g) ⇌ 4NO(g) + 6H₂O(g)
Here n_r = 9; n_p = 10, therefore n_p > n_r
∴ Equilibrium will shift backwards on increasing the pressure.

Question 27.
The equilibrium constant for the following reaction is 1.6 x 10⁵ at 1024 K.
H₂(g) + Br₂(g) ⇌ 2HBr(g)
Find the equilibrium pressure of all gases if 10.0 bar of HBr is introduced into a sealed container at 1024K.
Answer:
Given reaction is H₂(g) + Br₂(g)⇌ 2HBr(g); K_p = 1.6 x 10⁵ at 1024 K
Therefore, for the reaction 2HBr(g) ⇌ H₂(g)+Br₂(g), the equilibrium constant will be,

p = 2.5 x 1^-2(5.0 x 10^-3)p
p+(5.0 x 10^-3)p = 2.5 x 10^-2
(1005 x 10^-3)p = 2.5 x 10^-2
p = 2.49 x 10^-2 bar = 2.5 x 10^-2 bar
rherefore, at equilibrium,
[H₂] = [Br₂] = 2.49 x 10^-2 bar
[HBr] =10 — 2 x (2.49 x 10^-2) bar
= 9.95 bar = 10 bar

Question 28.
Dihydrogen gas is obtained from natural gas by partial oxidation with steam as per following endothermic reaction:
CH₄(g) + H₂O(g) ⇌ CO(g) + 3H₂(g)
(a) Write an expression for K_p for the above reaction.
(b) How will the values of k_p and composition of equilibrium mixture be affected by
(i) increasing the pressure
(ii) increasing the temperature
(iii) Using a catalyst?
Answer:
(a) The given reaction is
CH₄(g) + H₄O(g) ⇌ CO(g) + 3H₂(g)
\(K_{p}=\frac{p_{\mathrm{CO}} \times p_{\mathrm{H}_{2}}^{3}}{p_{\mathrm{CH}_{4}} \times p_{\mathrm{H}_{2} \mathrm{O}}}\)
(b) (1) According to LeChatelier’s principle, the equilibrium will shift in the backward direction.
(ii) According to Le-Chatelier’s principle, as the reaction is endothermic, the equilibrium will shift in the forward direction.
(iii) The equilibrium of the reaction is not affected by the presence of a catalyst. A catalyst only increases the rate of a reaction. Thus, equilibrium will be attained quickly.

Question 29.
Describe the effect of:
(a) addition of H₂
(b) addition of CH₃OH
(e) removal of CO (d) removal of CH₃OH
on the equilibrium of the reaction:
2H₂(g) + CO (g) ⇌ CH₃OH(g)
Answer:
2H₂(g) + CO(g) ⇌ CH₃OH(g)
According to Le Chatelier’s principle,
(a) Addition of H₂ (increase in concentration of reactants) shifts the equilibrium in forward direction (more product is formed).
(b) Addition of CH₃OH (increase in concentration of product) shifts the equilibrium in backward direction.
(c) Removal of CO also shifts the equilibrium in backward direction.
(d) Removal of CH₃OH shifts the equilibrium in forward direction.

Question 30.
At 473K, equilibrium constant K_c for decomposition of phosphorus pentachloride, PCl₅ is 8.3 x 10^-3. If decomposition is depicted as,
PCl₅(g) ⇌ PCl₃(g) + Cl₂(g); \(\Delta_{\boldsymbol{r}} \boldsymbol{H}^{\ominus}\) = 1240 kJ mol^-1
(a) Write an expression for K_c for the reaction.
(b) What is the value of K_c for the reverse reaction at the same temperature?
(c) What would be the effect on K_c if
(i) more PCl₅ is added
(ii) pressure is increased?
(iii) the temperature is increased?
Answer:
PCl₅(g) ⇌ PCl₃(g) + Cl₂(g); Kc = 8.3 x 10^-3
(a) K_c = \(\frac{\left[\mathrm{PCl}_{3}\right]\left[\mathrm{Cl}_{2}\right]}{\left[\mathrm{PCl}_{5}\right]}\)
(b) Value of K_c for the reverse reaction at the same temperature is
K’_c = \(\frac{1}{K_{c}}=\frac{1}{8.3 \times 10^{-3}}\) = 1.2048 x 10² = 120.48
(c) (i) Addition pf PCl₅ have no effect on K_c because K_c is constant at constant temperature.
(ii) K_c does not change with pressure.
(iii) The given reaction is endothermic, hence on increasing the temperature, K_c will increase.

Question 31.
Dihydrogen gas used in Haber’s process is produced by reacting methane from natural gas with high temperature steam. The first stage of two stage reaction involves the formation of CO and H₂. In second stage, CO formed in first stage is reacted with more steam in water gas shift reaction,
CO(g) +H₂O (g) ⇌ CO₂(g) + H₂(g)
If a reaction vessel at 400° C is charged with an equimolar mixture of CO and steam such that p_CO = P_H2O = 4.0 bar, what will be the partial pressure of H₂ at equilibrium? K_P = 10.1 at 400°C
Answer:
The given reaction is
CO(g) + H20(g) ⇌ C02(g) + H2(g)

p = 12.71 – 3.17p
4.17 p = 12.71
p = \(\frac{12.71}{4.17}\) = 3.04 bar
Hence PH₂ = 3.04 bar

Question 32.
Predict which of the following reaction will have appreciable concentration of reactants and products:
(a) Cl₂(g) ⇌ 2Cl(g);K_c = 5 x 10^-39
(b) Cl₂(g) + 2NO(g) ⇌ 2NOCl(g); Kc = 3.7 x 10⁸
(c) Cl₂(g) + 2NO₂(g) ⇌ 2NO₂Cl(g); K_c = 1.8
Answer:
Following conclusions can be drawn from the values of K_c:
(a) Since the value of K_c is very small, this means that the molar concentration of the products is very small as compared to that of the reactants.
(b) Since the value of K_c is quite large, this means that the molar concentration of the products is very large as compared to that of the reactants.
(c) Since the value of K_c is 1.8, this means that both the products and reactants have appreciable concentration.

Question 33.
The value of K_c for the reaction
3O₂(g) ⇌ 2O₃(g)
is 2.0 x 10^-50 at 25°C. If the equilibrium concentration of O₂ in air at 25°C is 1.6 x 10^-2, what is the concentration of O₃?
Answer:
The given reaction is
3O₂(g) ⇌ 2O₃(g)
Then K
It is given that Kc = 2.0 x 10^-50 and [02(g)] = 1.6 x 10^-2
Then, we have,
\(2.0 \times 10^{-50}=\frac{\left[\mathrm{O}_{3}\right]^{2}}{\left[1.6 \times 10^{-2}\right]^{3}}\)
⇒ [O₃]² = 2.0 x 10^-50 x (1.6 x 10^-2)³
⇒ [O₃]² = 8.192 x 10^-56
⇒ [O₃] = 2.86 x 10^-28 M
Hence, the concentration of O₃ is 2.86 x 10^-28 M.

Question 34.
The reaction, CO(g) + 3H₂(g) ⇌ CH₄(g) + H₂O(g) is at equilibrium at 1300 K in a 1L flask. It also contain 0.30 mol of CO, 0.10 mol of H2 and 0.02 mol of H20 and an unknown amount of CH4 in the flask. Determine the concentration of CH4 in the mixture. The equilibrium constant, Kc for the reaction at the given temperature is 3.90.
Answer:
The given equation is
CO(g) + 3H₂(g) ⇌ CH₄(g) + H₂O(g)
Therefore,
\(\frac{\left[\mathrm{CH}_{4}\right]\left[\mathrm{H}_{2} \mathrm{O}\right]}{[\mathrm{CO}]\left[\mathrm{H}_{2}\right]^{3}}=K_{c}\)
Given, K_c = 3.90, [CO] = 0.30 mol, [H₂] = 0.10 mol and [H₂O] \(\frac{\left[\mathrm{CH}_{4}\right] \times 0.02}{0.3 \times(0.1)^{3}}\) = 3.90
[CH₄] = \(\frac{3.90 \times 0.3 \times(0.1)^{3}}{0.02}=\frac{0.00117}{0.02}\)
= 0.0585 M= 5.85 x 10^-2M
Hence, the concentration of CH4 at equilibrium is 5.85 x 10^-2 M.

Question 35.
What is meant by the conjugate acid-base pair? Find the conjugate acid/base for the following species :
\(\mathrm{HNO}_{2}, \mathrm{CN}^{-}, \mathrm{HClO}_{4}, \mathrm{~F}^{-}, \mathrm{OH}^{-}, \mathrm{CO}_{3}^{2-} \text { and } \mathrm{S}^{2-}\)
Answe:
A conjugate acid-base pair is a pair that differs only by one proton.
The conjugate acid-base for the given species is mentioned in the table below:

Question 36.
Which of the followings are Lewis acids
\(\mathbf{H}_{2} \mathbf{O}, \mathbf{B F}_{3}, \mathrm{H}^{+} \text {and } \mathrm{NH}_{4}^{+}\)
Answer:
Lewis acids are those acids which can accept a pair of electrons. For example, BF₃, H⁺ and \(\mathrm{NH}_{4}^{+}\) are Lewis acids.

Question 37.
What will be the conjugate bases for the Bronsted acids : HF, H₂SO₄ and \(\mathrm{HCO}_{3}^{-}\)?
Answer:
The table below lists the conjugate bases for the given Bronsted acids :

Question 38.
Write the conjugate acids for the following Bronsted bases: \(\mathbf{N H}_{2}^{-}\), NH₃ andHCOC^–.
Answer:
The table below lists the conjugate acids for the given Bronsted bases : Bronsted base Conjugate acid

Question 39.
The species : H₂O, HCO^–₃, HSO^–₄ and NH₃ can act both as Bronsted acids and bases. For each case give the corresponding conjugate acid and base.
Answer:
The table below lists the conjugate acids and conjugate bases for the given species :

Question 40.
Classify the following species into Lewis acids and Lewis bases and show how these act as Lewis acid/base: (a) OH^– (b)F^– (c)H⁺ (d) BCl₃
OH^– and F^– are electron rich species and can donate electron pair. Hence, these act as Lewis base.

H⁺ and BCl₃ are electron deficient species and can accept electron pair. Hence, these act as Lewis acid.

Question 41.
The concentration of hydrogen ion in a sample of soft drink is 3.8 x 10^-3 M. What is its pH?
Answer:
Given,
[H⁺] = 3.8 x 10^-3 M
∴ pH value of soft drink = – log[H⁺] = – log(3.8 x 10^-3)
= – log3.8 – log10^-3 = – log3.8 + 3 log10
= – log3.8 + 3
= -0.58 + 3
= 2.42

Question 42.
The pH of a sample of vinegar is 3.76. Calculate the concentration of hydrogen ion in it.
Answer:
Given, pH = 3.76
We know that,
pH = – log[H⁺]
⇒ log[H⁺] = -pH
⇒ [H⁺] = antilog (-pH)
= antilog (-3.76) -1 +1 = antilog \(\overline{4} .24\) = 1.74 x 10-4 M Hence, the concentration of hydrogen ion in the given sample of vinegar is 1.74 x 10^-4 M.

Question 43.
The ionization constant of HF, HCOOH and HCN at 298 K are 6.8 x 10^-4, 1.8 x 10^-4 and 4 8 x 10^-9 respectively. Calculate the ionization constants of the corresponding conjugate base.
Answer:
If K_a is the ionization constant of a weak acid and Kb is the ionization constant of its conjugate base then K_a.K_b = K_w
or K_b = \(\frac{K_{w}}{K_{a}}\)
Given, K_a of HF = 6.8 x 10^-4
Hence, K_b of its conjugate base F^–
= \(\frac{K_{w}}{K_{a}}=\frac{1 \times 10^{-14}}{6.8 \times 10^{-4}}\)= 1.5 x 10^-11
(K_w = ionic product of water =1 x 10^-14 at 298 K)
Given, K_a of HCOOH = 1.8 x 10^-4
= \(\frac{K_{w}}{K_{a}}=\frac{1 \times 10^{-14}}{1.8 \times 10^{-4}}\) = 5.6 x 10^-11
Hence, K_b of its coagulate base CN^–
Given, K_a of HCN = 4.8 x 10^-9
Hence, K_b of its coagulate base HCOO^–
= \(\frac{K_{w}}{K_{a}}=\frac{1 \times 10^{-14}}{4.8 \times 10^{-9}}\) = 2.08 x 10^-6

Question 44.
The ionization constant of phenol is 1.0 x 10^-10. What is the concentration of phenolate ion in 0.05 M solution of phenol? What will be its degree of ionization if the solution is also 0.01 M in sodium phenolate?
Answer:
Ionization of phenol :
C₆H₅OH + H₂O ⇌ C₆H₅O^– + H₃O⁺

Question 45.
The first ionization constant of H2S is 9.1 x 10^-8. (i) Calculate the concentration of HS^– ion in its 0.1 M solution. (ii) How will this concentration be affected if the solution is 0.1 M in HCI also? (ifi) If the second dissociation constant of H₂S is 1.2 x 10^-13, calculate the concentration of S^2- under both conditions.
Answer:

Hence, concentration of [HS^–] is decreased in the presence of 0.1 M
HCI due to common-ion effect.
(iii) For second dissociation constant,
HS + H₂O ⇌ H₃O⁺ + S^2- (In absence of HCl)
[HS^–] = 9.54 x 10^-5 M
\(K_{a_{2}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{S}^{2-}\right]}{\left[\mathrm{HS}^{-}\right]}\)

Question 46.
The ionization constant of acetic acid is 1.74 x 10^-5. Calculate the degree of dissociation of acetic acid in its 0.05 M solution. Calculate the concentration of acetate ion in the solution and its pH.
Answer:
CH₃COOH CH₃COO^– + H⁺
K_a for CH₃COOH = 1.74 x 10^-5
[CH₃COOH] = c = 0.05 M
CH₃COOH CH₃COO^– + H⁺ [where α = degree of dissociation and c = molar concentration]

[CH₃COO^–] = 0.933 x 10^-3 = 9.33 x 10^-4 M
pH = – log[H⁺] = – log (9.33 x 10^-4)
= – (-4) – log9.3 = 4 – 0.9 = 3.03

Question 47.
It has been found that the pH of a 0.01M solution of an organic acid is 4.15. Calculate the concentration of the anion, the ionization constant of the acid and its pK_a.
Answer:
Let the organic acid be HA.
⇒ HA ⇌ H⁺ + A^–
Concentration of HA = 0.01 M
pH = 4.15
-log[H⁺] = pH= 4.15
log[H⁺] = – 4.15
log[H⁺] = 5.85
[H⁺] = antilog \(\overline{5} .85\)
= 7.080 x 10^-5
K_a = \(\frac{\left[\mathrm{H}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}\)
Now, [H⁺] = [A^–] = 7.08 x 10^-5 M
Then K_a = \(
K_a = 5.01 x 10^-7
PK_a = – logK_a = – log(5.01 x 10^-7)
pK_a = 7 – 0.699 = 6.301

Question 48.
Assuming complete dissociation, calculate the pH of the following solutions:
(a) 0.003 M HCl
(b) 0.005 M NaOH
(c) 0.002 M HBr
(d) 0.002 M KOH
Answer:
(a) HCl (aq) ⇌ H⁺ (aq) + Cl^–(aq)
[HCl]= 0.003 M
As HC1 is completely dissociated into H⁺ ions
∴ [H⁺] = [HCl] = 0.003 M
pH = – log[H⁺] = – log [3 x 10^-3]
= 3 + (-0.4771) = 2.523
(b) NaOH(aq) ⇌ Na⁺(aq) + OH^– (aq)
[NaOH] = 0.005 = 5 x 10^-3 M
[OH^–] = [NaOH] = 5 x 10^-3 M
∴ [latex]\left[\mathrm{H}^{+}\right]=\frac{K_{w}}{\left[\mathrm{OH}^{-}\right]}=\frac{1.0 \times 10^{-14}}{5.0 \times 10^{-3}}\)
[H⁺]= 2.0 x 10^-12
∴ pH = – log(2 x 10^-12) = – (-12) – log2
= 12 – 0.30 = 11.70
[log2 = 0.30]

(c)

[HBr] = 0.002 M
[H⁺]= [HBr] = 0.002 M= 2.0 x 10^-3 M
pH = – log[H⁺] = – log[2 x 10^-3]
=- (-3) – log2
= 3 – log2
= 3 – 0.3 = 2.70

(d)

[OH^–] = 0.002 M
[H⁺] = \(\frac{K_{w}}{\left[\mathrm{OH}^{-}\right]}=\frac{1.0 \times 10^{-14}}{0.002}\) = 2 x 10^-12
pH = – log[H⁺] = -(-12) – log 5 = 12 – 0.70 = 11.30

Question 49.
Calculate the pH of the following solutions:
(a) 2 g of TIOH dissolved in water to give 2 litre of solution.
(b) 0.3 g of Ca(OH)₂ dissolved in water to give 500 niL of solution.
(c) 0.3 g of NaOH dissolved in water to give 200 mL of solution.
(d) 1 mL of 13.6 M HC1 is diluted with water to give 1 litre of solution.
Answer:

(d) 1 mL of 13.6 M HC1 is diluted with water to give 1 litre of solution HC1 is completely dissociated to give H+ ions
[HCl] = ?
M₁V₁ = M₂V₂
1 mL of 13.6 M HCl = 1000 mL of M₂
M₂ = \(\frac{1 \times 13.6}{1000}\) = 0.0136 M
[HC1] = [H+] = 0.0136 M pH = – log[H+] = – log(1.36 x 10-2)
= – (-2) – log 1.36 = 2 – 0.13 = 1.87

Question 50.
The degree of ionization of a 0.1 M bromoacetic acid solution is 0.132. Calculate the pH of the solution and the pK_a of bromoacetic acid.
Answer:
α (Degree of ionization) = 0.132
c (molar cone.) = 0.1 M

∴ H⁺ = c x α = 0.1 x 0.132 = 0.0132
pH = – logH⁺ = – log(1.32 x 10^-2)
= – (-2) – log 1.32 = 2 – 0.12 = 1.88
pK_a = -logK_a
Now, K_a = cα²
K_a = 0.1 x (0.132)² = 1.74 x 10^-3
∴ pK_a = – log (1.74 x 10^-3) = – (-3) – log1.74 = 3 – 0.24 = 2.76

Question 51.
The pH of 0.005 M codeine (C₁₈H₂₁NO₃) solution is 9.95.
Calculate its ionization constant and pK_b.
Answer:
Molar cone, of codeine, c = 0.005 = 5 x 10^-3
pH = 9.95
pOH = 14 – 9.95 = 4.05 (∵ pH + pOH = 14)
pOH = – log [OH^–]
log[OH^–] = -4.05= \(\overline{5} .95\)
[OH^–] = antilog \(\overline{5} .95\)
= 8.91 x 10-5
k_b = \(\left(\frac{8.91 \times 10^{-5}}{5 \times 10^{-3}}\right)^{2}\) = 1.588 x 10^-6
pK_b = – logK_b = – log(1.588 x 10^-6)
= 6 + (-0.2009) = 5.7991 = 5.80

Question 52.
What is the pH of 0.001 M aniline solution? The ionization constant of aniline can be taken from table 7.7 (427 x 10^-10). Calculate the degree of ionization of aniline in the solution. Also calculate the ionization constant of the conjugate acid of aniline.
Answer:
Given, K_b = 4.27 x 10^-10, c = 0.001 M
\(\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{NH}_{2}+\mathrm{H}_{2} \mathrm{O} \rightleftharpoons \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{NH}_{3}^{+}+\mathrm{OH}^{-}\)

[0H] = 6.534 x 10^-7
pOH = — log(6.534 x 10^-7)
= 7+ (-0.8152)= 6.18
pH + pOH =14
pH 14—6.18=7.82

Thus, the ionization constant of the conjugate acid of aniline is 2.34 x 10^-5.

Question 53.
Calculate the degree of ionization of 0.05 M acetic acid if its pK_a value is 4.74.
How is the degree of dissociation affected when its solution also contains (a) 0.01 M (b) 0.1 M in HCl?
Answer:
PK_a = – log K_a,
4.74 =-logK_a
log K_a = -4.74 = \(\overline{5} .26\)
Ka = antilog \(\overline{5} .26\) = 1.82 x 10^-5

[CH₃COOH is a weak acid and HC1 is a strong acid, so we can assume
that (cα + 0.01) 0.01]

In the presence of strong acid, dissociation of weak acid i.e., CH₃COOH decreases due to common ion effect.

Q.54. The Ionization constant of dimethylanilne is 54 x 10.
Calculate Its degree of ionization in its 0.02 M solution. What
percentage of dimethylamine is ionized if the solution is also
0.1MInNaOH?
Ans. Given, Kb = 5.4 x 10
c=0.02M

It means that in the presence of 0.1 M NaOH, 0.54% of dimethylamine will get dissociated.

Question 55.
Calculate the hydrogen ion concentration in the following biological fluids whose pH are given below :
(a) Human muscle-fluid, 6.83 (b) Human stomach fluid, 1.2
(c) Human blood, 7.38 (d) Human saliva, 6.4.
Answer:
(a) pH of Human muscle fluid = 6.83
pH = – log[H+] log[H⁺] = -6.83 = \(\overline{7} .17\)
[H⁺] = antilog \(\overline{7} .17\)
[H⁺] = 1.48 x 10^-7 M

(b) pH of Human stomach fluid =1.2
log[H⁺] = -1.2 = \(\overline{2} .80\)
[H⁺] = antilog \(\overline{2} .80\)
.-. [H⁺] = 6.3 x 10^-2 M

(c) pH of Human blood = 7.38
log[H⁺] = – 7.38 = \(\overline{8} .62\)
.-. [H⁺] = antilog \(\overline{8} .62\) = 4.17 x 10^-8 M

(d) pH of Human saliva = 6.4
log[H⁺] =-6.4 = \(\overline{7} .60\)
[H⁺] = antilog \(\overline{7} .60\) = 3.98 x 10^-7 M

Question 56.
The pH of milk, black coffee, tomato juice, lemon juice and egg white are 6.8, 5.0, 4.2, 2.2 and 7.8 respectively. Calculate corresponding hydrogen ion concentration in each.
Answer:
The hydrogen ion concentration in the given substances can be calculated by using the given relation: pH = – log[H⁺]
(i) pH of milk = 6.8
Since, pH = -log[H⁺]
6.8 = -log[H+] log[H⁺] = -6.8 = \(\overline{7} .20\)
[H+] = antilog (\(\overline{7} .20\)) = 1.5 x 10~7 M

(ii) pH of black coffee = 5.0
Since, pH = – log[H⁺]
5.0 = – log[H+] log[H⁺] = – 5.0
[H⁺] = antilog (-5.00) = 10-5 M

(iii) pH of tomato juice = 4.2
Since, pH = – log[H⁺]
4.2 = – log[H⁺]
log[H⁺] = – 4.2 = \(\overline{5} .80\)
[H⁺] = antilog (\(\overline{5} .80\)) = 6.31 x 10^-5M

(iv) pH of lemon juice = 2.2
Since, pH = – log[H⁺]
2.2 = – log[H+]
log[H⁺] = -2.2 = \(\overline{3} .8\)
[H⁺] – antilog (\(\overline{3} .8\)) = 6.31 x 10^-3 M

(v) pH of egg white = 7.8
Since, pH = -log[H⁺]
7.8 = – log[H⁺]
log[H⁺]= -7.8 = \(\overline{8} .20\)
[H⁺] = antilog (\(\overline{8} .20\)) = 1.58 x 10^-8 M

Question 57.
0.561 g of KOH is dissolved in water to give 200 mL of solution at 298 K. Calculate the concentrations of potassium, hydrogen and hydroxyl ions. What is its pH?
Answer:
Molar cone, of KOH = \(\frac{0.561 \times 1000}{56.1 \times 200}\) = 0.05M
56.1 x 200
KOH being a strong electrolyte, is completely ionized in aqueous solution.
KOH(aq) ⇌ K⁺(aq) + OH^–(aq)
[OH^–] = 0.05 M = [K⁺]
[H⁺][OH^–] = k_w
[H⁺] = \(\) = 2 x 10^-13
pH = – log[H⁺] = – log[2 x 10^-13]
= – (-13) – log2 = 13 – 0.03
∴ pH = 12.70

Question 58.
The solubility of Sr(OH)₂ at 298 K is 19.23 g/L of solution. Calculate the concentrations of strontium and hydroxyl ions and the pH of the solution.
Answer:
Solubility of Sr(OH)₂ = 19.23 g/L
Then, concentration of Sr(OH)₂ = \(\frac{19.23}{121.63 \times 1}\) M = 0.1581 M
Sr(OH)₂(aq) Sr²⁺(aq) + 2(OH^–)(aq)
∴ [Sr²⁺] = 0.1581 M
[OH^–] – 2 x 0.1581 M = 0.3162 M
Now
K_w = [OH^–] [H⁺]
\(\frac{1 \times 10^{-14}}{0.3162}\) = [H⁺]
[H⁺] = 3.16 x 10^-14
pH = – log[H⁺]
pH = 14 – 0.4997 = 13.5003 ≈ 13.5

Question 60.
The pH of 0.1 M solution of cyanic acid (HCNO) is 2.34. Calculate the ionization constant of the acid and its degree of ionization in the solution.
Answer:
Given, pH = 2.34
Molar cone, (c) = 0.1 M
HCNO H⁺ + CNO^–
pH = – log[H⁺]
2.34 = -log[H⁺]
log[H⁺] =-2.34 = \(\overline{3} .66\)
.-. [H⁺] = antilog \(\overline{3} .66\) = 4.57 x 10^-3 M
[H⁺] = \(\sqrt{K_{a}^{c}}\)
4.57 x 10^-3 = \(\sqrt{K_{a}^{c}}\)
Ionization constant,
K_a = 2.088 x 10^-4
Degree of ionization α = \(\sqrt{\frac{K_{a}}{c}}=\sqrt{\frac{2.088 \times 10^{-14}}{0.1}}\)
α = 0.0457

Question 61.
The ionization constant of nitrous acid is 45 x 104. Calculate the pH of 0.04 M sodium nitrite solution and also its degree of hydrolysis.
Answer:
Hydrolysis constant K_h = \(\frac{K_{w}}{K_{a}}\)
where K_w = Ionic product of water, K_a = Ionisation constant of the acid

pOH = -log(9.42 x 10^-7)= 7-0.97= 6.03
∴ pH = 14 – pOH = 14 – 6.03 = 7.97

Question 62.
A 0.02 M solution of pyridinium hydrochloride has pH = 3.44. Calculate the ionization constant of pyridine.
Answer:
Given, pH = 3.44
We know that,
PH = – log[H⁺]
.-. [H⁺]= 3.63 x 10^-4
Then K_h = \(\frac{\left(3.63 \times 10^{-4}\right)^{2}}{0.02}\) (Concentration = 0.02M)
=> K_h = 6.6 x 10^-6
Now, K_h = \(\frac{K_{w}}{K_{a}}\)
K_a = \(\frac{K_{w}}{K_{h}}=\frac{1 \times 10^{-14}}{6.6 \times 10^{6}}\)
= 1.51 x 10^-9

Question 63.
Predict if the solutions of the following salts are neutral, acidic or basic:
NaCl, KBr, NaCN, NH₄NO₃, NaNO₂ and KF
Answer:

Question 64.
The ionization constant of chloroacetic acid is 1.35 x 10^-3 . What will be the pH of 0.1 M acid and its 0.1 M sodium salt solution?
Answer:
Given that Ka = 1.35 x 10^-3.
=> Ka = cα²
α = \(\sqrt{\frac{K_{a}}{c}}=\sqrt{\frac{1.35 \times 10^{-3}}{0.1}}\)
(∵ Concentration of acid = 0.1 M)
= \(\sqrt{1.35 \times 10^{-2}}\) =0.116
.-. [H⁺]= cα = 0.1 x 0.116 = 0.0116
=> pH = – log[H⁺] = – log[0.0116] = 1.94
To find pH of 0.1 M sodium salt, we use the formula
pH = – \(\frac{1}{2}\)[log C_w + log K_a – log c]
= –\(\frac{1}{2}\)[log1 x 10^-14 + log(1.35 x 10^-3) – log(0.1)]
= –\(\frac{1}{2}\)[-14 + (-3 + 0.1303) – (-1)]
= – \(\frac{1}{2}\) [-15.8697] = 7.93485 ≈ 7.94

Question 65.
Ionic product of water at 310 K is 2.7 x 10^-14. What is the pH of neutral water at this temperature?
Answer:
Ionic product,
K_w = [H₃O⁺] [OH^–]
= 2.7 x 10^-14 at 310 K
H₂O + H₂O *=* [H₃0⁺][OH^–]
[H₃0⁺]= [OH^–]
Therefore, [H₃0⁺] = \(\sqrt{2.7 \times 10^{-14}}\)
⇒ = 1.64 x 10^-7 M
⇒ [H₃0⁺] = 1.64 x 10^-7
⇒ pH = – log[H₃0⁺] = – log[1.64 x 10^-7 = 6.78
Hence, the pH of neutral water is 6.78.

Question 66.
Calculate the pH of the resultant mixtures :
(a) 10 mL of 0.2 M Ca(OH)₂ + 25 mL of 0.1 M HC1
(b) 10 mL of 0.01 M H₂SO₄ + 10 mL of 0.01 M Ca(OH)₂
(c) 10 mL of 0.1 M H₂SO₄ + 10 mL of 0.1 M KOH
Answer:

Question 67.
Determine the solubilities of silver chromate, barium chromate, ferric hydroxide, lead chloride and mercurous iodide at 298 K from their solubility product constants.
[K_sp(Ag₂CrO₄) = 1.1 x 10^-12, K_sp(BaCrO₄) = 1.2 x 10^-10,
K_sp[Fe(OH)₃] = 1.0 x 10^-38, K_sp(PbCl₂) = 1.6 x 10^-5
K_sp(Hg₂I₂) = 4.5 x 10^-29]
Determine also the molarities of individual ions.
Answer:
(i) Silver chromate : Ag₂CrO₄⇌ 2Ag⁺ + CrO₄^2-, K_sp = 1.1 x 10^-12
Then, K_sp = [Ag⁺]²[CrO₄^2-]
Let the solubility of Ag₂CrO₄ be s.
⇒ [Ag⁺] = 2s and [CrO₄^2-] = s
Then, K_sp = (2s)² s – 4s³
⇒ 1.1 x 10^-12 = 4s³
0.275 x 10^-12 = s³
s = 0.65 x 10^-4 M
Molarity of Ag⁺ = 2s = 2 x 0.65 x 10^-4
= 1.30 x 10^-4 M
Molarity of CrO₄^2- = s = 0.65 x 10^-4 M

(ii) Barium chromate : BaCrO₄ ⇌ Ba²⁺ + \(\mathrm{CrO}_{4}^{2-}\); K_sp = 1.2 x 10^-10
Then, K_sp = [Ba²⁺] [latex]\mathrm{CrO}_{4}^{2-}[/latex]
Let s be the solubility of BaCrO₄.
⇒ [Ba²⁺] = s and [latex]\mathrm{CrO}_{4}^{2-}[/latex] = s
⇒ K_sp = s²
⇒ 1.2 x 10^-10 = s²
⇒ s = 1.09 x 10^-5 M
Molarity of [Ba²⁺] = Molarity of [latex]\mathrm{CrO}_{4}^{2-}[/latex] = s = 1.09 x 10^-5 M

(iii) Ferric hydroxide: Fe(OH)₃ ⇌ Fe²⁺ + 3OH^–; K_sp = 1.0.x 10^-38

K_sp = [Fe²⁺][OH^–]³
Let s be the solubility of Fe(OH)₃
⇒ [Fe³⁺] = s and [OH^–] = 3s
⇒ K_sp = s. (3s)³ = s x 27x³
K_sp = 27x⁴
1.0 x 10^-38 = 27x⁴
0.037 x 10^-38 = s⁴
0.00037 x 10^-36 = s⁴
s = 1.39 x 10^-10 M
Molarity of [Fe³⁺] = s = 1.39 x 10^-10 M
Molarity of [OH^–] = 3s = 4.17 x 10^-10 M

(iv) Lead chloride : PbCl₂ ⇌ Pb²⁺ + 2Cl^–; K_sp = 1.6 x 10^-5
K_sp = [Pb²⁺][Cl^–]²
Let s be the solubility of PbCl₂.
⇒ [Pb²⁺] = s and [Cl^–] = 2s
Thus, K_sp = s. (2s)² = 4s³
⇒ 1.6 x 10^-5 = 4s³
⇒ 0.4 x 10^-5 = s³
4 x 10^-6 = s³
⇒ s = 1.59 x 10^-2 M
Molarity of [Pb²⁺] = s = 1.59 x 10^-2 M
Molarity of [Cl^–] = 2s = 3.18 x 10^-2 M

(v) Mercurous iodide : Hg₂I₂ ⇌ \(\mathrm{Hg}_{2}^{2+}\) + = 4.5 x 10^-29
K_sp = [\(\mathrm{Hg}_{2}^{2+}\) ] []I^–]
Let s be the solubility of [Hg²I²]
⇒ [Hg₂] = s and [I^–] = 2s
K_sp = (s).(2s)² = 4s³
⇒ 4s³ = 4.5 x 10^-29
⇒ s³ = 1.125 x 10^-29
s = 2.24 x 10^-10 M
Molarity of [ \(\mathrm{Hg}_{2}^{2+}\) ] = s = 2.24 x 10^-10 M
Molarity of [I^–] = 2s = 4.48 x 10^-10 M.

Question 68.
The solubility product constant of Ag₂CrO₄ and AgBr are
1.1 x 10^-12 and 5.0 x 10^-13 respectively. Calculate the ratio of the molarities of their saturated solutions.
Answer:
Let s be the solubility of Ag₂CrO₄
Thus, Ag₂CrO₄ ⇌ 2Ag²⁺ + \(\mathrm{CrO}_{4}^{-}\); K_sp = 1.1 x 10^-12
K_sp = [Ag²⁺]². [latex]\mathrm{CrO}_{4}^{-}[/latex]
=> [Ag²⁺] = (2s)² and [latex]\mathrm{CrO}_{4}^{-}[/latex] = s
K_sp = (2s)². s= 4s³
1.1 x 10^-12 = 4s³
s = 6.5 x 10^-5 M

Let s be the solubility of AgBr.
AgBr(s) ⇌ Ag⁺ + Br^–; K_sp = 5.0 x 10^-13
K_sp = s² = 5.0 x 10^-13
s = \(\sqrt{5.0 \times 10^{-13}}\)
∴ s = 7.07 x 10^-7 M

Therefore, the ratio of the molarities of their saturated solution is
\(\frac{s\left(\mathrm{Ag}_{2} \mathrm{CrO}_{4}\right)}{s(\mathrm{AgBr})}=\frac{6.5 \times 10^{-5} \mathrm{M}}{7.07 \times 10^{-7} \mathrm{M}}\) = 9.19

Question 69.
Equal volumes of 0.002 M solutions of sodium iodate and cupric chlorate are mixed together. Will it lead to precipitation of copper iodate? (For cupric iodate, K_sp = 7.4 x 10^-8).
Ans. 2NaIO₃ + Cu(ClO₃)3 → 2NaClO₃ + Cu(IO₃)₂
Molar cone, of both solutions before mixing = 0.002 M
Molar cone, of both solution after mixing
\(\left[\mathrm{IO}_{3}^{-}\right]=\left[\mathrm{Cu}^{2+}\right]=\frac{0.002}{2}\)= 0.001 M
Cu(IO₃)₂ ⇌ Cu²⁺ + \(2 \mathrm{IO}_{3}^{-}\)
[Cu²⁺] = 0.001 M
\(\) = 0.001 M
Ionic product = [Cu²⁺]\(\left[\mathrm{IO}_{3}^{-}\right]^{2}\)
– 1 x 10^-3 x [1 x 10^-3]² = 1 x 10^-9
K_sp = 7.4 x 10^-8
Cu(IO₃)₂ is precipitated if [Cu²⁺] .\(\left[\mathrm{IO}_{3}^{-}\right]^{2}\) > K_sp
Since, the ionic product is less than the solubility product. Hence there will be no precipitation.

Question 70.
The ionization constant of benzoic acid is 6.46 x 10^-5 and Ksp for silver benzoate is 2.5 x 10 . How many times is silver benzoate
more soluble in a buffer of pH 3.19 compared to its solubility in pure water?
Answer:

where s is the solubility of C₆H₅COOAg
pH = 3.19
pH = -log[H⁺]
log[H⁺] = – pH = -3.19 = \(\overline{4} .81\)
[H⁺] = antilog \(\overline{4} .81\) = 6.46 x 10^-4

C₆H₅COOAg is 3.2 times more soluble in buffer than in pure water.

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 6 Thermodynamics Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 6 Thermodynamics

PSEB 11th Class Chemistry Guide Thermodynamics InText Questions and Answers

Question 1.
Choose the correct answer. A thermodynamic state function is a quantity
(i) used to determine heat changes
(ii) whose value is independent of path
(iii) used to determine pressure volume work
(iv) whose value depends on temperature only.
Answer:
(ii) A thermodynamic state function is a quantity whose value is independent of path. Functions like p, V, T etc., depend only on the state of a system and not on the path.

Question 2.
For the process to occur under adiabatic conditions, the correct condition is:
(i) ΔT = 0 (ii) Δp = 0
(iii) q = 0 (iv) w = 0
Answer:
(iii) A system is said to be under adiabatic conditions if there is no exchange of heat between the system and its surroundings. Hence, under adiabatic conditions, q = 0.

Question 3.
The enthalpies of all elements in their standard states are:
(i) unity
(ii) zero
(iii) < 0
(iv) different for each element
Answer:
(ii) The enthalpies of all elements in their standard states are zero.

Question 4.
\(\Delta \boldsymbol{U}^{\ominus}\) of combustion of methane is – X kJ mol^-1. The value of \(\Delta \boldsymbol{H}^{\ominus}\) is
(i) = ΔU
(ii) > ΔU
(iii) \(\Delta \boldsymbol{U}^{\ominus}\)
(iv) = 0
Answer:
(iii) CH₄(g) + 2O₂(g) > CO₂(g) + 2H₂O(l)
Δ_ng = n_p-n_r = 1 – 3 =-2
Hence,\(\Delta \boldsymbol{H}^{\ominus}\) = \(\Delta \boldsymbol{U}^{\ominus}\) + Δ n_gRT
\(\Delta \boldsymbol{H}^{\ominus}\) = – X – 2RT
Hence, \(\Delta \boldsymbol{H}^{\ominus}\) < \(\Delta \boldsymbol{U}^{\ominus}\)

Question 5.
The enthalpy of combustion of methane, graphite and dihydrogen at 298 K are, -890.3 kJ mol^-1 – 393.5 kJ mol^-1 and -285.8 kJ mol^-1 respectively. Enthalpy of formation of CH₄(g) will be
(i) -748kJmol^-1
(ii) -52.27kJ mol^-1
(iii) +748kJ mol^-1
(iv) +52.26kJ mol^-1
Answer:
According to the equation
(i) CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(l); ΔH = -890.3 kJ mol^-1

(ii) C(s) + O₂(g) → CO₂(g); ΔH = – 393.5 kJ mol^-1

(iii) H₂(g) + \(\frac{1}{2}\)O₂(g) → H₂O(l); ΔH = -285.8 kJ mol^-1
Multiplying equation (iii) by 2, we get equation (iv).

(iv) 2H₂(g) + O₂(g) → 2H₂O(l); ΔH = – 571.6 kJ mol^-1
Adding eqs. (ii) and (iv), we get

(v) (C(s) +2H₂(g) + 2O₂(g) → CO₂(g) + 2H₂O(l); ΔH = – 965.1 kJ mol^-1
Reversing eqs. (i)

(vi) CO₂(g) + 2H₂O(l) → CH₄(g) + 2O₂(g); ΔH = +890.3 kJ mol^-1
Adding eqs. (v) and (vi), we get
C(s) + 2H₂(g) → CH₄(g); ΔH = – 74.8 kJ mol^-1
Hence, option (i) is correct.

Question 6.
A reaction, A + B → C + D +q is found to have a positive entropy change. The reaction will be
(i) possible at high temperature
(ii) possible only at low temperature
(iii) not possible at any temperature
(iv) possible at any temperature
Answer:
(iv) For a reaction to be spontaneous, AG should be negative.
ΔG = ΔH – TΔS
According to the question, for the given reaction,
ΔS = positive
ΔH = negative (since heat is evolved)
=> ΔG = negative
Therefore, the reaction is spontaneous at any temperature.
Hence, option (iv) is correct.

Question 7.
In a process, 701 J of heat is absorbed by a system and 394 J of work is done by the system. What is the change in internal energy for the process?
Answer:
According to the first law of thermodynamics,
ΔU = q + W …(i)
Given,
q = +701 J (heat is absorbed here, q is positive)
W=- 394 J
(work is done by the system hence W is negative)
Substituting the values in expression (i), we get
ΔU= +701 J + (-394 J)
ΔH = 307 J
Hence, the change in internal energy for the given process is 307 J.

Question 8.
The reaction of cyanamide, NH₂CN(s) with dioxygen was carried out in a bomb calorimeter, and ΔU was found to be – 742.7 kJ mol^-1 at 298K. Calculate enthalpy change for the reaction at 298 K.
NH₂CN(s) + \(\frac{3}{2}\)O₂(g) → N₂(g) + CO₂(g) + H₂O(l)
Answer:
The given reaction is
NH₂CN(s) + \(\frac{3}{2}\)O₂(g) → N₂(g) + CO₂(g) + H₂O(l)
Difference of moles of gaseous products and reactants,
Δ_ng = n_p – n_r = 2 – \(\frac{3}{2}=\frac{1}{2}\) = 0.5 mol
Given, ΔU=- 742.7kJ mol^-1
Enthalpy change ΔH = ΔU + Δ_ngRT
= – 742.7 + (0.5 x 8.314 x 10^-3 x 298)
= – 742.7 +1238.786 x 10^-3
= – 741.46 kJ mol^-1

Question 9.
Calculate the number of kJ of heat necessary to raise the temperature of 60.0 g of aluminium from 35°C to 55°C. Molar heat capacity of Al is 24 J mol^-1K^-1.
Answer:
Given, mass of Al = 60.0 g
ΔT= 55 – 35 = 20°C
No.of moles of Al = \(\frac{60.0}{27}\) mol
Molar heat capacity of Al
= 24 J mol^-1K^-1
Heat, q = n.C . ΔT
= [ \(\frac{60}{27}\) mol )(24 J mol^-1K^-1)(20 K)
q= 1066.7 J
q = 1.07 kJ

Question 10.
Calculate the enthalpy change on freezing of 1.0 mol of water at 10.0°C to ice at – 10.0°C. Δ_fusH = 6.03 kJ mol^-1 at 0°C.
C_p[H₂O(l)] – 75.3 J mol^-1K^-1
C_p[H₂O(s)] = 36.8J mol^-1K^-1
Answer:
(i) Heat change required to lower the temperature of water from 10.0°Cto0°C
ΔH₁= n x C_p x ΔT= 1.0 x 75.3 x (-10) = – 753 J mol^-1
(ii) Heat change required to convert 1 mol of H₂O(l) at 0°C to H₂O(s) at 0°C
ΔH₂ = ΔH_fusion = – 6.03 kJ mol^-1 as heat is given out
(iii) Heat change required to change 1 mole of ice from 0°C to -10.0° C
ΔH₃ = – 36.8 x 10 x 1 = – 368 J mol^-1
Total heat change
= ΔH₁ + ΔH₂ + ΔH₃ = (- 0.753 – 6.03 – 0.368) kJ mol^-1
∴ Total enthalpy change = – 7.151 kJ mol^-1
As in each step, heat is evolved, each step will have a negative sign with Δ_H

Question 11.
Enthalpy of combustion of carbon to CO₂ is -393,5 kJ mol^-1. Calculate the heat released upon formation of 35.2 g of CO₂ from carbon and dioxygen gas.
Answer:
The reaction for the combustion of carbon into CO₂ is
C(s) + O₂(g) → CO₂(g); ΔH = – 393.5 kJ mol^-1 (1 mole CO₂ – 44g)
Heat released in the formation of 44 g CO₂ = 393.5 kJ
∴ Heat released in the formation of 35.2 g CO₂
\(\frac{393.5 \mathrm{~kJ}}{44 \mathrm{~g}}\) x 5.2g = 314.8 kJ mol^-1

Question 12.
Enthalpies of formation of CO(g), CO₍₂₎(g), N₂O(g) and N₂O₄(g) are -110, -393, 81and 9.7 kJ mol^-1 respectively. Find the value of Δ_rH for the reaction:
N₂O₄(g) + 3CO(g) → N₂O(g) + 3CO₂(g)
Answer:
Δ_fH (CO) = -110 kJ mol^-1
ΔH_f(CO₂) = -393 kJ mol^-1
Δ_fH (N₂O)= 81 kJ mol^-1
Δ_fH (N₂O₄) = 9.7 kJ mol^-1
The given reaction is
N₂O₄(g) + 3CO(g) → N₂O(g) + 3CO₂(g); Δ_rH = ?

= [81 + 3 (-393)] – [9.7 + 3 (-110)] kJ = [81 -1179]-[9.7-330] kJ
Δ_rH = – 777.8 kJ.

Question 13.
Given : N₂(g) + 3H₂(g) → 2NH₃(g); \(\Delta_{\boldsymbol{r}} \boldsymbol{H}^{\ominus}\) = -92.4kJ mol^-1.
What is the standard enthalpy of formation of NH₃ gas?
Answer:
Given, N₂(g) + 3H₂(g) → 2NH₃(g); Δ_rH = – 92.4 kJ mol^-1
Chemical reaction for the enthalpy of formation of NH3(g) is as follows :
\(\frac{1}{2}\)N₂(g) + \(\frac{3}{2}\)H₂(g) → NH₃(g)
∴ Standard enthalpy of formation of NH₃(g)
= \(\frac{1}{2}\)\(\Delta H^{\theta}\) = \(\frac{1}{2}\) (-92.4 kJ mol^-1) = -46.2 kJ mol^-1

Question 14.
Calculate the standard enthalpy of formation of CH₃OH(l) from the following data:
CH₃OH(l) + \(\frac{3}{2}\)O₂(g) → CO₂(g) + 2H₂O(l); \(\Delta_{\boldsymbol{r}} \boldsymbol{H}^{\ominus}\) = -726 kJ mol^-1
C_(graphite) + O₂(g) → CO₂(g); \(\Delta_{\boldsymbol{c}} \boldsymbol{H}^{\ominus}\) = – 393 kJ mol^-1
H₂(g) + \(\frac{1}{2}\)O₂(g) → H₂O(l); \(\Delta_{\boldsymbol{f}} \boldsymbol{H}^{\ominus}\) = – 286 kJ mol^-1
Answer:

Question 15.
Calculate the enthalpy change for the process
CCl₄(g) → C(g) + 4Cl(g)
and calculate bond enthalpy of C—Cl in CCl₄(g).
\(\Delta_{\mathbf{v a p}} \boldsymbol{H}^{\ominus}\)(CCl₄) = 30.5kJ mol^-1. \(\Delta_{\boldsymbol{f}} \boldsymbol{H}^{\ominus}\)(CCl₄) = – 135.5kJ mol^-1.
\(\Delta_{a} \boldsymbol{H}^{\ominus}(\mathbf{C})\) = 715.0kJ mol^-1, \(\Delta_{\boldsymbol{a}} \boldsymbol{H}^{\ominus}\left(\mathbf{C l}_{\mathbf{2}}\right)\)(Cl2) = 242 kJ mol^-1; where \(\Delta_{\boldsymbol{a}} \boldsymbol{H}^{\ominus}\) is enthalpy of atomisation.
Answer:
Given,
(i) CCl₄(Z) → CCl₄(g); \(\Delta_{\mathrm{vap}} H^{\ominus}\) = +30.5 kJ mol^-1
(ii) C(s) → C(g); \(\Delta_{a} H^{\ominus}\) = 715.0 kJ mol^-1
(iii) Cl₂(g) → 2Cl(g); \(\Delta_{a} H^{\ominus}\) = 242 kJ mol^-1
(iv) C(s) + 2Cl₂(g) → CCl₄ a); \(\Delta_{f} H^{\ominus}\) = – 135.5KJ mol^-1

Enthalpy change for the given process
CCl₄(g) → C(g) + 4Cl(g); \(\Delta_{r} H^{\ominus}\) = ?

Add (i) and (iv) and subtract (ii) and (iii) x 2
CCl₄(l) + C(s) + 2Cl₂(g) – C(s) – 2Cl₂ (g) → CCl₄(g) + CCl₄(g) – C(g) – 4Cl(g)
or \(\Delta_{r} H^{\ominus}\) = 30.5 -135.5 – 715 – 484 = -1304 kJ
0 = CCl₄(g) – C(g) + 4Cl(g); \(\Delta_{r} H^{\ominus}\) = -1304kJ
CCl₄(g) → C (g) + 4Cl(g); \(\Delta_{r} H^{\ominus}\) = 1304 kJ
There are four bonds of C—Cl in CCl₄.
Bond enthalpy of C—Cl bond
= \(\frac{1304}{4}\) mol^-1
= 326 kJmol^-1

Question 16.
For an isolated system, ΔU = 0, what will be ΔS ?
Ans. For an isolated system, ΔU = 0 and for a spontaneous process, total entropy change must be positive. For example, consider the diffusion of two gases A and B into each other in a closed container which is isolated from the surroundings.

The two gases A and B are separated by a movable partition. When partition is removed, the gases begin to diffuse into each other and the system becomes more disordered. It shows that ΔS > 0 and ΔU = 0 for this process.
Moreover, ΔS =\(=\frac{q_{\mathrm{rev}}}{T}=\frac{\Delta H}{T}=\frac{\Delta U+p \Delta V}{T}=\frac{p \Delta V}{T}\) (∴ ΔU = 0)
i.e., TΔS or ΔS > 0

Question 17.
For the reaction at 298 K, 2A + B > C
ΔH = 400kJ mol^-1 and ΔS = 0.2kJK^-1mol^-1 At what temperature will the reaction become spontaneous considering ΔH and ΔS to be constant over the temperature range?
Answer:
Given, ΔH = 400 kJ mol^-1, ΔS = 0.2 kJ K^-1mol^-1
Gibbs free energy, ΔG = ΔH – TΔS
0 = 400 kJ mol^-1 – T x 0.2 kJ K^-1mol^-1
(ΔG = 0 at equilibrium)
T = \(\frac{400 \mathrm{~kJ} \mathrm{~mol}^{-1}}{0.2 \mathrm{~kJ} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}}\)
T = 2000 K
For the reaction to be spontaneous, ΔG must be negative. Hence, for the given reaction to be spontaneous, T should be greater than 2000 K.

Question 18.
For the reaction,
2Cl(g) → Cl₂(g), what are the signs of ΔH and ΔS?
Answer:
ΔH and ΔS are negative.
The given reaction represents the formation of chlorine molecule from chlorine atoms. Here, bond formation is taking place. Therefore, energy is being released. Hence, ΔH is negative.
Also, two moles of atoms have more randomness than one mole of a molecule. Since spontaneity is decreased, ΔS is negative for the given reaction.

Question 19.
For the reaction : 2A(g) + B(g) → 2D(g)
\(\Delta \boldsymbol{U}^{\ominus}\) = – 10.5 kJ and ΔS = – 441 JK^-1.
Calculate \(\Delta \boldsymbol{G}^{\ominus}\) for the reaction, and predict whether the reaction may occur spontaneously.
Answer:
For the given reaction,
2A(g) + B(g) → 2D(g)
Δn_g = 2 – 3 = -1 mol
Substituting the value of \(\Delta \boldsymbol{U}^{\ominus}\) in the expression ofΔH
\(\Delta H^{\ominus}=\Delta U^{\ominus}+\Delta n_{g} R T\)
= (-10.5 kJ) + (-1) x (8.314 x 10^-3kJK^-1 mol^-1) x (298 K)
= -10.5 kJ-2.48 kJ
\(\Delta H^{\ominus}\) = -12.98 kJ
We know that,
\(\Delta G^{\ominus}=\Delta H^{\ominus}-T \Delta S^{\ominus}\)
= -12.98 kJ – (298K) x ( – 44.1 JK^-1)
= -12.98 kJ + 13.14kJ
\(\Delta G^{\ominus}\) = +0.16 kJ
Since, \(\Delta G^{\ominus}\) is positive, the reaction will not occur spontaneously.

Question 20.
The equilibrium constant for a reaction is 10. What will be the value of \(\Delta G^{\ominus}\)? R = 8.314 JK^-1mol^-1, T = 300 K.
Answer:
\(\Delta G^{\ominus}\) = – 2303RT log K_c
Given, K_c = 10, T = 300 K, R = 8.314 J K^-1 mol^-1
\(\Delta G^{\ominus}\) = (- 2.303) (8.314 JK^-1mol^-1) (300K) (loglO) (∵ log 10 = 1)
= – 5744.14 Jmol^-1 = – 5.744 kJmol^-1

Question 21.
Comment on the thermodynamic stability of NO(g), given
\(\frac{1}{2}\)N₂(g) + \(\frac{1}{2}\)O₂(g) → NO(g); \(\Delta_{\boldsymbol{r}} \boldsymbol{H}^{\ominus}\) = 90 kJ mol^-1
NO(g) + \(\frac{1}{2}\)O₂(g) → NO₂(g); \(\Delta_{\boldsymbol{r}} \boldsymbol{H}^{\ominus}\) = – 74 kJ mol^-1
Answer:
NO(g) is unstable because formation of NO is endothermic (energy is absorbed) but NO₂(g) is formed because its formation is exothermic (energy is released).
Hence, unstable NO(g) changes to stable NO₂(g).

Question 22.
Calculate the entropy change in surroundings when 1.00 mol of H₂O(Z) is formed under standard conditions. \(\Delta_{\boldsymbol{f}} \boldsymbol{H}^{\ominus}\) = – 286
kJ mol^-1.
Answer:
Enthalpy change for the formation of 1 mol of H₂O(Z)
H₂(g) + \(\frac{1}{2}\)O₂(g) → H₂O(l); \(\Delta_{f} H^{\mathrm{s}}\) = -286 kJ mol^-1
Energy released in the above reaction is absorbed by the surroundings. * It means,
q_surr = + 286 kJ mol^-1
Entropy change ΔS_surr = \(=\frac{q_{\mathrm{surr}}}{T}=\frac{286 \mathrm{~kJ} \mathrm{~mol}^{-1}}{298 \mathrm{~K}}\)
ΔS_surr = 0.95973 kJ K^-1 mol^-1 = 959.73 J mol^-1K^-1

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 5 States of Matter Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 5 States of Matter

PSEB 11th Class Chemistry Guide States of Matter InText Questions and Answers

Question 1.
What will be the minimum pressure required to compress 500 dm3 of air at 1 bar to 200 dm³ at 30° C?
Answer:
Given,
Initial pressure, P₁ =1 bar
Initial volume, V₁ = 500 dm³
Final volume, V₂ = 200 dm³
Final pressure, P₂ = ?
Sipce the temperature remains constant at30°C.
According to Boyle’s law,
P₁V₁ = P₂V₂
⇒ P₂ = \(\frac{p_{1} V_{1}}{V_{2}}=\frac{1 \times 500}{200}\) bar = 2.5 bar
Therefore, the minimum pressure required is 2.5 bar.

Question 2.
A vessel of 120 mL capacity contains a certain amount of gas at 35°C and 1.2 bar pressure. The gas is transferred to another vessel of volume 180 mL at 35°C. What would be its pressure?
Answer:
Given,
Initial pressure, P₁ =1.2 bar
Initial volume, V₁ = 120 mL
Final volume, V₂ = 180 mL
Final pressure, P₂ = ?
Since the temperature remains constant at 35°C.
According to Boyle’s law,
⇒ P₂ = \(\frac{p_{1} V_{1}}{V_{2}}=\frac{1.2 \times 120}{180}\) bar = 0.8 bar
Therefore, the pressure would be 0.8 bar.

Question 3.
Using the equation of state pV = nRT; show that at a given temperature density of a gas is proportional to gas pressure p.
Answer:
The equation of state is given by
pV = nRT

or d = \(\frac{p M}{R T}\)
If T constant, then d ∝ p.

Question 4.
At 0°C, the density of a certain oxide of a gas at 2 bar is same as that of dinitrogen at 5 bar. What is the molecular mass of the oxide?
Answer:
Density (d) of the substance at temperature (T)
d = \(\frac{p M}{R T}\)
When T and d are same and R is constant then
p₁M₁ = p₂M₂
Given, P₁ = 2 bar
p₂ = 5 bar
Molecular mass of nitrogen, M₂ = 28g/mol
Now, M₁ = \(\frac{M_{2} p_{2}^{2}}{p_{1}}=\frac{28 \times 5}{2}\) = 70 g/mol
Hence, the molecular mass of the oxide is 70 g/ mol.

Question 5.
Pressure of 1 g of an ideal gas A at 27°C is found to be 2 bar. When 2 g of another ideal gas B is introduced in the same flask at same temperature the pressure becomes 3 bar. Find a relationship between their molecular masses.
Answer:
For ideal gas A, the ideal gas equation is given by
p_AV – n_ART …(i)
Where, p_A and n_A represent the pressure and number of moles of gas A. For ideal gas B, the ideal gas equation is given by
p_BV = n_BRT …(ii)
Where, p_B and n_B represent the pressure and number of moles of gas B.
Number of moles of A gas, n_A = \(\frac{1}{M_{A}}\) [M_A = molar mass of gas A]
Number of moles of B gas, n_B = \(\frac{2}{M_{B}}\) [M_B = molar mass of gas B]
Pressure of gas A, p_A = 2 bar
Total pressure P_total = p_A + p_B = 3 bar
Pressure of gas B, p_B = p_total – p_A = 3 – 2 = 1 bar
V, R and T are same for both the gases.
Hence from eqs. (i) and (ii)

Question 6.
The drain cleaner, Drainex contains small hits of aluminum which react with caustic soda to produce dihydrogen. What volume of dihydrogen at 20°C and one bar will be released when 0.15g of aluminum reacts?
Answer:

Question 7.
What will be the pressure exerted by a mixture of 3.2 g of methane and 4.4g of carbon dioxide contained in a 9 dm³ flask at 27°C?
Answer:
Mass of CH₄ = \(\frac{\text { Mass of } \mathrm{CH}_{4}}{\text { Molar mass of } \mathrm{CH}_{4}}\)
[Molar mass of CH₄ = 12 + 4 x 1 = 16]
= \(\frac{3.2}{16}\) = 0.2 mol
Mass of CO₂ = \(\frac{4.4}{44}\) = 0.1 mol
[Molar mass of CO₂ = 12 + 2 x 16 = 44]
Total moles = 0.2 + 0.1 = 0.3 mol
Pressure P = \(\frac{n R T}{V}=\frac{0.3 \times 8.314 \times 300}{9 \times 10^{-3}}\) = 8.314 x 10⁴ Pa

Question 8.
What will be the pressure of the gaseous mixture when o.5L of H₂ at 0.8 bar and 2.0 L of dioxygen at 0.7 bar are introduced in a 1L vessel at 27°C?
Answer:
To calculate the partial pressure of H₂, Le., pH₂
V₁ = 0.5L, V₂ = 1L, p₁ = 0.8 bar, p₂ = ?
Temperature remaining constant, applying Boyl&s Law
p₁V₁=p₂V₂
0.8 x 0.5= p₂ x 1
or P₂ = 0.4 bar
To calculate the partial pressure of O₂ i.e., PO₂
V₁ = 2.0L, V₂ = 1L, p₁ = 0.7 bar, P₂ = ?
Applying Boyle’s Law
p₁V₁ = p₂V₂
0.7 x 2.0 = 1 x p₂
or p₂ = 1.4 bar.
If p is final pressure of the gas mixture, then according to Dalton’s Law of partial pressures
p = pH₂ + pO₂ = (0.4 +1.4)
= 1.8 bar

Question 9.
Density of a gas is found to be 5.46 g/dm³ at 27°C at 2 bar pressure. What will be its density at STP?
Answer:
Given,
d₁ = 5.46 g/dm³
p₁ = 2 bar
T₁ = 27°C = (27 + 273)K = 300 K
P₂ = 1 bar
T₂ = °C = 273 K
d₂ = ?
Density a = \(\frac{M p}{R T}\)
For same gas at different temperatures and pressures

Question 10.
34.05 ml. of phosphorus vapour weighs 0.0625g at 546°C and 0.1 bar pressure. What is the molar mass of phosphorus?
Answer:
Given,
p= 0.1 bar
V= 34.05 mL = 34.05 x 10^-3L
R = 0.083 bar dm³K^-1 mol^-1
T = 546°C = (546 + 273) K = 819 K
Mass, M = 0.0625 g
Now, pV = nRT
n = \(\frac{p V}{R T}=\frac{0.1 \times 34.05 \times 10^{-3}}{0.083 \times 819}\)= 5.0 x 10^-5 mol^-1
∴ Molar mass of phosphorus = \(\frac{0.0625}{5.0 \times 10^{-5}}\) = 1250 g mol^-1
Hence, the molar mass of phosphorus is = 1250 g mol^-1

Question 11.
A student forgot to add the reaction nixture to the round bottomed flask at 27°C but instead he/she placed the flask on the flame. After a lapse of time, he realized his mistake, and using a pyrometer he found the temperature of the flask was 477°C. What fraction of air would have been expelled out?
Answer:
Let the volume of the round bottomed flask = V cm3 at 27°C = 300 K
V₁ = V, T₁ = (27 + 273)K = 300K, V₂ =?,
T₂ = 477° C = (477 + 273)K
According to Charles’s law,
\(\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\)
V₂ = \(\frac{V_{1} T_{2}}{T_{1}}=\frac{750 \mathrm{~V}}{300}\) = 2.5V
Therefore, volume of air expelled out = 2.5 V – V = 1.5 V
Hence, fraction of air expelled out = \(\frac{1.5 \mathrm{~V}}{2.5 \mathrm{~V}}\) = 0.6

Question 12.
Calculate the temperature of 4.0 mol of a gas occupying 5 dm³ at 3.32 bar. (R = 0.083 bar dm³K^-1 mol^-1).
Answer:
Given,
n = 4.0 mol, V = 5 dm³, p = 3.32 bar, R = 0.083 bar dm³K^-1mol^-1
Applying ideal gas equation ‘
pV = nRT
T = \(\frac{p V}{n R}=\frac{3.32 \times 5}{4 \times 0.083}\) = 50K
Hence, the required temperature is 50 K.

Question 13.
Calculate the total number of electrons present in 1.4g of dinitrogen gas.
Answer:
Molar mass of dinitrogen (N₂) = 28 g mol^-1 Mass
Moles = \(\frac{Mass}{Molar mass}\)
ⁿN₂ = \(\frac{1.4}{28}\) = 0.05 mol
1 mol = 6.022 x 10²³ molecules
0.05 mol = 0.05 x 6.022 x 10²³ molecules
= 0.3011 x 10²³ molecules
Now, 1 molecule of N₂ contains = 14 electrons.
Therefore, 0.3011 x 10²³ molecules will contain = 14 x 0.3011 x 10²³
= 4.214 x 10²³ electrons

Question 14.
How much time would it take to distribute one Avogadro number of wheat grains, if 10¹⁰ grains are distributed each second?
Answer:
Avogadro number, N_A = 6.022 x 10²³

Hence, the time taken would be 1.909 x 10⁶ years.

Question 15.
Calculate the total pressure in a mixture of 8 g of dioxygen and 4 g of dihydrogen confined in a vessel of 1 dm³ at 27°C.
R 0.083 bar dm³ K^-1 mol^-1
Answer:
Moles of O₂ = \(\frac{\text { Mass }}{\text { Molar weight }}=\frac{8}{32}\) = 0.25 mol
Moles of H₂ = \(\frac{4}{2}\) = 2 mol
Therefore, total number of moles in the mixture = 0.25 + 2- 2.25 mol
Given, V = 1 dm³
n = 2.25 mol
R = 0.083 bar dm³K^-1mol^-1
T = 27°C = 300K
pV= nRT
⇒ Pressure, p = \(\frac{n R T}{V}=\frac{2.25 \times 0.083 \times 300}{1}\) = 56.025 bar.
Hence, the total pressure of the mixture is 56.025 bar.

Question 16.
Pay load is defined as the difference between the mass of displaced air and the mass of the balloon. Calculate the pay load when a balloon of radius 10m, mass 100kg is filled with helium at 1.66 bar at 27°C.(Density of air = 1.2 kg m^-3 and R = 0.083 bar dm³K^-1 mol^-1)
Answer:
Given,
Radius of the balloon, r = 10m
∴ Volume of the balloon = \(\frac{4}{3} \pi r^{3}=\frac{4}{3} \times \frac{22}{7}\) x 10³ = 4190.5 m3(approx)
∴ Mass of displaced air = V_{displaced air} x density of air
= 4190.5 x 1.2 kg = 5028.6 kg
Now, mass of helium (m) filled in balloon
\(m_{\mathrm{He}}=\frac{M p V}{R T}\)
Here, M = 4 x 10^-3 kg mol^-1
p= 1.66 bar
V = Volume of the balloon = 4190.5 x 10³ dm³
R = 0.083 bar dm³K^-1mol^-1
T = 27°C = 300 K
Then m_He = \(\frac{4 \times 10^{-3} \times 1.66 \times 4190.5 \times 10^{3}}{0.083 \times 300}\) = 1117.5kg(approx)
Now, total mass of the balloon filled with helium
= (100 +1117.5)kg = 1217.5kg
Hence, pay load = mass of displaced air – mass of balloon
= (5028.6 -1217.5) kg = 3811.1 kg
Hence, the pay load of the balloon is 3811.1 kg

Question 17.
Calculate the volume occupied by 8.8g of CO2 at 31.1°C and 1 bar pressure. (R = 0.083 bar LK^-1 mol^-1).
Answer:
We know that,
pV = nRT m
pV = \(\frac{m}{M} R T\)
V = \(\frac{m R T}{M p}\)
Here, m = 8.8 g
R = 0.083 bar LK^-1mol^-1
T = 31.1°C = 304.1 K
M = 44 g mol^-1
p = 1 bar
Then, volume V = \(\frac{8.8 \times 0.083 \times 304.1}{44 \times 1}\) = 5.048 L
Hence, the volume occupied is 5.048 L.

Question 18.
2.9 g of a gas at 95°C occupied the same volume as 0.184 g of dihydrogen at 17°C, at the same pressure. What is the molar mass of the gas?
Answer:
Applying the ideal gas equation pV = nRT

Hence, the molar mass of the gas is 40 g mol^-1 .

Question 19.
A mixture of dihydrogen and dioxygen at one bar pressure contains 20% by weight of dihydrogen. Calculate the partial pressure of dihydrogen.
Answer:
Let the weight of dihydrogen be 20 g and the weight of dioxygen be 80g.
Moles of dihydrogen,
ⁿH₂ = 20/2 = 10 mol
Moles of dioxygen,
ⁿO₂ = 80/32 = 2.5 mol
Given,
Total pressure of the mixture, p_total = 1 bar
Then, partial pressure of dihydrogen,
^pH₂ = \(\frac{n_{\mathrm{H}_{2}}}{n_{\mathrm{H}_{2}}+n_{\mathrm{O}_{2}}} \times p_{\text {total }}=\frac{10}{10+2.5} \times 1\) = 0.8 bar
Hence, the partial pressure of dihydrogen is 0.8 bar.

Question 20.
What would be the SI unit for the quantity pV² T² / n?
Answer:
The SI unit of \(\frac{p V^{2} T^{2}}{n}\) is given by
= \(\frac{\left(\mathrm{Nm}^{-2}\right)\left(\mathrm{m}^{3}\right)^{2}(\mathrm{~K})^{2}}{\mathrm{~mol}}\) = Nm⁴K²mol^-1

Question 21.
In terms of Charles’ law explain why -273°C is the lowest possible temperature.
Answer:
According to Charles’ law,
V_t = V₀ [1 + \(\frac{t}{273}\) ]
At t = -273° C
V_t = V₀ = [1 – \(\frac{273}{273}\) ] = 0
Thus, at -273° C, volume of a gas becomes zero and below this temperature the volume becomes negative, which is meaningless.

Question 22.
Critical temperature for carbon dioxide and methane are 31.1° C and -81.9°C respectively. Which of these has stronger intermolecular forces and why?
Answer:
Higher is the critical temperature of a gas, easier is its liquefaction. This means that the intermolecular forces of attraction between the molecules of a gas are directly proportional to its critical temperature. Hence, intermolecular forces of attraction are stronger in the case of C02.

Question 23.
Explain the physical significance of van der Waals parameters.
Answer:
Significance of constant ‘a’ : The value of constant ‘a’ is a measure of the magnitude of intermolecular forces between the molecules of the gas. Its units are atm L mol^-2 . Larger the value of ‘a’ larger will be the intermolecular forces among the gas molecules.
Significance of constant ‘b’ : The constant ‘b’ is called co-volume or excluded volume per mol of a gas. Its units are litre mol^-1.The volume of V is four times the actual volume of the molecules. It is measure of effective size of the gas molecules.

Punjab State Board PSEB 11th Class Chemistry Book Solutions Chapter 4 Chemical Bonding and Molecular Structure Textbook Exercise Questions and Answers.

PSEB Solutions for Class 11 Chemistry Chapter 4 Chemical Bonding and Molecular Structure

PSEB 11th Class Chemistry Guide Chemical Bonding and Molecular Structure InText Questions and Answers

Question 1.
Explain the formation of a chemical bond.
Answer:
A chemical bond is defined as an attractive force that holds the constituents (atoms, ions etc.) together in a chemical species.
Various theories have been suggested for the formation of chemical bonds such as the electronic theory, valence shell electron pair repulsion theory, valence bond theory, and molecular orbital theory.

A chemical bond formation is attributed to the tendency of a system to attain stability. It was observed that the inertness of noble gases was because of their fully filled outermost orbitals. Hence, it was postulated that the elements having incomplete outermost shells are unstable (reactive). Atoms, therefore, combine with each other and complete their respective octets or duplets to attain the stable configuration of the nearest noble gases. This combination can occur either by sharing of electrons or by transferring one or more electrons from one atom to another. The chemical bond formed as a result of sharing of electrons between atoms is called a covalent bond. An ionic bond is formed as a result of the transference of electrons from one atom to another.

Question 2.
Write Lewis dot symbols for atoms of the following elements: Mg, Na, B, O, N, Br.
Answer:
Mg : There are two valence electrons in Mg atom (2, 8, 2). Hence, the Lewis dot symbol of Mg is :

Na : There is only one valence electron in an atom of sodium (2, 8,1). Hence, the Lewis dot Symbol is :

B : There are three valence electrons in Boron atom (2, 3). Hence, the Lewis dot symbol is :

0 : There are six valence electrons in an atom of oxygen (2, 6). Hence, the Lewis dot symbol is :

N: There are five valence electrons in an atom of nitrogen (2,5). Hence, the Lewis dot symbol is :

Br : There are seven valence electrons in bromine (2, 8, 18, 7). Hence, the
Lewis dot symbol is :

Question 3.
Write Lewis symbols for the following atoms and ions: S and S^2-; Al and Al³⁺; H and H^–
Answer:

Question 4.
Draw the Lewis structure for the following molecules and ions :
H₂S, SiCl₄, BeF₂, \(\mathrm{CO}_{3}^{2-}\), HCOOH
Answer:

Question 5.
Define octet rule. Write its significance and limitations.
Answer:
Octet rule : Atoms can combine either by transfer of valence electrons from one atom to another (gaining or losing) or by sharing of valence electrons in order to have an octet in their valence shell.
Significance of octet rule : It help to explain why different atom combine with each other to form ionic or covalent compounds. Limitations of the Octet Rule
Although octet rule can explain the formation of a large number of compounds but it has many exceptions also, which are discussed below :

(i) Electron deficient molecules : There are some molecules in which the central atom is surrounded by less than eight electrons, i.e., their octet is incomplete. Elements having less than four valence electrons generally form molecules of this category.
e.g., BeCl₂, BF₃, AlCl₃, LiCl, BeH₂ etc.

(ii) Odd electron molecules : Molecules like NO, NO₂, O₂ etc., are examples of such molecules in which bonded atoms have odd number of electron (usually 3) in between them. That’s why these are called odd electron molecules.
In case of these molecules, the octet rule is not satisfied for all the atoms, e.g.,

Species with one unpaired electron are called free radicals. These are paramagnetic and most of them are generally unstable.

(iii) Electron rich molecules : Elements of the third and higher periods of the periodic table, because of the availability of d orbitals can expand their covalency and -can accommodate more than eight valence electrons around the central atom. This is referred as expanded octet. Here, also the octet rule is not applicable, e.g., PF₅ (10 electrons around P atom), SF₆ (12 electrons around S atom), H₂SO₄ (12 electron around S atom).
Compounds having expanded octet are also termed as hypervalent compounds.

(iv) Other drawbacks : Other drawbacks of this theory are as follows:
1. Octet rule is based on the inertness of noble gases but some noble gases like xenon and krypton form several compounds with oxygen and fluorine like. XeF₂, XeF₄, XeF₆, XeOF₄, XeO₂F₂, KrF₂ etc.
2. It does not tell anything about the shapes of molecules and their relative stabilities.
3. It fails to explain the paramagnetic behaviour of oxygen. (Which should be diamagnetic according to this rule but it is infact paramagnetic in nature).

Question 6.
Write the favourable factors for the formation of ionic bond.
Answer:
The favourable factors for ionic bond formation are as follows :

(i) Low ionization enthalpy of element forming cation.
(ii) More negative electron gain enthalpy of element forming anion.
(iii) High lattice energy of the compound formed.

Question 7.
Discuss the shape of the following molecules using the VSEPR model:
BeCl₂, BCl₃, SiCl₄, ASF₅, H₂S, PH₃
Answer:
According to VSEPR theory, the shape of a molecule depends upon the number of valence shell electron pairs (bonded or non-bonded) around the central atom. Pairs of electrons in the valence shell repel each other. The order of their repulsion is as follows :
Ip -Ip > Ip -bp > bp – bp
(i) BeCl₂ or

The central atom Be has only 2 valence electrons which are bonded to Cl, so there are only 2 bond pairs and no lone pairs. It is of the type AB₂ and hence, the shape is linear.

(ii) BCl₃:

The central atom B has only 3 valence electrons which are bonded with three Cl atoms, so it contains only 3 bond pairs and no lone pair. It is of the type AB₃ and hence, the shape is trigonal planar.

(iii) SiCl₄ :

Similarly, the central atom Si has only 4 bond pairs and no lone pair. It is of the type AB₄ and hence, the shape is tetrahedral.

(iv) AsF₅:

The central atom As has only 5 bond pairs and no lone pair. It is of the type AB₅ and hence, the shape is trigonal bipyramidal.

(v) H₂S:

The central atom S has 6 valence electrons. Out of these only two are used in bond formation with two H-atoms while four (two pairs) remains as non-bonding electrons (i.e., lone pairs). So, it contains 2 bond pairs and 2 lone pairs. It is of the type AB₂E₂ and hence, the shape
is bent or V-shaped.

(vi) PH₃

The central atom P has 5 valence electrons. Out of which three are utilised in bonding with H atoms and one pair remains as lone pair. So, it contains 3 bond pairs and one lone pair. It is of the type AB₃E and hence the shape is pyramidal.

Question 8.
Although geometries of NH₃ and H₂O molecules are distorted
tetrahedral, bond angle in water is less than that of ammonia.
Discuss.
Answer:

In H₂O molecule there, is lone pair-lone pair repulsion due to the presence of two lone pairs of electrons while in NH₃ molecule there are only lone pair-bond pair repulsion. According to VSEPR theory the former one is more stronger and hence the bond angle in water is less than that of ammonia.

Question 9.
How do you express the bond strength in terms of bond order?
Answer:
Bond strength represents the extent of bonding between two atoms forming a molecule. The larger the bond energy, the stronger is the bond and the greater is the bond order.

Question 10.
Define the bond length.
Answer:
Bond length is defined as the equilibrium distance between the nuclei of two bonded atoms in a molecule.
Bond lengths are expressed in terms of Angstrom (10^-10 m) or picometer (10^-12 m) and are measured by spectroscopic X-ray diffractions and |
electron-diffraction techniques.

Question 11.
Explain the important aspects of resonance with reference to \(\mathrm{CO}_{3}^{2-}\) the ion.
Answer:
According to experimental findings, all carbon to oxygen bonds in \(\mathrm{CO}_{3}^{2-}\) are equivalent. Hence, it is inadequate to represent \(\mathrm{CO}_{3}^{2-}\) ion by a single Lewis structure having two single bonds and one double bond.
The \(\mathrm{CO}_{3}^{2-}\) ion is best described as a resonance hybrid of the canonical forms I, II and III.

All canonical forms have similar energy, same positions of atoms and same number of bonded and non-bonded pairs of electrons.

Question 12.
H₃PO₃ can be represented by structures 1 and 2 shown below. Can these two structures be taken as the canonical forms of the resonance hybrid representing H₃PO₃? If not, give reasons for the same.

Answer:
The given structures cannot be taken as the canonical forms of the resonance hybrid of H₃PO₃, because the positions of the atoms have been changed.

Question 13.
Write the resonance structures for SO₃, NO₂ and \(\mathrm{NO}_{3}^{-}\)
Answer:
The resonance structures are :
(a) SO₃:

(b) NO₂:

(c) \(\mathrm{NO}_{3}^{-}\)

Question 14.
Use Lewis symbols to show electron transfer between the following atoms to form cations and anions: (a) K and S (b) Ca and O (c) Al and N.
Answer:
(a) K and S :
The electronic configurations of K and S are as follows :
K : 2, 8, 8, 1
S : 2, 8, 6

Sulphur (S) requires 2 more electrons to complete its octet. Potassium (K) requires one electron more than the nearest noble gas i.e., Argon. Hence, the electron transfer can be shown as:

(b) Ca and O :
The electronic configurations of Ca and O are as follows :
Ca : 2, 8, 8, 2
O : 2, 6
Oxygen requires two electrons more to complete its octet, whereas calcium has two electrons more than the nearest noble gas i.e., Argon. Hence, the electron transfer takes place as :

(c) Al and N :
The electronic configurations of Al and N are as follows :
A1: 2, 8, 3
N : 2, 5
Nitrogen is three electrons short of the nearest noble gas (Neon), whereas aluminium has three electrons more than neon. Hence, the electron transference can be shown as :

Question 15.
Although both CO₂ and H₂O are triatomic molecules, the shape of H₂O molecule is bent while that of CO₂ is linear. Explain this on the basis of dipole moment.
Answer:
According to experimental results, the dipole moment of carbon dioxide is zero. This is possible only if the molecule is linear so that the dipole moments of C—O bonds are equal and opposite to nullify each other.

Resultant µ = 0 D
On the other hand, H₂O molecule is found to have a net dipole moment value of 1.84 D (thoughit is a triatomic molecule as CO₂). The value of the dipole moment suggests that the structure of H20 molecule is bent where the dipole moment of O—H bonds are unequal.

Question 16.
Write the significance/applications of dipole moment.
Answer:
The applications of dipole moment are as follows :
1. In determining the polarity of bonds : As µ = e x d, obviously greater is the magnitude of dipole moment, higher will be the polarity of the bond. This is applicable to molecules containing only one polar bond like HC1, HBr etc. In non-polar molecules like, H₂, O₂, N₂ the dipole moment is zero. It is because there is no charge separations in these molecules [e = 0]. Thus, dipole moment can also be used to distinguish between polar and non-polar molecules.

2. In the calculation of percentage ionic character :
Take the example of HCl. Its µ = 1.03 D
If HCl is 100% ionic, each end would carry charge of one unit
i.e., 4.8 x 10^-10 e.s.u.
d (bond length) in H—Cl = 1.275Å
∴ for 100% ionic character, dipole moment will be
µ_ionic = e x d
= 4.8 x 10^-10 e.s.u x 1.275 x 10^-8 cm
= 6.12 x 10^-18 e.s.u cm = 6.12 D
∴ Percentage of ionic character =

= \(\frac{1.03}{6.12}\) x 100 = 16.83.

3. In determining the symmetry (or shape) of the molecules : Dipole moment is an important property in determining the shape of molecules containing 3 or more atoms. For instant if any molecule possesses two or more polar bonds, it will not be symmetric if it possesses some net molecular dipole moment as in case of water (\(\mu_{\mathrm{H}_{2} \mathrm{O}}\) = 1-84 D) and ammonia (\(\mu_{\mathrm{NH}_{3}}\) = 1.49 D). But if a molecule contains a number of similar atoms linked to a central atom the overall dipole moment of the molecule is found out to be zero, this will imply that the molecule is symmetrical as in the case of CO₂, BF₃, CH₄,CCl₄,etc.

Question 17.
Define electronegativity. How does it differ from electron gain enthalpy?
Answer:
Electronegativity is the ability of an atom in a chemical compound to attract a bond pair of electrons towards itself. Electronegativity of any given element is not constant. It varies according to the element to which it is bound. It is not a measurable quantity. It is only a relative number.

On the other hand, electron gain enthalpy is the enthalpy change that takes place when an electron is added to a neutral gaseous atom to form an anion. It can be negative or positive depending upon whether the electron is added or removed. An element has a constant value of the electron gain enthalpy that can be measured experimentally.

Question 18.
Explain polar covalent bond with the help of suitable example.
Answer:
When two dissimilar atoms having different electronegativities combine to form a covalent bond, the bond pair of electrons is not shared equally. The bond pair shifts towards the nucleus of the atom having greater electronegativity. As a result, electron distribution gets distorted and the electron cloud is displaced towards the electronegative atom.

As a result, the electronegative atom becomes slightly negatively charged while the other atom becomes slightly positively charged. Thus, opposite poles are developed in the molecule and this type of a bond is called a polar covalent bond.

For example-In HF, the electron pair is attracted more towards F atom due to its higher electronegativity. HF may be written as

Question 19.
Arrange the bonds in order of increasing ionic character in the molecules : LiF, K₂O, N₂, SO₂ and ClF₃.
Answer:
More the difference of electronegativity, more the ionic character of the molecules
N₂ < SO₂ < ClF₂ < K₂O < LiF.

Question 20.
The skeletal structure of CH₃COOH as shown below is correct, but some of the bonds are shown incorrectly. Write the correct Lewis structure for acetic acid.

Answer:
The correct Lewis structure for acetic acid is given below :

Question 21.
Apart from tetrahedral geometry, another; possible geometry for CH₄ is square planar with the four H atoms at the comers of the square and the C atom at its centre. Explain why CH₄ is not square planar?
Answer:
Electronic configuration of carbon atom :
₆C : 1s² 2s² 2p²
In the excited state, the orbital picture of carbon can be represented as:

Hence, carbon atom undergoes sp³ hybridization in CH₄ molecule and takes a tetrahedral shape.

For a square planar shape, the hybridization of the central atom has to be dsp. However, an atom of carbon does not have d-orbitals to undergo dsp² hybridization. Hence, the structure of CH₄ cannot be square planar. Moreover, with a bond angle of 90° in square planar, the stability of CH₄ will be very less because of the repulsion existing between the bond pairs. Hence, VSEPR theory also supports a tetrahedral structure for CH₄.

Question 22.
Explain why BeH₂ molecule has a zero dipole moment although the Be—H bonds are polar.
Answer:
BeH₂ molecule is linear. The two equal bond dipoles point in opposite
directions and cancel the effect of each other.
That is why its dipole moment is zero.

Question 23.
Which out of NH₃ and NF₃ has higher dipole moment and why?
Answer:
In both molecules i.e., NH₃ and NF₃, the central atom (N) has a lone pair electron and there are three bond pairs. Hence, both molecules have a pyramidal shape. Since fluorine is more electronegative than hydrogen, it is expected that the net dipole moment of NF₃ is greater than NH₃. However, the net dipole moment of NH₃ (1.46 D) is greater than that of NF₃ (0.24 D).
This can be explained on the basis of the directions of the dipole moments of each individual bond in NF₃ and NH₃. These directions can be shown as :

Thus, the resultant moment of the N—H bonds add up to the bond moment of the lone pair (the two being in the same direction), whereas that of the three N—F bonds partly cancels the moment of the lone pair.
Hence, the net dipole moment of NF₃ is less than that of NH₃.

Question 24.
What is meant by hybridisation of atomic orbitals? Describe the shapes of sp, sp² , sp³ hybrid orbitals.
Answer:
Hybridisation : It is defined as the mixing of the atomic orbitals belonging to the same atom but having slightly different energies so that a redistribution of energy takes place between them resulting in the formation of new orbitals of equal energies and identical shapes. The new orbitals thus formed are known as Hybrid Orbitals. sp Hybridisation : Here one s and one p orbitals of same atom mix up to
give two sp hybrid orbitals with \(\frac{1}{2}\)s and \(\frac{1}{2}\)p character and linear shape with
bond angle of 180° between them. For example, in BeH₂, BeF₂ and C₂H₂, Be and C are sp-hybridised.

sp hybridization is also called diagonal hybridization.

sp² Hybridisation : Here one s and two p-orbitals of same atom mix up to form three sp²hybrid orbitals with \(\frac{1}{3}\)s and \(\frac{2}{3}\)p character. They form Trigonal Planar shapes with an angle of 120° with themselves. For example, in BH₃ and BF₃, boron is sp² hybridised and in C₂H₄, carbon is sp² hybridised.

sp³ Hybridisation : Here one s and three p orbitals of same atom mix up to give four sp³ hybrid orbitals with \(\frac{1}{4}\) s character and \(\frac{3}{4}\)p character. They form tetrahedral shapes with angles of 109°, 28′ with themselves. For example, in methane (CH₄), ethane (C₂H₆) and all compounds of carbon containing C—C single bonds, carbon is sp³ hybridised.

Question 25.
Describe the change in hybridisation (if any) of the A1 atom in the following reaction.
AlCl₃ + Cl^– → \(\mathbf{A l C l}_{\mathbf{4}}^{-}\)
Answer:
Electronic configuration of A1 in ground state is \(1 s^{2}, 2 s^{2}, 2 p^{6}, 3 s^{2}, 3 p^{\prime}{ }_{x}\) and it is \(1 s^{2}, 2 s^{2}, 2 p^{6}, 3 s^{\prime}, 3 p_{x}^{\prime}, 3 p^{\prime} y\) in excited state.

In the formation of AlCl₃ Al undergoes sp²-hybridisation and it is trigonal planar in shape. While in the formation of \(\mathrm{AlCl}_{4}^{-} \), Al undergoes sp³-hybridisation. It means empty 3p_z-orbital also involved in hybridisation. Thus, the shape of \(\mathrm{AlCl}_{4}^{-} \) ion is tetrahedral.

Question 26.
Is there any change in the hybridisation of B and N atoms as a result of the following reaction?
BF₃ + NH₃ → F₃B . NH₃
Answer:
In BF₃, B is sp² hybridised and in NH₃, N is sp³ hybridised. After the reaction hybridisation of B changes to sp³ but that of N remains unchanged.

Question 27.
Draw diagrams showing the formation of a double bond and a triple bond between carbon atoms in C₂H₄ and C₂H₂ molecules.
Answer:
Formation of C₂H₄ (ethylene)

Formation of C₂H₂ (acetylene)

Question 28.
What is the total number of sigma and pi bonds in the following molecules?
(a) C₂H₂ (b) C₂H₄
Answer:
(a) The structure of C₂H₂ can be represented as:

Hence, there are three sigma and two pi-bonds in C₂H₂.

(b) The structure of C₂H₄ can be represented as:

Hence, there are five sigma bonds and one pi-bond in C2H4.

Question 29.
Considering x-axis as the intemuclear axis which out of the following will not form a sigma bond and why?
(a) 1s and 1s (b) 1s and 2p_x, (c) 2p_y and 2p_y (d) Is and 2s.
Answer:
(c) 2p_y and 2p_y orbitals will not a form a sigma bond. Taking x-axis as
the intemuclear axis, 2p_y and 2p_y orbitals will undergo lateral overlapping, thereby forming a pair bond.

Question 30.
Which hybrid orbitals are used by carbon atoms in the following molecules?
(a) CH₃— CH₃; (b) CH₃—CH = CH₂; (c) CH₃—CH₂—OH;
(d) CH₃—CHO; (e) CH₃COOH
Answer:

Question 31.
What do you understand by bond pan’s and lone pah’s of electrons? Illustrate by giving one example of each type.
Ans. When two atoms combine by sharing their one or more valence electrons, a covalent bond is formed between them. The shared pairs of electrons present between the bonded atoms are called bond pairs. All valence electrons may not participate in bonding. The electron pairs that do not participate in bonding are called lone pairs of electrons.
For example, in C₂H₆ (ethane), there are seven bond pairs but no lone pair present.

In H₂O, there are two bond pairs and two lone pairs on the central atom (oxygen).

Question 32.
Distinguish between a sigma and a pi bond.
Answer:
The following are the differences between sigma and pi-bonds :

	Sigma (σ) Bond	Pi (π) Bond
(a)	It is formed by the end to end over lapping (axial over lapping) of atomic orbitals.	It is formed by the lateral overlapping (sideway overlapping) of atomic orbitals.
(b)	The orbitals involved in the overlapping are s—s, s—p or p—p.	These bonds are formed by the overlapping of p—p orbitals only.
(c)	It is a strong bond.	It is a weak bond.
(d)	The electron cloud is symmetrical about the line joining the two nuclei.	The electron cloud is not symmetrical.
(e)	It consists of one electron cloud, which is symmetrical about the internuclear axis.	There are two electron clouds lying above and below the plane of the atomic nuclei.
(f)	Free rotation about σ bonds is possible.	Rotation is restricted in case of pi-bonds.

Question 33.
Explain the formation of H₂ molecule on the basis of valence bond theory.
Answer:
Consider two hydrogen atoms A and B are approaching each other. Their nuclei are N_A and N_B and electrons present in them are represented by e_A and e_B. When the two atoms are far apart, there is no interaction between them but as these approach each other, some new ‘ attractive and repulsive force begin to operate.
Attractive forces generated between

(i) nucleus of one atom and its own electron i.e., N_A – e_A and N_B – e_B.
(ii) nucleus of one atom and electron of other atom i.e., N_A – e_B and N_B-e_A.
Similarly, repulsive forces originated in between
1. electrons of two atoms i.e., e_A – e_B
2. nuclei of two atoms N_A – N_B.
Attractive forces tend to bring the combining atoms close to each other “ whereas repulsive forces tend to push them apart as shown in the figure

The magnitude of the attractive forces is more than that of the repulsive forces. Hence, the two atoms approach each other. As a result, the potential energy decreases. Finally, a state is reached when the attractive forces balance the repulsive forces and the system acquires minimum energy. This leads to the formation of a dihydrogen molecule.

Question 34.
Write the important conditions required for the linear combination of atomic orbitals to form molecular orbitals.
Answer:
Conditions required for the Combination of Atomic Orbitals
The linear combination of atomic orbitals to form molecular orbitals is possible only when they satisfied the following conditions :
(i) Similar energy of combining atomic orbitals : The combining atomic orbitals must possess the same or nearly the same energy. It means that Is orbital can combine with another Is orbital but not with 2s orbital because the energy of 2s orbitals is appreciable higher than that of Is orbital. However, it is not true in case of very different atoms.
(ii) Similar symmetry of combining atomic orbitals : The combining atomic orbitals must possess the same symmetry about the molecular axis along with the same energy. If the orbitals have same energy but their symmetry is not same, they will not combine e.g., 2p_z orbital of one atom can combine with 2p_z orbital or 2s orbital of the other atom but not with the 2p_x or 2p_y orbitals as their symmetries are different.
(iii) Maximum overlap : The combining atomic orbitals must overlap to the maximum extent. Higher the extent of overlapping, more will be the electron-density between the nuclei of a molecular orbital.

Question 35.
Use molecular orbital theory to explain why the Be₂ molecule does not exist.
Answer:
The electronic configuration of Beryllium is 1s² 2s²
The electronic configuration of Be₂ molecule (4 + 4 = 8),
σ1s², σ* 1s², σ2s²s², σ* 2s²
Hence, the bond order of Be₂ is -(N_b – N_a).
where,
N_b = Number of electrons in bonding orbitals.
N_a – Number of electrons in anti-bonding orbitals.
∴ Bond order of Be₂ = \(\frac{1}{2}\) (4 – 4) = 0
A negative or zero bond order means that the molecule is unstable. Hence, Be2 molecule does not exist.

Question 36.
Compare the relative stability of the following species and indicate their magnetic properties ; \(\mathbf{O}_{2}, \mathbf{O}_{2}^{+}, \mathbf{O}_{2}^{-}\)(superoxide), \(\mathrm{O}_{2}^{2-}\) (peroxide)
Answer:

Question 37.
Write the significance of a plus and a minus sign shown in representing the orbitals.
Answer:
Molecular orbitals are represented by wave function. A plus sign in an orbital indicates a positive wave function while a minus sign in an orbital represents a negative wave function. Combination of two wave functions having similar sign gave bonding molecular orbital while that having opposite sign gave antibonding molecular orbital.

Question 38.
Describe the hybridisation in case of PCl₅. Why are the axial bonds longer as compared to equatorial bonds?
Answer:
The ground state and excited state outer electronic configurations of phosphorus (Z = 15) are as follows :

Phosphorus atom is sp³ d hybridised in the excited state. These orbitals are filled by the electron pairs donated by five Cl atoms as :

The five sp³d hybrid orbitals are directed towards the five corners of the trigonal bipyramidals. Hence, the geometry of PCl₅ can be represented as :

There are five P—Cl sigma bonds in PCl₅. Three P—Cl bonds lie in one plane and make an angle of 120° with each other. These bonds are called equatorial bonds.
The remaining two P—Cl bonds lie above and below the equatorial plane and make an angle of 90° with the plane. These bonds are called axial bonds.

As the axial bond pairs suffer more repulsion from the equatorial bond pairs, axial bonds are slightly longer than equatorial bonds.

Question 39.
Define hydrogen bond. Is it weaker or stronger than the van der Waals forces?
Answer:
A hydrogen bond is defined as an attractive force between the hydrogen attached to an electronegative atom of one molecule and an electronegative atom of a different molecule (may be of the same kind). Due to a difference between electronegativities, the bond pair between hydrogen and the electronegative atom gets drifted far away from the hydrogen atom. As a result, a hydrogen atom becomes electropositive with respect to the other atom and acquires a positive charge.

The magnitude of H-bonding is maximum in the solid state and minimum in the gaseous state.
There are two types of H-bonds:
(i) Intermolecular H-bonds e.g., HF, H₂O etc
(ii) Intramolecular H-bonds e.g., o-nitrophenol
Hydrogen bonds are stronger than Van der Waals forces since hydrogen bonds are regarded as an extreme form of dipole-dipole interaction.

Question 40.
What is meant by the term bond order? Calculate the bond order of: \(\mathrm{N}_{2}, \mathrm{O}_{2}, \mathrm{O}_{2}^{+}\) and \(\mathbf{O}_{2}^{-}\).
Answer:
Bond order is defined as half of the difference between the number of electrons present in the bonding and anti-bonding orbitals of a molecule.
Bond order = \(\frac{1}{2}\) (N_b – N_a)
If N_b > N_a, then the molecule is said be stable. However, if N_b ≤ N_a, then the molecule is considered to be unstable.
Bond order values 1, 2 or 3 correspond to single, double or triple bonds respectively.

Calculation of the bond order of \(\mathrm{N}_{2}, \mathrm{O}_{2}, \mathrm{O}_{2}^{+}\) and \(\mathbf{O}_{2}^{-}\).
Electronic configuration of N₂