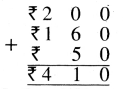
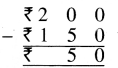
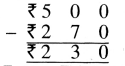
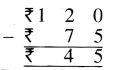
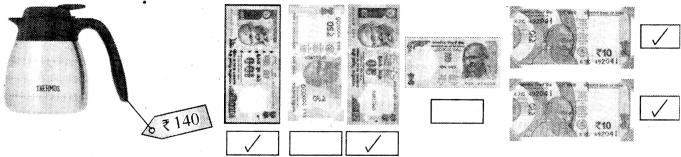
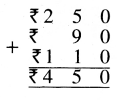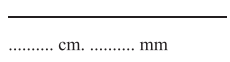Punjab State Board PSEB 10th Class Maths Book Solutions Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1
In each of the questions, give the justification of the construction also.
Question 1.
Draw a line segment of length 7.6 cm and divide ¡tin the ratio 5 : 8. Measure the two parts.
Solution:
Given: A line segment of length of 7.6 cm.
Steps of construction:
1. Take a line segment AB = 7.6 cm.
2. Draw any ray AX, making an acute angle ∠BAX.
3. Locate 5 + 8 = 13 (given ratio 5: 8) points A1, A2, A3, A4, A5, ………….., A10, A11, A12, A13 on ray AX such that A1A2 = A2A3 = A3A4 = …………. = A11A12 = A12 A13.
4. Join BA13.
5. Through point A5, draw a line A5C || A13B (by making an angle equal to ∠A13B) at A5 intersecting AB at ‘C’. Then AC : CB = 5 : 8;
Justification:
Let us see how this method gives us the required division.
In ∆AA13B,
Since A5C || A13B
∴ By Basic Proportionality Theorem
\(\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}=\frac{\mathrm{AC}}{\mathrm{CB}}\)
By construction, \(\frac{\mathrm{AA}_{5}}{\mathrm{~A}_{5} \mathrm{~A}_{13}}=\frac{5}{8}\)
∴ \(\frac{\mathrm{AC}}{\mathrm{CB}}=\frac{5}{8}\)
This shows that ‘C’ divides AB in the ratio 5 : 8.
On measuring the two parts, AC = 2.9 cm and CB = 4.7 cm.
Alternative Method:
Steps of construction:
1. Take a line segment AB = 7.6 cm
2. Draw any acute angle ∠BAX
3. Draw angle ∠ABY such that ∠ABY = ∠BAX.
4. Locate the points A1, A2, A3, A4, A5 on ray AX such that A1A2 = A2A3 = A3A4 = A4A5.
5. Locate the points B1, B2, B3, B4, B5, B6, B7, B8 on ray BY such that B1B2 = B2B3 = B3B4 = B4B5 = B5B6 = B6B7 = B7B8
6. Join A5B8 let it intersects AB at point Then AC : CB = 5 : 8.
justification:
In ∆ACA5 and ∆BCB8,
∠ACA5 = ∠BCB8 [vertically opp. ∠s]
∠BAA5 = ∠ABB8 [construction]
∴ AACA5 ~ ABCB8 [AA-similarity cond.]
∴ Their corresponding sides must be in the same ratio. ,
\(\frac{A C}{B C}=\frac{C A_{5}}{C B_{8}}=\frac{A_{5} A}{B_{8} B}\)
(I)(II) (III)
From I and III, \(\frac{A C}{B C}=\frac{A_{5} A}{B_{8} B}\)
But, \(\frac{A_{5} A}{B_{8} B}=\frac{5}{8}\) [construction]
\(\frac{A C}{C B}=\frac{5}{8}\).
Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac{2}{3}\) of corresponding sides of the first triangle.
Solution:
Steps of construction:
1. Construct a triangle ABC with given measurements. AB = 5 cm, AC = 4 cm and BC = 6 cm.
2. Make any acute angle ∠CBX below the side BC.
3. Locate three points (greater of 2 and 3 in \(\frac{2}{3}\))B1, B2, B3 on BX such that BB1 = B1B2 = B2B3.
4. Join B3C.
5. Through B2 (smaller of 2 and 3 in \(\frac{2}{3}\) draw a line parallel to B3C, which intersect BC in C’.
6. Through C’, draw a line parallel to CA meeting BA is A’.
Thus ∆A’BC’ is the required triangle whose sides are of corresponding sides of ∆ABC.
Justification of construction :
First we will show that first triangle and constructed triangle are similar.
i.e. ∆A’BC’ ~ ∆ABC.
Consider ∆A’BC’ and ∆ABC.
∠B = ∠B [Common]
∠A’C’B= ∠ACB [By construction]
∆A’C’B ~ ∆ACB [AA – similarity]
∴ Their corresponding sides must be in the same ratio.
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) …………….(1)
Now, consider ∆B2BC’ and ∆B3BC,
∠B = ∠B [common]
∠B2C’B = ∠B2CB [construction]
∴ ∆B2BC’ ~ ∆B3BC [AA -similarity]
∴ Their corresponding sides must be in the same ratio.
\(\frac{\mathrm{B}_{2} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{B}_{2}}{\mathrm{CB}_{3}}\)
I II III
Taking (I) and (II).
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{B}_{2} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}\)
But, \(\frac{\mathrm{B}_{2} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}=\frac{2}{3}\) [construction]
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{2}{3}\) ……………(2)
From (1) & (2),
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{2}{3}\)
⇒ A’B = \(\frac{2}{3}\) AB and BC’ = \(\frac{2}{3}\) BC; C’A’ = \(\frac{2}{3}\) CA.
Hence, the construction is Justified.
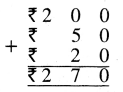
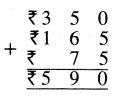
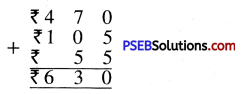
Question 3.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are of the corresponding sides of the first triangle.
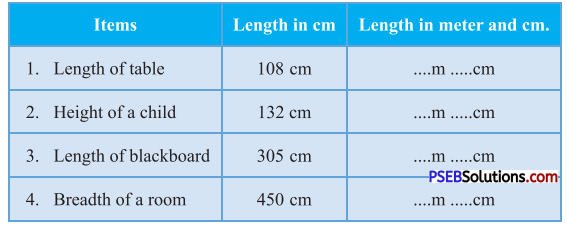
Solution:
Steps of construction :
1. Construct a triangle ABC in which AB = 7 cm, BC 6 cm and AC =5 cm.
2. Make any acute angle ∠BAX below the base AB.
3. Locate seven points A1, A2, A3, A4, A5, A6, A7 on the ray AX such that
AA1 = A1A2 = A2A3 = A3A4 = A4A5 = A5A6 = A6A7.
4. Join BA5.
5. Through A7, draw a line parallel A5B. Let it meets AB at B’ on being produced such that AB’= \(\frac{7}{5}\) AB.
6. Through B’, draw a line parallel to BC which meets AC at C’ on being produced.
∆AB’C’ is the required triangle.
Justification of the construction.
In ∆ABC and ∆AB’C’,
∠A = ∠A [common]
∠ABC = ∠AB’C’ [corresponding ∠s]
∴ ∠ABC – ∠AB’C’ [AA-similarity]
∴ Their corresponding sides must be in the same ratio.
\(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{\mathrm{BC}}{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}=\frac{\mathrm{CA}}{\mathrm{C}^{\prime} \mathrm{A}}\) ……………..(1)
Again, in ∆AA5B and AA7B’
∠A = ∠A [common]
∠AA5B = ∠AA7 B’ [corresponding ∠s]
∴ ∆AA5B ~ ∆AA7B’ [AA – similarity]
∴ Their corresponding sides must be in the same ratio.
\(\frac{\mathrm{AA}_{5}}{\mathrm{AA}_{7}}=\frac{\mathrm{A}_{5} \mathrm{~B}}{\mathrm{~A}_{7} \mathrm{~B}^{\prime}}=\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}\)
⇒ \(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{\mathrm{AA}_{5}}{\mathrm{AA}_{7}}\) [construction]
But, \(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{5}{7}\) …………….(2)
From (1) and (2),
\(\frac{\mathrm{AB}}{\mathrm{AB}^{\prime}}=\frac{\mathrm{BC}}{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}=\frac{\mathrm{CA}}{\mathrm{C}^{\prime} \mathrm{A}}=\frac{5}{7}\)
or \(\frac{A B^{\prime}}{A B}=\frac{B^{\prime} C^{\prime}}{B C}=\frac{C^{\prime} A}{C A}=\frac{7}{5}\)
⇒ AB’ = \(\frac{7}{5}\) AB; B’C’ = \(\frac{7}{5}\) BC and C’A’ = \(\frac{7}{5}\) CA
Hence, the sides of ∆AB’C’ are \(\frac{4}{4}\) of ∆ABC.
Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 12 times
the corresponding sides of the isosceles triangle.
Solution:
Given: Base of isosceles triangle is 8 cm and Altitude = 4 cm
To construct: A triangle whose sides are times the sides of isosceles triangle.
Steps of construction:
1. Take base AB = 8 cm.
2. Draw perpendicular bisector of AB. Let it intersect AB at ‘M’.
3. With M as centre and radius = 4 cm, draw an arc which intersects the perpendicular bisector at ‘C’
4. Join CA and CB.
5. ∆ABC is an isosceles with CA = CB.
6. Make any acute angle ∠BAX below the side BC.
7. Locate three (greater of ‘2’ & ‘3’ in 1\(\frac{1}{2}\) or \(\frac{3}{2}\))
A1, A2, A3 on ‘AX’ such that A A1 = A1 A2 = A2 A3.
8. Join A2 (2nd point smaller of ‘2 and ‘3’ in ) and B.
9. Through A3, draw a line parallel to A2B meet AB is B’ cm being produced.
10. Through B’, draw a line parallel to BC which meets AC in C’ on being produced. ∆AB’C’ is the required triangle whose sides are 1\(\frac{1}{2}\) times the corresponding sides of ∆ABC.
Justification of construction :
First we will prove ∆AB’C’ are ∆ABC and similar.
Consider ∆ AB’C’ and ∆ ABC
∠A = ∠A [Common]
∠AB’C’ = ∠ABC [By construction]
∠AB’C’ ~ ∠ABC [By AA – similarityj
∴ Their corresponding sides must be in the same ratio
\(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}}{\mathrm{CA}}\) ……………(1)
Now consider ∆ A3AB’ and ∆ A,AB
∠A = ∠A [common]
∠B’A3A = ∠BA2A [By construction]
∴∆ A3A B’ – ∆A2AB [AA – similarity]
∴ Their corresponding sides must be in the same ratio
\(\frac{A_{3} A}{A_{2} A}=\frac{A B^{\prime}}{A B}=\frac{B^{\prime} A_{3}}{B A_{2}}\)
I II III
Taking (I) & (II),
\(\frac{A B^{\prime}}{A B}=\frac{A_{3} A}{A_{2} A}\)
But, \(\frac{A_{3} A}{A_{2} A}=\frac{3}{2}\) [construction]
⇒ \(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{3}{2}\) ……………..(2)
From (1) & (2)m
\(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}=\frac{\mathrm{B}^{\prime} \mathrm{C}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}}{\mathrm{CA}}=\frac{3}{2}\left(1 \frac{1}{2}\right)\)
⇒ AB’ = 1\(\frac{1}{2}\) (AB); B’C’ = 1\(\frac{1}{2}\) BC and C’A’ = 1\(\frac{1}{2}\) (CA)
Hence, given result is justified.
Question 5.
Draw a triangle ABC with side BC = 6 cm, AB =5 cm and ¿ABC = 60°. Then construct a triangle whose sides are of the corresponding sides of the triangle ABC.
Solution:
Steps of construction :
1. Take a line segment BC = 6 cm
2. Construct an angle of measure 60° at point B. i.e., ∠CBX = 60°.
3. With B as centre and radius 5 cm draw an arc intersecting BX at ‘A’
4. Join A and C.
5. At B, make any acute angle ∠CBY below the side BC.
6. Locate four points (greater of 3 and 4 in \(\frac{3}{4}\)) B1, B2, B3, B4 on BY such that BB1 = B1B2 = B2B3 = B3B4. .
7. Join B4 and C.
8. Draw a line through B3 (smaller of 3 and 4 in ) parallel to B4C making corresponding angles. Let the line through B3 intersects BC in C’.
9. Through C’, draw a line parallel to CA which intersects BA at A’.
The ∆A’BC’ is the required triangle whose sides are \(\frac{3}{4}\) of sides of ∆ABC.
Justification of the construction:
Consider ∆A’BC’ and ∆ABC
∠B = ∠B [commoni
∠A’C’B = ∠ACB [corresponding ∠s]
∴ ∆A’BC’ ~ ∆ABC [AA – similarity]
∴ Their corresponding sides must be in the same ratio.
∴ \(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ……………..(1)
Now consider ∆B3B C’ and ∆B4BC.
∠B = ∠B [common]
∠ C’ B3B = ∠CB4B [corresponding ∠s]
∆B3BC’ ~ ∆B4BC [AA – similarity con.]
Their corresponding sides must be in the same ratio.
\(\frac{B_{3} B}{B_{4} B}=\frac{B C^{\prime}}{B C}=\frac{C^{\prime} B_{3}}{C B_{4}}\)
(I) (II) (III)
From (I) and (II),
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{B}_{3} \mathrm{~B}}{\mathrm{~B}_{4} \mathrm{~B}}\)
But, = \(\frac{\mathrm{B}_{3} \mathrm{~B}}{\mathrm{~B}_{4} \mathrm{~B}}=\frac{3}{4}\) [construction]
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{3}{4}\) ………..(3)
From (1) and (3)
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{3}{4}\)
and C’A’= \(\frac{3}{4}\) CA.
∆A’BC’ is the required triangle whose sides are \(\frac{3}{4}\) sides of ∆ABC.
Question 6.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°. ∠A = 105°. Then construct a triangle whose sides are j- times
the corresponding sides of ∆ABC.
Solution:
Steps of construction:
1. Construct the triangle ABC with the given measurements.
BC = 7 cm; ∠B = 45, ∠A = 105°
By angle sum property of triangle
∠A + ∠B + ∠C= 180°
105° + 45° + ∠C = 180°
∠C = 180 – 150° = 30°
2. Make any acute angle ∠CBX at point B, below the sides BC.
3. Locate four points (greater of 3 and 4 in \(\frac{4}{3}\)) B1, B2, B3, B4 on ‘BX’ such that BB1 = B1B2 = B2B3 = B3B4.
4. Join B3C (smaller of 3 and 4 in \(\frac{4}{3}\)).
5. Through B4, draw a line parallel to B3C meeting BC in C’ on being produced.
6. Through C’, draw another line parallel to CA meeting BA in A’ on being produced.
7. ∆A’BC’ is the required triangle whose sides are times the triangle ABC.
Justification of construction:
Consider the ∆ A’BC’ and ∆ ABC,
∠B = ∠B [common]
∠A’C’B = ∠ACB [construction]
∴ ∆A’BC’ ~ ∆ABC [AA – similarity]
∴ Their corresponding sides must be in the same ratio
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ………….(1)
Again, consider ∆B4B C’ and ∆B3BC,
∠B = ∠B [common]
∠C’B4B = ∠CB3B [By consiruction]
∴ BB C’ AB3BC [AA-si niilarity]
∴ Their corresponding sides must be in the same ratio
\(\frac{\mathrm{B}_{4} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{B}_{4}}{\mathrm{CB}_{3}}\)
I II III
Taking I and II members.
\(\frac{B C^{\prime}}{B C}=\frac{B_{4} B}{B_{3} B}\)
But, \(\frac{B_{4} B}{B_{3} B}=\frac{4}{3}\) (construction)
or \(\frac{B C^{\prime}}{B C}=\frac{4}{3}\) ………….(2)
From (1) and (2),
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{4}{3}\)
⇒ A’B = \(\frac{4}{3}\) AB; BC’ = \(\frac{4}{3}\) BC and C’A’ = \(\frac{4}{3}\) CA
Hence the construction is justified.
Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac{5}{3}\) times the corresponding sides of the given triangle.
Solution:
Steps of construction:
1. Draw a right triangle using given conditions. Consider the triangle as ABC in which BC = 4 cm; AB = 3 cm and
∠B = 90°.
2. Make any acute angle ∠CBX below the line BC.
3. Locate five points (greater of 5 and 3 in \(\frac{5}{3}\)) B1, B2, B3, B4. B5 on BX such that BB1 = B1B2 = B2B3 = B3B4 = B4B5.
4. Join B3 (smaller of ‘5’ and ‘3’ in \(\frac{5}{3}\)) and ‘C’.
5. Through B5. draw a line parallel to BC meeting BC is C’ on being produced.
6. Again draw a line through C’ parallel to CA meeting BA in A’ on being produced.
∆A’BC’ is the required triangle whose sides are \(\frac{5}{3}\) times the sides of ∆ABC.
Justification of construction :
Consider ∆A’BC’ and ∆ABC
∠B = ∠B [common]
∠A’C’B = ∠ACB [By construction]
∴ ∆A’BC’ ~ ∆ABC [AA-similarity condition]
∴ Their corresponding sides must be in the same ratio
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}\) ……………..(1)
Again, in ∆B5C’B and ∆XB3CB,
∠B = ∠B [common]
∠C’B5B = ∠CB3B [By construction]
∴ ∆B5C’B ~ ∆B3CB [AA-similarityj
∴ Their corresponding sidcs must be in the same ratio.
\(\frac{\mathrm{B}_{5} \mathrm{C}^{\prime}}{\mathrm{B}_{3} \mathrm{C}}=\frac{\mathrm{C}^{\prime} \mathrm{B}}{\mathrm{CB}}=\frac{\mathrm{BB}_{5}}{\mathrm{BB}_{3}}\)
I II III
Taking II and III members.
\(\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{B}_{5} \mathrm{~B}}{\mathrm{~B}_{3} \mathrm{~B}}\)
But, \(\frac{B_{5} B}{B_{3} B}=\frac{5}{3}\) [construction]
\(\frac{B C^{\prime}}{B C}=\frac{5}{3}\) ……………(2)
From (1) and (2),
\(\frac{\mathrm{A}^{\prime} \mathrm{B}}{\mathrm{AB}}=\frac{\mathrm{BC}^{\prime}}{\mathrm{BC}}=\frac{\mathrm{C}^{\prime} \mathrm{A}^{\prime}}{\mathrm{CA}}=\frac{5}{3}\)
⇒ A’B = \(\frac{5}{3}\) AB; BC’ = \(\frac{5}{3}\) BC and C’A’ = \(\frac{5}{3}\) CA
Hence the construction is justified.
