Punjab State Board PSEB 11th Class Economics Book Solutions Chapter 22 केंद्रीय प्रवृत्ति के माप-समान्तर माध्य Textbook Exercise Questions, and Answers.
PSEB Solutions for Class 11 Economics Chapter 22 केंद्रीय प्रवृत्ति के माप-समान्तर माध्य
PSEB 11th Class Economics केंद्रीय प्रवृत्ति के माप-समान्तर माध्य Textbook Questions and Answers
I. वस्तुनिष्ठ प्रश्न (Objective Type Questions)
प्रश्न 1.
केन्द्रीय प्रवृत्ति किसे कहते हैं ?
उत्तर-
आंकड़ों के विस्तार के अन्तर्गत एक ऐसे मूल्य को केन्द्रीय प्रवृत्ति कहते हैं जो शृंखला के सभी मूल्यों की प्रतिनिधता करता है।
प्रश्न 2.
समान्तर माध्य से क्या अभिप्राय है ?
उत्तर-
समान्तर माध्य किसी श्रृंखला की सभी मदों की औसत होती है।
प्रश्न 3.
समान्तर माध्य का कोई एक लाभ लिखें।
उत्तर-
समान्तर माध्य उपयोग तथा गणना की दृष्टि से / रूप से सरल औसत है।
प्रश्न 4.
समान्तर माध्य को स्थिति की औसत कहा जाता है।
उत्तर-
ग़लत।
![]()
प्रश्न 5.
समान्तर माध्य को गणित्क औसत कहा जाता है।
उत्तर-
सही।
प्रश्न 6.
किसी श्रृंखला के सभी मदों के योग को उनकी संख्या से विभाजन करने से ………………. प्राप्त होता है।
(a) समान्तर माध्य
(b) माध्यका
(c) बहुलक
(d) इनमें से कोई नहीं।
उत्तर-
(a) समान्तर माध्य।
प्रश्न 7.
समान्तर माध्य का सूत्र लिखो।
उत्तर-
\(\bar{X}=\frac{\Sigma X}{N}\)
प्रश्न 8.
समान्तर मध्य दो प्रकार की होती है :
(i) सरल समान्तर माध्य
(ii) ……………….
उत्तर-
भारित समान्तर माध्य।
प्रश्न 9.
खण्डित श्रृंखला में समान्तर माध्य के माप का सूत्र लिखो। ..
उत्तर-
\(\overline{\mathrm{X}}=\frac{\Sigma f \mathrm{X}}{\mathrm{N}}\)
प्रश्न 10.
समान्तर माध्य का कोई एक अवगुण लिखो।
उत्तर-
समान्तर माध्य सीमान्त मूल्यों द्वारा प्रभावित होती है।
प्रश्न 11.
पद विचलन विधि द्वारा समान्तर माध्य के माप का सूत्र ..
(a) \(\bar{X}=\frac{\Sigma X}{N}\)
(b) \(\overline{\mathbf{X}}=\mathrm{A}+\frac{\boldsymbol{\Sigma} f d x}{\mathbf{N}}\)
(c) \(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x^{\prime}}{\mathrm{N}} \times \mathrm{C}\)
(d) \(\overline{\mathbf{X}}=\frac{\Sigma f x}{\mathrm{~N}}\)
उत्तर-
(c) \(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x^{\prime}}{\mathrm{N}} \times \mathrm{C}\)
प्रश्न 12.
अशुद्ध समान्तर औसत को सही समान्तर माध्य की गणना का सूत्र लिखो।
उत्तर-
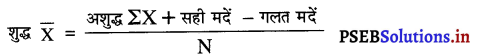
प्रश्न 13.
मदों में समान्तर से लिए गए विचलनों का योग शून्य होता है।
उत्तर-
सही।
प्रश्न 14.
यदि मदों में कोई स्थिर संख्या को जोड़, घटा, गुणा अथवा विभाजित किया जाए तो समान्तर में अन्तर आ जाता है।
उत्तर-
ग़लत।
II. अति लघु उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
एक अच्छी केन्द्रीय प्रवृत्ति के कोई दो गुण बताएं।
उत्तर-
1. स्पष्ट परिभाषा (Clear Definition)-एक अच्छी केन्द्रीय प्रवृत्ति अथवा औसत की परिभाषा स्पष्ट होनी चाहिए जिससे इसको समझना आसान हो जाता है। इससे अनुसन्धान का कार्य सरलता से किया जा सकता है। इसलिए यह अनिवार्य है कि औसतों की परिभाषा स्पष्ट तथा स्थिर हो।
2. समझने में आसानी (Easy to Understand)-अच्छी औसत का गुण बताते हुए प्रो० घूली तथा कैंडल का विचार है कि इसको आसानी से समझा जा सके। यदि औसत को सरल ढंग से स्पष्ट करने की जगह पर जटिल धारणाओं का रूप दिया जाता है तो साधारण लोग इन औसतों का प्रयोग अच्छी तरह नहीं कर सकते।
![]()
प्रश्न 2.
समान्तर औसत (Mean) से क्या अभिप्राय है ?
उत्तर-
केन्द्रीय प्रवृत्ति के माप में अच्छी औसत को समान्तर औसत कहा जाता है। गणित औसतों में यह सबसे अधिक प्रसिद्ध या लोकप्रिय है। समान्तर औसत की जगह पर मध्यमान (Mean) का प्रयोग किया जाता है। जब हम दी गई सभी मदों का जोड़ करके इस जोड़ को मदों की संख्या से विभाजित कर देते हैं तो इससे हमारे पास समान्तर औसत प्राप्त हो जाती है।
प्रश्न 3.
समान्तर औसत के कोई दो गुण बताएँ।
उत्तर-
- सरल-समान्तर औसत एक सरल औसत है, जिसकी स्पष्ट परिभाषा दी जा सकती है। आंकड़ा शास्त्री इस धारणा का सबसे अधिक प्रयोग करते हैं।
- आसान माप-समान्तर औसत का माप आसानी से किया जा सकता है। इससे एक समान परिणाम प्राप्त होते
प्रश्न 4.
समान्तर औसत के कोई दो दोष बताएँ।
उत्तर-
- गुणात्मक माप के लिए उचित नहीं-समान्तर औसत केवल उस स्थिति में ही माप सकते हैं, जब आंकड़े संख्याओं के रूप में दिए हों, यदि गुणात्मक माप जैसे कि बहादुरी, समझदारी इत्यादि के रूप में करना हो तो गणित औसत उचित नहीं होती।
- हद की मदों के लिए उचित नहीं-समान्तर औसत का मुख्य दोष यह होता है कि जब मदों के मूल्य में एक मद बहुत बड़ी अथवा बहुत छोटी होती है तो इस स्थिति में औसत सभी मदों का प्रतिनिधित्व नहीं करता। उदाहरणस्वरूप पांच विद्यार्थियों के अंक \(\frac{1+2+3+4+90}{5}=\frac{100}{5}\) = 20 तथा 90 हैं तो औसत अंक है, परन्तु यह विद्यार्थियों के अंकों की उचित प्रतिनिधित्व नहीं करती।
प्रश्न 5.
समान्तर औसत का माप कैसे ज्ञात किया जाता है ?
उत्तर-
प्रत्यक्ष विधि-आंकड़ा शास्त्र में समान्तर औसत को \(\bar{X}\) (एक्स बार) द्वारा लिखा जाता है। जिन मदों की औसत का माप करना होता है, उसको X1 X2…. XN प्रथम पद (X1) द्वितीय पद (X2) कुल पद (XN) कहते हैं। प्रत्यक्ष विधि द्वारा समान्तर औसत के माप के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है-
फार्मूला \(\overline{\mathrm{X}}=\frac{\mathrm{X}_{1}+\mathrm{X}_{2}+\mathrm{X}_{3}+\mathrm{X}_{4} \cdots \ldots \ldots \mathrm{X}_{\mathrm{N}}}{\mathrm{N}}=\frac{\Sigma \mathrm{X}}{\mathrm{N}} \)
अल्प विधि (Short Cut Method)-
\(\overline{\mathbf{X}}=\mathrm{A}+\frac{\Sigma f d x}{\mathrm{~N}}\)
पद विचलन विधि (Step Deviation Method)
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\boldsymbol{\Sigma} f d x^{\prime}}{\mathrm{N}} \times \mathrm{C}\)
प्रश्न 6.
खण्डित श्रेणी द्वारा समान्तर औसत की माप विधि बताएं।
उत्तर-
प्रत्यक्ष विधि \(\bar{X}=\frac{\Sigma f X}{N}\)
अल्पविधि \(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x}{\mathrm{~N}}\)
पद विचलन विधि \(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x^{\prime}}{\mathrm{N}} \times \mathrm{C}\)
III. लघु उत्तरीय प्रश्न (Short Answer Type Questions)
प्रश्न 1.
समान्तर औसत के माप की विधियों का सार लिखो।
उत्तर-
1. व्यक्तिगत श्रेणी (Individual Series)
- प्रत्यक्षं विधि
\(\bar{X}=\frac{\Sigma X}{N}\) - लघु विधि \(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma d x}{\mathrm{~N}}\)
खण्डित श्रेणी (Discrete Series)
- प्रत्यक्ष विधि \(\bar{X}=\frac{\Sigma f X}{N}\)
- लघु विधि \(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x}{\mathrm{~N}}\)
- पद विचलन विधि \(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x^{1}}{\mathrm{~N}} \times \mathrm{C} \)
3. अखण्डित श्रेणी (Continuous Series)
- प्रत्यक्ष विधि \(\overline{\mathrm{X}}=\frac{\sum f \mathrm{X}}{\mathrm{N}}\)
- लघु विधि \(\overline{\mathbf{X}}=\mathrm{A}+\frac{\sum f d x}{\mathrm{~N}}\)
- पद विचलन विधि \(\overline{\mathrm{X}}=\mathrm{X}+\frac{\Sigma f d x^{\prime}}{\mathbf{N}} \times \mathrm{C}\)
IV. दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)
प्रश्न 1.
एक अच्छी केन्द्रीय प्रवृत्ति औसत के गुणों का वर्णन करें। (Discuss the merits of good Central Tendency.)
- स्पष्ट परिभाषा (Clear Definition)-एक अच्छी केन्द्रीय प्रवृत्ति अथवा औसत की परिभाषा स्पष्ट होनी चाहिए जिससे इसको समझना आसान हो जाता है। इससे अनुसन्धान का कार्य सरलता से किया जा सकता है। इसलिए यह अनिवार्य है कि औसतों की परिभाषा स्पष्ट तथा स्थिर हो।
- समझने में आसानी (Easy to Understand)-अच्छी औसत का गुण बताते हुए प्रो० घूली तथा कैंडल का विचार है कि इसको आसानी से समझा जा सके। यदि औसत को सरल ढंग से स्पष्ट करने की जगह पर जटिल धारणाओं का रूप दिया जाता है तो साधारण लोग इन औसतों का प्रयोग अच्छी तरह नहीं कर सकते।
- माप में आसानी (Easy to Compute)-एक अच्छी केन्द्रीय प्रवृत्ति का निर्माण करते समय यह ध्यान रखना चाहिए कि जहां तक सम्भव हो औसतों को मापने तथा हल करने का ढंग आसान तथा सरल हो। यदि जटिल विधियों द्वारा माप किया जाता है तो इससे औसतों में शुद्धता प्राप्त करनी कठिन हो जाती है। परिणामस्वरूप उचित परिणाम प्राप्त नहीं होते।
4. सभी मदों पर आधारित (Based on All Items) – औसतों का माप करते समय सभी मदों को ही ध्यान में रखना चाहिए। यदि हम किसी मद को छोड़ देते हैं तो प्राप्त परिणाम में परिवर्तन नहीं होना चाहिए। उदाहरणस्वरूप पांच मनुष्यों की रोज़ाना आय ₹ 100, 200, 300, 400, 500 दी है तो औसत आय = \( \frac{100+200+300+400+500}{5}\) = \(\frac{1500}{5} \) = ₹ 300 प्राप्त होती है जोकि सभी मदों पर आधारित है। परन्तु यदि प्रति दिन की आय= \(\frac{100+200+300+400+4000}{5}=\frac{5000}{5}\) = ₹ 1000 औसत आएगी जोकि सभी मदों पर आधारित नहीं है।
5. हद की मदों से कम प्रभावित (Less Effected By Extreme Items) केन्द्रीय प्रवृत्तियों का एक गुण यह होना चाहिए बहुत बड़ी अथवा बहुत छोटी मदों का प्रभाव औसतों पर पड़ना चाहिए। इसलिए यह औसत आंकड़ों की प्रतिनिधिता उस समय करती है जब सभी आंकड़े लगभग समान होते हैं।
6. बीज गणित समीक्षा में आसानी (Easy Algebric Treatment) औसत ऐसी होनी चाहिए जिसकी बीज गणित समीक्षा हो सके। जब हम बीज गणित के आधार पर आंकड़ों का विश्लेषण करते हैं तो इससे अन्य विधियों में इन केन्द्रीय प्रवृत्तियों का प्रयोग किया जा सकता है।
![]()
प्रश्न 2.
समान्तर औसत से क्या अभिप्राय है ? समान्तर औसत के गुण तथा दोष बताओ। (What is Arithmetic Average ? Explain its Merits and Demerits.)
उत्तर-
केन्द्रीय प्रवृति के माप में अच्छी औसत को समान्तर औसत कहा जाता है। गणित औसतों में यह सबसे अधिक प्रसिद्ध या लोकप्रिय है। समान्तर औसत की जगह पर मध्यमान (Mean) का प्रयोग किया जाता है। जब हम दी गई सभी मदों का जोड़ करके इस जोड़ को मदों की संख्या से विभाजित कर देते हैं तो इससे हमारे पास समान्तर औसत प्राप्त हो जाती है।
उदाहरणस्वरूप तीन बच्चों की आयु 9 वर्ष, 10 वर्ष तथा 11 वर्ष दी है। हम इन बच्चों की औसत आयु निकालना चाहते हैं तो इस उद्देश्य के लिए तीन बच्चों की आयु का जोड़ करके उन बच्चों की संख्या ऊपर विभाजित किया जाता है तो इसको समान्तर औसत कहा जाता है। अर्थात् बच्चों की आयु का जोड़ 9 + 10 + 11 = 30 वर्ष
बच्चों की संख्या = 3
औसत आयु = ![]() = 10 वर्ष इसकी परिभाषा देते हुए प्रो० होरेश सीकरिस्ट ने कहा, “किसी श्रेणी के मदों के मूल्यों का योग करके उन मदों की संख्या से भाग देने पर जो संख्या प्राप्त होती है, उसको समान्तर औसत कहा जाता है।” (“The Arithmetic Mean is the amount secured by dividing the sum of values of the items in a series by their numbers.”-Harace Secrist)
= 10 वर्ष इसकी परिभाषा देते हुए प्रो० होरेश सीकरिस्ट ने कहा, “किसी श्रेणी के मदों के मूल्यों का योग करके उन मदों की संख्या से भाग देने पर जो संख्या प्राप्त होती है, उसको समान्तर औसत कहा जाता है।” (“The Arithmetic Mean is the amount secured by dividing the sum of values of the items in a series by their numbers.”-Harace Secrist)
समान्तर औसत के गुण-समान्तर औसत एक अच्छी औसत मानी जाती है। इसके मुख्य गुण इस प्रकार हैं-
- सरल-समान्तर औसत एक सरल औसत है, जिसकी स्पष्ट परिभाषा दी जा सकती है। आंकड़ा शास्त्री इस धारणा का सबसे अधिक प्रयोग करते हैं।
- आसान माप-समान्तर औसत का माप आसानी से किया जा सकता है। इससे एक समान परिणाम प्राप्त होते हैं।
- सभी मदों पर आधारित-समान्तर औसत में श्रेणी की सभी मदों को ध्यान में रखा जाता है। इसलिए यह औसत आंकड़ों पर अधिक प्रतिनिधित्व करती है।
- बीजगणित विवेचन-इस औसत का बीजगणित विवेचन किया जा सकता है। इसलिए आंकड़ा शास्त्र की दूसरी विधियों जैसे कि अपकिरण, सह-सम्बन्ध इत्यादि में इस औसत का अधिक प्रयोग किया जाता है।
- शुद्धता-समान्तर औसत निकालते समय प्रत्येक मद को ध्यान में रखा जाता है। इसलिए प्राप्त परिणामों में अधिक शुद्धता पाई जाती है।
- तुलना में आसानी-समान्तर औसत के आधार पर समुच्चयों की तुलना आसानी से की जा सकती है। उदाहरण स्वरूप विभिन्न देशों की प्रति व्यक्ति आय की तुलना से किसी देश के अमीर अथवा निर्धन होने का पता लगाया जा सकता है।
- स्थिर औसत-समान्तर औसत स्थिर औसत होती है, क्योंकि यदि नमूने में परिवर्तन किया जाए तो इससे औसत में अधिक परिवर्तन नहीं होता।
समान्तर औसत के दोष-समान्तर औसत के दोष इस प्रकार हैं-
1. गुणात्मक माप के लिए उचित नहीं-समान्तर औसत केवल उस स्थिति में ही माप सकते हैं, जब आंकड़े संख्याओं के रूप में दिए हों, यदि गुणात्मक माप जैसे कि बहादुरी, समझदारी इत्यादि के रूप में करना हो तो गणित औसत उचित नहीं होती।
2. हद की मदों के लिए उचित नहीं-समान्तर औसत का मुख्य दोष यह होता है कि जब मदों के मूल्य में एक मद बहुत बड़ी अथवा बहुत छोटी होती है तो इस स्थिति में औसत सभी मदों का प्रतिनिधित्व नहीं करता। उदाहरणस्वरूप पांच विद्यार्थियों के अंक 1, 2, 3, 4, तथा 90 हैं तो औसत अंक \(\frac{1+2+3+4+90}{5}=\frac{100}{5}\) = 20 यह विद्यार्थियों के अंकों की उचित प्रतिनिधित्व नहीं करती।
3. अनुचित परिणाम-समान्तर औसत द्वारा कई बार अनुचित परिणाम निकाले जाते हैं। उदाहरणस्वरूप देश A तथा देश B में लोगों की औसत आय ₹ 2000 है तो हम यह परिणाम निकालते हैं कि दोनों देशों में औसत आय समान है तथा लोगों की आर्थिक स्थिति एक समान है, परन्तु देश A में आय 10, 20, 30, 40 तथा 9000 है। इससे औसत आय \(\frac{100+200+300+400+9000}{5}=\frac{10000}{5}\) = ₹ 2000 है। देश B में 5 मनुष्यों की आय, दो-दो हज़ार रु० अंक है, परन्तु है तो औसत आय \(\frac{2000+2000+2000+2000+2000}{5}=\frac{10000}{5}\) = ₹ 2000 है परन्तु दोनों देशों में लोगों की आर्थिक स्थिति समान नहीं है। A देश में आय का वितरण असमान है, परन्तु औसत आय से इसका ज्ञान प्राप्त नहीं होता।
4. प्रतिनिधि औसत नहीं-कई बार औसत ऐसी संख्या हो सकती है जोकि मदों में नहीं पाई जाती जैसे कि \(\frac{1+2+3+10}{4}=\frac{16}{4}\)= 4 सट संख्याओं में नहीं पाई जाती। मद संख्याओं में नहीं पाई जाती।
5. ग्राफ द्वारा प्रदर्शन सम्भव नहीं-गणित औसत द्वारा ग्राफ विधि द्वारा औसत को प्रकट नहीं किया जा सकता। इस प्रकार यह औसत उचित नहीं है।
6.खले वर्गों में माप सम्भव नहीं-जब हमारे पास खुले वर्ग होते हैं, जैसे कि 10 से कम अथवा 100 से अधिक। ऐसी स्थिति में गणित समान्तर औसत का माप नहीं किया जा सकता क्योंकि इस स्थिति में मदों के उचित मूल्य को शामिल नहीं किया जाता। चाहे समान्तर औसत में कुछ दोष भी पाए जाते हैं परन्तु फिर भी इस औसत को दूसरी औसतों की तुलना में अच्छा माना जाता है, क्योंकि यह औसत न केवल सिद्धान्तक तौर पर ही अलग प्रयोग की जाती है, बल्कि व्यावहारिक तौर पर भी अधिक लाभदायक है।
![]()
1. व्यक्तिगत श्रेणी
(Individual Series)
प्रश्न 3.
समान्तर औसत का माप कैसे ज्ञात किया जाता है ?
उत्तर-
(A) प्रत्यक्ष विधि-आंकड़ा शास्त्र में समान्तर औसत को \(\bar{X}\) (एक्स बार) द्वारा लिखा जाता है। जिन मदों की औसत का माप करना होता है, उसको X1X2… XN प्रथम पद (X1) द्वितीय पद (X2) कुल पद (XN) कहते हैं। प्रत्यक्ष विधि द्वारा समान्तर औसत के माप के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है।
फार्मूला
\(\bar{X}=\frac{X_{1}+X_{2}+X_{3}+X_{4} \cdots \ldots \ldots X_{N}}{N}=\frac{\Sigma X}{N}\)
इस फार्मूले में
\(\overline{\mathrm{X}}\) = समान्तर औसत (Mean) . X1 X2……XN = यह मदों के मूल्य को प्रकट करते हैं। जैसे कि पहले विद्यार्थी के अंकों को X1 दूसरे विद्यार्थी के अंकों को X2 इत्यादि लिखा जाता है। ΣX = इसमें चिन्ह (Σ) को सिगमा (Sigma) कहते हैं। इसका अर्थ है मदों का कुल योग। X शब्द का प्रयोग मदों के मूल्य के लिए किया जाता है। मदों के मूल्य का कुल योग (ΣX) द्वारा प्रकट किया जाता है। N = मदों की कुल संख्या।
Short Cut Method :
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{d x}{\mathrm{~N}}\)
Step Deviation Method :
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma d x}{\mathrm{~N}} \times \mathrm{C}\)
प्रश्न 4.
ग्यारहवीं कक्षा के 10 विद्यार्थियों द्वारा अंग्रेज़ी के पेपर में से 100 अंकों में से प्राप्त अंक दिए हुए
अंक : 10 50 29 61 52 16 24 18 42 48
प्रत्यक्ष विधि द्वारा समान्तर मध्य का माप ज्ञात करो।
हल (Solution) :
प्रत्यक्ष विधि द्वारा समान्तर मध्य का माप…
| विद्यार्थियों की संख्या (Number of Students) | अंक (Marks) |
| 2 | 10 |
| 2 | 50 |
| 3 | 29 |
| 4 | 61 |

\( \overline{\mathrm{X}}=\frac{\Sigma \mathrm{X}}{\mathrm{N}}=\frac{350}{10}\) = 35 Marks उत्तर।
1 विद्यार्थी ने गणित के पेपर में 100 अंकों में से औसत 35 अंक प्राप्त किए हैं। इससे ज्ञात होता है कि ग्यारहवीं कक्षा के विद्यार्थी अंग्रेज़ी में कमज़ोर हैं।
प्रश्न 5.
साबुन बनाने वाले कारखाने में आठ मजदूरों की रोज़ाना मज़दूरी का विवरण निम्नलिखित अनुसार दिया गया है
रोज़ाना मज़दूरी (₹) 100 110 140 150 180 200 210 270 समान्तर औसत का माप ज्ञात करो।
हल (Solution):
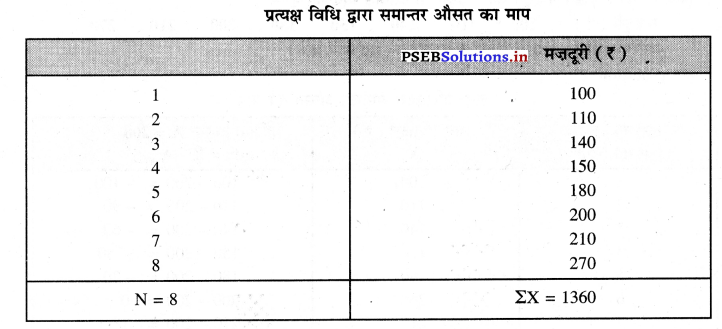
\(\bar{X}=\frac{\Sigma X}{N}=\frac{1360}{8}\) = ₹ 170 उत्तर।
साबुन बनाने के कारखाने में मजदूरों की रोज़ाना औसत मज़दूरी ₹ 170 प्रतिदिन प्राप्त होती है।
प्रश्न 6.
आठ मज़दूरों की प्रतिदिन मज़दूरी इस प्रकार दी है।
मज़दूरी : 100 110 140 150 180 200 210 270
हल (Solution) :
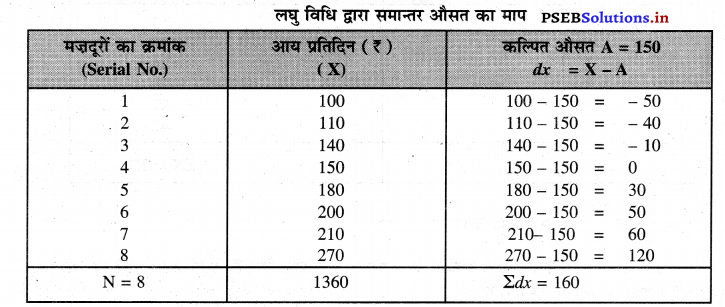
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma d x}{\mathrm{~N}}\)
सरल विधि अनुसार
\( \bar{X}=150+\frac{160}{8}=₹ 170\)
\(\bar{X}=\frac{\Sigma X}{N}=\frac{1360}{8}\)
\(\bar{X}\) = ₹ 170 उत्तर
मज़दूरों की प्रतिदिन औसत मज़दूरी = ₹ 170.
![]()
प्रश्न 7.
निम्नलिखित मजदूरों की मजदूरी के आंकड़े दिए गए हैं
मज़दूरी (₹) 100 110 140 150 180 200 210 270
कल्पित औसत 200 से लेकर समान्तर मध्य का माप करो।
हल (Solution) :
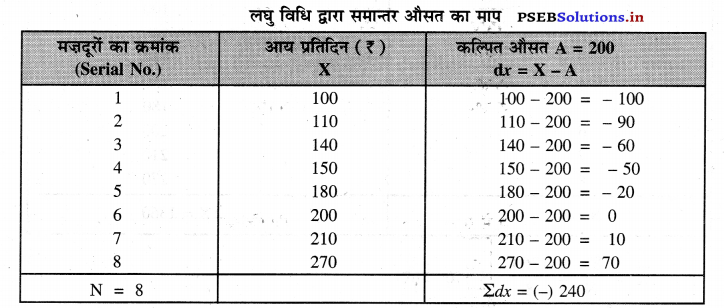
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma d x}{\mathrm{~N}}\)
\(\bar{X}=200+\frac{-240}{8}\)
\(\bar{X}\)= 200 – 30 = ₹ 170 उत्तर।
प्रश्न 8.
पद विचलन विधि द्वारा निम्नलिखित आंकड़ों की सहायता से समान्तर औसत का माप करो –
मज़दूरी (₹) 100 110 140 150 180 200 210 270
हल (Solution) :
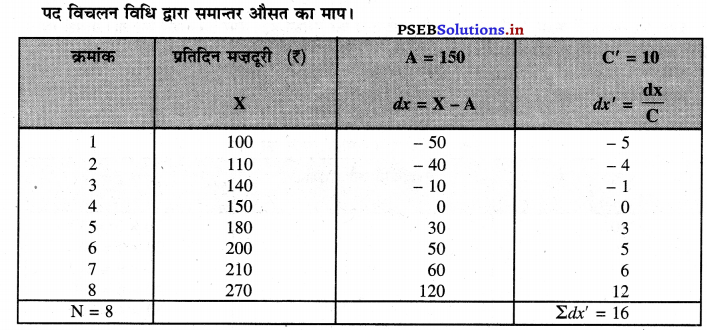
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma d x^{\prime}}{\mathbf{N}} \times \mathrm{C}\)
\( \bar{X}=150+\frac{16}{8} \times 10\) = ₹ 170 उत्तर
इस प्रकार प्रत्येक विधि से एक ही उत्तर आता है।
2. खण्डित श्रेणी में समान्तर औसत का माप (Calculation of Mean in Discrete Series)
प्रश्न 9.
खण्डित श्रेणी में समान्तर मद के माप की विधि स्पष्ट करो।
उत्तर-
खण्डित श्रेणी में मदों के साथ उनकी आवृत्ति दी होती है। इस स्थिति में औसत का माप तीन विधियों द्वारा किया जा सकता है।
- प्रत्यक्ष विधि
- लघु विधि
- पद विचलन विधि
1. प्रत्यक्ष विधि-प्रत्यक्ष विधि में समान्तर औसत मापने के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है-
\(\overline{\mathbf{X}}=\frac{\sum f x}{\mathbf{N}}\)
इस सूत्र में \(\bar{X}\) = समान्तर औसत
f = आवृत्ति
x = श्रेणी की मदें
N = मदों की संख्या
इसको Σf भी कहा जाता है।
2. लघु विधि \(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x}{\mathrm{~N}}\)
3. पद विचलन विधि \(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x^{\prime}}{\mathrm{N}} \times \mathrm{C}\)
प्रश्न 10.
ग्यारहवीं कक्षा के विद्यार्थियों की अर्थशास्त्र की परीक्षा हुई। पेपर 50 अंकों का था। प्रत्यक्ष विधि द्वारा समान्तर मध्य ज्ञात करो।
| अंक : | विद्यार्थियों की संख्या : |
| 10 | 3 |
| 20 | 8 |
| 30 | 9 |
| 40 | 6 |
| 50 | 4 |
हल (Solution) :
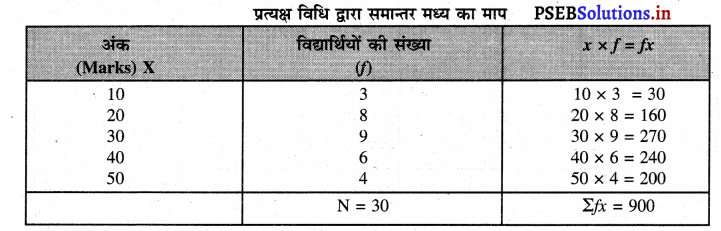
\(\overline{\mathrm{X}}=\frac{\Sigma f x}{f}=\frac{900}{30}\) = 30 अंक उत्तर।
अर्थशास्त्र के पेपर में ग्यारहवीं कक्षा के विद्यार्थियों के 50 अंकों में से औसत अंक 30 अंक हैं। इससे ज्ञात होता है कि विद्यार्थी अर्थशास्त्र में होशियार हैं।
![]()
प्रश्न 11.
कम्प्यूटर पर काम करने वाले 30 मजदूरों की प्रति घण्टा मजदूरी का विवरण निम्नलिखित अनुसार दिया गया है। लघु विधि से समान्तर मध्य ज्ञात करो।
| प्रति घण्टा मजदूरी (₹) | मज़दूरों की संख्या |
| 10 | 3 |
| 20 | 8 |
| 30 | 9 |
| 40 | 6 |
| 50 | 4 |
हल (Solution):
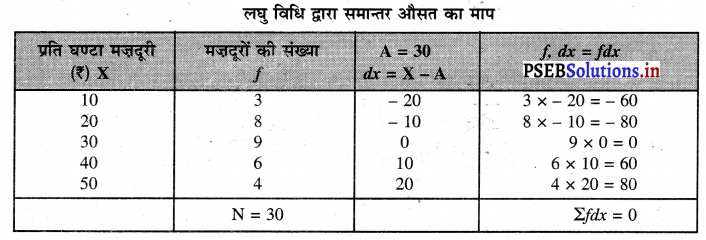
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x}{\mathrm{~N}}\)
x = 30+ 3 = 2 30 उत्तर।
कम्प्यूटर पर काम करने वाले की औसत प्रति घण्टा मज़दरी ₹ 30 है।
प्रश्न 12.
50 मजदूरों की मजदूरी के आंकड़े निम्नलिखित अनुसार दिए गए हैं। औसत मजदूरी का माप पद विचलन विधि द्वारा ज्ञात करो।
| मज़दूरी (₹) | मज़दूरों की संख्या |
| 20 | 6 |
| 30 | 8 |
| 40 | 10 |
| 50 | 12 |
| 60 | 9 |
| 70 | 5 |
हल (Solution) :
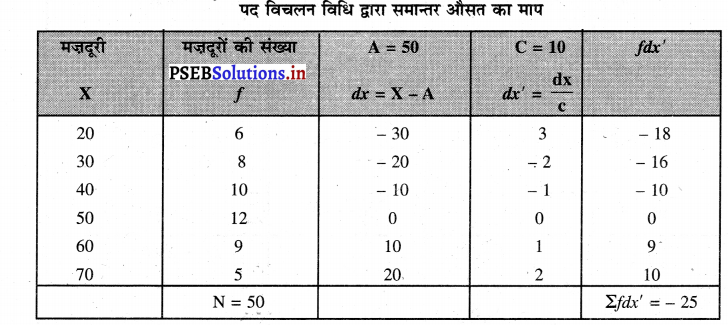
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x^{\prime}}{\mathrm{N}} \times \mathrm{C}\)
\(\bar{X}=50+\frac{-25}{50} \times 10\)
\(\bar{X}\) = 50 – 5 = ₹ 45 उत्तर।
इससे ज्ञात होता है कि मज़दूरों की औसत मज़दूरी ₹ 45 है।
3. अखण्डित श्रृंखला में समान्तर माध्य की गणना (Calculation of Arithmetic Mean in Continuous Series)
प्रश्न 13.
निम्नलिखित आंकड़ों की सहायता से प्रत्यक्ष विधि द्वारा समान्तर औसत ज्ञात करो।
| अंक: | विद्यार्थियों की संख्या: |
| 0-10 | 5 |
| 10 – 20 | 10 |
| 20 – 30 | 12 |
| 30 – 40 | 15 |
| 40-50 | 18 |
| 50 – 60 | 10 |
हल (Solution) :
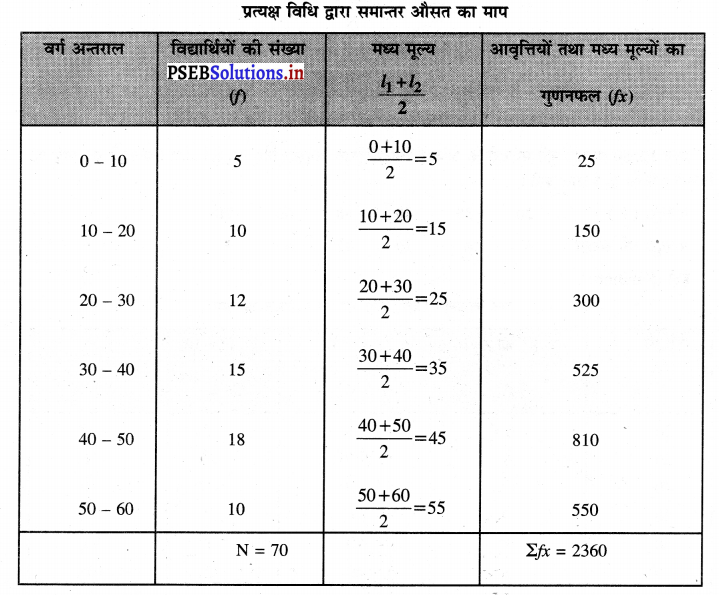
\(\overline{\mathbf{X}}=\frac{\Sigma f x}{\mathrm{~N}}\)
\(\bar{X}=\frac{2360}{70} \) = 33.71 अंक उत्तर।
इससे ज्ञात होता है कि विद्यार्थियों के 33.71/60 औसत अंक हैं। इसलिए विद्यार्थियों का स्तर अच्छा है।
![]()
प्रश्न 14.
50 विद्यार्थियों द्वारा प्राप्त किए अंकों का विवरण इस प्रकार दिया हुआ है। लघु विधि द्वारा समान्तर औसत का माप करो।
| अंक : | विद्यार्थियों की संख्या : |
| 0 – 10 | 8 |
| 10 – 20 | 12 |
| 20 – 30 | 15 |
| 30 – 40 | 10 |
| 40 – 50 | 5 |
हल (Solution):
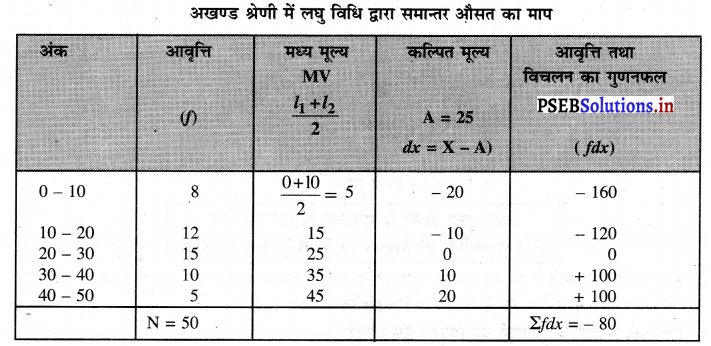
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x}{\mathrm{~N}}\)
\(\bar{X}=25+\frac{-80}{50}\)
\(\bar{X}\) = 25 – 1.6 = 23.4 अंक उत्तर
इससे ज्ञात होता है कि विद्यार्थियों का मध्यम स्तर है।
समावेशी श्रेणी में समान्तर मध्य का माप (Calculation of Arithmetic Mean in Inclusive Series)
नोट-खण्डित श्रेणी में यदि वर्गान्तर समावेशी है तो इसको अपवर्जी में परिवर्तन करने की कोई आवश्यकता नहीं होती। उसी तरह मध्य मूल्य निकालकर हल किया जाता है।
प्रश्न 15.
निम्नलिखित आंकड़ों की समान्तर औसत का माप करो।
| भूमि (एकड़): | किसानों की संख्या : |
| 10 – 19 | 8 |
| 20 – 29 | 10 |
| 30 – 39 | 16 |
| 40 – 49 | 10 |
| 50 – 59 | 6 |
हल (Solution) :
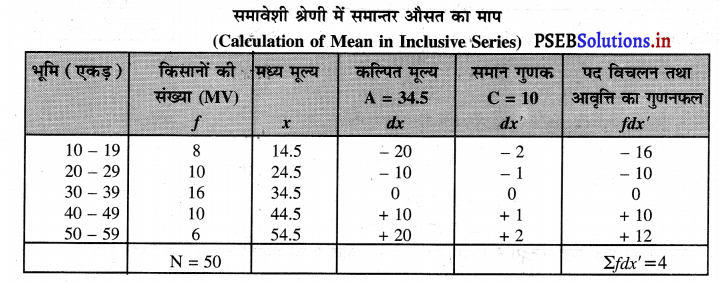
\(\overline{\mathbf{X}}=\mathrm{A}+\frac{\sum f d x^{l}}{\mathrm{~N}} \times \mathrm{C}\)
\(\bar{X}=34.5+\frac{-4}{50} \times 10\)
\(\bar{X}=34.5+\frac{-4}{5}=34.5-0.8=33.7\)
\(\bar{X}\) = 33.7 एकड़ उत्तर
मध्य मूल्य श्रेणी में समान्तर औसत का माप । (Calculation of Mean in Mid-Value Series)
मध्य मूल्यों वाली श्रेणी में समान्तर मध्य का माप वर्गान्तर श्रेणी में हम मध्य मूल्य (MV) निकाल कर प्रश्न का हल करते हैं। यदि मध्य मूल्य दिए होते हैं तो उसका हल इस प्रकार किया जाता है।
प्रश्न 16.
मजदूरों की मजदूरी का विवरण इस प्रकार है
| मध्य मज़दूरी : | मज़दूरों की संख्या : |
| 5 | 10 |
| 10 | 12 |
| 15 | 15 |
| 20 | 18 |
| 25 | 10 |
| 30 | 5 |
| 35 | 2 |
समान्तर मध्य का माप करो।
हल (Solution) :
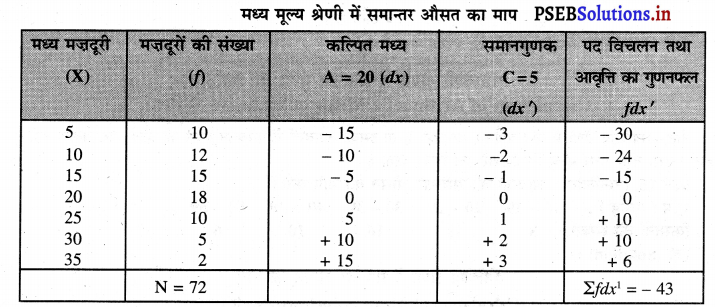
\(\overline{\mathrm{X}}=\mathrm{A}+\frac{\Sigma f d x^{\prime}}{\mathrm{N}} \times \mathrm{C}\)
\(\bar{X}=20+\frac{(-) 43}{72} \times 5\)
\(\bar{X}=20-\frac{215}{72}\)
\(\bar{X}\) = 20.2.99
\(\bar{X}\) = ₹ 17.01 उत्तर
मज़दूरों की प्रति घण्टा मज़दूरी ₹ 17.01 है। इससे ज्ञात होता है कि मज़दूरों की आर्थिक स्थिति ठीक है।
गलत समान्तर औसत को ठीक करना (Correcting the Incorrect Mean)
प्रश्न 17.
गलत समान्तर औसत को ठीक करने की विधि बताओ।
उत्तर-
समान्तर औसत का माप करते समय कई बार कुछ मदें अशुद्ध लिख ली जाती हैं परन्तु ठीक मदों का पता लगाने के लिए गलत समान्तर औसत को सही किया जा सकता है। इस उद्देश्य के लिए निम्नलिखित सूत्र का प्रयोग किया जाता है
\(\bar{X}=\frac{\Sigma X}{N}\)
N.\(\bar{X}\) = ΣX
इससे अशुद्ध ΣX प्राप्त हो जाता है। सही \(\bar{X}\) का माप इस प्रकार किया जाता है
\(\bar{X}\)= अशुद्ध Σ\(\bar{X}\) = – गलत मद + ठीक मद
प्रश्न 18.
50 विद्यार्थियों द्वारा प्राप्त किए गए औसत अंक 30 दिए गए हैं। उसके पश्चात् ज्ञात होता है कि एक विद्यार्थी के उचित अंक 60 हैं, जोकि गलती से 6 लिखे गए। ठीक समान्तर औसत का माप करो।
हल (Solution):
\(\bar{X}=\frac{\Sigma X}{N}\) = 30= \(\frac{\Sigma \mathrm{X}}{50}\)
N.\(\bar{X}\) = Σ\(\bar{X}\)
50 × 30 = Σ\(\bar{X}\)
गलत ΣX= 1500
ठीक अंक = 60 गलती से लिखे गए = 6
\(\bar{X}\) = गलत ΣX – गलत मद + ठीक मद
\(\bar{X}\) = \(\frac{1500-6+60}{50} \)
\(\bar{X}\) = \(\frac{1554}{50}\) = 31.08 अंक
विद्यार्थियों द्वारा औसत अंक 30 दिए गए हैं। परन्तु गलत अंकों के स्थान पर ठीक अंक जोड़ने से औसत अंक 31.08 हो गए हैं।
प्रश्न 19.
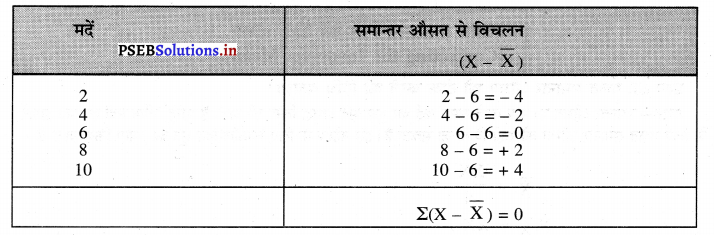
मदों के समान्तर औसत से लिए गए विचलनों का योग सिफर होता है। स्पष्ट करें।
उत्तर-
समान्तर औसत से लिए गए विचलनों का योग सिफर होता है। जब हम समान्तर औसत से मदों का विचलन निकाल कर योग करते हैं तो यह हमेशा सिफर होता है अर्थात्
Σ (X – \(\bar{X}\)) = 0
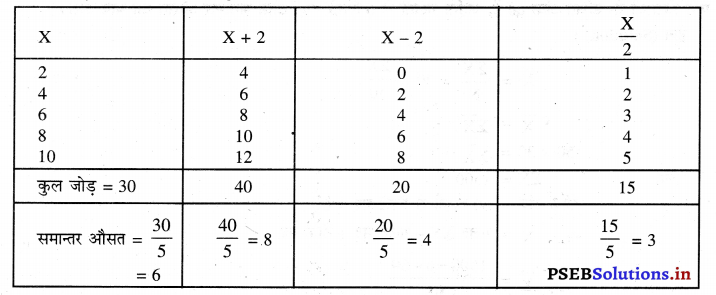
उदाहरण-मदें : 2 4 6 8 10
हल (Solution) :
\(\bar{X}=\frac{2+4+6+8+10}{5}=\frac{30}{5}\) = 6
मदों की औसत = 6
![]()
प्रश्न 20.
यदि मदों में स्थिर मूल्य, जोड़, घटाओ, गुणा अथवा वितरण किया जाए तो क्या प्रभाव पड़ता है ?
उत्तर-
यदि मदों में स्थिर मूल्य (मान लो 2) जोड़ दिया जाए, घटा दिया जाए, गुणा किया जाए अथवा वितरण किया जाए तो समान्तर औसत उसी अनुपात में बदल जाता है।
स्थिर मूल्य का जोड़, घटाओ, गुणा तथा वितरण प्रभाव