PSEB 8th Class Maths Solutions Chapter 4 Practical Geometry Ex 4.3

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 Practical Geometry Ex 4.3 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.3

1. Construct the following quadrilaterals:

Question (i).
Quadrilateral MORE
MO = 6 cm
OR = 4.5 cm
∠M = 60°
∠O = 105°
∠R = 105°
Solution:

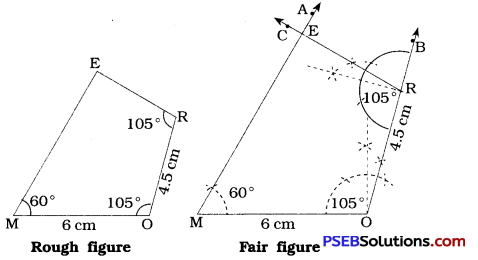
• Draw a line segment MO = 6 cm.
• At M, draw $\overrightarrow{\mathrm{MA}}$, such that ∠OMA = 60°
• At O, draw $\overrightarrow{\mathrm{OB}}$ such that ∠MOB = 105°.
• With O as centre and radius = 4.5 cm, draw an arc intersecting $\overrightarrow{\mathrm{OB}}$ at R.
• At R, draw $\overrightarrow{\mathrm{RC}}$ such that ∠ORC = 105°.
• Locate E at intersection of $\overrightarrow{\mathrm{RC}}$ and $\overrightarrow{\mathrm{MA}}$.

Thus, MORE is the required quadrilateral.

Question (ii).
Quadrilateral PLAN
PL = 4 cm
LA = 6.5 cm
∠P = 90°
∠A = 110°
∠N = 85°
Solution:

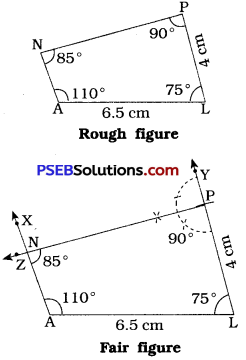
[Note : In □ PLAN, m∠P = 90°, m∠A = 110° and m∠N = 85°)
∴ m∠L = 360°- (m∠P + m∠A + m∠N)
= 360° – (90° + 110° + 85°)
= 360° – 285°
= 75°

Steps of construction:

• Draw a line segment AL = 6.5 cm.
• At A, draw $\overrightarrow{\mathrm{AX}}$ such that ∠XAL = 110°. (Use protractor)
• At L, draw $\overrightarrow{\mathrm{LY}}$ such that ∠YLA = 75°. (Use protractor)
• With L as centre and radius = 4 cm, draw an arc intersecting $\overrightarrow{\mathrm{LY}}$ at P.
• At P, draw $\overrightarrow{\mathrm{PZ}}$ such that ∠ZPL = 90°. (∵ ∠ ZPY = 90°)
• Locate N at intersection of $\overrightarrow{\mathrm{AX}}$ and $\overrightarrow{\mathrm{PZ}}$.

Thus, PLAN is the required quadrilateral.

Question (iii).
Parallelogram HEAR
HE = 5 cm
EA = 6 cm
∠R = 85°
Solution:

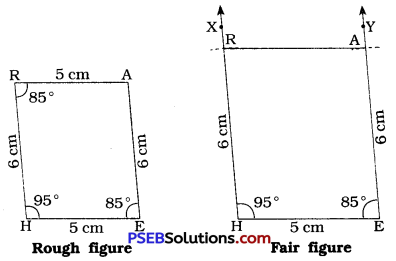
[Note : □ HEAR is a parallelogram.
Opposite sides of parallelogram are of equal lengths.]
HE = 5 cm, ∴ AR = 5 cm, EA = 6 cm, ∴ HR = 6 cm
Adjacent angles of a parallelogram arc supplementary.
m∠R = 85° (given)
∴ m∠H = 180° – 85° = 95°
Opposite angles of a parallelogram are of equal measures,
m ∠ R = 85°
∴ m ∠ E = 85°

Steps of construction:

• Draw a line segment HE = 5 cm.
• At H, draw $\overrightarrow{\mathrm{HX}}$, such that ∠ XHE = 95°. (Use protractor)
• With H as centre and radius = 6 cm, draw an arc intersecting $\overrightarrow{\mathrm{HX}}$ at R.
• At E, draw $\overrightarrow{\mathrm{EY}}$ such that ∠ HEY = 85°. (Use protractor)
• With E as centre and radius = 6 cm, draw an arc intersecting $\overrightarrow{\mathrm{EY}}$ at A.
• Draw $\overline{\mathrm{AR}}$.

Thus, HEAR is the required parallelogram.

Question (iv).
Rectangle OKAY
OK = 7 cm
KA = 5 cm
Solution:

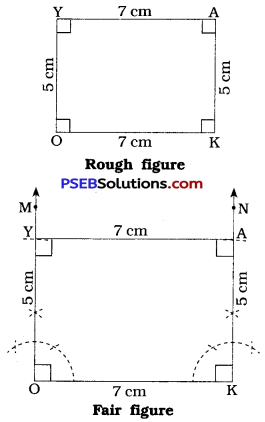
[Note: Here, OKAY is a rectangle. Opposite sides of a rectangle are of equal lengths.]
OK = 7 cm, ∴ AY = 7 cm and KA = 5 cm, ∴ OY = 5 cm
Moreover, all angles of a rectangle are right angles.

Steps of construction:

• Draw a line segment OK = 7 cm.
• At O, draw $\overrightarrow{\mathrm{OM}}$ such that ∠ MOK = 90°.
• With O as centre and radius = 5 cm, draw an arc intersecting $\overrightarrow{\mathrm{OM}}$ at Y.
• At K, draw $\overrightarrow{\mathrm{KN}}$ such that ∠ NKO = 90°.
• With K as centre and radius = 5 cm, draw an arc intersecting $\overrightarrow{\mathrm{KN}}$ at A.
• Draw $\overline{\mathrm{AY}}$.

Thus, OKAY is the required rectangle.