Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 3 Understanding Quadrilaterals Ex 3.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Maths Chapter 3 Understanding Quadrilaterals Ex 3.1
Question 1.
Given here are some figures.
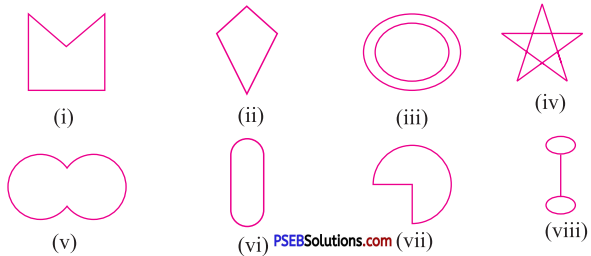
Classify each of them on the basis of the following:
(a) Simple curve
(b ) Simple closed curve
(c) Polygon
(d ) Convex polygon
(e) Concave polygon
Solution:
(a) Simple curves : (i), (ii), (v), (vi) and (vii)
(b) Simple closed curves : (i), (ii), (v), (vi) and (vii)
(c) Polygons : (i) and (ii)
(d) Convex polygon : (ii)
(e) Concave polygons : (i)
![]()
Question 2.
How many diagonals does each of the following have?
(a) A convex quadrilateral
(b) A regular hexagon
(c) A triangle
Solution :
(a) In a convex quadrilateral, number of sides (n) = 4
∴ Number of diagonals = \(\frac{n(n-3)}{2}\)
= \(\frac{4(4-3)}{2}\)
= \(\frac{4 \times 1}{2}\)
= 2
(b) In a regular hexagon, number of sides (n) = 6
∴ Number of diagonals = \(\frac{n(n-3)}{2}\)
= \(\frac{6(6-3)}{2}\)
= \(\frac{6 \times 3}{2}\)
= 9
(c) In a triangle, number of sides (n) = 3
∴ Number of diagonals = \(\frac{n(n-3)}{2}\)
= \(\frac{3(3-3)}{2}\)
= \(\frac{3 \times 0}{2}\)
= 0.
Question 3.
What is the sum of the measures of the angles of a convex quadrilateral ? Will this property hold if the quadrilateral is not convex ? (Make a non-convex quadrilateral and try!)
Solution:
The sum of measures of angles of a convex quadrilateral = 360°
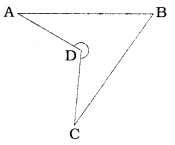
Yes, this property holds, even if the quadrilateral is not convex.
Here, quadrilateral ABCD is a non-convex quadrilateral.
m∠A + m∠B + m∠C + m∠D
= 40° + 55° + 35° + 230°
= 360°
![]()
Question 4.
Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
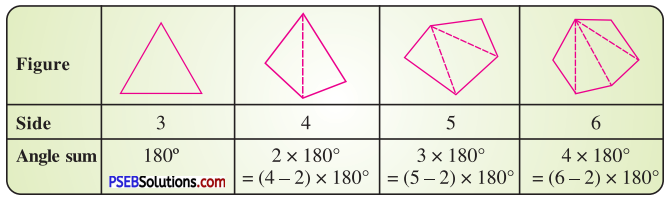
What can you say about the angle sum of a convex polygon with number of sides ?
(a) 7 (b) 8 (c) 10 (d) n
Solution :
From the above table, we conclude that sum of interior angles of polygon with n-sides = (n – 2) × 180°
(a) When n = 7
Sum of interior angles of a polygon of 7 sides = (n – 2) × 180°
= (7 – 2) × 180°
= 5 × 180°
= 900°
(b) When n = 8
Sum of interior angles of a polygon of 8 sides = (n – 2) × 180°
= (8 – 2) × 180°
= 6 × 180°
= 1080°
(c) When n = 10
Sum of interior angles of a polygon having n-sides = (n – 2) × 180°
= (10 – 2) × 180°
= 8 × 180°
= 1440°
(d) When n = n
Sum of interior angles of a polygon having n-sides = (n – 2) × 180°
Question 5.
What is a regular polygon ? State the name of a regular polygon of:
(i) 3 sides
(ii) 4 sides
(iii) 6 sides
Solution:
A polygon is said to be a regular polygon if:
(1) the measures of its interior angles are equal.
(2) the lengths of its sides are equal.
The name of a regular polygon having:
(i) 3 sides is a ‘equilateral triangle’.
(ii) 4 sides is a ‘square’.
(iii) 6 sides is a ‘regular hexagon’.
![]()
Question 6.
Find the angle measure x in the following figures.
(a)
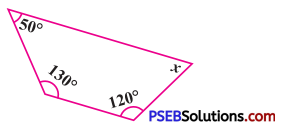
Solution:
The sum of the interior angles of a quadrilateral = 360°
∴ x + 120° + 130° + 50° = 360°
∴ x + 300° = 360°
∴ x = 360° – 300°
(Transposing 300° to RHS)
∴ x = 60°
(b)
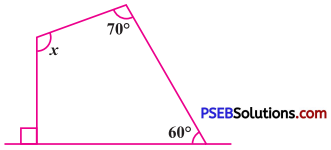
Solution:
The sum of the interior angles of a quadrilateral = 360°
∴ x + 60° + 70° + 90° = 360°
∴ x + 220° = 360°
∴ x = 360° – 220° (Transposing 220° to RHS)
∴ x = 140°
(c)
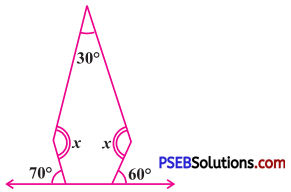
Solution:
Interior angles are : 30°, x, x,
(180° – 70°) = 110° (Linear pair) and
(180° – 60°) = 120° (Linear pair)
The given figure is a pentagon.
∴ Sum of interior angles of a pentagon = (n – 2) × 180°
= (5 – 2) × 180°
= 3 × 180° = 540°
∴ 30° + x + x + 110° + 120° = 540°
∴ 2x + 260° = 540°
∴ 2x = 540° – 260° (Transposing 260° to RHS)
∴ 2x = 280°
∴ \(\frac{2 x}{2}=\frac{280^{\circ}}{2}\)
(Dividing both the sides by 2)
∴ x = 140°
(d)
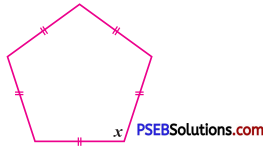
Solution:
It is a regular pentagon.
Sum of all interior angles of a pentagon
= (5 – 2) × 180°
= 3 × 180°
= 540°
∴ x + x + x + x + x = 540°
∴ 5x = 540°
∴ \(\frac{5 x}{5}=\frac{540^{\circ}}{5}\)
(Dividing both the sides by 5)
∴ x = 108°
![]()
7. (a).
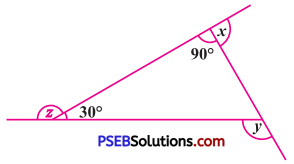
Find x + y + z
Solution:
x + 90° = 180° (Linear pair)
∴ x = 180° – 90°
∴ x = 90°
y = 30° + 90° = 120°
(Exterior angle of a triangle is equal to the sum of interior opposite angles)
z = 180° – 30° (Linear pair) = 150°
Now, x + y + z = 90° + 120° + 150°
= 360°
(b).
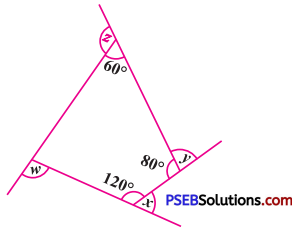
Find x + y + z + ω
Solution:
The sum of interior angles of a quadrilateral = 360°
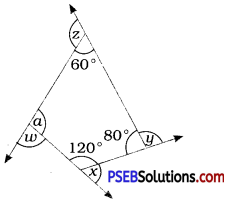
∴ a + 60° + 80° + 120° = 360°
∴ a + 260° = 360°
∴ a = 360° – 260° = 100°
Now, x + 120° = 180° (Linear pair)
∴ x = 180°- 120° = 60°
y + 80° = 180° (Linear pair)
∴ y = 180° – 80° = 100°
z + 60° = 180° (Linear pair)
∴ z = 180° – 60° = 120°
ω + 100° = 180°
∴ ω = 180° – 100° = 80°
Thus, x + y + z + ω = 60° + 100° + 120° + 80°
= 360°