Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.4
Question 1.
Parallelogram ABCD and rectangle ABEF are on the, same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
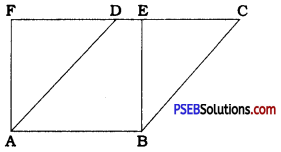
Rectangle ABEF is a parallelogram too.
Now, parallelograms ABCD and ABEF are on the same base AB and they have equal areas. Hence, they are between the same parallels FC and AB.
In ∆ AFD, ∠F, being an angle of rectangle ABEF, is a right angle and so, AD is the hypotenuse.
∴ AD > AF
∴ AD + AB > AF + AB
∴ 2 (AD + AB) > 2 (AF + AB)
∴ Perimeter of parallelogram ABCD > Perimeter of rectangle ABEF
![]()
Question 2.
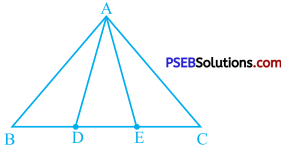
In the given figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you now answer the question that you have left in the ‘Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
[Remark : Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide AABC into n triangles of equal areas.]
Answer:
Here, in ∆ ABE, D is a point on BE such that BD = DE.
So, in ∆ ABE, D is the midpoint of BE and AD is a median.
∴ ar (ABD) = ar (ADE) ……………… (1)
Similarly, in A ADC, E is the midpoint of DC and AE is a median.
∴ ar (ADE) = ar (AEC) ……………. (2)
From (1) and (2),
ar (ABD) = ar (ADE) = ar (AEC)
Thus, in ∆ ABC, by joining the points of trisection of BC, i.e., D and E to vertex A, the triangle is divided into ∆ ABD, ∆ ADE and ∆ AEC which have the same area.
Now, the answer to the question which was left unanswered in the ‘Introduction’ is ‘Yes’. The manner in which Budhia divided her field, the area of all the three parts are equal.
![]()
Question 3.
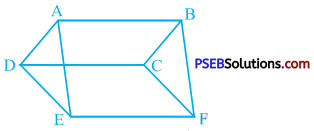
In the given figure, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
Answer:
Opposite sides of a parallelogram are equal.
∴ In parallelogram ABCD, AD = BC, in parallelogram DCFE, DE = CF and in parallelogram ABFE, AE = BF.
Now, in ∆ ADE and ∆ BCE
AD = BC, DE = CF and AE = BE
∴ By SSS rule, ∆ ADE = ∆ BCF
∴ ar (ADE) = ar (BCF)
Question 4.
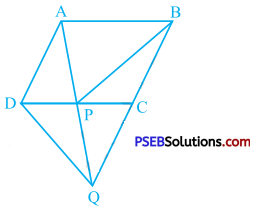
In the given figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at E show that ar (BPC) = ar (DPQ).
[Hint: Join AC.]
Answer:
Join AC.
In parallelogram ABCD, BC || AD and BC = AD.
BC is produced to point Q such that AD = CQ.
Thus, AD = CQ and AD || CQ.
∴ Quadrilateral ACQD is a parallelogram.
Diagonals of a parallelogram divide it into four triangles of equal areas.
∴ ar (DPQ) = ar (DPA) = ar (APC) = ar (CPQ)
∴ ar (DPQ) = ar (APC) ……………. (1)
Now, ∆ APC and ∆ BPC are on the same base PC and between the same parallels PC and AB.
∴ ar (APC) = ar (BPC) ………….. (2)
From (1) and (2),
ar (BPC) = ar (DPQ)
![]()
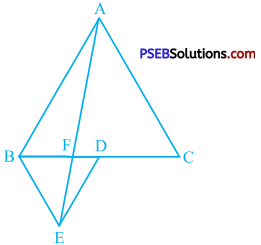
Question 5.
In the given figure, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = \(\frac{1}{4}\)ar (ABC)
(ii) ar (BDE) = \(\frac{1}{2}\)ar (BAE)
(iii) ar (ABC) = 2ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v ) ar (BFE) = 2ar (FED)
(vi) ar (FED) = \(\frac{1}{8}\)ar (AFC)
[Hint: Join EC and AD. Show that BE || AC and DE || AB, etc.]
Answer:
Join EC and AD.
In equilateral ∆ ABC, ∠ ACB = 60°
In equilateral ∆ BDE, ∠ DBE = 60°
∴ ∠ CBE = 60°
Thus, ∠ ACB = ∠ CBE
But, ∠ ACB and ∠ CBE are alternate angles formed by transversal BC of AC and BE and they are equal.
∴BE || AC .
Similarly, ∠ ABD = ∠ BDE = 60°
∴ DE || AB
Now, in ∆ ABC, D is the midpoint of BC.
Hence, AD is a median of ∆ ABC.
∴ ar (ADB) = ar (ADC) = \(\frac{1}{2}\)ar (ABC)
∆ ABC and AAEC are on the same base AC and between the same parallels AC and BE.
∴ ar (ABC) = ar (AEC)
∴ ar (ABC) = ar (ADC) + ar (EDC) + ar (AED) …………….. (1)
In ∆ EBC, ED is a median.
∴ ar (EDC) = ar (BDE) = \(\frac{1}{2}\)ar (EBC) ………………… (2)
∆ AED and ∆ BDE are on the same base DE and between the same parallels AB and DE.
∴ ar (AED) = ar (BDE) …………… (3)
From (1), (2) and (3),
ar (ABC) = \(\frac{1}{2}\)ar (ABC) + ar (BDE) + ar (BDE)
∴ ar (ABC) – \(\frac{1}{2}\) ar (ABC) = 2ar (BDE)
∴\(\frac{1}{2}\)ar (ABC) = 2ar (BDE)
∴ ar (BDE) = \(\frac{1}{4}\)ar (ABC) ….. Result (i)
∆ BAE and ∆ BCE are on the same base BE and between the same parallels BE and AC.
∴ ar (BAE) = ar (BCE) ……………. (4)
In ∆ BEC, ED is a median.
∴ ar (BDE) = \(\frac{1}{2}\)ar (BCE)
∴ ar (BDE) = \(\frac{1}{2}\)ar (BAE) [by (4)] ……. Result (ii)
The diagonals of trapezium ABED intersect at F.
∴ ar (AFD) = ar (BFE) ……………… (5)
The diagonals of trapezium ABEC intersect at F.
∴ ar (ABF) = ar (EFC) ………………….. (6)
In ∆ ABC, AD is a median. s
∴ ar (ABC) = 2ar (ADB) S
∴ ar (ABC) = 2[ar (ABF) + ar (AFD)l
∴ ar (ABC) = 2[ar (EFC) + ar (BFE)] [by (5) and (6)]
∴ ar (ABC) = 2ar (BEC) … Result (iii)
In trapezium ABED, AB || ED and diagonals intersect at F.
∴ ar (BFE) = ar (AFD) …….. Result (iv)
By result (i),
ar (BDE) = \(\frac{1}{4}\)ar (ABC)
∴ ar (BDE) = \(\frac{1}{4}\) 2ar (ABD)
∴ ar (BDE) = \(\frac{1}{2}\)ar (ABD)
∆ BDE and ∆ ABD have the common base s BD.
∴ Altitude on BD in ∆ BDE = \(\frac{1}{2}\) × altitude on BD in ∆ ABD.
Now, the altitude on base BD in ∆ BDE is the same as the altitude on base BF in ∆ BEF and the altitude on base BD in ∆ ABD is the same as the altitude on base FD in ∆ AFD.
∴ Altitude on base BF in ∆ BEF
= \(\frac{1}{2}\) × altitude on base FD in ∆ AFD.
But, ar (BFE) = ar (AFD) …Result (iv)]
∴ BF = 2 × FD
Now, in ∆ BFE and ∆ FED, the altitudes corresponding to base BF and FD respectively are the same.
∴ ar (BFE) = 2ar (FED) … Result (v)
Suppose, in ∆ ABD, the altitude on base BD = h.
∴ In ∆ AFC, the altitude on base FC = h.
Also, in ∆ BDE, the altitude on base BD = \(\frac{h}{2}\)
∴ In A FED, the altitude on base FD = \(\frac{h}{2}\).
Now, ar (FED) = \(\frac{1}{2}\) × FD × \(\frac{h}{2}\) = \(\frac{h \times \mathrm{FD}}{4}\).
∴ FD = \(\frac{4 {ar}(\mathrm{FED})}{h}\) ………….. (7)
and ar (AFC) = \(\frac{1}{2}\) × FC × h = \(\frac{h}{2}\) × FC
= \(\frac{h}{2}\) (CD + FD)
= \(\frac{h}{2}\) (BD + FD) [∵ BD = CD]
= \(\frac{h}{2}\) (BF + FD + FD)
= \(\frac{h}{2}\) (2FD + FD + FD) [∵ BF = 2FD]
= \(\frac{h}{2}\) × 4FD
∴ ar (AFC) = 2 × h × FD
= 2 × h × \(\frac{4 {ar}(\mathrm{FED})}{h}\) [by (7)]
∴ ar (AFC) = 8 ar (FED)
∴ ar (FED) = \(\frac{1}{8}\) ar (AFC) … Result (vi)
![]()
Question 6.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at E Show that
ar (APB) × ar (CPD) = ar (APD) × ar (BPC).
[(Hint: From A and C, draw perpendiculars to BD.]
Answer:
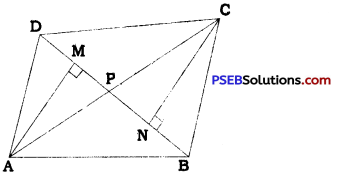
Draw AM ⊥ BD and CN ⊥ BD, where M and N are points on BD.
∴ ar (APB) × ar (CPD)
= (\(\frac{1}{2}\) × PB × AM) × (\(\frac{1}{2}\) × PD × CN)
= (\(\frac{1}{2}\) × PB × CN) × (\(\frac{1}{2}\) × PD × AM)
Thus, ar (APB) × ar (CPD) = ar (APD) × ar (BPC)
Question 7.
P and Q are respectively the midpoints of sides AB and BC of a triangle ABC and R is the midpoint of AR show that
(i) ar (PRQ) = \(\frac{1}{2}\) ar (ARC)
(ii) ar (RQC) = \(\frac{3}{8}\) ar (ABC)
(iii) ar (PBQ) = ar (ARC)
Answer:
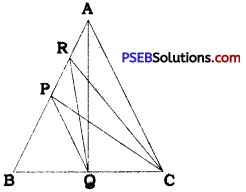
In ∆ ABC, AQ and CP are medians. In ∆ APC, CR is a median, In ∆ APQ, QR is a median. In ∆ PBC, PQ is a median, In ∆ RBC, RQ is a median.
(i) ar (PRQ) = ar(ARQ) }
= \(\frac{1}{2}\)ar (APQ)
= \(\frac{1}{2}\)ar (BPQ)
= \(\frac{1}{2}\)ar(PQC)
= \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (PBC)
= \(\frac{1}{4}\)ar (PBC)
= \(\frac{1}{4}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{8}\)ar (ABC)
\(\frac{1}{2}\)ar (ARC) = \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar(APC)
= \(\frac{1}{4}\)ar (APC)
= \(\frac{1}{4}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{8}\)ar (ABC)
∴ar (PRQ) = \(\frac{1}{2}\)ar (ARC)
![]()
(ii) ar(RQC) = ar(RBQ)
= ar (PBQ) + ar (PRQ)
= \(\frac{1}{2}\)ar (PBC) + \(\frac{1}{8}\)ar (ABC)
= \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (ABC) + \(\frac{1}{8}\)ar (ABC)
= \(\frac{1}{4}\)ar (ABC) + \(\frac{1}{8}\)ar (ABC)
= \(\frac{3}{8}\)ar (ABC)
(iii) ar (PBQ) = \(\frac{1}{2}\)ar (PBC) = \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{4}\)ar (ABC)
ar (ARC) = \(\frac{1}{2}\)ar (APC) = \(\frac{1}{2}\) ∙ \(\frac{1}{2}\)ar (ABC)
= \(\frac{1}{4}\)ar (ABC)
∴ ar (PBQ) = ar (ARC)
Question 8.
In the given figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN „ are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:
(i) ∆ MBC S ∆ ABD
(ii) ar (BYXD) = 2ar (MBC)
(iii) ar (BYXD) = ar (ABMN)
(iv) ∆ FCB ≅ ∆ ACE
( v ) ar (CYXE) = 2ar (FCB)
(vi) ar (CYXE) = ar (ACFG)
(vii) ar (BCED) = ar (ABMN) + ar (ACFG)
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler j! proof of this theorem in Class X.
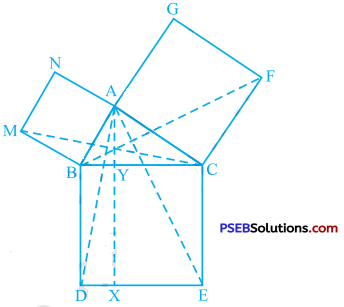
Answer:
(i) ∠ ABM = ∠ CBD = 90°
∴ ∠ABM + ∠ABC = ∠CBD + ∠ABC
∴ ∠ MBC = ∠ ABD
In ∆ MBC and ∆ ABD,
MB = AB, ∠ MBC = ∠ ABD and BC = BD
∴ By SAS rule, ∆ MBC ≅ ∆ ABD
![]()
(ii) ar (BYXD) = 2ar (ABD)
∴ ar (BYXD) = 2ar (MBC) [∆ MBC ≅ ∆ ABD]
(iii) ar (BYXD) = 2ar (ABD)
ar (ABMN) = 2ar (MBC)
But, ar (MBC) = ar (ABD)
∴ ar (BYXD) = ar (ABMN)
(iv) ∠ FCA = ∠ ECB = 90°
∴ ∠FCA + ∠ACB = ∠ECB + ∠ACB
∴ ∠FCB = ∠ACE
In ∆ FCB and ∆ ACE,
FC = AC, ∠ FCB = ∠ACE and CB = CE
∴By SAS rule, ∆ FCB ≅ ∆ ACE
(v) ar (CYXE) = 2ar (ACE)
∴ar (CYXE) = 2ar (FCB) [∵ ∆ FCB ≅ ∆ ACE]
(vi) ar (CYXE) = 2ar (FCB)
and ar (ACFG) = 2ar (FCB)
∴ ar (CYXE) = ar (ACFG)
![]()
(vii) ar (BCED) = ar (CYXE) + ar (BYXD)
∴ ar (BCED) = ar (ACFG) + ar (ABMN) [By result (iii) and (vi)]
∴ ar (BCED) = ar (ABMN) + ar (ACFG)