Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 9 Areas of Parallelograms and Triangles Ex 9.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles Ex 9.3
Question 1.
In the given figure, E is any point on median AD of a ∆ ABC. Show that ar (ABE) = ar (ACE).
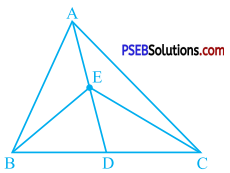
Answer:
As AD is a median of ∆ ABC, it divides ∆ ABC into two triangles with equal areas.
∴ ar (ADB) = ar (ADC) …………… (1)
In ∆ ABC, AD is a median.
∴ BD = CD
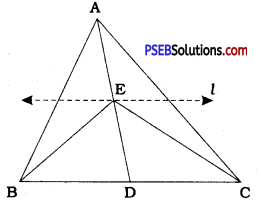
Draw a line l through E and parallel to BC. Then, ∆ EDB and ∆ EDC are on the equal bases and between the same parallels l and BC.
∴ ar (EDB) = ar (EDC) ……………… (2)
Subtracting (2) from (1),
ar (ADB) – ar (EDB) = ar (ADC) – ar (EDC)
∴ ar (ABE) = ar (ACE)
![]()
Question 2.
In a triangle ABC, E is the midpoint of median AD. Show that ar (BED) = \(\frac{1}{4}\)ar (ABC).
Answer:
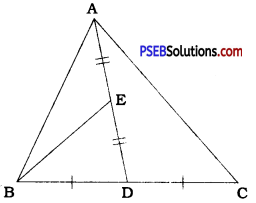
In ∆ ABC, AD is a median
∴ ar (ADB) = ar (ADC) = \(\frac{1}{2}\)ar (ABC)
Now, in ∆ ABD, E is the midpoint of AD.
∴ BE is a median of ∆ ABD.
∴ ar (BED) = ar (BEA) = \(\frac{1}{2}\)ar (ABD)
Thus, ar (BED) = \(\frac{1}{2}\)ar (ABD) and
ar (ABD) = \(\frac{1}{2}\)ar (ABC)
∴ ar (BED) = \(\frac{1}{2}\) × \(\frac{1}{2}\)ar (ABC)
∴ ar (BED) = \(\frac{1}{4}\)
![]()
Question 3.
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Answer:
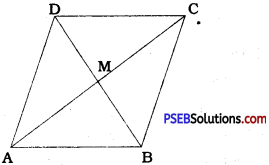
The diagonals of a parallelogram bisect each other.
Hence, in parallelogram ABCD, diagonals AC and BD bisect each other at M. Thus, M is the midpoint of AC as well as BD.
In ∆ ABC, BM is a median.
∴ ar (ABM) = ar (CBM) ……………. (1)
In ∆ BCD, CM is a median.
∴ ar (CBM) = ar (CDM) ……………. (2)
In ∆ ABD, AM is a median.
∴ ar (ABM) = ar (DAM) ……………. (3)
From (1), (2) and (3),
ar (ABM) = ar (CBM) = ar (CDM) = ar (DAM)
Thus, the diagonals of a parallelogram divide it into four triangles of equal areas.
![]()
Question 4.
In the given figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
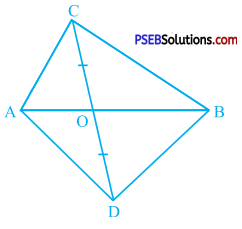
Answer:
Drawing a line through A and parallel to CD, ∆ AOC and A AOD are on the equal bases and between the same parallels.
∴ ar (AOC) = ar (AOD) ……………… (1)
Similarly, drawing a line through B and parallel to CD, A BOC and A BOD are on the equal bases and between the same parallels.
∴ ar (BOC) = ar (BOD) ……………. (2)
Adding (1) and (2),
ar (AOC) + ar (BOC) = ar (AOD) + ar (BOD)
∴ ar (ABC) = ar (ABD)
![]()
Question 5.
D, E and F are respectively the midpoints of the sides BC, CA and AB of a A ABC. Show that:
(i) BDEF is a parallelogram.
(ii) ar (DEF) = \(\frac{1}{4}\)ar (ABC)
(iii) ar (BDEF) = \(\frac{1}{2}\)ar (ABC)
Answer:
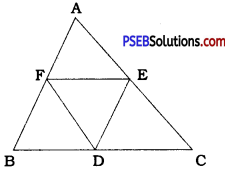
In ∆ ABC, F and E are the midpoints of AB and AC respectively.
∴ FE || BC
∴ FE || BD
In ∆ ABC, E and D are the midpoints of AC and BC respectively.
∴ ED || AB
∴ ED || FB
In quadrilateral BDEF, FE || BD and ED || FB.
∴ Quadrilateral BDEF is a parallelogram. …… Result (i)
Similarly, quadrilaterals AFDE and FDCE are parallelograms.
In parallelogram BDEF, FD is a diagonal.
∴ ar (BDF) = ar (DEF) ……………….. (1)
In parallelogram AFDE, EF is a diagonal.
∴ ar (AFE) = ar (DEF) ……………….. (2)
In parallelogram FDCE, ED is a diagonal.
∴ ar (DCE) = ar (DEF) ………………. (3)
∆ ABC is made up of four non-overlapping triangles, ∆ BDF, ∆ AFE, ∆ DCE and ∆ DEF.
∴ ar (ABC)
= ar (BDF) + ar (AFE) + ar (DCE) + ar (DEF)
∴ ar (ABC)
= ar (DEF) + ar (DEF) + ar (DEF) + ar (DEF) [From (1), (2) and (3)]
∴ ar (ABC) = 4ar (DEF)
∴ ar (DEF) = \(\frac{1}{4}\)ar (ABC) …………. Result (ii)
Now, ar (BDEF) = ar (BDF) + ar (DEF)
∴ ar (BDEF) = ar (DEF) + ar (DEF)
∴ ar (BDEF) = 2ar (DEF)
∴ ar (BDEF) = 2 × \(\frac{1}{4}\)ar (ABC)
∴ ar (BDEF) = \(\frac{1}{2}\)ar (ABC) ……. Result (iii)
![]()
Question 6.
In the given figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar (DOC) = ar (AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB and ABCD is a parallelogram. [Hint: From D and B, draw perpendiculars to AC.]
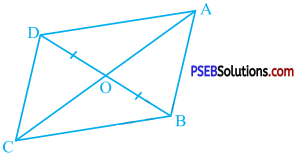
Answer:
Draw DM ⊥ AC and BN ⊥ AC, where M and N are points on AC.
In ∆ DMO and ∆ BNO,
DO = BO (Given)
∠ DOM = ∠ BON (Vertically opposite angles)
∠ DMO = ∠ BNO (Right angles)
∴ ∆ DMO ≅ ∆ BNO (AAS rule)
∴ DM = BN (CPCT)
Now, in ∆ DMC and ∆ BNA,
DM = BN
hypotenuse DC = hypotenuse BA (Given)
∠ DMC = ∠ BNA (Right angles)
∴ ∆ DMC = ∆ BNA (RHS rule)
∴ ar (DMC) = ar (BNA) ……………… (1)
Moreover, ar (DMO) = ar (BNO) (∵ ∆ DMO ≅ ∆ BNO) ………………… (2)
Adding (1) and (2),
ar (DMC) + ar (DMO) = ar (BNA) + ar (BNO)
∴ ar (DOC) = ar (AOB) (Non-overlapping triangles) … Result (i)
Now, adding ar (COB) on both the sides,
ar (DOC) + ar (COB) = ar (AOB) + ar (COB)
∴ ar (DCB) = ar (ACB) ……… Result (ii)
∆ DCB and ∆ ACB are on the same base BC and their areas are equal.
∴ ∆ DCB and ∆ ACB are between the same parallels DA and CB.
∴ DA || CB ……………… (3)
∆ DMO = ∆ BNO gives OM = ON
∆ DMC = ∆ BNA gives CM = AN
∴ OM + CM = ON + AN
∴ OC = OA
Also, OD = OB (Given)
Thus, in quadrilateral ABCD, diagonals AC and BD bisect each other at O.
∴ ABCD is a parallelogram. ……………….. (4)
Taking (3) and (4) together,
DA || CB and ABCD is a parallelogram. ………. Result (iii)
![]()
Question 7.
D and E are points on sides AB and AC respectively of ∆ ABC such that ar (DBC) = ar (EBC). Prove that DE || BC.
Answer:
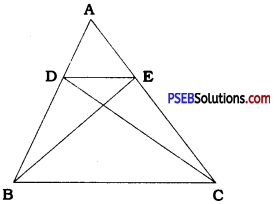
ar (DBC) = ar (EBC)
∴ ∆ DBC and ∆ EBC have equal areas.
Here, ∆ DBC and ∆ EBC are on the same base BC and their areas are equal.
∴ ∆ DBC and ∆ EBC are between the same parallels DE and BC.
∴ DE || BC
Question 8.
XY is a line parallel to side BC of a ‘triangle ABC. If BE II AC and CF II AB meet ( XY at E and F respectively, show that ar (ABE) = ar (ACF).
Answer:
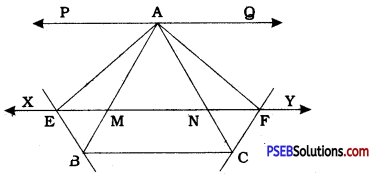
Suppose line XY drawn parallel to BC intersects AB and AC at M and N respectively.
In quadrilateral EBCN, EN || BC and BE || CN.
∴ EBCN is a parallelogram.
In quadrilateral MBCF, MF || BC and BM || CF.
∴ MBCF is a parallelogram.
Parallelograms EBCN and MBCF are on the same base BC and between the same parallels BC and EF
∴ ar (EBCN) = ar (MBCF)
∴ ar (BME) + ar (MBCN) = ar (MBCN) + ar (CFN)
∴ ar (BME) = ar (CFN) ……………….. (1)
Now, ∆ BME and ∆ CFN are between the same parallels EF and BC and their areas are equal.
∴ Their bases are equal.
∴ EM = NF
Through A, draw line PQ parallel to EF.
Then, ∆ AEM and ∆ ANF are on equal bases s and between the same parallels PQ and EF. !>
∴ ar (AEM) = ar (ANF) ……………… (2)
Adding (1) and (2),
ar (BME) + ar (AEM) = ar (CFN) + ar (ANF)
∴ ar (ABE) = ar (ACF)
![]()
Question 9.
The side AB of a parallelogram ABCD is ‘produced to any point P. A line through A and parallel to CP meets CB produced at and then parallelogram PBQR is completed (see the given figure). Show that: ar (ABCD) = ar (PBQR)
[Hint: Join AC and PQ. Now compare ar (ACQ) and ar (APQ).]
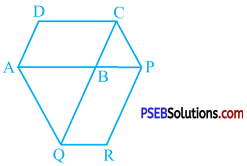
Answer:
Join AC and PQ.
∆ CAQ and ∆ PAQ are on the same base AQ and between the same parallels CP and AQ.
∴ ar (CAQ) = ar(PAQ)
∴ ar (ACB) + ar (ABQ) = ar (PBQ) + ar (ABQ) (Non-overlapping triangles)
∴ ar (ACB) = ar (PBQ) ……………. (1)
In parallelogram ABCD, AC is a diagonal.
∴ ar (ACB) = \(\frac{1}{2}\)ar (ABCD) ……………… (2)
In parallelogram PBQR, PQ is a diagonal.
∴ ar (PBQ) = \(\frac{1}{2}\)ar (PBQR) ………………. (3)
From (1), (2) and (3),
\(\frac{1}{2}\)ar (ABCD) = \(\frac{1}{2}\)ar (PBQR)
∴ ar (ABCD) = ar (PBQR)
![]()
Question 10.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).
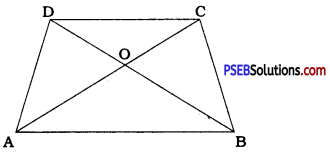
Answer:
∆ DAB and ∆ CBA are on the same base AB and between the same parallels AB and CD.
∴ ar (DAB) = ar (CBA)
∆ DAB and ∆ CBA are both formed by two non-overlapping triangles.
∴ ar (DAB) = ar (AOD) + ar (OAB) and
ar (CBA) = ar (BOC) + ar (OAB)
∴ ar (AOD) + ar (OAB) = ar (BOC) + ar (OAB)
∴ ar (AOD) = ar (BOC)
![]()
Question 11.
In the given figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)
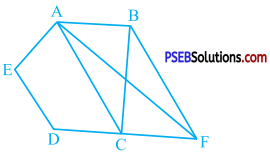
Answer:
∆ ACB and ∆ ACF are on the same base AC and between the same parallels AC and BF.
∴ ar (ACB) = ar (ACF)
Adding ar (AEDC) on both the sides,
ar (ACF) + ar (AEDC) = ar (ACB) + ar (AEDC)
∴ ACF and quadrilateral AEDC are two non-overlapping figures and they form quadrilateral AEDF.
Similarly, ∆ ACB and quadrilateral AEDC are two non-overlapping figures and they form pentagon ABCDE.
∴ ar (AEDF) = ar (ABCDE)
Question 12.
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the comers to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Answer:
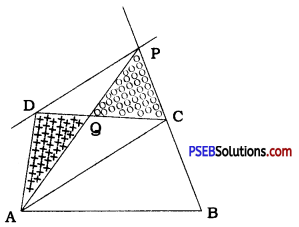
Suppose, quadrilateral ABCD is the plot of Itwaari in the shape of a quadrilateral.
Draw diagonal AC. Through D draw a line parallel to AC to intersect BC produced at P
Join PA to intersect CD at Q.
Here, ∆ DAC and ∆ PAC are on the same base AC and between the same parallels DP and AC.
∴ ar (DAC) = ar (PAC)
∴ ar (DAQ) + ar (QAC) = ar (PQC) + ar (QAC)
∴ ar (DAQ) = ar (PQC)
Thus, we get two triangles – ∆ DAQ and ∆ PQC of equal areas.
So, the Gram Panchayat should take triangular region DAQ from the plot of Itwaari and in exchange give him triangular region PQC. Then, the plot of Itwaari will be of the triangular shape PAB and its area will be the same as the area of original plot ABCD.
![]()
Question 13.
ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
[Hint: Join CX.)
Answer:
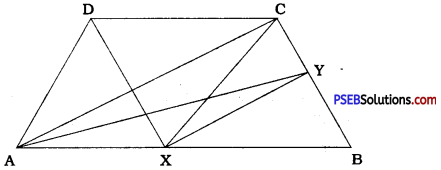
Join CX.
∆ ADX and ∆ ACX are on the same base AX and between the same parallels AB and CD.
∴ ar (ADX) = ar (ACX) …………… (1)
A ACX and A ACY are on the same base AC and between the same parallels AC and XY.
∴ ar (ACX) = ar (ACY) ……………. (2)
From (1) and (2),
ar (ADX) = ar (ACY)
Question 14.
In the given figure, AP || BQ || OR. Prove that ar (AQC) = ar (PBR).
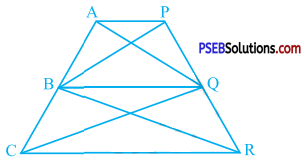
Answer:
∆ CBQ and ∆ RBQ are on the same base BQ and between the same parallels BQ and CR.
∴ ar (CBQ) = ar (RBQ) ……. (1)
∆ ABQ and ∆ PBQ are on the same base BQ and between the same parallels BQ and AE
∴ ar (ABQ) = ar (PBQ) ……… (2)
Adding (1) and (2),
ar (CBQ) + ar (ABQ) = ar (RBQ) + ar (PBQ)
∴ ar (AQC) = ar(PBR) (Non-overlapping triangles)
![]()
Question 15.
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a , trapezium.
Answer:
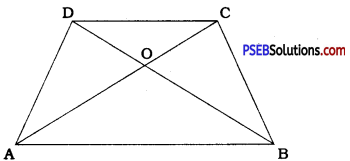
ar (AOD) = ar (BOC)
Adding ar (OAB) on both the sides,
ar (AOD) + ar (OAB) = ar (BOC) + ar (OAB)
∴ ar (DAB) = ar (CAB)
Thus, ∆ DAB and ∆ CAB are on the same base AB and their areas are equal.
Hence, by theorem 9.3, ∆ DAB and ∆ CAB are between the same parallel.
∴ DC || AB
In quadrilateral ABCD, DC || AB.
Hence, ABCD is a trapezium.
![]()
Question 16.
In the given figure, ar (DRC) = ar (DPC) and ar (BDP) = ar (ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.
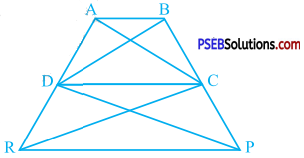
Answer:
ar (DRC) = ar (DPC)
Thus, ∆ DRC and ∆ DPC are on the same base DC and their areas are equal.
Hence, by theorem 9.3, they are between the same parallels.
∴ DC || RP
In quadrilateral DCPR, DC || RE .
∴ Quadrilateral DCPR is a trapezium.
Now, ar (BDP) = ar (ARC)
∴ ar (DPC) + ar (BDC) = ar (DRC) + ar (ADC) (Non-overlapping triangles)
But, ar (DPC) = ar (DRC)
∴ ar (BDC) = ar (ADC)
Thus, ∆ BDC and ∆ ADC are on the same base DC and their areas are equal.
Hence, by theorem 9.3, they are between the same parallels.
∴ AB || DC
In quadrilateral ABCD, AB || DC.
∴ Quadrilateral ABCD is a trapezium.