Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 8 Quadrilaterals Ex 8.2 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 8 Quadrilaterals Ex 8.2
Question 1.
ABCD is a quadrilateral in which F Q, R and S are midpoints of the sides AB, BC, CD and DA respectively (see the given figure 1). AC is a diagonal. Show that:
(i) SR || AC and SR = \(\frac{1}{2}\) AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
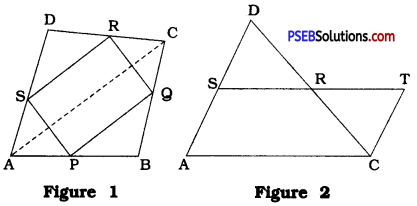
Answer:
In ∆ DAC, S and R are the midpoints of DA and DC respectively.
Through C draw a line parallel to AD which intersects line SR at T.
In ∆ DRS and ∆ CRT
∠ DRS = ∠ CRT (Vertically opposite angles)
∠ RSD = ∠ RTC (Alternate angles formed by transversal ST of DS || TC)
DR = CR (R is the midpoint of DC.)
∴ ∆ DRS ≅ ∆ CRT (AAS rule)
∴ DS = CT and SR = RT (CPCT)
As S is the midpoint of DA, we have DS = SA.
∴ SA = CT
And, by construction, SA || CT.
∴ Quadrilateral SACT is a parallelogram.
∴ ST || AC
∴ SR || AC ………… (1)
Now, SR = RT gives SR = \(\frac{1}{2}\)ST
In parallelogram SACT, ST = AC.
∴ SR = \(\frac{1}{2}\)AC ……………. (2)
Taking (1) and (2) together,
SR || AC and SR = \(\frac{1}{2}\)AC ….. Result (1)
Similarly, in ∆ ABC, P and Q are the midpoints of AB and BC respectively. ,
∴ PQ || AC and PQ = \(\frac{1}{2}\)AC
Now, SR = \(\frac{1}{2}\)AC and PQ = \(\frac{1}{2}\)AC
∴ PQ = SR …… Result (ii)
Similarly, SR || AC and PQ || AC.
∴ PQ || SR
Thus, in quadrilateral PQRS, PQ = SR and PQ || SR.
Hence, by theorem 8.8, PQRS is a parallelogram. … Result (iii)
![]()
Question 2.
ABCD is a rhombus and F Q, R and S are the midpoints of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Answer:
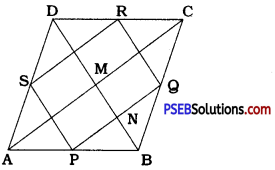
ABCD is a rhombus and F Q, R and S are the midpoints of sides AB, BC, CD and DA respectively.
∴ In ∆ ABC, PQ || AC and PQ = \(\frac{1}{2}\)AC.
∴ In ∆ ADC, SR || AC and SR = \(\frac{1}{2}\)AC.
Hence, in quadrilateral PQRS, PQ || SR and PQ = SR.
∴ Quadrilateral PQRS is a parallelogram.
Now, since ABCD is a rhombus, AC and BD bisect each other at right angles at M.
∴ ∠ AMB = 90°
Now, AC || PQ and MN is their transversal.
∴ ∠ AMN + ∠ MNP = 180° (Interior angles on the same side of transversal)
∴ ∠ AMB + ∠MNP = 180°
∴ 90° + ∠ MNP = 180°
∴ ∠ MNP = 90°
In ∆ ABD, P and S are the midpoints of AB and AD respectively.
∴ PS || BD and NP is their transversal.
∴ ∠ DNP + ∠ NPS = 180°
∴ ∠ MNP + ∠ NPS =180°
∴ 90° + ∠ NPS = 180°
∴ ∠ NPS = 90°
∴ ∠ SPQ = 90°
Thus, in parallelogram PQRS, one angle ∠P is a right angle.
Hence, quadrilateral PQRS is a rectangle.
![]()
Question 3.
ABCD is a rectangle and P, Q, R and S are midpoints of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Answer:
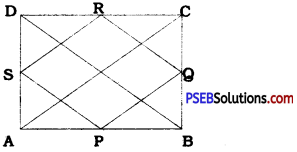
Since ABCD is a rectangle, its diagonals are equal.
∴ AC = BD
∴ \(\frac{1}{2}\)AC = \(\frac{1}{2}\)BD
In ∆ ABC, P and Q are the midpoints of AB and BC respectively.
∴ PQ = \(\frac{1}{2}\)AC
Similarly, in ∆ ADC, SR = \(\frac{1}{2}\)AC; in ∆ ABD, SP = \(\frac{1}{2}\) BD and in ∆ BCD, QR = \(\frac{1}{2}\) BD.
Now, PQ = SR = \(\frac{1}{2}\)AC, SP = QR = \(\frac{1}{2}\)BD and \(\frac{1}{2}\)AC = \(\frac{1}{2}\)BD
Hence, in quadrilateral PQRS,
PQ = QR = RS = SP
Thus, all the sides of quadrilateral PQRS are equal.
Hence, quadrilateral PQRS is a rhombus.
![]()
Question 4.
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the midpoint of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the midpoint of BC.
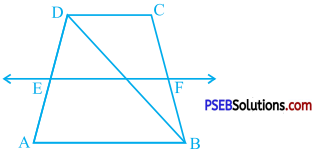
Answer:
Suppose line EF drawn through E and parallel to AB intersects BD at M.
EF || AB and AB || DC
∴ EF || DC
Trapezium ABCD is divided into two triangles, ∆ ABD and ∆ BCD, by diagonal BD.
In ∆ ABD, E is the midpoint of AD and a line through E and parallel to AB intersects BD at M.
Hence, by theorem 8.10, M is the midpoint of BD.
Now, in ∆ BCD, M is the midpoint of BD and a line through M and parallel to CD intersects BC at F.
Hence, by theorem 8.10, F is the midpoint of BC.
Note: The following result about the length of EF can also be derived:
EF = \(\frac{1}{2}\)(AB + CD)
Moreover, if X and Y are the midpoints of the diagonals of above trapezium ABCD, then XY = \(\frac{1}{2}\)|AB – CD|.
![]()
Question 5.
In a parallelogram ABCD, E and F are the midpoints of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
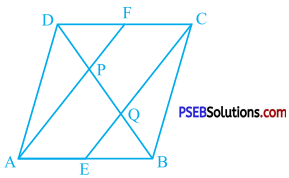
Answer:
E and F are the midpoints of AB and CD respectively.
∴ AE = \(\frac{1}{2}\)AB and CF = \(\frac{1}{2}\)CD
In parallelogram ABCD, AB = CD and AB || CD.
∴ AE = CF and AE || CF
Hence, quadrilateral AECF is a parallelogram.
∴ AF || EC
∴ AP || EQ
In ∆ ABP E is the midpoint of AB and EQ || AR
∴ Q is the midpoint of PB. (Theorem 8.10)
∴PQ = QB …………… (1)
Similarly, in ∆ DQC, F is the midpoint of DC and FP || CQ.
∴ P is the midpoint of DQ. (Theorem 8.10)
∴ DP = PQ …………….. (2)
From (1) and (2), DP = PQ = QB.
Moreover, DP + PQ + QB = BD.
Thus, AF and EC trisect the diagonal BD.
![]()
Question 6.
Show that the line segments joining the midpoints of the opposite sides of a quadrilateral bisect each other.
Answer:
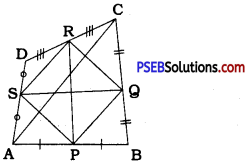
In quadrilateral ABCD, P Q, R and S are the midpoints of sides AB, BC, CD and DA respectively.
In ∆ ABC, P and Q are the midpoints of AB and BC respectively.
∴ PQ || AC and PQ = \(\frac{1}{2}\)AC …………….. (1)
In ∆ ADC, S and R are the midpoints of DA and DC respectively.
∴ SR || AC and SR = \(\frac{1}{2}\)AC ……………… (2)
From (1) and (2),
PQ = SR and PQ || SR.
Thus, in quadrilateral PQRS, sides in one pair of opposite sides are equal and parallel. Hence, quadrilateral PQRS is a parallelogram. The diagonals of a parallelogram bisect each other. [Theorem 8.6]
∴ PR and SQ bisect each other.
Thus, the line segments joining the midpoints of the opposite sides of a quadrilateral bisect each other.
![]()
Question 7.
ABC is a triangle right angled at C. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. Show that:
(i) D is the midpoint of AC.
(ii) MD ⊥ AC
(iii) CM = MA = \(\frac{1}{2}\)AB
Answer:
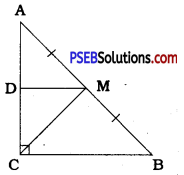
In ∆ ABC, ∠ C is a right angle and M is the midpoint of hypotenuse AB. A line through M and parallel to BC intersects AC at D.
Hence, by theorem 8.10, DM bisects AC.
∴ D is the midpoint of AC. ….. Result (i)
In ∆ ABC, ∠ C is a right angle.
∴ ∠ C = 90°
Now, BC || DM and DC is their transversal.
∴ ∠ MDC + ∠ DCB = 180° (Interior angles on the same side of transversal)
∴ ∠ MDC + 90° = 180°
∴ ∠ MDC = 90°
Thus, MD is perpendicular to AC.
∴ MD ⊥ AC …… Result (ii)
Now, in ∆ ADM and ∆ CDM,
AD = CD (D is the midpoint of AC)
∠ ADM = ∠ CDM (Right angles)
DM = DM (Common)
∴ ∆ ADM ≅ ∆ CDM (SAS rule)
∴ AM = CM (CPCT) ……………. (1)
Now, M is the midpoint of AB.
∴ AM = \(\frac{1}{2}\)AB …… (2)
< Prom (1) and (2),
CM = MA = \(\frac{1}{2}\)AB …… Result (iii)