Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 6 Lines and Angles Ex 6.3 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 9 Maths Chapter 6 Lines and Angles Ex 6.3
Question 1.
In the given figure, sides QP and RQ of ∆ PQR are produced to points S and T respectively. If ∠ SPR =135° and ∠ PQT = 110°, find ∠ PRQ.
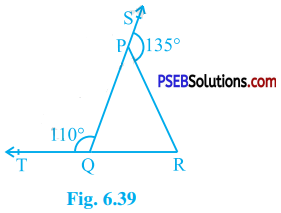
Answer:
Here, ∠ SPR and ∠ PQT are exterior angles.
Then, by theorem 6.8,
∠ SPR = ∠ PQR + ∠ PRQ and
∠ PQT = ∠ QPR + ∠ PRQ
∴ ∠ PQR + ∠ PRQ = 135° and
∠ QPR + ∠ PRQ = 110°
Adding these two equations,
∠ PQR + ∠ PRQ + ∠ QPR + ∠ PRQ = 135° + 110°
∴ 180° + ∠ PRQ = 245° (Theorem 6.7)
∴ ∠ PRQ = 245° – 180°
∴ ∠ PRQ = 65°
![]()
Question 2.
In the given figure, ∠ X = 62°, ∠ XYZ = 54°. If YO and ZO are the bisectors of ∠ XYZ and ∠ XZY respectively of ∆ XYZ, find ∠ OZY and ∠ YOZ.
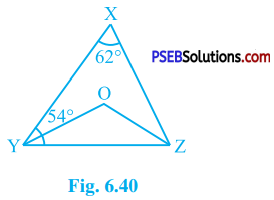
Answer:
In ∆ XYZ,
∠ X + ∠ XYZ + ∠ XZY = 180° (Theorem 6.7)
∴ 62° + 54° + ∠ XZY = 180°
∴ ∠ XZY = 180° – 62° – 54°
∴ ∠ XZY = 64°
YO and ZO are bisectors of ∠ XYZ and ∠ XZY respectively.
∴ ∠ OYZ = \(\frac{1}{2}\) ∠ XYZ = \(\frac{1}{2}\) × 54° = 27° and
∠ OZY = \(\frac{1}{2}\) ∠ XZY = \(\frac{1}{2}\) × 64° = 32°.
Now, in ∆ OYZ,
∠ OYZ + ∠ OZY + ∠ YOZ = 180° (Theorem 6.7)
∴ 27° + 32° + ∠ YOZ = 180°
∴ ∠ YOZ = 180° – 27° – 32°
∴ ∠ YOZ = 121°
![]()
Question 3.
In the given figure, if AB || DE, ∠ BAC = 35° and ∠ CDE = 53°, find ∠ DCE.
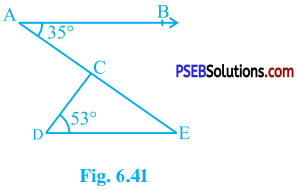
Answer:
AB || DE and AE is transversal for them.
∴ ∠ AED = ∠ BAE (Alternate interior angles)
∴ ∠ CED = ∠ BAC (Point C lies on line AE)
∴ ∠ CED = 35° (Given : ∠ BAC = 35°)
In ∆ CDE, by theorem 6.8
∠ CDE + ∠ CED + ∠ DCE = 180°
∴ 53° + 35° + ∠ DCE = 180°
∴ ∠ DCE = 180° – 53° – 35°
∴ ∠ DCE = 92°
![]()
Question 4.
In the given figure, if lines PQ and RS intersect at point T, such that ∠ PRT = 40°, ∠ RPT = 95° and ∠ TSQ = 75°, find ∠ SQT.
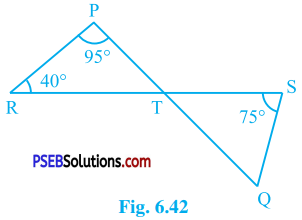
Answer:
In ∆ PRT,
∠ RPT + ∠ PRT + ∠ PTR = 180° (Theorem 6.7)
∴ 95° + 40° + ∠ PTR = 180°
∴ 135° + ∠ PTR = 180°
∴ ∠ PTR = 180°- 135°
∴ ∠ PTR = 45°
Lines PQ and RS intersect at point T.
∴ ∠ STQ = ∠ PTR (Vertically opposite angles)
∴ ∠ STQ = 45°
In ∆ STQ,
∠ TSQ + ∠ STQ + ∠ SQT = 180° (Theorem 6.7)
∴ 75° + 45° + ∠ SQT = 180°
∴ 120° + ∠ SQT = 180°
∴ ∠ SQT = 60°
![]()
Question 5.
In the given figure, if PQ ⊥ PS, PQ || SR, ∠ SQR = 28° and ∠ QRT = 65°, then find the values of x and y.
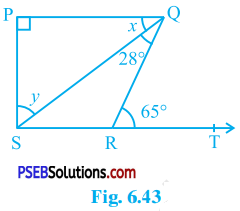
Answer:
PQ || SR and QR is transversal for them.
∴ ∠ PQR = ∠ QRT (Alternate interior angles)
∴ ∠ PQR = 65° (Given : ∠ QRT = 65°)
∴ ∠ PQS + ∠ SQR = 65° (Adjacent angles)
∴ x + 28° = 65° (Given : ∠ SQR = 28°)
∴ x = 65° – 28°
∴ x = 37°
PQ ⊥ PS
∴ ∠ SPQ = 90°
In ∆ PSQ,
∠ SPQ + ∠ PQS + ∠ PSQ = 180° (Theorem 6.7)
∴ 90° + 37° + y = 180°
∴ 127° + y = 180°
∴ y = 180°- 127°
∴ y = 53°
![]()
Question 6.
In the given figure, the side QR of ∆ PQR is produced to a point S. If the bisectors of ∠ PQR and ∠ PRS meet at point T, then prove that ∠ QTR = \(\frac{1}{2}\) ∠ QPR.
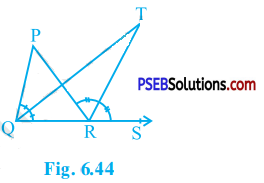
Answer:
QT is the bisector of ∠ PQR and RT is the bisector of ∠ PRS.
∴ ∠ TQR = \(\frac{1}{2}\) ∠ PQR and ∠ TRS = \(\frac{1}{2}\) ∠ PRS ……………… (1)
∠ PRS is an exterior angle of ∆ PQR.
∴ ∠ PRS = ∠ QPR + ∠ PQR
∴ \(\frac{1}{2}\) ∠ PRS = \(\frac{1}{2}\) ∠ QPR + \(\frac{1}{2}\) ∠ PQR
∴ ∠ TRS = \(\frac{1}{2}\) ∠ QPR + ∠ TQR [By (1)] …………… (2)
In ∆ TQR, ∠ TRS is an exterior angle.
∴ ∠ TRS = ∠ QTR + ∠ TQR ……………. (3)
From (2) and (3), we get
∠ QTR + ∠ TQR = \(\frac{1}{2}\) ∠ QPR + ∠ TQR
∴ ∠ QTR = \(\frac{1}{2}\) ∠ QPR