PSEB 9th Class Maths Solutions Chapter 11 Constructions Ex 11.1

Punjab State Board PSEB 9th Class Maths Book Solutions Chapter 11 Constructions Ex 11.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.1

Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Answer:

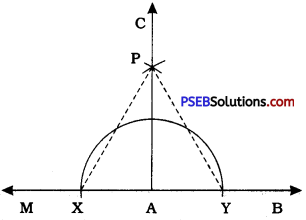
Steps of construction :

1. Ray AB is given. Produce ray AB on the side of A to get line MAB.
2. Taking A as centre and some radius, draw an arc of a circle to intersect line MAB at X and Y.
3. Taking X and Y as centres and radius more than \(\frac{1}{2}\)XY, draw arcs to intersect at P on one side of line MAB.
4. Draw ray AC passing through E
   Thus, ∠CAB is the required angle of 90°.

Justification:
Draw PX and PY.
In ∆ PAX and ∆ PAY,
AX = AY (Radii of same arc)
PX = PY (Radii of congruent arcs)
PA = PA (Common)
∴ By SSS rule, ∆ PAX ≅ ∆ PAY
∴ ∠PAX = ∠PAY (CPCT)
But, ∠PAX + ∠PAY = 180° (Linear pair)
∴ ∠PAY = \(\frac{180^{\circ}}{2}\) = 90°
∴ ∠CAB = 90°

Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Answer:

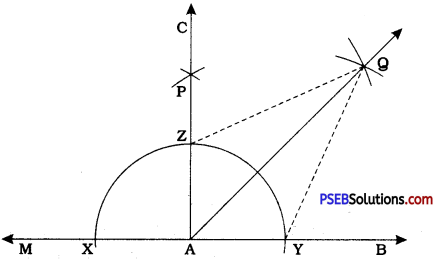
Steps of construction:

1. Ray AB is given. Produce ray AB on the side of A to get line MAB.
2. Taking A as centre and some radius, draw an arc of a circle to intersect line MAB at X and Y.
3. Taking X and Y as centres and radius more than \(\frac{1}{2}\)XY, draw arcs to intersect at P on one side of line MAB.
4. Draw ray AC passing through E Thus, ∠CAB of 90° is received.
5. Name the point of intersection of the arc with centre A and ray AC as Z.
6. Taking Y and Z as centres and radius more than \(\frac{1}{2}\)YZ, draw arcs to intersect each other at Q.
7. Draw ray AQ.
   Thus, ∠QAB is the required angle of 45°.

Justification:
In example 1, we have already justified that ∠CAB = 90°. So, we do not repeat that part’ here.
Draw QZ and QY.
In ∆ AYQ and ∆ AZQ,
AY = AZ (Radii of same arc)
YQ = ZQ (Radii of congruent arcs)
AQ = AQ (Common)
∴ By SSS rule, ∆ AYQ ≅ ∆ AZQ
∴ ∠QAY = ∠QAZ (CPCT)
But, ∠QAY + ∠QAZ = ∠ZAY = ∠CAB = 90°
∴ ∠QAY = \(\frac{90^{\circ}}{2}\) = 45°
∴ ∠QAB = 45°

Question 3.
Construct the angles of the following measurements:
(i) 30°
Answer:

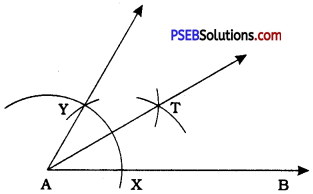
Steps of construction:

1. Draw any ray AB. With centre A and any radius, draw an arc to intersect AB at X.
2. With centre X and the same radius [as in step (1)], draw an arc to intersect the previous arc at Y. Draw ray AY. Then, ∠YAB = 60°.
3. Draw ray AT, the bisector of ∠YAB.
   Thus, ∠TAB is the required angle of 30°.

(ii) 22\(\frac{1}{2}\)°
Answer:

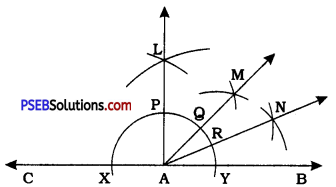
Steps of construction:

1. Draw any ray AB. Produce AB on the side of A to get line CAB.
2. Taking A as centre and any radius, draw an arc of a circle to intersect line CAB at X and Y.
3. Taking X and Y as centres and radius more than \(\frac{1}{2}\)XY, draw arcs to intersect each other at L on one side of line CAB. Draw ray AL. Then, ∠LAB = 90°.
4. Draw ray AM, the bisector of ∠LAB. Then, ∠MAB = 45°.
5. Draw ray AN, the bisector of ∠MAB. Then, ∠NAB = 22\(\frac{1}{2}\)°.
   Thus, ∠NAB is the required angle of 22\(\frac{1}{2}\)°.

(iii) 15°
Answer:

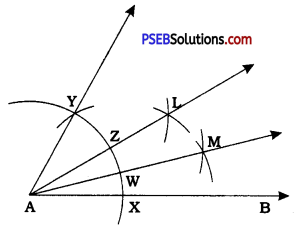
Steps of construction:

1. Draw any ray AB. Taking A as centre and any radius, draw an arc of a circle to intersect AB at X.
2. Taking X as centre and the same radius as before, draw an arc to intersect the previous arc at Y. Draw ray AY. Then, ∠YAB = 60°.
3. Draw ray AL, the bisector of ∠YAB. Then, ∠LAB = 30°.
4. Draw ray AM, the bisector of ∠LAB. Then, ∠MAB = 15°.
   Thus, ∠MAB is the required angle of 15°.

Question 4.
Construct the following angles and verify by measuring them by a protractor:
(i) 75° and (ii) 105°
Answer:

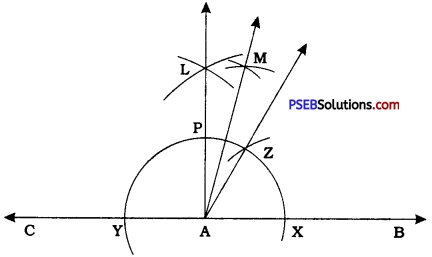
Steps of construction:

1. Draw any ray AB and produce it on the side of A to get line CAB. Taking A as centre and any radius draw an arc of a circle to intersect line CAB at X and Y.
2. Taking X and Y as centres and radius more than \(\frac{1}{2}\)XY, draw arcs to intersect each other at point L on one side of line CAB. Draw ray AL. Then, ∠LAB = 90°.
3. Taking X as centre and radius AX, draw an arc of a circle to Intersect the first arc (arc XY) with centre A at Z.
4. Draw ray AZ. Then, ∠ZAB = 60°.
5. Now, draw ray AM, the bisector of ∠LAZ. Then, ∠MAB = 75° and ∠MAC = 105°.
   Thus, ∠MAB and ∠MAC are the required angles of measure 75° and 105° respectively.

(iii) 135°
Answer:

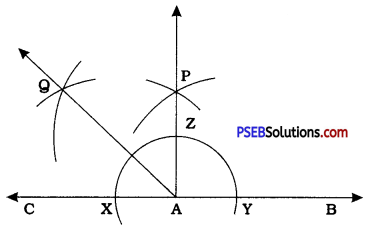
Steps of construction:

1. Draw line CAB. Taking A as centre and any radius, draw an arc of a circle to Intersect line CAB at X and Y.
2. Taking X and Y as centres and radius more them \(\frac{1}{2}\)XY, draw arcs to intersect each other at P on one side of line CAB.
3. Draw ray AP Then, ∠PAB = ∠PAC = 90°.
4. Draw ray AQ, the bisector of ∠PAC.
5. Then, ∠QAB = 135°.
   Thus, ∠QAB is the required angle of 135°.

Question 5.
Construct an equilateral triangle, given its side and justify the construction.
Answer:
Line segment XY is given. We have to construct an equilateral triangle with each side being equal to XY.

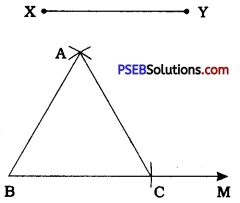
Steps of construction:

1. Draw any ray BM.
2. With centre B and radius XY, draw an arc of a circle to intersect BM at C.
3. Taking B and C as centres and rhdius XY, draw arcs to intersect each other at A on one side of line AC.
4. Draw AB and AC.
   Thus, ∆ ABC is the required equilateral triangle with each side being equal to XY.

Justification:
The arc drawn with centre B and radius XY intersects ray BM at C. ∴ BC = XY. The arcs drawn with centres B and C and radius XY intersect at A.
∴ AB = XY and AC = XY.
Thus, in ∆ ABC, AB = BC = AC = XY.
Hence, ∆ ABC is an equilateral triangle in which all sides are equal to XY.
Note: If the measure of sides are given numerically, e.g., 4 cm, 5 cm, etc., then we have to use graduated scale instead of straight edge.